Introducción
En muchos estudios quirúrgicos, y especialmente los relacionados con el cáncer, la variable principal que queremos valorar es el tiempo que transcurre hasta un suceso. A este tiempo, normalmente se le llama "supervivencia", aunque el suceso en cuestión no tiene por qué ser la defunción. Cuando el suceso que queremos evaluar ocurre en todos los pacientes, entonces disponemos de varias técnicas estadísticas que pueden aplicarse. Sin embargo, lo más habitual es que el suceso en cuestión (la defunción, la recidiva, la reaparición de los síntomas) no se presente en todos los individuos. Además, y aunque casi nunca los cirujanos evaluamos si los datos tienen una distribución normal, comprobar la distribución debería ser el primer paso antes de aplicar cualquier prueba, y es muy frecuente que estos datos de supervivencia no sigan la distribución normal, con lo cual la mayoría de las pruebas estadísticas que conocemos comúnmente los cirujanos, no son aplicables. En esta situación, hay una serie de técnicas estadísticas (análisis de la supervivencia) apropiadas para estudios en los que cada paciente es seguido durante un determinado período y en los que se recoge el intervalo que transcurre entre el hecho inicial y el hecho final, o hasta que acaba el seguimiento si no ocurre el hecho final. Además, entre estas técnicas, disponemos de pruebas para comparar curvas de supervivencia, y modelos más complejos basados en la regresión que permiten valorar el efecto de un conjunto de valores pronósticos.
El objetivo de este artículo es dar unas pinceladas básicas de la terminología que se usa en el análisis de supervivencia, unas nociones elementales sobre lo que nos dicen las curvas y los listados que obtenemos del famoso SPSS y cuatro trucos sencillos para saber interpretar correctamente una curva de supervivencia.
Introducción histórica
Los antecedentes más lejanos se pueden situar en la elaboración de las tablas de mortalidad que el astrónomo Edmon Halley publicó a partir del registro de funerales y nacimientos de la ciudad de Breslau1. El análisis de la supervivencia tal como se conoce hoy, sin embargo, tiene sus raíces en la ingeniería, y está encaminado a analizar la duración y fiabilidad de los diferentes elementos que forman una máquina. Como en tantas otras cosas (las famosas curvas ROC, por ejemplo), la Segunda Guerra Mundial aceleró el desarrollo de estas técnicas.
En ciencias de la salud, el auge de estas técnicas empieza hacia los años setenta. La ventaja que ofrecen estas técnicas y lo que las ha popularizado es que permiten generalizar el análisis de respuestas binarias (sí/no; fallecido/vivo), incluido el tiempo de seguimiento, es decir, el tiempo que ha transcurrido desde el inicio del seguimiento hasta producirse la respuesta o hasta el final del seguimiento si la respuesta no se ha producido. Además, este tiempo que se analiza se puede valorar en condiciones muy flexibles, porque la duración del período de observación puede ser muy diferente para cada sujeto.
Así pues, el análisis de la supervivencia es una técnica muy apropiada para analizar respuestas binarias en estudios longitudinales o de seguimiento que se caractericen por:
1. Duración variable del seguimiento: los estudios de seguimiento tienen fechas muy bien definidas de inicio y de cierre, pero los sujetos se incorporan al estudio en momentos diferentes.
2. Observaciones incompletas: en la fecha de cierre del estudio aún no se ha producido el evento terminal en ciertos sujetos (sujetos retirados "vivos"). Además, puede haber pérdidas (sujetos perdidos). Estas observaciones incompletas dan lugar a lo que se llama "datos censurados", y el análisis de supervivencia se caracteriza por incluir la información que aportan estos datos.
Para realizar un estudio de supervivencia, en realidad, sólo se necesitan un par de valores: el tiempo de seguimiento del sujeto y una variable binaria que indica si es un tiempo completo o censurado.
De hecho, un análisis que mide una respuesta binaria se puede hacer de muchas maneras: la prueba de la χ2, por ejemplo. Pero hay una característica muy importante del análisis de supervivencia y que precisamente es frecuentemente ignorada por los cirujanos y que permite que no se pierda una información muy importante: el ritmo al que se va presentando, es decir, la tasa de incidencia del evento. También podríamos hacer un análisis utilizando la variable "tiempo", pero esto es incorrecto, porque en realidad sólo es conocido en los sujetos que han presentado el evento.
Cuatro definiciones
Para clarificar la explicación, usaremos el ejemplo de un serie de pacientes con neoplasia de esófago operada y la evaluación de su supervivencia a los 5 años.
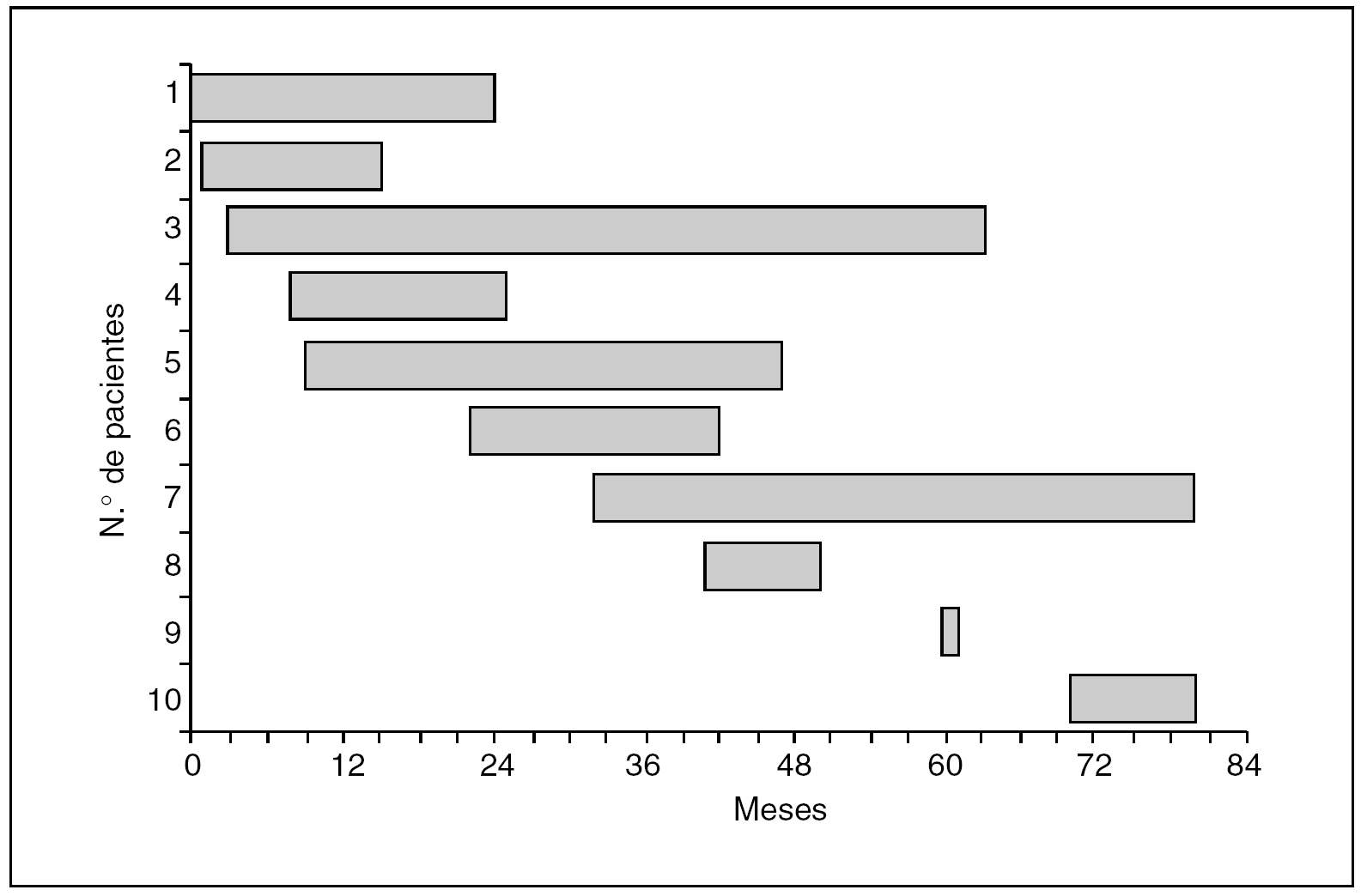
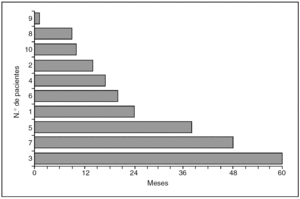
Tiempo calendario. En la figura 1, cada barra representa la fecha de inicio del tratamiento y la fecha de final de seguimiento a los 5 años o la fecha de último control en dispensario si no han transcurrido estos 5 años para cada uno de los 10 pacientes del estudio. Cada barra es pues el tiempo calendario de cada paciente.
Fig. 1. Tiempo calendario.
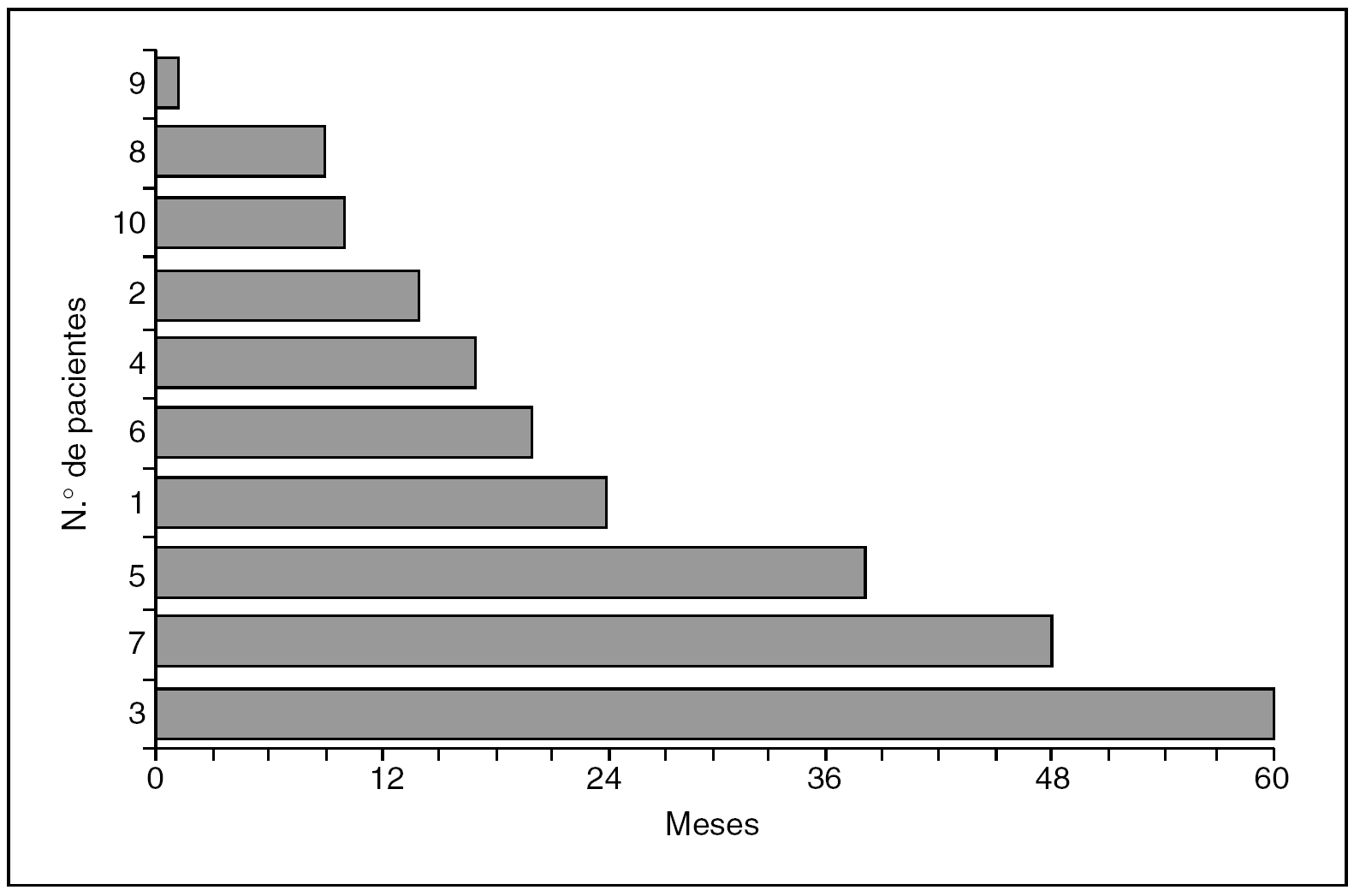
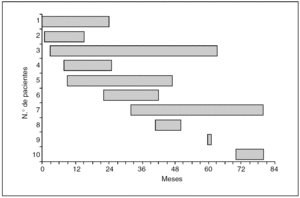
Tiempo de seguimiento. Representados en la figura 2, son los mismos datos que los de la figura 1, ordenados de menor a mayor tiempo de seguimiento, y preparados para hacer el análisis descriptivo.
Fig. 2. Tiempo de seguimiento.
Fecha de inicio y fecha de cierre. Determinan la duración del estudio. La primera diferencia a tener en cuenta con otros estudios es que los sujetos entran con una fecha diferente para cada uno, y que no tiene por qué coincidir con las fechas de inicio y final del estudio. En nuestro ejemplo, el estudio dura 80 meses.
Fecha de la última observación. La última noticia que se tiene de un sujeto marca la fecha de la última observación y, mucho más importante, el estado del sujeto, que puede ser "fallecido" (si el evento terminal se ha producido) o "vivo" en caso contrario.
Tiempo de seguimiento. Es el tiempo que transcurre entre la fecha de entrada en el estudio hasta la fecha registrada en la última observación. Será una de las dos variables fundamentales para efectuar el análisis.
Evento terminal. Los modelos básicos de análisis de supervivencia, que son los que tratamos en este artículo, consideran un solo estado terminal. En nuestro estudio sobre mortalidad de la neoplasia de esófago operada el evento terminal es la defunción del sujeto. Pero podría ser perfectamente la recidiva. Nuevamente, en los análisis básicos, el evento debe presentarse una sola vez; es decir, no podemos analizar a un paciente que presente una recidiva, se cure, y vuelva a presentar otra más adelante. Genéricamente, llamamos al estado terminal como "defunción", pero puede ser perfectamente el alta, la remisión de la enfermedad, la recaída, el fallo de sutura o cualquier otro incidente que pueda tener dos estados bien definidos: "vivo" y "fallecido". Este evento terminal es la segunda de las dos variables indispensables para el análisis de supervivencia.
Tiempo de supervivencia. Si el estado del sujeto es "fallecido", el tiempo de seguimiento se llama "tiempo de supervivencia". Se trata de un tiempo completo, o no censurado (uncensored time). En nuestro ejemplo, se conoce el tiempo de supervivencia de los sujetos 1, 2, 4, 6, 8 y 9 porque han fallecido durante el período del estudio.
Tiempos incompletos o censurados. Si el estado del sujeto es "vivo" porque en la última observación no se había producido el evento terminal, se trata de un tiempo incompleto o censurado (censored time). En nuestro ejemplo, son los sujetos 3, 5, 7 y 10. Estas observaciones llamadas incompletas por la derecha aportan información para estimar las probabilidades de supervivencia, y es una de las diferencias del análisis de supervivencia respecto de otros estudios. Los tiempos censurados pueden tener varios orígenes, por ejemplo sujetos retirados vivos o perdidos.
Sujetos "retirados vivos". Cuando se termina un estudio, hay sujetos que se han seguido regularmente y que en el momento del cierre del estudio no han presentado el evento terminal. En nuestro ejemplo, los sujetos 7 y 10 no han realizado el seguimiento completo de 60 meses y no han presentado el evento terminal.
Sujetos "perdidos". Los sujetos perdidos, bien porque han cambiado de domicilio o porque han fallecido por otras razones no relacionadas con el estudio, también producen tiempos incompletos. En nuestro ejemplo, el sujeto 5 dejó de acudir a seguimiento.
Tanto los retirados vivos como los perdidos producen tiempos incompletos censurados por la derecha que son analizados de manera idéntica, pero son muy diferentes. A nadie se le escapa que para los mismos 100 tiempos censurados no es lo mismo 90 perdidos y 10 retirados vivos que 10 perdidos y 90 retirados vivos. Por ello, hay que dar este dato adicional de sujetos perdidos al dar los resultados de cualquier análisis de supervivencia.
El censurado hace al análisis de supervivencia diferente
El análisis de supervivencia tiene una característica que lo diferencia claramente de otros análisis estadísticos, y es que algunos individuos experimentan el evento terminal y otros no, lo que hace que el tiempo de supervivencia de los que no lo han experimentado sea un tiempo desconocido. Ya hemos definido esta característica como tiempo censurado, pero nos interesa describir claramente cómo puede producirse un tiempo censurado. Puede suceder por 3 vías diferentes: a) el paciente no ha sufrido (aún) el evento terminal en la fecha de fin del estudio; b) el paciente se ha perdido, y c) el paciente experimenta un evento diferente pero que imposibilita el seguimiento. Pongamos ejemplos: el paciente de nuestro estudio, que es seguido durante 60 meses y al cual se le da el alta. Es importante entender que un sujeto seguido durante 60 meses (ha seguido, por tanto, todo el protocolo) y ya dado de alta, es un sujeto retirado vivo, y por tanto, da un "tiempo incompleto o censurado". Hay que recordar que lo que define un tiempo completo es la presencia del evento terminal, no que el paciente ya haya sido dado de alta por no necesitar más seguimiento en nuestro ejemplo. Éste es precisamente uno de los conceptos más difíciles de entender a los no iniciados. Otro ejemplo: un paciente operado de un cáncer de esófago dentro de un estudio que mide la mortalidad por cáncer y que fallece a los 6 meses por accidente de tráfico, es un "retirado vivo" y por tanto un tiempo censurado porque el evento terminal, la defunción por cáncer, no se ha presentado. Esto, que puede parecer una curiosa trampa estadística, en realidad ha de quedar muy bien definido en cualquier estudio con una correcta metodología: ¿qué vamos a medir; la mortalidad global o la mortalidad por cáncer? Si medimos la mortalidad por cáncer, entonces los que fallecen por otras causas son "retirados vivos" y por tanto, censurados por la derecha. La clave es que quien lee el artículo también tenga muy claro lo que se mide.
Vale la pena comentar que los tiempos censurados por la derecha están subestimando la verdadera supervivencia del sujeto, y por tanto, que los estudios de supervivencia normalmente subestiman la supervivencia de la población.
Aunque no se pretende entrar en el fondo del asunto, también hay que comentar que los tiempos pueden ser censurados por la izquierda. Esto sucede, por ejemplo, si incluimos en el estudio a un paciente que había sido operado hacía un año. Incluso, puede haber intervalos censurados (períodos dentro del seguimiento), pero esto corresponde a otro artículo.
Supervivencia y riesgo
Los datos de supervivencia se pueden dar y estudiar con dos tipos de probabilidades diferentes: supervivencia y riesgo. Casi todos nosotros hemos visto en alguna ocasión una curva de supervivencia. La "probabilidad de supervivencia" (también llamada función de supervivencia) o S(t) es la probabilidad de que un individuo sobreviva desde la fecha de entrada en el estudio hasta un momento determinado en el tiempo t. Estos valores van a describir la supervivencia global de toda nuestra población.
Pero incluso más interesante que la probabilidad de supervivencia, aunque muchísimo menos conocida, es la "función de riesgo" h(t): la probabilidad de que a un individuo que está siendo observado en el tiempo t le suceda el evento en ese momento. Es decir: ¿cuál es la probabilidad de que fallezca un paciente operado de cáncer de esófago a los 16 meses de la operación (suponiendo que haya sobrevivido hasta ese momento)? Hay que destacar las diferencias entre ambas probabilidades. Mientras que la función de supervivencia se centra sobre todo en la "no ocurrencia" del evento (el paciente no ha fallecido; o no ha recidivado), la función de riesgo se centra en la "ocurrencia" del evento. Proporciona información tan valiosa como la tasa de incidencia, es decir, puede contestarnos preguntas como "¿en qué momento voy a tener el pico de recidivas?" que pueden implicar cambios en nuestro quehacer clínico diario. Si en el ejemplo del cáncer de esófago, la función de riesgo nos dice que el pico máximo de recidivas se sitúa alrededor de los 12 meses, podríamos plantearnos un seguimiento más exhaustivo de los pacientes hacia los 8 meses, con el objeto de detectarlas en una fase más precoz que ofreciera posibilidades terapéuticas. No deja de sorprender que una herramienta tan potente como ésta y que tanta información puede darnos, esté totalmente infrautilizada en los ambientes médicos (no sólo los quirúrgicos).
Datos y SPSS
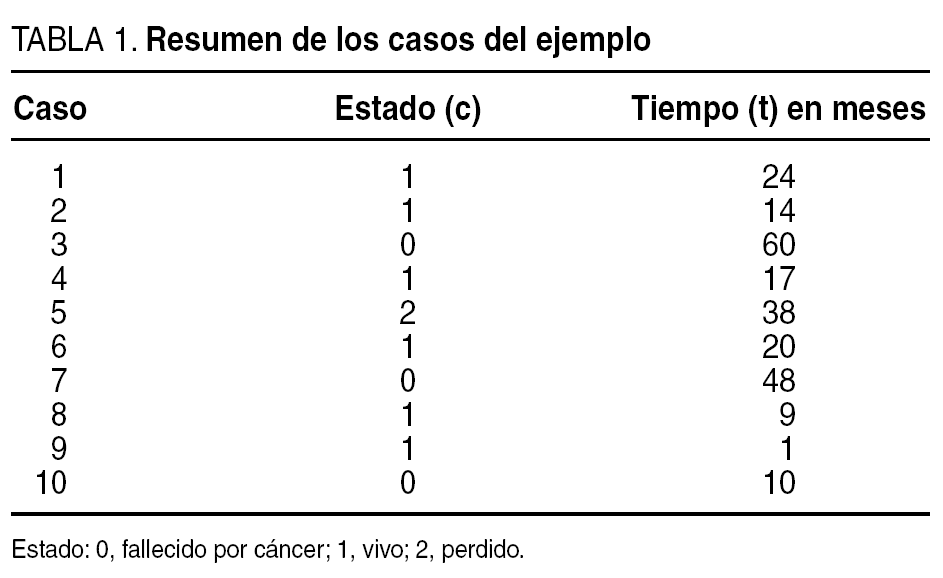
Todos conocemos la potente herramienta estadística llamada SPSS. También es capaz de hacer estudios de supervivencia, pero antes hemos de preparar los datos para que sea capaz de usarlos. Existen 2 variables indispensables que son las que usará el programa para los cálculos: estado y tiempo. La tabla 1 recoge los datos de nuestro estudio simulado preparados para el análisis por SPSS.
La variable estado puede tener varios valores como en nuestro ejemplo (0 = fallecido por cáncer; 1 = vivo; 2 = perdido), pero el sistema nos pedirá sólo un valor: el que marca la ocurrencia del evento terminal y que en nuestro estudio es la defunción por cáncer (el valor de c = 0). En realidad, lo que nos pide el programa es que le definamos qué tiempos son censurados (incompletos) y cuáles no censurados (completos). Así, la variable estado puede tener varios valores (fallecido por cáncer, fallecido por otras causas, perdido, vivo) pero sólo uno será el evento terminal que se analizará. Los demás valores que se recojan serán interesantes para saber cuántos han fallecido por otras causas, o cuántos se han perdido, y por tanto, aumentan la calidad de nuestro estudio, pero debemos tener claro que son tiempos censurados (incompletos).
Método de Kaplan-Meyer
Otra de las sorpresas cuando se explica el análisis de supervivencia es que no es sinónimo de Kaplan-Meyer. La probabilidad de supervivencia se puede estimar de manera no paramétrica basándose en los tiempos de observación (censurados y no censurados) usando el método de Kaplan-Meyer. Pero también puede estimarse la probabilidad de supervivencia con otros métodos como el actuarial. Centrémonos de momento en el más conocido en nuestro ámbito: el método de Kaplan-Meyer.
Si asumimos que el evento terminal es independiente para cada paciente (un requisito fundamental en el análisis, pero sobre el que no profundizaremos), las probabilidades de sobrevivir en un tiempo t(j) determinado se calculan gracias a una ley (ley multiplicativa de las probabilidades) que nos dice que esta probabilidad es igual a la probabilidad de sobrevivir hasta el momento anterior t(j1) por la probabilidad condicionada de sobrevivir un tiempo t(j) después de haber sobrevivido un tiempo t(j1). Esto dicho así es considerablemente árido. Pero veamos la tabla 2 y comprobemos que no es tan difícil de calcular.
¿Cómo se interpreta la tabla anterior (que nos da el SPSS)? Pues que en el tiempo t(20) (a los 20 meses de la cirugía) la probabilidad acumulada de supervivencia es del 45,71%.
El listado original de SPSS nos da también una media, que en realidad no puede calcularse, porque nos falta el tiempo completo de todos los sujetos. Pero pueden hacerse estimaciones basadas en Lee y es la cifra que nos da la tabla original de SPSS. La mediana es un índice más adecuado porque su cálculo no requiere conocer el tiempo de todos los pacientes. La mediana se estima con el percentil 50 de la distribución, que corresponde al primer tiempo con una proporción de supervivencia (probabilidad acumulada de supervivencia) igual o inferior a 0,5. En nuestro ejemplo, la mediana de supervivencia es de 20 meses.
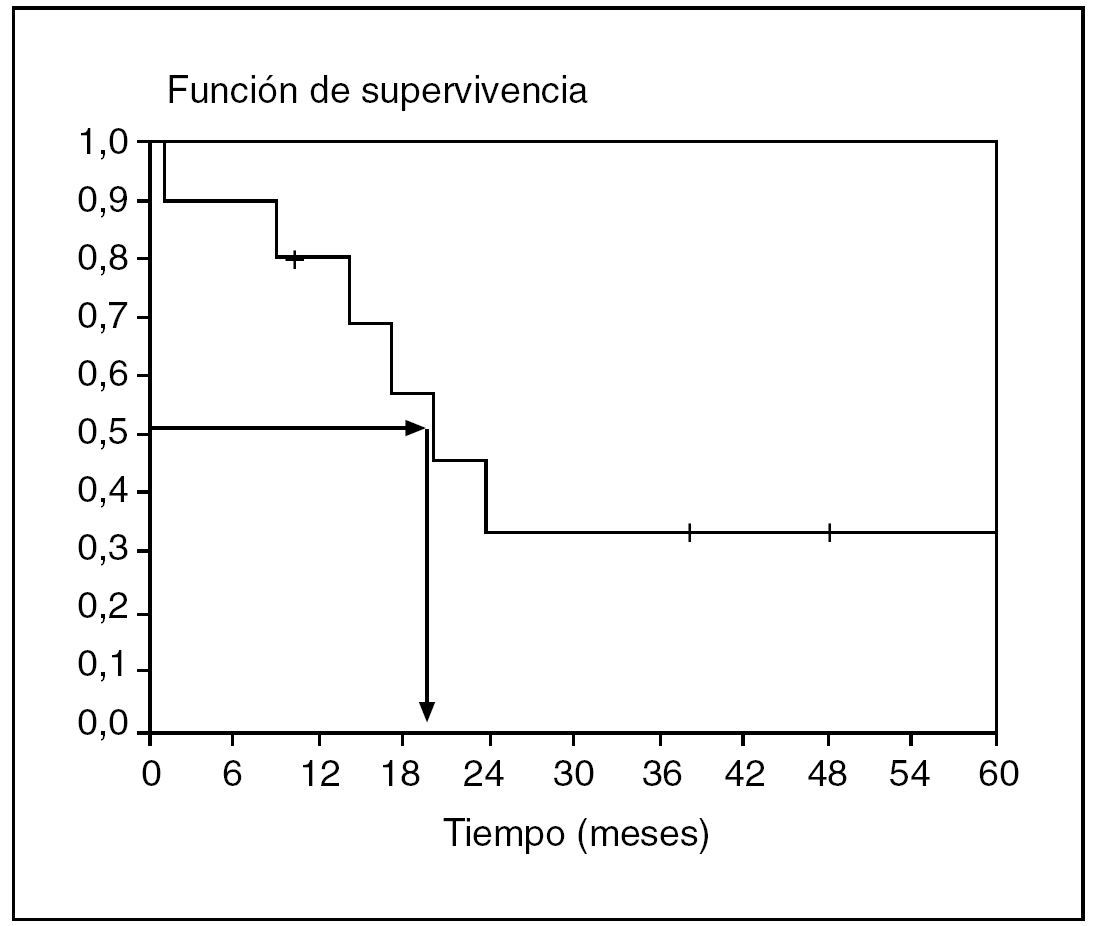
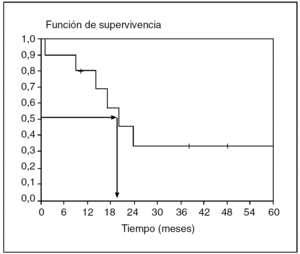
La curva de supervivencia que todos hemos visto alguna vez (fig. 3) es una representación de la probabilidad de supervivencia acumulada frente al tiempo. Nos da una forma de resumir los datos muy visual que además permite estimar claramente la mediana. Sólo se trata de proyectar la probabilidad de supervivencia del 0,5 sobre la curva y comprobar a qué tiempo le corresponde.
Fig. 3. Curva de supervivencia y cálculo de la mediana.
Método actuarial
Tal como hemos dicho más arriba, no sólo se puede analizar la supervivencia con el método de Kaplan-Meyer. El método actuarial o método de la tabla de vida consiste en agrupar el tiempo de participación de cada sujeto en intervalos predeterminados y al igual que en el método de Kaplan-Meyer, calcular las probabilidades de supervivencia mediante la misma fórmula que hemos utilizado.
Hay ventajas e inconvenientes en usar este método. El principal inconveniente es que da estimaciones poco precisas cuando el número de sujetos es pequeño. Pero en muestras grandes, ofrece una ventaja fundamental. Primero porque influye muy poco sobre las estimaciones, segundo porque ofrece una curva de supervivencia muy clara, pero la más importante: nos permite dar una función riesgo.
¿Función de riesgo?
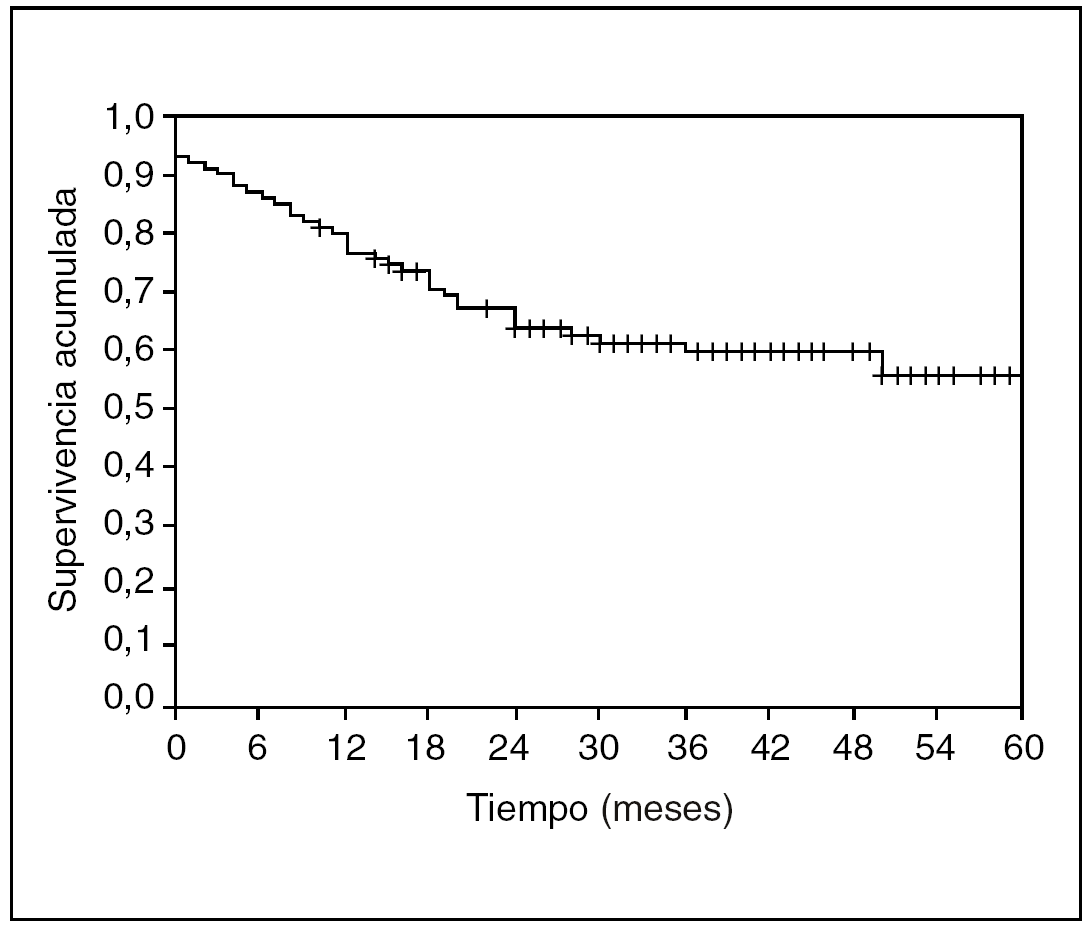
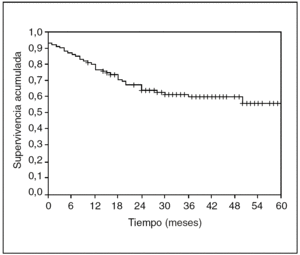
No sólo es interesante saber la supervivencia de nuestra población. Probablemente, en el ejemplo del cáncer de esófago, sería muy interesante saber en qué momento existe el máximo riesgo de que se presente una recidiva. Pues bien, ampliemos nuestro ejemplo a 100 pacientes seguidos durante 60 meses y veamos su curva de supervivencia, calculada tal como hemos explicado antes, con el método de Kaplan-Meyer (fig. 4).
Fig. 4. Curva de supervivencia Kaplan-Meyer.
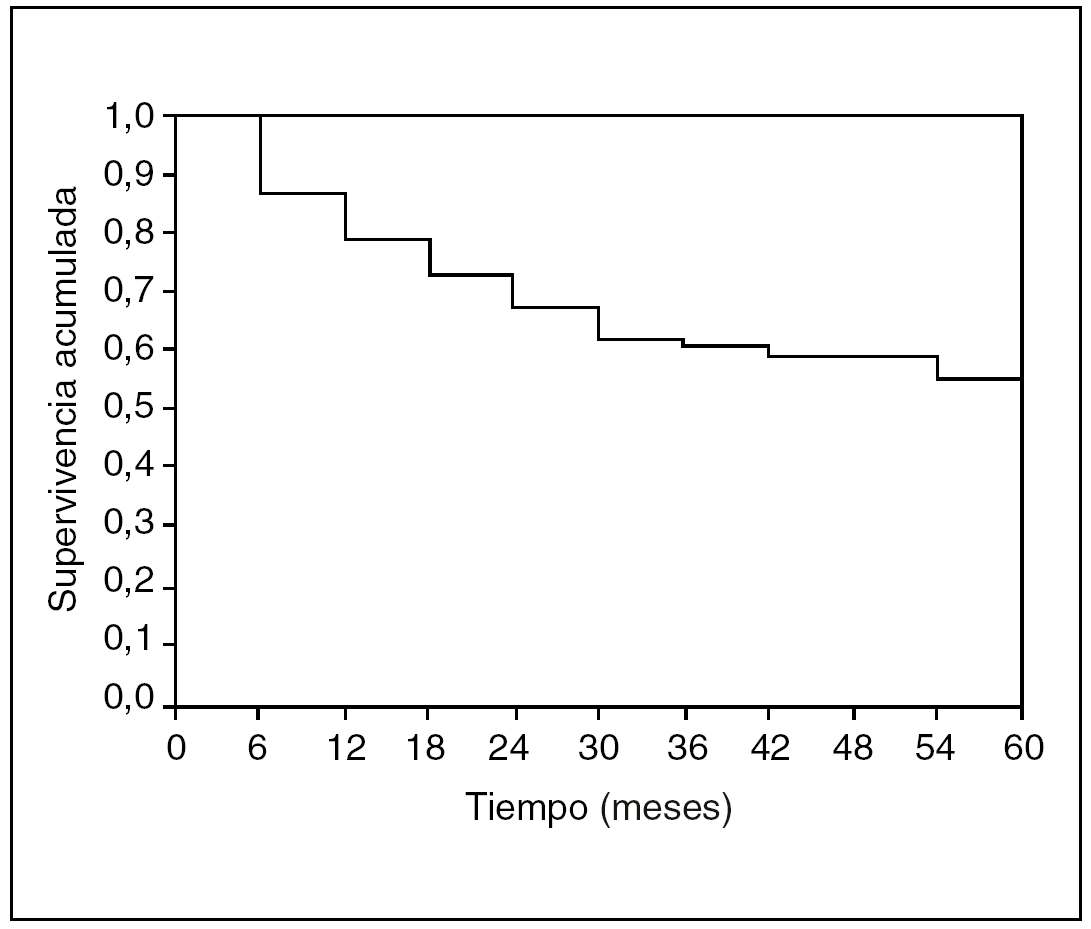
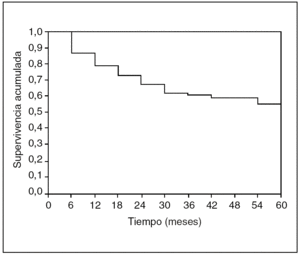
Comparémosla con la misma curva pero basada en los datos analizados con el método actuarial (fig. 5). Son muy parecidas, incluso nos gusta más la realizada con Kaplan-Meyer. Pero veamos la función de riesgo de defunción, es decir, cuál es el momento de mayor riesgo de que el sujeto fallezca (y que sólo se puede calcular con el método actuarial) (fig. 6).
Fig. 5. Curva de supervivencia actuarial.
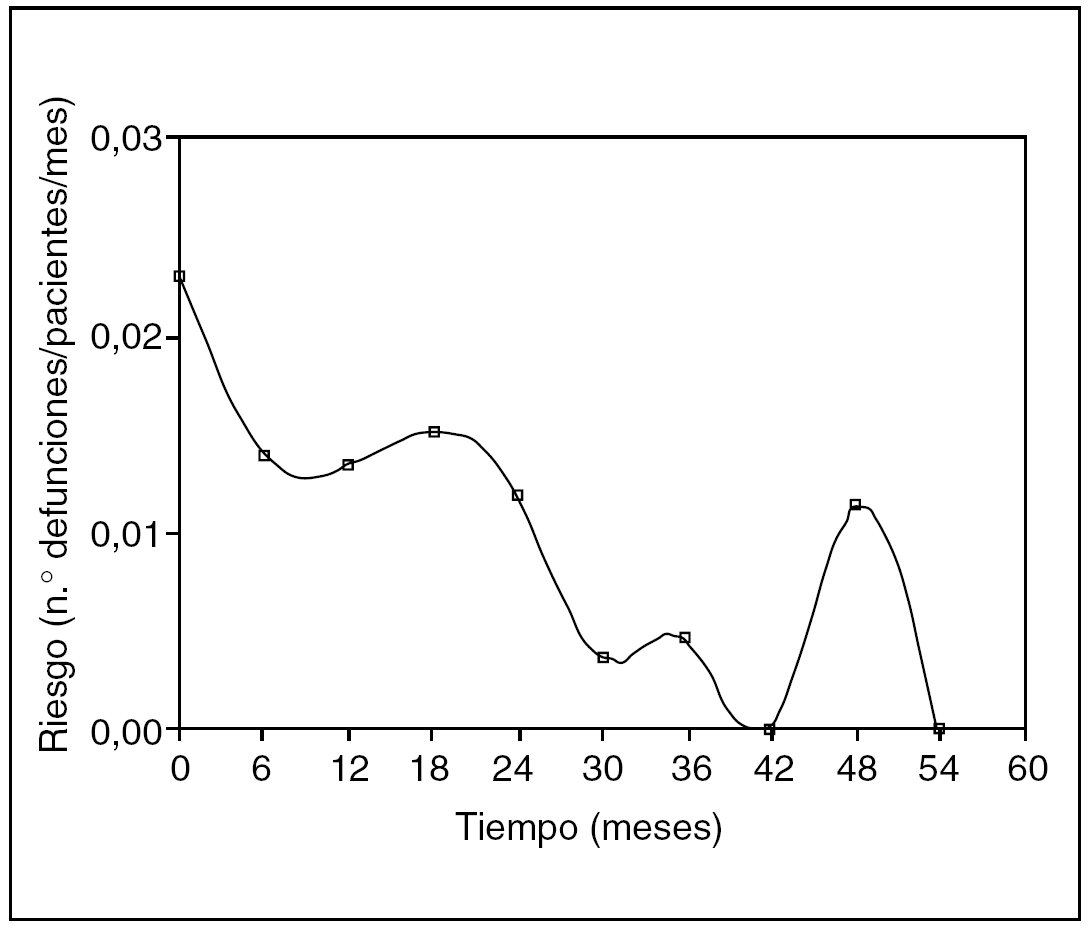
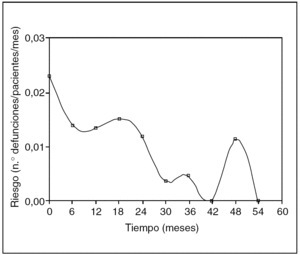
Fig. 6. Función de riesgo.
De la observación de la curva anterior se puede sacar varias conclusiones "visuales", es decir, sólo mirando la curva (y sin "p"...) y es que en el tiempo 0 es el momento de máximo riesgo de defunción (es decir, la intervención quirúrgica), que luego hay un repunte de mortalidad a los 18 meses y un pico aislado a los 48 meses.
La función de riesgo, pues, es mucho más adecuada para describir la dinámica del proceso que estamos estudiando, porque sus valores nos dan una adecuada aproximación a la tasa de incidencia del evento en cuestión. Sirve por tanto para contestar la pregunta ¿cuándo fallecen más los pacientes?, o ¿cuándo recidivan más? Vale la pena recordar que una tasa de incidencia de la mortalidad, por ejemplo, es una medida del riesgo de morir en un intervalo concreto.
Comparaciones entre curvas
Otro de los aspectos útiles en las curvas de supervivencia es que pueden compararse entre sí. Existe una prueba no paramétrica, el log-rank2 que es la más ampliamente usada para comparar dos o más curvas de supervivencia. En este caso, las curvas pueden corresponder a dos grupos de pacientes con diferentes tratamientos, o dos grupos de pronóstico diferente. El método calcula para cada tiempo el número de eventos terminales que se esperarían asumiendo que no hay diferencias entre ambos grupos. Se obtiene un valor final que puede compararse mediante una distribución de χ2 y que puede dar un valor de p que permita valorar la existencia de diferencias estadísticamente significativas entre ambas curvas. Aunque existen otros métodos para comparar curvas, se considera que el de log-rank es tan robusto3, a pesar de depender del número de pacientes, que la utilización de cualquier otro método debe estar muy bien justificada4.
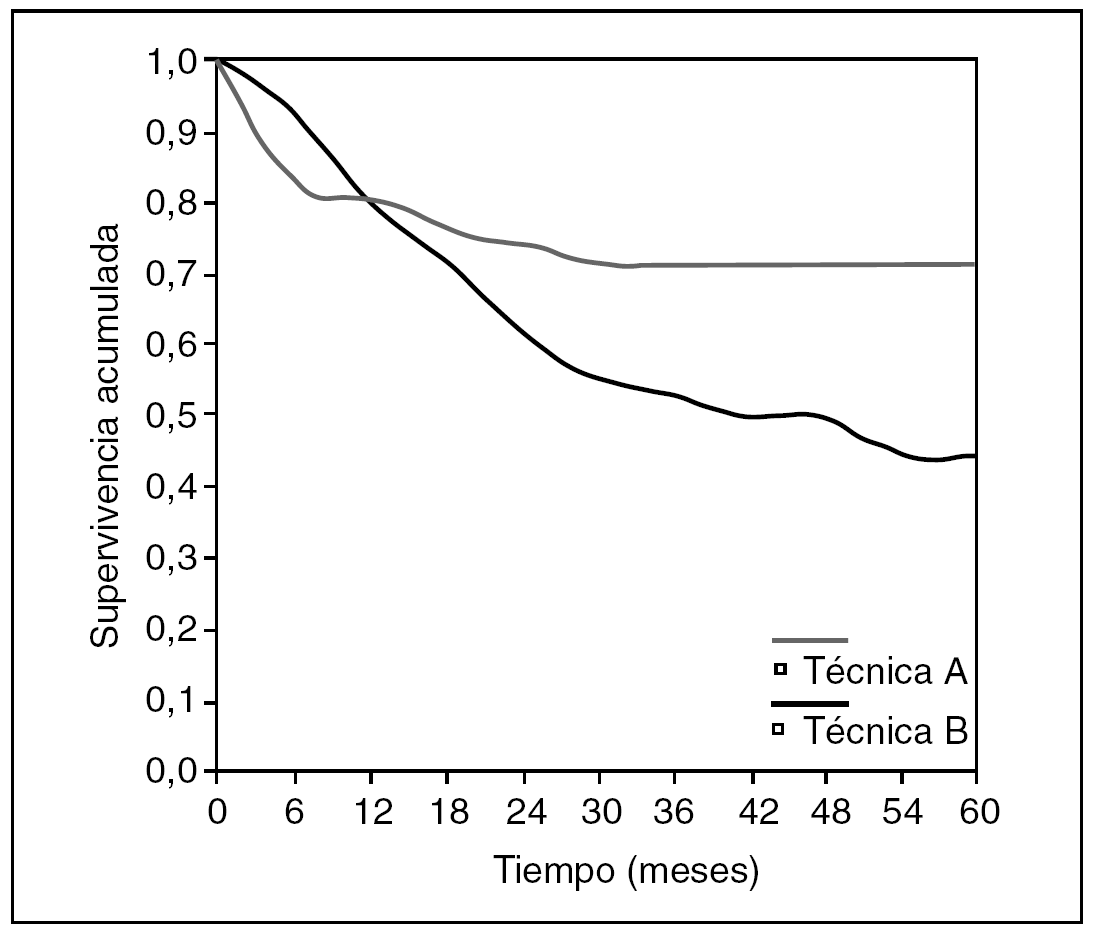
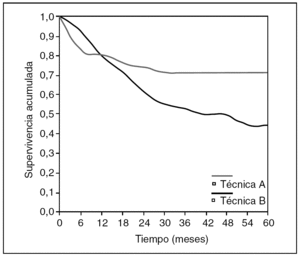
Vayamos otra vez al ejemplo de los 100 cánceres de esófago operados. Supongamos que en el diseño del estudio se recogió la variable técnica quirúrgica, y que además en 50 casos se utilizó la técnica A y en otros 50 casos la técnica B. Sin entrar en más consideraciones sobre la comparabilidad de los grupos, la asignación aleatoria y otros detalles, veamos cómo son las dos curvas de supervivencia de estos dos grupos, con el método actuarial (fig. 7).
Fig. 7. Comparación entre dos curvas de supervivencia.
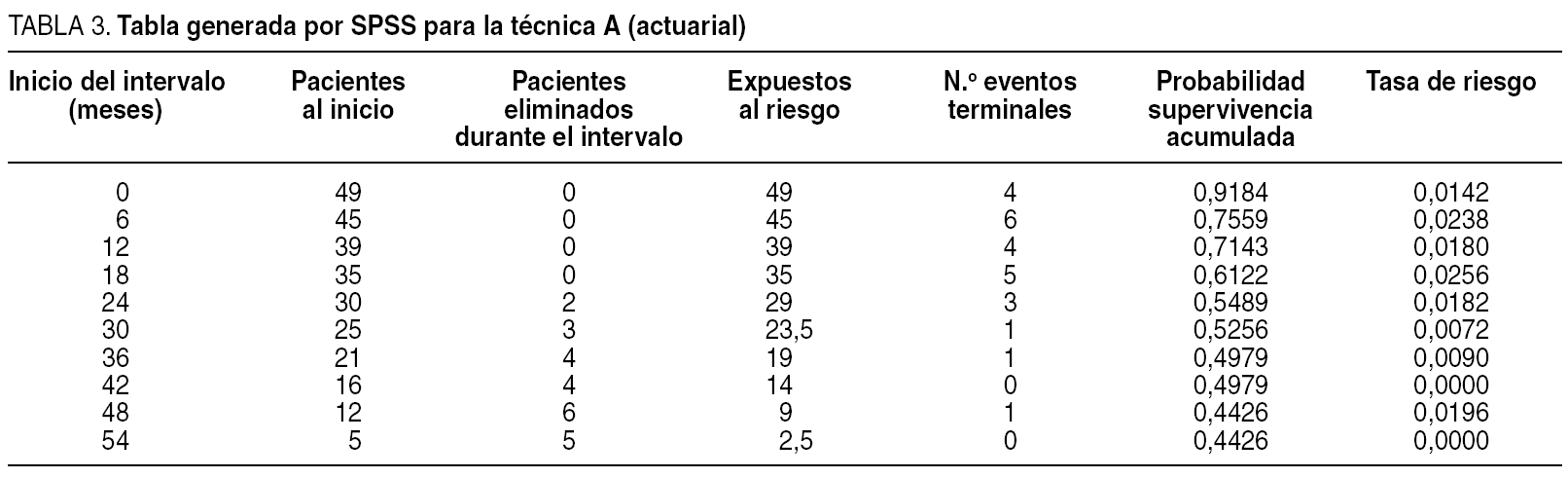
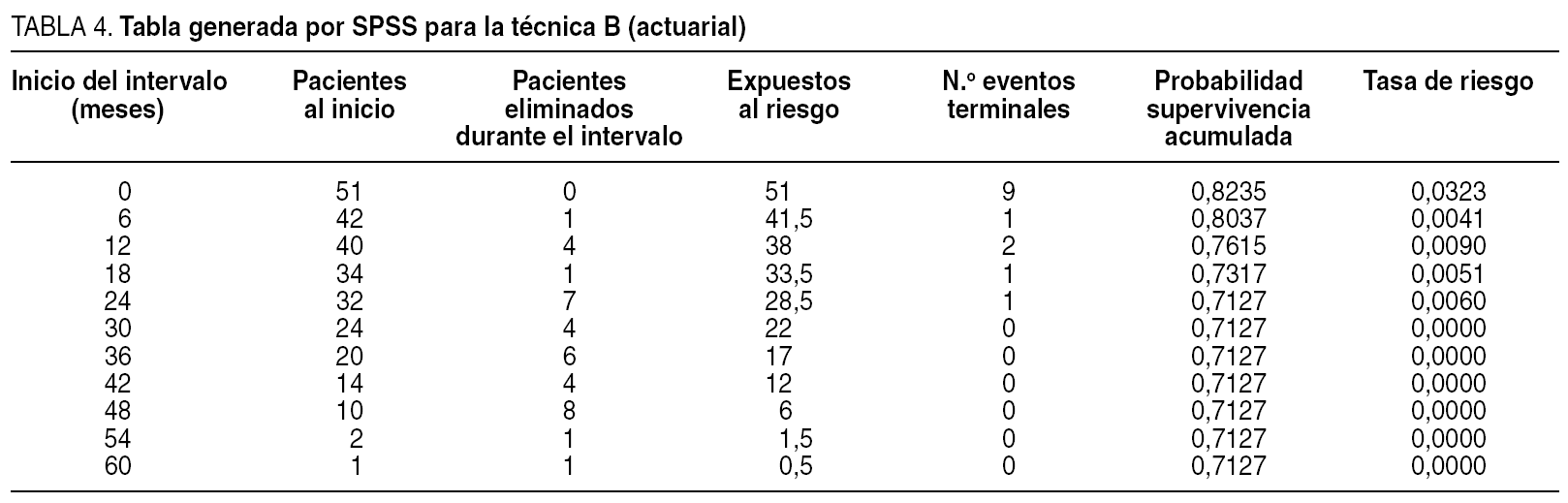
Lo primero que hay que fijarse es que la gráfica no se parece en nada a la escalera que habíamos representado en la curva anterior de toda la población: es una pequeña trampa que nos ofrece el SPSS: permite representar los datos de supervivencia en forma escalonada o en forma lineal. Pero lo realmente importante es el listado numérico que nos ofrece el SPSS, que se ofrece en las tablas 3 y 4.
¿Qué quiere decir cada columna? La primera marca los intervalos en los que calcularemos la supervivencia. La segunda, el número de sujetos al inicio del intervalo. La tercera, el número de sujetos con el tiempo censurado durante el intervalo. La cuarta son los que están en riesgo durante el intervalo. La quinta es el número de eventos que se producen durante el intervalo. La siguiente columna importante es la sexta: señala la probabilidad de supervivencia acumulada, y que es la que se representa en la curva. Y la última transcendente por hoy es la séptima: la tasa de riesgo, y que también será la que representaremos en forma de curva de riesgo. Para un no iniciado, con estas columnas es suficiente (SPSS da más, pero éstas son suficientes por hoy).
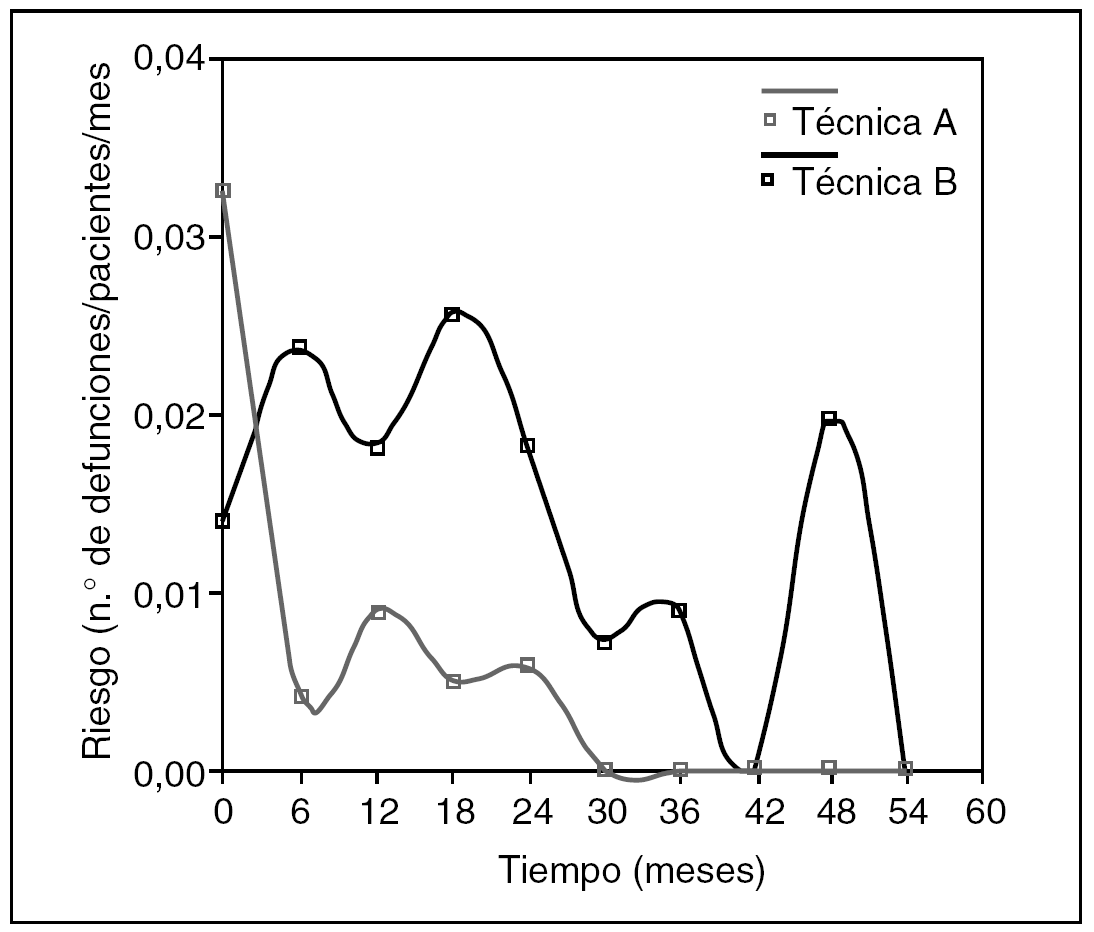
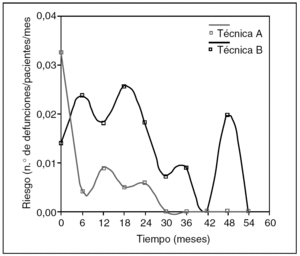
Volvamos a la gráfica comparativa de las dos técnicas quirúrgicas en esofagectomía. No hacen falta las "p": se puede ver que la técnica A está castigada con más mortalidad inicial, seguramente operatoria, que la técnica B. Pero en cambio, la supervivencia a partir del mes 12 pasa a beneficiar a la técnica A, probablemente porque la técnica B tiene un mayor porcentaje de recidiva. Y esto que acabamos de decir, ¿se puede ver de alguna manera? Pues sí: usemos una función de riesgo (fig. 8).
Fig. 8. Comparación entre dos funciones de riesgo.
La observación de la función de riesgo no ofrece dudas: el riesgo de morir con la técnica A es máximo al inicio, es decir, al operar. Luego hay un pequeño pico a los 12 meses, y los que sobreviven a los 24 meses ya no van a morir por la neoplasia. En cambio, la técnica B no tiene demasiada mortalidad operatoria pero está castigada con dos picos de mortalidad a los 6 y 18 meses, y su riesgo siempre es mayor a la de la técnica A. Y sin "p".
Requerimientos críticos del análisis de supervivencia
Censurado no informativo: pérdidas
Los métodos para el análisis de datos de supervivencia son válidos sólo si los pacientes censurados (aquellos en los que no se ha presentado el evento terminal) han sido censurados por un motivo "no informativo". En la práctica, sí son pacientes perdidos. Esto tiene un sentido clínico que hay que explicar. Al menos en teoría, un paciente perdido puede presentar el evento terminal en cualquier momento una vez lo hemos perdido. Nada nos hace pensar que tenga alguna característica que lo haga diferente de los que permanecen en el estudio y no se han perdido y, por tanto, es comparable a los que se quedan en el estudio. En cambio, el censurado "informativo" es una situación diferente. Por ejemplo, son los pacientes que han fallecido por cualquier otro motivo, o aquellos que salen del estudio porque la situación clínica ha empeorado, o han presentado un efecto adverso grave. Esto los hace no comparables a los que se han quedado en el estudio. Precisamente por este motivo, no es muy adecuado hacer un análisis de supervivencia teniendo como variable de evento terminal la mortalidad por cáncer: ¿y los que fallecen por un accidente de tráfico? Los fallecidos por un accidente de tráfico es un caso claro de tiempo censurado (tiempo incompleto: no se ha presentado el evento terminal, que era la defunción por cáncer) pero informativo: sabemos perfectamente lo que le ha pasado al paciente, y además, no podemos decir que sea comparable a los que siguen en el estudio. Otro ejemplo es el paciente que acaba el seguimiento a los 60 meses y sale del estudio: es un censurado informativo, sabemos lo que le ha pasado exactamente, y además, vuelve a no ser para nada comparable con los que siguen en el estudio. Un ejemplo muy claro de cómo puede variar la "supervivencia" de un mismo paciente según el evento terminal que se estudie se encuentra en un trabajo que compara las supervivencias del cáncer de colon por diferentes eventos terminales5. Una buena parte de los ejemplos que hemos presentado son "riesgos competitivos". Los riesgos competitivos son aquellos eventos que no son el evento terminal pero que imposibilitan el seguimiento posterior, dando por tanto un tiempo censurado por la derecha6. En un artículo de conceptos básicos como éste, con conocer que existen y que deberían ser tenidos en cuenta es suficiente.
Duración del seguimiento
Normalmente es el diseño de un estudio lo que marca cómo se analizará y qué seguimiento se hará. Por ejemplo, para estudios de cáncer digestivo, con un seguimiento de 5 años suele ser suficiente. El pronóstico de la enfermedad y su gravedad deben ser los parámetros a evaluar de cara a calcular el seguimiento óptimo. No hay reglas fijas.
Seguimiento completo
Cada paciente que no tenga el evento terminal puede ser incluido en el análisis de supervivencia por el período en que se ha recogido su seguimiento, y será un tiempo censurado. Sin embargo, el seguimiento completo de estos pacientes es muy importante y se relaciona con lo que hemos dicho de los censurados no informativos. Un seguimiento desigual entre los dos grupos que se comparen sesgará el análisis. Contar simplemente las pérdidas en cada brazo del estudio ya es un indicador de la calidad del seguimiento, pero no nos informa de cuánto tiempo hemos perdido. En general, cuando las pérdidas no se distribuyen igual en los dos grupos, deben ser investigadas.
Efecto cohorte sobre la supervivencia
El método de Kaplan-Meyer asume que las probabilidades de supervivencia son las mismas para todos los pacientes del estudio, tanto los que se incluidos hace 10 años como los que se incluyeron anteayer. Es evidente que en períodos largos los avances en medicina pueden distorsionar completamente esta asunción. Existen métodos de ajuste que pueden compensar este hecho, pero corresponden a partes más avanzadas del análisis de supervivencia.
Estudios multicéntricos
El problema es el mismo que en el apartado anterior. Diferentes hospitales pueden aplicar diferentes técnicas de diagnóstico, por ejemplo, que permitan detectar una recidiva 3 meses antes que en otro hospital. Esto, obviamente, afectará al análisis de supervivencia, introduciendo un sesgo.
Conclusión
El análisis de supervivencia es un conjunto de métodos estadísticos muy apropiado cuando lo que estamos investigando es el tiempo hasta que algo ocurre. Precisa recoger como mínimo dos variables: el tiempo y la ocurrencia o no del evento terminal. Los datos pueden presentarse como función de supervivencia y como función de riesgo. Disponemos de pruebas que permiten comparar dos curvas de supervivencia.