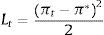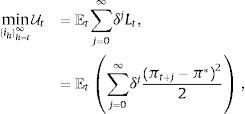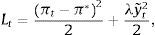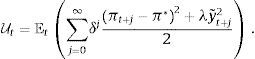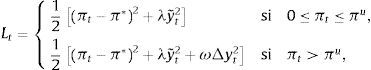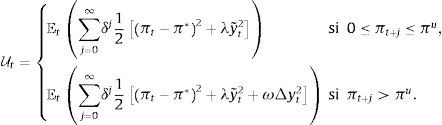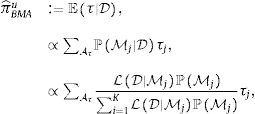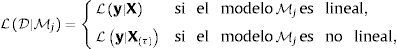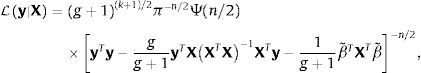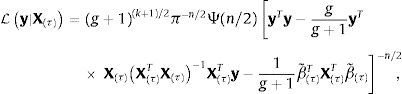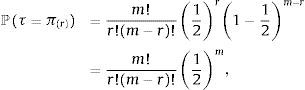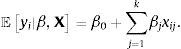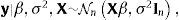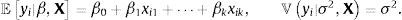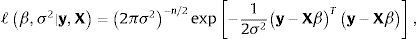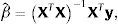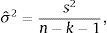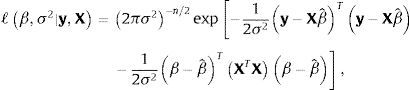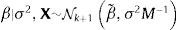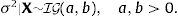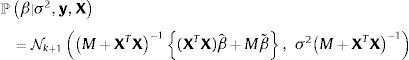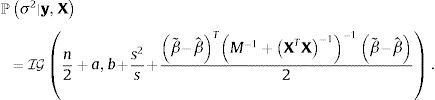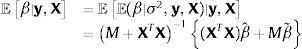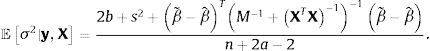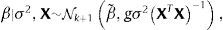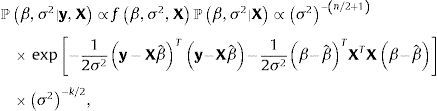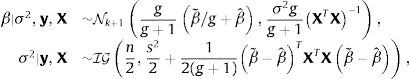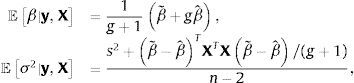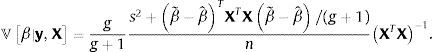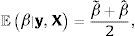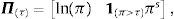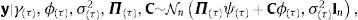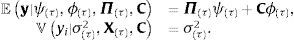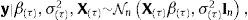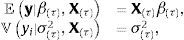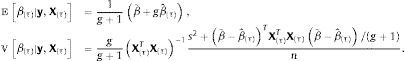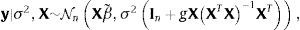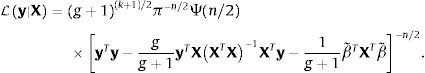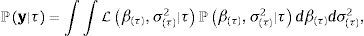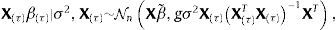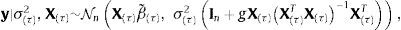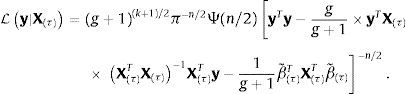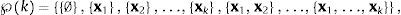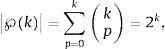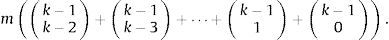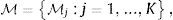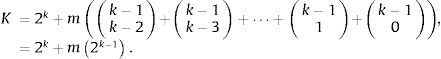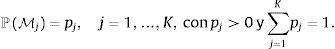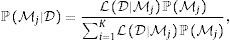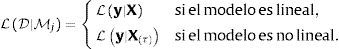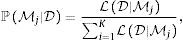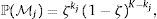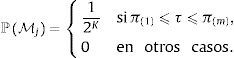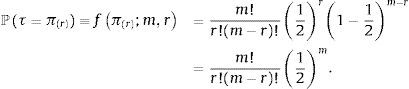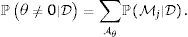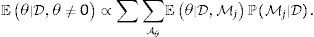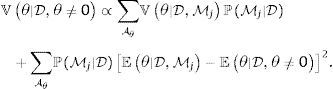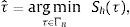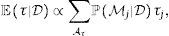Después de la crisis internacional se sugirió elevar las metas de inflación para dar más espacio a la política monetaria durante épocas contractivas del producto. Este estudio propone que el límite para elevar la meta de inflación debería ser el umbral de inflación, definido como aquel por encima del que la variación de precios es perjudicial para el crecimiento económico. Para estimar este umbral se proponen métodos Bayesianos. Los resultados muestran que encima del umbral existe una relación negativa y estadísticamente significativa entre la inflación y las variaciones del producto.
After the international crisis, it was suggested that inflation targets should be raised in order to allow more space to monetary policies during contractionary product times. The present study proposes that the limit to raise the inflation target should be threshold inflation, defined as the rate above which price variability is detrimental to economic growth. Bayesian methods are proposed to estimate this threshold. Results suggest that over the threshold there is a negative and statistically significant relationship between inflation and variations in the product.
Para Blanchard, Giovanni, and Mauro (2010) las reducciones en la variabilidad en la inflación y el crecimiento sostenido del producto en EE. UU. durante la Gran Moderación (Stock & Watson, 2003) de los ochenta motivaron a los macroeconomistas y hacedores de política a creer que sabían exactamente cómo conducir la política monetaria; sin embargo, las crisis globales de 2008 y 2009 mostraron las limitaciones de la política monetaria y abrieron el debate acerca de la posibilidad de incrementar las metas de inflación para evitar el tope de tasa de interés cero y tener así más espacio para aplicar una política expansiva si existen choques contraccionarios sobre la economía (Williams, 2009)1. Ball (2013), por ejemplo, sugirió elevar la meta de inflación en países desarrollados al 4% para liberar a la política monetaria de las restricciones del límite inferior cero de las tasas de interés y reducir así la severidad de las crisis económicas. El importante beneficio que resulta de incrementar la meta de inflación tendría un costo mínimo, ya que —en opinión de Ball— una inflación del 4% no dañaría significativamente a la economía. En una posición similar, Krugman (2014) argumentó que una meta de inflación más alta es necesaria y deseable debido a la alta probabilidad de episodios de límite inferior cero, sumado a la dificultad de realizar ajustes al salario real cuando la inflación es muy baja (lo que reduce la competitividad, estancando la actividad), y sobre todo porque una meta de inflación demasiado baja puede llevar a una «trampa de la economía»si los consumidores posponen sistemáticamente su consumo esperando que los precios bajen, ocasionando un bucle autoperpetuado y autoalimentado entre debilidad económica e inflación baja, que deprime persistentemente la actividad real2.
Si el beneficio de incrementar la meta de inflación es superior al costo de esta política, surge la interrogante de qué tan alta tiene que ser la nueva tasa del objetivo inflacionario. Esta investigación sugiere que el umbral de inflación, definido como aquel por encima del que la inflación tiene un efecto perjudicial sobre el crecimiento económico, es el límite para incrementar la meta de inflación, ya que encima de ese umbral la inflación comienza a perjudicar al crecimiento económico. Una estimación del umbral permitiría a la Banca Central conducir una política monetaria con objetivos múltiples, que busque no solamente la estabilidad de precios sino que evite también los efectos perjudiciales de la alta inflación sobre el crecimiento económico: si los objetivos de inflación de una autoridad monetaria son estrictos, la función de pérdida periodo-a-periodo (Lt) del Banco Central será simplemente una función de desviaciones de la inflación observada (πt) respecto al objetivo inflacionario (π*),
por lo que el problema de política del Banco Central en t es elegir la trayectoria actual y futura de un instrumento de política monetaria {ih}h=t∞, con el propósito de minimizar la suma esperada descontada de las desviaciones de la inflación observada respecto a la meta explícita o implícita de inflación,siendo δ∈(0, 1) el factor de descuento y Et un operador de esperanza condicional al conjunto de información en el momento t. Si el Banco Central tiene como mandato estabilizar la magnitud de la brecha del producto además de la inflación, la función de pérdida será (Svensson, 1999),en la que λ≥0 mide la importancia relativa que el Banco Central asigna a los movimientos cíclicos del producto (y˜t). La suma esperada de pérdidas de política descontada será ahora,En el caso de contar con una medida de inflación de umbral (πu), la función de pérdida se vuelve condicional,
al igual que la función de pérdida intertemporal de la autoridad monetaria,En esta ecuación, el crecimiento económico está incluido entre los mandatos del Banco Central, por lo que, si la inflación registrada (πt) o anticipada (πt+j) es mayor que el umbral (πu), la autoridad monetaria comienza a asignar una importancia relativa (ω>0) al crecimiento económico (Δyt2), además de a la estabilidad inflacionaria y a la reducción de la brecha del producto, ya que encima del umbral la inflación comenzaría a afectar al crecimiento económico. Debajo del umbral, si el Banco Central tiene metas estrictas (λ=0), su mandato es solamente la estabilidad de precios; pero cuando λ>0, considera también la estabilización de la brecha del producto, como en modelos de metas inflacionarias flexibles.
Esta investigación proporciona un método bayesiano para estimar el umbral de inflación. El uso de métodos bayesianos permite obtener resultados que consideran la incertidumbre sobre las variables potencialmente explicativas del crecimiento económico. Se presenta una aplicación al caso de Nicaragua, un país que sufrió una hiperinflación —seguida por tasas de inflación por encima y debajo de los 2 dígitos— y tasas crecimiento económico negativas durante crisis económicas.
La estimación de más de 24 mil regresiones indicó que el umbral de inflación por encima del que la variación de precios sería perjudicial para el crecimiento económico en Nicaragua es aproximádamente del 14%. Encima de este umbral, la relación entre el crecimiento y la inflación es negativa. Debajo del umbral, la relación de la inflación con el crecimiento resultó no estadísticamente significativa.
Los fundamentos teóricos y la evidencia empírica se revisan en la sección 2. La metodología de estimación del umbral se describe en la sección 3. La sección 4 muestra la aplicación a Nicaragua. La sección 5 discute los resultados y las implicaciones de política.
2Fundamentos teóricos y evidencia empírica previa2.1Inflación y crecimiento económico: teoríaTeóricamente, existe un consenso general acerca de que la relación entre la inflación y el crecimiento económico es no-lineal; véase inter aliaChoi, Smith, and Boyd (1996), Azariadis and Smith (1996), Sarel (1996), Ghosh and Phillips (1998), Khan and Senhadji (2001), Burdekin, Denzau, Keil, Sitthiyot, and Willett (2004), Hineline (2007) o Bick (2010). La no-linealidad se refiere a que el crecimiento económico se vería perjudicado si la inflación es igual o mayor a una determinada tasa, llamada umbral de inflación, mientras que si la inflación está por debajo de este umbral, la variación general de precios tendría una ligera relación positiva o ningún efecto sobre la actividad económica. En el modelo teórico de Minea and Villieu (2009), por ejemplo, un incremento en el señoreaje (y por tanto en la inflación, ya que la inflación en el largo plazo depende positivamente del señoreaje) se dedica a gastos públicos productivos que fomentan el crecimiento, pero si el incremento del señoreaje está por encima de un umbral se incrementa el costo de la inversión privada, lo que daña el crecimiento económico. Choi et al. (1996) explican que la inflación afecta adversamente a la economía debido a que las altas tasas de inflación exacerban las fricciones del mercado al reducir las tasas de retorno reales recibidas por los ahorristas en los mercados financieros, interfiriendo con la provisión de capital de inversión y su colocación, ya que los prestamistas serán menos propensos a otorgar créditos ante tasas de interés reales bajas y alto riesgo, limitando la provisión de crédito y reduciendo así la actividad económica en el largo plazo. El modelo de Choi et al. (1996) predice además que si las tasas de inflación son bajas (por debajo de un umbral), no se producirá un racionamiento de crédito y la inflación estará positivamente relacionada con el crecimiento. Este enfoque es similar al presentado en Azariadis and Smith (1996), quienes construyen un modelo de crecimiento neoclásico con dinero y mercados crediticios activos, en el que el dinero es un sustituto cercano del capital físico en portafolios de capital privado y la utilidad de ser un depositante depende (positivamente) de los retornos de los depósitos bancarios, por lo que aumentos en la inflación reducen los retornos e incentivan a prestamistas de baja calidad a buscar créditos. Para disuadir a estos prestamistas, se crean mayores restricciones de acceso al crédito, lo que afecta a prestamistas legítimos, racionando el crédito. Según la inflación aumenta, el racionamiento se vuelve más severo, estableciendo un enlace negativo entre la inflación y la acumulación de capital. El equilibrio del modelo cae en 2 posibles regiones: si las tasas de inflación son bajas, se produce el efecto Mundell-Tobin, por lo que la inflación y el producto estarán positivamente relacionados en el largo plazo; pero si la tasa de creación de dinero excede un umbral, el crédito comienza a racionarse, revirtiendo el efecto Mundell-Tobin y ocasionando una relación negativa entre inflación y crecimiento.
2.2Inflación y crecimiento económico: evidencia empíricaKormendi and Meguire (1985), Levine and Zervos (1993), Fischer (1993), Barro (1995), y Bruno and Easterly (1998) se encuentran entre los primeros estudios que analizan la relación empírica entre la inflación y el crecimiento económico. Kormendi and Meguire (1985) encuentran una relación negativa y altamente significativa de la inflación con el crecimiento, que interpretan como evidencia contundente en contra del efecto Mundell-Tobin y a favor de la posición teórica de Stockman (1981). Fischer (1993) encuentra una relación positiva entre la inflación y el crecimiento, que se vuelve negativa según la inflación aumenta. Barro (1995), por su parte, encuentra también una relación negativa entre la inflación y el crecimiento, pero solamente si las tasas de inflación son altas, al igual que Bruno and Easterly (1998).
Algunos estudios que evalúan la relación entre inflación y crecimiento en Latinoamérica, empleando métodos lineales, son inter aliaDe Gregorio (1992) y De Gregorio (1993), Faria and Carneiro (2001), Dabus and Viego (2003), Grier and Grier (2006) y Bittencourt (2012). En De Gregorio (1992) y De Gregorio (1993) se estudia los determinantes del crecimiento en 12 países de Latinoamérica durante el periodo 1950-1985, encontrando que la inflación, así como su variabilidad, tiene efectos negativos sobre el crecimiento, un resultado que no solo sería válido en países con altas tasas de inflación (De Gregorio & Lee, 1999). Analizando el caso de Brasil, Faria and Carneiro (2001) encuentran evidencia empírica de una relación negativa entre la inflación y el producto en el corto plazo, pero no en el largo plazo. Dabus and Viego (2003) hallan una relación negativa entre inflación y crecimiento, particularmente en periodos de inflación extrema —10% de acuerdo a Dabus and Viego (2003), aunque este valor no se estima sino que se escoge arbitrariamente—, analizando 7 economías de Latinoamérica (Argentina, Brasil, Perú, Colombia, México, Uruguay y Venezuela). Grier and Grier (2006) encuentran que la incertidumbre inflacionaria (calculada con un modelo multivariante generalizado de heterocedasticidad condicional) tiene un efecto negativo y significativo sobre el crecimiento en México. Bittencourt (2012) emplea datos de panel de Argentina, Bolivia, Brasil y Perú en el periodo 1970 y 2007, concluyendo que inflaciones altas tienen un efecto perjudicial en el crecimiento económico.
La literatura empírica más reciente trata de estimar el valor del umbral por encima del que la inflación tiene una relación negativa con las variaciones del producto:
- •
Sarel (1996) analiza la información de 87 países entre 1970 y 1990, y encuentra un umbral de inflación del 8% por encima del que la inflación tiene un efecto negativo contundente sobre el crecimiento, mientras que si la variación general de precios se encuentra debajo de este valor, la inflación no tiene ningún efecto o tiene un ligero efecto positivo.
- •
Ghosh and Phillips (1998) analizan 145 países entre 1960 y 1996; empleando árboles de regresión binarios encuentran una relación positiva entre la inflación y el crecimiento con bajas tasas anuales de inflación (2-3%), además de una relación negativa y convexa por encima de estos valores.
- •
Doyle and Christoffersen (1998) utilizaron un panel no balanceado de economías en transición, siendo la serie más larga de 1990 a 1997, y encontraron un umbral del 13% con pérdida del 1% del producto por encima del umbral.
- •
Gylfason and Herbertsson (2001) analizan 170 países desde 1960 a 1992, encontrando que una inflación por encima del 10-20% por año es en general perjudicial para el crecimiento.
- •
Khan and Senhadji (2001) —posiblemente uno de los estudios más influyentes, en el sentido del número de veces que ha sido citado— analizan 140 países y concluyen que el umbral de inflación es del 1-3% para países industrializados, y del 11-12% para países en desarrollo.
- •
Rousseau and Wachtel (2002), con datos de 84 países entre 1990 y 1965, estiman un umbral del 13-24% y opinan que las altas tasas de inflación dificultan la intermediación financiera, al aumentar la incertidumbre acerca de los proyectos de inversión y los retornos, además de erosionar la utilidad de los activos monetarios.
- •
Burdekin et al. (2004) utilizando splines encuentran un umbral del 8% para países industrializados y un umbral del 3% para países en desarrollo.
- •
David, Gomis-Porqueras, and Hernandez-Verme P. (2005) emplean un panel no-balanceado de 138 países en el periodo 1950-2000 y encuentran evidencia contundente de que la inflación tiene un efecto no-lineal sobre el crecimiento. David et al. (2005) estiman un umbral del 19,16% para la muestra completa y los países no-industrializados, y del 12,51% para la muestra de países industrializados.
- •
Pollin and Zhu (2006) analizan 80 países entre 1961 y 2000; encuentran un umbral del 14-16% para países de ingreso medio, y del 15-23% para países de ingresos bajos.
- •
Vaona and Schiavo (2007) estudian 167 países entre 1960 y 1999, empleando métodos no-paramétricos y semiparamétricos, y encuentran un umbral del 12% debajo del cual la inflación no sería perjudicial para el crecimiento, aunque no obtienen resultados claros para países en desarrollo, un resultado que Vaona and Schiavo (2007) piensan que se debe a las diferentes experiencias de los países agrupados como en desarrollo.
- •
Bick (2010) analiza 40 países en desarrollo, entre 1960 a 2004, y encuentra un umbral del 19% que cae al 12% si se incluye un intercepto de régimen.
- •
Trupkin and Ibarra (2011) emplean un panel de 120 países en modelos de regresión de transición suave; encuentran un umbral del 4,1% para países industrializados y del 19,1% para países no industrializados, por debajo de los cuales la inflación no tendría efectos sobre el crecimiento. Eligiendo un grupo de países en desarrollo con mejores cualidades institucionales, la estimación del umbral de Trupkin and Ibarra (2011) cae sin embargo al 7,9%.
- •
Kremer, Bick, and Nautz (2011) utilizando regresiones de panel dinámicas de 124 países encuentran un umbral del 2% para países industrializados, mientras que para países no-industrializados, una inflación por encima del 17% estaría asociada con un menor crecimiento económico.
Debido a que Gokal and Hanif (2004) consideran que la relación de umbral entre inflación y crecimiento depende de la estructura particular de cada economía, otros estudios se enfocan en estimar el valor del umbral de inflación para determinados países, como inter aliaMubarik and Riazuddin (2005), que calculan un umbral del 9% para Pakistan; Pattanaik and Nadhanael (2011) que estiman un umbral del 6% para India; Sargsyan (2005), que calcula un valor del 4,5% para Armenia; Mireku (2012) que estima un umbral de inflación del 9% para Ghana; o Leshoro (2012) que estima que el umbral de inflación para Sudáfrica es 4%.
Investigaciones más recientes intentan incluir efectos no-lineales y la incertidumbre sobre las variables explicativas del crecimiento, empleando métodos bayesianos: Crespo-Cuaresma and Doppelhofer (2007) miden el efecto no-lineal de umbral del producto per cápita inicial y la apertura de una economía, con regresiones de crecimiento en presencia de incertidumbre de modelos, analizando 88 países con Bayesian Averaging of Thresholds. Usando Bayesian Model Averaging (BMA) Hineline (2007) examina si los efectos de la inflación sobre el crecimiento económico son consistentes con la incertidumbre acerca de las variables explicativas del crecimiento económico; sus resultados con datos de panel y efectos fijos sugieren que la inflación es una de las variables más importantes para explicar el crecimiento. Aunque Hineline (2007) utiliza BMA para evaluar los efectos de la inflación en el crecimiento, no estima el valor del umbral de inflación sino que lo escoge arbitrariamente igual al 10%, una deficiencia metodológica que esta investigación pretende mejorar.
3Metodología: estimación bayesiana del umbral de inflación ante incertidumbre sobre los determinantes del crecimiento económicoLa teoría económica y la evidencia empírica postulan una gran cantidad de variables explicativas del crecimiento económico: según Durlauf, Johnson, and Temple (2005), existen al menos 145 variables potencialmente explicativas del crecimiento, agrupadas en 43 teorías conceptualmente distintas. Esta multiplicidad dificulta identificar cuáles variables son realmente determinantes para el crecimiento: Levine and Renelt (1992) mostraron que, aunque varias variables tengan la misma validez teórica, la significancia estadística de estas variables depende del conjunto de información utilizado, i.e. los resultados son frágiles ante cambios en las variables incluidas en la regresión. Debido a la poca cantidad de observaciones disponibles, no es posible incluir todas las variables en la regresión, ya que con esta estrategia los estimadores serían ineficientes (Cotteleer, 2009). Más aún, «probar»arbitrariamente diferentes variables y mostrar los resultados de un solo modelo puede llevar a una inferencia espuria, por el sesgo de variables omitidas (Sala-i-Martin, Doppelhofer, & Miller, 2004). Aunque varios modelos puedan parecer razonables, implican conclusiones disímiles acerca de los parámetros de interés, haciendo difícil identificar apropiadamente el valor del umbral de inflación.
Otra forma más científica de proceder es admitir que no se conoce cuál modelo de regresión es el adecuado y asignar a cada modelo una probabilidad de ser el correcto, para luego promediar los resultados de todos los modelos. Este procedimiento se conoce como BMA y es empleado en este estudio para calcular el umbral de inflación por encima del que la variación de precios es perjudicial para el crecimiento económico, controlando la incertidumbre sobre las variables explicativas del crecimiento económico, según la teoría económica y la evidencia empírica3.
Un estimador bayesiano BMA del umbral de inflación πˆBMAu puede obtenerse sumando los j-posibles valores del umbral τj ponderados por la probabilidad condicional de que sean correctos ℙMj|D, dada la incertidumbre sobre las variables que afectan al crecimiento,
siendo LD|Mj funciones de verosimilitud marginales del conjunto de datos D usado en la estimación, ℙMj probabilidades prior de que un modelo Mj de crecimiento sea correcto y τj los j-posibles valores de la inflación de umbral. Dados los datos del crecimiento del producto contenidos en un vector y y las covariantes contenidas en una matriz X, la función de verosimilitud marginal será,con,y, para un valor dado del umbral τ,siendo g el escalar de Zellner (1986) y β˜ estimadores de los efectos de las variables que pueden afectar el crecimiento económico, incluyendo la inflación. La probabilidad prior de que cada modelo sea correcto ℙMj sigue una distribución Binomial ℙMj∼B(m,r),con los π(1), π(2), ..., π(m) valores ordenados de menor a mayor de la inflación histórica observada (π(1)⩽π(2)⩽⋯⩽π(m)). Esta distribución asigna a priori una mayor probabilidad a los valores históricos de la inflación cercanos a la tendencia central; aproximación apropiada dado que, como sugirió Enders (2009), para que el umbral tenga un significado práctico los datos tienen de hecho que cruzar el umbral frecuentemente, lo que no ocurrirá si la inflación de umbral se encuentra en los extremos de la distribución4. Detalles sobre la estimación del umbral de inflación se encuentran en el Anexo A.4Aplicación: estimación del umbral de inflación de NicaraguaDatos. La base de datos contiene una muestra de n=41 años (desde 1972 a 2012) de k=9 variables potencialmente explicativas del crecimiento económico en Nicaragua,x1 es la inflación, calculada como la tasa de crecimiento del promedio anual del índice de precios al consumidor, es la tasa de fertilidad total (la cantidad de hijos que tendría una mujer si viviera hasta el final de sus años de fertilidad y tuviera hijos de acuerdo con las tasas de fertilidad actuales específicas por edad), es el crecimiento de la población, es la esperanza de vida al nacer (en años), es la formación bruta de capital fijo (en moneda local constante con base 1990), son los términos de intercambio, es la matriculación escolar en primaria, expresada como el porcentaje de la población en edad oficial para recibir educación primaria, es el volumen de crédito del sistema financiero, es la proporción de manufacturas en las exportaciones (como proxy de la industrialización de Nicaragua).
El crecimiento económico (y) se aproximó con el crecimiento porcentual del producto interno bruto de Nicaragua. Los datos de la inflación se obtuvieron de las Estadísticas Financieras Internacionales del Fondo Monetario Internacional, y los datos del crecimiento del producto y las variables potencialmente explicativas del crecimiento provienen del Banco Mundial (http://databank.worldbank.org/data/home.aspx). Las variables explicativas fueron elegidas por estar entre las encontradas como significativas para el crecimiento en otros estudios empíricos, como e.g. Grier and Tullock (1989), Barro (1991), Sala-i-Martin et al. (2004), Hendry and Krolzig (2004) o Moral-Benito (2010). Limitaciones en la disponibilidad de series largas para Nicaragua restringieron la inclusión de otras variables que podrían ser explicativas del crecimiento. Incluir los términos de intercambio como covariante de control permite eliminar la correlación espuria entre la inflación y el producto generada por cambios en los términos de intercambio (Doyle & Christoffersen, 1998)5.
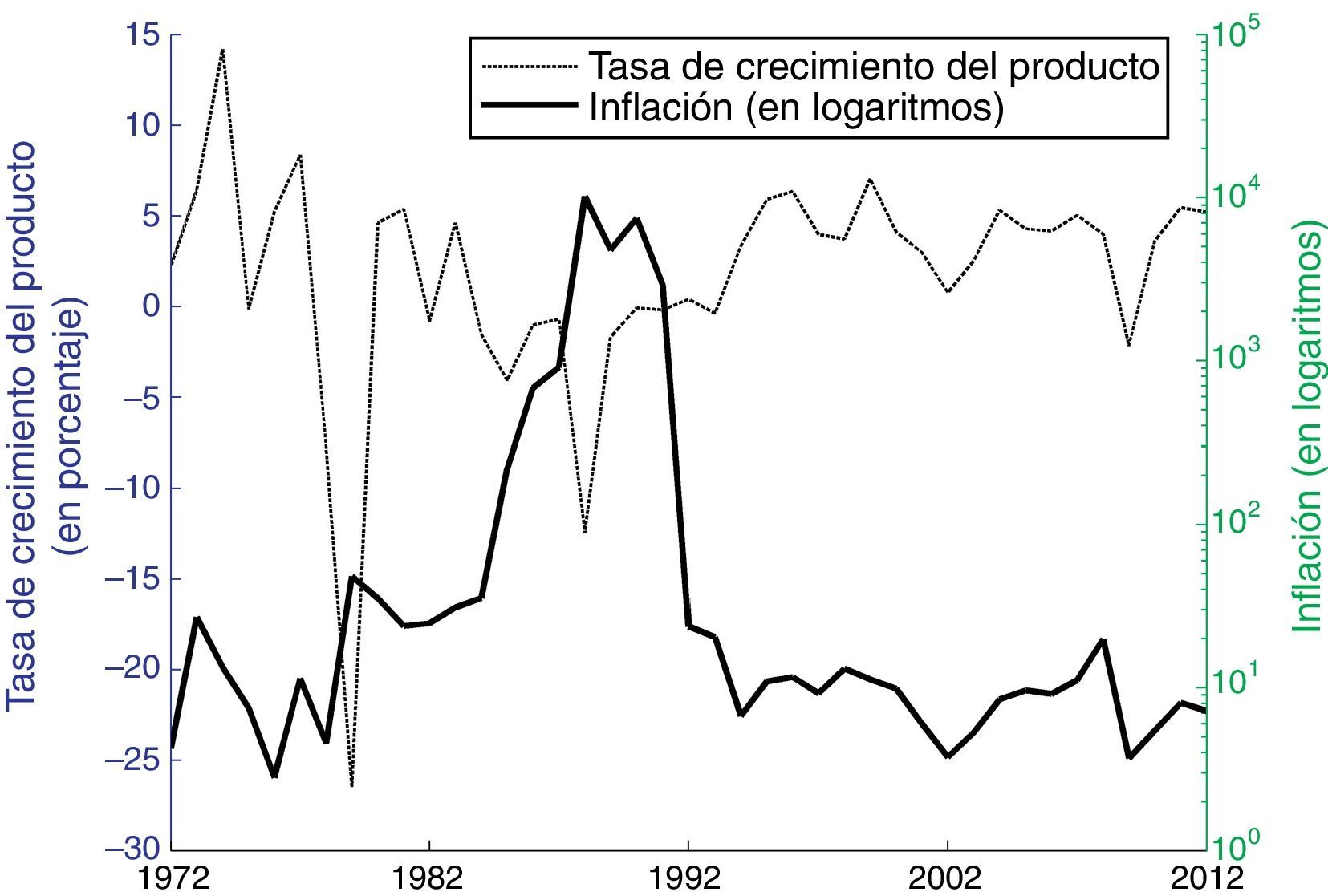
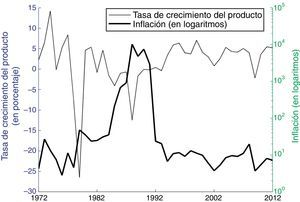
La figura 1 muestra el comportamiento anual del crecimiento del producto y la inflación en Nicaragua, desde 1972 a 2012. Durante este periodo, el crecimiento del producto en Nicaragua fue en promedio del 1,69%, siendo notoria la caída del producto del −26,5% en 1979, por la guerra insurreccional, y la contracción continua del producto entre 1984 y 1993, que en promedio fue del −2,18% y que estuvo relacionada con el modelo estatizante de economía que adoptó el régimen del gobierno sandinista en Nicaragua y el conflicto cívico militar que ocasionó la revolución, causando una reducción del empleo y de las exportaciones y una caída abrupta de la inversión privada, que fue sustituida por inversión pública de baja eficacia y eficiencia (Arana, Chamorro, DeFranco, Rivera, & Rodriguez, 2000). En este mismo periodo, Nicaragua experimentó un periodo hiperinflacionario, en el que la inflación pasó del 219% en 1985 al 681% en 1986; 912% en 1987 y 10.205% en 1988. Entre 1994 y 2012, la inflación se mantuvo aún alta, fue en promedio del 9%, alternando años de baja inflación (e.g. 3.8% en 2002) con años en los que la inflación estuvo por encima de 2 dígitos (e.g. 19,8% en 2008).
Tratamiento de los datos de la inflación. El estudio siguió las recomendaciones de Sarel (1996) y Khan and Senhadji (2001) y utilizó el logaritmo de la tasa de inflación de Nicaragua como regresor, debido a que la distribución altamente asimétrica de la tasa de inflación implica colocar un enorme peso en las pocas observaciones que registran una alta inflación, mientras que la transformación logarítmica permite obtener una distribución más simétrica: el coeficiente de asimetría de la distribución de la tasa de inflación de Nicaragua es 3,62 lo que indica una fuerte asimetría positiva relacionada con las pocas observaciones extremas del periodo hiperinflacionario. En cambio, la asimetría de la distribución del logaritmo natural de la inflación se reduce a 1,686. Por otra parte, al igual que en Crespo-Cuaresma and Doppelhofer (2007), se acotó la distribución de la tasa de inflación para evitar que alguno de los regímenes resultantes tenga muy pocas observaciones, lo que llevaría a estimadores no confiables. La acotación elegida fue del 15% al principio y al final de la muestra, quedando m=30 datos para la búsqueda del umbral.
Sensibilidad de los resultados al escalar g. Se evaluó la sensibilidad de los resultados a la elección de diferentes valores del escalar g, empleando g-priors comunes en la literatura de crecimiento económico (para Poirier (1988) es importante mostrar cómo diferentes priors afectan las conclusiones de un resultado empírico):
- g=1/k2,
dado que existen 9 variables explicativas, será igual a g=1/k2=1/92 = 0,011 por lo que se asignará una penalidad bastante pequeña a los modelos y como resultado existirán varios modelos relativamente no importantes que pesarán sobre los resultados de las estimaciones bayesianas.
- g=1/n,
ya que se tiene 41 observaciones, g=1/n=1/41 = 0,1562, siendo un caso intermedio en el que habrá una menor penalidad asintótica para los modelos grandes (i.e. con varios regresores).
- g=1
que es equivalente a poner la misma cantidad de información en el prior que en la muestra, por lo que la masa de probabilidad estará menos dispersa y existirán unos pocos modelos importantes que pesarán sobre los resultados de las estimaciones bayesianas.
Diseño de la estimación bayesiana. Ya que el estudio analiza k=9 variables explicativas, el espacio de modelos está formado por K=29+30×28=8.192 especificaciones, divididas en dos grupos: 29=512 modelos lineales y 30×28=7.680 modelos no-lineales. En el primer grupo de modelos el crecimiento económico se modela como la combinación lineal de un intercepto y una o varias variables predictoras, i=1, ..., 41, j=1, 2, ..., 9.
En los modelos no-lineales es necesario estimar regresiones del crecimiento contra la inflación y combinaciones de las 8 covariantes de control restantes, para cada uno de los m=30 posibles umbrales históricos de inflación, por lo que existirán 30×28=7.680 combinaciones a estimar.Debido a que el espacio de modelos lineales y no-lineales es de 8.192 modelos y se probaron 3 tipos de g-priors, se estimaron en total 24.576 modelos. Dado que el número de modelos no fue computacionalmente inviable de estimar7, en la investigación se estimaron todos los modelos, lo que permitió calcular estimadores BMA exactos para la inflación de umbral, basados en la enumeración completa del espacio de modelos, sin necesitar aproximaciones MC3 (Markov Chain Monte Carlo Model Composition) que toman muestras del espacio de modelos para calcular estimadores BMA aproximados; véase por ejemplo Madigan, York, and Allard (1995).
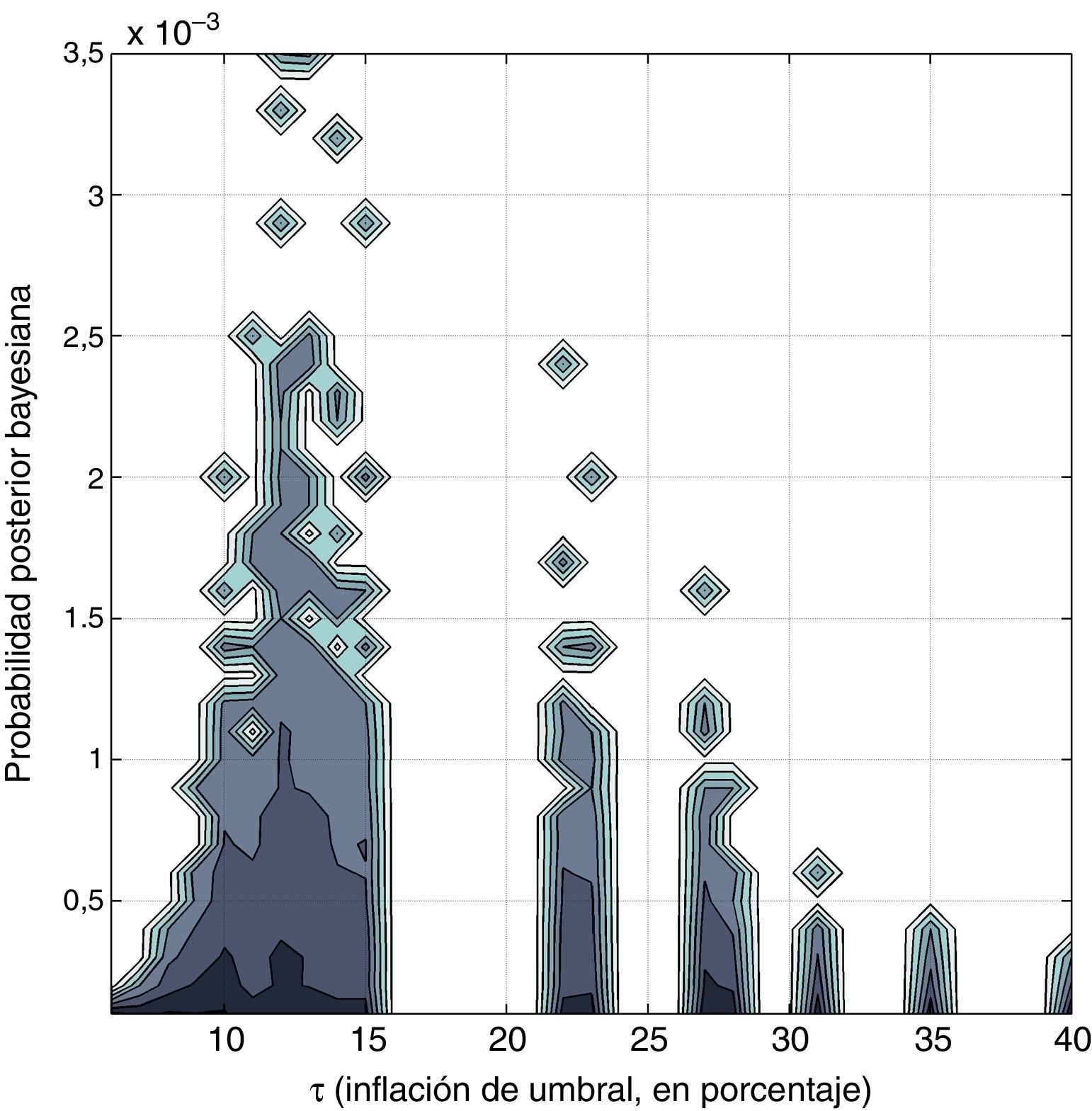
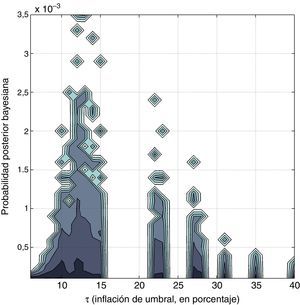
Resultados de las estimaciones bayesianas del umbral de inflación. La tabla 1 y la figura 2 muestran la estimación bayesiana del umbral de inflación en Nicaragua, obtenida con los 24.576 modelos considerados en el estudio. El umbral de inflación de Nicaragua está alrededor del 14%, con resultados no sensibles a la elección del escalar g (tabla 1).
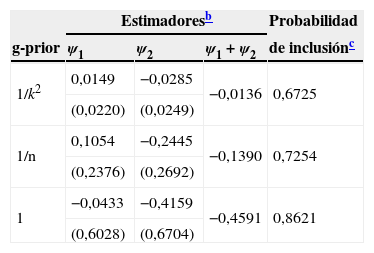
Efecto de la inflación en el crecimiento económico de Nicaragua. La tabla 2 muestra el efecto estimado de la inflación sobre el crecimiento de Nicaragua por encima y por debajo del umbral del 14%. El signo de la estimación bayesiana muestra un efecto negativo de la inflación sobre el crecimiento cuando la inflación supera el umbral inflacionario del 14%, mientras que si la inflación se encuentra debajo del umbral, el signo del estimado muestra una relación positiva entre la inflación y el crecimiento. Sin embargo, debido al alto valor del error estándar asociado al estimador bayesiano del efecto debajo del umbral, es posible que la relación de la inflación con el crecimiento sea no significativa en lugar de positiva. El efecto neto de la inflación sobre el crecimiento, medido por ψ1+ψ2, es predominantemente negativo, e indica que la magnitud de la caída del producto en Nicaragua (e−eψ2) estaría entre el 1,7% (g=1/k2) y el 2% (g=1) si la inflación en este país se duplica por encima del umbral (tabla 2).
Estimadores bayesianos del efecto de la inflación sobre el crecimiento económico (prior ℙMj binomial)a
| Estimadoresb | Probabilidad | |||
|---|---|---|---|---|
| g-prior | ψ1 | ψ2 | ψ1+ψ2 | de inclusiónc |
| 1/k2 | 0,0149 | −0,0285 | −0,0136 | 0,6725 |
| (0,0220) | (0,0249) | |||
| 1/n | 0,1054 | −0,2445 | −0,1390 | 0,7254 |
| (0,2376) | (0,2692) | |||
| 1 | −0,0433 | −0,4159 | −0,4591 | 0,8621 |
| (0,6028) | (0,6704) | |||
Entre paréntesis debajo de cada estimador: errores estándar calculados como la raíz cuadrada de la varianza entre modelos
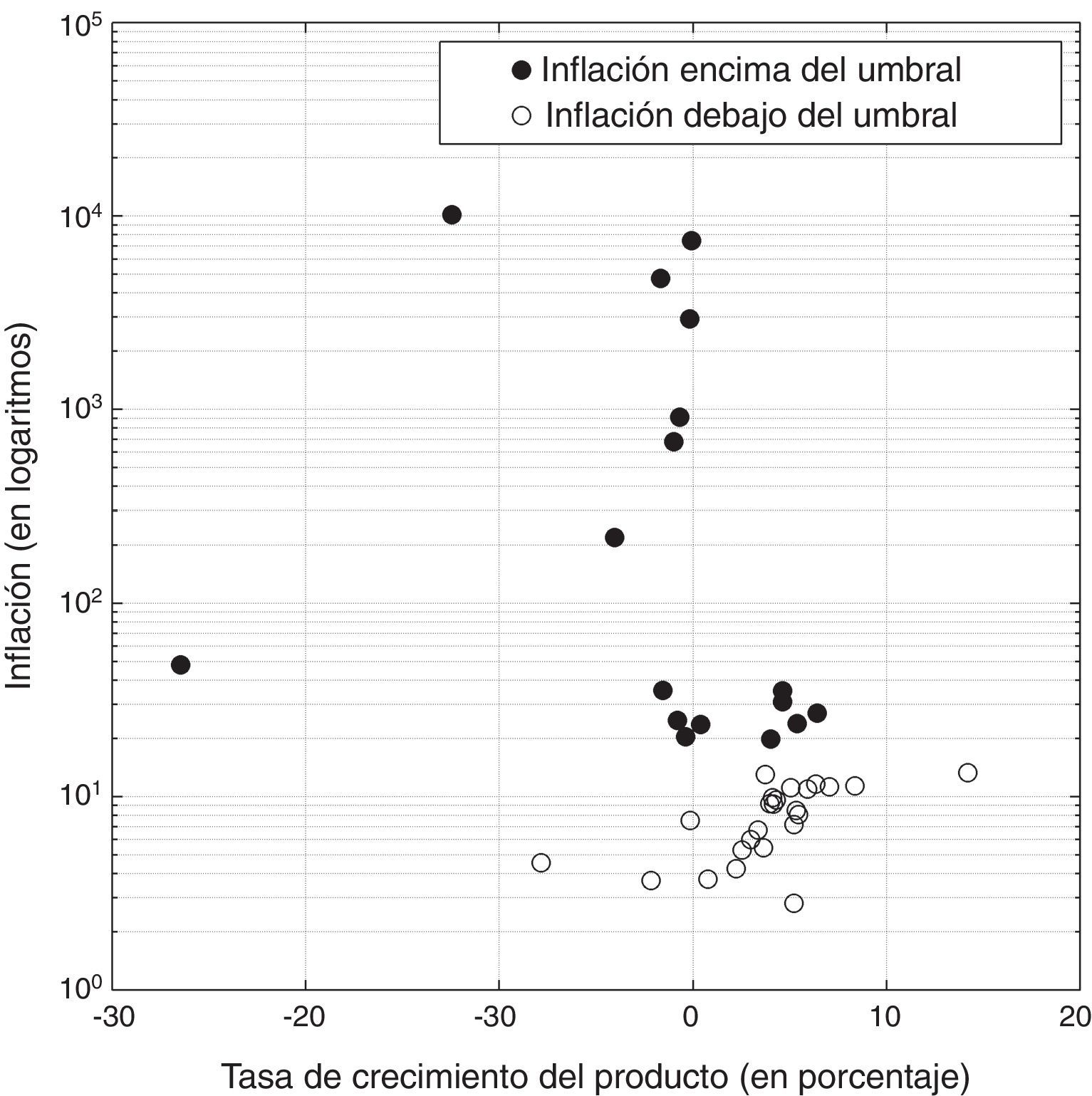
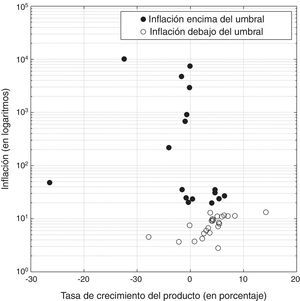
Para ilustrar estos efectos, la figura 3 muestra la relación entre la inflación y el producto, dividiendo las observaciones entre aquellas que estuvieron históricamente por encima y por debajo del umbral. La fuerte relación inversa entre el producto y la variación general de precios en Nicaragua es evidente cuando la inflación está por encima del umbral (•), pero en cambio si la inflación está debajo del umbral (○), la relación producto-inflación se observa ligeramente positiva, aunque posiblemente no estadísticamente significativa, como sugieren los resultados numéricos de la estimación bayesiana.
Diagrama cruzado - Crecimiento del producto e inflación en Nicaragua, considerando la estimación del umbral. Las observaciones de la inflación encima del umbral tienen una clara relación negativa con el producto; debajo del umbral, la inflación y el producto parecen tener una relación nula o ligeramente positiva
Se propuso un estimador bayesiano del umbral de inflación. El estimador se utilizó para estimar el umbral por encima del cual la inflación es perjudicial para el crecimiento económico de Nicaragua. La estimación se obtuvo con más de 24 mil regresiones, y por tanto no es condicional a un sólo modelo particular, como en estudios tradicionales8. Las estimaciones bayesianas indican que una inflación mayor del 14% sería perjudicial para el crecimiento en Nicaragua, mientras que si la inflación está debajo de este umbral, la relación de la variación de los precios con el producto podría ser ligeramente positiva o nula. Este resultado confluye con las teorías económicas de e.g. Choi et al. (1996), Azariadis and Smith (1996) o Gillman and Kejak (2005), y es congruente con la evidencia empírica de inter aliaBarro (1995), Bruno and Easterly (1998), De Gregorio (1992), Faria and Carneiro (2001), Dabus and Viego (2003) o Bittencourt (2012), quienes encontraron que solo cuando la inflación supera un cierto umbral existe una relación negativa y significativa entre la inflación y el crecimiento económico. El hecho de que el umbral de inflación en Nicaragua sea alto concuerda también con investigaciones que estimaron un umbral de inflación más alto para países en vías de desarrollo respecto a países desarrollados, e.g. Khan and Senhadji (2001), David et al. (2005), Pollin and Zhu (2006), Trupkin and Ibarra (2011) o Kremer et al. (2011). Khan and Senhadji (2001) conjeturan que el motivo de esta diferencia es que la larga historia inflacionaria o hiperinflacionaria de los países en desarrollo los llevó a adoptar sistemas de indexación que atenúan los efectos adversos de la inflación; por tanto, siendo que no se producen grandes cambios en los precios relativos, se requiere un mayor nivel de inflación para reducir el contenido de información de las señales de precios y distorsionar el uso eficiente de recursos, perjudicando el crecimiento (Agénor & Montiel, 2008). Las estimaciones de la magnitud del efecto de la inflación sobre el crecimiento muestran que si la tasa de inflación en Nicaragua se duplica por encima del umbral, el producto se contraería en 1,7% o en 2%, un efecto contundente y similar al obtenido por Sarel (1996) con un panel de 87 países. Debajo del umbral, se encontró una relación entre inflación y crecimiento estadísticamente no significativa, mostrando que debajo del umbral pueden reducirse los costos del fomento al crecimiento económico con políticas de control inflacionario, ya que estas son más fáciles de implementar que aquellas que promueven la inversión en capital humano o el desarrollo de nuevas tecnologías (Hineline, 2007). Finalmente, cualquier aumento en las metas de inflación puntuales o interválicas —para dar más espacio a la política monetaria, como se ha sugerido después de la reciente crisis económica y financiera internacional —debería tener como cota superior el umbral de inflación, ya que encima de este umbral la inflación comienza a perjudicar al crecimiento económico. Para la Banca Central en Nicaragua, es imperativo mantener metas de inflación puntuales e interválicas debajo del 14%.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
El autor agradece el apoyo de Sergio Gottret en la elaboración de la versión final del documento. Los comentarios de Julián Andrés Parra y 2 revisores anónimos fueron extremadamente útiles para aclarar y mejorar el enfoque de la investigación. Cualquier error remanente es responsabilidad del autor.
Sea n el tamaño de la muestra (el número de datos). El conjunto de datos está compuesto por el vector con datos de crecimiento económico, y=y1,…,yn, y las k-variables que explicarían el crecimiento económico, contenidas en una matriz n×(k+1),
En el modelo de regresión lineal gaussiano ordinario,y por tanto,El vector de parámetros β=β0β1⋯βk puede estimarse con máxima verosimilitud. Asúmase que X es de rango completo (rank(X)=k+1) para evitar problemas de identificabilidad (i.e. no existe multicolinealidad perfecta entre las variables explicativas potenciales). La verosimilitud del modelo de regresión lineal gaussiano ordinario es
y el estimador máximo verosímil de β es,que resulta también de la solución al problema de minimización de mínimos cuadrados,por lo que el estimador máximo verosímil coincide (en este caso) con el estimador de mínimos cuadrados ordinarios. El estimador insesgado clásico de σ2 es,dado s2=y−XβTy−Xβ. La expresión σˆ2XTX−1 aproxima la matriz varianza-covarianza del estimador clásico (frecuentista) βˆ.La forma gaussiana/gamma inversa de la función verosimilitud basada en los estimadores clásicos,
sugiere que un conjugado natural gaussiano para β y un conjugado gamma inversa para σ2 pueden utilizarse para obtener estimadores bayesianos. La distribución prior de β seráen la que M es una matriz positiva definida simétrica de dimensiones (k+1)×(k+1). El prior de σ2 seráLa distribución posterior de los estimadores seráyLos estimadores bayesianos de β y σ2, asumiendo pérdida cuadrática, serán las medias posteriores de ℙβ|σ2,y,X y ℙσ2|y,X. Estos estimadores pueden calcularse analíticamente; serán iguales a,
y (para n≥2),La elección de los valores que se asignan a los hiperparámetros a,b,β˜ y M es importante porque afecta el valor de los estimadores bayesianos. Para reducir el efecto subjetivo de esta elección, Zellner (1986) sugirió utilizar g-priors informativos que se fundamentan en emplear un prior (condicional) gaussiano para β,
y un prior impropio de Jeffrey, ℙσ2|X∝σ−2, para σ2. La elicitación se restringe por tanto a la elección de valores de β˜ y la constante g, que da nombre a este tipo de priors. Con los g-priors de Zellner, la distribución de probabilidad posterior conjunta de los estimadores se simplifica acon las distribuciones marginales,por lo que los estimadores bayesianos serán,y el estimador bayesiano de la matriz varianza-covarianza es,Véase Marin and Robert (2007).El escalar g es una medida de la cantidad de información prior respecto a la muestra. Feldkircher and Zeugner (2009) mostraron que los resultados son sensibles a la elección de g, ya que el valor de g determina cómo la masa posterior se distribuye entre modelos: si se asignan valores grandes a g, la masa se concentra en pocos modelos —el llamado efecto de supermodelo por Feldkircher and Zeugner (2009)—, mientras que valores más pequeños asignan una masa de probabilidad posterior más uniformemente, sin considerar el tamaño del modelo o su penalidad. Por tanto, si existe un solo modelo «verdadero», este se recupera asintóticamente asignando valores grandes a g.
En la literatura, se han sugerido varias formas de calcular el escalar g. Fernández, Ley, and Steel (2001) por ejemplo recomendaron que g sea igual a g=(max(n,k2))−1. Existen sin embargo otras opciones comúnmente utilizadas para elegir g:
- g=1/n
Este prior implica asignar la misma cantidad de información al prior condicional de β que la contenida en una sola observación, por lo que es similar a los priors uip (unit information priors) de Kass and Wasserman (1995), pero con una media igual a cero en lugar del estimador máximo verosimil. Eicher et al. (2011) mostraron que los priors uip tienden a ser superiores a otro tipo de priors, sin embargo Ley and Steel (2009) en un estudio sobre los efectos de los priors en el análisis BMA aplicado al crecimiento económico, recomendaron no utilizar g=1/n, ya que implica asignar una penalidad bastante pequeña a los modelos, y como resultado existirán varios modelos relativamente no importantes.
- g=1/n
En este caso hay una menor penalidad asintótica para los modelos grandes (i.e. aquellos con varios regresores).
- g=1/k2
Este prior es sugerido por el criterio de inflación de riesgo de Foster and George (1994) y George and Foster (1997). Foster and George (1994) mostraron que este criterio es superior al criterio de Akaike (1974) y de Schwarz (1978) si los regresores son ortogonales. Ley and Steel (2009) recomendaron emplear este prior si existen un gran número de regresores y pocas observaciones.
- g=1
Es equivalente a poner la misma cantidad de información en el prior que en la muestra, en este caso, por ejemplo, el estimador,
es el promedio entre el prior medio y el estimador máximo verosímil; véase Marin and Robert (2007).
Siendo que en modelos de crecimiento económico normalmente se tiene que k2≫n, los priors de referencia serán siempre g=1/k2 si se sigue la recomendación de Fernández et al. (2001). Empero, probar con diferentes valores de g permite analizar la sensibilidad de los resultados a la elección de este escalar.
Los modelos no-lineales de umbral fueron originalmente propuestos por Quandt (1958), aunque fueron popularizados por inter aliaTong and Lim (1980) o más recientemente Tong (2010). Un tratamiento bayesiano de estos modelos puede verse en Oleg (2009).
Sea τ el valor del umbral de inflación por encima del cual la inflación π tiene un efecto sobre el crecimiento económico. Si se permite que el efecto de la inflación sea continuo mediante la variable de spread respecto al umbral πs=ln(π)−ln(τ), la relación no-lineal de umbral entre la inflación y el crecimiento puede capturarse con una matriz,
en la que 1π>τ es un vector indicador con valores iguales a uno cuando la inflación es mayor al umbral τ y cero en otros casos. Si se incluye una matriz de variables de control C que contiene otras potenciales variables explicativas del crecimiento económico, el modelo de regresión gaussiano resultacon,En el vector ψ=ψ1ψ2, ψ1 mide el efecto de la inflación sobre el crecimiento económico cuando la inflación es igual o está debajo de un τ porcentaje, mientras que ψ2 mide el efecto de la inflación sobre el crecimiento económico cuando la inflación está por encima del umbral τ. El vector ϕτ son los parámetros que miden el efecto de otras variables (de control) que podrían también afectar al crecimiento económico.Si X(τ)=[Π(τ)C] resume los datos de los regresores en una sola matriz, y β(τ)=[ψϕτ] resume los parámetros asociados a los regresores en un solo vector, el anterior modelo no-lineal puede expresarse como
con,que para un valor conocido de τ es igual al modelo de regresión lineal gaussiano descrito previamente, por lo que los estimadores bayesianos de los parámetros y la matriz varianza-covarianza de los parámetros, empleando g-priors informativos de Zellner son simplementeEn los modelos lineales se tiene,
integrando en σ2 con el prior ℙ(σ2)=1/σ2 (con g-priors informativos de Zellner), se obtiene la función de verosimilitud marginal para modelos lineales,En el caso de modelos no-lineales, para un valor dado de τ, la verosimilitud marginal puede ser calculada de manera estándar,ya que βτ|στ2,Xτ∼Nk+1β˜τ,gστ2XτTXτ−1, la transformación lineal de βτ satisface,lo que implica que,integrando en σ2 con ℙ(σ2)=1/σ2, nuevamente con g-priors de Zellner, se obtiene la función de verosimilitud marginal para los modelos no-lineales,Dadas k-variables potencialmente explicativas del crecimiento x1, …, xk, el espacio de todos los posibles modelos lineales que se pueden estimar con estas variables está definido por el conjunto potencia ℘k,
es decir que se puede estimar un modelo sin ninguna variable explicativa (el conjunto vació ∅, que corresponde a un modelo solo con intercepto), modelos con solo una variable explicativa, modelos con combinaciones de 2 o más variables explicativas o un modelo con todas las variables explicativas. El número total de modelos lineales a estimar queda definido por la cardinalidad del conjunto potencia,siendo kp el coeficiente binominal, kp=k!p!(k−p)!.En el caso de modelos no-lineales los estimadores dependen de un valor específico del umbral de inflación τ, por lo que si existen m-posibles valores de τ, τ1, τ2, ..., τm, m∈ℕ, m<n, entonces se tendrán m-posibles modelos que midan el impacto no-lineal de la inflación sobre el crecimiento económico con k−1 covariantes de control (las variables restantes que potencialmente podrían explicar el crecimiento). El número total de modelos no-lineales resulta de multiplicar las posibles combinaciones de estas variables de control por los m-posibles valores del umbral inflacionario τ,
En consecuencia, en el espacio de modelos M,conformado por los 1, 2, ..., K modelos lineales y no-lineales a estimar, el número total de modelos K está dado por la cardinalidad de los modelos lineales y la cardinalidad de los modelos no-lineales de crecimiento económico,La incertidumbre acerca de cuál o cuáles variables son realmente importantes para explicar el crecimiento económico es equivalente a conocer cuáles de los K-posibles modelos que incluyen estas variables son apropiados para explicar el crecimiento dentro de todos los posibles modelos del espacio M.
Con un enfoque bayesiano, lidiar con esta incertidumbre implica en principio asignar a priori una probabilidad ℙMj de que cada modelo sea correcto,
Sea D el conjunto de datos conformado por la información del crecimiento económico y las variables potencialmente explicativas de este crecimiento. La probabilidad posterior de que un modelo sea el correcto, una vez observados los datos (i.e., la probabilidad condicional a D), será,donde LD|Mj es la verosimilitud marginal de que cada modelo sea apropiado. En este estudio, la función de verosimilitud marginal de cada modelo será igual aSi se considera que todos los modelos son igualmente válidos, entonces ℙMj=12K y la probabilidad posterior de que un modelo sea el correcto,es simplemente la proporción de verosimilitud de cada modelo respecto a todos los modelos estimados. No existe empero una restricción de cómo elegir la probabilidad ℙMj de que cada modelo sea correcto.Sea Mj el modelo con 0≤kj≤K regresores. Las probabilidades prior de cada modelo se especifican comúnmente como (Ley & Steel, 2009)
asumiendo que cada regresor ingresa en un modelo independientemente de otros con probabilidad ζ. Raftery et al. (1997) y Fernandez et al. (2001) escogen ζ = 0,5, lo que implica que el tamaño esperado de modelos será igual a K/2 y se asigna a todos los modelos la misma probabilidad a priori de ser correctos, ℙMj=2−K,Esto implica asignar una probabilidad de 1/2 de que cada regresor pertenezca al modelo explicativo del crecimiento y establecer una probabilidad 1/m de que τ tome un valor igual a la inflación π(r), con r=1, 2, ..., m y siendo m menor al número de datos n. En el caso de modelos no-lineales de umbral, parece más prudente utilizar un prior que asigne mayor masa de probabilidad a valores del umbral que se encuentren cerca de la tendencia central histórica de la inflación, ya que para que el umbral tenga un uso práctico, la serie tiene de hecho que cruzar este umbral (Enders, 2009). Puede permitirse por ejemplo que ℙMj siga una distribución binomial ℙMj∼B(m,r), con función de masa de probabilidad f(π(r);m, r),
Sea Θ∈ℝK el espacio paramétrico y θ∈Θ un parámetro de interés dentro de este espacio (como e.g. el parámetro que mide el efecto de cualquier variable potencialmente explicativa del crecimiento económico). Si Aθ denota al subconjunto del espacio de modelos (Aθ⊂M) en los que aparece θ, entonces la probabilidad de que una variable explique el crecimiento económico puede calcularse agregando las probabilidades posterior ℙMj|D de los modelos en los que está incluida la variable asociada a θ,
El estimador BMA de θ se obtiene sumando los estimadores calculados en cada modelo, ponderados por la probabilidad posterior de que cada modelo sea el correcto,La varianza total de θ es (Brock & Durlauf, 2001),que resulta de agregar la varianza dentro de cada modelo (whitin-variance, el primer término de la anterior ecuación) y la varianza entre modelos (el segundo término de la anterior ecuación), ponderadas por la probabilidad posterior asociada a cada modelo.La estrategia frecuentista para encontrar el valor del umbral τ es realizar una búsqueda de grilla que implica estimar h-modelos con valores de τ desde 1 a h y calcular el estimador concentrado,
en el que Sh(τ) es la suma de residuos al cuadrado de cada h-modelo y Γn=Γ∩q1,...,qh es el espacio de búsqueda, que resulta de la intersección del conjunto cerrado [τ_,τ¯]=Γ que contiene el mínimo y el máximo valor de τ en el que se realiza la búsqueda, y los q1, ..., qh cuantiles de la muestra disponible. Véase inter aliaChan (1993), Hansen (1997), Hansen (2000) o Gonzalo and Pitarakis (2002).La estrategia bayesiana para estimar el valor de τ es similar en principio al procedimiento frecuentista, pero el estimador no resulta de elegir aquel que minimiza los residuos del modelo sino de considerar todos los posibles valores de τ ponderados por la probabilidad de que sean correctos. Sean π(1), π(2), ..., π(m) los valores ordenados de menor a mayor de la inflación histórica observada, de forma que π(1)⩽π(2)⩽⋯⩽π(m). Enders (2009) considera que para que el valor del umbral tenga significado es necesario que se encuentre entre el valor mínimo y máximo de los datos históricos observados, por lo que el valor del umbral τ puede escogerse entre los valores de la inflación histórica, excluyendo las tasas más bajas y más altas para asegurar que exista un número adecuado de observaciones a cada lado del umbral (m<n). Un estimador bayesiano del umbral τ se obtiene ponderando cada posible valor de τ por la probabilidad posterior de que el modelo en el que τ toma un valor específico sea correcto,
siendo Aτ el subconjunto de aquellos modelos en los que aparece el umbral τ; véase inter aliaLubrano (1998), Koop and Potter (2003), Koop, Poirier, and Tobias (2007) u Oleg (2009).Para Williams (2009) una inflación promedio más alta, y por tanto tasas de interés nominales iniciales más altas, habrían hecho posible un mayor recorte de las tasas de interés, y de ese modo se habría reducido la caída del producto y el deterioro de la posiciones fiscales durante la crisis internacional. Blanchard et al. (2010) y Walsh (2011) tienen una posición similar y discuten los beneficios de aumentar la meta de inflación. Una posición contraria, puede encontrarse inter alia en Bean, Paustian, Penalver, and Taylor (2010) o Issing (2011).
En una posición contraria, Ascari and Sbordone (2013) arguyeron sin embargo que elevar la meta de inflación provoca mayor volatilidad e inestabilidad en la economía, además de desestabilizar las expectativas de inflación, requiriendo una intervención más agresiva por parte de la autoridad monetaria para estabilizar los precios. Véase también Coibion, Gorodnichenko, and Wieland (2012) para un argumento en contra del incremento de la meta de inflación como medio para reducir los costos del límite inferior cero.
Siguiendo los trabajos seminales de Kormendi and Meguire (1985), Grier and Tullock (1989) y Barro (1991), las investigaciones clásicas que buscan obtener evidencia empírica acerca de la relación que tienen las variables mostradas por la teoría económica con el crecimiento corren una regresión del crecimiento económico contra una o varias variables potencialmente explicativas del crecimiento, escogiendo finalmente el modelo que al investigador le parece más apropiado. En lugar de escoger un solo modelo, BMA implica estimar todas las posibles combinaciones de modelos y promediar los resultados de acuerdo a la probabilidad de que cada modelo sea el correcto. Debido a esta superioridad de los métodos bayesianos, BMA es una de las técnicas más empleadas en el análisis del crecimiento económico: fue utilizada por, inter alia, Fernandez, Ley, and Steel (2001), Brock and Durlauf (2001), Sala-i-Martin et al. (2004), Leon-Gonzalez and Montolio (2004), Masanjala and Papageorgiou (2008), Crespo-Cuaresma and Doppelhofer (2007), Ley and Steel (2007), Moral-Benito (2010), Eicher, Papageorgiou, and Raftery (2011), y Salimans (2012) para identificar apropiadamente los determinantes del crecimiento económico. Existen también técnicas frecuentistas para promediar modelos, como e.g. Weighted Average Least Squares (WALS) o Frequentist Model Averaging (FMA). Amini and Parmeter (2012) compararon los métodos BMA con las técnicas frecuentistas WALS de Magnus, Powell, and Prüfer (2010) y FMA sugerida por Hansen (2007), y concluyen que BMA tiene una característica superior sobre WALS y FMA: BMA permite obtener las probabilidades de inclusión de las variables potencialmente explicativas del crecimiento económico. Para una explicación más técnica de BMA y el problema de elección de variables explicativas en una regresión, véase inter aliaLeamer (1978), Raftery, Hoeting, and Madigan (1997), Hoeting, Madigan, Raftery, and Volinsky (1999), George (1999), Wasserman (2000), Cotteleer (2009), Eicher et al. (2011), Magnus et al. (2010) o Zhou, Liu, and Dannenberg (2012).
No parece coherente incluir valores de inflación extrema como los que se observan durante periodos de hiperinflación, ya que en periodos de hiperinflación la reducción de los precios es el objetivo primordial de la autoridad monetaria y al conseguir esta reducción se evita el impacto que causa la distorsión de precios sobre el sector real. Con valores de inflación bajos, como los observados durante contracciones económicas, el impulso al producto se vuelve paulatinamente más relevante que el control de precios. Fuera de estas situaciones extremas en las colas de la distribución, casos intermedios en los que la inflación de umbral se encuentra cerca de la tendencia central serán de utilidad práctica para el manejo cotidiano de la política monetaria con objetivos múltiples ya que, de forma análoga a los sistemas de alerta temprana, el umbral de inflación es un valor de alerta que permite a la autoridad monetaria tomar decisiones de política oportunamente, antes de que la inflación supere el umbral.
Fischer (1993) sugirió que los términos de intercambio estimulan tanto el producto como los precios, por lo que si se omite de las regresiones del producto contra la inflación, el costo que implica la inflación al producto estará sesgado hacia abajo; pero si los términos de intercambio aumentan por una caída de los precios de importación, en lugar de un aumento de los precios de exportación, se revertirá la dirección del sesgo porque los términos de intercambio estimularán el producto pero reducirán los precios.
Khan and Senhadji (2001) proveen además una justificación económica para relacionar el crecimiento económico a los logaritmos de la inflación, en lugar de a la inflación en niveles: en niveles, los choques inflacionarios serían aditivos y tendrían efectos idénticos en el crecimiento durante momentos de alta y baja inflación, mientras que la transformación logarítmica es más plausible porque asume que los choques son multiplicativos; es decir, se requiere que la inflación se duplique para tener efectos similares sobre el crecimiento, tanto en periodos de baja como de alta inflación. Por ejemplo, sin la transformación logarítmica, un aumento del 1% de la inflación tiene el mismo efecto sobre el crecimiento cuando la inflación es del 10% que cuando es del 100%.
La estimación de los 24.576 modelos tardó aproximadamente 20 min en un ordenador Dell Optiplex con un procesador Intel Core i5-2500 de 3.30GHz y memoria RAM de 4 GB, usando la versión R2012a (7.14.0.739) de MatLab para un sistema operativo de 64 bits.
El análisis tradicional está basado en valores de probabilidad exactos (p-values) de estimadores calculados con un solo modelo de regresión. La interpretación de estos p-values es cuestionable y poco confiable debido (i) a la gran cantidad de posibles modelos explicativos de crecimiento, (ii) a que los p-values no proporcionan probabilidades para las hipótesis (aunque lo aparenten) y (iii) a que los valores p no son suficientemente informativos para analizar la compleja evidencia sobre el fenómeno del crecimiento y su relación no-lineal con la inflación, ya que solo proveen una respuesta binaria al problema de identificar la importancia de una variable: aceptar o rechazar que sea significativa. Críticas más severas al uso de p-values para evaluar la significación estadística de una variable pueden encontrarse en Goodman (1999) y Hubbard and Lindsay (2008). Con BMA en cambio, se obtiene la probabilidad de que una variable sea determinante para el crecimiento económico calculando todas las posibles combinaciones de la variable con otras covariantes. Además, a diferencia de los métodos econométricos clásicos, que son asintóticos y requieren grandes muestras, los métodos bayesianos son igual de válidos con muestras grandes o muestras pequeñas (muestras finitas), ya que, como indicó Sims (2007), la inferencia bayesiana con muestras finitas es aproximádamente correcta si los supuestos paramétricos son aproximádamente correctos. Véase el sugestivo artículo de Sims (2007), Bayesian methods in applied econometrics, or why econometrics should always and everywhere be bayesian, disponible en http://sims.princeton.edu/yftp/EmetSoc607/AppliedBayes.pdf.