Morphologic analysis of the temporal change of forest cover

Resumen

En este trabajo se presenta un análisis morfológico de cobertura forestal en un lapso de doce años. Se emplearon dos imágenes multiespectrales LANDSAT TM-4 de los años 1989 y 2001. Estas imágenes cubren un área forestal donde han ocurrido cambios significativos en tales años. Estas imágenes fueron expandidas en términos de variables canónicas que describen la respuesta espacialespectral de las masas forestales. Las imágenes fueron modeladas como un campo vectorial de tantas dimensiones como bandas empleadas en el análisis. Se construyó un campo vectorial usando las bandas de variables canónicas.El conjunto de variables canónicas fue usado para cuantificar el cambio vectorial de las masas forestales. Este cambio vectorial cuantifica el grado de alteración de las masas forestales. Se empleó un algoritmo de crecimiento de regiones para segmentar las áreas ocupadas por el bosque. Este algoritmo emplea como entrada las variables canónicas. El resultado de tal segmentación es una imagen binaria llamada el bitmap. A partir de este bitmap, se llevó a cabo un análisis morfológico del área ocupada por el bosque. Se empleó un DEM generado a partir de un par interferométrico del satélite RADARSAT-1 para realizar una referencia cruzada con los bitmaps. Esta referencia cruzada conduce a la determinación de las elevaciones a las cuales ocurren los cambios de las masas forestales.

Abstract

A morphologic analysis of forest cover in a time span of twelve years is presented in this work. Two multispectral LANDSAT TM-4 images of the years 1989 and 2001 were used. These images cover a forest area where significant changes have occurred in such years. These images were expanded in terms of canonical-expansion variables that describe the spatial-spectral response of the forest masses. The images were modeled as a vector field of as many dimensions as the number of bands employed in the analysis. A vector field was constructed using canonical-variable bands. The set of canonical variables for each year was used to quantify a vector change of the forest masses. This vector change quantifies the degree of alteration of the forest masses. A region-growth algorithm was used to segment the areas occupied by the forest. This algorithm uses as input the canonical variables. The result of such segmentation is a binary image named the bitmap. From this bitmap, a morphologic analysis of the area occupied by the forest was undertaken. A DEM generated from a radar interferometric pair of the RADARSAT 1 satellite, was used to perform a cross-reference with the bitmaps. This cross-reference leads to the derivation of the elevation of occurrence of changes in the forest masses.

Introduction

The analysis of vector change is used in this work to quantify the change of forest cover in the environs of Mexico City. The vector change is combined with morphologic analysis to derive quantitative evolution of the forest cover. A number of methods of vector change have been published in the literature (Allen and Kupfer, 2000; Fraser et al., 2005; Nackaerts et al., 2005; Sanchez Flores and Yool, 2007).

A number of change indices have been used to quantify change of temporal phenomena such as deforestation, desertification, urban growth or land cover change (Johnson and Kasischke, 1998; Le Hégarat-Mascle and Seltz, 2004; Cakir et al, 2006). A detailed account of change detection methods is given in Coppin et al. (2004). Several methods of change detection in remote sensing are given in Canty (2007). Recent advances in tropical forest cover used parametric classification and change vector analysis to detect unchanged and changed areas in the tropical forest of Amazonia (Raši et al., 2013).

In the present work, a multispectral image is modeled as a vector field of as many dimensions as bands employed in the analysis (Lira and Rodriguez, 2006; Lira, 2010). In this model, a pixel is defined as a vector of an equal number of elements as the number of bands. Two LANDSAT TM-4 images are used in this model to obtain the change of forest cover in a time span of twelve years. A co-registration of the images was applied in order to implement our method and to evaluate the forest cover change in the time span.

In the present research, the vector change that experiences the vector field associated to the image was considered (Lambin and Strahler, 1994; Warner, 2005; Sanchez and Yool, 2007; Kontoes, 2008). A set of variables were calculated from a canonical-expansion of the image (Lira and Garcia, 2003). This expansion produces three basic canonical variables that characterize the spatial-spectral state of the forest cover. The use of variables to study land cover change, as a basis for change vector analysis, has been proposed (Lambin and Strahler, 1994; Lambin and Ehrlich, 1997). The original Landsat bands define a 6-dimensional vector field. Instead, the canonical variables define a 3-dimensional vector field.

The set of variables were used in a region-growth algorithm to segment the forest cover. This segmentation produced a two-class image named the bitmap. The bitmap depicts the area of the forest cover and the rest of the image. From the bitmaps of the images, morphologic change was evaluated. A digital elevation model (DEM) was constructed using an interferometric pair of the RADARSAT 1 satellite. The DEM was combined with the bitmaps to derive conclusions on morphologic change of forest cover.

In the present work, one vector field was considered: the vector field formed by the canonical variables. Principal component analysis (PCA) was applied to the set of variables of both images. From PCA, changes of the vector field were assessed. The analysis of vector change based on PCA is used there upon and conclusions on the forest cover change were derived. In the ensuing section of methods, details are provided on the vector field analysis.

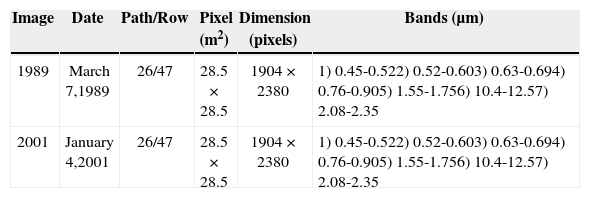
Materials and methods

Materials

Two multi-spectral LANDSAT TM-4 images are used in this research. From these images, an area was extracted; the resulting sub-images are dubbed 1989 and 2001. Figure 1 depicts a false color composite of the images of 1989 and 2001. Table 1 shows basic technical details of these images. With the exception of band 6, all the bands of the images were used in our research analysis. Band 6 is not included in the analysis due to a different pixel size.

Figure 1.

RGB = [7,4,1] of the images of 1989 (a) and 2001 (b).

Table 1.

Basic technical details of multi-spectral Landsat TM-4 images.

Image	Date	Path/Row	Pixel (m^2)	Dimension (pixels)	Bands (μm)
1989	March 7,1989	26/47	28.5 × 28.5	1904 × 2380	1) 0.45-0.522) 0.52-0.603) 0.63-0.694) 0.76-0.905) 1.55-1.756) 10.4-12.57) 2.08-2.35
2001	January 4,2001	26/47	28.5 × 28.5	1904 × 2380	1) 0.45-0.522) 0.52-0.603) 0.63-0.694) 0.76-0.905) 1.55-1.756) 10.4-12.57) 2.08-2.35

These images cover an area located to the east of Mexico City where a forest mass surrounds two volcanoes. This forest mass is formed by a mixture of coniferous trees, namely pine, oyamel and cedar (Hernandez García and Granados Sánchez, 2006). From March 1989 to January 2001, this forest mass has experienced a change in extension, morphology and heterogeneity (Rzedowski and Rzedowski. 2005; Hernandez García and Granados Sánchez, 2006). This forest masses will be referred in this research as forest cover. In addition to the LANDSAT TM-4 images, an interferometric pair from the RADARSAT 1 satellite was considered (Table 2). From this interferometric pair, a digital elevation model (DEM) was extracted.

Table 2.

Basic technical details of interferometric RADARSAT 1 images.

Image 1	Image 2	Pixel (m^2)	Size (km^2)	Looks	Band
May 19, 1998	July 6, 1998	24 × 24	144.74 × 226.89	4	C(5.6 cm)

The LANDSAT TM-4 images were geometrically corrected and corregistered using the ephemerides of the orbit. On the generation of the DEM from the RADARSAT 1, ground control points were used to corregister the interferometric pair. In this sense, the DEM produced by the interferometric pair was corregistered with the LANDSAT TM-4 images. Both, the LANDSAT TM-4 images and the DEM were resampled to have the same pixel dimension of 28.5 × 28.5 m².

Methods

In order to quantify the temporal change of the forest cover, two multi-spectral images were considered. On the grounds of these images, a model to characterize the spatial-spectral state of the forest cover was defined. The model was defined by means of a set of variables. Using the model, a segmentation of the area covered by the forest cover was undertaken. The segmentation based on this model results in a binary image dubbed the bitmap as explained in section 2.2.3. The validity of the model was assessed on the grounds of a multivalued probabilistic logic combination of the variables that define the model as explained in section 3.3. The bitmap was used to derive morphologic parameters that quantify the temporal change of the forest mass (Section 3.4). A method of vector change by means of the principal component analysis was considered to quantify the degree of forest cover change (Section 2.2.4). Details of the above rationale follow (Figure 2).

Figure 2.

Workflow of the methodology of analysis.

The selected variables that describe the spatial-spectral behavior of the forest cover are Reflectance of vegetation, Texture and the Greenness band of the Kauth and Thomas transformation. These variables define the spatial-spectral state of the forest cover. The texture determines the spatial roughness of vegetation, and Reflectance and Greenness establishes the spectral state of vegetation. Details of the calculation of these variables are provided in section 2.2.1. Such variables form a canonical expansion of the image (Lira and Garcia, 2003). In brief, the model is designed as (a) A canonical expansion of the multispectral image, (b) A set of variables to describe the spatial and spectral behavior of the forest cover and (c) To define a vector field of three dimensions from which vector change can be assessed.

A segmentation of forest cover was achieved using the variables as input to a hierarchical region-growth algorithm RHSEG (http://techtransfer.gsfc.nasa.gov/RHSEG). The result is a segmented image with a certain number of regions (Tilton et al., 2006). Details of this segmentation are provided in section 2.2.3.

RHSEG stands for Recursive Hierarchical Segmentation. This algorithm establishes a segmentation hierarchy where an image is segmented at different levels of detail. Segmentation at coarser levels of detail can be generated from merges of regions at finer levels of detail. In this procedure, an object in the image is represented by multiple image segments in finer level of detail in the segmentation hierarchy. In region-growing, spatially adjacent regions iteratively merge to represent and object with spatial-spectral homogeneity (Tilton et al., 2006).

The morphology of the forest cover was calculated using a group of morphologic parameters. A large number of connected areas dubbed patches form the forest cover. The evaluation of the morphology consists in the calculation of two groups of parameters, a) the number of patches and its area and b) the heterogeneity of the patches. The first group is to assess the extension of the forest cover and the second group is to assess the complexity of the landscape form by the forest cover. The calculation of the two groups of parameters for the images 1989 and 2001, permit the quantification of the evolution of the extension of the forest cover and the change of its heterogeneity. Morphologic parameters were calculated using the Fragstats software (http://www.umass.edu/landeco/research/fragstats/fragstats.html). Details are given in section 3.4.

Since PCA is used to quantify the temporal vector change, no radiometric normalization was required for the variables that define the spatial-spectral model (Canty, 2007, Chapter 8). Details of this are provided in section 2.2.2. Once the images were corregistered, PCA was applied to the vector field formed by the variables of both images. Section 2.2.4 describes such change. Figure 2 depicts the workflow of the methodology above described.

In order to corroborate that the selected variables adequately depicts the state of the forest cover a multivalued probabilistic logic is employed. The variables of the two images are combined by means of multivalued probabilistic logic (Nilson, 1986) to generate an image where the change of the forest cover is described. Section 2.2.5 provides details of such combination.

Canonical expansion

A canonical expansion is a representation of the image in terms of a set of variables with low or null correlation among them (Lira and Garcia, 2003). The variables selected for such expansion were Reflectance, Texture and Greenness of the forest masses. The calculation of these variables was the following. The Greenness is the second band of the Kauth and Thomas transformation of the LANDSAT TM-4 image. The Reflectance of the forest cover is derived using a variant of the principal component analysis (Lira, 2006). In this variant, a set of pixels related only to the forest cover is manually extracted from the image. The covariance matrix of such set is calculated. The set of eigenvectors is obtained from this covariance matrix. These eigenvectors define a kernel of transformation. This kernel is then applied to the whole image. The result is the variant of the principal component analysis related only to the forest cover. The Texture is generated using a divergence operator applied upon the first three principal components of the LANDSAT TM-4 images (Lira and Rodriguez, 2006). These variables represent the spatial-spectral state of the forest masses. Figure 3 shows a false color composite of canonical variables for the images of 1989 and 2001. Let these variables be named as follows: X₁ – Greenness, X₂ – Reflectance and X₃ – Texture. These variables form an expansion of the image in agreement with the following expression

Figure 3.

RGB false color composite of canonical variables for the 1989 (left) and 2001 (right) images.

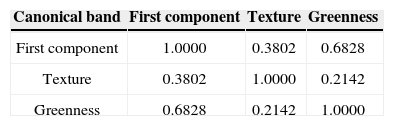
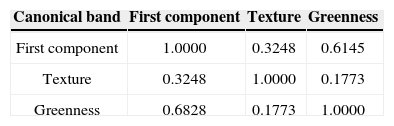
Where (k, l) are the coordinates of a pixel in the image, μ_i is the mean of the image bands and (M, N) are the dimensions of the image. The index i is a band of the image, while j is a dummy index. The coefficients a_ij in this case are set to one. Hence, the image g is expressed as a linear combination of the variables abovementioned. When the correlation between variables X_i is low, expression (1) approximates a canonical expansion of the image (Dougherty 1999). The moderate correlation (Table 3 and 4) among these variables for the images used in this work corroborates that expression (1) is approximately valid as a canonical expansion of the images. A linear histogram expansion was applied to the three variables to have the digital range [0,255]. No units were associated to the variables.

Table 3.

Linear regression between canonical bands of image 1989.

Canonical band	First component	Texture	Greenness
First component	1.0000	0.3802	0.6828
Texture	0.3802	1.0000	0.2142
Greenness	0.6828	0.2142	1.0000

Table 4.

Linear regression between canonical bands of image 2001.

Canonical band	First component	Texture	Greenness
First component	1.0000	0.3248	0.6145
Texture	0.3248	1.0000	0.1773
Greenness	0.6828	0.1773	1.0000

Radiometric normalization and co-registration

Although the same sensor produces the images used in this research, the conditions of illumination and geometry of acquisition are not exactly the same. From one date to the other, the solar illumination is different due to variations in the elevation angle and changes of the azimuth angle of the Sun. Even more, the satellite orbit experiences small fluctuations that lead to a geometry of different observation for the acquisition of the images. Due to this, it is necessary to carry out a co-registration process of the images. The co-registration is made by means of an orthorectification model using the satellite ephemerides applied to each image. The radiometric normalization is not required since the vector change is assessed using the PCA applied upon the ensemble of spectral variables of both images (Canty, 2007, Chapter 8). The combined histogram of the variables for the images of 1989 and 2001 show that a radiometric normalization is achieved (Figure 4). To obtain the combined histogram, an RGB false color composite of the canonical variables was prepared. This RGB is an image of 24-bits depth. Then, a compression of 24-bits to 8-bits was applied. The histogram of the compressed image is the combined histogram. The co-registered bands were used in turn to derive the above-described variables.

Figure 4.

Combined histogram of indicators of image 1989 (a) and image 2001 (b).

Generation of a bitmap

The region-growth algorithm RHSEG was applied to the set of canonical variables abovementioned. This algorithm was applied to each group of variables for the images of 1989 and 2001. The region-growth algorithm generated a segmented image where certain regions are associated with the forest masses. In an iterative process, the regions were grouped until reaching a binary image that represents a thematic map dubbed the bitmap. This iterative process consists in the aggregation of regions related to the forest cover. Regions not associated to the forest cover are grouped into a single class dubbed rest of the image. The identification of regions related to forest cover is done on the grounds of the image obtained by multivalued probabilistic logic (section 2.2.5). The part of the clouds in the image 1989 is entirely over the forest masses; therefore, that cloud-region was integrated into the class forest cover. This procedure was carried out manually.

This bitmap is a binary image with two values or states: 1 − forest cover, and 0 − rest of the image. The bitmap set the grounds for the quantification of the associated morphologic parameters of the forest cover as explained in section 3.4. Figure 5 displays the bitmap of the images of 1989 and 2001. The bitmaps were also used to assess the temporal change of the forest cover as explained in sections 2.2.5, 3.1 and 3.2.

Figure 5.

Bitmap of the images of 1989 (left) and 2001 (right).

Vector change

In a multispectral image g_η(r) of η bands, a pixel is a vector of η elements

Where b_k is the value of the pixel in the k − band. The interval of variation of b_k is 0 ≤ b_k ≤ 2^n-1, where n = 8 in most cases. The set of vectors {r_i} forms the vector field associated to the multispectral image (Lira and Rodriguez, 2006; Lira 2010), represented as

Where the hooks {} indicate the set of vectors associated to an image. Let r_i be the vectors of the vector field of the 1989 image and r_j those of the 2001 image. According to this, two vector fields are considered. The region of the vector field associated to the forest masses experience a change from the year 1989 to 2001. A measurement of such change is required to asses the modification of the forest cover.

The vector change can be measured in several ways: (a) By means of a measurement of similarity between the vectors {r_i} and {r_j} (Sanchez Flores and Yool, 2007; Warner, 2005). (b) Using the principal component analysis of the whole ensemble of bands of the two images (Canty, 2007). (c) Using the principal component analysis of the set of canonical variables of the two images.

The principal component analysis was applied on two sets of bands, namely

(i) Principal component analysis of the ensemble of bands.

The principal component analysis was applied to the ensemble of bands of the images 1989 and 2001. None of the first three components shows valuable details to quantify the change of the forest cover.

(ii) Principal component analysis of the set of canonical variables.

The vector change was measured using the principal component analysis of the ensemble of canonical variables of the images 1989 and 2001. Six canonical variables, three variables from the image of 1989 and three from the image of 2001 determine such ensemble. Therefore, a 3-dimensional vector field is defined for 1989 and a 3-dimensional vector field for 2001. This vector field experiences a change from 1989 to 2001. This vector field change can be measured by the use of principal component analysis applied on the ensemble of 6-canonical variables for 1989 and 2001. The first component carries most of the variance of the vector change from 1989 to 2001. Figure 6 shows the first principal component of the vector change.

Figure 6.

(a) First principal component of vector change. Forest cover alteration is appreciated in bright tones, the brightest, the greater the change. Forest mass appears in medium and dark gray. (b) Amplification of two selected zones from the top left (left) and from the middle (right) of figure 6a.

The regions of the vector field that did not experience a change from 1989 to 2001 have a high degree of similarity. Those that did change have a low similarity. That change is depicted in the first principal component. In figure 6, the values of the measurement of similarity and principal components are standardized at the interval [0, 255], where zero indicate no change and 255 the maximum change. This is translated into an image where forest cover change is gradually appreciated from dark tones to bright tones. Forest cover alteration is appreciated in bright tones, the brightest, the greater the change.

Multivalued probabilistic logic

The canonical expansion produced three variables X_i that characterize the spatial-spectral state of the forest vegetation of the scene. These variables can be combined using multivalued probabilistic logic (Nilsson, 1986) by means of the expression

Where X is the resulting image of such combination. Image X is the probability of occurrence of forest cover.

Equation (4) requires the variables X_i to be considered as probabilities. To accomplish this, it is assumed that the pixel distribution values of the variables X_i are probabilities. In this sense, the higher the value of the pixel in X_i, the higher the probability. The histogram of X_i characterizes such probability distribution. The higher the value of a pixel in X_i the higher the probability of occurrence of a forest cover. Therefore, the multivalued logic allows the corroboration that the selected variables characterize the forest cover properly. Figure 7 shows the multivalued probabilistic logic for the set of variables of the images of 1989 and 2001. The results for the multivalued probabilistic logic are high probability for forest zones (dark tones) and low probability for the rest of image (medium and bright tones). In multivalued probabilistic logic, distinctive probabilities occur for the forest masses and the rest of the image.

Figure 7.

Multivalued probabilistic logic of 1989 (a) and 2001 (b). Forest masses appear in dark gray. Borders from the bitmap of 2001 are overlaid with the probabilistic logic of 2001.

Digital elevation model

An interferometric pair from the RADARSAT 1 satellite was used to generate a digital elevation model (DEM) of the area of study. This interferometric pair was acquired from the Alaskan Satellite Facility by means of an ASF Project Agreement. Table 2 shows basic parameters of this interferometric pair.

The DEM is depicted in figure 8. A cross-reference of this DEM with the bitmaps that depict the forest cover change (Figure 5) permits the estimation of the elevations of the forest masses and an identification of the areas of forest loss. With the cross-reference, forest loss-type may be related to altitude as explained in section 3.5.

Figure 8.

Digital elevation model derived from a RADARSAT 1 interferometric pair. Elevation scale is shown on the left-bottom.

Results

Production of a bitmap

The classification with the region−growth algorithm using the canonical variables produced the bitmap of the years 1989 and 2001. The bitmap was used as the basis to evaluate the morphology of the forest areas (Figure 5 and Table 5). Figure 9 depicts an overlay of the bitmaps of 1989 and 2001. The forest cover change is shown in red. The reduction of forest masses occur in the perimeter and in numerous spots within the forest.

Table 5.

Morphologic parameters of the forest areas.

Image	Patches	Area (m^2)	Density/patches (m^2)	Form/landscape	Perimeter/Area (1/m)
1989	3,691	1,028,905,504	1.0049	53.9582	1.3341
2001	4,002	926,230,606	1.0896	58.8024	1.3267

Figure 9.

Overlay of bitmaps of 1989 (white plus red) and 2001 (white). Change appears in red.

Vector change

Two methods were considered using the principal component analysis applied to the original bands or to the set of variables (section 2.2.4). Best result was obtained with the set of six canonical variables from the images 1989 and 2001. As figure 6 shows, the bright spots that indicate forest change match well with the borders of the bitmap of 2001. In this figure, the perimeter of the forest cover coincides well with the edges produced by the bitmap.

Figure 6 is an overlay of the first principal component of the ensemble of canonical variables with the bitmap of 2001. In this component, forest cover changes are depicted in varying shades of gray. Instead, the bitmap depicts the total forest loss. Therefore, some of the gray shades indicating medium or moderate forest cover change are not marked by the bitmap. These results corroborate that the use of variables, instead of the original bands, is an appropriate model of the spectral response of the forest cover.

Multivalued probabilistic logic

The combination of the variables of forest cover with multivalued probabilistic logic produced an enhancement of the forest zones and an inhibition of the rest of the image. This corroborate that the selected canonical variables are well adapted to characterize the spatial-spectral response of the forest masses (Figure 7). The histogram of the probabilistic image is bimodal with a sharp decrease around digital value of 80. A sharp change in gray shades from forest cover to non-forest occurs in this probabilistic image. The borders coincide well with the multivalued probabilistic logic of image 2001. Therefore, when the borders from the bitmap of 2001 are overlaid with the probabilistic logic of 2001 such sharp changes is identified.

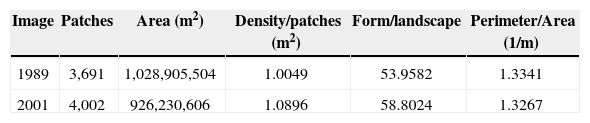
Morphology of forest cover

With the bitmap associated to the segmentations of the forest cover, it is feasible to quantify the morphologic parameters of the forest zones. These morphologic parameters are area, number of patches, density of patches, form of the landscape and fractal dimension. The first three parameters determine the extension of the forest cover. The last two parameters describe the complexity of the forest cover.

Table 5 summarizes the values of these parameters. The area associated to each pixel is 28.5 × 28.5 m² = 812.25 m². The definition and units of these parameters is the following

• •

  Area - Number of pixels of the forest area of the bitmap multiplied by the area associated to the dimension of the pixel. This quantity is expressed in m².

• •

  Patches - Number of connected zones under connectivity 8 that include the forest area. This quantity is dimensionless.

• •

  Density of patches - Number of patches divided by the forest area. This quantity is expressed in m^-2.

• •

  Form of the landscape - Measure of the aggregation or desegregation of patches. As the value of this parameter increases, the patches become increasingly disaggregated. This quantity is dimensionless.

• •

  Perimeter/Area, fractal dimension -Double of the slope of the line of regression of the logarithm of the patch area against the logarithm of the patch perimeter. This quantity is expressed in 1/m.

From the year 1989 to the year 2001, the forest area was reduced by 102,674,898 m² (Table 5). The fragmentation and reduction of the forest areas is the result of illegal cutting, fires and plagues (Aceves Pastrana, 2005).

The values of the morphologic parameters of table 5 prove clearly that the forest area (the landscape) becomes more complex as forest mass is lost. A great number of patches of diverse size form the forest areas depicted in the bitmap; the set of patches is equal to the total area occupied by the forest mass. For a quad-core i7 PC running at 3.4 GHz at 64-bit operating system, the total computing time for the images used in the present investigación is less than 10 minutes.

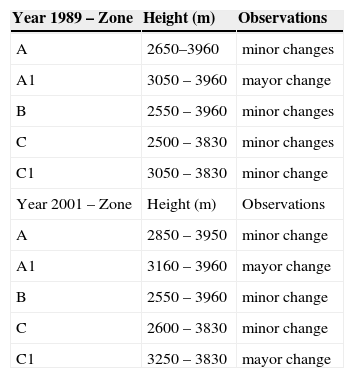
Cross-reference of DEM with forest cover

A cross-reference of DEM with forest cover (bitmap) is shown in figure 10. Table 6 resumes forest changes related to the elevation of the study area. The boxes in figure 10 indicate several zones of major forest change (Table 6).

Figure 10.

Cross-reference of DEM with bitmaps of 1989 (yellow plus red) and 2001 (red). Yellow depict change areas. Boxes show three alteration zones (see table 6).

Table 6.

Modification of forest areas in relation to the elevation.

Year 1989 – Zone	Height (m)	Observations
A	2650–3960	minor changes
A1	3050 – 3960	mayor change
B	2550 – 3960	minor changes
C	2500 – 3830	minor changes
C1	3050 – 3830	minor change
Year 2001 – Zone	Height (m)	Observations
A	2850 – 3950	minor change
A1	3160 – 3960	mayor change
B	2550 – 3960	minor change
C	2600 – 3830	minor change
C1	3250 – 3830	mayor change

As figure 10 shows, minor changes in the forest areas occur in the periphery and in numerous spots inside the forest. Major changes are localized in two zones: to the north and to the southeast in two large gullies. The forest cover of the study area occurs in the environs of two major volcanoes. The elevation variation in this area is from the hills at 2105 meters to the summit of the highest volcano at 5543 meters. The forest cover are present from the hills to an altitude of about 4000 meters. A cross-reference of DEM with the bitmap allows the localization of forest cover in relation to the altitude of the study area. Therefore, on the grounds of this cross-correlation the elevation of forest change occurrences can be identified. Table 6 has three columns. The left column shows five selected areas where forest change occurs. The column on the middle indicates the elevations of that change, and the column on the right the degree of change.

Conclusions

A segmentation of the areas that occupy the forest masses in a zone to the east of the Mexico City generated a binary image dubbed the bitmap. This bitmap was produced using an algorithm of region−growth that employs as input the canonical variables that characterize the state of the spatial-spectral response of the forest masses. From the bitmap, it is possible to obtain the morphologic variables that describe the spatial structure of the forest areas. The associated vector change to the vector fields of the images of two dates in a lapse of twelve years allows the quantification of the degree and location of the change of the forest mass. The use of a DEM obtained from an interferometric pair allows the identification of elevation-related spots where changes in forest cover occur. A search of the social, geographic and physical situation of the forest masses in area of study (Aceves Pastrana, 2005) complement the image analysis developed in this research. From these bases the following conclusions are derived

i). Such fragmentation is heterogeneous, within the forest mass and some edges of the forest area. The density of patches increases since the area is reduced and the number of patches increases (Table 5), this result in an increase of heterogeneity of the landscape formed by the forest cover patches.

ii). The morphologic structure of the areas becomes more complex as the forest area fragments. The form of the landscape (Table 5) gives the measurement of the complexity of the forest area. The value of this parameter increases from 1989 to 2001 indicating that the complexity of the forest cover area has increased.

iii). The forest spots are reduced in a considerable area. The area of the forest cover is reduced by slightly more than 100 km2 (Table 5).

iv). The canonical variables describe better the spatial-spectral state of the forest areas than the original bands. The application of principal component analysis to the ensemble of the 12-bands of the images of 1989 and 2001 did not produce meaningful results. The canonical variables are designed to characterize the spatial (texture) and the spectral (reflectivity and greenness) response of the forest cover.

v). The multivalued probabilistic logic corroborates that the canonical variables provide an adequate description of the forest areas.

vi). The cross-reference with the DEM identified small spots of deforestation at higher altitudes and mayor changes of forest cover at lower altitudes (Table 6).

Acknowledgment

The author thanks Professor J. Tilton for a temporal license of the region-growth software RHSEG. The author thanks the Alaska Satellite Facility for the free-delivery of radar images.