El 2 de febrero del 2021 se publicó en la presente revista un importante artículo que evaluó la asociación estadísticamente significativa (p<0,05) mediante la medida de odds ratio (OR). El estudio estimó una correlación del uso de benzodiacepinas y el sexo femenino (OR=2,5) en 350 pacientes que asistieron a consulta de reumatología1.
Se recomienda la replicación de las investigaciones clínicas basadas en las pruebas de significación para generar una evidencia con mayor credibilidad en el área de la reumatología.
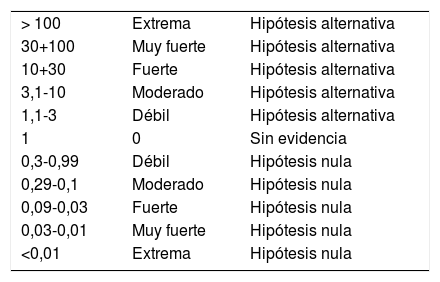
El factor Bayes es el método idóneo para evaluar más allá de la interpretación dicotómica de rechazo o aceptación de la hipótesis nula, pues cuantifica el valor de evidencia o certeza con que los datos respaldan la hipótesis alterna respecto a la hipótesis nula (hipótesis alterna vs. hipótesis nula)2,3. La replicación estadística de hallazgos significativos mediante el factor Bayes permite reforzar la credibilidad práctica de futuros artículos del área de la reumatología (ensayos clínicos, intervenciones y tratamientos, entre otros), que se precisa cuando la inferencia bayesiana reporta una evidencia concluyente (fuerte) o superior (FB10 > 10), a partir del esquema de clasificación de Jeffreys4: débil, moderado, fuerte, muy fuerte y extremo (tabla 1).
Valores de interpretación cuantificable del factor Bayes
| > 100 | Extrema | Hipótesis alternativa |
| 30+100 | Muy fuerte | Hipótesis alternativa |
| 10+30 | Fuerte | Hipótesis alternativa |
| 3,1-10 | Moderado | Hipótesis alternativa |
| 1,1-3 | Débil | Hipótesis alternativa |
| 1 | 0 | Sin evidencia |
| 0,3-0,99 | Débil | Hipótesis nula |
| 0,29-0,1 | Moderado | Hipótesis nula |
| 0,09-0,03 | Fuerte | Hipótesis nula |
| 0,03-0,01 | Muy fuerte | Hipótesis nula |
| <0,01 | Extrema | Hipótesis nula |
Elaboración propia según la escala de clasificación de Jeffreys4.
Esta carta tiene como objetivo reportar 2ejemplos de reanálisis bayesiano con base en el tamaño de la muestra y el valor estadístico de la OR, el cual fue convertido a coeficiente de correlación (r) mediante una calculadora en línea5 que reportó un valor de r=0,245.
El factor Bayes consta de 2interpretaciones: FB10 (a favor de la hipótesis alternativa) y FB01 (a favor de la hipótesis nula) y el intervalo de credibilidad a partir de los datos6.
Los resultados obtenidos mediante el factor Bayes son FB10=3.000 y FB01=0,0003, con intervalo de confianza (IC) de 0,143-0,340 y una evidencia muy fuerte, lo cual respaldó el resultado significativo. Asimismo, se estimaron los parámetros del factor Bayes máximo (máxFB10=48,61; máxFB10=6.133), para determinar la estabilidad de los resultados, cuyos valores de mayor magnitud fortalecen la estimación de la reevaluación bayesiana.
La conversión del tamaño de efecto y otras medidas estadísticas, que se basan en las hipótesis de significación (AUC, d, f, η2, OR, x2, Z) al efecto de correlación (r) de mayor uso universal en las ciencias de la salud, permite afianzar futuros análisis y reanálisis bayesianos. Estas estimaciones son fáciles de llevar a cabo mediante la calculadora de Lenhard y Lenhard5. El factor Bayes es útil en otras pruebas estadísticas de significación7,8 (regresión lineal, ANOVA, entre otras), cuyas medidas de tamaño de efecto también son convertibles. Se recomienda el manual de Goss-Sampson6 para la inferencia bayesiana de los análisis más utilizados en la investigación en reumatología.
El uso inclusivo de diferentes magnitudes de efecto convertible afianza el incremento de investigaciones con diversos métodos estadísticos para futuros metaanálisis. A su vez, la aplicación del factor Bayes es beneficiosa para seleccionar aquellos tamaños de efecto con una mayor solidez de evidencia (FB10 > 10) para los estudios sistemáticos cuantitativos, lo que refuerza la credibilidad en las conclusiones metaanalíticas.
En conclusión, el uso inclusivo de la conversión del tamaño de efecto u otras medidas estadísticas y el factor Bayes es un gran aporte metodológico que presenta una implicancia práctica en la toma de decisiones clínicas esenciales a partir de la confirmación de resultados que sean eficazmente concluyentes, de mayor importancia en el contexto de la COVID-19.
FinanciaciónLa presente investigación no ha recibido ninguna beca específica de agencias de los sectores público, comercial o sin ánimo de lucro.
Conflicto de interesesNinguno.