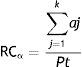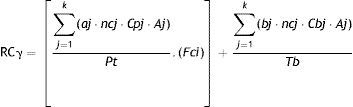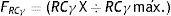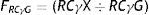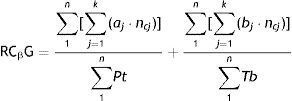El algoritmo RC evalúa de forma cualitativa el factor de impacto personal de la producción científica de investigadores aislados. Los autores proponen una adaptación de RC para evaluar el factor de impacto personal de centros de investigación, hospitales y otras agrupaciones de investigadores. Así, estas podrían ser clasificadas en función del impacto acreditado de los resultados de su labor científica entre los investigadores de su mismo ámbito científico, algo que podría ser de utilidad para canalizar presupuestos y ayudas a la investigación.
The RC algorithm quantitatively evaluates the personal impact factor of the scientific production of isolated researchers. The authors propose an adaptation of RC to evaluate the personal impact factor of research centers, hospitals and other research groups. Thus, these could be classified according to the accredited impact of the results of their scientific work between researchers of the same scientific area. This could be useful for channelling budgets and grants for research.
La contratación de investigadores, o la asignación de ayudas para investigar en convocatorias competitivas, así como la captación de fondos económicos para los diferentes centros de investigación (sean hospitalarios o no), o la estimación de su influencia científica entre iguales, requieren, cada vez más, que se introduzcan medidas de racionalidad para adoptar las mejores decisiones posibles.
Eso requiere disponer de procedimientos de evaluación objetivos y mensurables que permitan calibrar mejor a los candidatos.
Una de las formas de valorar con cierto rigor las aptitudes investigadoras de un individuo, o de un centro, más allá de que publique mucho o poco, es medir la trascendencia que tiene su investigación en el contexto científico en el que se mueve. O, lo que es lo mismo, evaluar el impacto que producen los resultados de sus investigaciones entre sus colegas. Y un modo de realizar esa valoración radica en anotar el número de veces que sus artículos son citados por sus colegas. Lo que podría llamarse el factor de impacto personal (fip) del sujeto, de un laboratorio, de un servicio médico, de un hospital o de un centro de investigación.
Pero el fip de un sujeto, o un centro, no es el mismo que tienen las revistas en las que publica sus artículos. Porque el factor de impacto de una revista refleja el número de veces que son citados los artículos que ella publica, no el de los investigadores que transmiten sus resultados en ella. Se sabe que el 50% de las citas recibidas por una revista están producidas, únicamente, por el 15% de los artículos publicados en ella1. Eso significa que se puede publicar en una revista con un gran factor de impacto y ser, sin embargo, poco citado1, con lo que la influencia propia es muy limitada, por elevada que sea la de la revista donde se publican los artículos.
El fip debe reflejar el número de veces que son citados los artículos publicados por un determinado sujeto, o la producción científica de un centro concreto, pues ese es el verdadero impacto que producen sus investigaciones entre sus colegas del mismo campo.
El algoritmo RC es uno de esos indicadores2. Tiene la peculiaridad de realizar un recuento cualitativo del número de citas que recibe cada artículo y libro publicado por un individuo (y a continuación se verá que también por los centros), teniendo en cuenta las autocitas, el lugar que ocupa el investigador entre los firmantes, la densidad de ese impacto en su producción total, el tipo de artículo o libro evaluado (revisiones o investigaciones originales), y el tiempo que el investigador ha permanecido inactivo. Resulta más completo y explicativo que el índice h, el cual se limita a señalar el número h de artículos que tienen al menos un número h de citas3.
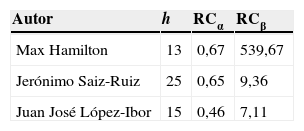
Y aunque el índice h es un indicador con alguna utilidad4, no resulta demasiado informativo. Un ejemplo de ello se refleja en la tabla 1. En ella se muestran el fip de Max Hamilton (muy conocido por su famosa escala para evaluar la depresión) y de algunos psiquiatras españoles, utilizando los datos proporcionados por la ISI Web Of Knowledge y PubMed-NCBI. La tabla 1 muestra los índices h, el RCα y el RCβ (se omite para este ejemplo el RCγ por su más complejo cálculo). El índice h de Max Hamilton es inferior al de Saiz-Ruiz y López-Ibor, aparte de no decir gran cosa sobre la verdadera dimensión de ese fip. Indica, sí, que 13 de sus publicaciones son citadas más de 13 veces, pero no hay forma de saber si más de 13 significa 50, 200 o 1.000. Por la información proporcionada por h, parece que Hamilton es menos influyente, a nivel internacional, que Saiz-Ruiz y López-Ibor, algo que los psiquiatras saben que no es real. Pero RCβ (y RCγ, más sofisticado y explicativo) muestra la auténtica dimensión de la diferencia al señalar el colosal fip de Hamilton (RCβ=539,67) frente al de los otros 2 autores.
Índice h y RC de algunos autores
| Autor | h | RCα | RCβ |
|---|---|---|---|
| Max Hamilton | 13 | 0,67 | 539,67 |
| Jerónimo Saiz-Ruiz | 25 | 0,65 | 9,36 |
| Juan José López-Ibor | 15 | 0,46 | 7,11 |
Se ha consultado Web Of Knowledge y PubMed-NCBI con fecha 23/04/2013. Filtros de búsqueda: Hamilton M and depression (solo con Hamilton M se obtienen 4.842 resultados, la mayoría de los cuales no le corresponden); Lopez-Ibor JJ or Lopez Ibor JJ; Saiz-Ruiz J or Saiz Ruiz J (SaizRuiz J no arroja resultados).
El 71% del valor de RCβ de Max Hamilton procede de las citas recibidas por su seminal artículo A rating scale for depression5, que tenía un total de 15.477 citas, y un 24% de ese valor de RCβ corresponde a su segundo artículo más citado (5.217), Development of a rating scale for primary depressive illness6, relacionado, también, con su famosa escala.
Es una razón de peso para preferir determinar el fip personal de los investigadores o grupos de investigadores con RC en lugar del índice h.
La versión α de RC (expresada como en [1]) refleja la proporción de artículos publicados por un sujeto que han tenido alguna cita. Oscila entre 0 y 1. Y cuanto más próximo a 1 esté RCα, significa que la mayor parte de la producción del investigador influye en otros.
Donde aj son los artículos citados y Pt la producción total de artículos.
Si un sujeto tiene un RCα=0,85 señala que una gran parte de su producción es tenida en cuenta por sus colegas; mientras que otro sujeto con un RCα=0,15 muestra que una proporción pequeña de su producción es influyente.
El fip bruto de un investigador a lo largo de su vida productiva estaría representado por el número de citas totales recibidas por sus artículos, dividido por el número total de artículos publicados:
Donde, a efectos de cálculo, aj representa un artículo (y tiene como valor «1») y ncj el número de veces que es citado.
RCα y RCβ son 2 formas un tanto «toscas» de expresar el fip de un sujeto, pues no aportan información cualitativa relacionada con el tipo de artículo publicado (original o revisión, por ejemplo), el lugar ocupado por el firmante, las autocitas, el tiempo transcurrido sin actividad científica, etc., aunque no dejan de ser 2 indicadores ciertamente informativos.
Bastante más ilustrativa es RCγ (expresado como en [3]), que recoge los aspectos cualitativos mencionados anteriormente de cada artículo y libro citados.
Donde aj=es un artículo (con valor «1» para el cálculo); ncj=número de citas del artículo (en la fracción situada entre corchetes); Aj=el orden del firmante en el artículo (en la fracción situada entre corchetes); Cpj=corrección por el tipo de artículo (originales, revisiones, cartas al director, editoriales); Fci=factor de corrección por inactividad; Pt=total de artículos publicados. Y donde bj=es un libro (con valor «1» para el cálculo); ncj=número de citas del libro (en la fracción situada fuera de los corchetes); Aj=el orden del firmante del libro (en la fracción situada fuera de los corchetes); Cbj=corrección por el tipo de libro (original, revisión, editor, un capítulo); Tb=total de libros publicados2.
Con RCγ es posible proporcionar un valor de fip para un sujeto y, así, establecer comparaciones entre varios. Bien porque a un determinado centro le interese contratar al de mayor influencia entre sus pares, bien porque a una institución le importe conceder una ayuda económica para investigar a quien le da mayor confianza de que obtendrá resultados de alto interés para sus colegas.
Con el fin de saber si un mismo valor RCγ corresponde a un sujeto de corta trayectoria profesional, con escasas publicaciones, pero de gran influencia (100 citas cada uno, por ejemplo), respecto a otro con una trayectoria más larga y con artículos menos citados (30 cada uno), bastará con conocer el valor Pt (producción total de artículos) y el Tb (producción total de libros) de cada uno de ellos.
Desarrollo y discusiónPero también es posible calificar con RCγ a centros del mismo campo de investigación y compararlos entre sí. Incluso se puede establecer un fip estándar que permita catalogar a los diferentes servicios hospitalarios, laboratorios de investigación, hospitales o centros, en función de la distancia que les separa de ese fip estándar de excelencia autonómico, interautonómico o estatal.
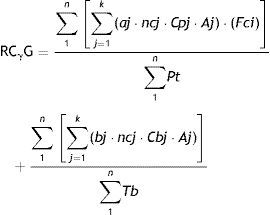
Para ello, basta aplicar una adaptación de RCγ para su cálculo en grupos: RCγG.
Donde los numeradores de las fracciones contienen la suma de las k citas ponderadas de cada uno de los artículos publicados por cada «n» sujeto del grupo que se analiza, y el denominador, la suma de la producción total (Pt: artículos; Tb: libros) de esos mismos «n» sujetos.
Bastará con sumar todas las citas (debidamente ponderadas en función del lugar de la firma, autocita, originalidad, etc., como en RCγ) recibidas por cada uno de los artículos publicados por los sujetos que componen el cuerpo científico del centro, y dividirlo por la producción total de todos ellos.
Es una cuestión a decidir si Pt y Tb deben ser todas las publicaciones del grupo o solo las indexadas a nivel internacional (las que realmente pueden ser rastreadas, leídas y citadas por sus pares). Es una decisión que debe adoptarse, y asumirse, por consenso entre los implicados en el proceso de evaluación y las autoridades interesadas en ello.
Otra decisión a tomar es el tiempo que se adopta como referencia para evaluar la repercusión de la actividad científica, ya sea de un sujeto o de un centro.
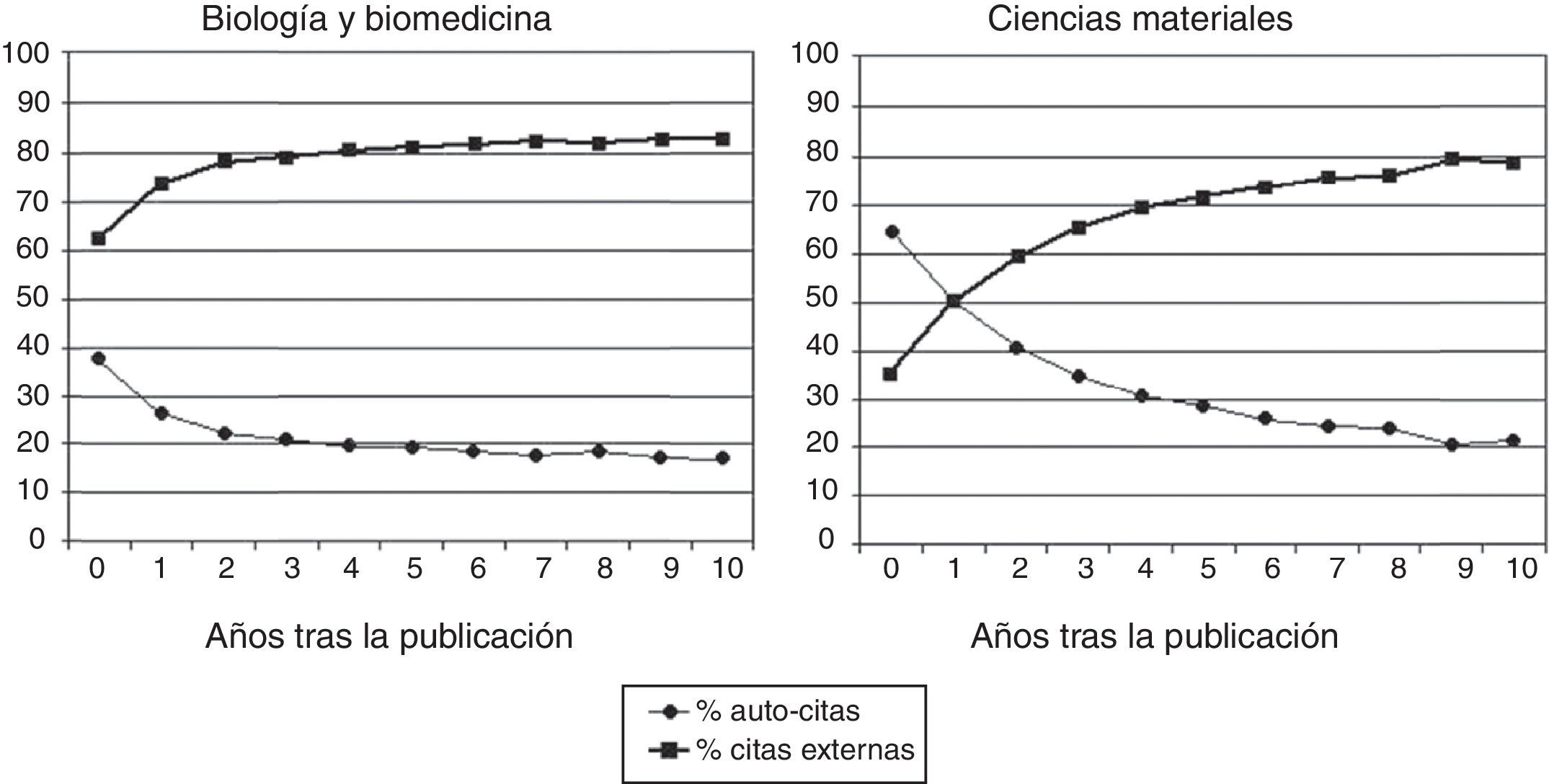
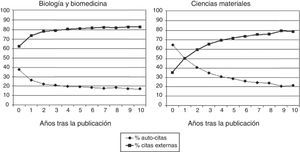
Nosotros pensamos que debería tomarse en consideración toda la vida científica de sujetos y centros. Circunscribirla a unos pocos años anteriores a la evaluación introduce un sesgo importante, porque, al menos los artículos biomédicos y de las Ciencias Materiales, comienzan a ser citados por otros entre 3 y 7 años después de ser publicados (fig. 1)7. Circunscribir la evaluación a las citas recibidas en los 5 años anteriores, por ejemplo, resulta poco útil. Es cierto que la vida de un centro es más larga que la de los individuos que lo componen y, por lo tanto, puede recibir un considerable número de citas (mayor, en cualquier caso, que un posible candidato a pertenecer a él). Pero también es cierto que publica más artículos y no todos serán citados, lo que reduce la posible distorsión inflacionista introducida por el factor tiempo en RCγG al aumentar también el denominador de la ecuación [4].
Evolución, a lo largo del tiempo, de la proporción de autocitas y citas externas según el ámbito científico de trabajo. Adaptada de Costas et al., 20107.
Por otra parte, hay que tener en cuenta que, con frecuencia, los miembros de un mismo laboratorio o servicio colaboran firmando un mismo artículo. Este ha de ser considerado tan solo una vez para evaluar a grupos con RCγG; en caso contrario, se incrementaría artificialmente el fip de ese artículo al multiplicar el número de citas recibidas por el número de firmantes del mismo centro.
Tanto RCγ como RCγG permiten realizar diferentes tipos de evaluaciones.
Comparación entre sujetosBien porque se desea contratar a un investigador de gran repercusión entre sus pares, bien porque se pretende prestar una ayuda económica a la investigación a aquellos sujetos que alcanzan mayor impacto entre sus colegas con sus resultados, el uso de RCγ puede permitir adoptar la mejor decisión.
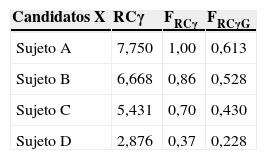
Supóngase que el Centro Z desea seleccionar a 3 investigadores con el mejor fip posible. Una vez calculado el RCγ de cada uno de los presentados, se puede proceder de varios modos (tabla 2). Uno de ellos es, simplemente, ordenar de mayor a menor los RCγ de cada candidato y seleccionar a los 3 primeros. Otra forma de proceder resulta más gráfica y, quizás, más útil. Consistiría en escoger el mayor RCγ de los candidatos como referencia y obtener la fracción de RCγ (FRCγ) de todos los demás aspirantes, expresada en tantos por uno [5]. El Centro Z adopta la decisión de admitir solo a aquellos candidatos que se encuentren en el último cuartil de FRCγ (0,75). En el ejemplo de la tabla 2, solo el Sujeto B (además del Sujeto A, que se ha tomado de referencia) se encuentra en esa situación, lo que significa que el Centro Z debe elegir entre dejar una plaza vacante o flexibilizar su criterio FRCγ.
Uso de RCγ en la evaluación de individuos
| Candidatos X | RCγ | FRCγ | FRCγG |
|---|---|---|---|
| Sujeto A | 7,750 | 1,00 | 0,613 |
| Sujeto B | 6,668 | 0,86 | 0,528 |
| Sujeto C | 5,431 | 0,70 | 0,430 |
| Sujeto D | 2,876 | 0,37 | 0,228 |
| RCγG | |||
|---|---|---|---|
| Centro Z | 12,638 | 1,000 |
Donde FRCγ=(RCγ X÷RCγ máx.); es decir, el RCγ del Sujeto X dividido entre el RCγ más alto de los candidatos presentados (el sujeto A, en el ejemplo).
En la comparación del fip de los sujetos respecto al del centro, FRCγG=(RCγ X÷RCγG). Donde RCγG corresponde al fip del centro según [4], que en el ejemplo tiene el valor de 12,638.
FRCγ es el RCγ del Sujeto X dividido por el RCγ más alto de los candidatos presentados.
Pero el Centro Z puede obrar de otro modo. Después de todo, las 2 formas anteriores seleccionan a los mejores candidatos que se presentan, no tanto al que el Centro Z necesita realmente. Una forma más exigente de actuar es analizar de forma comparativa la fracción entre los RCγ de los candidatos con el del propio Centro Z, tal y como se calcula con [4], como referencia. Utilizando FRCγG [6], el Centro Z se garantiza así incorporar al candidato más afín al perfil fip de su grupo. En el ejemplo de la tabla 2, el Centro Z tiene un RCγG=12,638. Dividiendo los RCγ de los candidatos entre el RCγG del Centro Z, se obtienen los valores FRCγG de la columna de la derecha. Si mantiene la exigencia de admitir a los sujetos que se aproximen a su RCγG en un 0,75 tendrá que rechazar a todos los candidatos que se han presentado, pues carecen del fip que le interesa mantener al Centro Z, por su propio prestigio y para salir airoso en posibles evaluaciones externas.
Donde RCγX corresponde al Sujeto X y RCγG es el del centro.
Pero supóngase que el Centro Z no es un lugar de investigación, sino un organismo que presta ayuda financiera a la investigación, como el Instituto de Salud Carlos III, por ejemplo, o cualquier otro. Un criterio para prestar esa ayuda podría ser no tanto lo que investiga un sujeto, ni lo que publica, sino su fip. Como RCγ refleja el impacto de ese investigador entre sus colegas, podría interesar ayudar a investigar, precisamente, al sujeto que más influencia consigue con el resultado de sus trabajos.
El Centro Z puede seleccionar candidatos comparándolos con un estándar prefijado, para calcular FRCγG. Ese modelo de referencia puede ser un grupo de investigadores (del mismo ramo que el candidato, que son los verdaderamente comparables) a quienes ya haya prestado ayuda y tenga calculado su RCγG; o puede asumir como propio el RCγG de algún servicio de esa especialidad que ya conozca como una buena referencia (ver infra). E, igualmente, puede asumir como criterio de selección que los candidatos alcancen el 0,75 (o cualquier otra proporción) del RCγG de ese servicio.
Comparación entre centrosTambién los servicios de un hospital, los propios hospitales, las cátedras universitarias, las mismas universidades y otros centros de investigación pueden ser clasificados por el fip que obtienen de sus investigaciones, calculado con RCγG, como en [4] (ver supra).
Es evidente que estos centros no pueden catalogarse únicamente con este criterio. Pero parece muy útil mantener una clasificación competitiva de aquellos bajo este concepto; por prestigio (que atraiga a investigadores y/o médicos en formación especializada) y, también y sobre todo, si eso atrae presupuestos.
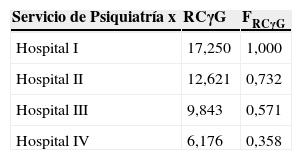
La forma de actuar ya se ha descrito previamente. En la tabla 3 se muestra un ejemplo. Imagínese que se calcula el RCγG de todos los servicios de Psiquiatría (y de cualquier otra especialidad) de los hospitales generales donde existen. El que más destaque por su fip será el que se tome como referencia; y, así, podrá elaborarse un catálogo de tales servicios en función del valor de su FRCγG calculado como en [6].
Uso de RCγG en la evaluación de centros
| Servicio de Psiquiatría x | RCγG | FRCγG |
|---|---|---|
| Hospital I | 17,250 | 1,000 |
| Hospital II | 12,621 | 0,732 |
| Hospital III | 9,843 | 0,571 |
| Hospital IV | 6,176 | 0,358 |
Donde FRCγG=(RCγG X÷RCγG máx.).
RCγG X correspondería al del Servicio de Psiquiatría del Hospital X, y RCγG máx. corresponde al Servicio de Psiquiatría con mayor RCγG.
El objetivo de esta catalogación es introducir un elemento de competencia entre los servicios de Psiquiatría a fin de alcanzar el máximo valor de FRCγG (1,000) e, incluso, superarlo. Si el Servicio de Psiquiatría del Hospital III consigue con el tiempo mejorar su rendimiento hasta superar el valor del Servicio del Hospital I (por ejemplo, con un RCγG=23,457 lo sobrepasaría con un FRCγG= 1,360) y lo mantiene un quinquenio, por ejemplo, ese se convertiría en el nuevo valor RCγG de referencia y la catalogación de los citados servicios se modificaría.
Lo mismo podría hacerse para clasificar las cátedras de la misma asignatura en las universidades. Y con los laboratorios de investigación. Y con los hospitales en su conjunto. Y con las universidades.
Para evitar que solo sea un servicio (centro, facultad, etc.) el que ofrezca el RCγG de referencia podría calcularse tomando como base los 2 o 3 con mayor fip del Estado. Así se obtendría un modelo estándar de referencia, modificable solo cuando esos 2 o 3 servicios sean superados de forma estable por otros, que pasarían a ser los nuevos referentes.
Mantener una adecuada FRCγG sería un objetivo que mejoraría la calidad de la investigación producida por tales centros, buscando no solo publicar en las mejores revistas, sino, también, convertirse en los mayores referentes entre sus iguales.
Naturalmente, los cálculos realizados hasta aquí con [4] podrían hacerse igualmente, y con los mismos fines, con la modificación grupal de RCβ (a la que se habría añadido el elemento relacionado con la publicación de libros), reflejada en [7]. Sin duda alguna es más sencilla de aplicar, pero se perderían los aspectos cualitativos que ofrece RCγ.
Donde los numeradores de las fracciones contienen la suma de las k citas de cada uno de los artículos publicados por cada «n» sujeto del grupo que se analiza; y el denominador, la suma de la producción total (Pt: artículos; Tb: libros) de esos mismos «n» sujetos.
ConclusionesEl algoritmo RC, tanto en su formulación individual (RCγ) como grupal (RCγG), aporta un procedimiento interesante para expresar con un guarismo el impacto personal de las publicaciones de investigadores particulares2, o agrupaciones de ellos, atendiendo a diversos valores cualitativos de su producción científica. También proporciona un procedimiento para catalogar los centros de investigación de diverso tipo en función del impacto (FRCγG) que producen sus resultados entre los investigadores del mismo ramo.
Eso permite introducir elementos racionales para la toma de decisiones en la contratación de investigadores, en la prestación de ayudas a la investigación a sujetos e instituciones, y en la distribución de los presupuestos, institucionales o privados, entre los diferentes centros de investigación.
LimitacionesEn la actualidad existen bases de datos accesibles (Science Citation Index, Web Of Knowledge, Embase, Scopus, PubMed) que, combinadas, permiten obtener el número de citas que reciben los artículos de investigadores concretos, el lugar que ocupan en la firma de los artículos, las autocitas, el tipo de artículo del que se trata y sus fechas de publicación. Google lleva tiempo probando su propia herramienta de localización de citas (incluso de libros), que también podría ser útil para estos fines (Google Académico). Quizás la más completa para estos fines sea Web Of Knowledge.
Una de las limitaciones del algoritmo RC viene, precisamente, de su dependencia de tales fuentes bibliográficas, que tienen una fuerte preeminencia de textos escritos en inglés. La bondad de los resultados de RC depende del esfuerzo que realicen esas fuentes en añadir revistas escritas en otras lenguas y homologar la firma de los investigadores indexados8,9. Los científicos españoles, por ejemplo, tienden a figurar en tales bases de datos con 2 o 3 variaciones de sus nombres, lo que obstaculiza su identificación y el cálculo de cualquier indicador basado en esas fuentes de datos10. Quizás por eso, los autores y las propias revistas deberían esforzarse en conseguir, también, esa homologación de firmas.
Mientras se consigue que tales bases de datos sean lo más completas posibles, el algoritmo RC será siempre infrainclusivo. Una limitación injusta respecto a las producciones totales reales, cierto, pero que afecta a todos los miembros de la misma especialidad, lo que anularía sus efectos restrictivos.
Otra limitación procedería de que para utilizar RC se requiere de acuerdos generales entre los miembros de la comunidad científica y los evaluadores, a fin de unificar sus criterios de uso. Por eso, quizás, la evaluación de los servicios, hospitales, facultades, universidades, etc., debería ser acometida por organismos ministeriales centrales, sobre un listado de investigadores adscritos a los diferentes centros, que podrían proporcionar ellos mismos.
Pese a todo, y al esfuerzo que supone realizar esa tarea evaluadora, parece que el uso del algoritmo RC podría ser de gran utilidad por su capacidad para valorar aspectos cualitativos de la producción científica individual y grupal y su impacto sobre otros investigadores del mismo ramo2.
Responsabilidades éticasProtección de personas y animalesLos autores declaran que para esta investigación no se han realizado experimentos en seres humanos ni en animales.
Confidencialidad de los datosLos autores declaran que en este artículo no aparecen datos de pacientes.
Derecho a la privacidad y consentimiento informadoLos autores declaran que en este artículo no aparecen datos de pacientes.
AutoríaAmbos autores han contribuido a partes iguales al contenido del artículo, aprobando su versión final.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.