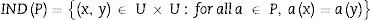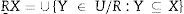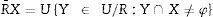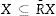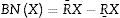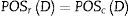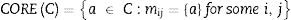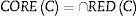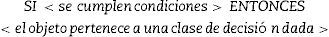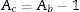El objetivo de este trabajo busca definir posibles escenarios futuros (quiebra o estabilidad financiera) de las empresas participantes de este estudio (Mipymes), para lo cual se ha analizado el riesgo operativo a partir de los indicadores financieros (variables de estudio) utilizando una herramienta considerada dentro del campo de la inteligencia artificial y conocida como «metodología de Conjuntos Rugosos o Inestables» (Rough Set methodology) y que dentro del campo de las finanzas se denomina indicadores de fracaso o quiebra empresarial.
La muestra utilizada en este trabajo se compone de Mipymes operando actualmente y de empresas ya quebradas. Esta metodología genera unas «reglas de decisión» (criterios) que sirven para evaluar a otras empresas operando al momento del estudio y con esto anticipar su probable quiebra o estabilidad financiera futura. El presente análisis generó como resultado una distribución con escenarios probables, aplicado al universo de casi 1,5 millones de Mipymes colombianas.
The objective of this work seeks to anticipate possible future scenarios (bankruptcy or financial stability), of the participating companies in this study (SME's), for which it has been analyzed operational risk on the basis of the financial indicators (variables of study). Thus, it has used a tool considered within the field of Artificial Intelligence (AI), knowing as: “Rough Sets methodology”, wich one is known within the field of finance, as indicators of corporate bankruptcy or failure.
With the analysis of a sample of SME's in operation and another of companies already broken, this methodology generates a “decision rules” (criteria) that are used to evaluate other companies operating at same time that this study, and anticipate their probable bankruptcy or financial stability. For this work resulted in a distribution of likely scenarios for the universe of almost 1.5 million Colombian SME's.
Ante la pregunta: ¿Cuál será la distribución de la probabilidad de quiebra de las Mipymes, en Colombia, a partir del análisis de sus principales variables operativas (indicadores financieros)?, se consideró pertinente explorar herramientas y aplicaciones útiles en el análisis de conjuntos de variables y su interrelación, como la teoría de conjuntos, dentro de la cual se encuentran los Conjuntos Borrosos (Fuzzy Set) (Bellman y Zadeh, 1977), y más específicamente los llamados Conjunto Rugosos o Inestables (Rough Set) (Pawlak, Grzymala-Busse, Slowinski y Ziarko, 1995). Dentro del campo de las finanzas, esta metodología ha sido aplicada para prever la quiebra empresarial, apoyándose de 25 variables (indicadores financieros) que miden el desempeño operativo desde el punto de vista económico y financiero de las organizaciones objeto de este estudio.
Así, el objetivo de este trabajo radica en la aplicación de esta herramienta de tipo prospectivo para generar posibles escenarios futuros y con esto producir análisis de riesgo de operación de las empresas de tamaño micro, pequeñas y medianas, y determinar la probabilidad de éxito o fracaso de este sector económico fundamental.
Inteligencia artificialEl campo de la inteligencia artificial fue introducido a la comunidad científica en 1950 por el inglés Alan Turing en su artículo «Maquinaria Computacional e Inteligencia», que buscaba contestar la pregunta: ¿Pueden las máquinas pensar? Este trabajo fue continuado en Estados Unidos por John von Neumann durante la década de los cincuenta.
Dentro de estas técnicas de reciente implementación se pueden mencionar: los sistemas borrosos (fuzzy systems), la teoría de los conjuntos aproximados (rough sets theory) y los sistemas caóticos (systems chaotics). Los sistemas borrosos y la teoría de los conjuntos aproximados se pueden emplear con las técnicas de la inteligencia artificial simbólica, y las aplicaciones numéricas, en el tratamiento de la información imprecisa e incompleta.
Estos sistemas están diseñados para servir de soporte a los complejos análisis que se requieren en el descubrimiento de las tendencias del negocio, con el fin de tomar decisiones eficientes y oportunas (Jiménez, Urrutia, Galindo y Zaraté, 2016).
Conjuntos BorrososBetancur (2006) comenta que los modelos económicos y financieros son representaciones aproximadas de la realidad, a diferencia de los modelos usados en la física o la mecánica. Según Sen (1989), de poco sirve realizar representaciones extremadamente precisas de un concepto identificado como incierto o borroso. Por ejemplo, cuando se está considerando la compra de una casa mediante financiación hipotecaria, la evolución futura del tipo de interés de financiación a 15 o 20años es un asunto más borroso que aleatorio, que debe tratarse mediante intervalos de confianza.
De acuerdo con Haugen y Baker (1996), en un contexto de mercados imperfectos el cálculo del costo de capital y de la deuda no debería fundamentarse solo en modelos teóricos precisos basados en sistemas de ecuaciones simultáneas y muy apropiados para entornos de menor complejidad, sino en sistemas de ecuaciones aproximadas que reflejen un enfoque más evolutivo y cambiante.
Se observa que un alto grado de posibilidad no implica un alto grado de probabilidad, es decir, lo que es probable debe ser posible; en cambio, lo que es posible no siempre es probable. Por lo tanto, la teoría de probabilidades y la teoría de posibilidades (subconjuntos borrosos) no son sustitutivas entre sí pero son complementarias (Fernández, 2016).
Rough SetLa teoría de Rough Set (conjuntos aproximados) ha encontrado muchas aplicaciones interesantes, áreas de aprendizaje de la máquina, adquisición de conocimientos, análisis de decisiones, bases de datos, sistemas expertos, razonamiento inductivo y reconocimiento de patrones, sin embargo como lo señala Segovia, Gil, Heras y Vilar (2003), ya que muchas decisiones financieras requieren clasificar en categorías o grupos, una observación (empresa, título de una cartera, etc.) lo que genera problemas de clasificación binaria, es decir, cuando el número de grupos se limita a dos, por ejemplo clasificar créditos entre fallidos y no, fusiones y adquisiciones, clasificación de bonos, etc., fundamentalmente en la predicción del fracaso empresarial.
Lazzari, Machado y Pérez (1998) comentan que los primeros en abordar la teoría de los conjuntos borrosos son Bellman y Zadeh (1970) en su artículo «Fuzzy sets», y concluyen que en el estudio de los sistemas complejos llega un momento en el cual la precisión choca con la significatividad: a más precisión menos significatividad, añadiendo además que es un paso hacia una proximidad entre la precisión de la matemática clásica y la sutil imprecisión del mundo real, un acercamiento nacido de la incesante búsqueda humana por lograr una mejor comprensión de los procesos mentales y del conocimiento.
Diversos autores, como Gómez y Vázquez (2013), Pawlak et al. (1995) y Coaquira (2007), concuerdan que el autor más representativo de la teoría del modelo de Rough Set es Pawlak (1982), quien propuso esta herramienta matemática para el análisis de datos imperfectos, la ambigüedad y la incertidumbre de la información, y además es muy efectiva para el análisis de los sistemas de información financiera de una colección de objetos descritos por un conjunto de ratios financieros y variables cualitativas.
Por otro lado, Blanco, Miranda y Segovia (2012) afirman que la teoría Rough Set está relacionada con la incertidumbre que se produce cuando algunos objetos se caracterizan por tener la misma información, es decir, que para un conjunto de variables presentan los mismos valores (por lo tanto, no se pueden diferenciar, son indiscernibles), sin embargo, se clasifican en distintas clases o categorías.
Para Bravo y Pinto (2008) esta teoría es una poderosa herramienta matemática para manejar la imprecisión y la incertidumbre inherente al proceso de toma de decisiones, y citan a Pawlak (1991, p. 1) para ejemplificar acerca de las ventajas y beneficios que tiene el empleo del modelo Rough Set:
Una de las principales ventajas de la teoría Rough Set es que esta no necesita información preliminar o adicional sobre ningún tipo acerca de los datos, tales como distribución de probabilidad en estadísticas o grado o probabilidad de pertenencia en la teoría de conjuntos difusos (fuzzy set theory).
De la misma manera, Filiberto, Bello, Caballero y Frías (2011) hacen mención que en la Teoría de los Conjuntos Aproximados la información es representada por una tabla donde cada fila representa un objeto y cada columna un rasgo. Esta tabla es llamada Sistema de Información; más formalmente, es un par S=U,A, donde U es un conjunto finito no vacío de objetos llamado Universo y A es un conjunto finito no vacío de atributos.
Mosqueda (2010) ubica al modelo Rough Set como un método perteneciente a los Sistemas de Inducción de Reglas y Árboles de Decisión (o métodos de criterio múltiple), cuyo enfoque, a su vez, se encuadra dentro de las aplicaciones de la inteligencia artificial.
Indicadores de fracasoDiversos autores (Bravo y Pinto, 2008; Coaquira, 2007; Miranda, 2012; Pawlak, 2002; Samaniego y Vázquez, 2007) concuerdan con una metodología lógica para llegar a resultados confiables a través de la metodología Rough Set, la cual es ampliamente aplicada en estudios a empresas de tamaño micro, pequeño y mediano. Por ejemplo, en el continente europeo Cueto, Diéguez y Oliver (2015) han aplicado la metodología Rough Set como predictora de fracaso o de quiebra empresarial. En su estudio, realizado a un total de 3.872 empresas solventes y 4.517 del Reino Unido, concluyen que esta técnica puede ayudar a la preselección de las variables (entre financieras y no financieras) más importantes para una buena clasificación y, para el caso particular de las microempresas, mostrando la significatividad de variables que no son estrictamente financieras.
Otro ejemplo de aplicación, ahora en la industria hotelera de micro y pequeñas empresas, es el de Vivel-Búa, Lado-Sestayo y Otero-González (2015), que definen algunos determinantes de quiebra a partir de una muestra de 1.679 hoteles utilizando modelos de probabilidad condicional (probit y logit) y variables financieras (rentabilidad, endeudamiento, equilibrio económico-financiero, estructura económica, liquidez y actividad), concluyendo que las variables de nivel de endeudamiento y porcentaje de activo corriente influyen de manera positiva, mientras que la rentabilidad y el nivel de actividad influyen de manera negativa hacia la probabilidad de quiebra del hotel.
Por último se puede mencionar a De Llano, Piñeiro y Rodríguez (2016), quienes elaboran un análisis comparativo de la eficacia de ocho métodos de pronóstico populares: univariante, regresiones lineal, discriminante y logit, particionamiento recursivo, rough sets, redes neuronales artificiales y Data Envelopment Analysis (DEA), lo que surge a partir de una crítica que realizan Joy y Tollefson (1975) al modelo Z-core de Altman, 1968, Altman (1968 y 1977) acerca de la inestabilidad de los modelos discriminantes debido a la ausencia de procedimientos de contraste intertemporal, ya que el decisor no dispone de criterios para aventurar si los pronósticos obtenidos en un momento dado son fiables o no. También concluyen que se pueden emitir predicciones fiables usando cuatro variables que contienen información acerca de rentabilidad, estructura financiera, rotación y flujos de caja.
Descripción de la Metodología de Indicadores de FracasoSistema de informaciónTradicionalmente en sistema de información, en las filas de la tabla se indican el conjunto de objetos U=x1, x2,…,x7, mientras que las columnas denotan los atributos A=a1, a2,…,a7 de estos objetos y la variable de decisión d. Las entradas en este tipo de sistemas son los valores de los atributos o descriptores. Cada fila de la tabla contiene descriptores que representan información correspondiente a un objeto. La relación de no diferenciación ocurrirá si dos objetos para todos los atributos tomasen los descriptores el mismo valor.
Tabla de decisiónDebido a la imprecisión que existe en los datos en el mundo real, siempre existirá conflicto en los datos contenidos en una tabla de decisión. Aquí el conflicto se refiere a dos o más objetos idénticos usando cualquier conjunto de atributos de condición; sin embargo, ellos tienen una diferente clase de decisión. Tales objetos son llamados inconsistentes. Esta tabla de información es llamada tabla de decisión inconsistente.
La relación indiscernible. La teoría de los conjuntos aproximados se basa en la relación indiscernible. Sea T=U,A,C,D una decisión datos del sistema, donde U es un conjunto finito no vacío llamado universo. CyD son subconjuntos.
Los elementos de la U se denominan objetos, casos u observaciones. Los atributos son interpretados como funciones, variables o características de condiciones, dada una característica, tales que:
Sea a∈A, P⊆A la relación indiscernible, IND(P) se define de la siguiente manera:
La relación indiscernible define una partición de U. Permitir U/INDP denota una familia de todas las clases de equivalencia de la relación INDP, llamados conjuntos elementales. Otras dos clases de equivalencia U/INDC y U/INDD, llamadas condicional y clase decisional, respectivamente, también pueden ser definidas.
Aproximación inferior:
Deje que R⊆CyX⊆U, el R−aproximación inferior conjunto de X es el conjunto de todos los elementos de la U que puede ser clasificados como elementos de X.
Así, puede verse que la aproximación inferior R es un subconjunto de X:
Aproximación superior:
La R−superior aproximación conjunto de X es el conjunto de todos los elementos de U, que posiblemente puede pertenecer al subconjunto de interés X:
Obsérvese que X es un subconjunto de la R-superior aproximación. Así:
Región fronteriza.
Es la colección de conjuntos definidos por elementales:
Estos juegos se incluyen en R−superior pero no en R−aproximaciones inferior.
Reduzca (reductos):
Un sistema T=U,A,C,D es independiente si todos los c de c son indispensables. Un conjunto de características R⊆C se denomina reducto de C de T′=U,A,R,D, es independiente y POSRD=POSCD. Además, no existe T⊂R. De tal forma que:
Un reducto es un conjunto mínimo de características que conserva la relación indiscernible producida por una partición de C pudiendo haber varios subconjuntos de atributos R objetos similares o insignificantes pueden estar representados varias veces sobre una tabla de información, algunos de los atributos pueden ser superfluos o irrelevantes, y pueden ser destituidos sin perder la calidad en la clasificación.
El núcleo
El conjunto de todas las características indispensables en C es denotada por COREC. El núcleo es el conjunto de todas las entradas de un solo elemento de la matriz, que es discernible. Tenemos:
Donde REDC es el conjunto de todos los reductos de C. Por lo tanto, el núcleo es la intersección de todos los reductos de un sistema de información. El núcleo no considera las características prescindibles y que puede ampliarse mediante reductos.
Reglas de decisión.
De hecho, esta es la cuestión más importante del enfoque Rough Set. Una regla de decisión puede expresarse como una sentencia lógica que relaciona la descripción de condiciones y las clases de decisión. Toma la siguiente forma:
Las reglas generadas pueden ser determinísticas o no determinísticas. Por determinística (consistente, precisa, exacta) entendemos siC→D; en otro caso es no determinística (inconsistente, aproximada), que sería cuando las condiciones pueden conducir a varias posibles decisiones.
MetodologíaDefinición de las variablesDiversos autores (Rubio y Fernández, 2016; Samaniego y Vázquez, 2007; Caro, 2016; García, 2015) emplean en su trabajos a los ratios financieros como variables del modelo Rough Set para el cálculo de la aplicación de tal modelo.
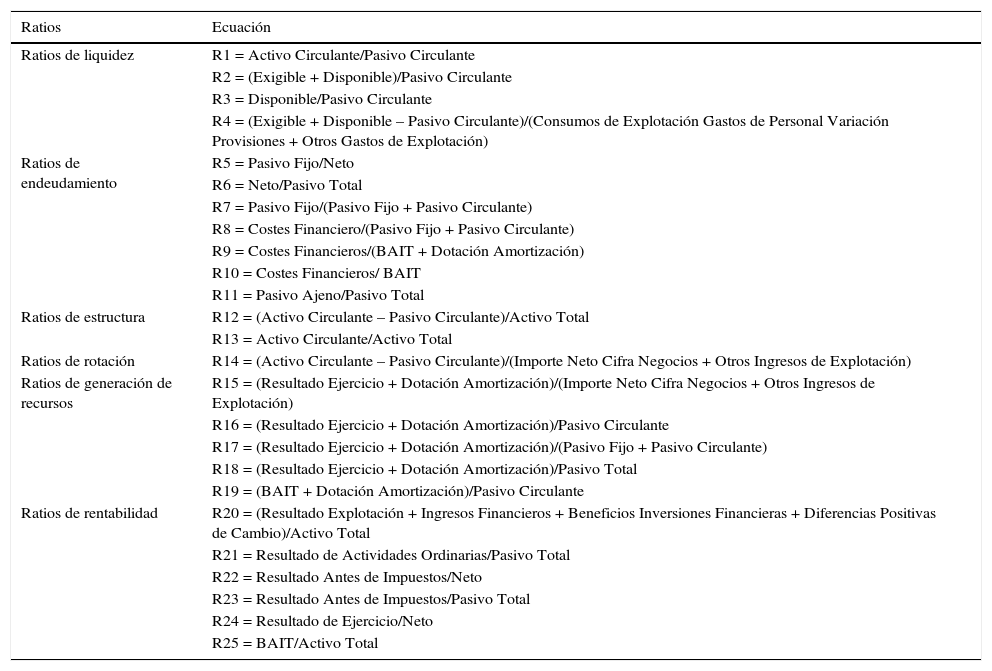
En la tabla 1 se muestran las variables clasificadas en ratios de liquidez, endeudamiento, estructura, rotación, generación de recursos y rentabilidad.
Ratios financieros que actúan como variables del estudio
| Ratios | Ecuación |
|---|---|
| Ratios de liquidez | R1 = Activo Circulante/Pasivo Circulante |
| R2 = (Exigible + Disponible)/Pasivo Circulante | |
| R3 = Disponible/Pasivo Circulante | |
| R4 = (Exigible + Disponible – Pasivo Circulante)/(Consumos de Explotación Gastos de Personal Variación Provisiones + Otros Gastos de Explotación) | |
| Ratios de endeudamiento | R5 = Pasivo Fijo/Neto |
| R6 = Neto/Pasivo Total | |
| R7 = Pasivo Fijo/(Pasivo Fijo + Pasivo Circulante) | |
| R8 = Costes Financiero/(Pasivo Fijo + Pasivo Circulante) | |
| R9 = Costes Financieros/(BAIT + Dotación Amortización) | |
| R10 = Costes Financieros/ BAIT | |
| R11 = Pasivo Ajeno/Pasivo Total | |
| Ratios de estructura | R12 = (Activo Circulante – Pasivo Circulante)/Activo Total |
| R13 = Activo Circulante/Activo Total | |
| Ratios de rotación | R14 = (Activo Circulante – Pasivo Circulante)/(Importe Neto Cifra Negocios + Otros Ingresos de Explotación) |
| Ratios de generación de recursos | R15 = (Resultado Ejercicio + Dotación Amortización)/(Importe Neto Cifra Negocios + Otros Ingresos de Explotación) |
| R16 = (Resultado Ejercicio + Dotación Amortización)/Pasivo Circulante | |
| R17 = (Resultado Ejercicio + Dotación Amortización)/(Pasivo Fijo + Pasivo Circulante) | |
| R18 = (Resultado Ejercicio + Dotación Amortización)/Pasivo Total | |
| R19 = (BAIT + Dotación Amortización)/Pasivo Circulante | |
| Ratios de rentabilidad | R20 = (Resultado Explotación + Ingresos Financieros + Beneficios Inversiones Financieras + Diferencias Positivas de Cambio)/Activo Total |
| R21 = Resultado de Actividades Ordinarias/Pasivo Total | |
| R22 = Resultado Antes de Impuestos/Neto | |
| R23 = Resultado Antes de Impuestos/Pasivo Total | |
| R24 = Resultado de Ejercicio/Neto | |
| R25 = BAIT/Activo Total |
Fuente: Samaniego y Vázquez (2007), citando el trabajo de Trujillo (2002).
Los datos requeridos son extraídos de los estados financieros de las empresas (fallidas o sanas), y con ellos se calculan los 25 ratios económico-financieros a partir de las ecuaciones mostradas en la tabla 1. Dichos ratios tienen que ser calculados para cada una de las 50 empresas que conforman la muestra utilizada para este estudio, realizando un «emparejamiento» entre 25 de ellas consideradas como fallidas1, y otras 25 empresas consideradas como sanas2 financieramente hablando. Para este cálculo se aplicó la siguiente ecuación:
dónde:
Ac= Año de cálculo del ratio.
Ab= Año base.
Una vez calculados los ratios de cada una de las empresas se obtiene un sistema de decisión (tabla 2), de 50×25, añadiendo una columna en la cual se clasifica cada una de las empresas con un criterio dumy (sanas=1 y fallidas=0), quedando entonces una tabla modificada de 50×26 datos.
Criterios para la generación de la tabla de distribución de frecuencias
| Número de datos | Total de resultados de los ratios calculados |
| Valor máximo | El dato más grande de todo el conjunto de datos |
| Valor mínimo | El dato más pequeño de todo el conjunto de datos |
| Rango | Es la resta del valor mínimo al valor máximo |
| No. de intervalo | La técnica más recomendable es la de la regla de Sturges, la cual nos dice que k = 1+3.3 log N; donde N es el número de datos o elementos de la muestra |
| Amplitud de clase | Se divide el rango entre el número de intervalos, y el cociente de tal división es la amplitud de cada clase |
| Diferencia | Es a criterio del usuario, es solo para dar un espacio a cada intervalo, normalmente se utiliza la unidad para diferenciación |
Fuente: elaboración propia.
La información financiera de la muestra de las 50 empresas emparejadas (25 fallidas y 25 sanas) fue tomada de la base de datos que proporciona el sistema de información financiera y reporte empresarial (SIREM) de la Superintendencia de Sociedades de Colombia.
Dicha base de datos contiene la información de los estados financieros básicos (balance general, estado de resultados, y flujo de efectivo) de cerca de 25.000 empresas colombianas, las cuales a su vez están clasificadas por tamaño, sector, actividad económica, etc.
Los criterios de selección para este trabajo fueron: en cuanto a tamaño3, las micro, pequeñas y medianas empresas. En cuanto al sector: comercio, servicios y transformación. En cuanto a capacidad económica, se consideró su activo total, como criterio para «emparejar» las empresas en cuanto a su riqueza se refiere.
La determinación del número de empresas que sería estudiada (50 empresas: 25 sanas y 25 fallidas) está fundamentado en un proceso no aleatorio y por conveniencia, debido a que la selección de cada una de las empresas requiere, además de los criterios de selección antes mencionados, un proceso de análisis extra escudriñando empresas con historial antes del año base (2015), para determinar así su estatus de sanas o fallidas.
Descripción de la aplicación de la metodología Rough Set- a)
Como primer paso se genera una tabla con el total de los ratios calculados de cada una de las empresas de la muestra, con la que se obtiene un sistema de decisión (tabla 2) de 50×25.
- b)
Posteriormente se añade una columna en la cual se clasifica cada una de las empresas con un criterio dumy (sanas=1, fallidas=0), quedando entonces una tabla modificada de 50×26 datos.
- c)
El siguiente paso es codificar los datos de la tabla anterior de manera manual, con la ayuda de una tabla de la distribución de frecuencia, por lo que es necesario computar algunos datos específicos, los cuales se muestran en la tabla 2.
- d)
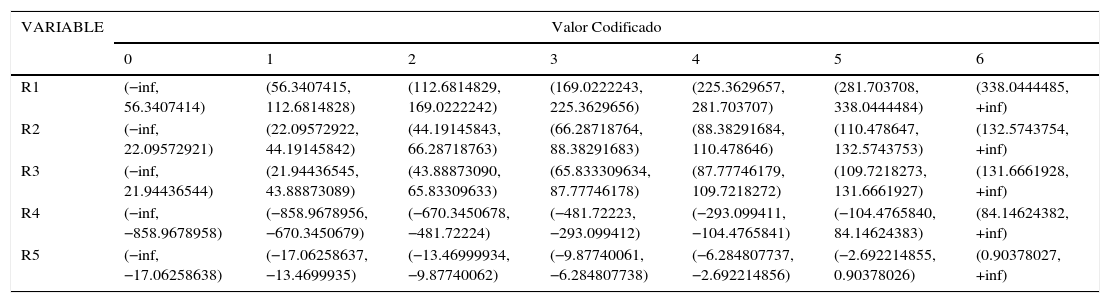
Una vez que se tiene la tabla con los 25 ratios, ya ordenadas en intervalos, se asigna un código a cada intervalo, como se muestra en la tabla 3 (solo se muestra una parte de la tabla generada, a manera de ilustración).
Tabla 3.Parte de la tabla de intervalos generados
VARIABLE Valor Codificado 0 1 2 3 4 5 6 R1 (−inf, 56.3407414) (56.3407415, 112.6814828) (112.6814829, 169.0222242) (169.0222243, 225.3629656) (225.3629657, 281.703707) (281.703708, 338.0444484) (338.0444485, +inf) R2 (−inf, 22.09572921) (22.09572922, 44.19145842) (44.19145843, 66.28718763) (66.28718764, 88.38291683) (88.38291684, 110.478646) (110.478647, 132.5743753) (132.5743754, +inf) R3 (−inf, 21.94436544) (21.94436545, 43.88873089) (43.88873090, 65.83309633) (65.833309634, 87.77746178) (87.77746179, 109.7218272) (109.7218273, 131.6661927) (131.6661928, +inf) R4 (−inf, −858.9678958) (−858.9678956, −670.3450679) (−670.3450678, −481.72224) (−481.72223, −293.099412) (−293.099411, −104.4765841) (−104.4765840, 84.14624383) (84.14624382, +inf) R5 (−inf, −17.06258638) (−17.06258637, −13.4699935) (−13.46999934, −9.87740062) (−9.87740061, −6.284807738) (−6.284807737, −2.692214856) (−2.692214855, 0.90378026) (0.90378027, +inf) Fuente: elaboración propia.
- e)
Con apoyo del programa computacional denominado ROSE24 se obtiene una tabla de datos codificada (tabla 4).
Tabla 4.Tabla codificada (solo se muestra una parte, a manera de ejemplo)
Empresa R1 R2 R3 R4 R5 R6 R7 R8 R9 R10 R11 R12 R13 R14 R15 R16 R17 R18 R19 R20 R21 R22 R23 R24 R25 Atributo de Decisión 1 0 0 0 5 5 0 6 0 2 2 1 6 0 0 6 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 5 5 0 0 1 2 2 0 6 0 0 6 5 0 0 4 0 0 0 0 0 0 0 3 0 0 0 5 5 0 0 0 6 6 0 6 4 0 6 5 0 0 4 0 0 0 0 0 0 0 26 0 0 0 5 5 0 3 1 2 2 0 6 1 0 6 5 0 0 4 0 0 0 0 0 0 1 27 0 0 0 5 5 0 0 0 2 2 0 6 1 0 6 5 0 0 4 0 0 0 0 0 0 1 28 0 0 0 5 5 1 0 1 2 2 0 6 2 0 6 5 0 0 4 0 0 0 0 0 0 1 Fuente: elaboración propia.
Los valores que aparecen en la tabla 4 serán utilizados por el ROSE2 para realizar cálculos posteriores que serán aplicados a las 50 empresas que forman parte de este estudio, con los cuales se generan los siguientes:
ResultadosComo ya se mencionó, con la tabla codificada y con el apoyo del programa ROSE2 se construyeron los llamados reductos, lo cual implica un resumen de los ratios que tienen una alta significancia (tabla 5).
Reductos generados
| 1 | {R4, R5, R6, 67, R8, R9, R12, R13, R20} |
| 2 | {R4, R5, R6, R7, R8, R10, R12, R13, 20} |
| 3 | {R4, R5, R6, R7, R8, R9, R12, R13, R25} |
| 4 | {R4, R5, R6, R7, R8, R10, R12, R13, R25} |
| 5 | {R4, R6, R7, R8, R9, R12, R13, R22} |
| 6 | {R4, R6, R7, R8, R10, R12, R13, R22} |
| 7 | {R4, R6, R7, R8, R9, R12, R13, R24} |
| 8 | {R4, R6, R7, R8, R10, R12, R13, R24} |
Fuente: elaboración propia.
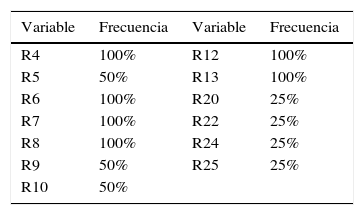
Estos reductos se agruparon en una tabla de frecuencias de cada variable (tabla 6).
Con la tabla 6 se puede identificar que los ratios R4, R6, R7, R8, R12, R13 son variables que aparecen en todos y cada uno de los reductos; por lo tanto, no pueden dejar de considerarse. Por otro lado, los ratios R5, R9, R10 aparecen en un 50%. Por último, las ratios R20, R22, R24, R25 aparecen únicamente en un 25%. El resto de los 25 ratios no tienen una frecuencia menor; por lo tanto, no se toman en cuenta en esta investigación.
Con el apoyo de la distribución de frecuencias se generaron 25 reglas de decisión con la ayuda del programa ROSE2 (mediante la función LEMS2). Se presentan en la tabla 7.
Reglas de decisión resultantes
| Regla 1 | = | (R4=5) y (R5=5) y (R11=0) y (R13=0) y (R16=5) entonces (D1=0) |
| Regla 2 | = | (R5=5) y (R13=4) y (R16=5) entonces (D1=0) |
| Regla 3 | = | (R11=2) entonces (D1=0) |
| Regla 4 | = | (R7=3) y (R8=0) y (R11=0) entonces (D1= 0) |
| Regla 5 | = | (R3=0) y (R7=6) entonces (D1=0) |
| Regla 6 | = | (R6=0) y (R16=4) entonces (D1=0) |
| Regla 7 | = | (R4=6) y (R6=1) entonces (D1=0) |
| Regla 8 | = | (R20=6) entonces (D1=0) |
| Regla 9 | = | (R8=6) entonces (D1=0) |
| Regla 10 | = | (R6=1) y (R13=5) entonces (D1=0) |
| Regla 11 | = | (R12=0) entonces (D1=1) |
| Regla 12 | = | (R13=2) entonces (D1=1) |
| Regla 13 | = | (R9=4) entonces (D1=1) |
| Regla 14 | = | (R7=1) y (R16=5) entonces (D1=1) |
| Regla 15 | = | (R4=5) y (R5=5) y (R11=0) y (R13=1) entonces (D1=1) |
| Regla 16 | = | (R7=5) entonces (D1=1) |
| Regla 17 | = | (R1=4) entonces (D1=1) |
| Regla 18 | = | (R6=2) entonces (D1=1) |
| Regla 19 | = | (R1=1) entonces (D1=1) |
| Regla 20 | = | (R4=6) y (R6=0) entonces (D1=1) |
| Regla 21 | = | (R6=3) entonces (D1=1) |
| Regla 22 | = | (R5=0) entonces (D1=1) |
| Regla 23 | = | (R8=1) y (R13=6) entonces (D1=1) |
| Regla 24 | = | (R6=0) y (R7=0) y (R13=5) entonces (D1=0) o (D1=1) |
| Regla 25 | = | (R8=0) y (R10=2) y (R11=0) y (R12=6) y (R13=6) y (R24=0) entonces (D1=0) o (D1=1) |
Fuente: elaboración propia, resultante del proceso LEMS2 de ROSE2.
Puede observarse que las primeras 10 reglas identifican a las empresas fallidas. Las siguientes 13 muestran a las empresas que no son fallidas, es decir, las empresas sanas. Las últimas dos reglas de decisión nos muestran que pueden resultar sanas o fallidas.
Por ejemplo, la regla 5 establece que si el ratio 3 es igual a 0 y el ratio 7 es igual a 6, la empresa se clasificara como empresa fallida (D1=0). Por el contrario, en la regla 14, si el ratio 7=1 y el ratio R16=5, entonces la empresa se clasificara en empresa sana (D1=1). Estas 25 reglas se clasifican con un 82% en los elementos que fueron utilizados.
Las anteriores reglas de decisión se aplicaron a una nueva muestra de 100 empresas extraídas de la base de datos ya señalada. Esta muestra se conformó con los siguientes criterios.
El número de empresas obedece a que es un número cerrado para determinar de manera directa un porcentaje de distribución; adicionalmente, este número considera también la dificultad de tiempo y cantidad de trabajo para determinar la selección de cada una de ellas:
- •
La selección es totalmente aleatoria.
- •
La muestra considera una proporcionalidad numérica para cada uno de los criterios:
- •
En cuanto a su actividad económica: industrial (33%), comercial (33%), servicio (33%).
- •
En cuanto a tamaño de las empresas: micro (50%), pequeña (30%) y mediana (20%).
Con el objetivo de realizar un análisis rápido de los posibles escenarios para cada empresa se consideró codificar con colores cada escenario, los cuales se muestran en la tabla 8).
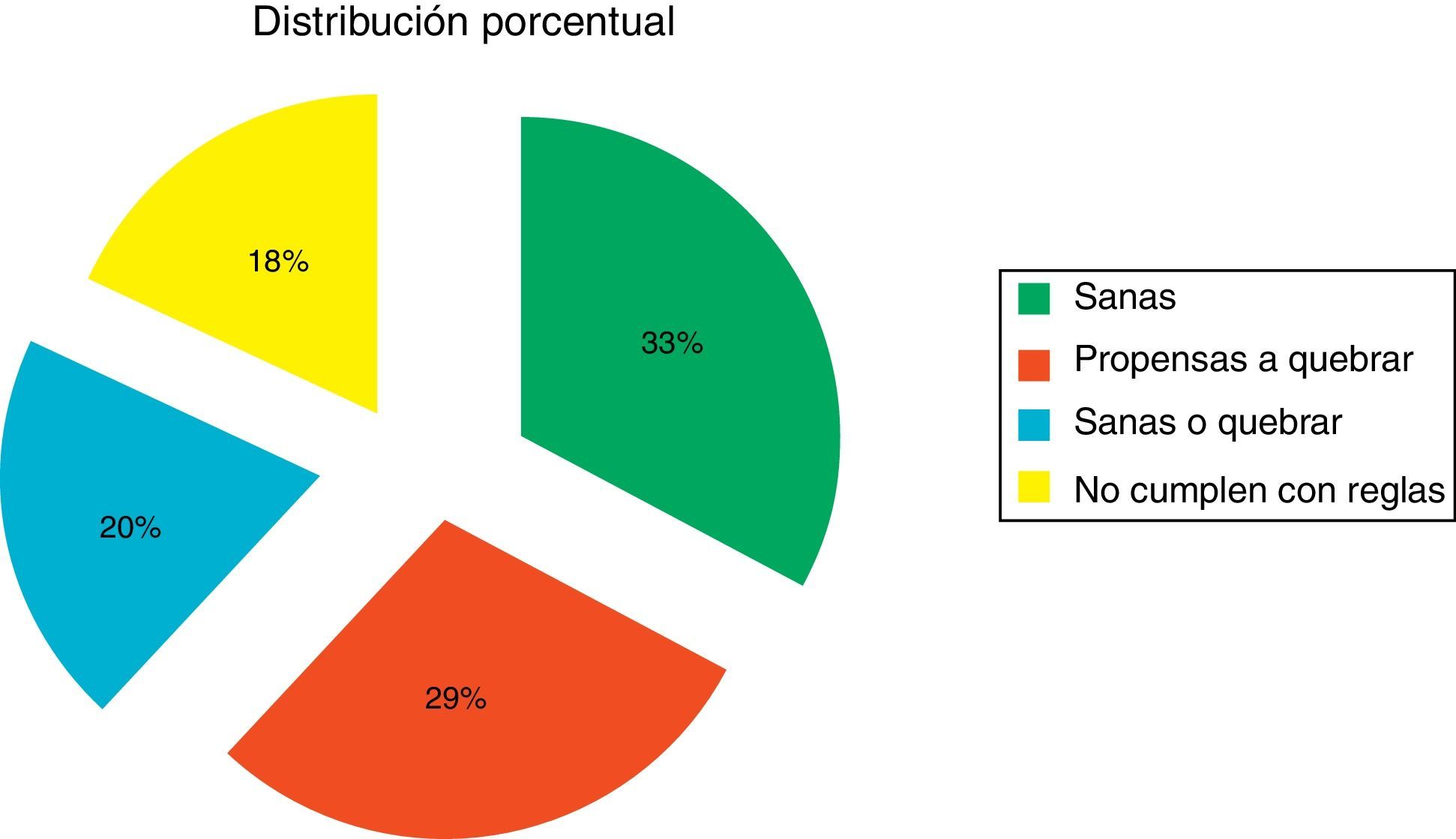
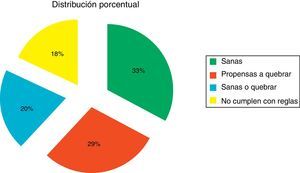
Esta codificación se aplicó a cada una de las 100 empresas de esta nueva muestra, y se determinó una distribución porcentual de los posibles escenarios futuros. Dicha distribución se muestra en la figura 1.
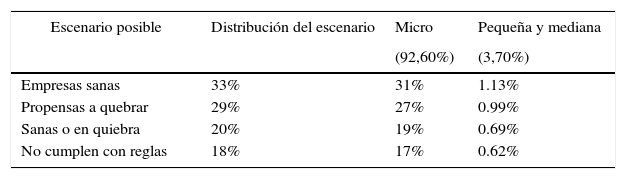
Considerando esta información y la distribución calculada en este trabajo, se establece la siguiente suposición de la ponderación considerando los posibles escenarios futuros determinados en este trabajo, aplicado al universo de las 1.422.117 empresas colombianas que, según Espinosa, Molina y Vera-Colina (2015), han sido censadas por el DANE5, quienes establecen que el 96,4% de las empresas se clasifican como Mipymes, de las cuales el 92,6% son microempresas y el 3,7% son pequeñas y medianas.
La tabla 9 muestra una ponderación del porcentaje de empresas que se espera se encuentren en alguno de los escenarios pronosticados.
Distribución supuesta del universo de las Mipymes colombianas
| Escenario posible | Distribución del escenario | Micro | Pequeña y mediana |
|---|---|---|---|
| (92,60%) | (3,70%) | ||
| Empresas sanas | 33% | 31% | 1.13% |
| Propensas a quebrar | 29% | 27% | 0.99% |
| Sanas o en quiebra | 20% | 19% | 0.69% |
| No cumplen con reglas | 18% | 17% | 0.62% |
Fuente: elaboración propia.
Los resultados que se generaron de este trabajo son consistentes con la mayoría de los estudios referentes a las Mipymes, como por ejemplo el de Espinosa et al., 2015, donde consta que aproximadamente el 30% de las empresas Mipymes se mantienen sanas y operando, mientras que el índice de mortandad está alrededor del 70%.
Este trabajo determinó que alrededor del 30% se consideran plenamente sanas financieramente hablando, en tanto que el 29% de las empresas son propensas a quiebra, el 20% podrían continuar financieramente sanas o quebrar y el 18% no cumplen con las reglas, por lo que es complicado determinar su futuro financiero.
La aplicación de la metodología Rough set empleada ha resultado útil para la determinación del riesgo operativo de las Mipymes colombianas a partir del análisis de patrones detectados en los índices financieros, con lo cual se ha podido predecir el desempeño operativo de las Mipymes.
Esta aplicación busca sentar las bases para generar una tendencia innovadora denominada «Prospectiva Financiera», útil en el análisis y la determinación anticipada del riesgo operativo de las empresas, primordialmente de tamaño micro, pequeño y mediano, ya que tomando en cuenta que más del 90% de las empresas son Mipymes según lo han demostrado diversos y variados estudios, se considera importante desarrollar herramientas aplicables a estas unidades fundamentales para el desempeño económico de cualquier país.
Hay que considerar en estudios futuros que esta metodología (Rough Set) presenta una evolución importante, encontrando innovaciones y herramientas que pueden y deben ser abordados, por ejemplo: clustering y multi-granulation, herramientas que forman parte de la inteligencia artificial, útiles en el manejo de sistemas de información para toma de decisiones (por ejemplo, los trabajos de Sun y Ma, 2015; Xu y Guo, 2016; Yao y She, 2016; Li y Xu, 2015), ya que dichas herramientas se aplican no solo en el límite superior o inferior, como lo determina la metodología Rough Set, sino en las diversas opciones que se presentan dentro de dichos rangos, lo que implica una amplitud de opciones de análisis.
Las empresas que desaparecieron para el año base (2015) y que en años anteriores sí habían reportado operaciones.
Premio al mejor artículo del número.
Las empresas que reportan al menos 10 años atrás al año base (2015) y que se han mantenido operando.
Según la ley del 905 del 2004, donde define el tamaño en función del número de empleados, que para micro empresa está establecido con 0 a 10 empleados, y activos de hasta 500 salarios mínimos (SMLV); para la pequeña empresa se consideran de 11 a 50 empleados con activos mayores de 501-5.000 SMLV, y para la mediana empresa, personal entre 50 y 200 trabajadores o activos totales entre 5.001 y 30.000 SMLV.