Las gráficas cumulative sum (CUSUM) se engloban dentro de gráficas de control de calidad, son posiblemente las que mejor se adaptan y las más utilizadas en la monitorización de los procesos clínico-asistenciales.
Una de sus principales ventajas es su empleo en casos raros y en eventos con baja incidencia, en los cuales sería necesario obtener una muestra y un tiempo de seguimiento amplio, imposible en determinados casos, mediante métodos estadísticos convencionales. También por ello, son útiles para estudiar curvas de aprendizaje, la introducción de nuevas tecnologías y, en general, para valorar la calidad de los propios resultados asistenciales, porque su perfil es sensible a cambios de tendencias (positivas o negativas) muy sutiles en los resultados, que no se observarían con otros métodos.
Por otra parte, su uso se puede expandir más allá de lo que es el control o la monitorización de calidad, aspecto que resulta novedoso en investigación clínica.
Cumulative sum graphs are quality control charts that are possibly the most frequently used for monitoring clinical-care processes.
One of their main advantages is the use in rare cases and in events with low incidence, where it would be necessary to obtain a large sample and a long follow-up time with conventional statistical methods, which is impossible in certain cases. This is also why they are useful for studying learning curves, the introduction of new technologies and, in general, for assessing the quality of care outcomes themselves, because their profile is sensitive to very subtle changes in trends (positive or negative), which would not be observed with other methods.
On the other hand, their use can be expanded beyond quality control or monitoring, which is a new aspect in clinical research.
Las técnicas estadísticas de control de calidad fueron desarrolladas por primera vez en los años 20 del siglo pasado por Walter Shewhart. Debido a la exitosa aplicación en el campo de la industria armamentística en EE. UU. durante la segunda guerra mundial y posteriormente en la revolución industrial japonesa, durante los años 50 se inició su uso en el campo de la medicina, concretamente para la monitorización de valores de laboratorio de análisis clínicos o bancos de sangre1,2. Actualmente, está aumentando el interés sobre estas técnicas de control de calidad, tanto para auditar (controlar) procesos clínicos como para la monitorización de resultados asistenciales3. Su campo de aplicación es ilimitado, ya que cualquier actividad humana es susceptible de ser cuantificada y por tanto monitorizada para mejorar su calidad.
Fundamentalmente, estas técnicas se emplean para monitorizar un proceso mientras este transcurre y lo hacen de modo visual mediante gráficas de control. Si es cierto que una imagen vale más que mil palabras, no es menos cierto que una gráfica comunica mejor que una tabla con una amalgama de cifras. De este modo, si se observan signos que indiquen la existencia de un problema, es decir, una desviación importante sobre lo previsto o sobre lo deseable, el proceso puede detenerse y comprobarse precozmente. Así pues, el principal objetivo de estas gráficas es identificar la tendencia del proceso, de modo que si la tendencia está yendo a peor es necesario detener el proceso y analizar posibles errores, mientras que si esta está yendo mejor de lo esperado, también es interesante identificar las razones.
En cualquier proceso existe siempre una variabilidad inherente al mismo, de modo que el resultado de cada unidad monitorizada rara vez es igual o idéntico. El objetivo de los procesos de control de calidad es definir cuál es la variabilidad aceptable para un proceso, marcando unos límites máximos y mínimos donde se considera que el proceso se encuentra bajo control, estableciendo así un rango óptimo de variabilidad que distinga la variabilidad común o asignable propia del proceso de una variabilidad especial o excesiva, con el objetivo de garantizar el buen funcionamiento del proceso4.
En la interpretación de estos límites de control no hay que olvidar la posibilidad de aparición de errores estadísticos, tal como ocurre en las técnicas estadísticas habituales. El error α o tipo I, corresponde con un falso positivo, es decir rechazar la hipótesis nula cuando esta es verdadera. En el caso de los gráficos control de calidad correspondería a un valor correcto del proceso que se situaría por fuera del rango de variabilidad común. Así, en el caso de que el rango aceptado corresponda a la media±2 SD el error tipo I será del 5%. El error β o tipo II, equivale a un falso negativo, es decir aceptar la hipótesis nula cuando esta es falsa. En los procesos de control de calidad este error aparece cuando se hace caso omiso de un resultado que en realidad se debe a una causa especial. Así pues, las gráficas de control no son otra cosa que la reproducción visual del resultado de una prueba estadística de significación, en la que se puede observar si el proceso se desvía significativamente del objetivo deseable, pero con la ventaja añadida de permitir ver si el proceso tiene tendencia, o no, a acercarse a esa desviación crítica. Por lo tanto, permiten activar una alerta antes de que salte la alarma.
Gráficas cumulative sumDentro del amplio abanico de las gráficas de control estadístico de procesos se encuentran las gráficas cumulative sum (CUSUM), que son posiblemente las que mejor se adaptan y las más utilizadas en la monitorización de los procesos clínico-asistenciales. Pueden emplearse también para comparar resultados de diversas instituciones, servicios, o incluso sujetos individuales. Fueron descritas por Page5 en el año 1954, siendo las preferidas en el campo de la medicina por su sencillez y su fácil interpretación. En el año 1977, Herbert Wohl6 publicó en la prestigiosa revista The New England Journal of Medicine el primer artículo en el cual estas curvas se empleaban con el objetivo de monitorizar un proceso clínico, más concretamente los cambios en la temperatura corporal de pacientes sépticos. Posteriormente, este método de monitorización se extendió a otros procesos clínicos y quirúrgicos; así, de Levar7 fue el primero en utilizar este método para el control de calidad en cirugía, más concretamente para monitorizar la transposición de grandes vasos en neonatos con o sin defecto asociado en el tabique interventricular en función del cirujano responsable. Gracias a este y a diversos trabajos8–11, su uso está actualmente muy extendido en el campo de la cirugía cardiaca y torácica.
Suma acumulada, en realidad, quiere decir sumar la diferencia observada en el resultado de cada unidad que compone el proceso (cada caso clínico, por ejemplo) con respecto a un valor que se considera el estándar u objetivo de calidad. Si esa diferencia de cada unidad se ordena acumuladamente en la gráfica en cuanto al orden temporal de ejecución, o por cualquier otro criterio de ordenación, lo que nos dibujará la gráfica es la tendencia del proceso a separarse o a acercarse al objetivo establecido.
Estas gráficas se pueden construir siguiendo las indicaciones recogidas en la bibliografía en simples hojas de cálculo como Excel o SPSS, aunque también se pueden obtener automáticamente con programas estadísticos específicos (STATA ver. 12 para Windows).
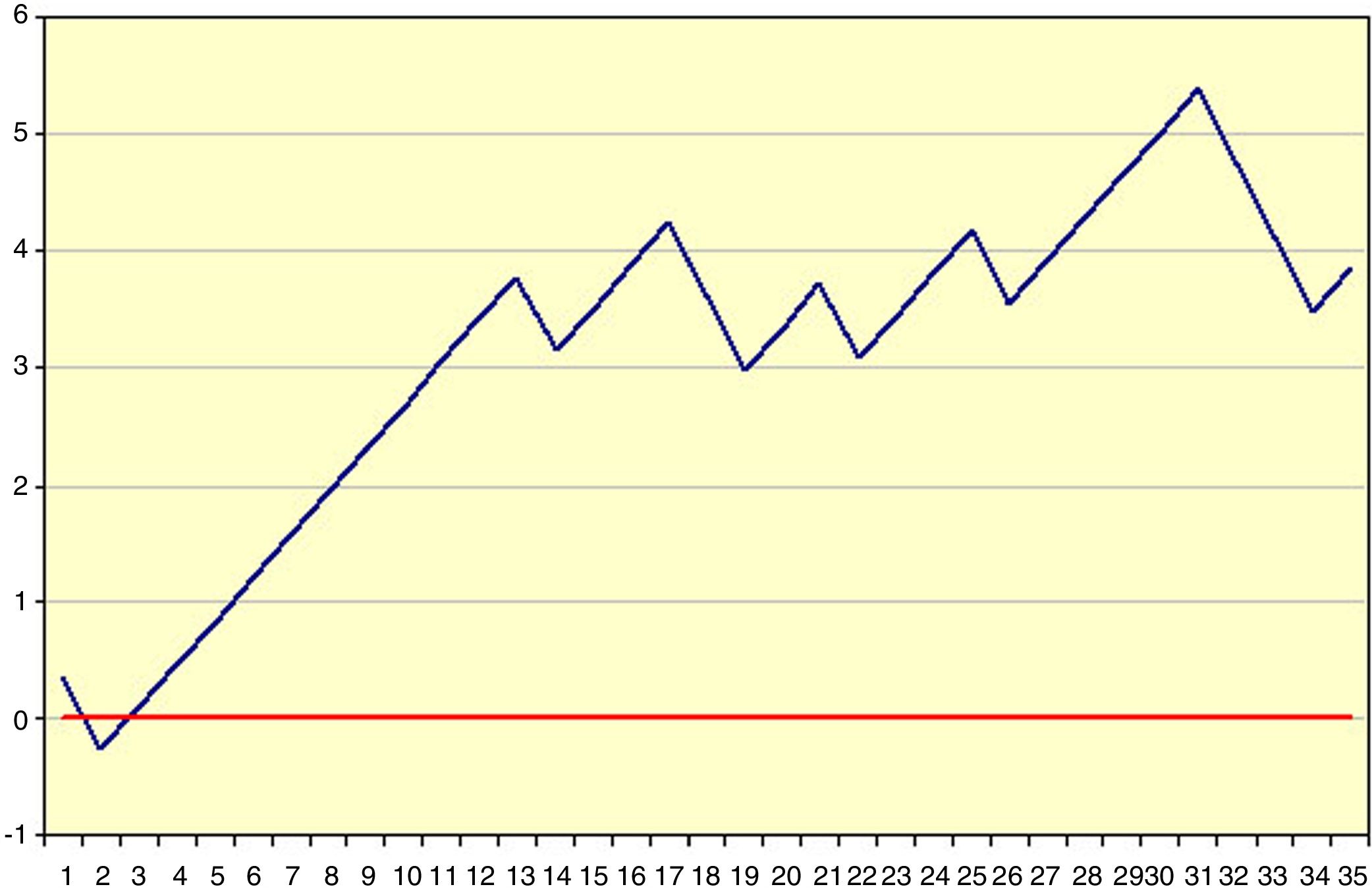
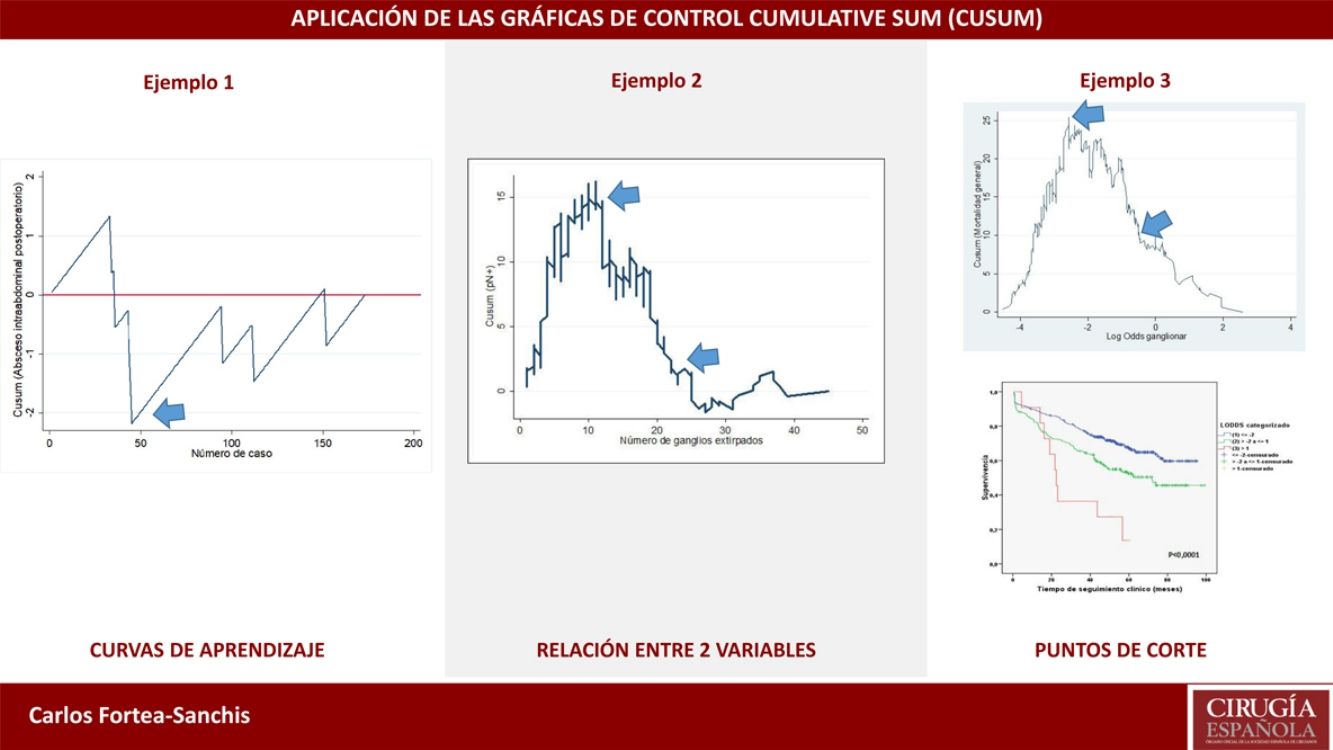
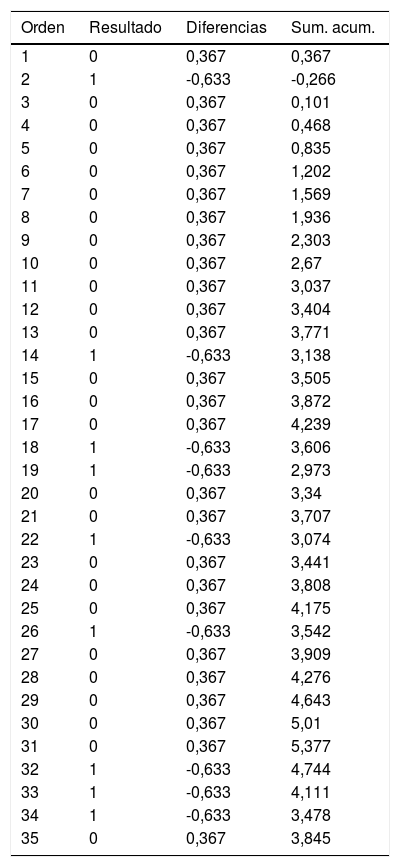
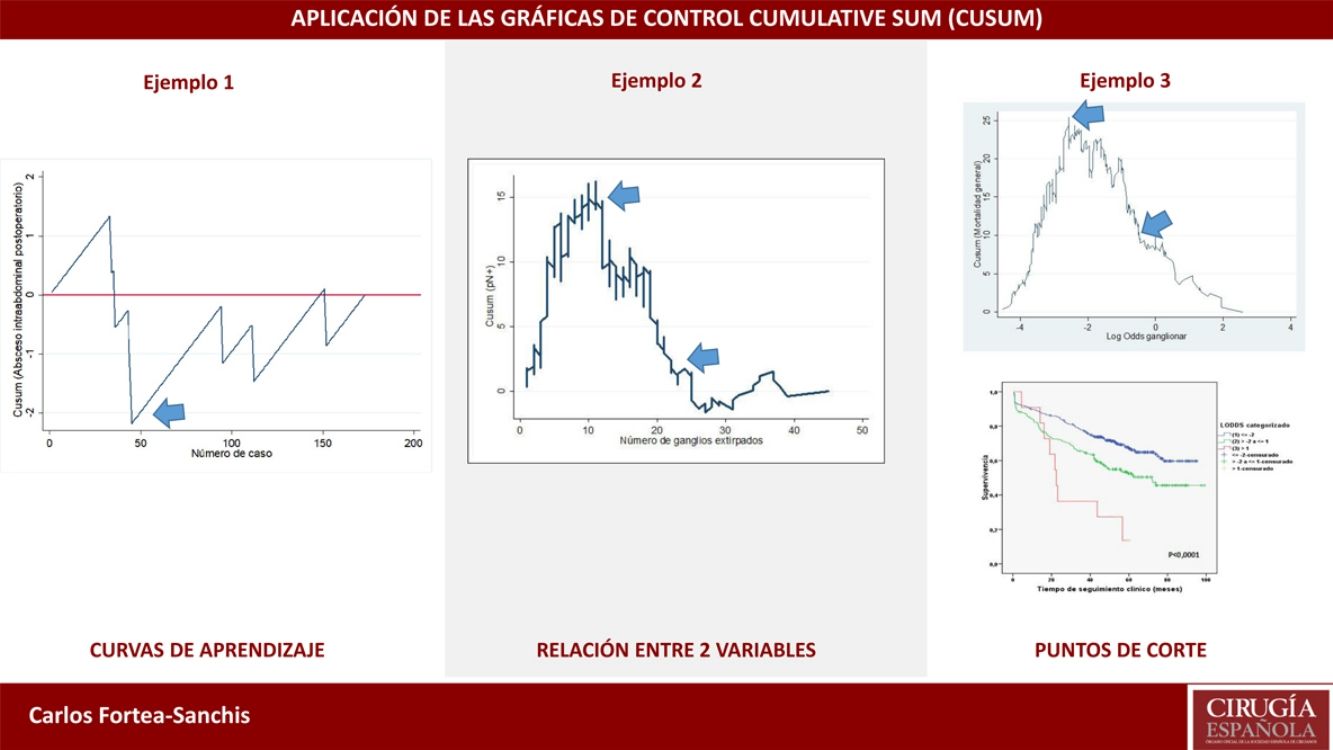
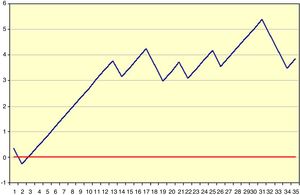
Ejemplo 1En la tabla 1 y la figura 1 se ejemplifica visualmente la construcción de una gráfica CUSUM. Se trataría de una intervención quirúrgica urgente cuyo resultado final tiene un indicador de calidad de 36,7% de muertes. Inicialmente se ordenan los pacientes temporalmente con su resultado, en este ejemplo 0=vivos y 1=éxitos. Posteriormente se calcula para cada paciente la diferencia entre el resultado obtenido (0 o 1) frente al esperado (indicador de calidad: 0,367). Finalmente se realiza la suma acumulada de estas diferencias en la que el nivel 0 corresponde al indicador de calidad, y estas se representan mediante una gráfica. En este ejemplo vemos que existe un aumento en el riesgo de mortalidad hasta aproximadamente 12 casos y a partir de esta cifra la tendencia se estabiliza.
Ejemplo de gráficas CUSUM
| Orden | Resultado | Diferencias | Sum. acum. |
|---|---|---|---|
| 1 | 0 | 0,367 | 0,367 |
| 2 | 1 | -0,633 | -0,266 |
| 3 | 0 | 0,367 | 0,101 |
| 4 | 0 | 0,367 | 0,468 |
| 5 | 0 | 0,367 | 0,835 |
| 6 | 0 | 0,367 | 1,202 |
| 7 | 0 | 0,367 | 1,569 |
| 8 | 0 | 0,367 | 1,936 |
| 9 | 0 | 0,367 | 2,303 |
| 10 | 0 | 0,367 | 2,67 |
| 11 | 0 | 0,367 | 3,037 |
| 12 | 0 | 0,367 | 3,404 |
| 13 | 0 | 0,367 | 3,771 |
| 14 | 1 | -0,633 | 3,138 |
| 15 | 0 | 0,367 | 3,505 |
| 16 | 0 | 0,367 | 3,872 |
| 17 | 0 | 0,367 | 4,239 |
| 18 | 1 | -0,633 | 3,606 |
| 19 | 1 | -0,633 | 2,973 |
| 20 | 0 | 0,367 | 3,34 |
| 21 | 0 | 0,367 | 3,707 |
| 22 | 1 | -0,633 | 3,074 |
| 23 | 0 | 0,367 | 3,441 |
| 24 | 0 | 0,367 | 3,808 |
| 25 | 0 | 0,367 | 4,175 |
| 26 | 1 | -0,633 | 3,542 |
| 27 | 0 | 0,367 | 3,909 |
| 28 | 0 | 0,367 | 4,276 |
| 29 | 0 | 0,367 | 4,643 |
| 30 | 0 | 0,367 | 5,01 |
| 31 | 0 | 0,367 | 5,377 |
| 32 | 1 | -0,633 | 4,744 |
| 33 | 1 | -0,633 | 4,111 |
| 34 | 1 | -0,633 | 3,478 |
| 35 | 0 | 0,367 | 3,845 |
Resultado (0=vivo, 1=éxitus).
Si se establecen unos límites de desviación podremos detectar el momento preciso en el que esa desviación pasa a ser estadísticamente significativa, que supondría que el proceso ha entrado en un estado de «fuera de control». En cierto modo son como un gráfico bursátil, aunque en este lo que se acumula es la diferencia de un índice con respecto al valor del momento anterior, sean h o días, mientras que en la CUSUM se acumulan diferencias con respecto a un valor de referencia. En cualquier caso, lo que se muestra es la tendencia del resultado con respecto al criterio de ordenación, sea temporal o de otro tipo1,2,12,13.
Las principales ventajas de estas gráficas son su sencillez, interpretación visual intuitiva y la capacidad de detectar cambios en las tendencias. Al ser capaces de distinguir anomalías no explicadas por la variabilidad común del proceso, estas gráficas se pueden aplicar para identificar en qué tramos de un resultado influye, en mayor o menor intensidad, un determinado factor14. Al respecto, es necesario puntualizar que las gráficas de control no identifican por sí mismas las causas de una desviación especial o asignable. La identificación de estas causas forma parte de un proceso separado de investigación, pero, al menos, constituyen la forma más rápida y segura de conocer que algo indeseable está ocurriendo.
Por otra parte, una de sus principales ventajas es su empleo en casos raros y en eventos con poca incidencia, en los cuales sería necesario obtener una muestra y un tiempo de seguimiento amplio, imposible en determinados casos, mediante métodos estadísticos convencionales. Sin embargo, mediante las gráficas CUSUM se consigue monitorizar el proceso en tiempo real desde su inicio15. También por ello, son útiles para estudiar curvas de aprendizaje1,9,13,16. De este modo, presentan como ventajas respecto a otros métodos: actualización de los resultados tras cada procedimiento, y aplicación de distintos objetivos en función de los cirujanos, así como monitorización en tiempo real del proceso. Del mismo modo, pueden emplearse para la introducción de nuevas tecnologías y, en general, para valorar la calidad de los propios resultados asistenciales, porque su perfil es sensible a cambios de tendencias (positivas o negativas) muy sutiles en los resultados, que no se observarían con otros métodos14,17–21.
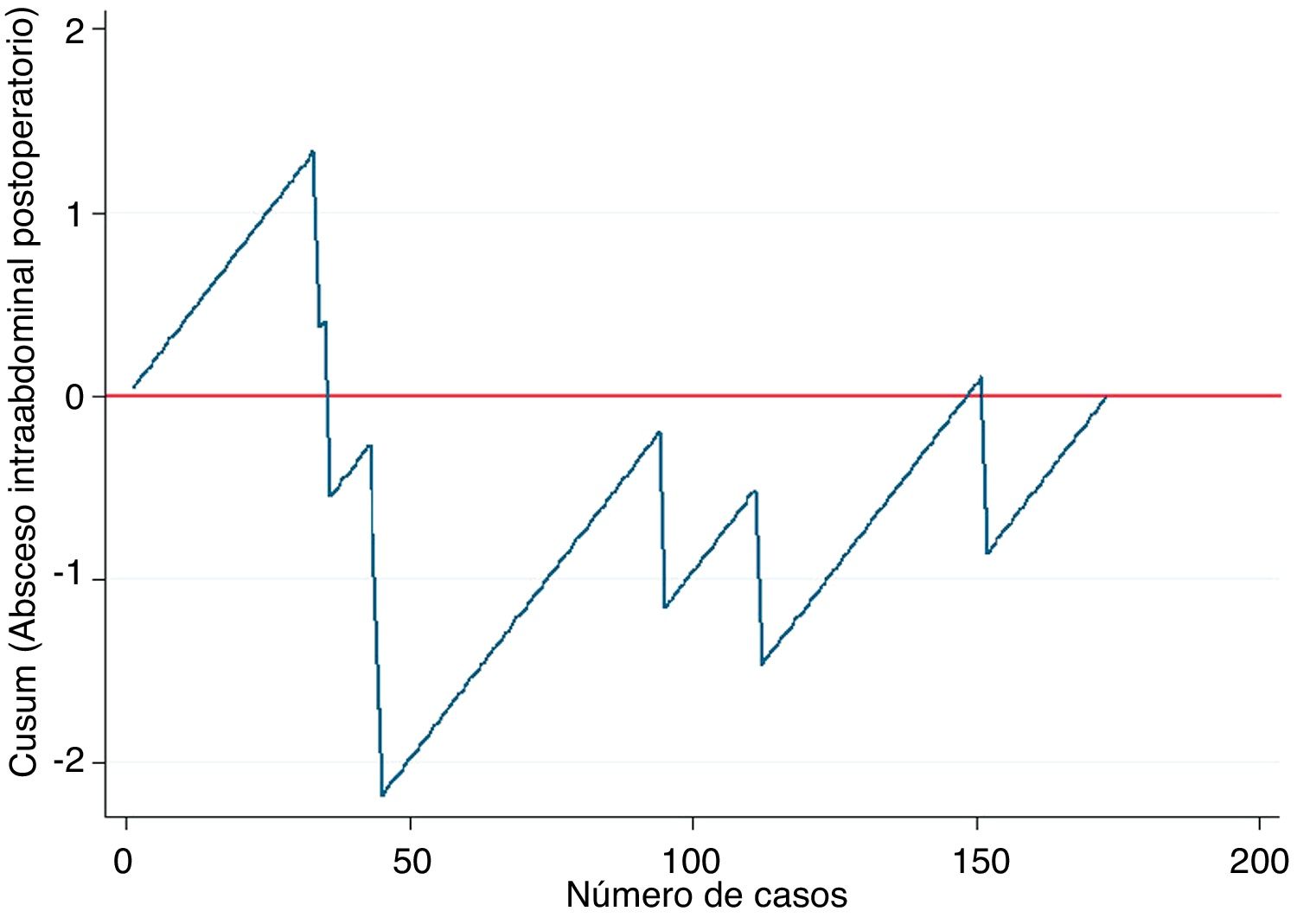
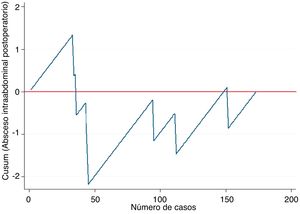
Ejemplo 2En este ejemplo mostraremos su empleo en las curvas de aprendizaje, en este caso para la apendicectomía laparoscópica en residentes de un hospital general. Como medida de una correcta técnica quirúrgica se empleó la aparición de abscesos intraabdominales postoperatorios sobre un objetivo deseable de no sobrepasar el 5%. De este modo, tal como se observa en la figura 2, el riesgo de aparición de abscesos intraabdominales aumenta hasta aproximadamente los 40 casos realizados (línea ascendente), y a partir de esta cifra se produce un descenso del riesgo de aparición, situándose por debajo de la línea 0 durante el resto de la secuencia temporal. Esto se traduce que en este centro se necesitaron 40 casos para que el grupo de residentes superaran la curva de aprendizaje para la realización de apendicectomías laparoscópicas.
Otras utilidadesNo obstante, su uso se puede expandir más allá de lo que es control o monitorización de calidad, aspecto que resulta novedoso en investigación clínica. Por ejemplo, pueden resultar útiles en la investigación de las relaciones de dos variables clínicas de interés, más allá de la relación promedio que pueda haber entre ellas y que habitualmente se escruta mediante pruebas estadísticas convencionales. Por ejemplo, es posible determinar cómo aumenta paulatinamente la probabilidad de encontrar ganglios afectados por un tumor conforme se disecan más ganglios en una linfadenectomía, o a partir de qué cantidad de ganglios disecados esa probabilidad ya no aumenta de forma manifiesta, o dibujar la tendencia de la edad, año a año, a producir más complicaciones postoperatorias, o a partir de qué día de la evolución de un cuadro clínico aumenta la tendencia a que se produzcan más muertes, o a partir de qué cantidad de intervenciones realizadas se invierte la tendencia a emplear más tiempo quirúrgico (curva de aprendizaje), entre otras muchas.
Este tipo de gráfica CUSUM fue propuesta por Royston20 y representa la diferencia acumulada entre la prevalencia general del indicador analizado en una serie de casos, y la probabilidad de un resultado calculado mediante regresión logística entre 2 variables: una de resultado (de tipo cualitativo binario situada en el eje Y) y otra variable pronosticadora de dicho resultado (de tipo cuantitativo ubicada en el eje X). Al dibujar la tendencia del resultado desde esta relación, se puede observar cuándo se producen cambios en el perfil de la curva para cada valor de la variable pronosticadora, especialmente si existe algún cambio sustancial o extraordinario. Como siempre, la línea 0 de la gráfica representa el valor de referencia que en este caso corresponde a la prevalencia general del factor analizado.
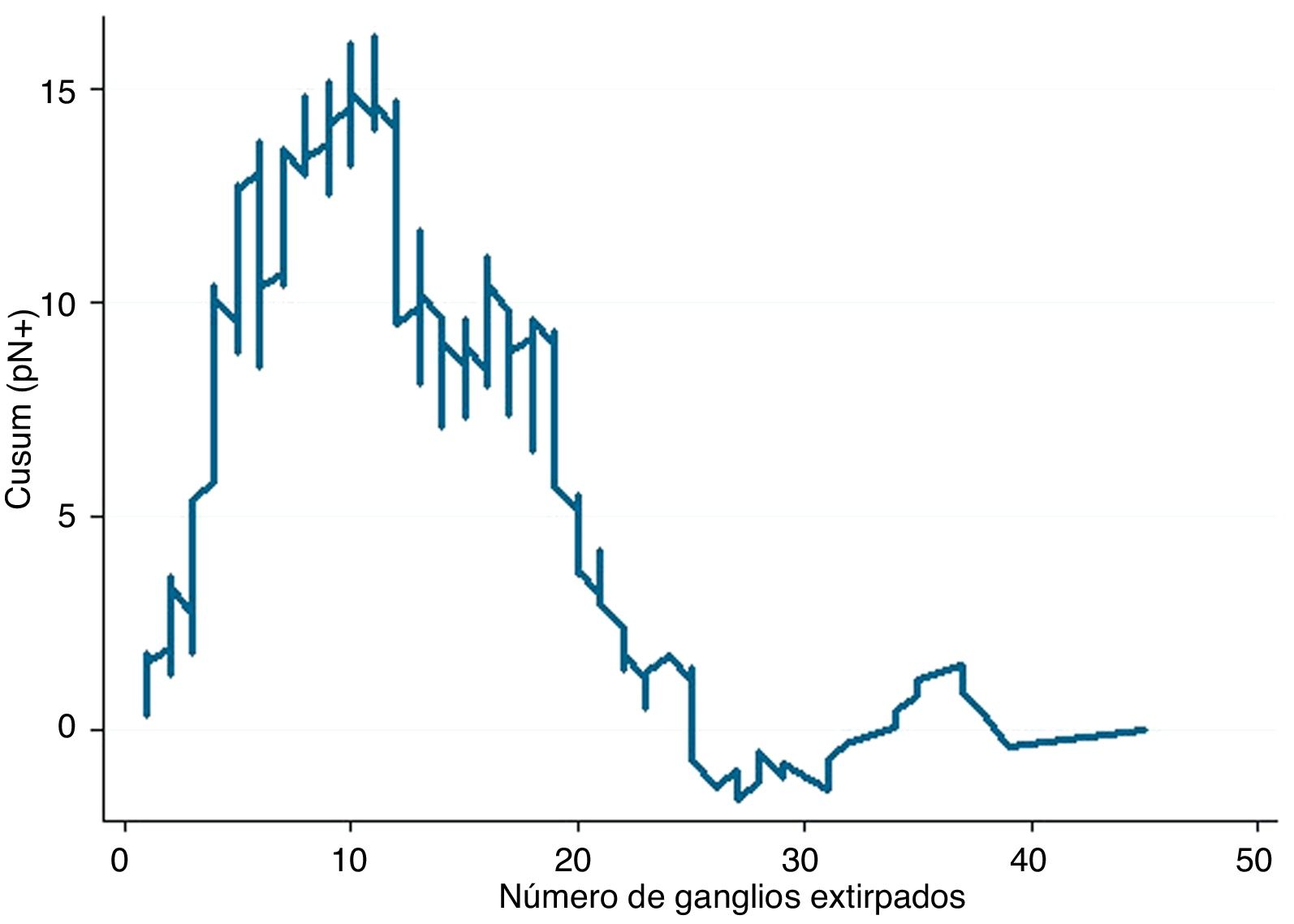
Ejemplo 3Si estudiamos la relación entre afectación ganglionar de un tumor maligno (variable binaria Sí-No) y número total de ganglios analizados, el valor de referencia será la prevalencia general de ganglios afectados en una serie de casos. Cuando el objetivo principal es aquilatar la tendencia del resultado y sus cambios con respecto a la variable pronosticadora no es estrictamente necesario establecer límites de control, puesto que este objetivo no está relacionado con la calidad. Si la curva adopta una forma de U invertida nos indicará que a más ganglios analizados hay una mayor probabilidad de encontrar ganglios afectados, mientras que si adoptara una forma de U no invertida nos indicaría lo contrario. Si el perfil de la curva fuera oscilante nos indicaría que no hay una clara relación entre la variable pronosticadora y la de resultado. Tras esta valoración general, en el caso de existir una relación evidente entre las variables, nos hemos de fijar en los cambios de perfil que muestra la curva. Debe puntualizarse que, basándose en el fundamento matemático de los cálculos, la interpretación de los resultados debe hacerse de una forma aproximada, es decir, debemos señalar que un cambio de tendencia en la curva se produce aproximadamente en un momento determinado, y no que se produce exactamente en ese momento. Se trata, pues, de una forma de análisis más detallado que el proporcionado por cualquier prueba estadística que se base en cifras promedio (media, mediana, etc.) de las variables que se estudien4.
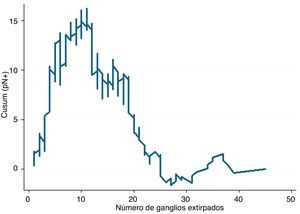
En la figura 3 se puede observar que, en general, a más ganglios analizados es más probable encontrar ganglios positivos. Y ya entrando en detalles, hasta unos 12 ganglios analizados la diferencia acumulada entre la prevalencia general de ganglios afectados y la hallada para cada cifra de ganglios analizados (esperados-observados) tiende a aumentar, es decir, realmente estamos obteniendo menos ganglios afectados que los que cabría esperar. A partir de cifras de 12 ganglios analizados esta diferencia va menguando de forma mantenida, es decir, ya obtenemos más ganglios positivos que los esperados pero la probabilidad acumulada de obtener ganglios afectados con respecto al promedio general representado en la línea 0 todavía discurre por encima de ella, es decir, va en aumento conforme se analizan más ganglios. Ya a partir de unos 26 ganglios analizados, la probabilidad acumulada de obtener más ganglios afectados que los esperados tiende a estabilizarse, es decir, por más ganglios que se analicen a partir de unos 25-26 ganglios, no varía sustancialmente la probabilidad de encontrar ganglios afectados. En términos prácticos podríamos deducir que, en este tumor, por debajo de 12 ganglios analizados existe el riesgo de infraestadificar el estadio ganglionar de los pacientes, y que a partir de unos 26 ganglios analizados este riesgo prácticamente desaparece en términos de probabilidad acumulada. Por lo tanto, por una parte sería deseable no obtener menos de 12 ganglios en ningún caso y, por otra, la cifra mínima de ganglios que se debe obtener para una estadificación ganglionar absolutamente segura de acuerdo con los datos disponibles en la serie que se analiza sería de unos 25-26 ganglios, aproximadamente.
Otro de los usos de este tipo de gráfica, paralelo al descrito y provisto del mismo fundamente matemático, es el cálculo de puntos de corte óptimos clínicamente bien fundados en variables continuas, cuando se quiere categorizarlas para su análisis estadístico, debido a su capacidad de detectar estos sutiles cambios en las tendencias. El objetivo es, pues, establecer puntos de corte óptimos para la creación de subgrupos de riesgo, más bien basados en el riesgo propiamente dicho que en artificios matemáticos dirigidos a maximizar el poder estadístico (como son los cortes por percentiles). El principal problema de los métodos de estadificación basados en la obtención de scores de riesgo, es establecer los puntos de corte correctos para la obtención de los diversos subgrupos de pronóstico diferenciado. La muchas veces utilizada división por percentiles obtiene unos subgrupos muy similares en cuanto al número de casos, por lo tanto, el tamaño de la muestra está maximizado para cada uno de ellos, y como consecuencia, el poder estadístico, motivo por el cual es más fácil obtener diferencias estadísticamente significativas, pero tiene el inconveniente de poder mezclar dentro de cada subgrupo casos con distinto riesgo que redunda en una escasa significación clínica.
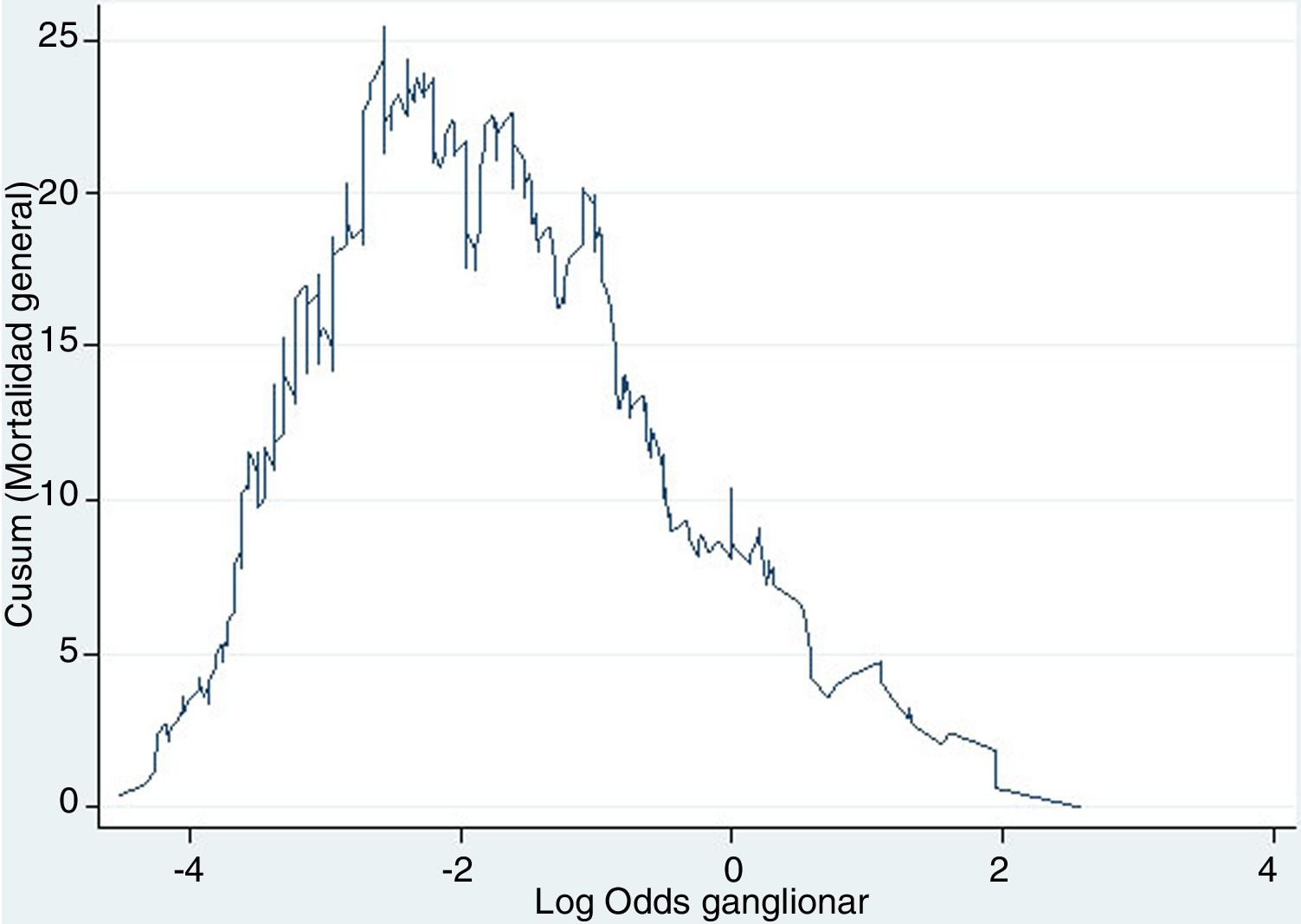
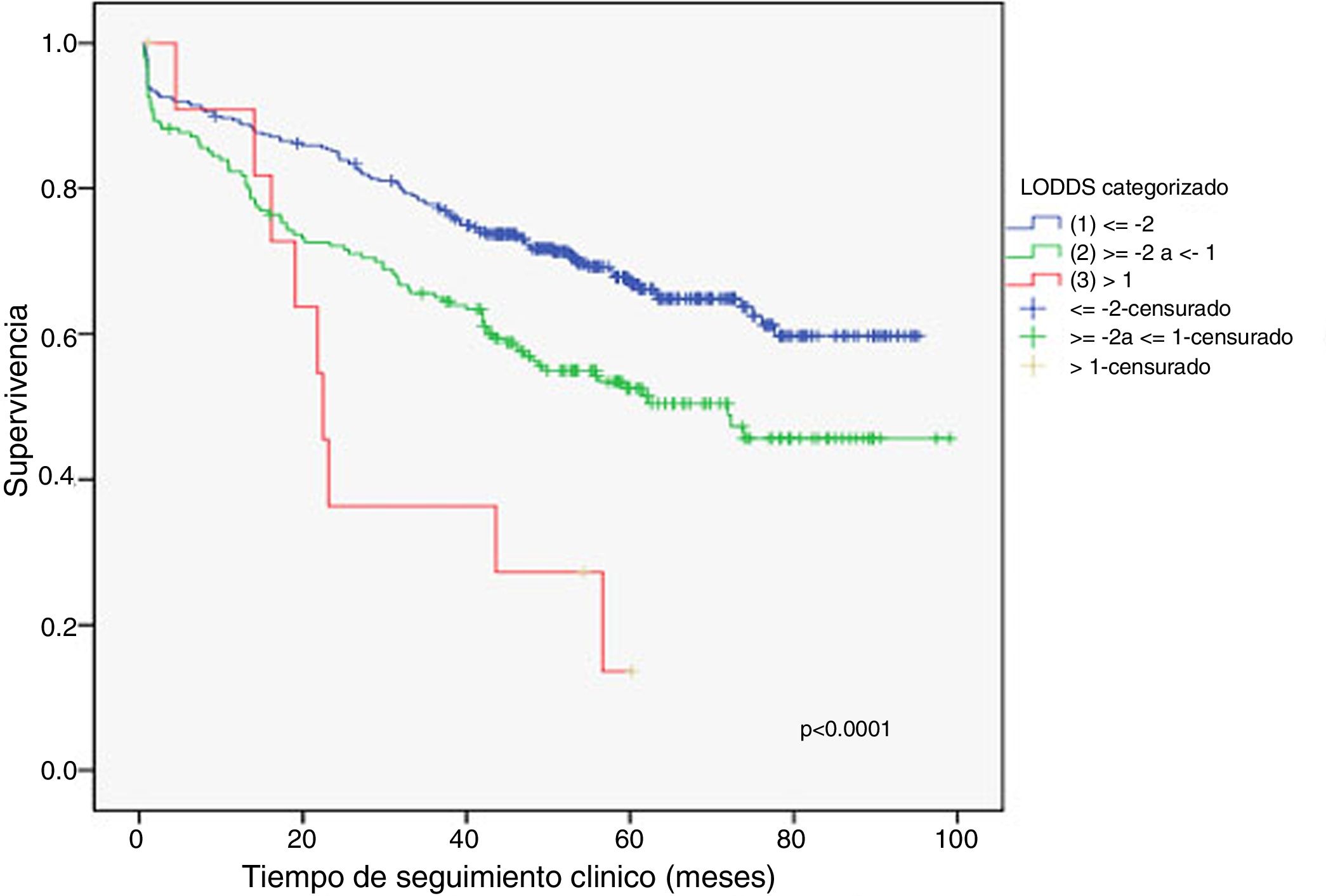
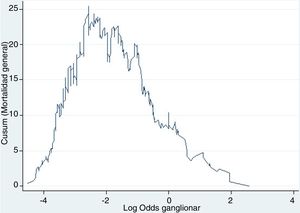
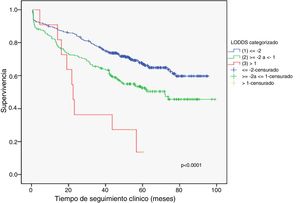
Ejemplo 4El logaritmo de odds ganglionar (LODDS) se trata de un método de estadificación ganglionar y se define como el logaritmo del cociente entre ganglios positivos y negativos+una constante, para evitar la singularidad. En la figura 4 se calcularon los puntos de corte para el logaritmo de odds ganglionar (LODDS) en el cáncer de colon. A simple vista, llama la atención un acúmulo del riesgo de mortalidad general hasta una cifra de LODDS alrededor de -2, para posteriormente descender este riesgo de forma hasta -1 y finalmente una fase con descenso del riesgo más suave. Por ello, estos cambios de tendencia definirán a 3 subgrupos de riesgo para LODDS: bajo riesgo: LODDS <-2; riesgo intermedio: LODDS de -2 a -1; y alto riesgo: LODDS de>-1, que corresponden con 3 grupos con supervivencias diferenciadas, tal como puede observarse en la figura 5.
En resumen, las gráficas CUSUM presentan múltiples aplicaciones en el campo de la cirugía, desde el control de calidad hasta la obtención de puntos de corte de una variable cuantitativa que tengan verdadero sentido clínico. Sería de gran interés generalizar su empleo con el objetivo tanto de monitorizar la actividad asistencial como para la mejora de la investigación clínica.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.