El análisis mediante elementos finitos (AEF) viene aplicándose en la bibliografía al estudio biomecánico de las prótesis de rodilla1-3. El diseño de los componentes de las artroplastias totales de rodilla tiene importantes consecuencias en la posterior función de la articulación, siendo la congruencia entre los mismos uno de los factores más relevantes, aunque también desempeña un papel importante el grosor del polietileno. Las alteraciones que se producen en las superficies articulares de las prótesis de rodilla aumentan con el tiempo de implantación, es decir, los ciclos de carga, y con el peso de los pacientes, es decir, la tensión causada por contacto. Por tanto, el daño es causado por la fatiga provocada por las solicitaciones cíclicas que soportan tanto la superficie como el interior del polietileno. Las prótesis de rodilla son mucho menos congruentes que las de cadera, tienen áreas de contacto significativamente menores y tienen que soportar mayores tensiones4.
Los objetivos generales de este trabajo han sido efectuar un modelo de articulación de rodilla, simulando el tejido óseo (fémur, tibia, peroné y rótula), meniscos (lateral y medial), ligamentos cruzados (anterior y posterior), ligamentos colaterales (medial y lateral), y el aparato extensor (tendón rotuliano y cuádriceps). Se han simulado las superficies óseas articulares (femororrotuliana y femorotibial) y la superficie de cartílago articular (femoral, tibial y rotuliana). También se ha realizado un modelo de artroplastia de rodilla, simulando el implante femoral, el implante tibial, el polietileno del implante tibial y el polietileno de la rótula. Para ello hemos estudiado el efecto de las cargas sobre el modelo anatómico, en la fase de soporte unilateral a 0º y 15º de flexión.
Se han estudiado los desplazamientos en los tres ejes del espacio, las tensiones en dirección vertical para los meniscos y tejido óseo (cortical y esponjosa), y las tensiones en dirección longitudinal para los ligamentos. También se ha analizado el efecto de las cargas sobre el modelo de artroplastia de rodilla en la fase de soporte unilateral a 0º y 15º de flexión, y los desplazamientos en los tres ejes, las tensiones en dirección vertical para el tejido óseo, las tensiones de Von Mises para los implantes femoral y tibial, y las tensiones en dirección longitudinal para los ligamentos y el aparato extensor.
MATERIAL Y MÉTODO
Se ha realizado la geometría y el mallado de un modelo de rodilla en 3D con elementos finitos, a partir de la geometría y mallado de un fémur estudiado previamente5. El procesador de cálculo utilizado para la simulación fue ABAQUS, v. 5.8. y el preprocesador I-DEAS MASTER SERIES, v.7. Simulamos en 3D un modelo de rodilla anatómica con los siguientes elementos: fémur distal, tibia y peroné proximales, rótula, meniscos, ligamentos cruzados anterior y posterior, ligamentos colaterales (externo e interno), aparato extensor (tendón rotuliano y cuádriceps), y las superficies articulares femorotibial y femoropatelar.
Se introdujeron las propiedades no lineales a los ligamentos trabajando sólo cuando estaban a tensión. Además de su no-linealidad y viscoelasticidad existía una gran variabilidad en las propiedades de los tejidos atendiendo a diversos factores como edad, localización anatómica, y exposición previa a diversos niveles tensionales. Por lo tanto, resultó imposible utilizar un único valor mecánico para todos los ligamentos. Los parámetros de rigidez utilizados en la simulación se recogen en la tabla 1. Los elementos de unión entre el ligamento y el hueso se solucionaron mediante elementos barra B32.
En el modelo se diferenciaron dos tipos de tejido óseo: hueso cortical y esponjoso, que se consideraron como materiales homogéneos, lineales e isótropos, con unas características determinadas siguiendo a Heegaard et al6 (tabla 2). Los valores de módulo elástico introducidos en el modelo se recogen en la tabla 3. A pesar del comportamiento anisótropo y heterogéneo de los meniscos, aplicamos un módulo de Young de 55 MPa, y Poisson de 0,37, y para el cartílago articular un módulo de Young de 5 MPa y Poisson de 0,478.
El contacto entre superficies cartílago de la rótula-cartílago del fémur distal se realizó mediante los pares de contacto («contact pair») de ABAQUS, mientras que para la unión menisco-cartílago del fémur y menisco-tibia se llevó a cabo un proceso de separación de nodos de la malla, es decir, se separaron de la malla los nodos en los que aparecían tensiones a tracción, manteniendo en aquella las zonas donde existían tensiones a compresión. Se estimó un coeficiente de fricción constante entre superficies de contacto de 0,001. La malla resultante tenía 17.684 elementos y 18.355 nudos.
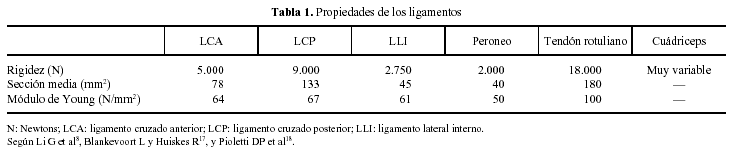
Además simulamos en 3D el modelo de artroplastia natural de rodilla (Sulzer Orthopedics, Inc, Austin, Texas) con los siguientes elementos: componente tibial, componente femoral, polietileno del platillo tibial y polietileno de la rótula. Se seleccionó un tamaño de prótesis adecuado a las características de la malla de rodilla previamente realizada. Resecamos el ligamento cruzado anterior (LCA) conservando el ligamento cruzado posterior (LCP). El polietileno utilizado para el modelo fue congruente de 7 mm de espesor. El módulo de Young y de Poisson se refleja en la tabla 4. El resultado final fue una malla de 495 elementos y 709 nudos (fig. 1).
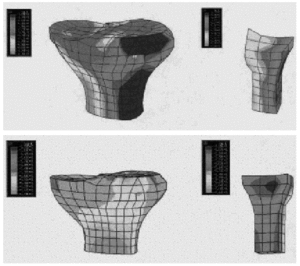
Figura 1. Malla en 3D del modelo de rodilla protésica.
A causa de la dificultad de reproducir en la simulación las restricciones al movimiento debidas a la articulación del tobillo y a los músculos que actúan sobre la rodilla, limitamos sus desplazamientos en la zona inferior, suficiente para obtener resultados cualitativos fiables de los estados tensionales y deformaciones de la articulación. Para simular el contacto entre los componentes, femoral y tibial, se separaron los nodos sometidos a tracción en la superficie de contacto. El contacto entre componente femoral y rótula se simuló mediante los elementos de contacto «contact pair» de ABAQUS.
Analizamos las tensiones de la rodilla a partir de las cargas que actúan sobre el extremo proximal del fémur en la fase media de apoyo, con un ángulo de giro de la rodilla de aproximadamente 15º, que siguiendo a Verdonschot y Huiskes9, fueron la carga por el peso corporal y la resultante de la acción de los músculos abductores (glúteo mayor, menor y medio) en el trocánter mayor (tabla 5).
Se analizó en dos posiciones diferentes: a 0º, en extensión completa de la rodilla, y a 15º de flexión o posición de apoyo final. El apoyo fue igual que en el caso de la rodilla sana, empotrando los nodos de la zona inferior de la tibia y peroné. Estudiamos los desplazamientos obtenidos en los tres ejes del espacio (U1, U2 y U3) y las tensiones en dirección vertical (S33) para el tejido óseo y meniscos; las tensiones en dirección longitudinal (S11) para los ligamentos y las tensiones de Von Mises para los componentes protésicos.
RESULTADOS
Desplazamientos
Rodilla anatómica a 0° de flexión
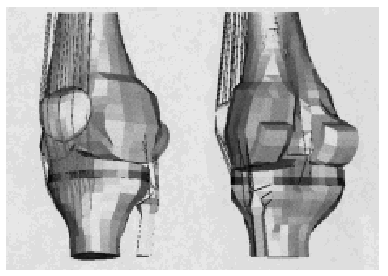
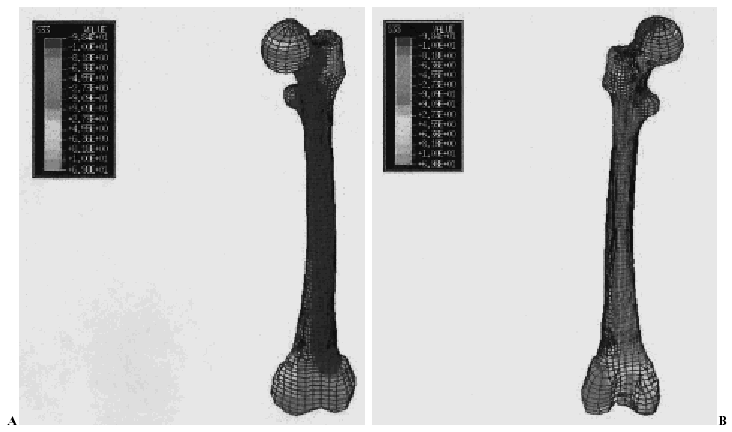
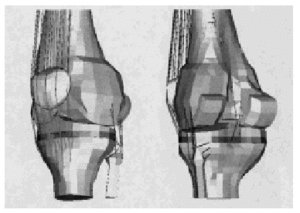
El mayor desplazamiento de la rodilla anatómica fue en dirección U2 con tendencia a desplazarse hacia delante (U2: 19 mm). También se desplazó hacia lateral (U1: 17mm) (fig. 2).
Figura 2. Desplazamientos del modelo de rodilla anatómica a 0º y 15º de flexión.
Rodilla anatómica a 15° de flexión
El desplazamiento fue mayor en dirección U2 (60 mm) y se desplazó hacia atrás. En el eje U1 se desplazó hacia medial (6 mm) (fig. 2).
Rodilla protésica a 0° de flexión
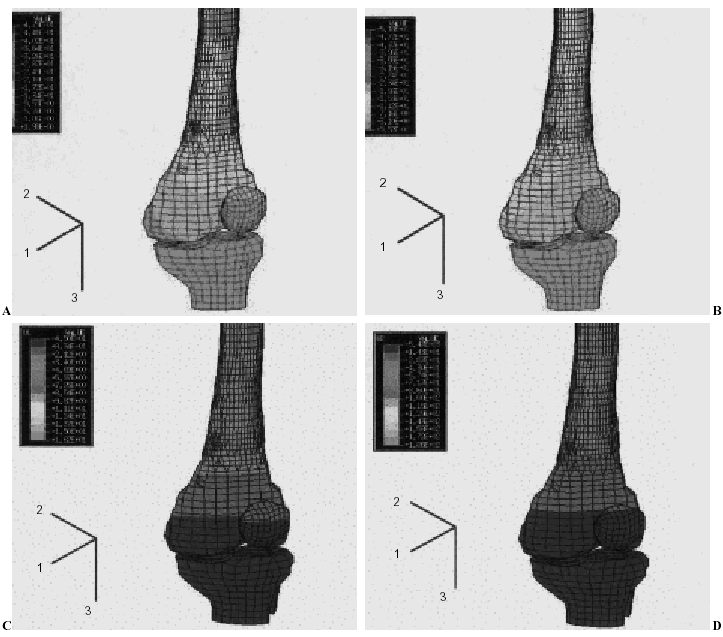
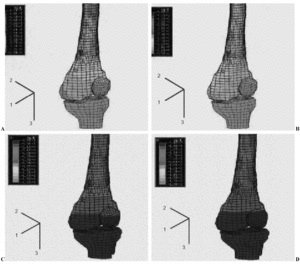
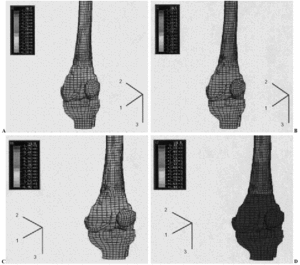
Coincidiendo con la rodilla anatómica, los desplazamientos fueron mayores en el eje U2 hacia delante (4 mm), seguidos de U1 hacia lateral (2 mm) y de U3 hacia arriba (1 mm). Sin embargo, estos valores se redujeron enormemente, alrededor de un 80%, debido a que la unión era mucho más rígida (fig. 3).
Figura 3. Desplazamientos del modelo de artroplastia de rodilla a 0º y 15º de flexión.
Rodilla protésica a 15° de flexión
El desplazamiento siguió siendo mayor en U2 (11 mm) hacia atrás, seguido de U1(3 mm) hacia medial (fig. 3). En comparación con la rodilla sana los desplazamientos en los tres ejes disminuyeron alrededor de un 70%. Además se observó que el desplazamiento en U1 fue mínimo hacia medial.
Tensiones
Rodilla anatómica a 0° de flexión
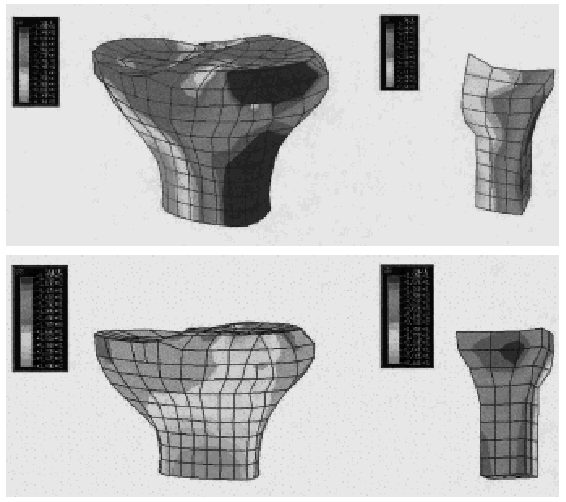
En las tensiones S33 sobre el fémur (fig. 4) se observó que la cara anterior del fémur trabajó a compresión, mientras que la posterior lo hizo a tracción, con tensiones máximas de 70 MPa en tracción y 100 MPa en compresión. En la zona de tejido esponjoso del fémur los valores de las tensiones disminuyeron casi 100 veces. En la tibia se obtuvieron tensiones a compresión en el platillo externo y a tracción en el platillo interno (fig. 5). Los valores de las tensiones máximas fueron menores que en el fémur (40 MPa a tracción y 35 MPa a compresión), debido a la acción de los meniscos.
Figura 4. Tensiones principales sobre el fémur en modelo de rodilla anatómica a 0º de flexión.
Figura 5. Tensiones principales en tibia y peroné en modelo de rodilla anatómica a 0º y 15º de flexión.
Las tensiones que aparecen en el peroné fueron muy pequeñas o prácticamente nulas. En la rótula las tensiones también fueron despreciables. Los elementos del menisco trabajaron a compresión en la zona superior donde contactaban con los cóndilos femorales. En la cara inferior de contacto con los platillos tibiales existió algún elemento trabajando mínimamente a tracción. El LCP (alrededor de 300 MPa) y el colateral interno trabajaban a tracción. Por tanto, la carga a la que está sometido el tejido óseo se encontraba en torno al 80% de su resistencia y el elemento más afectado por las condiciones del modelo fue el LCP, traccionando a 300 MPa.
Rodilla anatómica a 15° de flexión
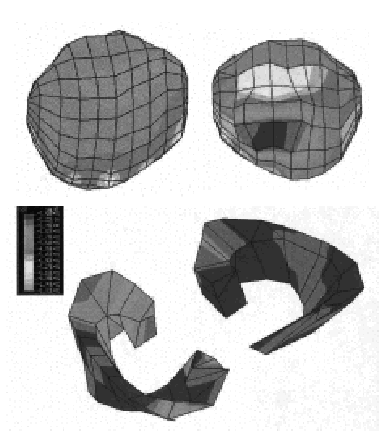
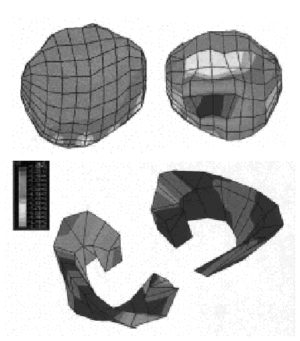
Las tensiones máximas de tracción fueron de 90 MPa en la cara anterior y de compresión de 110 MPa en la cara posterior. Sobre la tibia la zona traccionada correspondió a la zona anterior (110 MPa) y la zona comprimida a la posterior (130 MPa) (fig. 5). El peroné apenas apareció tensionado. La rótula mostró tensiones importantes sobre su superficie. Por un lado apareció el contacto con la tróclea femoral que comprimía la zona posterior (90 MPa) y, por otro, el ligamento rotuliano traccionó la superficie anterior (120 MPa) (fig. 6). Los meniscos trabajaron a compresión en su cara superior (70 MPa). En algunas zonas de la cara inferior se observaron concentraciones de tensiones a tracción (130 MPa) (fig. 6). El tendón rotuliano y el cuádriceps aparecieron más traccionados que en el caso anterior.
Figura 6. Tensiones en rótula y meniscos en modelo de rodilla anatómica a 15º de flexión.
Rodilla protésica a 0° de flexión
En el fémur se produjo compresión anterior (100 MPa) y tracción (70 MPa) en la zona posterior. Encontramos concentraciones de esfuerzos en el cuello femoral, tanto en tracción como en compresión, mientras que en el modelo anatómico la distribución de tensiones fue más uniforme. En la tibia, igual que en el modelo anatómico, se produjo compresión en el platillo externo y tracción en el interno. Los valores de las tensiones fueron similares a las del fémur (40 MPa en tracción y 45 MPa en compresión), ya que se eliminaron los meniscos. Las tensiones en el peroné fueron muy pequeñas o prácticamente nulas, igual que las tensiones en la rótula.
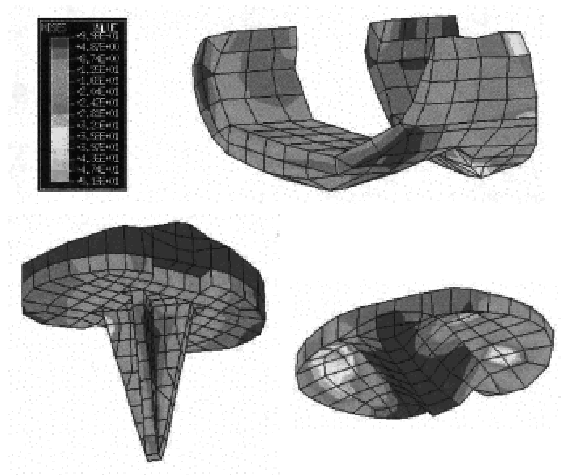
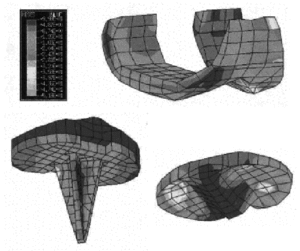
Respecto al análisis de tensiones según el criterio de Von Mises, vimos concentraciones de esfuerzo en el componente tibial. El vástago fue la zona más desfavorable, alcanzando tensiones de 260 MPa (fig. 7), lejos del límite de rotura. En el componente femoral encontramos más tensiones en la zona anteroexterna, en la zona de contacto con el componente tibial y en la zona de contacto con el hueso femoral, alcanzando tensiones máximas pequeñas (50 MPa) (fig. 7). En la bandeja de polietileno se observaron concentraciones de esfuerzo en la zona de contacto con el cóndilo femoral externo (10 MPa), lejos del límite de rotura (36 MPa) (fig. 7). La transmisión de tensiones en la prótesis se realizó a través de las zonas centrales de los cóndilos, mientras que en el modelo anatómico el menisco permitió una transmisión de tensiones sobre la periferia de los cóndilos. Y como se eliminó el LCA, el LCP tuvo que absorber todas las tensiones.
Figura 7. Tensiones de Von Mises en el componente femoral, tibial y polietileno en modelo de prótesis de rodilla a 0º.
Rodilla protésica a 15° de flexión
Como en el caso anatómico, se produjeron tensiones de tracción en la cara anterior (90 MPa) y compresión en la cara posterior (100 MPa), con valores similares a la rodilla sana. Por su parte, en la tibia, la zona traccionada correspondió a la anterior y la comprimida a la posterior, con valores de 120 MPa tanto a tracción como a compresión. Como en los casos anteriores, el peroné no sufrió tensión y en la rótula se encontraron tensiones importantes.
Respecto a las tensiones de Von Mises, las máximas concentraciones aparecieron en el vástago del componente tibial, con tensiones de 650 MPa. En el componente femoral las zonas con mayores tensiones fueron la zona anterior e interna, y la zona de contacto con el hueso femoral y con el componente tibial, con valores máximos de 300 MPa. El componente de polietileno sufrió menor tensión (47 MPa) que la bandeja metálica del componente tibial. Esta concentración se hizo máxima en la zona posterior de los platillos. Sin embargo, la tensión superó el límite de rotura del material (36 MPa), por lo que el polietileno podría romperse. El aparato extensor (tendón rotuliano y cuádriceps) y el ligamento lateral interno (LLI) trabajaron a tracción.
DISCUSIÓN
El AEF es un método aproximado de cálculo, que se acerca al valor de los desplazamientos mediante funciones polinómicas definidas por su valor en un conjunto de puntos del sólido. La investigación en esta materia supone la realización de experimentos muy costosos con especímenes reales. De ahí el interés por encontrar modelos numéricos que simulen de forma suficientemente aproximada el comportamiento del fémur. En este trabajo, el AEF nos ha permitido elaborar la simulación de una estructura tan compleja como es la rodilla, y a partir de la malla realizada hemos estudiado el comportamiento biomecánico de un modelo de prótesis de rodilla. Se trata de una aproximación e idealización de una estructura anatómica, con multitud de limitaciones que convendría destacar cuidadosamente. Se han simplificado aspectos importantes como el apoyo en la zona superior de la tibia y peroné, el estado de cargas a nivel del fémur en el apoyo monopodal durante el ciclo de la marcha, y la caracterización del comportamiento del hueso, cartílago, meniscos y ligamentos.
Las características particulares de los distintos tejidos y materiales son datos aproximados, que entran dentro del rango de valores tomados de estudios previos. Puesto que buscamos datos cualitativos y comparativos, hemos considerado para nuestra simulación el tejido óseo como un material homogéneo, lineal e isótropo. Trabajos previos también analizan sus limitaciones del modelo y destacan la anisotropía del hueso esponjoso en la tibia proximal, sin conocerse el efecto que podría tener esta anisotropía en los resultados. En los 6 modelos de componentes tibiales simulan una unión perfecta. Comparan los diseños exclusivamente en función del nivel de tensión, lo cual probablemente no es suficiente para explicar todos los tipos de aflojamiento.
Hemos analizado los desplazamientos y la distribución de tensiones en dos momentos determinados del apoyo monopodal del ciclo de la marcha: con la rodilla en extensión completa y a 15º de flexión, que corresponde a la posición de apoyo final y es la más desfavorable. En nuestro modelo con la rodilla en flexión de 0º observamos que los desplazamientos obtenidos en el modelo de la rodilla anatómica son mayores en las tres direcciones que en la rodilla con artroplastia. Esto es debido a que la rigidez del polietileno es mayor que la de los meniscos. Además, al colocar la artroplastia de rodilla se reseca el LCA y se conserva el LCP, produciéndose una mayor rigidez en la unión. Lo mismo ocurre cuando estudiamos los desplazamientos con la rodilla en flexión de 15º. En el eje transversal (eje 1) el desplazamiento hacia medial de la rodilla anatómica es superior que en la rodilla artroplastia, que prácticamente no se desplaza.
El desplazamiento es diferente en función del ángulo de flexión de la articulación, manteniendo las condiciones de apoyo y la distribución de cargas. En el caso de extensión completa, en ambos casos, el fémur tiende a desplazarse hacia la posición anterior, con un mayor trabajo para los ligamentos cruzados. En el caso de 15º de flexión, el fémur tiende a desplazarse hacia atrás, con mayor trabajo del cuádriceps y tendón rotuliano. Kraemer et al10 analizan los micromovimientos a nivel del platillo tibial en dos modelos no cementados, debido a cargas axiales (lateral, medial, anterior, posterior), de cizallamiento y torsionales. La fijación con tetones y con vástago no son adecuados y producen micromovimientos importantes, mientras que la asociación de vástago con tornillos produce la fijación más estable, lo cual favorece una buena integridad ósea.
Respecto a las tensiones producidas en el tejido óseo, en la rodilla con artroplastia en extensión, los valores son los mismos que en el modelo de rodilla anatómica. Sin embargo, se produce una mayor concentración de tensiones a nivel de la cabeza femoral, mientras que en el modelo de rodilla anatómica la distribución es más uniforme. Esto podría explicar la existencia de fracturas subcapitales por tensión en portadores de prótesis de rodilla11. Al pasar de extensión a flexión, las tensiones tibiales alternan de compresión lateral a compresión posterior, y de tracción medial a tracción anterior.
Otro factor a tener en cuenta es la distribución de tensiones en la rodilla anatómica que se transmite del fémur a la tibia por medio de los meniscos, de manera que la superficie de contacto de los cóndilos femorales sea la máxima posible. Sin embargo, la transmisión de la carga a través de la artroplastia se realiza de manera más localizada. Esta zona más delimitada de contacto depende de la posición de flexión en la que se encuentre la rodilla y del diseño de la prótesis 4,12,13.
Bartel et al4 compararon mediante AEF las tensiones y las deformaciones relativas producidas por el contacto, en 8 modelos de prótesis coexistentes. Las condiciones del estudio han sido las peores, es decir con un polietileno del menor espesor disponible, con la rodilla en flexión y en máxima carga. La tensión de contacto era mayor en aquellos modelos que presentaban superficies articulares poco congruentes. La fatiga era mayor en los componentes no conformados que en aquellos otros que sí lo estaban. Las máximas deformaciones relativas ocurrieron donde las tensiones de Von Mises eran mayores, es decir, a 1 ó 2 mm por debajo de la superficie articular. En este estudio se confirman las ventajas de los diseños de prótesis de rodilla con mayor congruencia en las superficies articulares y mayor espesor del componente de polietileno. Aconsejan un espesor mínimo de polietileno de 8 mm para disminuir las tensiones que producen el daño en la superficie12.
Postak et al14 estudiaron la influencia de la geometría en la distribución de tensiones y las áreas de contacto en 8 modelos de prótesis de rodilla, a 0º, 60º y 90º de flexión. Elbert et al15 estudian mediante AEF las tensiones producidas a nivel de la articulación femororrotuliana con la rodilla en flexión, en dos diseños de implantes rotulianos, ambos con soporte metálico. Se simula un contacto simétrico en los dos cóndilos femorales. El diseño de superficie cóncava aumenta la superficie de contacto con una menor producción de tensiones. Una rótula de poco espesor disminuiría el grado de desplazamiento y el área de contacto, y aumentaría las tensiones de contacto. Sólo se estudia la influencia del diseño de la geometría de superficie de la rótula. Las propiedades del polietileno asimismo son importantes y también cambian.
Rakotomanana et al16 compararon mediante AEF la transferencia de cargas a través de la bandeja tibial en el hueso subyacente en dos modelos de prótesis de rodilla. Observaron que el pico de tensión que se producía en la interfaz por debajo de la bandeja metálica tibial era menor en la prótesis no cementada (PCA --«porous coated anatomic»--) que en la cementada (MTTC --«cemented metal tray total condylar»--). Los micromovimientos por cizallamiento se observaron en ambos modelos.
En cuanto a las tensiones obtenidas en la artroplastia de rodilla, el componente tibial es el que más trabaja, sobre todo en la zona del vástago pero también en la bandeja metálica. Sin embargo, las tensiones obtenidas en ambas situaciones, en extensión y en flexión de 15º, están muy por debajo del límite elástico de rotura del material.
Las tensiones obtenidas sobre el polietileno con la rodilla en flexión de 15º pueden superar su límite tensional. Estos valores sólo se encuentran en una zona concreta del polietileno, por lo que podría ser un problema de mallado. Además, sólo se considera el efecto de una carga estática, sin tener en cuenta otros factores como modificación de áreas de contacto, coeficiente de fricción, y tensiones sobre superficie y subsuperficie del polietileno. El componente femoral es el que menos tensiones sufre, lo cual puede explicar una evolución más favorable.
A pesar de las limitaciones del modelo podemos afirmar que el AEF permite realizar un estudio biomecánico comparando el comportamiento estructural de la rodilla anatómica y la rodilla con artroplastia. Se trata de un modelo válido para obtener los primeros resultados, que permitan profundizar en el estudio del comportamiento de la articulación de la rodilla.