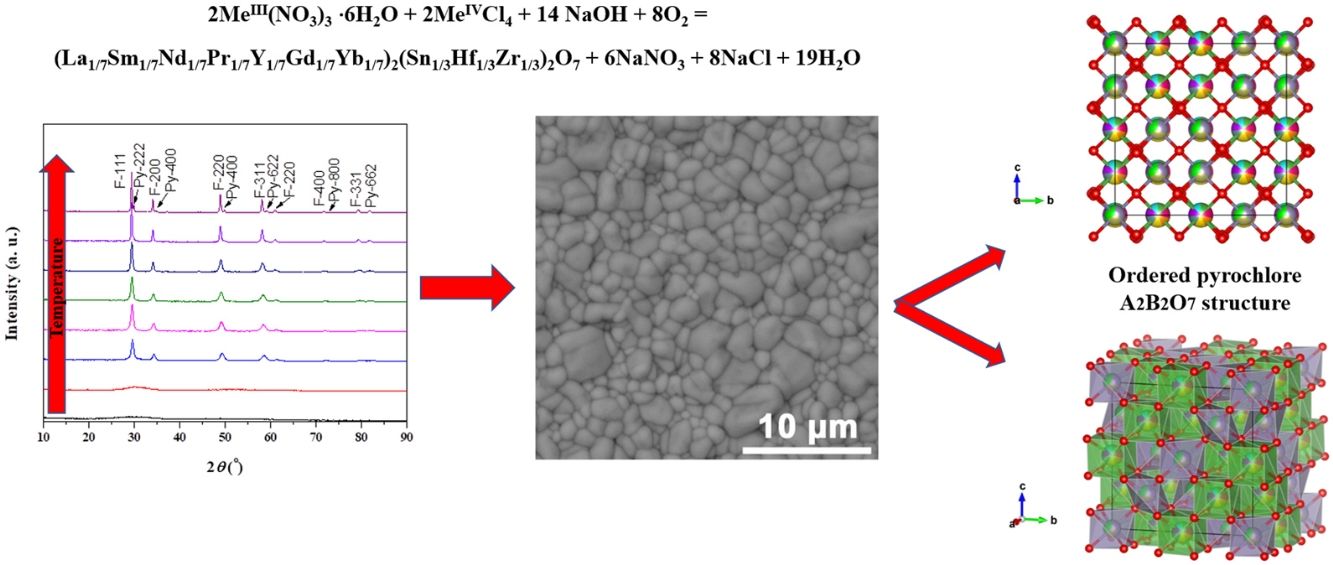
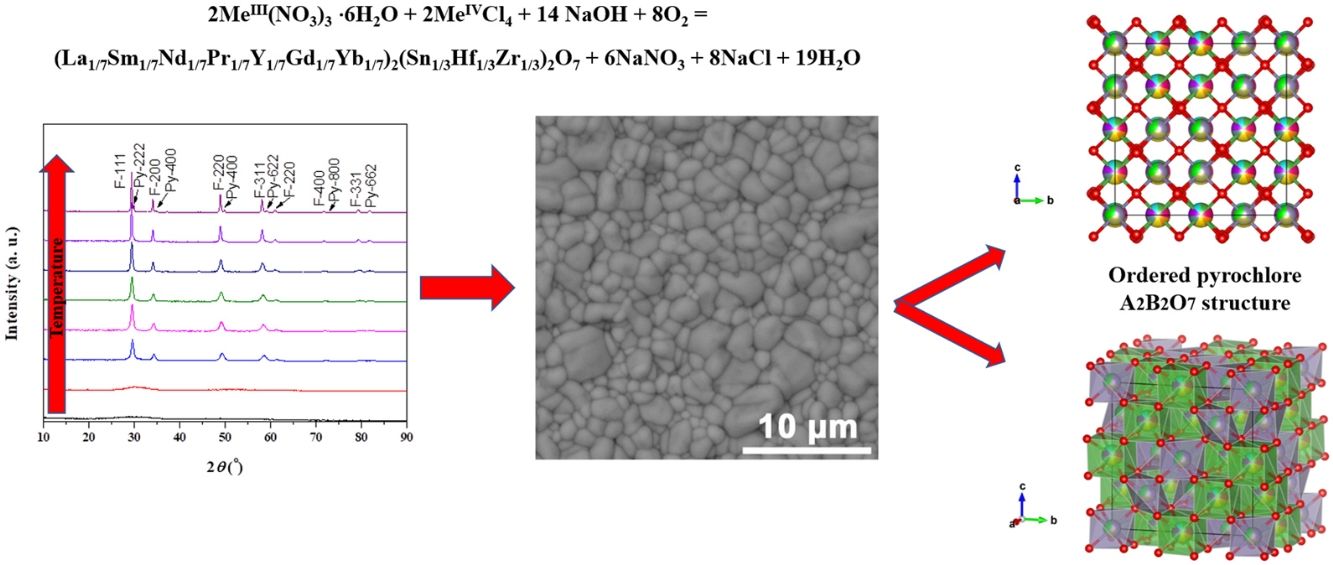
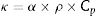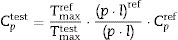Multicomponent oxide with pyrochlore structure (A2B2O7), containing 7 different A-site cations and 3 B-site cations in equiatomic amounts, was synthesized. Powders with nominal composition (La1/7Sm1/7Nd1/7Pr1/7Y1/7Gd1/7Yb1/7)2(Sn1/3Hf1/3Zr1/3)2O7 were fabricated through a reaction of metal nitrates (A-site) and metal chlorides (B-site) with sodium hydroxide during the solid state displacement reaction. Room temperature synthesis initially resulted in the obtainment of amorphous powders, which crystallized after subsequent calcination to form single crystalline compounds. Crystalline high-entropy ceramic powders formation took place at temperatures as low as 750°C. During calcination, defective fluorite (F-A2B2O7) and crystal pyrochlore (Py-A2B2O7) structures coexist. A large number of cations induce the obtainment of stable high-entropy pyrochlores. Results showed that sintering at 1650°C lead to pure crystalline single-phase pyrochlore formation. High-density ceramic, free of additives, was obtained after powders were compacted and subjected to pressureless sintering at 1650°C. Multicomponent pyrochlore structure was investigated using the theoretical and experimental multi-methodological approach.
Se sintetizó un óxido multicomponente con estructura de pirocloro (A2B2O7), conteniendo siete diferentes sitios catiónicos A y tres sitios catiónicos B en cantidades equiatómicas. Se fabricaron polvos con composición nominal (La1/7Sm1/7Nd1/7Pr1/7Y1/7Gd1/7Yb1/7)2(Sn1/3Hf1/3Zr1/3)2O7, a través de una reacción de nitratos metálicos (sitios A) y cloruros metálicos (sitios B), usando hidróxido de sodio durante la reacción de desplazamiento en estado sólido. Inicialmente, la síntesis a temperatura ambiente produjo polvos amorfos, los cuales fueron cristalizados después de someterlos a calcinación para formar compuestos monocristalinos. La formación de polvos cerámicos cristalinos de alta entropía se obtuvo a temperaturas tan bajas como 750°C. Durante la calcinación coexisten estructuras de fluorita desordenada (F-A2B2O7) y pirocloro cristalino (Py-A2B2O7). Un número significativo de cationes induce la obtención de pirocloros estables de alta entropía. Los resultados mostraron que la sinterización a 1.650°C condujo a la formación de un pirocloro cristalino puro monofásico. Se obtuvo una cerámica de alta densidad y libre de aditivos después de compactar los polvos y someterlos a sinterización sin presión a 1.650°C. La estructura del pirocloro multicomponente se investigó utilizando el enfoque multimetodológico teórico y experimental.
The pyrochlore compound has a general formula of A2B2O6O′, where A and B sites are usually occupied by +3 and +4 cations, respectively, while oxygen at the same time occupies two different positions (O and O′) [1,2]. The formation of a stable A2B2O7-type pyrochlore structure is determined by a geometric factor defined as a ratio of the A-site cation radius, r(A), and the B-site cation radius, r(B). Namely, for the formation of a stable A2B2O7-type pyrochlore structure, the above-mentioned radius ratio must be in the range between 1.46 and 1.78 [3,4]. A few years ago, this concept of high-entropy alloys, i.e. solid solutions with five or more elements in equal or near-equal molar ratio, was introduced into ceramic materials engineering [5–7].
Among all high-entropy oxides, pyrochlores can be singled out as the most prominent compounds for the future practical applications due to their diverse compositions and properties, such as thermal conductivity [8,9], ionic conductivity [10,11], geometrically frustrated magnetism [1], neutron absorption [2], nuclear waste storage capacity [12], and excellent high-temperature stability [11]. The high application potential of these materials can also be attributed to their easily-controllable properties achievable through the change of constituent ions.
Many different methods can be used to fabricate pyrochlore ceramics. The most commonly used methods are solid state reaction [13], precipitation and combustion synthesis [5,6], hydrothermal route [7], sol–gel method [14], mechanical milling [15], and molten salt reaction [3]. Although the solid state displacement reaction (SSDR) is established as a low energy consumption method that is highly efficient, simple and results in the obtainment of powders with uniform morphology, it is rarely used in practice. Since the solid state displacement method is successfully used for the synthesis of a significant number of diverse oxide compounds and their solid solutions [16–19] it can be assumed that this method could be also effectively employed for the synthesis of multicomponent oxides, such as high-entropy pyrochlores.
Therefore, the aim of this study was to obtain high-entropy multicomponent oxide with the A2B2O7 pyrochlore structure that contains 7 different cations in site A and 3 cations in site B in equiatomic amounts by applying the solid state displacement reaction at room temperature and subsequent calcination at different temperatures. This synthesis route was chosen since it provides an excellent mixing of the constituent elements enabling in that way the formation of desired compound composition at a relatively low temperature. The phase evolution during calcination, the sinterability of the obtained powders, as well as some mechanical properties of the sintered high-entropy multicomponent oxide was investigated.
Materials and methodsExperimental proceduresMaterial synthesisStarting reactants for the synthesis of multicomponent oxide with pyrochlore structure were trivalent lanthanide (La, Sm, Nd, Pr, Gd, Yb, Y) nitrate powders in the hydrate form, tetravalent Zr, Hf, and Sn chloride powders, and sodium hydroxide granule supplied by Merck, USA. Amounts of all starting reactants were calculated according to the nominal composition of the final reaction product, i.e. (La1/7Sm1/7Nd1/7Pr1/7Y1/7Gd1/7Yb1/7)2(Sn1/3Hf1/3Zr1/3)2O7. Usually, in the case of entropic materials, only one sublattice is filled with several different elements (≥5 elements) while the other sublattice is occupied by a single element. The aim of the present work was, therefore, to achieve the stable A2B2O7 structure in which both (A and B) cationic sites in the compound are multi-elemental with 10 different elements in total, i.e. the objective was to attain the stable structure with a very complex chemical composition which was not synthesized before.
The synthesis reaction was proposed according to the following equation:
The calculated fractions of starting reactants were hand-mixed in an alumina mortar for 5min. The by-products of the synthesis reaction are NaNO3 and NaCl. To remove the formed by-products, the reaction mixture was centrifuged for 10min at 3500rpm three times in distilled water and two times in alcohol using the Centurion 1020D centrifuge, Centurion Scientific Ltd., UK.
The synthesized powders were then calcined for 2h at temperatures ranging from 600°C to 1500°C. Calcined powder, obtained after the heat treatment at 1350°C, is afterward subjected to a uniaxial pressure of 30MPa, and then cold-isostatically pressed at 150MPa without any binder utilizing the Riken Power press, Riken Seiki Co. Ltd., Japan, into the cylindrical green bodes with 10mm in radius and 10mm in height. The compacted cylindrical samples were additionally conventionally sintered for 4h in a furnace at 1650°C with a heating rate of 10°Cmin−1 in a statistic air atmosphere.
Materials characterizationThe synthesized and calcined powders were characterized by the X-ray diffraction (XRD) technique using a RIGAKU Ultima IV diffractometer with Ni-filtered Cu Kα radiation (λ=1.54178Å). Crystal structure of these powders was analyzed in the 2θ range from 10 to 90°. For the phase analysis the PDXL2 software (version 2.0.3.0) [21], with reference to the patterns of the International Centre for Diffraction Data (ICDD) [22], was used.
The experimental data obtained during the powders XRD analysis were used for the Rietveld structural refinement calculations by means of the Full Prof software [23] to derive relevant structural parameters. In a typical Rietveld refinement, individual scale factors and profile, background, and lattice parameters are varied. In favorable cases, the atomic positions and site occupancies can also be successfully varied to obtain the most correct structural models.
In order to clarify the structure of sintered multicomponent ceramics at the chemical bond's level, the Fourier-transform infrared spectroscopic (FT-IR) analysis was performed. The sintered ceramic samples were for that purpose finely powdered, evenly mixed with potassium bromide (KBr) (2mg of the sintered sample was mixed with 150mg of KBr) and vacuum-pressed at 200MPa into lozenges. Pure KBr lozenge was used as a reference. The FT-IR measurements were performed at room temperature using a Bomem MB-100 spectrometer, Hartmann & Braun, Canada, to obtain sub-formed spectra. All spectral data of the sintered multicomponent ceramics were collected in the range of 4000–400cm−1 with a resolution of 2cm−1.
The as-synthesized and calcined powders’ morphology and elemental distribution were analyzed by a JSM-IT300LV scanning electron microscope (SEM), JEOL, USA, operated at 20keV and coupled with an X-max energy dispersive spectrometer (EDS), Oxford Instruments, UK, and Aztec software.
A Micromet 5101 Vickers microindentation hardness tester, Buehler, Germany, was utilized to determine the sintered samples’ microhardness. The microhardness measurements were conducted by applying a load of 1kgf (9807mN) for a dwell time of 15s at 10 measuring points of each sample with excellent reproducibility.
The sintered samples’ density was measured by applying the Archimedes principle in distilled water. The theoretical density was calculated based on the crystal structure of pyrochlore with the space group 227 and the proportional ratio of cations according to the desired nominal composition.
The DXR Raman Microscope, Thermo Fisher Scientific Inc. USA, equipped with an Ar laser operating at an irradiation wavelength of 532nm was used for recording the sintered high-entropy pyrochlore ceramics Raman spectra. Multiple Raman spectra were recorded under the laser power of 5mW for a collect exposure time of 5s at different sample positions to confirm the samples’ homogeneous structure.
Thermal conductivity, κ, of the sintered samples was calculated from the experimentally determined thermal diffusivity, α, density, ρ, and specific heat capacity, Cρ, according to Eq. (2):
Thermal diffusivity was measured by an LFA427 laser flash apparatus, Netzsch, Germany, in a nitrogen atmosphere at temperatures up to 1000°C. The specific heat capacity was determined by a comparative method using two identical (size/diameter) samples, i.e. reference and investigated sintered sample, under the same conditions [24]. The Cp was calculated by Eq (3):
where Tmax refers to the maximum temperature recorded on a sample, ρ is the sample density, and l is the sample thickness. Superscripts ref and test are referring to the reference and test samples, respectively. A Pyroceram 9606, Netzsch, Germany, was used as reference material.Theoretical investigationsMulticomponent solid solution with pyrochlore structure was investigated using a multi-methodological approach [25,26]. Structure candidates were generated using the Primitive Cell Approach for Atom Exchange (PCAE) method [27] and the supercell approach [28] within the Crystal17 program package [29,30], while investigation of disordered systems and multicomponent solid solutions was conducted using the group action theory [31]. Full structural optimization on the ab initio level was performed using the Quantum Espresso code [32,33]. Moreover, non-stochiometric systems were additionally investigated in the Crystal17 code [29,30] where build-in tools allow adding/removing atoms to reach the stoichiometric multicomponent system of interest [34,35]. Results of such calculations, which are highly important in the exploration of energy landscapes under extreme conditions [36], were successfully applied and discussed previously [25,37,38]. Density functional theory (DFT) calculations were utilized, using the generalized gradient approximation (GGA) with the Perdew, Burke, and Ernzerhof (PBE) functional [39] in both quantum mechanical codes.
The Quantum Espresso (QE), as plane wave-based code with 600eV cutoff energy and 6×6×6K-point mesh [32,33], was used for the present investigations. In particular, the QE basis sets used in this study included the set for lanthanum labeled as La.pbe-spfn-kjpaw_psl.1.0.0.UPF, the set for gadolinium labeled as Gd.pbe-spdn-kjpaw_psl.1.0.0.UPF, the set for neodymium labeled as Nd.pbe-spdn-kjpaw_psl.1.0.0.UPF, the set for prasedinium labeled as Pr.pbe-spdn-kjpaw_psl.1.0.0.UPF, the set for samarium labeled as Sm.pbe-spdn-kjpaw_psl.1.0.0.UPF, the set for yttrium labeled as Y.pbe-spn-kjpaw_psl.1.0.0.UPF, the set for ytterbium labeled as Yb.pbe-spn-kjpaw_psl.1.0.0.UPF, the set for hafnium labeled as Hf.pbe-spn-kjpaw_psl.1.0.0.UPF, the set for zirconium labeled as Zr.pbe-spn-kjpaw_psl.1.0.0.UPF, the set for tin labeled as Sn.pbe-dn-kjpaw_psl.1.0.0.UPF, and the set for oxygen labeled as O.pbesol-n-kjpaw_psl.0.1.UPF [40,41]. Convergence tolerance for the structure relaxation was fixed to 10−8.
In the case of the Crystal17 program, which is based on the linear combination of atomic orbitals [42], for calculations with 8×8×8K-point mesh using the Monkhorst-Pack scheme [43] the effective core pseudopotential (ECP) basis set for lanthanum denoted as La_ECP_Heifets_2013 [44], the basis set for gadolinium denoted as Gd_ECP_Doll_2008 [45], the all-electron basis set (AEBS) for yttrium denoted as AEBS_buljan_1999 [46], the basis set for samarium, neodymium, ytterbium and praseodymium denoted as ECP Sm, Nd, Yb, Pr ERD Small Core 2017 [47], the AEBS basis set for oxygen [48,49], the basis set for zirconium denoted as Zr_ECP_HAYWSC_311d31G_dovesi_1998 [50], the basis set for tin denoted as Sn_DURAND-21G*_causa_1991 [51], as well as the basis set for hafnium denoted as Hf_ECP_Stevens_411d31G_munoz_2007 [52] were used. The calculated structure symmetry was analyzed using the SFND algorithm [53] and RGS algorithm [54] implemented in the KPLOT software [55], while investigated pyrochlore structures were visualized using the VESTA code [56].
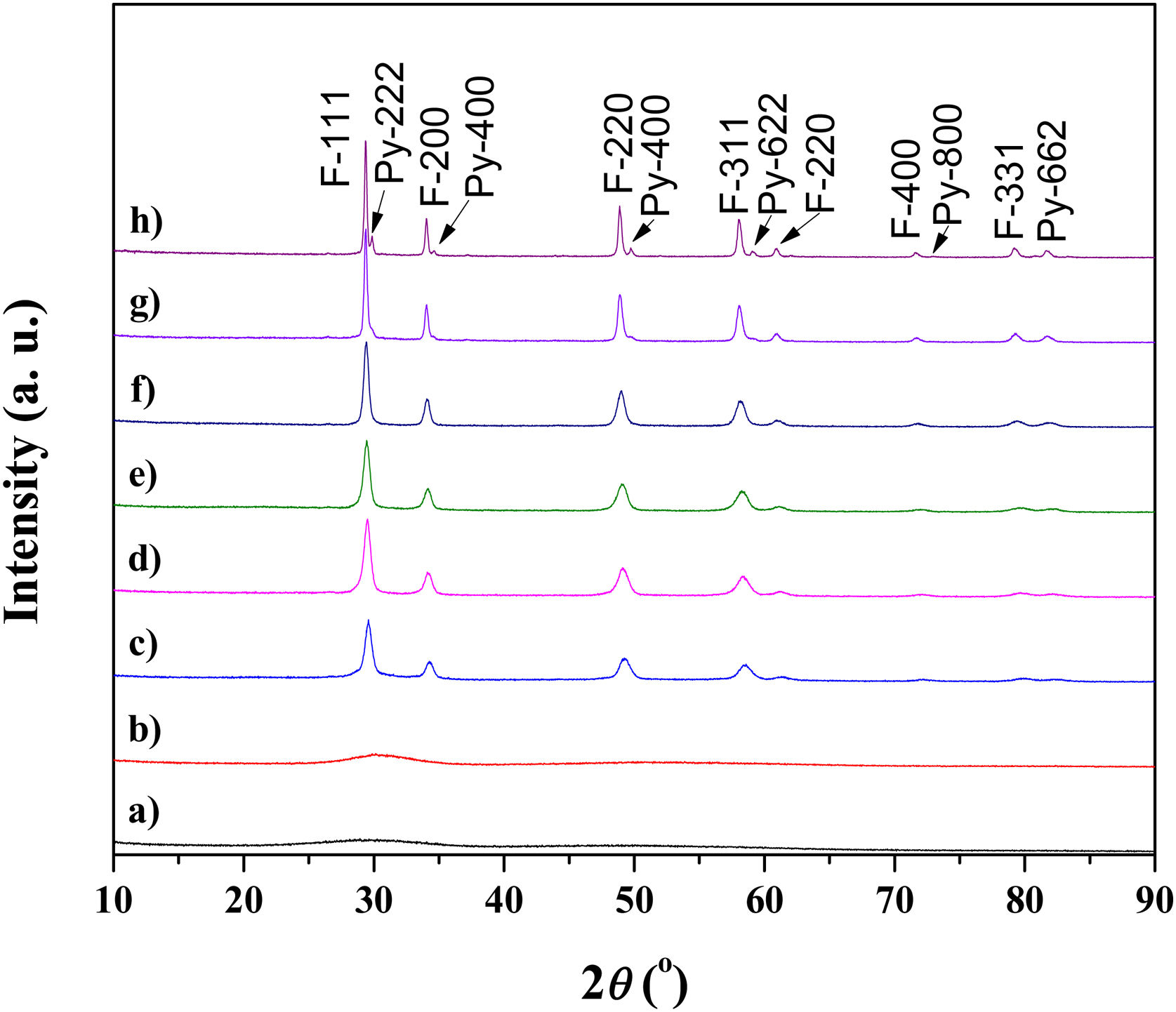
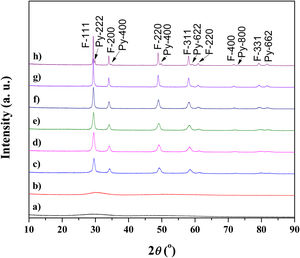
Results and discussionExperimental study of the multicomponent solid solution with pyrochlore structureThe formation of a stable A2B2O7-type pyrochlore structure, as previously emphasized, is expected if the ratio of A-site and B-site cations radius, r(A)/r(B), is in the range between 1.46 and 1.78. In the present study, the r(A)/r(B) ratio is 1.52 and a necessary geometric factor condition for the formation of a pyrochlore structure is completely fulfilled. Therefore, the formation of a stable pyrochlore structure during the presented experimental procedure is considered through the XRD analysis of the experimentally obtained powders. The XRD patterns of powders calcined at different temperatures for 2h are shown in Fig. 1.
The XRD patterns presented in Fig. 1 clearly indicate that the samples calcined at room temperature and 600°C show typical amorphous behavior without a long-range of atom ordering. The appearance of the first reflections occurs for the sample calcined at 750°C with very broad diffraction lines indicating its low crystallinity state. In the XRD pattern of the powder calcined at 750°C the strongest reflection, located at the 2θ value of ∼29°, can be assigned to the {111} reflection of the defect fluorite structure. Moreover, the other reflections present in this XRD pattern correspond to the fundamental fluorite structure with the 225 space group: F{200}, F{220}, and F{311}. However, at higher temperatures, calcination temperature causes narrowing of the diffraction lines and an increase in their intensities, which is the result of increased crystallite size. The powders thermally treated at 1500°C show that in addition to the defective fluorite-type structure, the phase with the pyrochlore-type structure also appears. A new phase exhibits an ordered pyrochlore-type structure which is characterized by the presence of typical superstructure diffraction peaks reviled using Cu Kα radiation [57,58].
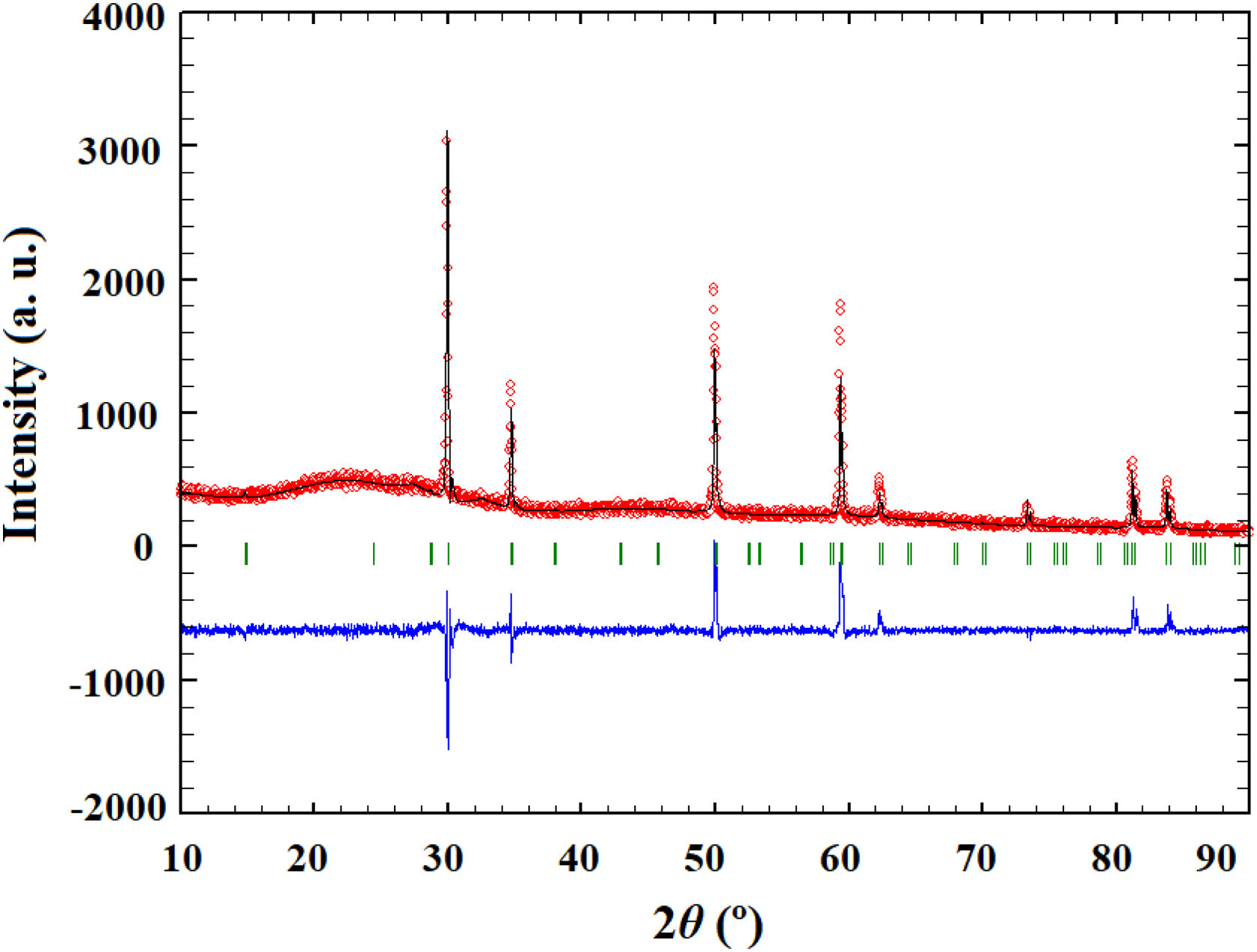
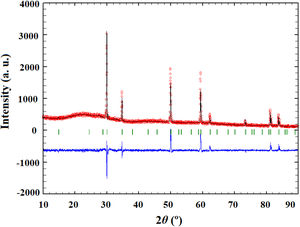
Powder calcined at 1350°C was subjected to an additional sintering process at 1650°C and Rietveld's method was employed to conduct structural refinement of its XRD pattern.
Pure crystalline pyrochlore phase in space group 227 (F d 3¯ m) was adopted for the Rietveld structural refinement of the XRD pattern obtained for the sample sintered at 1650°C. Among structural parameters, only unit cell parameter a and x coordinate for the O1 were refined. All other atoms were in special positions. Performed Rietveld refinement resulted in the obtainment of refined unit cell parameter a=10.3179(2) and oxygen coordinate x(O1)=0.363(1). The composition of the refined phase was set as (La1/7Sm1/7Nd1/7Pr1/7Y1/7Gd1/7Yb1/7)2(Sn1/3Hf1/3Zr1/3)2O7. The best fit between the calculated and observed XRD pattern of the sample sintered at 1650°C is shown in Fig. 2, where all allowed Bragg reflections are shown by vertical bars. Red line denotes the observed experimental diffraction pattern, while the black line represents the calculated diffraction pattern. The difference between experimental and theoretical diffraction patterns is shown as the blue line in Fig. 2. The accuracy of fitting obtained for the sample sintered at 1650°C can be monitored through the values of reliability (R) factors. The values of Goodness of Fit (GoF), Chi2, and RB factors are determined to be 2, 3.36, and 15.3, respectively, indicating good refinement of the experimentally obtained diffraction pattern.
Line-broadening analysis was performed using the Rietveld method in conjunction with the Warren–Averbach procedure to attain crystallite size and lattice strain parameters. In the present approach, the grain size broadening was represented by a Lorentzian function, while the micro strain broadening was depicted by a Gaussian function. The convolution of these functions is a pseudo-Voigt function, which is approximated by a modified Thompson-Cox-Hastings pseudo-Voigt.
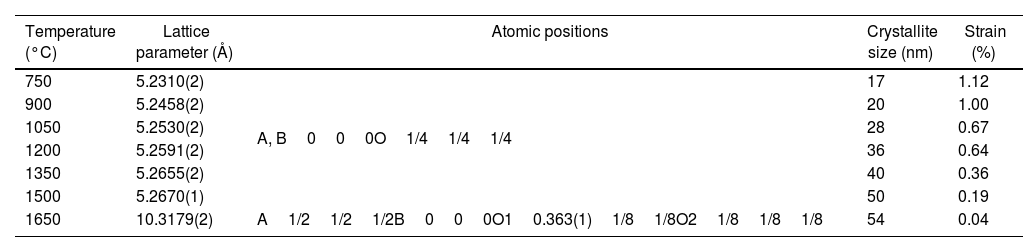
The contribution of the instrument is very important during the size-strain analysis. Keeping this in mind, a well crystallized CeO2 powder was refined to determine instrumental peak broadening and its contribution was implemented in the Rietveld refinement through the instrumental resolution irf file. The values of cell parameters along with the values of crystallite size and strain for powders calcined at different temperatures for 2h are presented in Table 1. The obtained crystallite sizes are in the nanometric range with crystallites (coherent domain) between 17nm and 50nm (Table 1).
Cell parameters, crystallite size, and internal strain of the calcined (La1/7Sm1/7Nd1/7Pr1/7Y1/7Gd1/7Yb1/7)2(Sn1/3Hf1/3Zr1/3)2O7 powders treated for 2h at different temperatures.
| Temperature (°C) | Lattice parameter (Å) | Atomic positions | Crystallite size (nm) | Strain (%) |
|---|---|---|---|---|
| 750 | 5.2310(2) | A, B000O1/41/41/4 | 17 | 1.12 |
| 900 | 5.2458(2) | 20 | 1.00 | |
| 1050 | 5.2530(2) | 28 | 0.67 | |
| 1200 | 5.2591(2) | 36 | 0.64 | |
| 1350 | 5.2655(2) | 40 | 0.36 | |
| 1500 | 5.2670(1) | 50 | 0.19 | |
| 1650 | 10.3179(2) | A1/21/21/2B000O10.363(1)1/81/8O21/81/81/8 | 54 | 0.04 |
Data presented in Table 1 clearly indicate that the average crystallite size increases with an increase in calcination temperature due to the growth of crystal domains and, accordingly, the number of imperfections present in the crystal is decreasing. On the other side, the internal strain decreases with a temperature increase. It could be assumed that this decrease is a consequence of an ordering of atomic arrangement during calcination. Namely, since the significant amount of strain is localized at the surface of crystallites as a result of a high concentration of broken bonds, the ordering of atoms leads to a reduction in internal strain.
This behavior can be clearly observed if data obtained in the case of synthesized powders thermally treated at lower temperatures, i.e. 750°C, are compared to data of powders calcined at higher temperatures. Accordingly, the internal strain decreases with an increase in crystallite size due to a decrease in the surface disordered region accompanied by grain growth during higher temperature calcination. Powder sample heat-treated at 1350°C, as well powder calcined at 1500°C, exhibit a very small internal strain.
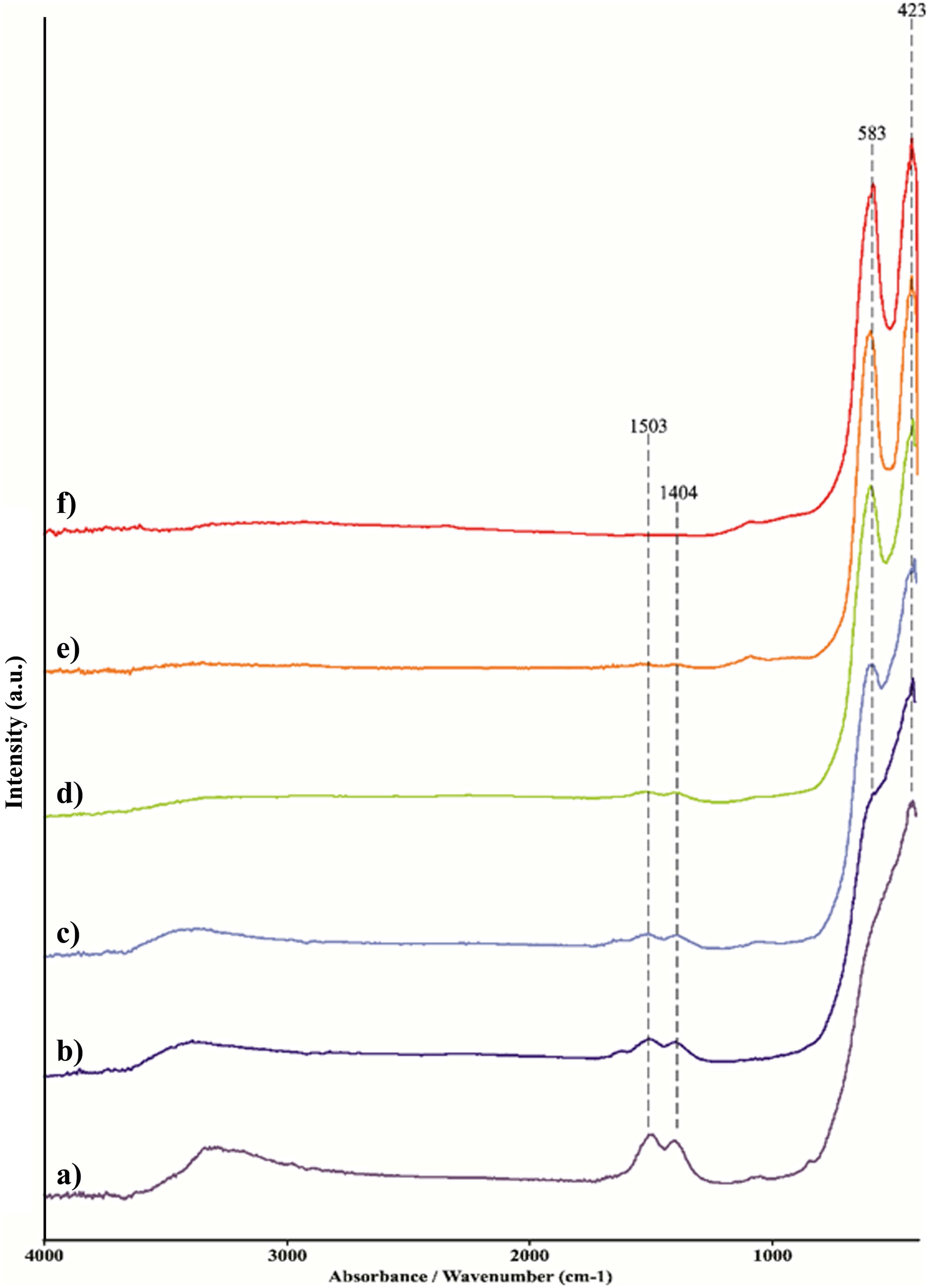
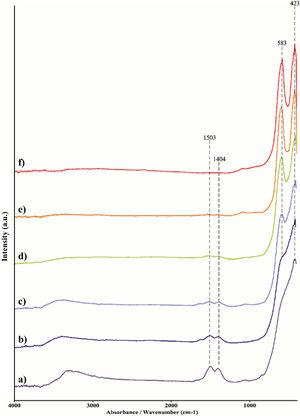
Since the synthesis reaction presented in Eq. (1) is very complex, and infrared active optic modes originate from the bending and stretching vibrations of the metal-oxygen bonds, the FT-IR spectroscopic analysis was carried out to observe the nature of metal-oxygen bonds in the calcined samples at different temperatures [59]. Fig. 3 shows the FT-IR spectra of the obtained calcined powders. The recorded FT-IR spectra indicate that powders heat-treated up to 1350°C (Fig. 3a–e) show hygroscopic behavior. Namely, the broad band present in the wave number range of 3600–3200cm−1 is characteristic of the stretching vibration of the O–H bond in water. The bending mode presented as peaks at 1503cm−1 and 1404cm−1 can be ascribed to water or M–OH bonds [60]. With an increase in the calcination temperature, the intensity of the O–H band decreases due to the manifestation of lower hygroscopicity, i.e. due to the total surface area reduction and enhanced atomic ordering. As a consequence, the sample treated at 1500°C shows no signs of hygroscopicity. The chemical bonds between numerous cations and oxygen exhibit metal–oxygen (M–O) stretching regimes in the 600–400cm−1 region. In contrast to the reduction and disappearance of the O–H bond, samples heated up to 900°C show new M–O peaks at 583cm−1 and 425cm−1. These peaks become even more intense for samples exposed to higher temperatures and are attributed to the octahedral group complexes (smaller tetravalent 6-coordinated cation, i.e. Sn, Zr, Hf) due to the phase transition onset from fluorite to pyrochlore structure.
SEM microstructural observations, as well as results of the EDS multi-elemental analysis of the obtained (La1/7Sm1/7Nd1/7Pr1/7Y1/7Gd1/7Yb1/7)2(Sn1/3Hf1/3Zr1/3)2O7 pyrochlore compound sintered at 1650°C for 4h are presented in Fig. 4. The synthesized high-entropy pyrochlore powder shows good sinterability. The attained sintered sample density was 98% of theoretical density, indicating a relatively fast densification process during sintering at 1650°C for 4h without the use of sintering additives. The microstructure of sintered sample is shown in Fig. 4a. The sintered pyrochlore ceramic material exhibits a bimodal structure which is mainly composed of grains with equiaxed morphology and size in the range from 1μm to 4μm, revealing the tendency of microparticles to coarsen during the sintering regime of 4h at 1650°C. Namely, it can be assumed that smaller grains are consumed by larger grains during pressureless sintering inducing in that way the formation of a bimodal structure. Furthermore, the absence of porosity through a large sample area is evident in the SEM micrograph (Fig. 4a). The high density and therefore low porosity of the sintered sample was accompanied by a relatively high hardness of 13.1GPa. This hardness value is sufficiently high to consider this sintered pyrochlore ceramic as a promising material for thermal barrier coatings. The corresponding EDS elemental mapping images demonstrate that all cations are randomly and homogeneously distributed throughout the sintered sample (Fig. 4b and c).
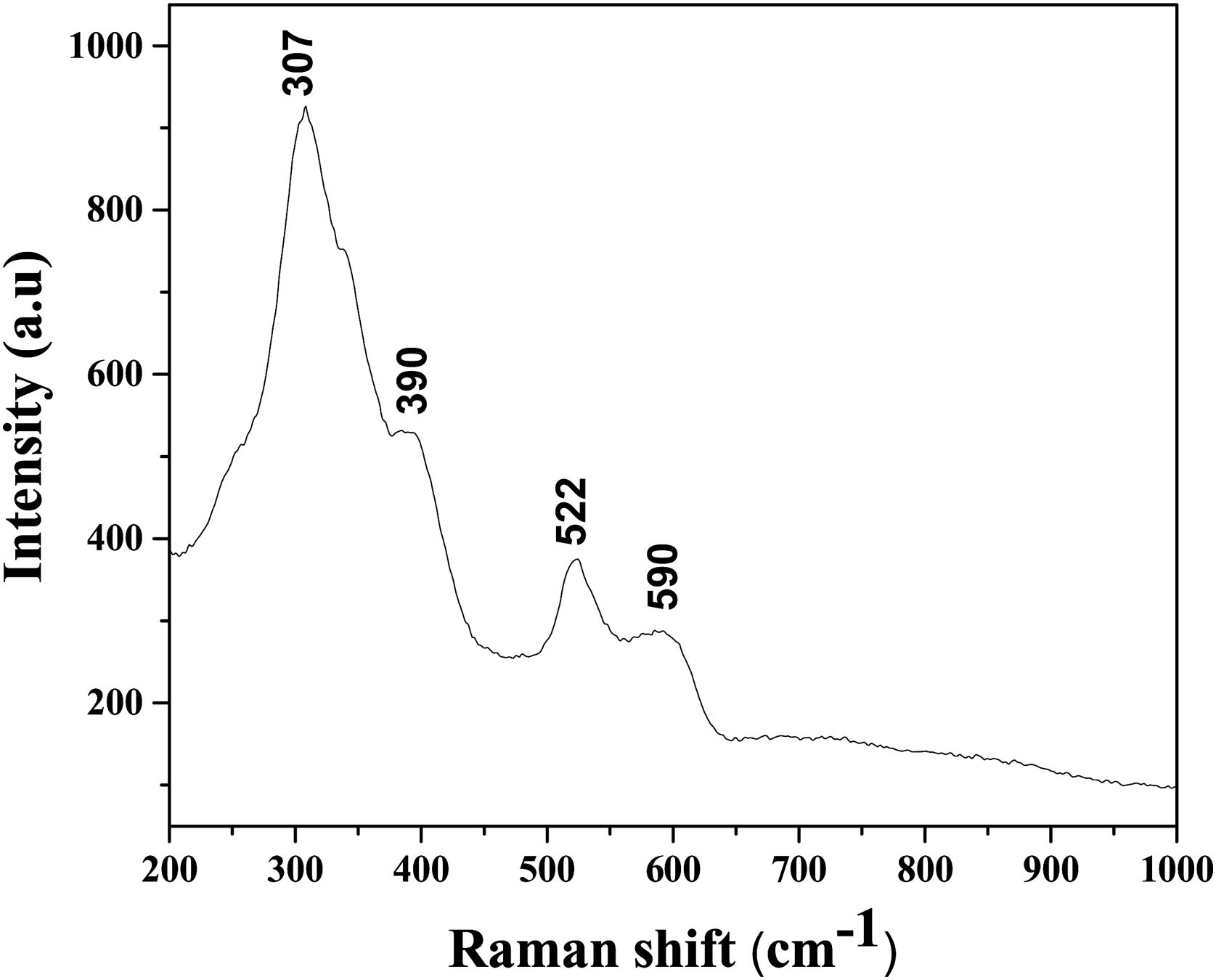
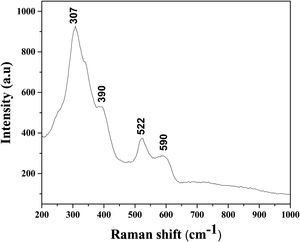
Based on the Raman spectrum, presented in Fig. 5, it can be confirmed that the sintered sample shows a pyrochlore and not a fluorite structure. Generally, the pyrochlore structure possesses the most intense Raman band at 307cm−1, which can be ascribed to the Eg mode due to the (Hf, Zr, Sn)O6 bending, two peaks at around 390 and 590cm−1 that could be attributed to the T2g modes, and Raman band at 522cm−1 that can be identified as the A1g mode due to the O–(Hf, Zr, Sn)–O bending vibrations.
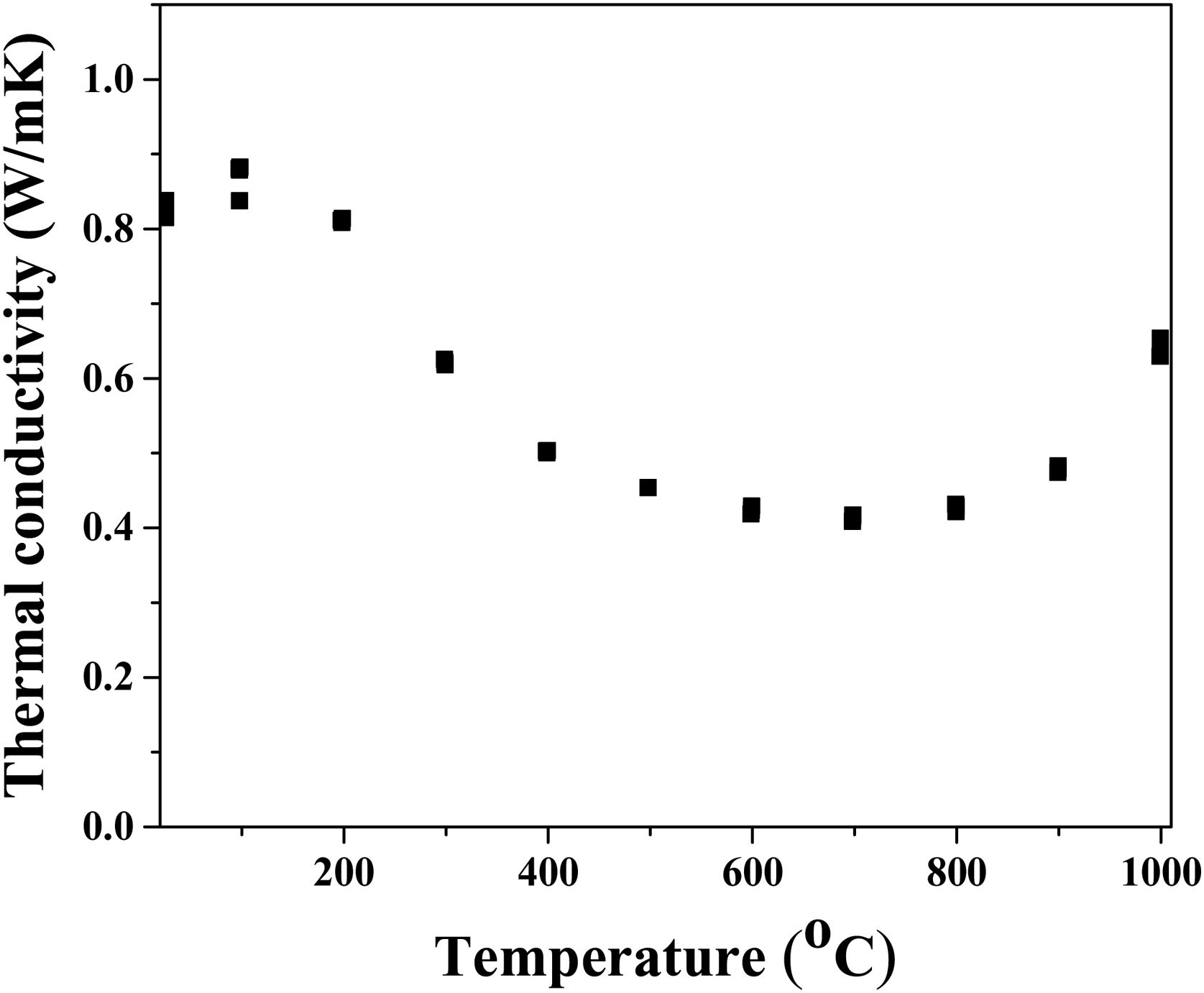
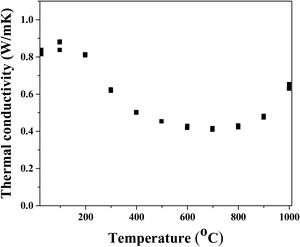
Since phonon propagation is the dominant mechanism of heat conduction in insolating materials, thermal conductivity reduction in multicomponent solid solutions, such as high-entropy multicomponent solid solutions, occurs as a result of the appearance of lattice distortion and lattice defects [61]. The thermal conductivity of sintered high-entropy pyrochlore ceramic material is presented in Fig. 6. The obtained results show that the lowest thermal conductivity (less than 0.5W/mK) was measured in the temperature range from 500°C to 800°C. It is assumed that low thermal conductivity in this temperature range is probably due to the weak vibrations of the crystal lattice that occur as a result of the weak covalent bond. In this study, the pyrochlore structure with 10 different cations with random distribution creates the scattering of phonon waves, i.e. reduces thermal conductivity through the material. At 1000°C the determined thermal conductivity was 0.7W/mK, representing the lowest conductivity value among other high-entropy pyrochlores, as well as a much lower value compared to yttria-stabilized zirconia as reference material for thermal barrier coating materials [62,63].
Even though the most simple binary pyrochlores with one cation in position A and one cation in site B show quite similar values of thermal conductivity ranging from 1.6W/m to 1.9W/mK, the high-entropy pyrochlores are characterized with a significantly reduced thermal conductivity value due to a significant phonon scattering that occurs as a result of different cation distributions in positions A and B [64]. In fact, substitutions with both, bigger or smaller, sized cations provide the rattling effect due to a mismatch of their mass and size [65]. Moreover, in the structure of pyrochlores, there are about 12.5% of vacancies which are significantly affecting their thermal conductivity.
Theoretical study of the multicomponent solid solution with pyrochlore structureA multi-methodological approach was applied to investigate multicomponent solid solution system with the variable composition of the ordered and disordered pyrochlore structures using quantum mechanics, group action theory, PCAE, and supercell methods. The final multicomponent (La1/7Sm1/7Nd1/7Pr1/7Y1/7Gd1/7Yb1/7)2(Sn1/3Hf1/3Zr1/3)2O7 compound synthesized at extremely high temperature of 1650°C crystallizes in the cubic F d 3¯ m (no. 227) space group with prototypic pyrochlore A2B2O7 structure, where A atoms are located at 16d, B atoms at 16c, and O atoms at 48f and 8b Wyckoff positions.
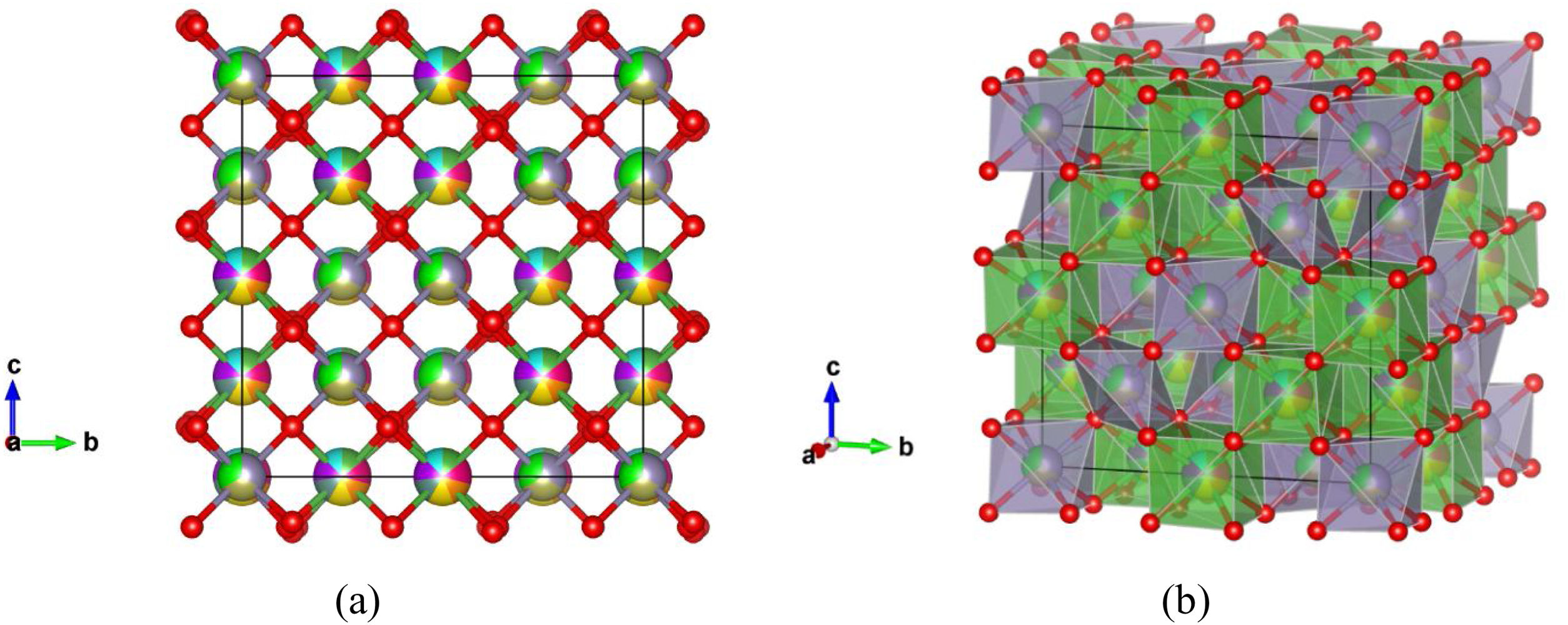
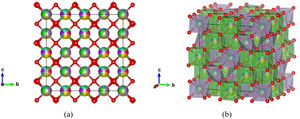
Fig. 7 shows experimentally observed ordered pyrochlore structure, with partial occupancy on A cation (16d) Wyckoff position sharing 8-fold coordinated polyhedra with 14.3% of La, Y, Gd, Yb, Pr, Nd, and Sm, respectively. On the other hand, Zr, Sn, and Hf atoms are sharing 33.3% at the B site (16c) Wyckoff position appearing in the 6-fold coordinated octahedral environment.
Ordered pyrochlore A2B2O7 structure obtained from the recorded XRD data: (a) visualization with partial occupancy of the atomic positions; (b) visualization with coordination polyhedra. The A cation polyhedra with 14.3% of La, Y, Gd, Yb, Pr, Nd, and Sm, are presented in light green color, while B cation polyhedra with 33.3% Zr, Sn, and Hf atoms are shown in purple, and oxygen atoms are shown in red color.
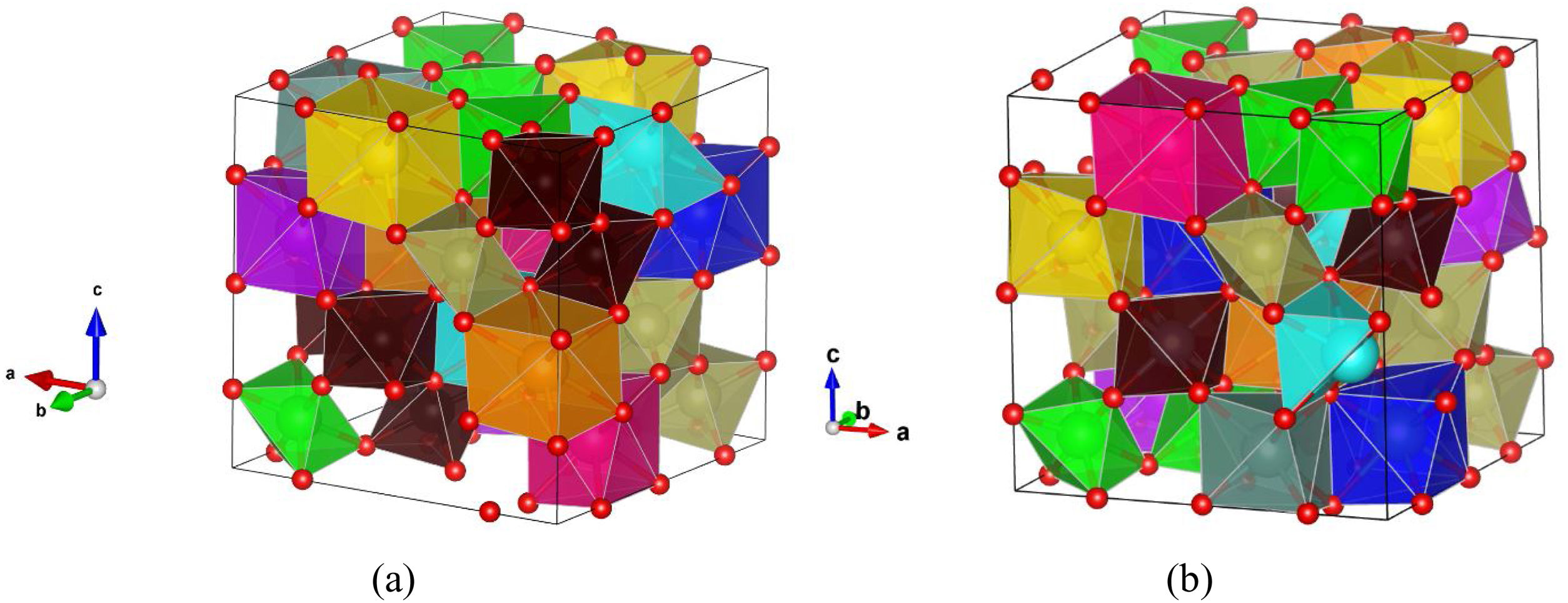
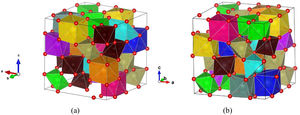
A large number of supercell structures were created to investigate the variable composition of ordered and disordered pyrochlore structures and the PCAE method was applied to create various doped La2Zr2O7 compositions, as it was already successfully applied in our previous study [25]. The most promising structure candidates, created for the synthesized multicomponent (La1/7Sm1/7Nd1/7Pr1/7Y1/7Gd1/7Yb1/7)2(Sn1/3Hf1/3Zr1/3)2O7 compound, are shown in Fig. 8. After the structural optimization using GGA-PBE functional was undertaken, the unit cell parameters were calculated and the obtained values were compared with the experimentally obtained XRD results showing good agreement with only a slight overestimation of ∼3%.
Two most favorable structure candidates for the multicomponent (La1/7Sm1/7Nd1/7Pr1/7Y1/7Gd1/7Yb1/7)2(Sn1/3Hf1/3Zr1/3)2O7 compound generated using the PCAE and supercell methods and relaxed using GGA-PBE functional. Atoms of La are presented in dark blue color, Yb in light blue, Pr in yellow, Gd in light purple, Nd in orange, Sm in pink, Y in gray, Hf in light brown, Zr in light green, Sn in dark brown, and O atoms are presented in red color.
Presented experimental and theoretical results indicate that the obtained high-entropy pyrochlore ceramic material shows significant potential for diverse industrial and technological applications [66,67].
ConclusionsA study on the properties of synthesized multicomponent solid solution with pyrochlore structure (high-entropy pyrochlore ceramics) using the combined experimental and theoretical approach was presented. A new approach to the synthesis of pyrochlore, i.e. solid state displacement reaction, with a large number of different cations (7 cations in positions A and 3 in site B: (La1/7Sm1/7Nd1/7Pr1/7Y1/7Gd1/7Yb1/7)2(Sn1/3Hf1/3Zr1/3)2O7) was successfully applied. Densification of the green compacts was achieved without the addition of sintering aids. A relative density of 98%, as well as microhardness of 13.1GPa were achieved by applying the pressureless sintering at 1650°C for 4h. The microstructure of the obtained sintered high-entropy pyrochlore ceramic exhibits low porosity and bimodal structure with equiaxed grains, ranging from 1μm to 4μm in size. The thermal conductivity of obtained pyrochlore material was determined to be 0.7W/m K at 1000°C, which is the lowest value of thermal conductivity for this type of material. A relatively high hardness combined with a low thermal conductivity of this high-entropy pyrochlore ceramic makes this material a promising candidate for diverse high-temperature applications. Theoretical study of the multicomponent solid solution with pyrochlore structure was performed using the multi-methodological approach involving several different computational methods. Predicted and experimentally observed multicomponent pyrochlore structures were generated using the PCAE and supercell approach, and ab initio structure optimization shows good concurrence with the experimentally obtained XRD data.
Conflict of interestsThe authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
This research was financially supported by the Ministry of Science, Technological Development and Innovation of the Republic of Serbia (Grant Nos. 451-03-68/2022-14/200017 and 451-03-68/2022-14/200135) and the Visiting Professor Program of the Chinese Academy of Sciences (2021VEA0003).