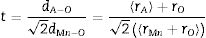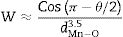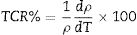Structural, electrical transport and optical properties of doped La0.7Ca0.3MnO3 ceramics

Abstract

In this study, we have investigated the structural, electrical transport and UV–Visible properties of polycrystalline La_0.7Ca_0.3−xK_xMnO₃ (x = 0.0, 0.05, 0.10, 0.20) ceramic samples prepared by conventional solid-state reaction. The structure characterized by X-ray diffraction shows that the samples possess orthorhombic perovskite structure belonging to Pnma space group with some impurity for higher doping level (x = 0.10, 0.20) and cell volume is enlarged with Ca²⁺ substitution by K¹⁺. The surface morphology was investigated by field emission scanning electron microscope, which indicates that the samples with better crystallization having higher density. The electrical transport properties were measured by the standard four-probe method, which demonstrates that the resistivity decreases non-monotonically and the metal–insulator transition temperature (T_P) shifts to higher temperature with increasing K¹⁺ content, the electrical transport behavior for metal and insulator region was explained using Zener double exchange model and small polaron hopping model respectively. Furthermore, the progressive substitution of Ca²⁺ by K¹⁺ broadens the metal–insulator transition and reduces the temperature coefficient of resistivity. Room temperature UV–Vis studies show that the optical band gap changes with the partial replacement of Ca²⁺ with K¹⁺. The investigations clearly show the effect of impurity present on structural, electrical transport and UV–visible response of the prepared ceramic samples.

Resumen

En este estudio, hemos investigado las propiedades estructurales, de transporte eléctrico y UV-visible de muestras cerámicas policristalinas de La_0.7Ca_0.3-xK_xMnO₃ (x = 0,0, 0,05, 0,10, 0,20) preparadas por reacción convencional en estado sólido. La estructura comprobada por difracción de rayos X muestra que las muestras poseen una estructura perovskita ortorrómbica perteneciente al grupo espacial Pnma con algunas impurezas para niveles de dopaje más altos (x = 0,10, 0,20) y el volumen de las celdas se amplía con la sustitución de Ca²⁺ por K¹⁺. La morfología de la superficie se investigó mediante un microscopio electrónico de barrido de emisión de campo, que indica que las muestras con mejor cristalización tienen mayor densidad. Las propiedades de transporte eléctrico se midieron mediante el método estándar de cuatro sondas, que demuestra que la resistividad disminuye de forma no monótona y la temperatura de transición metal-aislante (TP) se desplaza a una temperatura más alta con el aumento del contenido de K¹⁺, el comportamiento de transporte eléctrico para la región de metal y aislante se explicó utilizando el modelo de intercambio doble de Zener y el modelo de esperanza de polaron pequeño, respectivamente. Además, la sustitución progresiva de Ca²⁺ por K¹⁺ amplía la transición metal-aislante y reduce el coeficiente de temperatura de la resistividad. Los estudios de UV-Vis a temperatura ambiente muestran que la brecha de banda óptica cambia con la sustitución parcial de Ca²⁺ por K¹⁺. Las investigaciones muestran claramente el efecto de la impureza presente en la respuesta estructural, de transporte eléctrico y de UV-visible de las muestras cerámicas preparadas.

Introduction

Colossal magnetoresistance and metal to insulator transition (T_P) reported in hole doped ABO₃ type perovskites have aroused great interest among researchers in these manganites. The structural disorder and size variance effect is due to an ionic size mismatch between the doped ions and La³⁺ induced by the substitution of tetravalent, trivalent and/or monovalent ions at the A-site, which consequently modifies the physical properties and their interrelations. The interplay and correlation between spin, charge, charge and orbital ordering, structure and property, etc. exhibited by these perovskites, prompted researchers to do detailed investigations to understand the concurrent occurrence of metal-ferromagnetic states in manganites. The mechanism that governs the transfer of charge carriers was adequately explained by C. Zener [1–4]. However, ZDE (Zener Double Exchange) alone cannot entirely clarify all the features proclaimed by mixed valent oxide manganites and, hence, additional mechanisms are recommended to understand the physical properties exhibited by doped manganites, which might reasonably explain the role of the Jahn–Teller ion in the ascription of the CMR phenomenon exhibited by these mixed valent oxides when they are subjected to external magnetic fields. It was suggested by Goodenough et al. that, apart from DE, ferromagnetism is also governed by the distinct nature of the super-exchange interaction (SE) in Mn³⁺OMn³⁺ and Mn³⁺OMn⁴⁺ chains [5]. Ferromagnetic and metallic properties in the La_1−xA_xMnO₃ (A = divalent alkaline earth) system concurrently appear. However, there is no comprehensive explanation to date of the dependence of these properties on each other. The influence of DE and SE interactions largely depends on alteration in the Mn³⁺/Mn⁴⁺ ratio, but these exchange models do not take into account the spin-lattice/charge-lattice interactions of polarons, as they influence the resistivity in the paramagnetic/insulating phase [6].

The parameters like average ionic radii rA and size variance (σA2) play a critical role in the modifications of electrical and also magnetic properties in divalent ion-doped oxide manganites [7,8]. Magneto-resistive properties of manganites (doped as well as undoped systems) have been extensively examined owing to their significance in basic research as well as possible exercises in technological industries [9,10].

LaMnO₃, an antiferromagnetic insulator compound accompanied by a ferromagnetic component, is the most fascinating hole-doped mixed oxide manganite system. The partial replacement of La³⁺ by divalent alkaline earth ions improves the mean manganese valency to conserve overall electrical neutrality and produces Mn⁴⁺ ions with (S = 3/2) configuration and the electrons of Mn³⁺ are predicted to be delocalized and play the role of charge carriers. These oxide systems have metal to insulator phase transformation, 33% doping of alkaline earth at the A-site [11,12] and a huge magneto resistivity near the Curie temperature [13]. Therefore, it was essentially needed to understand the electrical conduction concerning polarons. Previous investigations into manganites have revealed that the magnetic transition temperature is largely influenced by the mean A-site cation size [14]. However, subsequent studies have proved that the mismatch effect, frequently signified by the size variance of the A-site cation, also impacts T_C and T_P. It has also been demonstrated that electrical and magnetic transitions in manganites progress toward higher temperature regions with increasing tolerance. The discrepancy in this linear relationship between transition temperature, T_P and the tolerance factor has also been reported because of the size variance of A-site cations [7].

Our previous studies on structural, electrical transport and magneto-transport properties by the nonmagnetic Ga³⁺ and smaller Sb⁵⁺ doping at larger Mn³⁺ ion-site in La_0.67Ca_0.33MnO₃ manganites have shown the orderly variation in resistivity and metal to insulator transition temperature with Ga³⁺/Sb⁵⁺ doping. The variations are explained in the light of Mn-site ionic size variations accompanied by structural and magnetic lattice modifications [11,12].

There are several reports available on the substitution effect of Ca²⁺ by a monovalent alkali metal [15–20]. As the larger K¹⁺ ion prompts a large structural deformation because of the size mismatch as well as the valency mismatch, it will synchronously modify the Mn³⁺/Mn⁴⁺ ratio. Also, the replacement of Ca²⁺ with K¹⁺ will alter the MnOMn bond angle and MnO bond length. Subsequently, they changed the electrical transport, optical and magnetic response of the manganites. All these reports discussed various properties of the single phasic sample without any traces of impurity.

To understand the size mismatch, cationic disorder and aforementioned effects, in this communication, the results of the investigations on partial replacement of Ca²⁺ by K¹⁺ in La_0.7Ca_0.3−xK_xMnO₃ (LCKMO) and the effect of the presence of a very little impurity on the electrical resistivity as well as on the optical bandgap of the manganite system have been discussed.

Experimental details

Polycrystalline ceramic samples of La_0.7Ca_0.3−xK_xMnO₃ (LCKMO) with x = 0.00, 0.05, 0.10 and 0.20 (hereafter referred to as K-0, K-05, K-10 and K-20 respectively) were prepared using a standard Solid-State Reaction (SSR) technique. The starting La₂O₃, CaCO₃, MnO₂, and K₂CO₃ (Sigma–Aldrich) precursors were firstly preheated at 400 °C then mixed in stoichiometric proportions and calcined at 800 °C for 12 h. Samples were then molded into pellets (having 10 mm diameter and ∼2 mm thickness) and sintered in air at 1175 °C for 48 h with intermediate grinding and heating. X-ray diffraction (XRD) data was collected on PW 3040/60, an X’pert PRO Philips diffractometer using Cu-Kα radiation at RT. Structures were analyzed using Rietveld refinement using the Fullprof code [21]. Field effect scanning electron microscopy (FE-SEM) measurements were taken on the ZEISS Merlin/VP compact model at RT for surface microstructural studies.

Electrical resistivity measurements were performed using the standard four-probe dc method (Quasar Tech made XPLORE 1.2 PQMS system), and UV–Vis data was recorded on the Shimadzu UV-1700 model at RT.

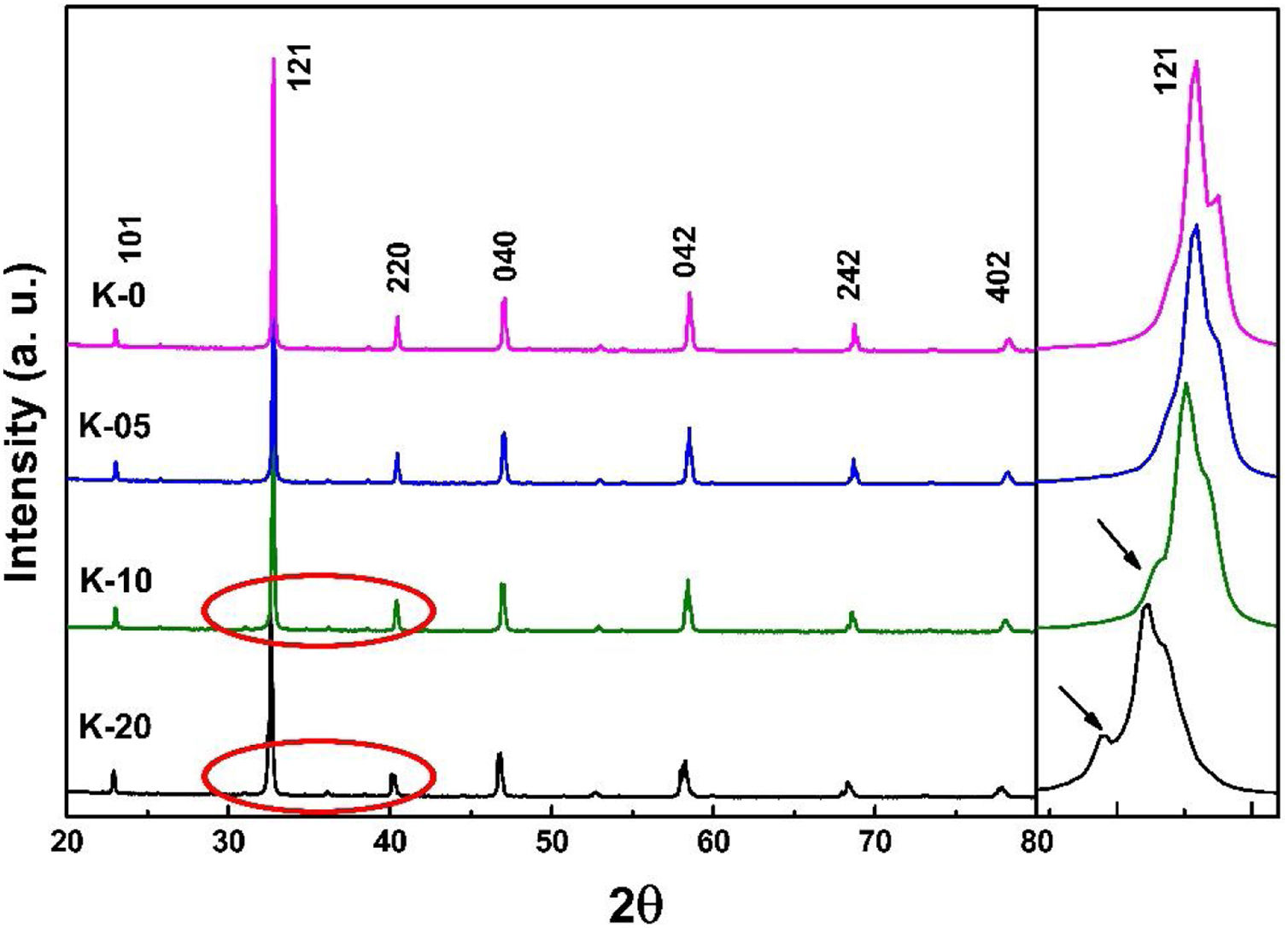
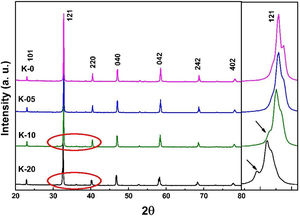
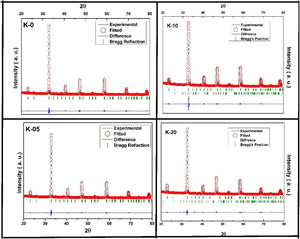
Results and discussion

Structural studies: XRD

Room temperature XRD studies were performed to identify the structural phases in all the La_0.7Ca_0.3−xK_xMnO₃ (LCKMO) (with x = 0.00, 0.05, 0.10, and 0.20) ceramic samples. Fig. 1 shows the XRD raw data of LCKMO ceramic samples reveals that K-0 and K-05 have a single phasic nature without any noticeable impurities, whereas the ceramic samples K-10 and K-20 show the presence of a very little amount of Mn₃O₄ impurity may be because of the insufficient sintering temperature treatment (shown by arrows in the enlarged view of the 121 peaks and the circles drawn). The side panel in Fig. 1 displays an enlarged view of the most intense (121) XRD peak of LCKMO ceramic samples. The shifting of the (121) peak toward the lower 2θ angle depicted can be accredited to the substitution of larger K¹⁺ (1.37 Å) at a smaller Ca²⁺ (1.12 Å) site, which in turn increase the unit cell lattice parameters and volume.

Fig. 1.

XRD patterns (raw data) of LCKMO ceramic samples and enlarged view of (121) XRD peak of LCKMO ceramic samples.

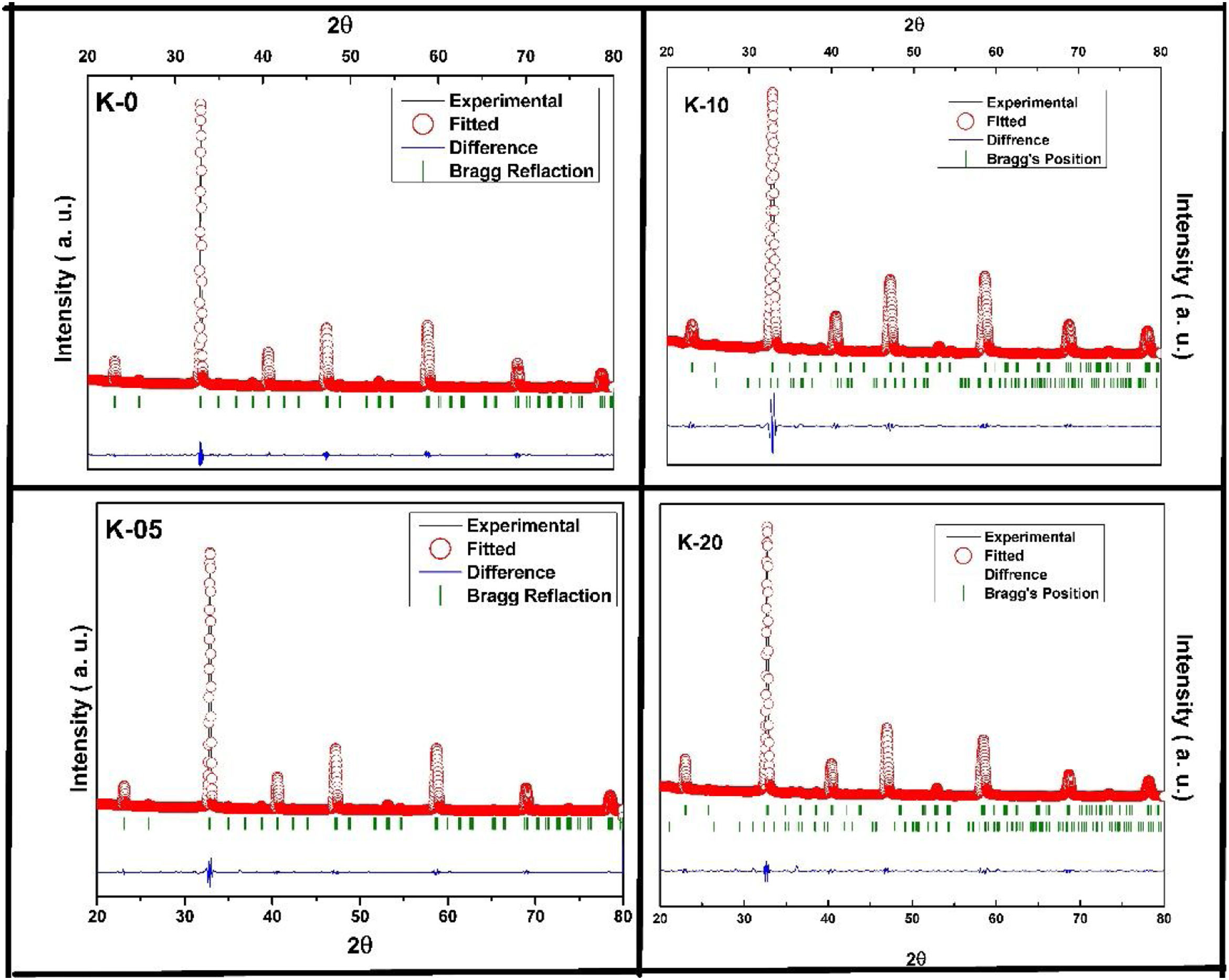
Also, according to Bragg's formula, the spacing between the crystal faces is increasing, with the diffraction peak shifted to a lower theta value, while the cell volume increases, respectively. To prove this trend, we have refined the XRD results of the LCKMO ceramic samples by the Rietveld refinement using the FULLPROF program [21].

Fig. 2 shows the Rietveld refined XRD patterns of LCKMO ceramic samples, carried out to check the structural phase. All the refinements confirm that the samples are crystallized in the orthorhombic structure having a Pnma space group (Card No. 62). It can be seen from Fig. 2 that the observed data is in good agreement with the theoretical data. The values of refined unit cell parameters, cell volume and R-factors and estimated values of average A-site radius, tolerance factor, size variance, and relative densities for the LCKMO ceramic samples are depicted in Table 1. Further the Mn₃O₄ phase present in K-10 and K-20 ceramic samples are found to be 2.51% and 2.26% respectively.

Fig. 2.

Rietveld refined XRD patterns of (a) K-0, (b) K-05, (c) K-10 and (d) K-20 LCKMO ceramic samples.

Table 1.

Summary of Reitveld refined structure, R-factors and estimated values of average A site radius, tolerance factor, size variance, average crystallite size for La_0.7Ca_0.3−xK_xMnO₃ ceramic samples.

Sample	K-0	K-05	K-10	K-20
System	Orthorhombic	Orthorhombic	Orthorhombic	Orthorhombic
Space group	Pnma	Pnma	Pnma	Pnma
Lattice constants (Å)
a	5.44964(8)	5.44323(9)	5.4502(8)	5.45697(9)
b	7.68217(9)	7.69141(8)	7.70536(6)	7.72037(7)
c	5.43872(7)	5.45773(9)	5.47195(7)	5.49069(2)
Cell volume V (Å^3)	227.692(3)	228.494(7)	229.799(7)	231.322(5)
Bond distances (Å)
MnMn	3.84108(6)	3.8457(7)	3.8527(4)	3.86020(7)
MnO1	1.96023(3)	1.96095(4)	1.95519(6)	1.96394(4)
MnO2	1.83261(2)	2.01147(3)	2.13992(8)	1.96424(5)
Bond angles (°)
MnO1Mn	156.9009(5)	157.3734(6)	160.294(3)	158.6983(11)
MnO2Mn	165.0235(0)	163.2664(3)	161.4558(5)	160.9988(3)
W	0.092905	0.092863	0.094272	0.092573
Volume density (gm/cm^3)	6.34	6.16	6.12	6.39
Relative density %	82.06	80.02	79.98	84.15
Rp%	9.51	9.91	11.8	9.90
Rwp%	8.67	9.58	10.9	9.47
Rexp%	5.91	6.15	6.75	6.16
Bragg R-factor	4.94	1.61	1.83	12.1
Rf-factor%	4.70	2.89	2.90	8.71
χ^2	2.30	2.54	2.61	2.36
σ2 (Å)	1.288	1.3005	1.313	1.338
t	0.9570	0.97156	0.97676	0.98536
σ2 (Å^2)	0.012096	0.0108647	0.009321	0.005296

The room temperature XRD data implies that the structure and the space group symmetry remain unchanged, concerning the substitution of Ca²⁺ with K^1+, but, the lattice constants and cell volume increase monotonically with the fractional replacement of Ca²⁺ by larger ionic radii of the alkaline earth ion K¹⁺.

The Goldschmidt tolerance factor, used to evaluate the distortion in the perovskite crystal structure [22], reflects the degree of distortion induced by the partial introduction of larger K¹⁺ in place of smaller Ca²⁺ in this case. The tolerance factor can be calculated using relationships.

where rA and rB are the average ionic radii of A (La) site and B (Mn) sites, and rO is the radii of oxygen ion. There is an increase in tolerance factor from 0.9570 (for K-0) to 0.98536 (for K-20), which reduces the distortion in MnO₆ and that in turn promotes the hopping integral (t = cos(θ/2)) and reduces the charge localization which is further supported by the resistivity data.

The estimated values of t and size variance σA2 are shown in Table 1. The values of ionic radii were taken from the Shannon ionic radii database [23].

Microstructure: SEM studies

The surface morphologies obtained at RT by FE-SEM for all the LCKMO ceramic samples are shown in Fig. 3. The micrographs show interconnected disk-like grains with an average grain size in the micrometer range. It can also be seen that the grain size and grain boundaries vary with the amount of K¹⁺ doping agent. The samples have a high-volume density and few, if any, pores. Moreover, there is an abrupt change in the grain size and grain boundaries. Comparison of (c) and (d) with (a) and (b) reveals the fact that K-10 has a very abrupt distribution of grain size and higher grain boundaries density. This may be because of the presence of Mn₃O₄ impurities and K-20 shows comparatively large grains and a smaller number of grain boundaries compared to other samples and this is reflected in the resistivity of the samples as well. The grain sizes calculated by the linear interception method are found to be 3.8 μm, 2.3, μm, 2.6 μm and 3.7 μm for K-0, K-05, K-10, K-20 ceramic samples respectively.

Fig. 3.

FE-SEM micrographs of (a) K-0, (b) K-05, (c) K-10 and (d) K-20 ceramic samples.

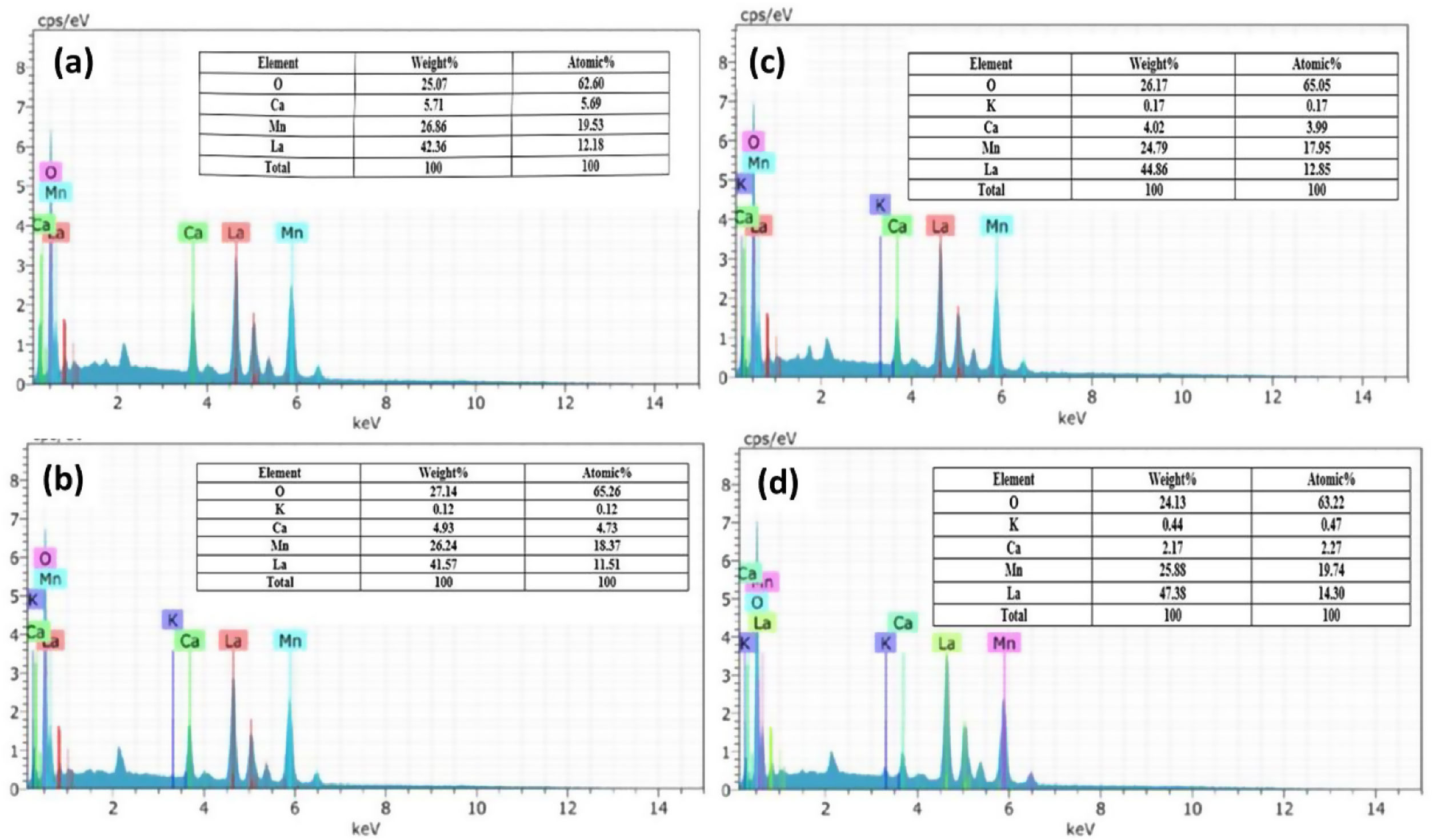
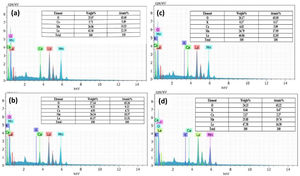
The EDS spectrum (Fig. 4) shows the distribution of the elements present in the LCKMO ceramic samples. The spectrum shows that K¹⁺ is replacing Ca²⁺ and hence there is a change in the weight percentages of the elements present in the samples.

Fig. 4.

EDS spectrum of (a) K-0, (b) K-05, (c) K-10 and (d) K-20 ceramic samples.

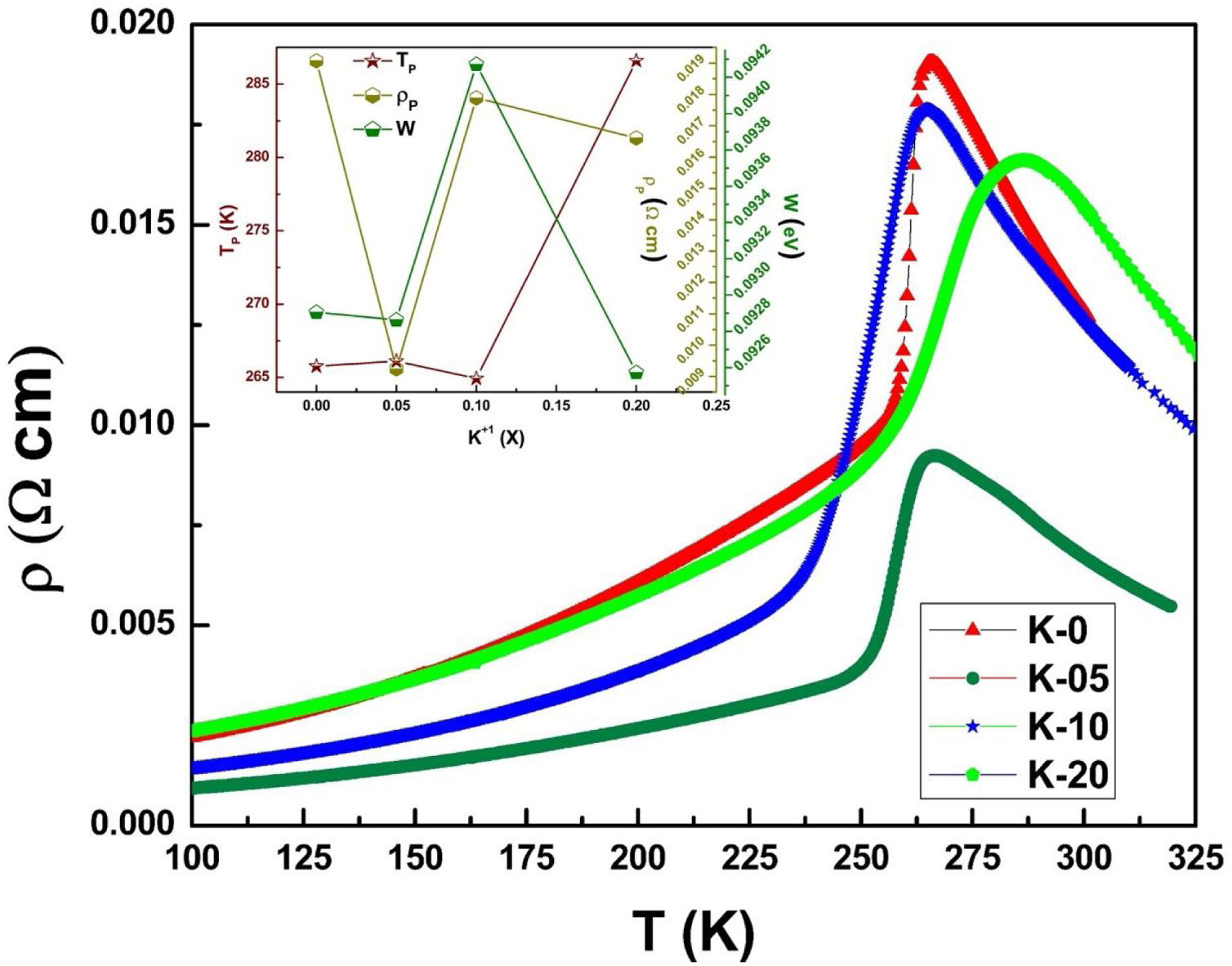
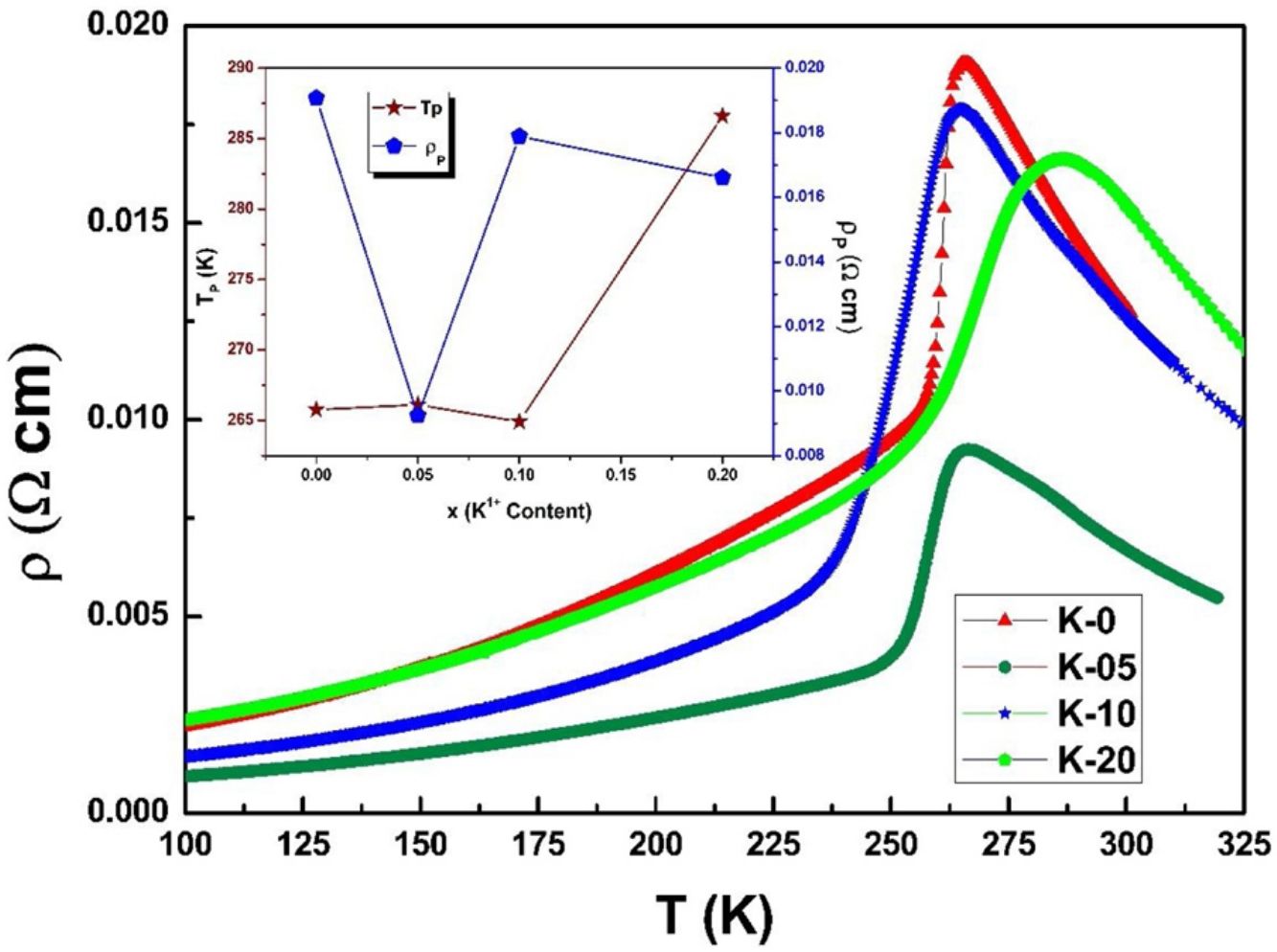
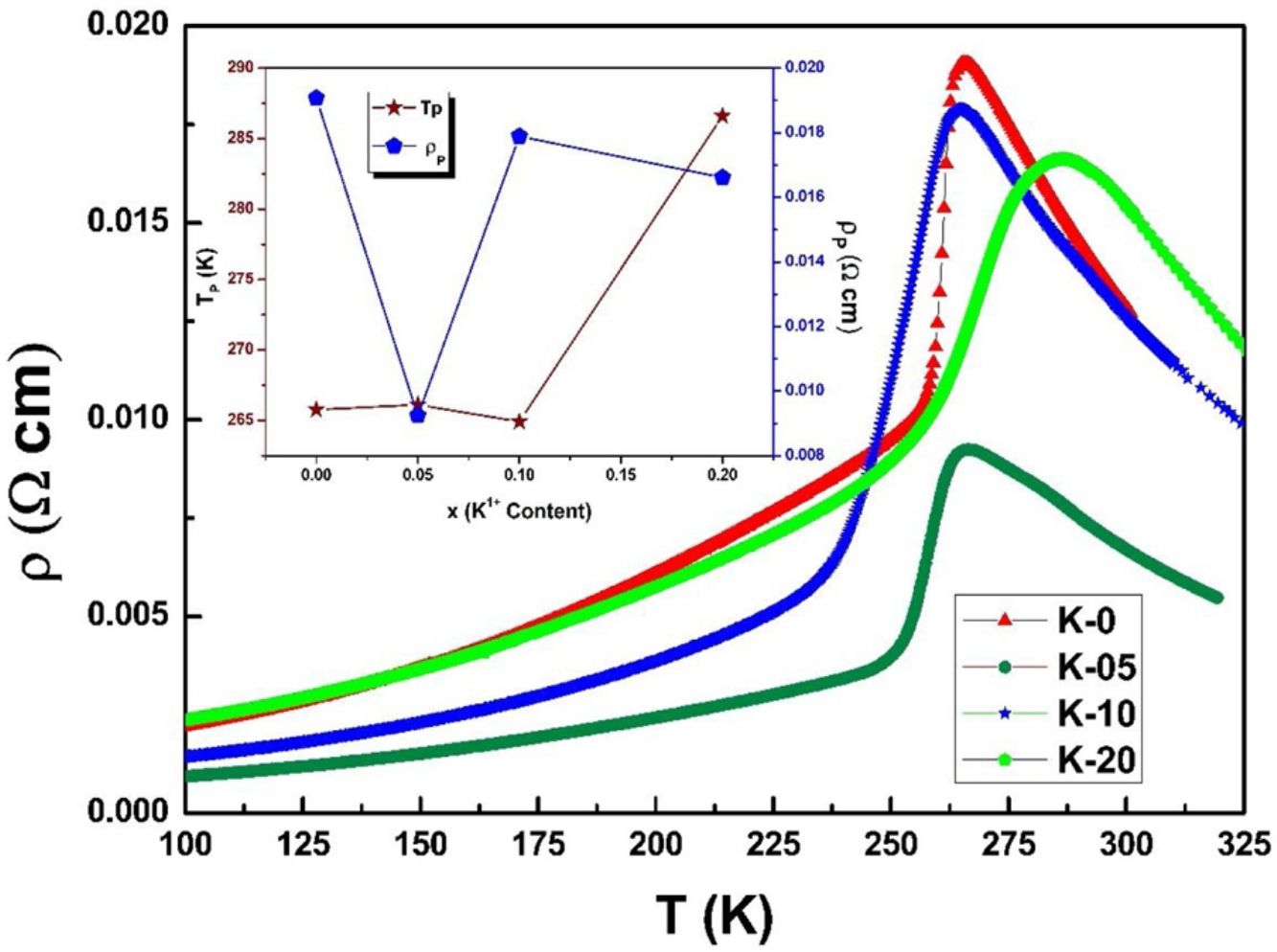
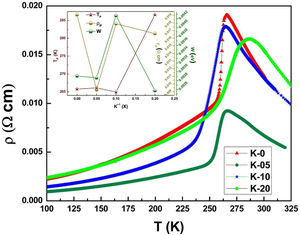
Electrical transport studies

Fig. 5 depicts the electrical resistivity-temperature relationship for the LCKMO ceramic sample studies in the temperature range of 100–325 K.

Fig. 5.

Temperature dependence of resistivity under zero applied filed for LCKMO ceramic samples. Inset: the variation in T_P, ρ_P and W with K¹⁺ content (x) for LCKMO ceramic samples.

It can be seen all the LCKMO ceramic samples show an insulator like behavior above T_P, and below T_P they show a metal-like behavior. At T_P, all the LCKMO ceramic samples show the highest resistivity, ρ_P. It is also noteworthy that, with an increase in K¹⁺ content (x), from K-0 to K-05, the resistivity decreases whereas T_P moves toward a higher temperature. This could be attributed to the higher conductivity gained due to K¹⁺ doping. From K-05 to K-10, the resistivity slightly increases again, possibly due to the presence of insulating Mn₃O₄ at the grain boundaries, and T_P moves toward a lower temperature. From K-10 to K-20, the resistivity slightly decreases again, possibly because of smaller value of electronic bandwidth W of e_g electrons explained below and hence decreasing the resistivity of the sample, and T_P moves toward a lower temperature. Change in peak resistivity and transition temperature with the x content is shown in the inset of Fig. 5.

This variation in the values of peak resistivity (ρ_P) and transition temperature (T_P) shown in Fig. 5 can also be understood in the light of the W, electronic bandwidth of e_g electrons, as follows.

The decrease/increase in resistivity is ascribed to broadening/narrowing of the electron bandwidth. XRD data advocates that the average < MnO > bond length and MnOMn bond angle increase non monotonically with increasing the average ionic radius of A-site. These parameters play a vital role in deciding the electronic bandwidth W of e_g electrons. The electronic bandwidth W can be estimated using the relationship [24],

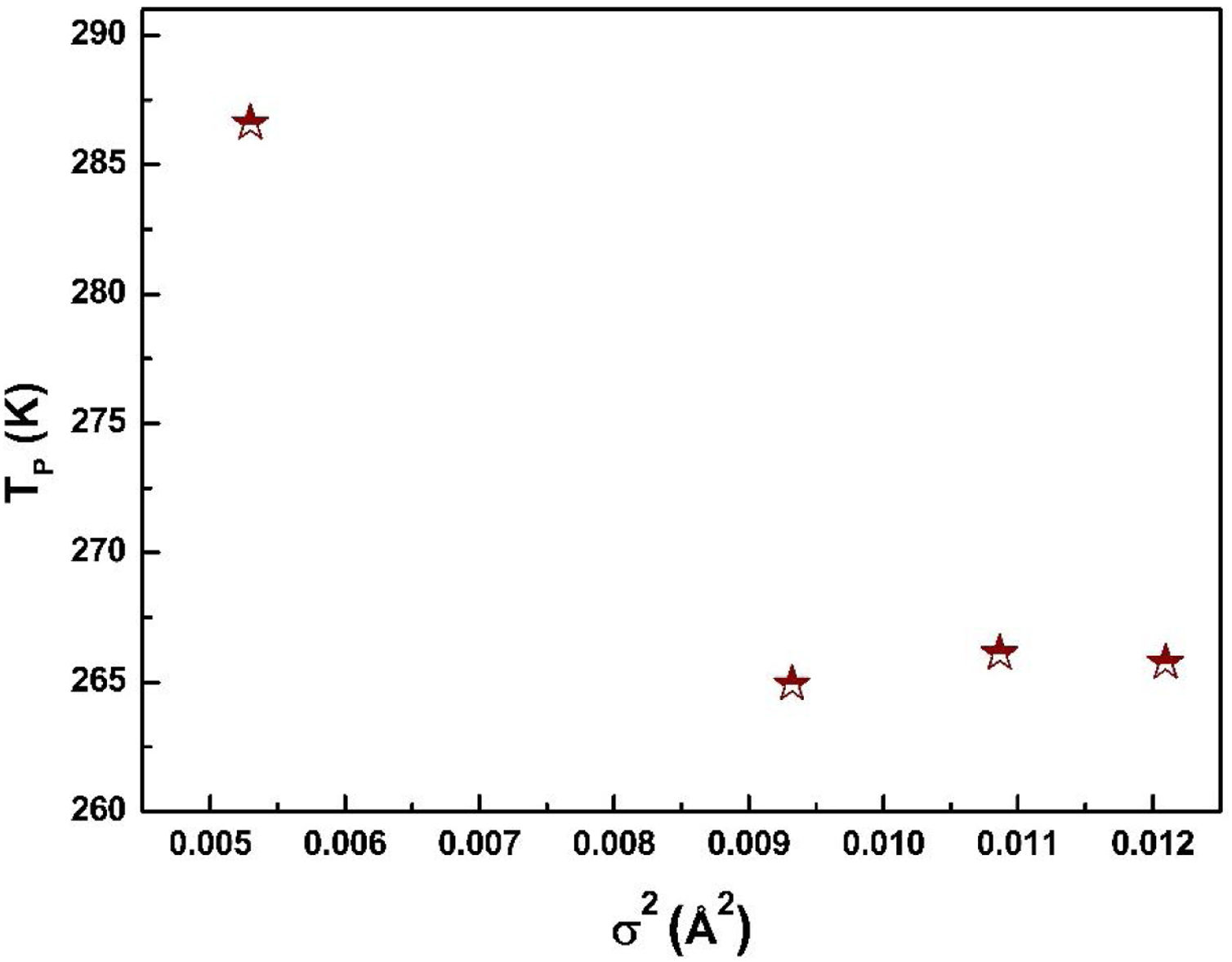
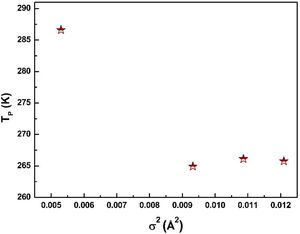
where W is electronic bandwidth of the e_g electrons, π−θ/2 and d_MnO represent angle of tilt in MnOMn bond plane and MnO bond length respectively. There is an overall decrement in the value of W with an increasing value of the average A site ionic radius, which implies the improvement of the hybridization between Mn-3d and O-2p electrons, hence boosting the delocalization of conduction electrons and hence decreasing the resistivity of the system.

Size-variance (σ²) is a factor that quantifies the extent of mismatch and plays a significant role in the metal-insulator transition temperature, T_P[7,25]. As shown in Fig. 6, T_P initially decreases with size variance, but at higher levels of doping (x = 0.10 and 0.20), T_P does not change linearly, and resistivity does not vary monotonically with doping level, possibly due to the presence of insulating Mn₃O₄.

Fig. 6.

Variation of T_P with A site cation size variance σ2.

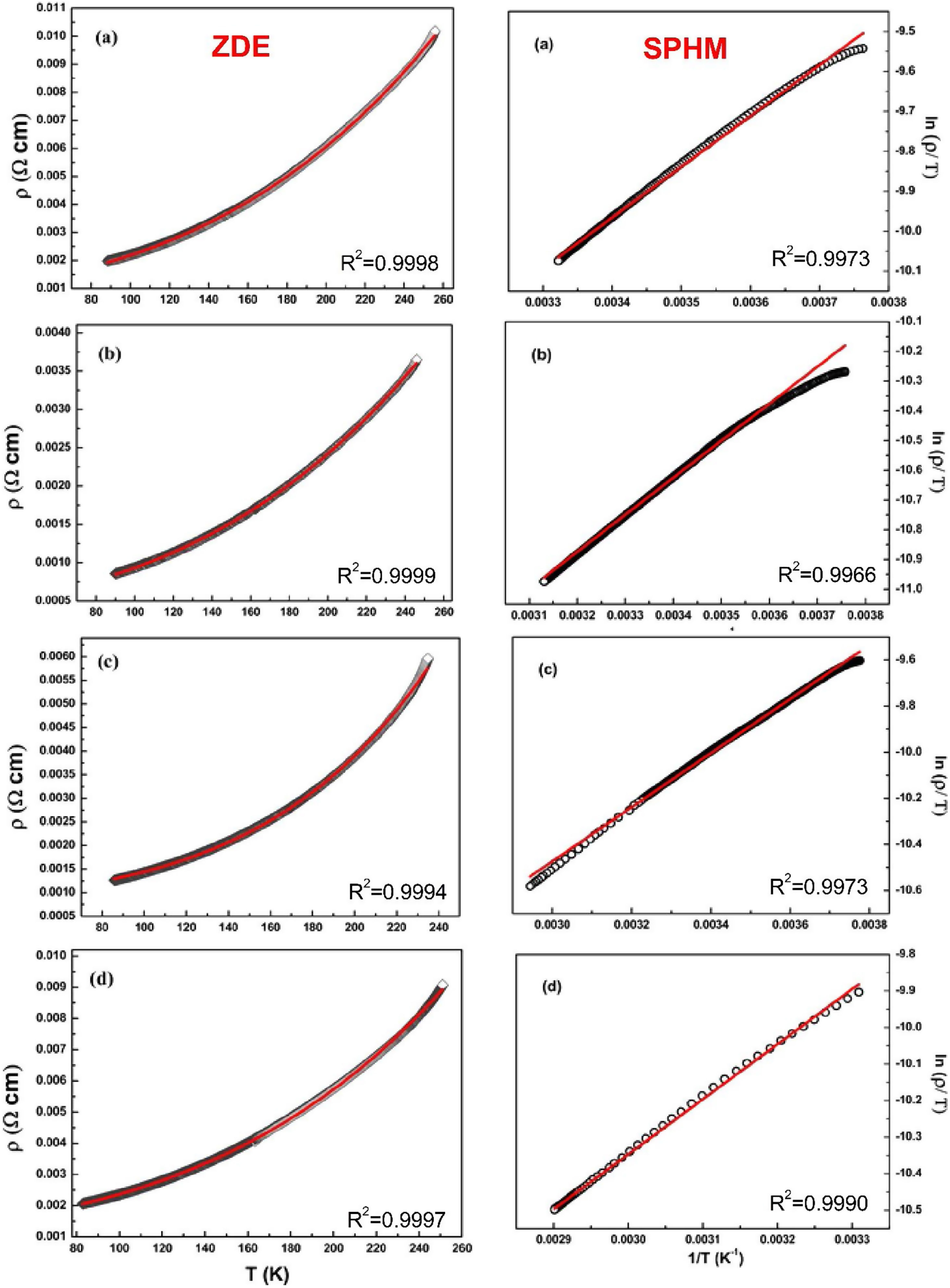
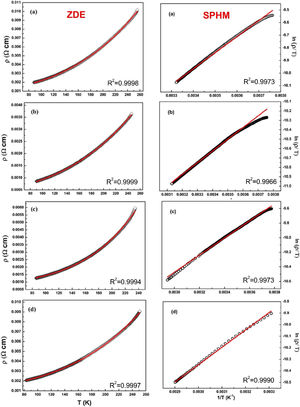
The electrical transport mechanisms responsible for the metallic region (∼90–250 K) of LCKMO ceramic samples can be inferred by fitting the resistivity data to a Zener double exchange (ZDE) polynomial law: ρ (T) = ρ₀ + ρ₂T² + ρ_nTⁿ fit (n=4.5), where ρ₀ is the residual resistivity, ρ₂ is the resistivity contribution by the electron-electron, electron-phonon, and electron – magnon scattering mechanism, n is a higher-order term and ρ_n is the corresponding resistivity coefficient [26]. Fig. 7 (left panel) shows the fittings for the resistivity in the metallic region for the LCKMO ceramic samples.

Fig. 7.

Low temperature fits using Zener Double Exchange polynomial law ρ (T) = ρ₀ + ρ₂T² + ρ_4.5T^4.5 (Left panel) and High temperature linear fits using the adiabatic small polaron hopping model (right panel) for (a) K-0, (b) K-05, (c) K-10 and (d) K-20 ceramic samples.

Here are all the LCKMO ceramic samples, Zener double exchange (ZDE) polynomial law: ρ (T) = ρ₀ + ρ₂T² + ρ_nTⁿ fit (hollow squares are the data recorded whereas the red curves are the fittings) propose that for all the samples, two magnon scattering phenomena accountable for the metallic behavior of the samples below the transition temperature T_P.

As depicted in Fig. 5, all the LCKMO ceramic samples studied show insulating regions above T_P. Electrical transport behavior in manganites usually depends on various mechanisms depending on the temperature environment. The electrical conduction in the insulating phase is dominated by the hopping mechanism, whereas the scattering phenomena become dominant in the low temperature magnetically ordered phase.

For different temperature ranges, various models [27–31] were used to explain the mechanism responsible for electrical conduction. At high temperatures (T > T_P), the resistivity follows the small polaron hopping model (SPH) expressed by equation ρT=ATexpEa/kBT[32] and is best fitted for all LCKMO ceramic samples.

Here, polaron binding energy Ea is associated with activation energy; T is the absolute temperature, and A is a constant that is independent of temperature. Above the transition temperature (T > T_P), the electrical resistivity follows the adiabatic small polaron hopping model as shown in Fig. 7 (right panel). Hollow spheres are the observed data, whereas the red line is the fitting line.

The fitting parameters values are listed in Table 2. It is noticed that ρ2≫ρ4.5 indicating that the electron-electron scattering dominates electrical transport at low-temperatures. It can be seen from Table 2 that activation energy decreases monotonously with increasing x, which can be accredited to the structural disorders induced by the larger K¹⁺ ion substitution at smaller Ca²⁺ ion sites.

Table 2.

Values of various fitting parameters obtained from fits of the electrical resistivity data and optical bandwidth.

Sample code & content (x)	ρ0×10−4 (Ω cm)	ρ2×10−8 (Ω cm K^−2)	ρ4.5×10−14 (Ω cm K^−4.5)	Activation energy Ea (meV)	EgeV
K-0 (0.00)	10.50	11.05	2.57	110.16	3.21
K-05 (0.05)	4.89	4.34	0.85	109.13	3.36
K-10 (0.10)	9.21	4.73	4.77	102.05	3.32
K-20 (0.20)	14.10	9.28	2.66	100.36	3.26

TCR studies

For the possible applications of these materials in future devices such as bolometers and infrared detectors, materials possessing high TCR values are highly desired [33,34]. To explore the application potential of the presently studied LCKMO ceramic samples, the temperature sensitivities have been calculated using the relation:

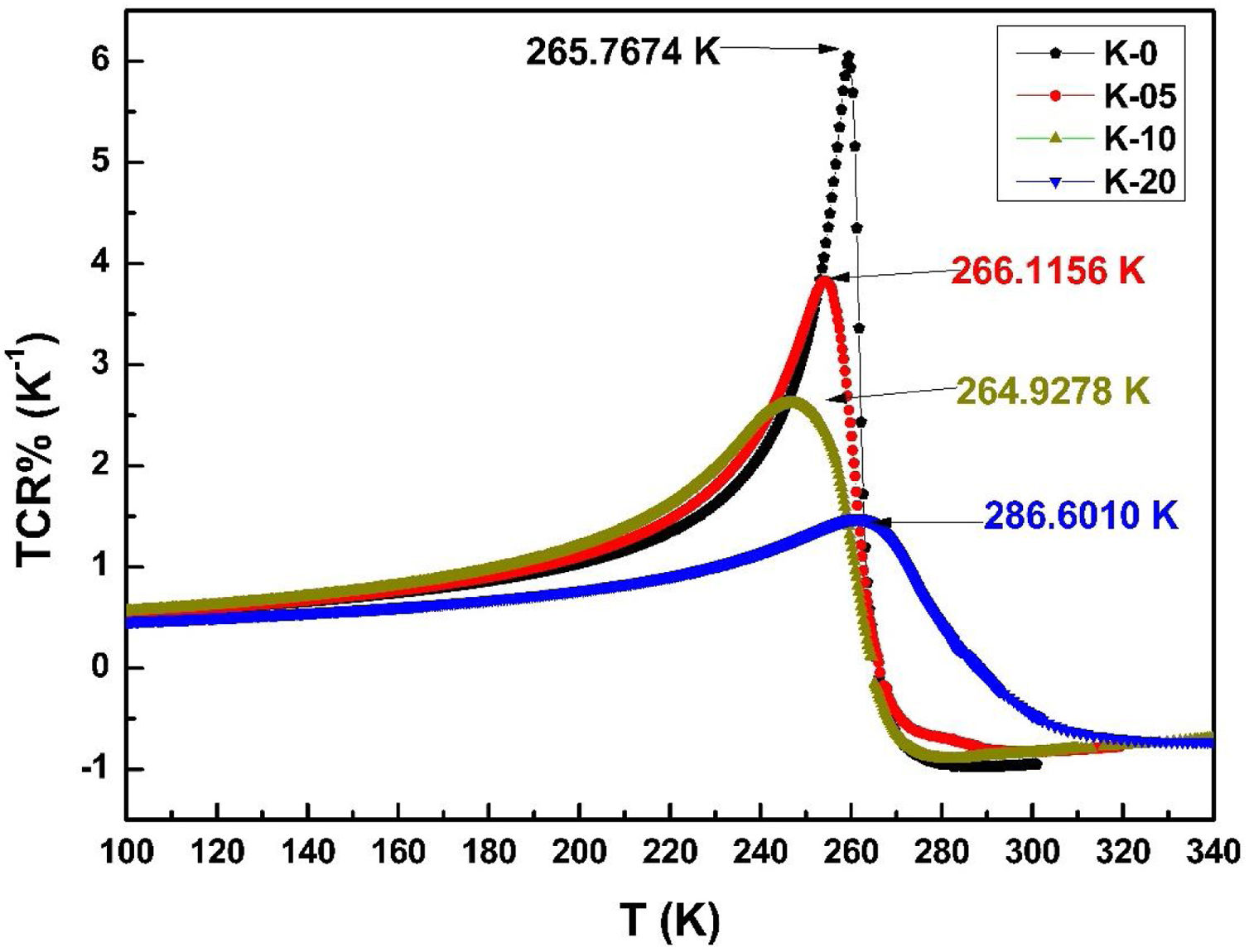
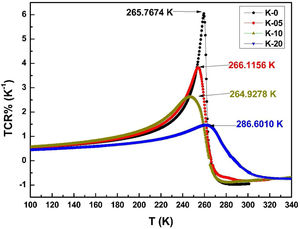
The variation in calculated values of TCR (%) with temperature for LCKMO ceramic samples is shown in Fig. 8. It can be noticed from the figure that TCR values increase with increasing temperature until the transition temperature. For temperatures greater than the transition temperature T_P, the TCR values decrease with increasing temperature. The positive and negative values of TCR show the signature of metallic and insulating phases, respectively.

Fig. 8.

Variation in TCR (calculated at T_P) with temperature for LCKMO ceramic samples.

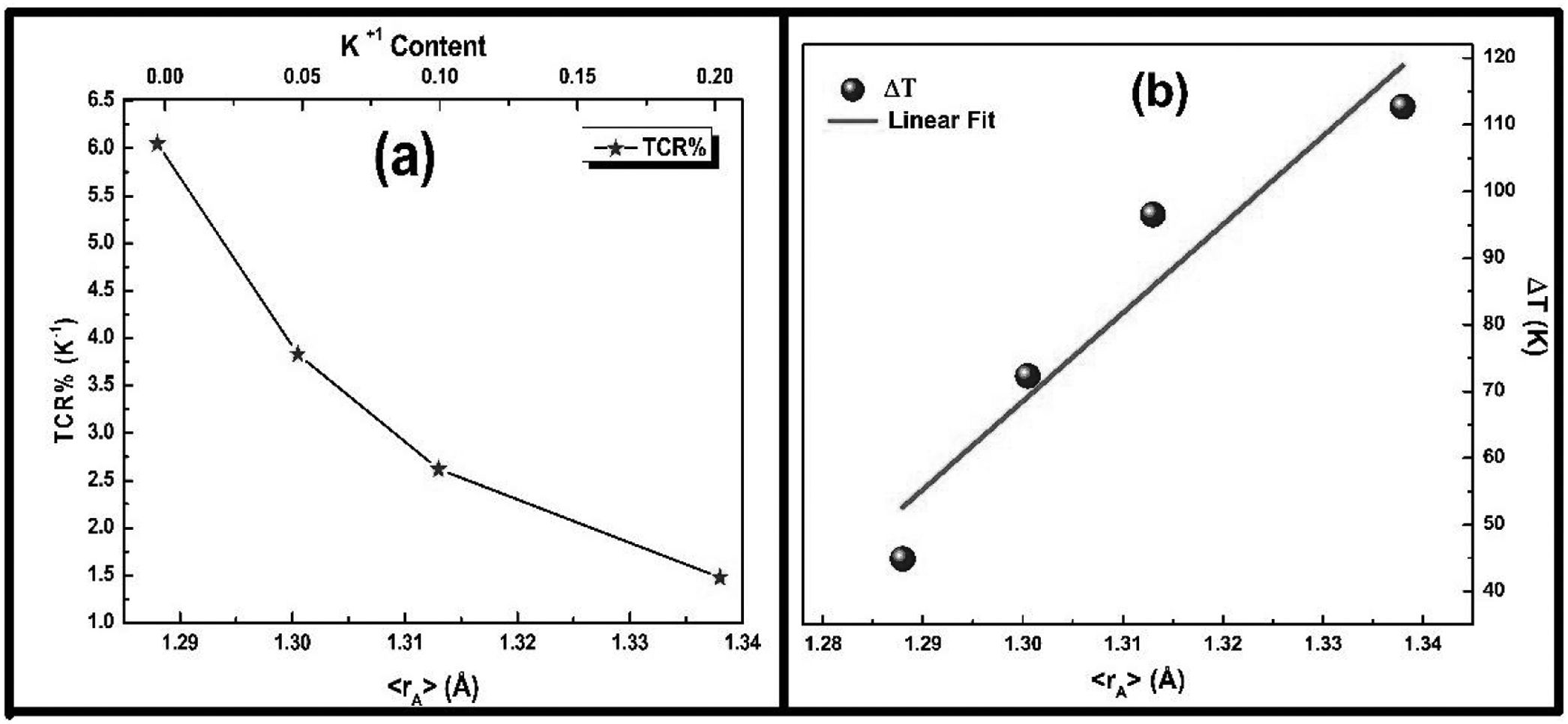
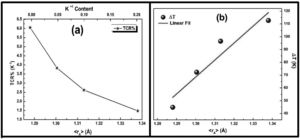
It is very clear from the figure that the maximum value of TCR (TCR_max) decreases from 6.05% K¹⁺ for x = 0.0–1.48% K¹⁺ for x = 0.20 non-monotonically. The reason for this non-monotonic change in the TCR values may be attributed to the non-monotonic changes in the resistivity of the samples. According to Wang et al. [35], the TCR_max value is largely affected by the width of the Gaussian distribution, the metal to insulator transition temperature, and the activation energy. According to the definition, TCR is influenced by two factors: resistivity and transition broadening temperature (T). The ΔT is calculated using the relation ΔT=Tinsulator−Tmetal from Fig. 5. The slope of the metal-insulator transition curve decreases with increasing K¹⁺ content, which broadens ΔT and the resistivity decreases non-monotonically. As a result, the TCR_max decreased.

Fig. 9(b) depicts the variation of ΔT with rA, indicating that ΔT increases with increasing rA. As a result, the metal to insulator transformation gets slower, and ΔT becomes larger. Fig. 9(a) clearly shows that TCR_max decreases with increasing rA. The decrement in the TCR_max values can be ascribed to the decreasing resistivity and the increasing ΔT. As discussed above, the resistivity is decreasing non-monotonically and, concurrently, ΔT increases rapidly. It is possible to conclude that the TCR values are primarily influenced by resistivity and ΔT, which can be altered by rA[36].

Fig. 9.

(a) Variation in TCR% and (b) Transition broadening temperature, ΔT with average A site radius, rA.

Optical properties

It is a very well-known fact now that the doping of any divalent alkaline earth ion in LaMnO₃ manganites introduces holes into the material that will lead to variations in Mn3+/Mn4+ ratio. Hence, like other manganites, this ratio very largely controls the electronic properties of the materials. This kind of hole doping plays a role in the shifting of the Fermi level, which is responsible for conduction and valence band behavior [37]. Thus, the electron–hole coexistence in manganites nominates them as a promising candidate for optical devices.

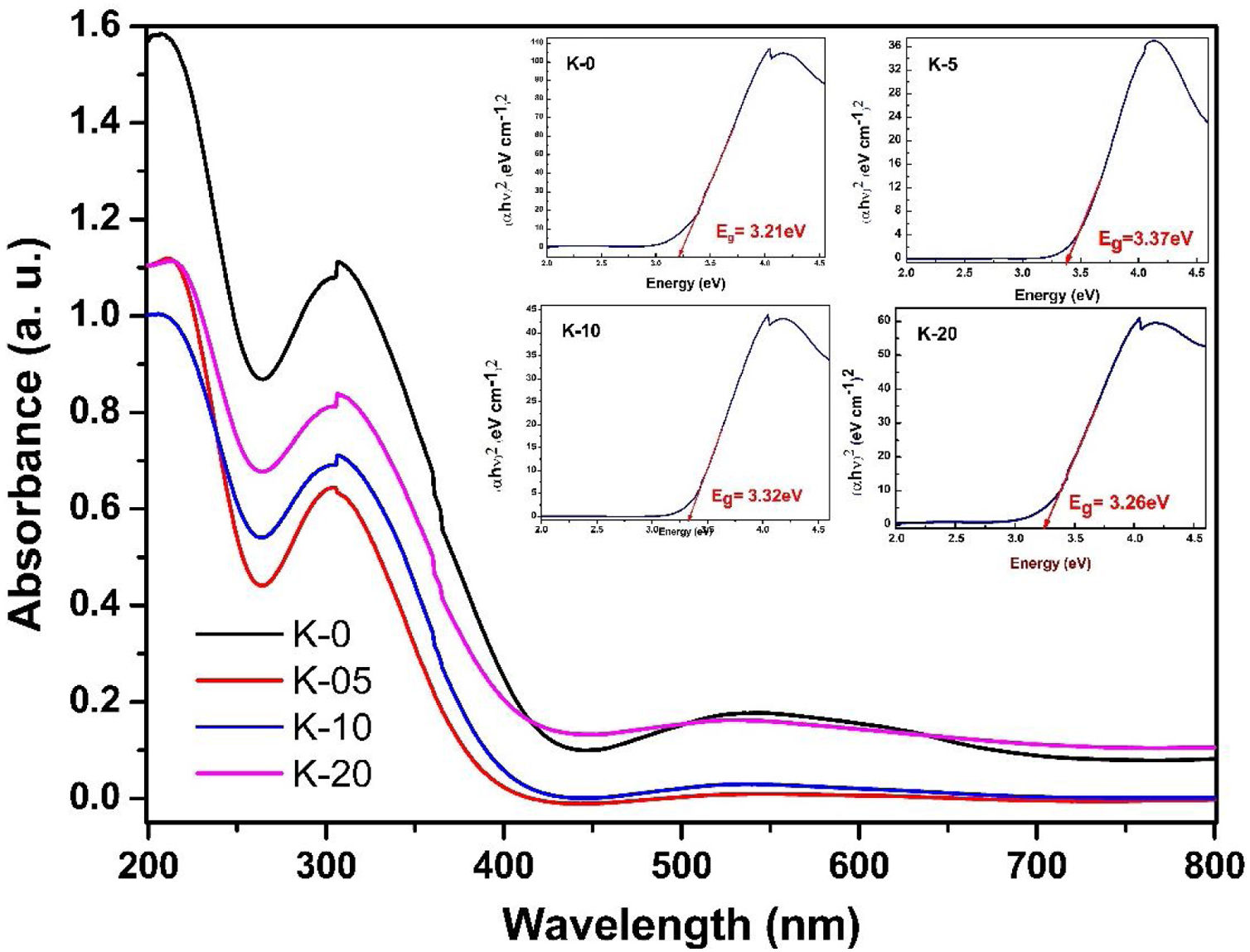
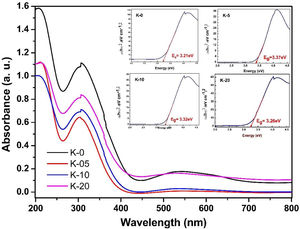
To investigate the optical response of the LCKMO ceramic samples, the absorbance spectrums of the samples were obtained and are shown in Fig. 10. The bandgap energy (Eg) has been estimated using the relation αhν2=Ahν−Eg, where α is the absorption coefficient; hν is the energy of the photon and A is a constant dependent on the effective masses of the charge carriers and the refractive index of the material. [38], as shown in the insets of Fig. 10. In which three obvious peaks are observed due to the optical response of the material. The first peak is observed near 207 nm, another strong absorption is observed at the wavelength of 304–307 nm and the third peak occurs around 528–545 nm

Fig. 10.

Room-temperature UV–Vis spectra of (a) K-0, (b) K-05, (c) K-10 and (d) K-20 ceramic samples.

It can be noticed that E_g values first increase from K-0 to K-05, then decrease with the increase in the K¹⁺ doping in LCKMO ceramics. This shift of the E_g for these ceramic samples may be attributed to the modification in the MnO bond length and MnOMn bond angle, since cation incorporation plays a crucial role in changing the bandwidth (W) and the optical bandgap of the LCKMO ceramics, which is consistent with our XRD results. The bandwidth (W) depends on both the bond angle and bond length as derived earlier. In addition, E_g is connected with W as: Eg=Δ−W, where D is the charge-transfer energy [24,39]. In the present case, all these structural changes show first an increase and then a decrease in the electron bandwidth (W). Further, it is evident from the spectra that the fundamental absorption edge shows a shift, which is related to the grain size, consequently there are variations in the value of optical bandgap E_g[40].

Conclusions

Investigations on structural, microstructural, resistivity-temperature, and optical properties dependence on the smaller ionic sized Ca²⁺ ion substitution by larger monovalent alkali metal K¹⁺ at A site have been discussed in this communication, considering the structural effects. Rietveld analysis of La_0.70Ca_0.30−x K_xMnO₃ (LCKMO) manganites is crystallized in a single phase without any noticeable impurity phase (for K-0 and K-05) and the presence of a small amount of Mn₃O₄ impurity (for K-10 and K-20) in the samples, having an orthorhombic unit cell structure with a Pnma space group. Resistivity-temperature studies reveal the change in electrical resistivity and metal to insulator transition temperature (T_P) with K¹⁺ content (x), attributed to the ionic size mismatch induced by structural distortions. The low-temperature electrical transport behavior of all the ceramic samples studied has been explained in the light of the electron-electron scattering mechanism owing to weak localization and average A-site cationic radius induced structural disorder in the LCKMO ceramics and the metallic region of the resistivity-temperature plots of the LCKMO ceramic samples studied has been explained using the Zener double exchange polynomial law. This shows doping induced alterations in the fit parameters for LCKMO ceramic sample systems. The insulating regime of resistivity temperature has been fitted using a small polaron hopping model and it has been observed that activation energy increases monotonically with increasing x in the LCKMO system. TCR_max values are decreasing with increasing doping. RT UV–Vis studies show that the optical bandgap of the LCKMO ceramic samples first increases and then decreases with doping that can be attributed to different grain sizes and grain boundaries.