El Excel Trial1 es sin duda el paradigma de cómo lo que debería ser colaboración entre diferentes especialidades termina generando confusión y crispación entre profesionales, con el efecto potenciador derivado de la industria farmacéutica. En este ensayo clínico se aleatorizan casi dos mil enfermos a cirugía (CABG) o angioplastia (PCI) para el tratamiento de la enfermedad de tronco coronariano izquierdo (TCI) con Syntax score de 0-22 (riesgo bajo-intermedio). Se analizan los resultados de un end-point combinado de muerte, accidente cerebrovascular e infarto a 3 años (estudio de no inferioridad) y posteriormente a 5 años (estudio de superioridad). A 5 años se observa un 22% de eventos en la rama PCI y un 19,2% en la rama CABG (p: 0,13). Así, a pesar de una diferencia de mortalidad llamativa (PCI: 13,0% vs CABG: 9,9%, p: 0,002) los autores concluyen que ambas estrategias son equivalentes. Si los resultados del Excel a 5 años se hubieran analizado como un estudio de no inferioridad como era el protocolo inicial, la diferencia observada del 2,8% (IC 95% -0,9 – 6,5%) hubiese impedido descartar la hipótesis nula (PCI es inferior) confirmando así la inferioridad de la rama PCI. Desgraciadamente los autores no explicaron el motivo del cambio en el análisis. El Excel Trial fue capital a la hora de modificar las guías clínicas europeas y equiparar la recomendación de tratamiento de TCI de bajo riesgo entre ambas opciones.
David Taggart, miembro inicial del comité del ensayo, retira su nombre de la publicación y acusa a los investigadores de manipulación2 entre otros motivos por el cambio en la definición de infarto perioperatorio. Bastaba una elevación enzimática para considerar dicho evento, que además formaba parte de un end-point primario combinado. El 90% de los infartos fueron definidos exclusivamente en base a criterios bioquímicos. Así, la rama CABG salía claramente perjudicada con porcentajes de infarto periprocedimiento claramente superiores a otros ensayos clínicos (6,3% vs 1,7% en Freedom o 2,9% en Syntax). De este modo, una diferencia de mortalidad del 38% a favor de la cirugía (9.9% PCI vs 13.0% CABG) queda diluida en la salsa bioquímica de un end-point combinado. La polémica en redes sociales e incluso en medios de comunicación ha sido intensa y la repercusión clínica posiblemente excesiva dada la escasa evidencia clínica para equiparar ambas estrategias.
En un intento de aportar más evidencia científica, James Brophy utiliza sus conocimientos en teoría bayesiana para dar otro enfoque a los datos del Excel Trial en un artículo presentado en JAMA3.
Thomas Bayes (1702-1761) fue un pastor presbiteriano inglés cuya fama procede de la presentación de su teorema por parte de su amigo Richard Price en la Royal Society de matemáticas dos años tras su muerte. De manera resumida, el teorema de Bayes determina, si aparece un determinado efecto, cuál es la probabilidad de que haya actuado una determinada causa. No hay alteración del orden temporal de los sucesos, lo que ocurre es que se recibe la información en sentido inverso. Este flujo de información es el que solemos procesar en la práctica clínica. En nuestro caso, en base a los síntomas que definen el end-point se busca la probabilidad de que se haya realizado PCI o CABG. Además, el enfoque bayesiano parte de una probabilidad condicionada al conocimiento previo que una vez más simula la práctica clínica. En el estudio que analizamos, la probabilidad previa (priors) son los ensayos clínicos que analizan el mismo problema (Syntax4, Freedom5 y Pre-Combat6). Los ensayos clínicos presentan un análisis frecuentista en el que se “simplifica” el análisis estadístico a aceptar o rechazar una hipótesis en base a una diferencia preestablecida a priori como significativa. El enfoque bayesiano permite estimar la probabilidad para cualquier diferencia.
En el artículo que analizamos, se realizan 100.000 muestras aleatorias de los datos iniciales y, partiendo del evento, se observa qué porcentaje era “provocado” por CABG (x) o por PCI (y). La diferencia de porcentaje (x-y) se sitúa en el eje de abscisas de una gráfica siendo el eje de ordenadas el porcentaje de muestras que presentan dicha diferencia. Por ejemplo si el 10% de las 100.000 muestras presentan una diferencia de porcentaje entre CABG y PCI de 2 (51% de los eventos son de PCI y 49% son de CABG), obtendremos en la gráfica un punto situado en abscisa 2 y en ordenada 0,.1 (10%). El análisis de todas las muestras y de las diferencias permite completar esta gráfica y obtener así una curva de densidad de probabilidad. Dicha curva presenta un área (área bajo la curva: AUC) de 1. El análisis del AUC a partir de un determinado punto puede interpretarse como la probabilidad de obtener una diferencia. Por ejemplo, en la figura 1 del artículo se obtiene una curva de densidad de probabilidad en la que el 95% del AUC se sitúa por encima de 0. Esto puede interpretarse como un 95% de probabilidad de que la diferencia en el porcentaje de veces que PCI-CABG causa un efecto es mayor que 0. Dicho de otro modo, hay un 95% de probabilidades de que PCI cause más efecto que CABG. La curva de densidad de probabilidad permite estimar la probabilidad para cada magnitud de efecto evitando la simplicación del análisis frecuentista y dejando al clínico la valoración de la importancia de cada magnitud.
Según este análisis hay un 95% de probabilidades de que haya más eventos primarios a 5 años con PCI y un 87% de que la diferencia sea al menos del 1%.
Considerando sólo muerte (fig. 2), la probabilidad de que haya más de un 1% de diferencia de mortalidad asciende al 94%. El análisis de los datos nos permite decir por ejemplo que hay un 95% de probabilidad de que por cada mil casos tratados la cirugía salve entre 9 y 27 vidas.
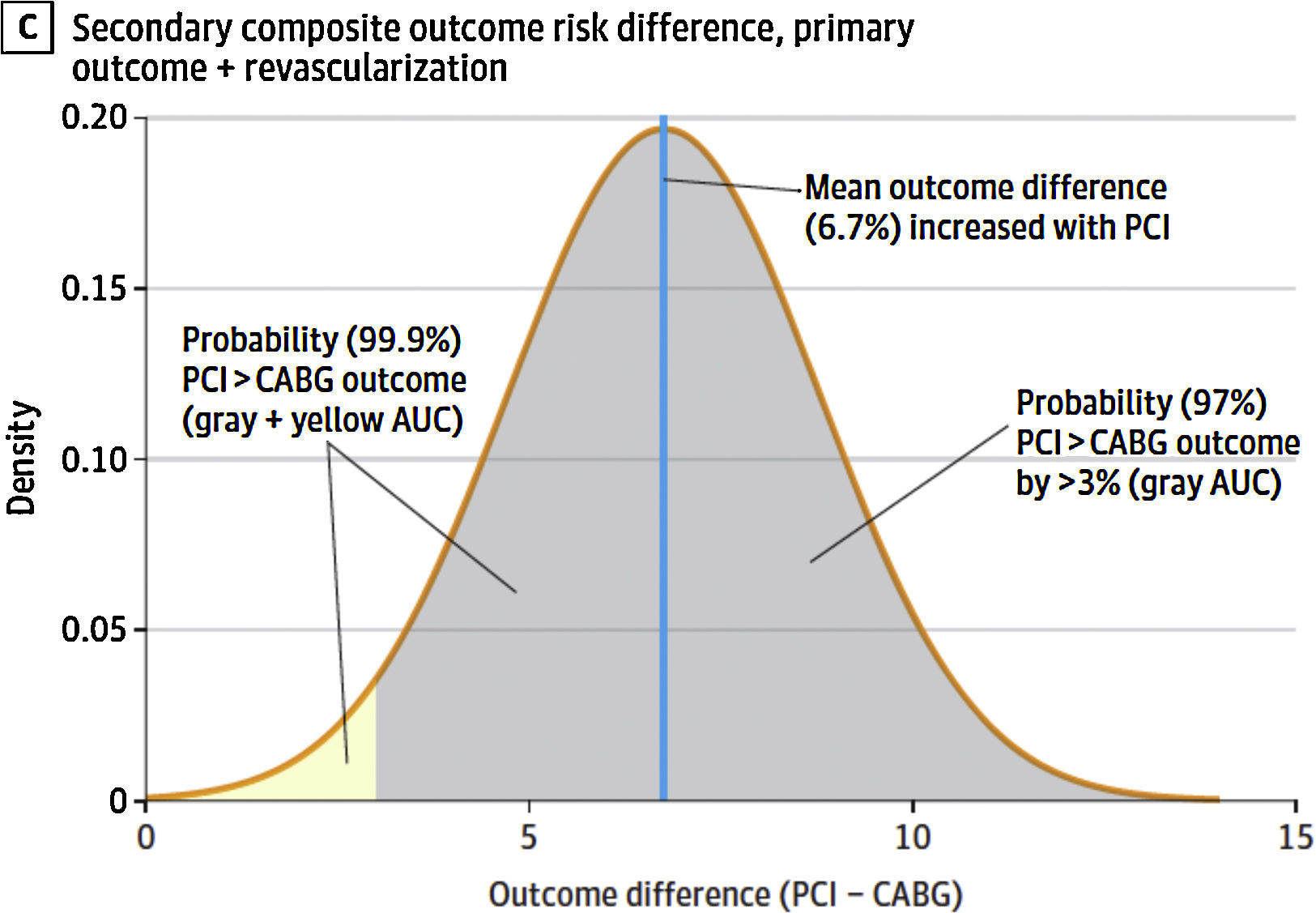
Fijándonos en el end-point secundario, en el que se incluye necesidad de nueva revascularización (NNR), la curva de densidad de probabilidad nos ofrece varios detalles importantes (fig. 3). La media de diferencia de eventos es de 6,7. Por otro lado, el 98% de la curva está situada por encima de los 4 eventos. Y el 90% por encima de 5. Dicho de otro modo, a 5 años existe un 90% de probabilidades de que los enfermos tratados con PCI para la enfermedad de TCI de riesgo bajo-intermedio tengan al menos 5 eventos más (infarto, muerte, accidente cerebrovascular o necesidad de revascularización) que si son operados. En un segundo análisis, el autor incorpora la probabilidad a priori de los ensayos clínicos disponibles y equiparables (SYNTAX, FREEDOM Y PRECOMBAT) para mostrar nuevas curvas de densidad de probabilidad. Estas nuevas curvas condicionadas muestran resultados similares con probabilidades algo inferiores.
En la misma revista, se analiza la influencia de la industria en los ensayos clínicos. M. Gaudino7 analiza cómo más de la mitad de los ensayos están esponsorizados. En este grupo, curiosamente, hay un mayor número de end-points combinados, más estudios de no inferioridad y más pérdidas en el seguimiento con hasta un 40% de discrepancia con respecto al protocolo.
El artículo que presentamos intenta aportar un enfoque matemático complementario que permita desligar de pasión “twitera” el tratamiento de la enfermedad de tronco coronario. La simplificación del software informático necesario para dicho análisis bayesiano y su disponibilidad en internet sin duda generará más artículos en el futuro. La comprensión del teorema de Bayes y de la probabilidad condicionada serán obligatorias para un correcto análisis de la evidencia científica. A pesar de las limitaciones derivadas de la ausencia de datos individuales y de la ausencia de determinadas medidas de precisión en algunos estudios, el enfoque bayesiano del Excel Trial redunda en el beneficio de la actuación quirúrgica en el tratamiento de la lesión de riesgo bajo-intermedio del tronco coronario izquierdo y permite una interpretación más rica. Sin embargo, los clínicos deben valorar la evidencia científica en el contexto de la situación de cada paciente para tomar la decisión más razonable. La angioplastia y la cirugía para el tratamiento de la enfermedad de tronco son elecciones tanto más válidas cuanto más se adapten a las necesidades del paciente y no del “operador”.