Systematic Reviews With Meta-analysis of Clinical Trials: Is There Enough Evidence?

Abstract

Systematic reviews with meta-analysis are essential tools to reliably summarize the effectiveness of health interventions. A meta-analysis based exclusively on a small number of trials will often not be conclusive or may yield false positive results. The estimation of the OIS — optimal information size — can reduce the risk of obtaining false positive results and determine if additional clinical trials are required. The estimation of the OIS is very similar to that used to estimate the sample size of a clinical trial. The required number of participants for the meta-analysis should be at least as large as a single trial with adequate power. The OIS concept provides a statistical framework in which the accumulated information is convincing to indicate whether more clinical trials are needed to address the effects of the intervention.

Resumen

Las revisiones sistemáticas con meta-análisis son pruebas esenciales para resumir de manera fiable la eficacia de las intervenciones sanitarias. Un meta-análisis basado exclusivamente en un pequeño número de ensayos a menudo no será concluyente o puede aportar resultados positivos falsos. La estimación del OIS -tamaño óptimo de la información- puede reducir el riesgo de obtener resultados falsos positivos y determinar si se requieren ensayos clínicos adicionales. El cálculo del OIS tiene similitudes al realizado para calcular el tamaño de la muestra de un ensayo clínico. El número requerido de participantes para el meta-análisis debe ser al menos tan grande como un solo ensayo con la potencia adecuada. El concepto del OIS proporciona un marco estadístico en el que la información acumulada es convincente para indicar si se necesitan más ensayos clínicos para abordar los efectos de la intervención.

Introduction

Systematic reviews (SR) with meta-analysis (MA) are essential to reliably synthesize the effectiveness of healthcare interventions.¹ SR with MA are research studies that identify the maximum number of relevant studies, evaluate their quality and summarize their results using rigorous and explicit scientific methodology. Surgeons use these tools to stay up-to-date in their field, and they are essential for developing clinical practice guidelines.² Certain government research funding agencies also require SR before granting funding for new research projects.³

SR can include MA as a statistical method to summarize the results of individual clinical trials.⁴ The main objective of an MA is to provide a more accurate estimate that combines the numerical information of the individual clinical trials. However, an MA based exclusively on a small number of trials will often not be conclusive⁵ or may result in type I errors, meaning that a difference is accepted between the 2 interventions evaluated, even though that difference does not exist.⁶ In the literature, there are several studies that conclude that the results of an MA with a large number of patients are probably more valid than the results of an MA with a small number of patients and events (<200 events).^7–9

Although it is currently debated and even questioned whether statistical significance values (P values) should still be used categorically,¹⁰ so far the most widespread method has been to set a risk value less than or equal to 5% or less than or equal to 1% of committing a type I error. In this manner, at least, that same risk value should be preserved in the MA. Updating an MA every time a new clinical trial appears (a common practice) increases the risk of overestimating the effect observed in the MA; this is mainly related to the effect of statistical multiplicity, which means that a benefit may be assumed when it really does not exist. Thus, each time a new trial is incorporated or a different outcome is analyzed, the value of α will be consumed and the type I error may be greater than 5%. A significant result would be obtained which, in reality, would result from an overestimation of the actual effect of the intervention. However, it is likely that a large number of clinicians and researchers are oblivious to these situations and consider MA results ‘definitive’.

The objective of this study is to describe the concept of the sample size in MA, the optimal information size (OIS) of an MA, its calculation, its interpretation and the influence of the OIS analysis on the interpretation of the evidence.

Sample Size in the Meta-analysis

From a classical (frequentist) statistical approach, the calculation of the sample size is an essential requirement when developing the protocol of a clinical trial. This is reflected in the number of patients or other experimental units that should be included in a study in order to reliably address the research question.¹¹ The sample size of an MA can be defined as the number of participants and events necessary to detect or reject the effect of an intervention assumed a priori in an MA. Here, a similar criterion could also be applied to that of the individual clinical trials, assuming that if the sample is too small, it will not be possible to detect an effect and that a sample that is too large may be a waste of time and money, while even raising ethical issues.¹² This would be mainly explained by the fact of continuing to carry out clinical trials when an MA had already demonstrated a firm result in favor or against the intervention; therefore, patients would be exposed to an ineffective intervention or an effective intervention would not be offered to patients in the case this was demonstrated in the MA. Among the scientific community and healthcare professionals, the idea may have spread that MA provide reliable results simply because they are MA.

However, when can an MA be considered definitive evidence? Is it possible to calculate the sample size in the MA as in the clinical trial?

Almost in parallel to the beginnings of the evidence-based medicine movement, the number of MA published annually has increased almost exponentially. Currently, it is estimated that around 8000 systematic reviews are published per year.¹³ However, not all MA include the appropriate number of patients to obtain reliable conclusions, and the lack of an adequate number of patients and events is one of the reasons for the imprecision in the estimated effect.¹⁴

How to Calculate the Optimal Information Size of a Meta-analysis

In an effort to obtain more reliable conclusions using MA, the risk of obtaining false positive results can be reduced by estimating the OIS, while determining whether additional clinical trials are required in a certain area of knowledge. Specifically, the OIS can be defined as the minimum amount of information required in the literature to reach reliable conclusions about an intervention.¹⁵ The calculation of the OIS is similar to the calculation of the sample size for a clinical trial. The concept of OIS for an MA was initially developed and proposed by Pogue in 1998.¹⁵ Several options have been proposed for OIS calculation. The simplest method to calculate this number of patients, similar to the sample size calculation, is to execute it as if it were a clinical trial with adequate study power. This can be done by assuming a value for α (false positive or type I error), β (false negative or type II error), power, effect size and experimental event rate in the control group.

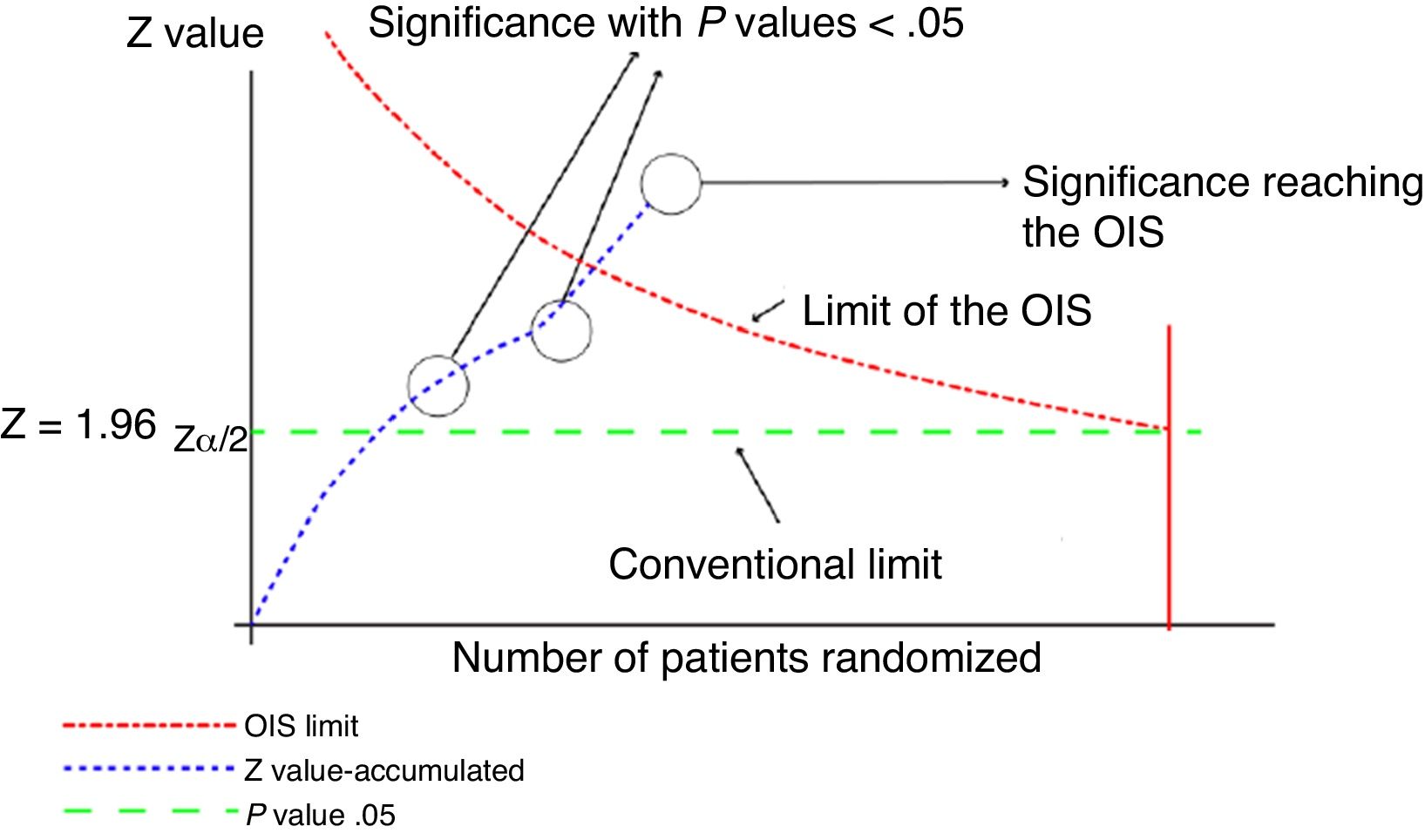
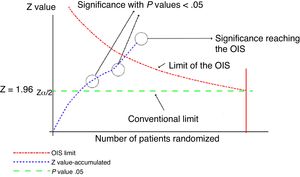
This analysis can be represented graphically, similar to that of sequential clinical trials, as shown in Fig. 1. For this calculation, software can be used to calculate the sample size, such as the free-access PS-Power (http://biostat.mc.vanderbilt.edu/wiki/Main/PowerSampleSize).

Fig. 1.

Graphical representation of the sequential analysis applied to the meta-analysis. Adapted with permission from Imberger et al.²²

In this graph, the cumulative z score line represents the information accumulated from each of the trials included in the meta-analysis. Where the line of the cumulative z score crosses the P value .05 line (conventional limit), which represents the traditional value of significance, a statistically significant result is obtained, but this does not indicate that the OIS has been reached. The appropriate volume of information will be reached when the cumulative z value line crosses the OIS limit line, as shown in the graph.

A decade later, in 2008 Brok et al.¹⁶ proposed including statistical heterogeneity in the estimation of the OIS, considering it an essential parameter in an MA. Statistical heterogeneity quantifies the variability between the results of the studies, and this variability may be due to the actual differences in approach and execution among the studies included or to other causes. For the estimation of this OIS, including heterogeneity, at least one specific and freely available software has been designed that enables the OIS to be calculated with an assumed heterogeneity value that can be entered manually or assumed by default according to the calculation made by the software (http://www.ctu.dk/tsa/downloads.aspx).

As mentioned in previous paragraphs, a key step to estimate the OIS is to decide which parameters to include in the calculation. A step that is no less important but more controversial is how to estimate the parameters that will be assumed for the calculation. Regarding the first point, the parameters necessary may include the estimated effect, event rate in the control group and heterogeneity (I²). Other necessary parameters include the value of α, the value of β and the statistical power. For these last three, there is greater consensus and the following values are usually assumed: α = 0.05; β = 95%; power = 80%. In the case of the estimated effect, there are authors who use the estimated effect in the MA, others use a value of 20% expressed as a relative risk reduction. As for the event rate, mainly the event rate in the control group, one author proposes that the most stable option is the median value of the proportion of events in the control group.¹⁷ Regarding heterogeneity, the value of the heterogeneity observed in the MA is usually used. Wetterslev et al. have proposed what they have called diversity, expressed as D2, and according to the authors it seems a better alternative than I² to consider the variation of the model in any random-effects MA.¹⁸ However, other options are perhaps more appropriate, such as the use of estimated values with a priori distributions of heterogeneity.^19,20

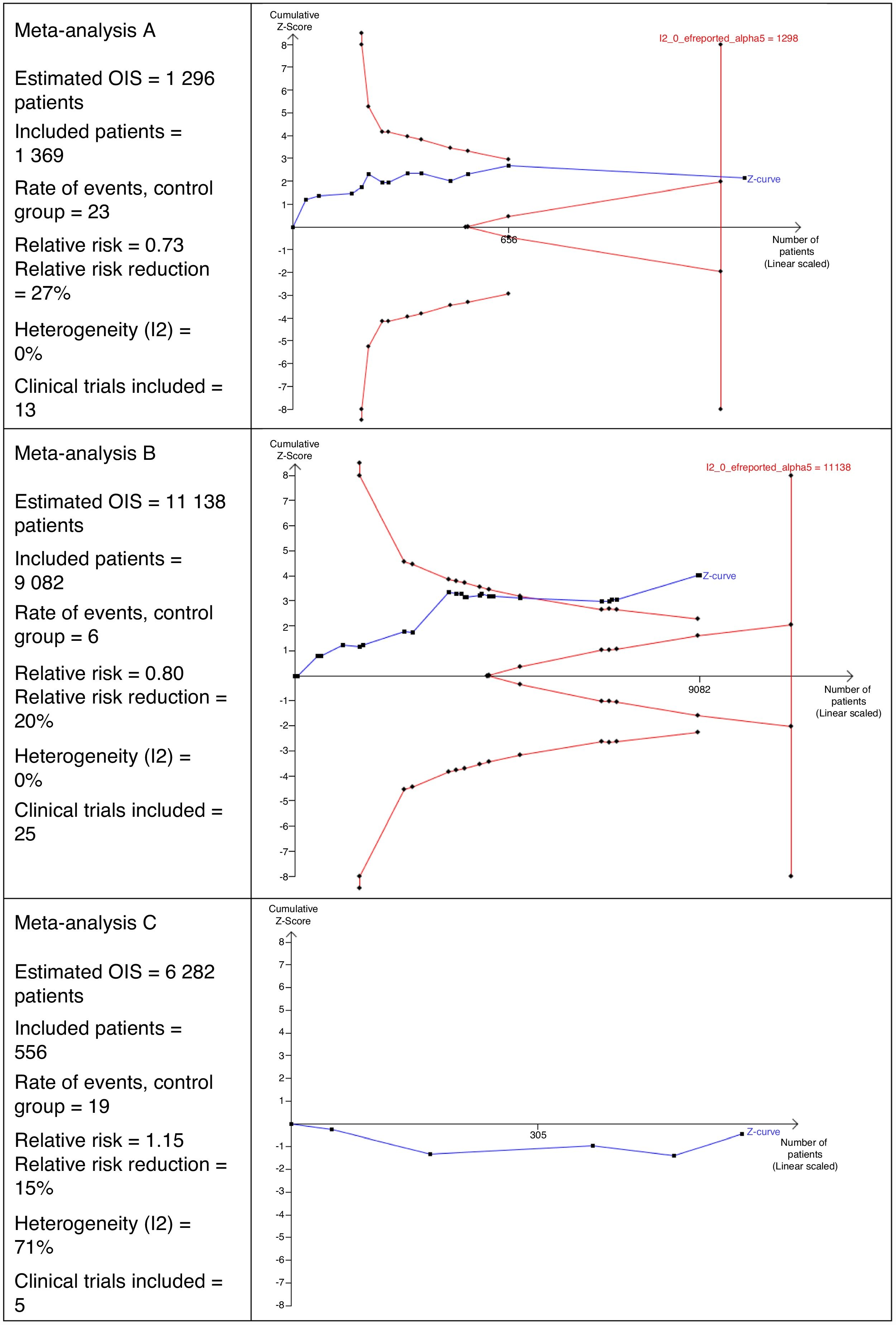
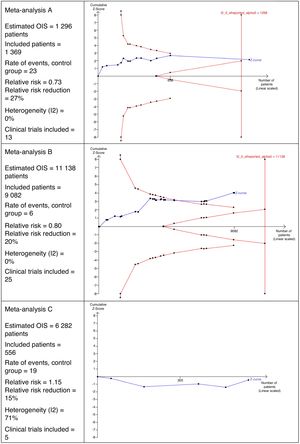
Interpretation of the Optimal Size of the Information

Fig. 2 shows 3 different scenarios of the calculation for OIS and its interpretation that could be perfectly applicable to MA in the field of surgery. It shows that MA A includes 13 clinical trials with a total of 1369 patients. This number of patients is sufficient to reach the OIS of 1298 patients and, therefore, the z curve crosses the vertical line. This is a good example in which a sufficient sample size is reached to be confident in the result obtained in the MA.

Fig. 2.

Examples of calculations for the optimal information size, showing 3 different scenarios (meta-analyses A, B y C).

In MA B, we can observe that there are 25 clinical trials with a total of 9082 patients. This number is insufficient to reach the OIS of 11,138 patients and, therefore, the z curve does not cross the vertical line. However, it is close to reaching it because, in addition, the trend is observed and it crosses the line of the curve of significance (downward curve of the limit of patients to be included).

MA C includes a total of 5 clinical trials, contributing 556 patients. The estimated OIS is 6282 patients. Due to this low number of patients collected, it is not even possible to draw the downward curve. Another interesting detail of this figure is that the z curve runs below the horizontal line because the observed relative risk is >1.

Optimal Information Size and Interpretation of the Evidence

The concept of OIS provides a statistical framework in which the accumulated information reliably indicates whether more clinical trials are needed to evaluate the effects of the intervention in the general population. The calculation of the OIS is a statistical tool that provides more precise information about the estimated effect observed in an MA. It can also report whether the volume of information accumulated in the MA, mainly the number of studies, is sufficient to answer the research question under certain assumptions. OIS estimations are already considered useful by the GRADE working group, which evaluates the quality of evidence and establishes the degree of recommendation for a particular medical or surgical intervention. The GRADE system considers the estimation of OIS to be an informative parameter to evaluate the imprecision of the results obtained in an MA. In this manner, it also determines the confidence that the result provides and, based on that, it establishes a degree of recommendation or another for the intervention studied.¹⁴

In systematic reviews with MA, the OIS is being increasingly used: there are already several MA published in the surgical field that incorporate the calculation of the OIS.^21–23 Despite this, it is still under development, and there is debate about how to estimate the parameters recommended for the calculation.²⁴ However, despite its methodological limitations, it is necessary to have a tool of this type that provides more precise information to interpret the evidence, thereby avoiding on more than one occasion the well-known phrase, “There is not enough evidence to assess the effect of this intervention. Further studies are needed to determine its effect.” In the event that this phrase is used, we should be more precisely indicate how many patients are needed in these studies to provide more accurate and reliable information.

Funding

This present article has received no specific funding from public, commercial or non-profit organizations.

Conflict of Interests

None.