Aplicación del análisis Rasch en la investigación enfermera: una introducción metodológica

Resumen

El diseño y la validación de herramientas constituye un pilar fundamental de la investigación enfermera, donde es imprescindible incorporar las metodologías y los análisis más actuales para poder garantizar la validez y la fiabilidad en su aplicación clínica.

El objetivo de este trabajo es describir las características del análisis Rasch y la metodología para su desarrollo, así como discutir su relevancia y aplicabilidad en la investigación enfermera, destacando su potencial contribución a la mejora de la calidad y precisión de los instrumentos de medición en la disciplina.

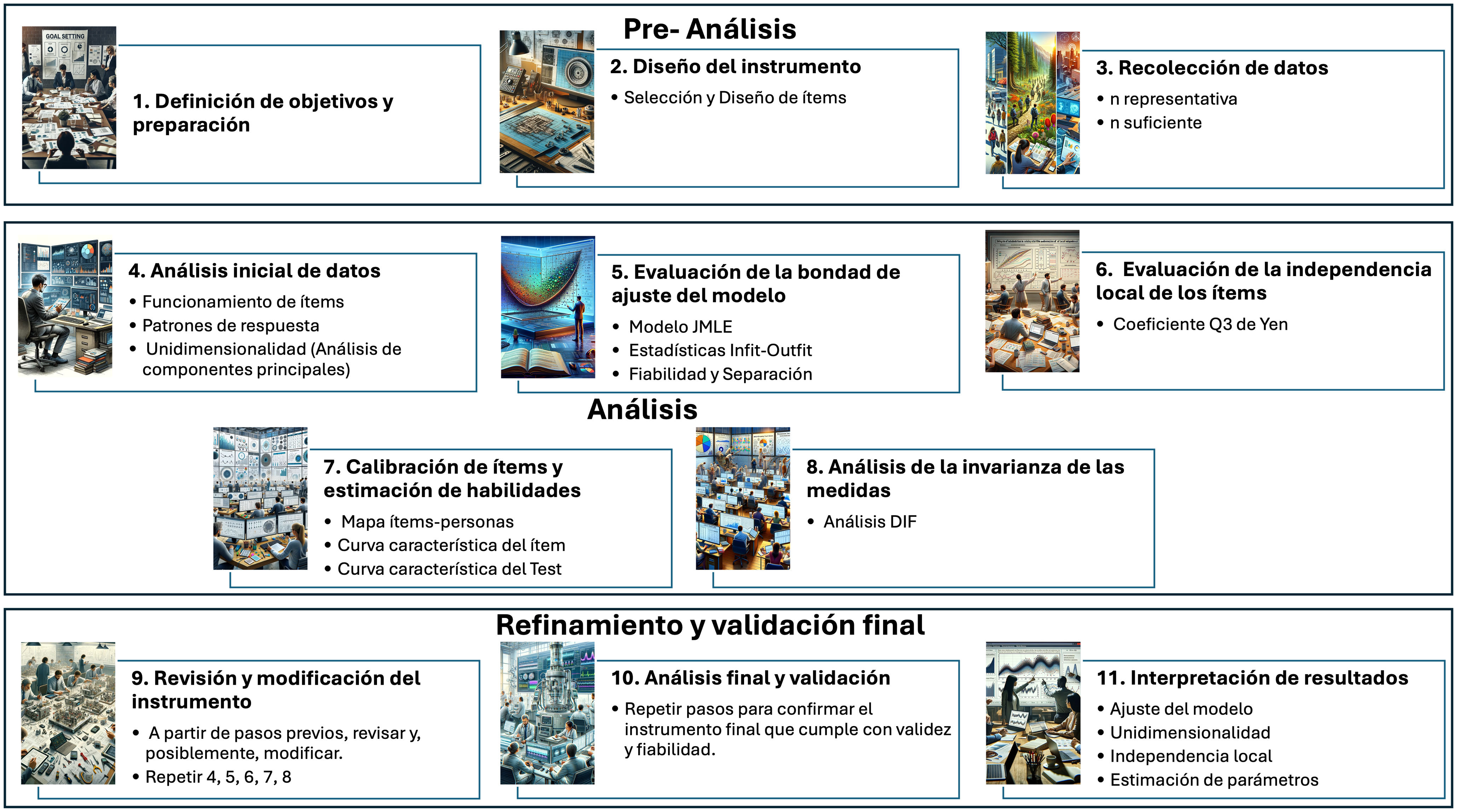
A través de una síntesis narrativa se describen los fundamentos teóricos del análisis Rasch, y se presentan las características y los supuestos que se deben cumplir para llevar a cabo este tipo de análisis. Posteriormente, se presenta la metodología de implementación en 11 pasos: definición de objetivos y preparación, diseño de instrumento, recolección de datos, análisis inicial y de la unidimensionalidad, evaluación de la bondad de ajuste (infit y outfit, fiabilidad y separación), evaluación de la independencia local de los ítems (coeficiente Q3 de Yen), calibración de ítems y estimación de las habilidades, análisis de la invarianza de la medida (análisis DIF), revisión y modificación del instrumento, análisis final y validación, interpretación de los resultados. Se presentan ejemplos de uso, así como las ventajas y las limitaciones del método. Como conclusión, el análisis Rasch proporciona una metodología valiosa para la evaluación de competencias y las habilidades clínicas, así como para el desarrollo y la validación de instrumentos de medición de gran utilidad para la investigación en cuidados, aunque sería necesario potenciar la formación y estandarización en su uso.

Abstract

The design and validation of tools constitutes a fundamental pillar of nursing research, where it is essential to incorporate the most current methodologies and analyses in order to guarantee validity and reliability in their clinical application.

The aim of this paper is to describe the characteristics of the Rasch analysis and the methodology for its development as well as to discuss its relevance and applicability in nursing research, highlighting its potential contribution to the improvement of the qual

ity and accuracy of measurement instruments in the discipline.

Through a narrative synthesis, the theoretical foundations of Rasch analysis are described and the characteristics and assumptions that must be fulfilled to carry out this type of analysis are presented. Subsequently, the implementation methodology is presented in 11 steps: definition of objectives and preparation, instrument design, data collection, initial and unidimensionality analysis, goodness-of-fit assessment (infit-outfit, reliability and separation), item local independence assessment (Yen's Q3 coefficient), item calibration and estimation of skills, measurement invariance analysis (DIF analysis), review and modification of the instrument, final analysis and validation, interpretation of results. Examples of use are presented, as well as the advantages and limitations of the method. In conclusion, the Rasch analysis provides a valuable methodology for the evaluation of clinical competencies and skills, as well as for the development and validation of measurement instruments of great utility for research in care, although it would be necessary to promote training and standardization in its use.

Introducción

La enfermería, como disciplina centrada en el cuidado de la salud, requiere de herramientas de evaluación precisas para garantizar la calidad y la eficacia de los cuidados proporcionados. Así pues, juega un papel crucial en el desarrollo de instrumentos de medida, especialmente en áreas relacionadas con la salud, el bienestar, la calidad de vida y la evaluación de cuidados. Las enfermeras contribuyen de forma activa junto a otras disciplinas de la salud y las ciencias sociales en la consecución de avances en la creación y validación de estos instrumentos.

El análisis Rasch, dentro del ámbito de la investigación en enfermería, se destaca como una herramienta estadística poderosa y refinada para la evaluación y la mejora de instrumentos de medición, especialmente en lo que respecta a encuestas y evaluaciones de competencias. Originario de la teoría de respuesta al ítem (TRI)¹, el análisis Rasch permite a los investigadores superar limitaciones inherentes a los métodos de escala tradicionales, proporcionando un marco más sólido y detallado para la interpretación de datos en estudios de salud. Ofrece una metodología sólida para la construcción y la validación de instrumentos de medición, permitiendo a los investigadores y profesionales clínicos desarrollar escalas y pruebas que reflejan con precisión las competencias y habilidades clínicas².

Así pues, en el contexto de la investigación enfermera, el análisis Rasch se utiliza para validar y refinar instrumentos de medición, asegurando que estos sean tanto fiables como válidos para medir los fenómenos específicos dentro de la disciplina³. Esto es de suma importancia, ya que los instrumentos de alta calidad son esenciales para la recopilación de datos precisos y útiles, los cuales, a su vez, informan de las prácticas basadas en evidencia y políticas de salud pública⁴.

En este contexto, los objetivos de este artículo son describir el análisis Rasch y discutir su relevancia y aplicabilidad en la investigación enfermera, destacando cómo esta metodología puede contribuir significativamente a la mejora de la calidad y precisión de los instrumentos de medición. Al hacerlo, se busca iluminar la importancia del análisis Rasch, no solo como una herramienta estadística, sino también como un enfoque que puede facilitar la investigación significativa y relevante en enfermería, la cual es crítica para el avance de la práctica y la formulación de políticas basadas en evidencia.

La comprensión y aplicación del análisis Rasch ofrece varias ventajas. No solo mejora la capacidad de desarrollar y validar instrumentos de medición robustos, sino que también proporciona una base sólida para la interpretación de los resultados de la investigación, asegurando que las decisiones basadas en estos datos sean lo más informadas y precisas posible. Además, el énfasis del análisis Rasch en la calidad de los datos refuerza la importancia de la rigurosidad metodológica en la investigación en enfermería, contribuyendo así al cuerpo general de conocimiento en la disciplina.

Fundamentos teóricos del análisis Rasch

El análisis Rasch, nombrado así por el matemático danés Georg Rasch⁵, es un enfoque dentro de la TRI que proporciona una base sólida para la medición objetiva en las ciencias sociales y de la salud. A diferencia de otros modelos estadísticos que pueden basarse en suposiciones menos estrictas sobre los datos, el modelo Rasch se caracteriza por su capacidad para transformar respuestas cualitativas (p. ej., correcto/incorrecto, de acuerdo/en desacuerdo) en medidas cuantitativas a lo largo de un continuo de habilidad o actitud, de modo que valores bajos en este continuo de la variable latente representan características de la variable latente que ocurren frecuentemente o que son fácilmente observables. Por otro lado, valores altos en este continuo indican características que son raramente observadas o bien que son más difíciles de conseguir⁶.

Descripción del modelo Rasch

El modelo Rasch es, fundamentalmente, un modelo matemático, con función de probabilidad logística, que asume que la probabilidad de una respuesta correcta a un ítem (o la elección de una respuesta particular en una escala) depende, únicamente, de la diferencia entre el nivel de habilidad del individuo y la dificultad del ítem⁷. Esta característica singular permite que el modelo Rasch proporcione mediciones independientes de las personas y los ítems, una propiedad conocida como «invarianza de la medida»⁸, lo que significa que las mediciones no dependen del grupo específico de ítems presentados o de la población de respondientes en la muestra.

Otro componente crucial de este modelo es la «jerarquía o calibración de ítems»⁹, un proceso mediante el cual se estima la dificultad de cada ítem dentro de un conjunto de datos. Es decir, se ordenan a los ítems y a las personas en el mismo continuo, en el que los ítems más probables se sitúan en la parte inferior del continuo¹⁰. La jerarquía de los ítems a lo largo del continuo determina el orden de las ubicaciones de los ítems en relación con la distribución de las personas⁹. Esta calibración es fundamental para asegurar que los ítems sean adecuadamente comparables, y para facilitar la construcción de pruebas equitativas y justas. Por último, la «estimación de habilidades» de los individuos es igualmente importante, permitiendo la evaluación precisa del nivel de habilidad o competencia de una persona en relación con el constructo medido.

También hay que tener en cuenta que el modelo Rasch se basa en 2 suposiciones clave que se deben cumplir^6,11. Si no es posible asumir estas suposiciones, se deberían aplicar otros métodos de validación de instrumentos. Estas suposiciones son:

• -

  Asunción de unidimensionalidad: Es la asunción básica del análisis Rasch¹². Este concepto implica que todas las preguntas o ítems en la prueba están diseñados para medir una única dimensión subyacente o constructo. En otras palabras, un conjunto de ítems se considera unidimensional si todas las variaciones en las respuestas de los individuos pueden atribuirse a diferencias en el nivel de esa única dimensión que se está evaluando, y no a otras dimensiones o factores irrelevantes.

  Por ejemplo, si estamos evaluando la habilidad de comprensión lectora en una prueba, queremos que todos los ítems midan esta habilidad y no estén influenciados por otras habilidades como la memoria o el conocimiento enciclopédico. Si la prueba es unidimensional, podemos confiar en que las diferencias en las respuestas de los individuos reflejan verdaderamente diferencias en su comprensión lectora y no están distorsionadas por otros factores.

• -

  Independencia local de los ítems^6,11: Esta propiedad implica que las respuestas de los individuos a cada ítem son independientes entre sí, una vez que se ha tenido en cuenta su habilidad en la dimensión que se está evaluando. En otras palabras, la independencia local significa que la probabilidad de que un individuo responda correctamente a un ítem determinado no está influenciada por sus respuestas a otros ítems, una vez que se ha considerado su nivel de habilidad en la dimensión que se está evaluando.

  Esta propiedad es fundamental en el modelo de Rasch porque permite que cada ítem contribuya de manera única a la medición de la habilidad del individuo en la dimensión específica. Si no se cumple esta independencia local, puede haber sesgos en la interpretación de las puntuaciones de la prueba y se podría afectar la validez y la fiabilidad de la medida.

A diferencia de otros modelos de la TRI, el análisis Rasch no requiere que los datos se ajusten a una distribución específica, lo que lo hace particularmente versátil y robusto para diferentes tipos de evaluaciones¹. Esta característica subraya la importancia del modelo Rasch en la creación de instrumentos de medición fiables y válidos, facilitando su aplicación en un amplio espectro de contextos.

Así pues, a diferencia de otros modelos de la TRI o de los métodos de la teoría clásica de los tests (TCT), el modelo Rasch ofrece varias ventajas únicas:

• –

  Medición conjunta¹³: Significa que los parámetros de las personas y de los ítems se expresan en las mismas unidades y se localizan en el mismo continuo. En consecuencia, la interpretación de las puntuaciones no se fundamenta necesariamente en normas de grupo, sino en la identificación de los ítems que la persona tiene una alta o baja probabilidad de resolver correctamente. Esta característica dota al modelo de Rasch de una gran riqueza diagnóstica.

• –

  Invarianza de medida: Como se mencionó anteriormente, una de las contribuciones más significativas del análisis Rasch es su capacidad para facilitar comparaciones válidas entre ítems y personas, independientemente de la muestra de ítems o la población de personas a las que se aplica el test⁴.

• –

  Objetividad específica¹⁴: Una medida solo puede ser considerada válida y generalizable si no depende de las condiciones específicas con que ha sido obtenida. Es decir, la diferencia entre 2 personas en un atributo no debe depender de los ítems específicos con los que sea estimada. Igualmente, la diferencia entre 2 ítems no debe depender de las personas específicas que se utilicen para cuantificarla. En consecuencia, si los datos se ajustan al modelo, las comparaciones entre personas son independientes de los ítems administrados y las estimaciones de los parámetros de los ítems no estarán influenciadas por la distribución de la muestra que se usa para la calibración. En la propiedad de objetividad específica se fundamentan aplicaciones psicométricas muy importantes como la equiparación de puntuaciones obtenidas con distintos tests, la construcción de bancos de ítems y los tests adaptados al sujeto.

• –

  Validación de los ítems: El análisis Rasch permite una revisión detallada de cada ítem en un test, identificando aquellos que no se ajustan al modelo y que, por tanto, podrían ser ambiguos o mal interpretados por diferentes subgrupos¹⁵.

• –

  Escala de intervalo: Otro aspecto distintivo es que el modelo Rasch convierte las respuestas en una escala de intervalo, lo que facilita la interpretación de las diferencias entre puntuaciones y mejora la precisión de las mediciones¹⁶.

El modelo Rasch original y sus extensiones a modelos de datos politómicos

En el contexto del desarrollo de instrumentos y escalas de medida, los ítems pueden tener diferentes opciones o tipos de respuesta. Así, los datos dicotómicos se refieren a ítems que tienen solo 2 posibles categorías de respuestas: correcto/incorrecto, verdadero/falso, etc. En contraposición, los datos politómicos se refieren a ítems que pueden tener 3 o más categorías de respuesta, algo común en muchos instrumentos de medida desarrollados para medir diferentes constructos, como los instrumentos de calidad de vida, de actitud o de satisfacción. Es frecuente que estos instrumentos utilicen categorías de respuesta ordinales que pueden ir, por ejemplo, desde «totalmente de acuerdo» hasta «totalmente en desacuerdo».

En el caso de datos dicotómicos nos referimos al modelo Rasch original, también conocido como el modelo de Rasch para medidas logísticas uniparamétricas^1,7. Sus características principales, además de las ya enunciadas, son la simplicidad, puesto que su análisis es relativamente sencillo, ya que cada ítem contribuye con un punto a la puntuación total, facilitando su interpretación y análisis; y ser un modelo uniparamétrico, donde solo se estima un parámetro por ítem, la dificultad del ítem, manteniendo la modelación y la interpretación más simple. Este modelo es ideal para pruebas que determinan si una respuesta es simplemente correcta o incorrecta, como en el caso de pruebas de conocimientos o habilidades de enfermería.

En el caso de los datos politómicos, donde estamos utilizando escalas tipo Likert, se utilizan extensiones del modelo Rasch como el «modelo de crédito parcial de Masters» (Credit Partial Model)¹⁷ o el «modelo de clasificación de Andrich» (Rating Scale Model)¹⁸. En este caso sus características, en contraposición al modelo original, son la complejidad, dado que puede manejar la complejidad de los ítems con múltiples categorías de respuesta, permitiendo una evaluación más matizada de las actitudes o habilidades; y el uso de modelos multiparamétricos que permiten, además de la estimación de la dificultad del ítem, estimar parámetros adicionales como el umbral de categorías de respuesta.

El modelo de escala de clasificación Rating Scale Model

El Rating Scale Model (RSM) de Andrich se utiliza para analizar datos de respuesta politómica donde todas las preguntas o ítems comparten el mismo conjunto de categorías de respuesta. Por ejemplo, en una encuesta donde las respuestas varían de 1 a 5, donde 1 es «Totalmente en desacuerdo» y 5 es «Totalmente de acuerdo», todas las preguntas utilizan esta misma escala de 5 puntos, de modo que:

• -

  Las categorías de respuesta son comunes a todos los ítems.

• -

  Se asume que los umbrales entre las categorías de respuesta (la transición de una categoría a la siguiente) son los mismos a través de todos los ítems.

• -

  El modelo estima un conjunto de parámetros de umbral que son aplicables a todos los ítems.

El modelo de crédito parcial Partial Credit Model

El Partial Credit Model (PCM), desarrollado por Geoff Masters, es más flexible que el RSM y se utiliza cuando las preguntas o ítems tienen diferentes números de categorías de respuesta o cuando no se espera que los umbrales entre categorías sean los mismos a través de todos los ítems. Por ejemplo, algunas preguntas pueden tener una escala de respuesta de 1 a 4, mientras que otras pueden tener respuestas de 1 a 5. Así, este modelo:

• -

  Permite manejar diferentes conjuntos de categorías de respuesta para cada ítem.

• -

  Los umbrales entre categorías de respuesta se estiman por ítem, no asumiéndose que son iguales a través de todos los ítems.

• -

  Ofrece una mayor flexibilidad para manejar ítems con una estructura de respuesta variada.

¿Cuándo elegir uno u otro modelo?

La elección entre RSM y PCM depende de la estructura del instrumento de medición y los objetivos del análisis. El RSM puede ser preferible por su simplicidad y la facilidad de interpretación cuando todas las preguntas utilizan la misma escala de respuesta. PCM ofrece mayor flexibilidad y es adecuado para instrumentos con variedad en las escalas de respuesta, permitiendo un análisis más detallado y específico para cada ítem. Para datos dicotómicos, donde las respuestas a los ítems son de naturaleza binaria (p.ej., correcto/incorrecto, sí/no), el modelo de Rasch original, como hemos visto, es el más adecuado y directamente aplicable.

Metodología de aplicación del análisis Rasch

La implementación efectiva del análisis Rasch en la investigación implica varios pasos críticos, desde el diseño inicial del estudio hasta la interpretación de los resultados. A continuación, se detallan 11 pasos esenciales en este proceso (fig. 1):

• 1.

  Paso/definición de los objetivos y preparación: El primer paso es establecer claramente los objetivos de la investigación y determinar cómo el análisis Rasch puede contribuir a alcanzarlos, ya sea mediante la evaluación de la validez de un instrumento existente, el desarrollo de uno nuevo, el refinamiento o reducción de instrumentos ya existentes o, incluso, la equiparación de diferentes tests en la medida.

• 2.

  Paso/diseño del instrumento de medición: Seleccionar o diseñar ítems que sean representativos del constructo que se desea medir. Esto incluye asegurar que los ítems sean claros, unidimensionales y adecuados para el grupo objetivo.

• 3.

  Paso/recolección de datos: Realizar la recolección de datos asegurando una muestra representativa y suficientemente amplia para el análisis estadístico. No obstante, en la literatura no hay acuerdo sobre el tamaño muestral necesario para este tipo de análisis. Así, Stolt et al.³ presentan estudios que usan muestras que van desde 43 hasta 13.113 participantes. El análisis Rasch puede funcionar relativamente bien independientemente del tamaño de la muestra por las características mencionadas, que le otorga una ventaja frente a otros tipos de análisis como el análisis factorial. Habitualmente, muchos estudios hacen referencia a la cita de Polit y Beck¹⁹ sobre la utilización de muestras en base a 5-20 participantes por cada ítem del instrumento a analizar.

• 4.

  Paso/análisis inicial de los datos: Usar un software de análisis Rasch para realizar un análisis inicial, identificando ítems que no funcionan bien, patrones inesperados en las respuestas y la alineación general de los datos con el modelo Rasch. En muchas ocasiones, este análisis inicial se combina con análisis sencillos de la TCT para estudiar la dificultad, desconocimiento y discriminación. Esto permite identificar ítems que no aportan beneficios al constructo y que se pueden eliminar previamente a la realización del análisis Rasch.

  En esta fase, es habitual, en la literatura, encontrar que para estudiar la unidimensionalidad se lleve a cabo un análisis de componentes principales de los residuos del modelo²⁰. Los criterios habituales son que el primer componente explique al menos el 50% de la varianza y que el segundo componente explique menos del 5% (o un autovalor —Eigenvalue— inferior a 2,0)²¹. Otra opción es, en el marco de un análisis factorial, calcular diferentes índices de unidimensionalidad, tal y como proponen Ferrando y Lorenzo-Seva²². El cálculo de los valores Unidimensional Congruence (UniCo), Explained Common Variance (ECV) y Mean of Item REsidual Absolute Loadings (MIREAL) pueden ayudar a evaluar si los datos pueden ser tratados como esencialmente unidimensionales²².

• 5.

  Paso/evaluación de la bondad de ajuste: nos proporciona datos de validez interna de la escala y de validez de la respuesta de las personas. Se utilizan estadísticas de ajuste, normalmente, los denominados infit y outfit^4,23. Los ítems o respuestas que no se ajustan pueden indicar problemas con el ítem o la unidimensionalidad del constructo. Es crucial identificar los ítems que no se ajustan al modelo de Rasch. La inclusión de ítems con un ajuste deficiente dificulta la calidad de la medición y disminuye la precisión del instrumento. Estos ítems deben eliminarse, revisarse o reescribirse, y volver a someterse a prueba. Las estadísticas de bondad de ajuste indican hasta qué punto cada ítem se ajusta al constructo subyacente de la prueba⁴.

  El modelo de estimación conjunta de máxima verosimilitud, o modelo Joint Maximum Likelihood Estimation (JMLE, por sus siglas en inglés) se refiere a una técnica estadística utilizada para la estimación de parámetros dentro de modelos de la TRI, incluido el análisis Rasch. Este enfoque se caracteriza por estimar simultáneamente los parámetros de los ítems y los parámetros de habilidad de los sujetos basándose en la máxima verosimilitud conjunta de todos estos parámetros dados los datos observados⁶.

  En el contexto de la TRI y el análisis Rasch, los parámetros de los ítems generalmente incluyen la dificultad de los ítems (y potencialmente otros parámetros, como la discriminación, dependiendo del modelo específico de TRI utilizado). Los parámetros de los sujetos, por otro lado, suelen referirse a las habilidades o competencias de los individuos que responden a los ítems. La estimación conjunta significa que el proceso de estimación busca aquel conjunto de valores de parámetros de ítems y sujetos que, en conjunto, tienen la mayor probabilidad de haber generado los datos observados.

  Este modelo presenta ventajas como son la «eficiencia», pues permite la estimación simultánea de parámetros de ítems y sujetos, lo que puede ser más eficiente desde el punto de vista computacional en comparación con los enfoques que estiman estos parámetros por separado, y la «aplicabilidad», que es especialmente útil en situaciones donde no se dispone de información previa sobre los parámetros de los ítems o las habilidades de los sujetos, permitiendo una estimación directa a partir de los datos recogidos. Pero este modelo también presenta limitaciones como son la «inexactitud en extremos» (la estimación conjunta puede ser menos precisa para los sujetos con habilidades extremadamente altas o bajas, ya que la información para estimar sus habilidades de manera precisa puede ser limitada en los datos observados) y la «estabilidad» (pues puede ser susceptible a problemas de estabilidad y convergencia, especialmente en conjuntos de datos pequeños o con patrones de respuesta poco comunes).

  Aunque el JMLE es una técnica poderosa dentro del análisis Rasch y otros modelos de la TRI, es importante que los investigadores sean conscientes de sus limitaciones y consideren la posibilidad de utilizar métodos alternativos de estimación, como el Marginal Maximum Likelihood Estimation (MMLE) o el Conditional Maximum Likelihood Estimation (CMLE), dependiendo de las características específicas de sus datos y los objetivos de su estudio. La elección del método de estimación debe basarse en una consideración cuidadosa de estos factores para asegurar la precisión y la validez de los resultados del análisis.

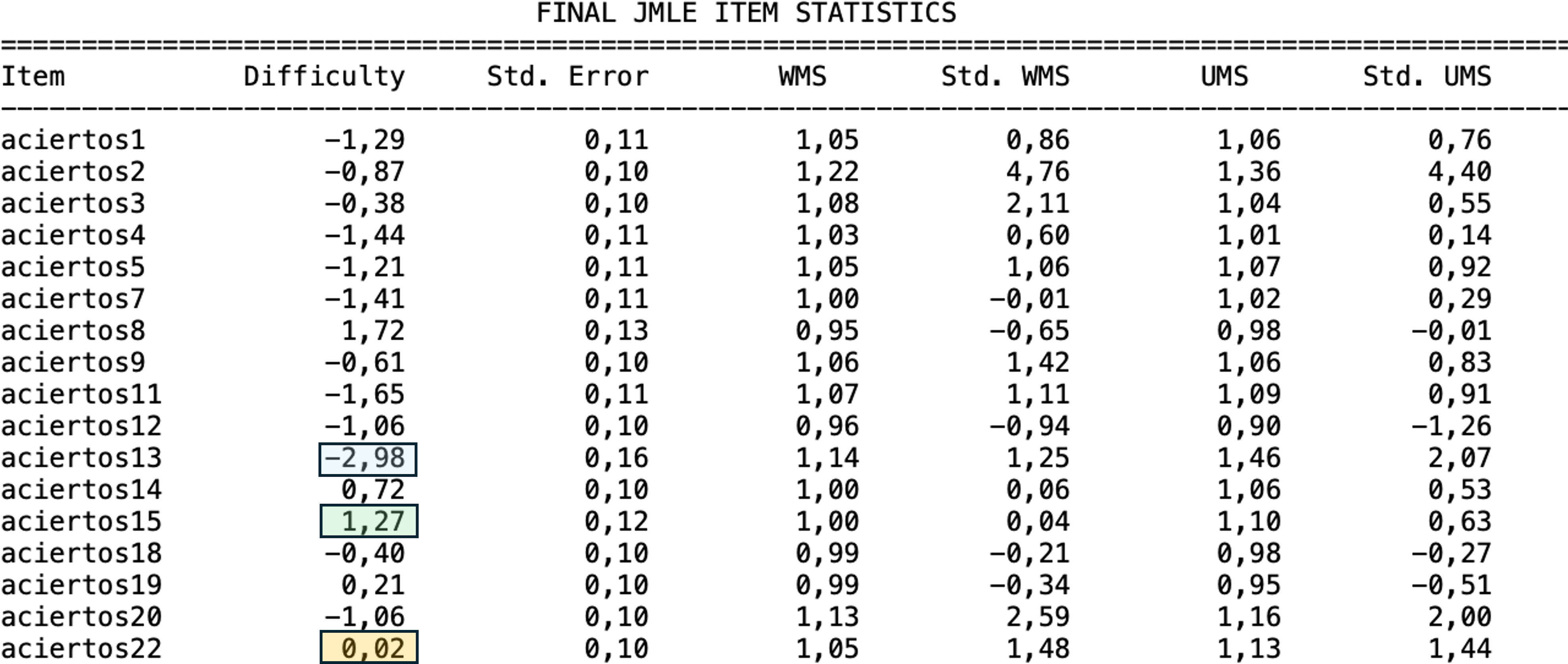
  Desde el modelo JMLE, el infit (información/ponderada), o Weighted Mean Square Fit Statistic (WMS), es una medida de ajuste que es especialmente sensible a los patrones de respuesta en los ítems que están cerca del nivel de habilidad del individuo. El outfit(Outlier-Sensitive Fit), o Unweighted Mean Square Fit Statistic (UMS), es una estadística de ajuste crudo, más sensible a respuestas inusuales o atípicas («outliers») entre los ítems que están lejos del nivel de habilidad del individuo. Estos valores se expresan como cuadrados medios. Un valor de 1 indica un ajuste perfecto al modelo. Así, los valores de los índices de ajuste comprendidos entre 0,8 y 1,2 representan un buen ajuste¹⁵ y los valores comprendidos entre 0,5 y 1,5 significan un ajuste aceptable¹¹, pero también se recomienda ajustar los valores según el tamaño de la muestra²⁴. En la figura 2 se representa un resultado parcial de un hipotético análisis, donde se pueden ver: la dificultad y los valores de infit (WMS) y outfit (UMS) con sus respectivos errores estándar.

  
  

  Figura 2.

  Representación parcial de una tabla de valores estimados por JMLE para un hipotético instrumento de medida (dificultad, infit [WMS] y outfit [UMS]).

  A modo de ejemplo, el ítem 13 sería el más fácil, el 22 estaría cercano a 0 (dificultad media) y el 15 sería el más difícil de los presentados en esta tabla.

  En el caso de la dificultad, valores cercanos a cero estarían en la mitad de dificultad, mientras valores mayores de cero, a medida que se alejan indican mayor dificultad; valores menores de cero indican una menor dificultad. En dos los valores se encuentran en el rango de valores que indican buen ajuste al modelo.

  Como hemos visto, el análisis de estos parámetros es de vital importancia pues nos permite el «Diagnóstico de ítems». Estas estadísticas permiten identificar ítems que no se comportan según lo esperado, ya sea porque son demasiado predecibles o porque presentan una variabilidad inesperada en las respuestas y la «Mejora del instrumento», ya que, al analizar el infit y el outfit, los desarrolladores de pruebas pueden tomar decisiones informadas sobre la revisión o eliminación de ítems para mejorar la validez y fiabilidad del instrumento. Finalmente, este análisis se relaciona directamente con la «Adaptación al modelo»; la evaluación del ajuste de los ítems al modelo Rasch (o cualquier modelo de TRI aplicado) es crucial para asegurar que las mediciones reflejen con precisión el constructo de interés.

  Otras medidas que nos aporta el análisis de bondad de ajuste son los estadísticos de calidad de la escala⁶, fiabilidad y separación, que pueden calcularse tanto para los ítems como para las personas. La fiabilidad de la persona es similar al coeficiente de fiabilidad de la TCT, siendo deseables valores superiores a 0,8. La separación de personas es similar a la fiabilidad en el sentido de que representa hasta qué punto una medida puede reproducir y clasificar las puntuaciones de forma coherente. Los valores de separación superiores a 2 son deseables, lo que indica que el instrumento puede separar a las personas en al menos 2 estratos, por ejemplo, baja y alta capacidad²⁵. La fiabilidad de los ítems se refiere al grado en que las dificultades de los ítems pueden ordenarse por rango. La separación entre ítems proporciona información similar sobre la calidad de la localización de los ítems en el rasgo latente.

• 6.

  Paso/evaluación de la independencia local: Normalmente, se lleva a cabo un análisis de la correlación los residuos estandarizados, lo que se conoce como el coeficiente Q3 de Yen, una medida estadística desarrollada por Yen²⁶ en 1984, y utilizada para evaluar la independencia local de los ítems en el contexto de los modelos de la TRI, incluido el análisis Rasch. Es una medida de correlación residual entre pares de ítems. En otras palabras, evalúa la correlación entre las respuestas a 2 ítems después de haber controlado por la habilidad general del respondiente. Si 2 ítems son verdaderamente independientes uno del otro, dada la habilidad de un individuo, entonces se espera que el coeficiente Q3 sea cercano a cero. Un valor de Q3 significativamente distinto de cero sugeriría que existe una dependencia entre los ítems, lo cual podría indicar una violación de la suposición de independencia local, propiedad necesaria para asumir el modelo Rasch, tal y como se expuso inicialmente.

  El coeficiente Q3 de Yen se aplica en el análisis de la validez de un instrumento de medición por varias razones:

  • -

    Identificación de Ítems dependientes: Permite identificar pares de ítems que pueden estar influyéndose mutuamente, lo cual es particularmente útil en la revisión y mejora de instrumentos de medición. Por ejemplo, 2 ítems pueden ser redundantes o pueden estar midiendo el mismo sub-rasgo o habilidad específica, en lugar de aspectos únicos del constructo general.

  • -

    Mejora del diseño del instrumento: Al identificar ítems con dependencias, los investigadores y desarrolladores de pruebas pueden tomar decisiones informadas sobre qué ítems modificar o eliminar para mejorar la independencia local, la validez y la fiabilidad del instrumento.

  • -

    Evaluación de la estructura del constructo: En algunos casos, las dependencias identificadas entre ítems pueden proporcionar información valiosa sobre la estructura subyacente del constructo que se está midiendo. Esto puede llevar a una mejor comprensión de las dimensiones del constructo y a la refinación teórica del mismo.

Figura 1.

Esquema que representa los 11 pasos para aplicar el análisis RASCH.

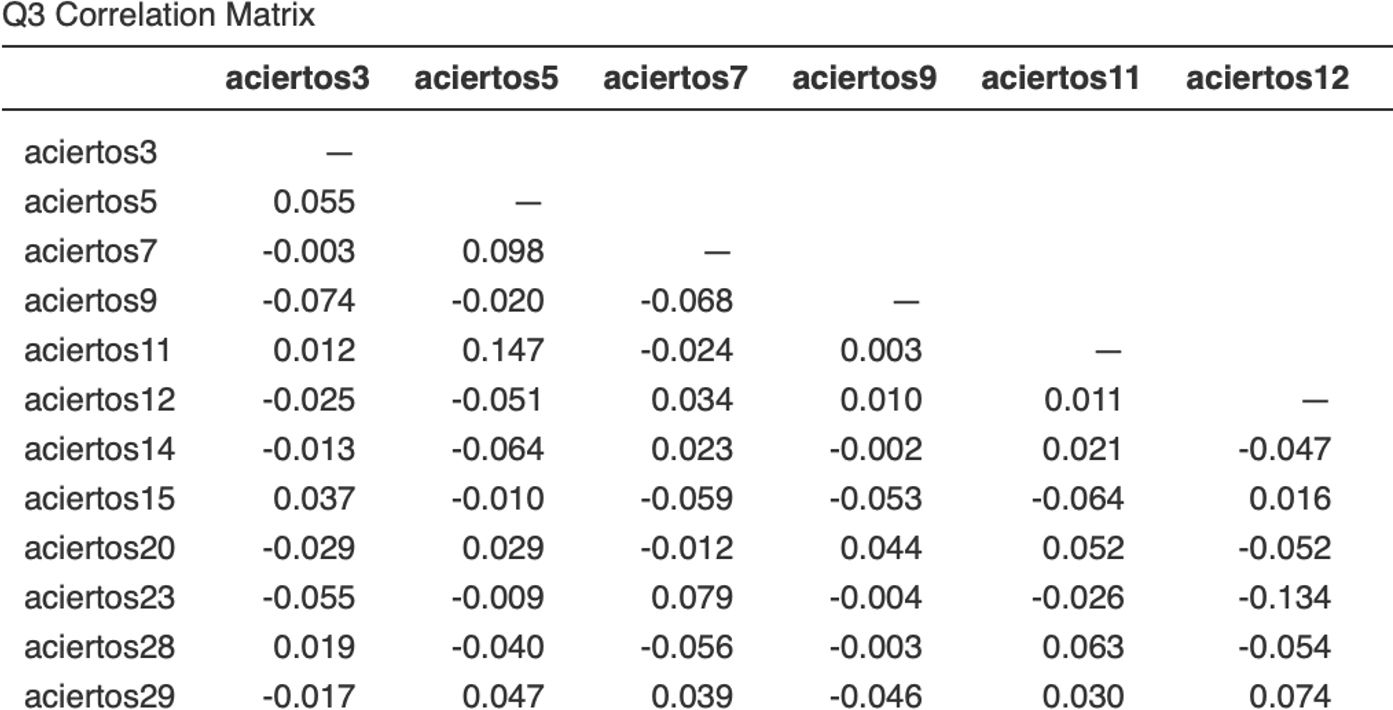
Es importante notar que la implementación de este análisis requiere el uso de software estadístico especializado que pueda manejar modelos de la TRI y calcular correlaciones residuales. Valores altos de Q3 pueden indicar problemas con la independencia de los ítems, pero también pueden reflejar aspectos multidimensionales del constructo que no necesariamente invalidan el uso del instrumento. Por tanto, los hallazgos deben ser evaluados en el contexto de la teoría subyacente del constructo y el propósito del instrumento de medición. Así pues, la interpretación de los valores del coeficiente Q3 de Yen, específicamente el umbral en el cual se considera que un valor de Q3 indica una dependencia inaceptable entre ítems, puede variar dependiendo del contexto del estudio y las normas establecidas por el investigador o la disciplina. Sin embargo, hay algunas guías generales que se pueden considerar. Yen, en su trabajo original, no especificó un umbral estricto para determinar cuándo un valor de Q3 es inaceptablemente alto, lo que sugiere que la interpretación depende en gran medida del contexto específico del análisis y del instrumento. En la práctica, algunos investigadores y metodólogos han adoptado enfoques pragmáticos para interpretar los valores de Q3, considerando valores por encima de ciertos puntos de corte como indicativos de una posible dependencia entre ítems. Un enfoque común es considerar valores de Q3 superiores a 0,2 o 0,3 como indicativos de una correlación residual significativa entre pares de ítems, sugiriendo que estos ítems podrían no ser independientes entre sí después de controlar por la habilidad general de los respondientes. Esta recomendación general debe usarse con precaución; algunos contextos pueden requerir un umbral más conservador o más liberal, dependiendo de la naturaleza del constructo medido y el propósito del instrumento de evaluación. En realidad, no existe un criterio uniforme, ya que este valor depende del tamaño de la muestra, del número de ítems y del número de categorías de respuesta²⁷. A modo de ejemplo, en la figura 3, se presenta una sección de una matriz de correlaciones de Q3 de Yen donde se puede observar que todos los valores son inferiores a 0,2 en valor absoluto, lo que estaría indicando independencia local de los ítems.

Figura 3.

Representación parcial de una matriz de correlaciones Q3 de Yen.

También es importante destacar que un valor alto de Q3 no necesariamente indica que los ítems deban ser eliminados o que el instrumento sea inválido. En su lugar sugiere la necesidad de una revisión más detallada de los ítems implicados para entender la razón de la dependencia. Esto podría llevar a considerar aspectos como la redacción de los ítems, la estructura del cuestionario, o incluso la posibilidad de dimensiones subyacentes no reconocidas dentro del constructo que se está midiendo.

• 7.

  Paso/calibración de ítems y estimación de habilidades¹: A través del análisis Rasch se estima la dificultad de cada ítem y se calculan las habilidades o niveles del constructo para cada participante. Una vez llevado a cabo todo lo anterior, los datos pueden representarse en gráficos que permiten una mejor interpretación. Son comunes los mapas ítems-personas o gráfico de Wright, que se compone de 2 grandes histogramas (graficados de forma vertical). El lado izquierdo presenta el histograma de la distribución de habilidades de las personas. El lado derecho presenta el histograma de la distribución de dificultades de los ítems. Los 2 histogramas comparten el eje de valores (línea vertical).

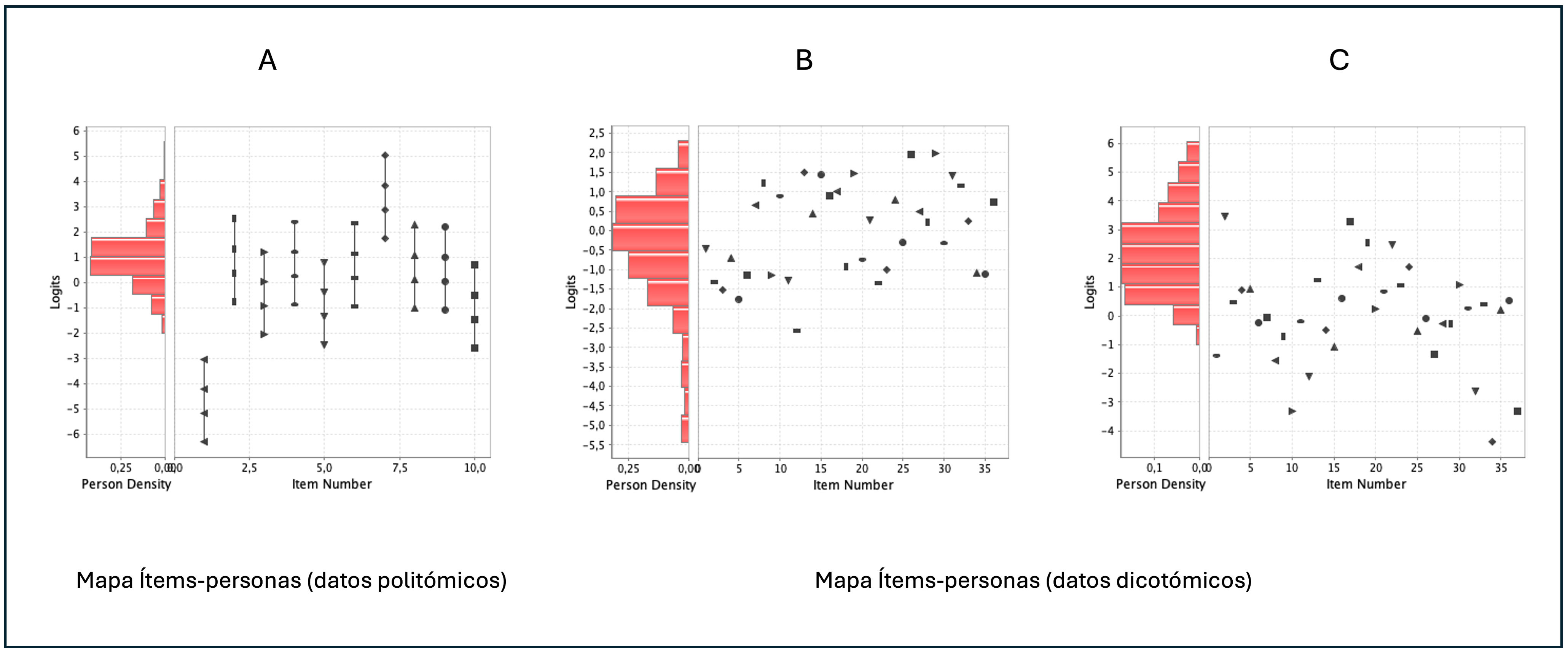
En la figura 4 se presentan 3 gráficos de Wright diferentes diferentes. En el primero es un gráfico de un modelo con datos politómicos. Por ello, en la parte derecha del gráfico aparecen líneas verticales con 4 marcas que representan cada ítem y la dificultad de cada categoría (10 ítems con 4 categorías de respuesta). En la izquierda estaría el histograma de personas. Ambos están en la misma escala logit, lo que permite comparar ambos elementos en la misma escala. Vemos, que, aunque se ve una distribución bastante normal, esta está desplazada hacia arriba en habilidad. En el caso de los ítems, hay una distribución homogénea a lo largo de la escala logit, lo que indica que hay ítems más fáciles (el que está más abajo) y otros más difíciles (el que está más arriba), aunque excepto para el primero, la distribución de personas e ítems se encuentra prácticamente igual.

Figura 4.

Ejemplos de gráficos de Wright o mapas de ítems/personas.

En el caso de los otros 2 gráficos, son modelos con datos dicotómicos (los ítem se representan con diferentes símbolos). En el gráfico central vemos que hay un grupo de personas que tienen una tendencia a puntuaciones bajas en el instrumento y que los ítems están más arriba, lo que puede suponer que este instrumento (si fuera de conocimientos) presenta preguntas relativamente difíciles para una parte de la muestra. En el gráfico de la derecha es todo lo contrario, las personas se desempeñan muy bien y los ítems parecen más fáciles.

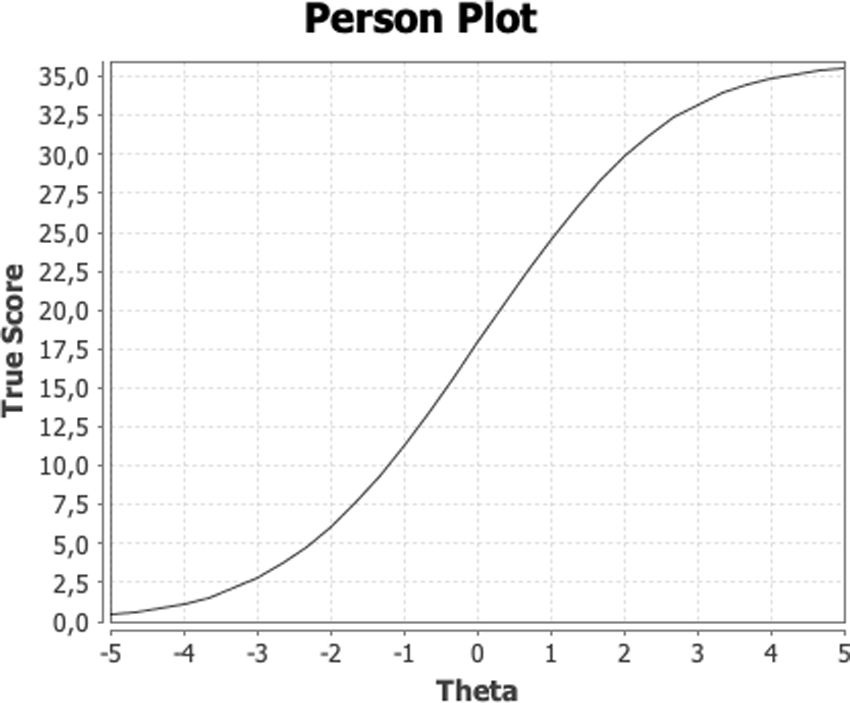
Los gráficos de la curva característica de los ítems (CCI), que ofrece una representación gráfica de las características del ítem, y por otra parte muestra la relación entre el nivel de habilidad y la repuesta al ítem, en términos probabilísticos; y la curva característica del test (CCT) (fig. 5), que muestra la relación existente entre la puntuación total en un test (no solamente en un ítem como sucede con la CCI) y el nivel de habilidad de una persona. En el caso de la figura 5 el gráfico presenta la curva característica de un test que se ajusta al modelo Rasch con una curva sigmoide que enfrenta la puntuación en la variable latente (theta) frente a las puntuaciones verdaderas de las personas.

• 8.

  Paso/análisis de la invarianza de las medidas: asegurando que las mediciones son consistentes a través de diferentes subgrupos de la muestra, como por género, edad u otras características. Esto es crucial para confirmar que el instrumento mide de manera equitativa para todos los participantes. Normalmente, se lleva a cabo mediante un análisis del funcionamiento diferencial de los ítems (DIF)^4,6.

Figura 5.

Curva característica del test.

El análisis de funcionamiento diferencial del ítem (DIF, por sus siglas en inglés) es una técnica estadística que se utiliza para identificar si diferentes grupos de individuos responden de manera distinta a un ítem específico, a pesar de tener el mismo nivel de habilidad o rasgo latente.

Aunque el análisis DIF y el análisis Rasch son conceptos distintos, pueden estar relacionados en la práctica de la evaluación psicométrica. El análisis Rasch proporciona un marco para medir un rasgo latente basado en las respuestas a los ítems de un test, y uno de sus principales atractivos es la capacidad de generar mediciones independientes de la muestra de ítems y la población de respondientes. Incorporar el análisis DIF en este contexto ayuda a garantizar que los ítems del instrumento sean justos para todos los grupos de individuos, lo que es esencial para la validez de las mediciones obtenidas a través del modelo Rasch. Por tanto, el propósito principal del análisis DIF es asegurar la equidad y la imparcialidad en la evaluación, identificando ítems que puedan ser sesgados o funcionar de manera diferente para subgrupos específicos dentro de la población, como pueden ser subgrupos definidos por género, etnicidad, edad, o cualquier otra variable demográfica o de agrupación relevante. Un ítem que muestra DIF sugiere que algo, además de la habilidad general que se está midiendo afecta cómo diferentes grupos responden a ese ítem.

El análisis DIF se puede realizar mediante varios métodos, incluidos enfoques gráficos, pruebas estadísticas y técnicas basadas en modelos como la regresión logística o el propio análisis Rasch. Los métodos basados en modelos Rasch, en particular, permiten evaluar el DIF mientras se mantiene la estructura del modelo, facilitando la interpretación de cómo el sesgo de ítem afecta la medición del rasgo latente.

En el contexto del análisis Rasch, el DIF se evalúa comparando la dificultad del ítem (parámetro de localización del ítem) entre diferentes grupos, controlado por la habilidad general. Este proceso se realiza manteniendo la estructura del modelo Rasch, lo que significa que la estimación de la dificultad del ítem y la habilidad del respondiente se basa en el principio de máxima verosimilitud, asumiendo que los ítems son independientes y que la probabilidad de una respuesta correcta solo depende de la diferencia entre la habilidad del respondiente y la dificultad del ítem.

Algunos métodos que pueden servir a este cometido son:

• -

  Análisis de contraste de grupos: una técnica común es dividir la muestra según el grupo de interés (p. ej., género, etnicidad) y realizar un análisis Rasch por separado para cada grupo. Luego, se compara la dificultad estimada de cada ítem entre los grupos. Un cambio significativo en la dificultad del ítem indica la presencia de DIF.

• -

  Modelos de Rasch multifacéticos: Algunas versiones del modelo Rasch permiten incorporar directamente el grupo como una «faceta» en el análisis. Esto facilita la estimación simultánea de los efectos del grupo sobre la dificultad del ítem, proporcionando una forma directa de evaluar el DIF.

• -

  Pruebas estadísticas específicas: Se utilizan pruebas estadísticas diseñadas para detectar diferencias en los parámetros de los ítems entre grupos, como el test de Mantel-Haenszel o pruebas basadas en la regresión logística, adaptadas al contexto del modelo Rasch. Estas pruebas comparan la dificultad del ítem entre grupos después de ajustar por la habilidad del respondiente.

La evaluación DIF en el contexto del análisis Rasch puede utilizar las odds ratio (OR) como una herramienta para medir la magnitud del DIF entre grupos. Las OR ofrecen una forma cuantitativa de comparar las probabilidades de que los individuos de diferentes grupos (p. ej., varones vs. mujeres, o grupos etarios distintos) respondan correctamente a un ítem, dado un nivel similar de habilidad o rasgo latente. Así, las OR se calculan para cada ítem y comparan la probabilidad de una respuesta correcta entre 2 grupos de interés. Un valor de OR de 1 indica que los grupos tienen la misma probabilidad de responder correctamente al ítem, después de ajustar por la habilidad. Valores significativamente mayores o menores que 1 sugieren la presencia de DIF, es decir, que un ítem favorece a un grupo sobre el otro.

Proceso para evaluar DIF con odds ratio en análisis Rasch

La secuencia sería la siguiente:

• –

  Estimación de la habilidad: Primero, se utiliza el análisis Rasch para estimar las habilidades de los individuos basadas en sus patrones de respuesta a los ítems del test.

• –

  Cálculo de las OR: Luego, para cada ítem, se calculan las OR de responder correctamente para los individuos en diferentes grupos, controlando por la habilidad. Esto se hace comparando las OR de éxito en un grupo con las del otro.

• –

  Análisis estadístico: Se realiza un análisis estadístico para determinar si las diferencias en las OR son significativas, lo que puede implicar el uso de pruebas de hipótesis o intervalos de confianza. La interpretación según la OR:

• –

  OR > 1: Indica que el grupo de referencia tiene mayores odds de responder correctamente al ítem en comparación con el grupo de comparación, sugiriendo un posible sesgo a favor del grupo de referencia.

• –

  OR < 1: Sugiere que el grupo de comparación tiene mayores odds de responder correctamente, indicando un sesgo a favor de este grupo.

• –

  OR ≈ 1: Implica que no hay evidencia significativa de DIF para ese ítem entre los grupos comparados.

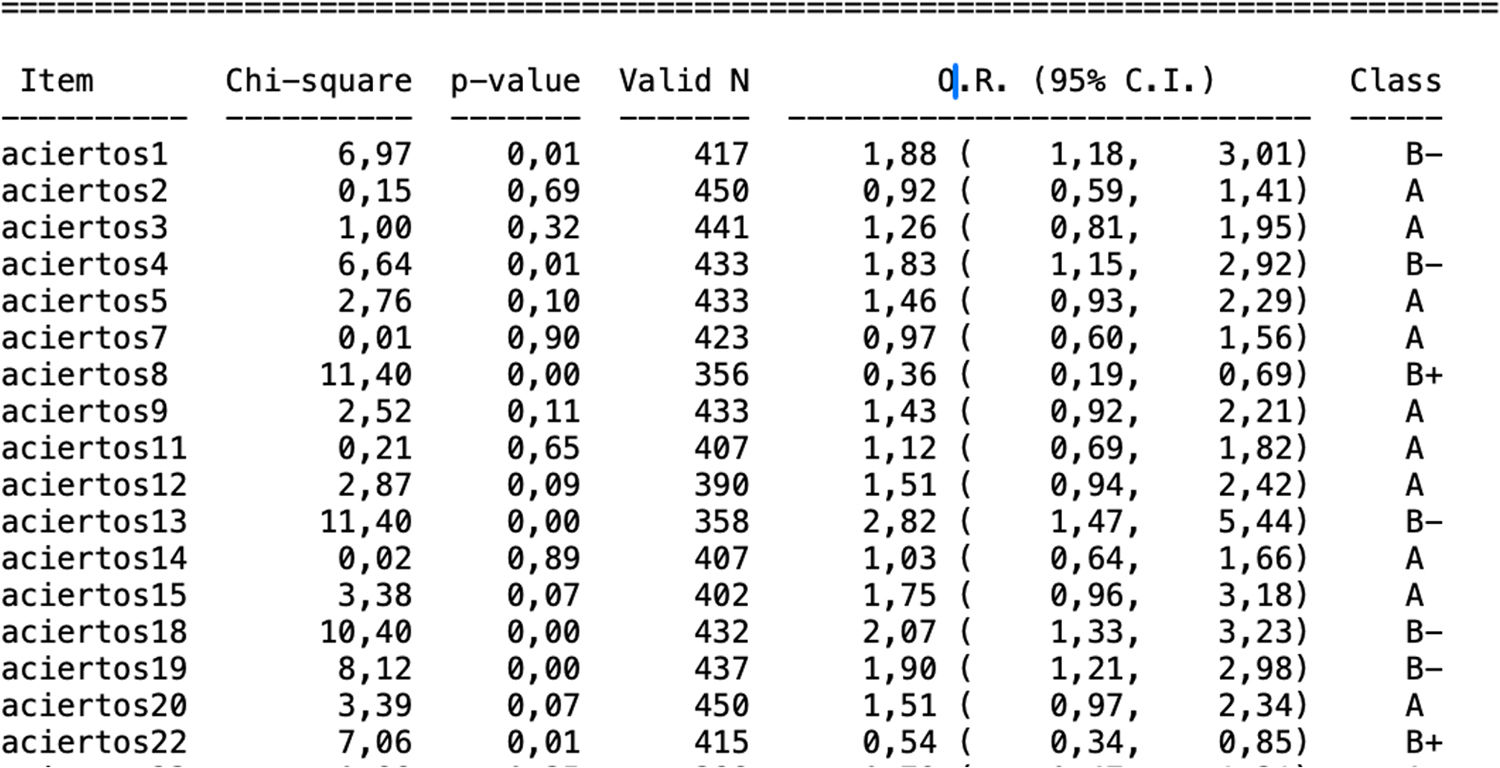
Es importante tener en cuenta que al utilizar las OR para evaluar DIF en el análisis Rasch, es crucial considerar el tamaño del efecto y la significción estadística. No todos los ítems con OR significativamente distintos de 1 necesariamente tienen un impacto práctico significativo en la medición. Por lo tanto, es esencial interpretar las OR en el contexto de la relevancia práctica y en combinación con otras medidas de DIF y análisis cualitativos de los ítems. En la figura 6 se presentan resultados parciales de un análisis DIF mediante prueba de Mantel-Haenszel para estimar la OR de un grupo de referencia frente a un grupo focal (estudiantes de 1.°-2.° curso frente a estudiantes de 3.°-4.° curso en un test de conocimientos). Como se puede observar hay una serie de ítems que presentan DIF moderado (B+ o B− en función de qué grupo tiene más habilidad para ese ítem). Esto nos ayuda a evaluar los ítems que tienen un funcionamiento diferente y que, por tanto, pueden estar midiendo otro constructo o que presentan diferencias por determinados elementos del grupo en cuestión. Esto violaría los supuestos del modelo Rasch. Por tanto, los ítems que presentan DIF (en este caso moderado, representado por la letra B) deberían ser eliminados.

• 9.

  Paso/revisión y modificación del instrumento: Basándose en los resultados del análisis inicial (pasos 4, 5, 6 y 7), revisar y posiblemente modificar el instrumento. Esto puede implicar eliminar ítems que no se ajustan bien, ajustar el formato de respuesta o clarificar el enunciado de los ítems. Este paso puede requerir más de un ajuste.

• 10.

  Paso/análisis final y validación del instrumento: Realizar un análisis Rasch final con el instrumento revisado para validar su estructura y determinar la fiabilidad y validez del mismo (repitiendo los pasos anteriores).

• 11.

  Paso/interpretación de resultados: Interpretar los resultados en el contexto de los objetivos del estudio, centrándose en la calidad de las mediciones, la validez del instrumento y las implicaciones para la práctica y la investigación futura. Esto implica examinar varios aspectos clave de los datos y el instrumento de medición. También incluye interpretar las escalas, los mapas de ítems/personas y las curvas de información.

  Algunos elementos a tener en cuenta:

  • a.

    Ajuste al modelo: Evaluar cómo los datos se ajustan al modelo Rasch, incluyendo el ajuste de los ítems individuales y el ajuste general del instrumento. Esto se hace mediante estadísticas de ajuste, como los residuos estandarizados y las medidas de infit y outfit.

  • b.

    Unidimensionalidad: Confirmar que el conjunto de ítems mide un único constructo o dimensión, lo cual es fundamental para la validez del instrumento.

  • c.

    Independencia local: Verificar que las respuestas a los ítems son independientes entre sí, después de controlar por la habilidad de la persona, lo que es esencial para la fiabilidad del instrumento.

  • d.

    Estimación de parámetros: Interpretar los parámetros estimados por el modelo, incluyendo la dificultad de los ítems y la habilidad de las personas. Esto proporciona información valiosa sobre las propiedades del instrumento y las características de la población estudiada.

  • e.

    Implicaciones prácticas: Finalmente, es crucial considerar las implicaciones prácticas de los resultados, incluyendo cómo pueden informar la práctica clínica, la educación en enfermería o la investigación futura.

Figura 6.

Representación parcial de un análisis DIF por medio de la OR.

Herramientas y software recomendados

Para llevar a cabo el análisis Rasch, existen varias herramientas y software especializados que facilitan este proceso. Algunas de las opciones más populares incluyen:

• •

  RUMM2030® (https://www.rummlab.com.au): Una herramienta poderosa para el análisis Rasch, especialmente útil para el análisis de datos politómicos y la evaluación de la calidad del ajuste de los ítems.

• •

  Winsteps® (http://www.winsteps.com)¹¹: Ampliamente utilizado en la comunidad de análisis Rasch, Winsteps ofrece una amplia gama de funcionalidades para el análisis de datos dicotómicos y politómicos.

• •

  FACETS²⁸: Específicamente diseñado para el análisis de datos multifacéticos, FACETS es ideal para estudios que involucran evaluadores múltiples o ítems con complejidades adicionales.

• •

  JMetrik® [https://itemanalysis.com]⁶: Una herramienta gratuita que ofrece capacidades para el análisis Rasch, junto con otras técnicas estadísticas comunes.

La elección del software adecuado dependerá de las necesidades específicas del estudio, incluyendo el tipo de datos a analizar, la complejidad del modelo y las preferencias del investigador.

Aplicación del análisis Rasch en enfermería

En esta sección, se explora cómo el análisis Rasch se aplica en la disciplina, destacando estudios de caso relevantes que ilustran su impacto práctico.

• •

  Evaluación de competencias y habilidades clínicas

La evaluación precisa de las competencias y habilidades clínicas es fundamental en la formación de enfermería y en la práctica profesional continua. El análisis Rasch ofrece un marco robusto para esta evaluación, permitiendo a los educadores y administradores identificar con precisión las áreas de fortaleza y las necesidades de desarrollo entre los estudiantes y las enfermeras.

• -

  Modelado de competencias: Mediante el uso del análisis Rasch, se puede modelar la complejidad de las competencias clínicas, diferenciando entre niveles de habilidad y asegurando que las evaluaciones sean adecuadas para el nivel de competencia esperado.

• -

  Desarrollo curricular: Los resultados del análisis Rasch pueden guiar el desarrollo curricular y las intervenciones educativas, asegurando que los programas de formación en enfermería estén alineados con las necesidades de competencia identificadas.

  • •

    Desarrollo y validación de instrumentos de medición en enfermería.

El desarrollo de instrumentos de medición fiables y válidos es otro ámbito crucial donde el análisis Rasch tiene un impacto significativo. Estos instrumentos son esenciales para la investigación en enfermería, la evaluación de programas educativos y la medición de resultados en la práctica clínica.

• -

  Construcción de instrumentos: El análisis Rasch facilita la construcción de instrumentos de medición al proporcionar un método para evaluar la unidimensionalidad de las escalas y la adecuación de los ítems, lo que permite la obtención de herramientas de evaluación más precisas y fiables.

• -

  Validación de escalas: A través del análisis Rasch, es posible validar escalas de medición existentes, refinando los ítems para mejorar la precisión y la relevancia clínica de las mediciones. Esto incluye la capacidad de identificar ítems sesgados culturalmente o que no funcionan de manera uniforme entre diferentes subgrupos de población.

  • •

    Estudios de caso relevantes

Los siguientes estudios de caso ilustran la potencial aplicación práctica y los beneficios del análisis Rasch en el campo de la enfermería:

• –

  Uso y calidad de reporte sobre análisis Rasch en enfermería: Stolt et al³ llevan a cabo una revisión exploratoria donde destacan que el uso de esta metodología en enfermería es poco sistemática, pero que es recomendable el uso de este enfoque metodológico.

• –

  Desarrollo de instrumentos para medir el conocimiento en profesionales y estudiantes en diferentes áreas: diferentes autores han utilizado el análisis Rasch para desarrollar y validar instrumentos para medir conocimiento en diferentes áreas, por ejemplo, el cuidado del Alzheimer²⁹, instrumentos de calidad de vida en adolescentes³⁰ o conocimientos sobre la prevención de las lesiones por presión^31,32.

• –

  Instrumentos para medir condiciones clínicas: como por ejemplo el desarrollado para medir el síndrome visual por ordenador en el lugar de trabajo³³. En este caso, también es un ejemplo de combinación de métodos desde la perspectiva de TCT y la TRI.

• –

  Refinamiento o revalidación de instrumentos: en este caso, mediante el análisis Rasch se redujo el número de ítems de la escala de úlceras por presión en lesionados medulares, mejorando su validez y fiabilidad³⁴.

• –

  Vinculación o equiparación de diferentes instrumentos: La vinculación de las escalas de 2 puntos de medición es un requisito previo para examinar un cambio en la competencia a lo largo del tiempo. En las evaluaciones educativas a gran escala, los formularios de pruebas no idénticas que comparten una serie de ítems suelen escalarse y vincularse utilizando modelos de respuesta al ítem, como en el caso del artículo publicado por Fischer et al³⁵.

Estos ejemplos muestran cómo el análisis Rasch se aplica para abordar desafíos específicos en la educación y la práctica de enfermería, desde la evaluación de competencias hasta el desarrollo y la validación de herramientas de medición. La metodología Rasch ofrece una base sólida para la mejora continua en estos ámbitos, contribuyendo a elevar los estándares de atención y educación en enfermería.

Ventajas, limitaciones y desafíos de la aplicación de este método

A modo de resumen, a continuación se presentan los beneficios de utilizar esta metodología:

• –

  Medición precisa y objetiva: El análisis Rasch permite la conversión de respuestas cualitativas a mediciones cuantitativas en una escala de intervalo, lo que proporciona una base sólida para la toma de decisiones basada en evidencia.

• –

  Validación de instrumentos: Facilita la validación y refinamiento de instrumentos de medición, asegurando que sean tanto fiables como válidos para evaluar las competencias y habilidades clínicas en enfermería.

• –

  Comparabilidad de mediciones: Una de las ventajas más significativas es la capacidad de comparar mediciones a través de diferentes grupos de población o momentos en el tiempo, lo que es fundamental para los estudios longitudinales y la evaluación de intervenciones.

• –

  Identificación de ítems problemáticos: El análisis detallado que ofrece el análisis Rasch permite identificar ítems con funcionamiento inadecuado, ya sea por su dificultad, ambigüedad o sesgo cultural, contribuyendo a mejorar la calidad de los instrumentos de medición.

• –

  Desarrollo profesional y educativo: Los resultados del análisis Rasch pueden informar el desarrollo curricular y las estrategias de enseñanza en programas de enfermería, alineando la educación con las competencias clínicas requeridas en la práctica.

Por todo lo expuesto, se puede considerar el análisis Rasch una valiosa herramienta metodológica, pero que no está exenta de desafíos y limitaciones, como:

• –

  Complejidad metodológica: A pesar de sus beneficios, el análisis Rasch puede ser metodológicamente complejo, requiriendo para el investigador de una comprensión sólida de sus principios y suposiciones para su aplicación adecuada.

• –

  Requisitos de datos: La aplicación efectiva del modelo Rasch requiere conjuntos de datos completos y bien estructurados, lo que puede ser un desafío en estudios con tasas altas de no respuesta o datos faltantes.

• –

  Interpretación de resultados: La interpretación de los resultados del análisis Rasch, especialmente en lo que respecta a las estadísticas de ajuste y la unidimensionalidad, puede ser compleja y requiere una consideración cuidadosa.

• –

  Limitaciones en la flexibilidad del modelo: Aunque el análisis Rasch es poderoso, puede ser menos flexible que otros modelos de la TRI, en términos de modelado de datos que no se ajustan perfectamente a sus suposiciones. El análisis Rasch asume que todos los ítems de una prueba tienen la misma importancia y que las respuestas de los participantes se pueden modelar utilizando una sola dimensión latente. Esta suposición puede no ser válida para todos los conjuntos de datos, especialmente en áreas donde los constructos son multidimensionales⁴.

Algunas propuestas de solución a las limitaciones o recomendaciones para mejorar el conocimiento, difusión y aplicación del análisis Rasch en la investigación enfermera podrían ser:

• a.

  Formación y capacitación: Fomentar la formación en análisis Rasch entre los investigadores en enfermería, ofreciendo talleres, cursos y recursos en línea para mejorar la comprensión y aplicación de esta metodología.

• b.

  Uso de software especializado: Aprovechar las herramientas y software diseñados específicamente para el análisis RASCH, muchos de los cuales incluyen guías y soporte para facilitar su uso.

• c.

  Estrategias de recolección de datos: Implementar estrategias robustas para la recolección de datos, como el seguimiento intensivo de los participantes y el diseño cuidadoso de los cuestionarios, para minimizar los datos faltantes o incompletos y asegurar la calidad de los datos.

• d.

  Colaboración multidisciplinaria: Trabajar en colaboración con profesionales estadísticos o metodólogos especializados en análisis Rasch puede ayudar a superar algunos de los desafíos metodológicos y de interpretación, asegurando la aplicación correcta del modelo.

• e.

  Consideración de modelos alternativos: En casos donde el análisis Rasch pueda no ser el más adecuado debido a las características de los datos, considerar el uso de otros modelos de la TRI que puedan ofrecer la flexibilidad necesaria o, incluso, el uso de modelos basados en la TCT. También sería adecuado la combinación de metodologías de la TRI y de la TCT para obtener resultados más robustos.

Conclusiones y perspectivas de futuro

El análisis Rasch proporciona una metodología valiosa para la evaluación de competencias y habilidades clínicas, así como para el desarrollo y validación de instrumentos de medición en enfermería. A través de su aplicación práctica, se pueden obtener mediciones precisas y objetivas, lo que facilita la toma de decisiones basada en evidencia en la educación y la práctica de enfermería. Los estudios de caso destacados ilustran el potencial del análisis Rasch para mejorar la calidad de la atención al paciente y la efectividad de los programas de formación en enfermería, subrayando su importancia como herramienta en la investigación y práctica de enfermería.

La aplicación del análisis Rasch en la enfermería es un campo rico en oportunidades para la investigación futura. Algunas direcciones prometedoras incluyen:

• –

  Innovación en instrumentos de medición: Desarrollo de nuevos instrumentos de medición para áreas emergentes de práctica y cuidado en enfermería, utilizando el análisis Rasch para garantizar su validez y fiabilidad.

• –

  Evaluación longitudinal de competencias: Aplicación del análisis Rasch en estudios longitudinales para evaluar el desarrollo de competencias a lo largo del tiempo, identificando factores que contribuyen al crecimiento profesional continuo.

• –

  Integración de tecnologías digitales: Exploración de cómo las tecnologías digitales y los datos masivos pueden integrarse con el análisis Rasch para mejorar la recopilación y análisis de datos en la investigación y práctica de enfermería.

• –

  Estudios comparativos internacionales: Utilización del análisis Rasch para facilitar estudios comparativos internacionales sobre la educación y práctica de enfermería, contribuyendo a la armonización de estándares y prácticas a nivel global.

Declaración de IA generativa y tecnologías asistidas por IA en el proceso de redacción

Durante la preparación de este trabajo los autores utilizaron «ChatGPT Plus/Academic Assistant Pro®» con el fin de mejorar/aumentar la calidad, la relevancia y el recuento preciso de palabras. Después de utilizar esta herramienta/servicio, se revisó y editó el contenido según fuera necesario, asumiendo los autores plena responsabilidad por el contenido de la publicación.

Conflicto de intereses

Los autores declaran que no tienen ningún conflicto de intereses en relación con este manuscrito.