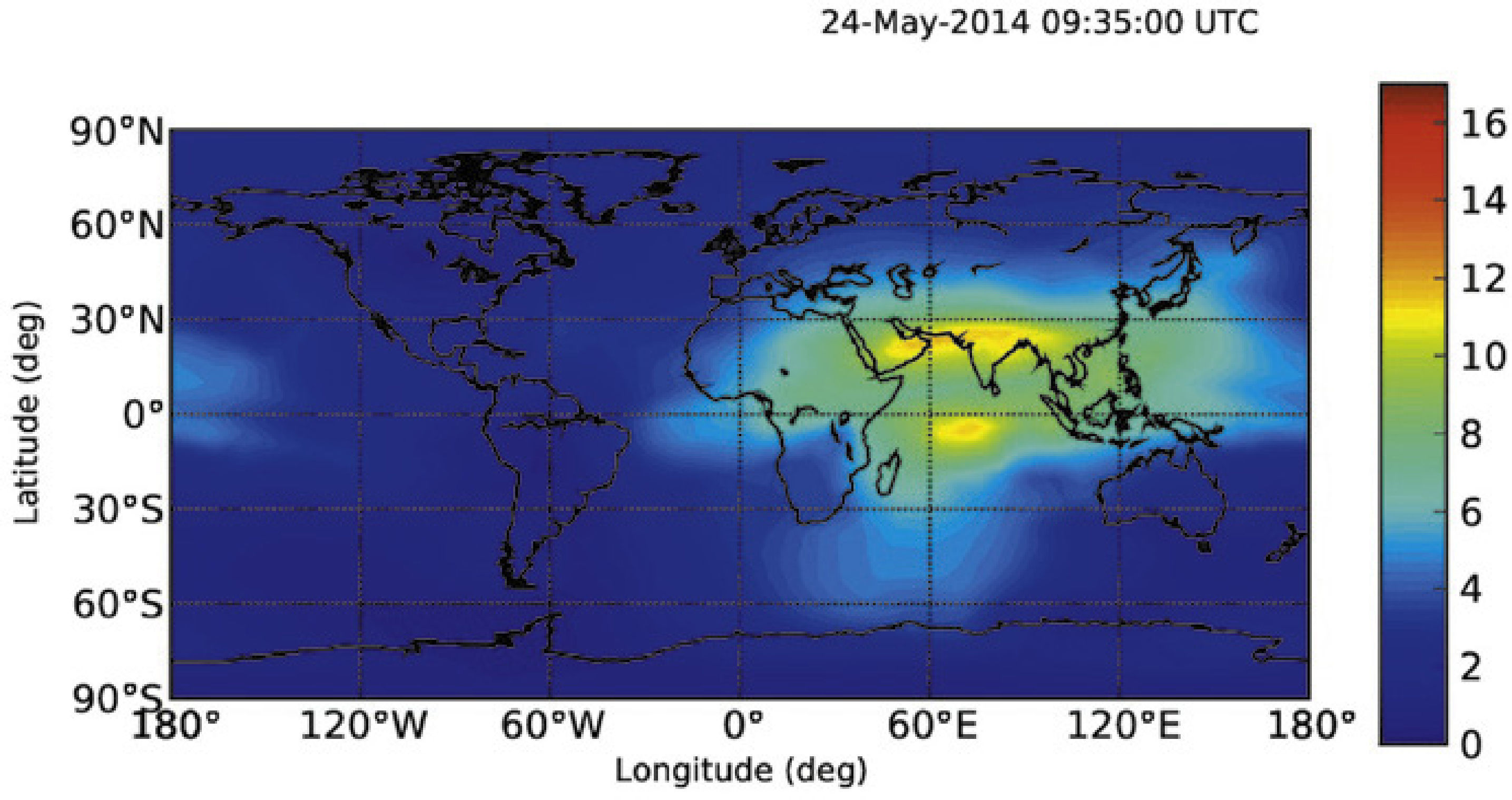
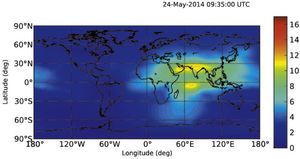
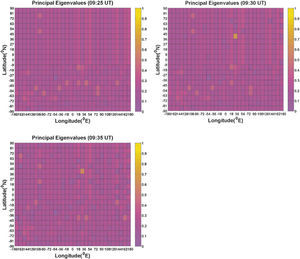
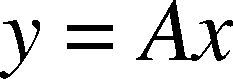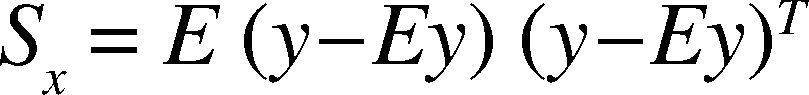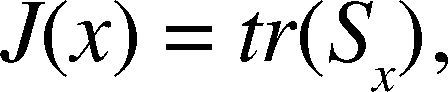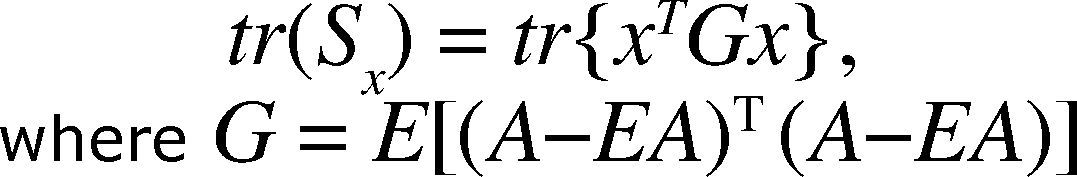Se utilizó el análisis de componentes principales de dos dimensiones (2DPCA) para determinar el contenido total de electrones de la ionosfera (TEC), una anomalía de dos dimensiones después del terremoto Egeo-Sea en 09:25:03 (UT) el 24 de mayo del 2014 (Mw = 6.4). Posterior al terremoto la anomalía TEC fue la más intensa y se localizó en 9:30-09:35 (UT). Ésta es una razón potencial para la formación de la anomalía TEC, lo que podría ser una fluctuación fuera de lo normal. Por ejemplo, la variación de la densidad de los electrones se elevó a alta velocidad de la onda de choque acústico con la velocidad de al menos 1.818,18km/h.m/s, dada por el movimiento principal del terremoto. El tiempo de duración de la anomalía TEC era de al menos cinco minutos. El tsunami fue causado por un terremoto con epicentro en el mar, la fluctuación anómala podría ser un signo precoz para las regiones lejanas del epicentro cuando comenzó a propagarse, ya que el tsunami llegó a ellas más lentamente que las fluctuaciones anómalas.
Two-dimensional principal component analysis (2DPCA) has been used to determine ionospheric two-dimensional total electron content (TEC) anomaly after Aegean-Sea earthquake at 09:25:03(UT) on 24 May, 2014 (Mw = 6.4). The TEC anomaly was more intense localized at 09:30 to 9:35 (UT) post the earthquake. Potential reason of the TEC anomaly, which might be a anomalous fluctuation e.g., electron density variation, is rising high speed acoustic shock wave with the speed of at least 1818.18 Km/h. m/s resulted by the mainshock of the earthquake. The duration time of the TEC anomaly was at least 5minutes. The anomalous fluctuation could be an early warning for the regions far from the epicenter when it began to propagate because the tsunami arrived at the far regions very slower than anomalous fluctuation if the tsunami was caused by earthquake with epicenter in the sea.
Ionospheric total electron content (TEC) anomalies associated with large earthquakes have been widely researched both as precursors and aftereffects (Artru & Lognonné, 2001; Garcia et al., 2005; Hegai et al., 2006; Liu et al., 2009; Liu et al., 2006; Lognonné et al., 2006; Marchand et al., 2008; Pulinets et al., 2000; Pulinets & Boyarchuk, 2004; Pulinets, 2007; Singh, et al., 2010; Zhao et al., 2008). The exact causes of earthquake associated precursor TEC anomalies are not known; however, there are many possibilities including gravity waves generated by the solid-earth and sea, as well as lower atmospheric electric fields resulting from earthquake preparation processes that can be transferred into the ionosphere along geomagnetic lines (Pulinets, 2004). Regardless of the specific causes of earthquake-precursor TEC anomalies, their earthquake association has been established statistically using deviations from running TEC median values after eliminating other possible causes of TEC disturbance such as solar flare and geomagnetic storm activity (Lin, 2010). The TEC anomalies were most likely caused by acoustic gravity waves traveling from the earth's surface into the ionosphere (Artru et al., 2001; Garcia et al., 2005; Lognonné et al., 2006; Marchand et al., 2008; Pulinets et al., 2000). The mechanism for this is thought to be earth's atmosphere acting as a natural amplifier. During an earthquake tiny amounts of kinetic energy are transferred from the solid earth to the lower atmosphere. If this kinetic energy is conserved, then given the exponential decline in atmospheric density with height, waves of great amplitude can result in the ionosphere. It has been estimated that millimeter disturbances at the earth's surface can be amplified to waves of amplitude 100 m at 100km altitude (Artru, et al., 2001; Lognonné et al., 2006). A study by Lognonné et al. (2006) using ground based GPS receivers to detect post-seismic ionospheric disturbance found that the measurable impact of the gravity waves resulting from the Nov. 3. Denali, Alaska M=7.9 earthquake produced small but detectable changes in the TECu count of 0.1% peak to peak. This disturbance was detected by 6 other satellites. Lognonné et al. (2006) also measured the effects of near field seismic waves for the Hokkaido Tokacho – Oki earthquake of Sept. 25, 2003. In that experiment, they found that acoustic waves could be detected as high as 800km, they also measured the gravity wave impact for the same earthquake and got similar results to those for the Alaskan Denlai earthquake in terms of TECu disturbance. One issue, however, with all TEC measurement is the nature of the ionosphere. The electron content of the ionosphere is highly dynamic plasma so that establishing anomalies and event association is not easy. For example, determining a running median of TEC content before large earthquakes to search for precursor TEC anomalies is difficult and may not always be reliable because TEC can be affected by many factors. Pulinets (2004) makes an extensive list of possible causes, including radon gas release, causing lower atmospheric electric fields which travel up into the ionosphere along geomagnetic lines. Freund (2003) suggests P-type semiconductor effect as the cause of lower atmosphere electric fields. Recent studies have shown that earthquake-related TEC anomalies are detectable using principal component analysis (PCA) (Lin, 2010, 2011). PCA is an alternative pure mathematical method for the measuring TEC anomalies. The method relies on exploiting signal delay between global positioning system (GPS) satellites and ground receiver stations without direct observation of ionospheric TEC. The long term period variance of ionospheric TEC (Lin, 2010) does not affect the outcome of the results using PCA and the potential influence of other factors such as solar flares and geomagnetic disturbance are eliminated using relevant Kp indexes statistically. While these PCA experiments were able to detect and even describe the spatial pattern or physical shape of earthquake-related TEC anomaly (Lin, 2011), PCA might not be as useful as two-dimensional principal component analysis (2DPCA) in the detection of TEC anomalies when applying to two-dimensional TEC data. Therefore, the goal of this study is to examine the ionospheric TEC anomaly related to Aegean-Sea earthquake (40.313°N, 25.453°E) at 09:25:03UT on 24 May, 2014 (Mw = 6.4) with the depth of 10.0km (U.S. Geological Survey) using 2DPCA. Possible causes of discovered anomaly will be discussed. It is expected that at the time 09:25 to 09:35 UT, ionospheric TEC behavior should be complicated showing large earthquake-related anomaly shortly after or during the mainshock like the results of Liu et al's work (2011) while tsunami did not occur to affect the ionosphere. The TEC data (two dimensional TEC data, F-layer) are derived NASA Global Differential GPS system (GDGPS) and global TEC maps (GIMs) in this study are derived using TEC data from ∼100 real-time GDGPS tracking sites, augmented with additional sites that are available on 5minutes basis. The integrated electron density data along each receiver-GPS satellite link is processed through a Kalman filter. Processing to estimate TEC value needs to consider some biases (influences) during restore of TEC values from measurements of dual-frequency delays of GPS signals, which related with cycle slips, resolving of carrier phase ambiguity, determination hardware delays for phase, code measurements, tropospheric and multipath problems. The Kalman filter has been used to estimate the TEC with less bias (Kechine et al., 2004; Ouyang et al., 2008) (http://www.gdgps.net/system-desc/index.html).
2Method2.12DPCAFor 2DPCA, let signals are represented by a matrix A (the dimension of n x m). Linear projection of the form is considered as followed (Sanguansat, 2012),
Here x is an n dimensional project axis and is the projected feature of signals on x called principal component vector.
Here Sx is the covariance matrix of the project feature vector.
The trace of Sx is defined;
The matrix G is called signal covariance matrix. The vector x maximizing Eq. 4 corresponds to the largest (principal) eigenvalue of G, and let the largest eigenvalue be the most dominant component of the data, therefore largest eigenvalue is represented the principal characteristics of the data (Sanguansat, 2012, Jeong et al., 2009). 2DPCA can be removed small sample signal size (SSS) problem for two dimensional TEC data (Fukunnaga, 1991). The PCA converts the measurements into one-dimensional data before covariance matrix calculation (Yang et al., 2004). The covariance matrix of PCA is based on an input matrix with the dimension of m x n, which is reshaped from one-dimensional data (length of m multiplying n). Reshaping data will cause computing error because PCA is a tool to deal with one-dimensional data. It means that the spatial structure and information can not be well preserved due to some original information loss when inverting to original dimension (Kramer, 1991) under the condition of the matrix being small sample size (SSS). Such information loss is called SSS problem. However, the covariance matrix in 2DPCA is full rank for a matrix of low dimension. Therefore the curse of dimensionality and SSS problem (low dimensional data problem) can be avoided (Kong et al., 2005; Sanguansat, 2012). TEC data are examined to detect earthquake-related TEC anomaly and GIMs are only used to observe TEC situation in this study.
2.2TEC Data Processing 2DPCAFigure 1(a) shows the GIMs during the time from 09:25 to 09:35. The earthquake-related TEC anomalies are not easy to observe using e.g. determining a running median of TEC content to detect a TEC anomaly (Liu et al., 2006). The TEC data of the global region (not dividing the GIM for image processing) in Figure 1(a) are divided into 600 smaller areas 5 and 2.5 degrees in longitude and latitude, respectively. The size of each small area is 12° in longitude and 9° in latitude. The spatial resolution of the TEC data for GDGPS system is 5 and 2.5 degrees in longitude and latitude, respectively (Hernández-Pajares et al., 2009; Chen and Gao, 2005; Gao and Chen, 2006) (http://www.gdgps.net/system-desc/references.html) and therefore 4 TEC data (two-dimensional data) are take in each area. The TEC were anomalies usually spread widely from the epicenters of large earthquakes from the results of Artru, et al. (2001) and Lognonné et al. (2006) and Hobara Parrot (2005). Therefore earthquake-related TEC anomaly is detectable for such selected size of an area. The 4 TEC data form a matrix A of Eq. 1 with the dimensions of 2 x 2 as small sample signal size (SSS) in each are of Figure 1(a). This allows for principal eigenvalues to be computed for each of the 600 smaller areas.
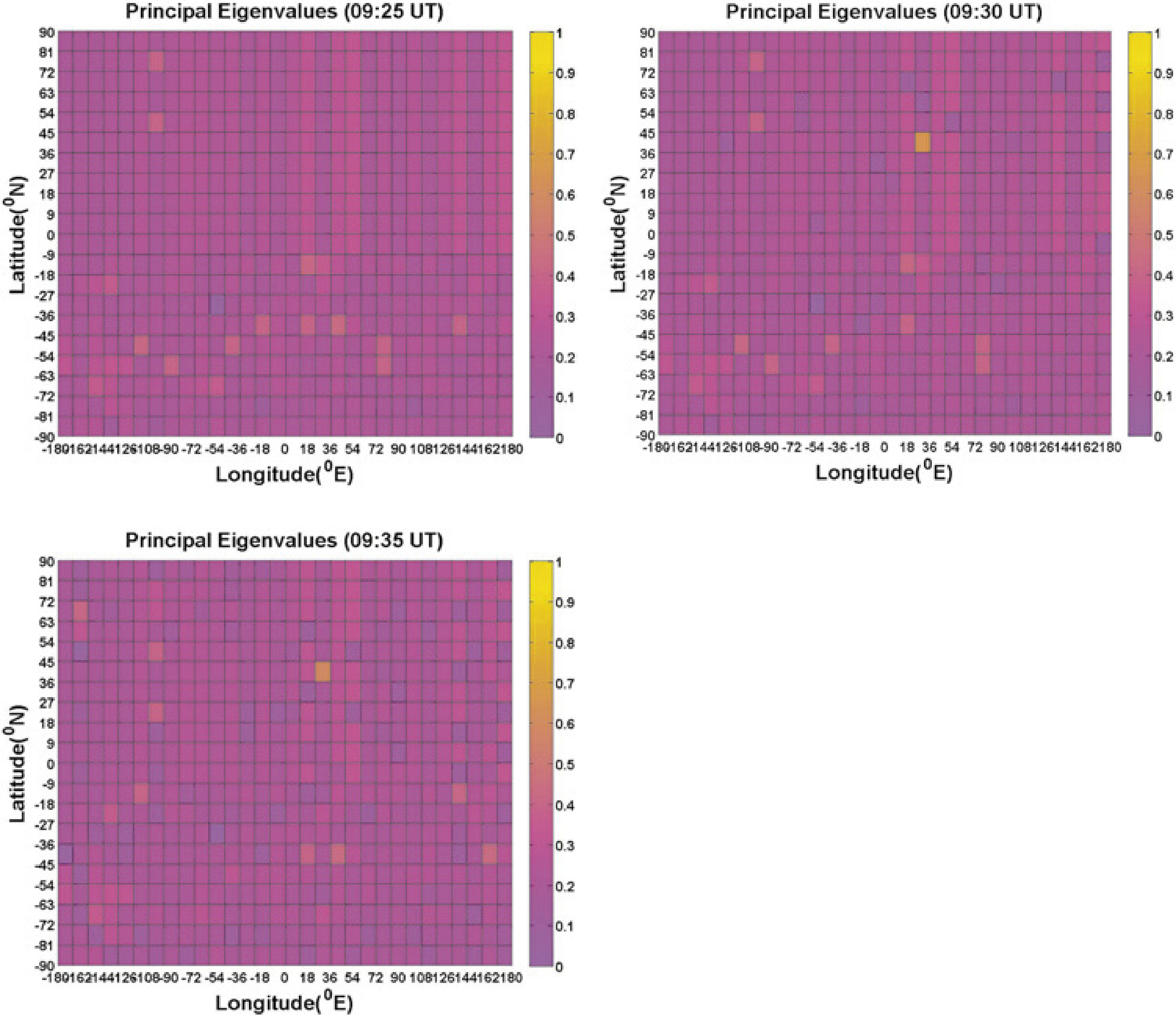
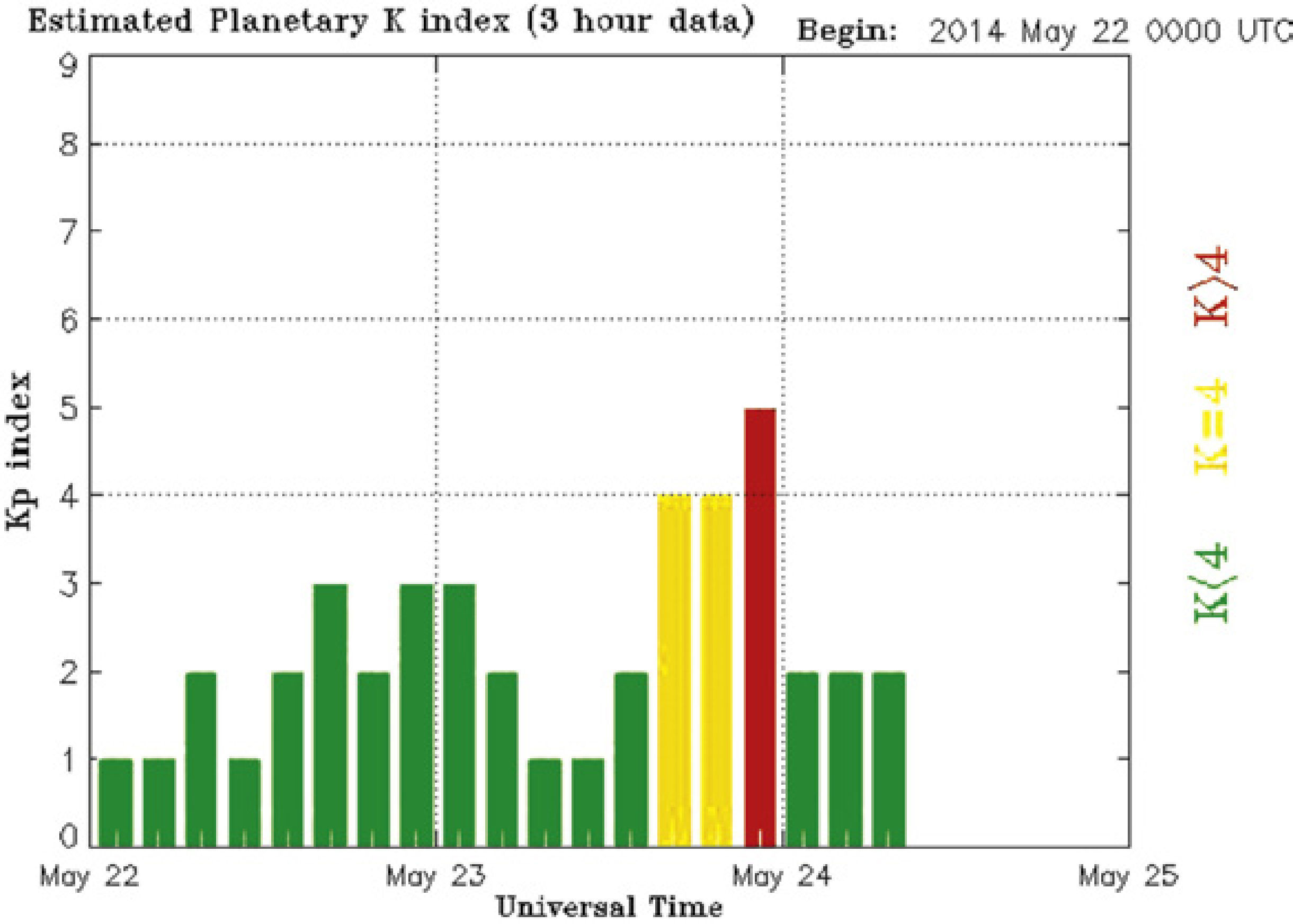
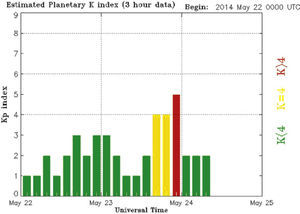
3ResultsThe respective results are given in Figure 1(b). The representative of large principal eigenvalues in the Figs 1(b) shows the existence of earthquake-related TEC anomaly represented by a large principal eigenvalue at the time 09:30-09:35. Non-earthquake TEC anomalies (e.g. EIA) are therefore suppressed by large principal eigenvalues defining as earthquake-related TEC anomaly. It means that if the largest principal eigenvalue related to the earthquake was taken out, then non-earthquake TEC anomalies would reveal clearly. Therefore the TEC anomaly related to this earthquake should be very large due to its large magnitude (Mw = 6.1) and shallow depth (10.0km). The possibility of other factors such as solar flare and geomagnetic effects affecting the results are considered by examining Kp indices (Elsner and Kavlakov, 2001; Hamilton et al., 1986; Mukherjee, 1999). July, 2 was geomagnetic quiet day shown in Figure 3 (Kp<4).
The figures give a color-coded scale of the magnitudes of principal eigenvalues of 2DPCA corresponding to Figure 1(a). The color within an area denotes the magnitude of a principal eigenvalue corresponding to Figure 1(a), therefore there are 600 principal eigenvalues assigned, respectively.
2DPCA was able to detect a TEC anomaly related tot this Earthquake at the time 09:30 to 09:35 UT. Identifying precise cause of earthquake related TEC anomalies is not easy. One reason for this is the number of potential causes of earthquake related TEC anomalies that arise during earthquake preparation, the mainshock, and aftershocks. For example during the earthquake preparation phase, Pulinets and Boyarchuk (2004) suggested that radon emanating from active faults and cracks before earthquakes ionize the near ground atmosphere to produce large vertical electric fields. Freund (2000) proposed that mobile positive holes in the earth's crust could be activated by low-energy impact, sound waves, and micofractures, creating charge clouds that could explain electromagnetic activity. Gravity waves arising from fine vibrations in the earth's surface leading to gas release are another possibility. This results in lower atmospheric turbulence and eventual ionospheric perturbations (Molchanov and Hayakawa, 1998). However, once an earthquake occurred, then the most evident physical mechanism was ground motion and fine surface vibrations. Accordingly, studies of electromagnetic disturbance suggested two possible explanations for earthquake-related anomalies at this altitude. One was acoustic gravity waves caused by Joule heating (Hegai et al., 1997) and the other was the presence of an electric field creating large scale ionospheric density irregularities (Liu et al., 2004; Pulinets and Legen’ka, 2003) coupled with potential drift of the anomaly toward the equator. However, this anomaly resembled what one would expect from rising acoustic gravity waves because of strong motion. As discussed in the introduction earth's atmosphere could act as a natural amplifier due to declining atmospheric density with height. A large earthquake, such as this earthquake, was characterized by many fine vibrations at the earth's surface which could produce a vertical stark acoustic pressure wave of great amplitude by the time it reached the ionosphere. Such a description could possibly represent the stark and concentrated energy of an acoustic shockwave being formed in the lower atmosphere after the earthquake traveling up into the ionosphere (Jin et al., 2010). This was the possibility described in the introduction to this study whereby high speed acoustic shock wave with the speed of at least 1818.18 Km/h. m/s caused by stark strong motion at the earth's surface are amplified through the atmosphere to affect an anomalous fluctuation e.g., electron density variation in the ionosphere from the earthquake zone. The computing process of the shock wave speed was as follows; the time difference from original time of the earthquake to beginning time of TEC anomaly is 297sec, and the F-lay is above 150km, then 150km ÷ 297sec is about 1818.18 Km/h. The duration time of earthquake-related TEC anomaly was estimated at least 5minutes. The duration time of TEC anomaly might correlate with the damping of ionospheric plasma. The anomalous fluctuation could be an early warning for far regions when this anomalous fluctuation beginning to propagate. The tsunami arrived at the far regions very slower than such anomalous fluctuation when the tsunami was caused by earthquake with epicenter in the sea (Liu et al., 2011). Afraimovich et al. (2001) researched shock acoustic wave due to occurring of the earthquakes to affect ionosphere. They studied the earthquake effects in Turkey on 17 August and 12 November 1999 and in Southern Sumatra on 04 June 2000 and found the ionospheric response related to the earthquakes due to shock acoustic wave is 180-390 s. Compared with the result of this study, 2DPCA has shown its advantage and credibility to estimate the duration time of earthquake-related TEC anomaly.
5Conclusion2DPCA had the advantage to detect the TEC anomaly related to the 24, May 2014 Aegean-Sea Earthquake. Results have shown that a local ranging TEC anomaly was detectable at the time 09:30 to 09:35 UT. The earthquake-related TEC anomaly could be indicative of a rising high speed acoustic shock wave with the speed of at least 1818.18 Km/h. m/s and might cause a TEC anomalous fluctuation e.g. density variance. The duration time of the TEC anomaly was at least 5minutes. The anomalous fluctuation could be an early warning for far regions when this anomalous fluctuation propagating.
The author is grateful to: NASA Global Differential GPS system (GDGPS) for their useful references Data.