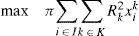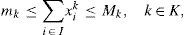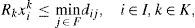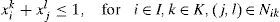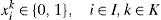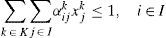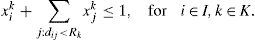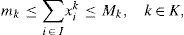Approximate Packing Circles in a Rectangular Container: Valid Inequalities and Nesting

Abstract

A problem of packing a limited number of unequal circles in a fixed size rectangular container is considered. The aim is to maximize the (weighted) number of circles placed into the container or minimize the waste. This problem has numerous applications in logistics, including production and packing for the textile, apparel, naval, automobile, aerospace and food industries. Frequently the problem is formulated as a nonconvex continuous optimization problem which is solved by heuristic techniques combined with the local search procedures. A new formulation is proposed based on using a regular grid approximated the container and considering the nodes of the grid as potential positions for assigning centers of the circles. The packing problem is then stated as a large scale linear 0–1 optimization problem. The binary variables represent the assignment of centers to the nodes of the grid. The resulting binary problem is then solved by the commercial software. Two families of valid inequalities are proposed to strengthening the formulation. Nesting circles inside one another is also considered. Numerical results are presented to demonstrate the efficiency of the proposed approach.

Resumen

Se considera el problema de empaquetar un número limitado de círculos de radios diferentes en un contenedor rectangular de dimensiones fijas. El objetivo es maximizar el número (ponderado) de círculos dentro del contenedor o minimizar el desperdicio de espacio dentro del mismo. Este problema tiene numerosas aplicaciones dentro de la logística, incluyendo la producción y empaquetado para la industria textil, naval, automotriz, aeroespacial y la industria de alimentos. Frecuentemente, el problema es formulado como un problema de optimización continua no convexo que es resuelto con técnicas heurísticas combinadas con procedimientos de búsqueda local. Se propone una nueva formulación basada en el uso de una malla regular que cubre el contenedor y donde se considera a los nodos de la malla como posiciones potenciales para la asignación de centros de los círculos. El problema de empaquetamiento se escribe entonces, como un problema de optimización 0–1 a gran escala y es resuelto con software comercial. Resultados numéricos son presentados para demostrar la eficiencia del enfoque propuesto y realizar una comparación con los resultados conocidos.

1

Introduction

Packing problems constitute a family of natural combinatorial optimization problems, which occur in many fields of study such as computer science, industrial engineering, logistics and manufacturing and production processes. For instance, several real life industrial applications require the allocation of a set of pieces to a larger standardized rectangular stock unit. They generally consist of packing a set of items of known dimensions into one or more large objects in order to minimize a certain objective (e.g. the unused part of the objects or waste).

The circle packing problem is a well studied problem [12] whose aim is the packing of a certain number of circles, each one with a fixed known radius (not necessary the same for each circle) inside a container. The shape of the container may vary from a circle, a square, a rectangular, etc.

This problem has been applied in different areas, such as the coverage of a geographical area with cell transmitters, storage of a cylindrical drums into containers o stocking them into an open area, packaging bottles or cans into the smallest box, planting trees in a given region as to maximize the forest density and the distance between the trees, and so forth [2,5,8]. Other applications one can find in the motor cycle industry, circular cutting, communication networks, facility location and dashboard layout [5,10,11].

In this paper we address the problem of packing a set of circular items in a rectangular container. There are two principal types of objectives that have been used in the literature: a) regard the circles (not necessary equal) as being of fixed size and the container as being of variable size and b) regard the circles and the container as being of fixed size and minimize “waste”.

Examples of the first approach include [17]:

• •

  For the square container minimize the length of the side and hence minimize the perimeter and area of the square;

• •

  Minimize the perimeter of the rectangle;

• •

  Minimize the area of the rectangle;

• •

  Considering one dimension of the rectangle as fixed, minimize the other dimension. Problems of this type are often referred to as strip packing problems (or as circular open dimension problems).

For the second approach various definitions of the waste can be used. The waste can be defined in relation to circles not packed (e.g. the number of unpacked circles or the perimeter/area of unpacked circles), or introducing a value associated with each circle that is packed (e.g. area of the circles packed), etc.

Many variants of packing circular objects in the plane have been formulated as nonconvex (continuous) optimization problems with decision variables being coordinates of the centres. The nonconvexity is mainly provided by no overlapping conditions between circles. These conditions typically state that the Euclidean distance separating the centres of the circles is greater than a sum of their radii.

The nonconvex problems can be tackled by available nonlinear programming (NLP) solvers, however most NLP solvers fail to identify global optima. Thus, the nonconvex formulation of circular packing problem requires algorithms which mix local searches with heuristic procedures in order to widely explore the search space. It is impossible to give a detailed overview on the existing solution strategies and numerical results within the framework of a single short paper. We will refer the reader to review papers presenting the scope of techniques and applications for the circle packing problem (see, e.g. [1,4,17,18] and the references therein).

In this paper we propose a new formulation for approximate solution of circular packing problems using a regular grid to approximate the container. The nodes of the grid are considered as potential positions for assigning centers of the circles. The packing problem is then stated as a large scale linear 0–1 optimization problem. Two classes of valid inequalities are proposed to strengthening the formulation. Nesting circles inside one another is also considered. Numerical results are presented to demonstrate efficiency of the proposed approach.

To the best of our knowledge, the idea to use a grid was first implemented by Beasley [3] in the context of cutting problems. This approach was recently applied in [9,15,16] for packing problems. This work is a continuation of [15].

2.

The model

Suppose we have non-identical circles C_k of known radius R_k, k ∈ K = {1,2,…K}. Let at most M_k circles C_k are available for packing and at least m_k of them have to be packed. Denote by i ∈ I = {1,2…,n} the node points of a regular grid covering the rectangular container. Let F ⊆ I be the grid points lying on the boundary of the container. Denote by d_ij the Euclidean distance between points i and j of the grid. Define binary variables xik=1 if centre of a circle C_k is assigned to the point i; xik=0 otherwise.

In what follows we will distinguish two cases of circle packing, depending on whether nesting circles inside one another is permitted o not. To the best of our knowledge, nesting problem was first mentioned in [10] in the context of packing pipes of different diameters into a shipping container. Comparing to the standard packing, packing with nesting is much less investigated.

Consider first the problem without nesting. In order to the circle C_k assigned to the point i be non-overlapping with other circles being packed, it is necessary that xjl=0 for j ∈ I, l ∈ K, such that d_ij < R_k + R_l. For any fixed i, k let N_ik = {j, l: i ≠ j, d_ij < R_k + R_l}. Let n_ik be the cardinality of N_ik: n_ik = |N_ik|. Then the problem of maximizing the area covered by the circles can be stated as follows:

Then the problem of maximizing the area covered by the circles is as follows:

Constraints (2) ensure that the number of circles packed is between m_k and M_k; constraints (3) that at most one centre is assigned to any grid point; constraints (4) that the point i can not be a centre of the circle C_k if the distance from i to the boundary is less than R_k; pair-wise constraints (5) guarantee that there is no overlapping between the circles; constraints (6) represent the binary nature of variables.

Note that for the particular case of packing equal circles of radius we may simply reduce the dimensions of the container by and then apply the above model to a smaller container dropping the boundary conditions (4).

We may expect that the linear programming relaxation of the problem (1)–(6) provides a poor upper bound for the optimal objective. For example, for K = 1 and suitably chosen M_k,m_k, set xik=0.5 for all i ∈ I. This solution is feasible to no overlapping constraints (5) and corresponding objective value grows linearly with respect to the number of grid points.

To tightening the LP-relaxation of (1)–(6) we propose two families of valid inequalities. The first ensure that no grid point is covered by two circles, while the second guarantee that there is at most one centre assigned to the area covered by a circle.

To present the first family, define matrix ¿ijk as follows. Let ¿ijk=1 ford_ij < R_k; ¿ijk=0 otherwise. By this definition, ¿ijk=1 if the circle C_k centered at i covers point j. The following constraints ensure that no points of the grid can be covered by two circles:

Note that (7) is not equivalent to non-overlapping constraints (5). Constraints (7) ensure that there is no overlapping in grid points, while (5) guarantee that there is no overlapping at all. Similar to set-covering formulations it is natural to refer to (7) as point-covering constraints.

The second family of inequalities is stated as follows:

To demonstrate that (8) is valid for the problem (1)–(6) assume that xik=1 in (8). That is the centre of the circle C_k is assigned at i. By (8) we have ∑j:diji ∈ I, k ∈ K and then it follows that xjk=0 for j:d_ij < R_k. That is there are no other centres assigned to points inside the circle centred at i. For xik=0 we have ∑j:diji, at most one point can be assigned as a centre. This is true since the distance between any pair of these points is less than 2R_k and assigning the centres of C_k violates non overlapping constraints.

To consider nesting circles inside one another, we only need to modify the non-overlapping constraints. In order to the circle C_k assigned to the point i be non-overlapping with other circles being packed (including circles places inside this circle), it is necessary that xjl=0 for j ∈ I, l ∈ K, such that R_k − R_l < d_ij < R_k + R_l. Note that the later condition is always fulfilled for R_k < R_l (d_ij ≥ 0), such that only smaller circles can be placed inside a given circle. For fixed i, k let ¿_ik = {j,l : i ≠ j, R_k − R_l < d_ij < R_k + R_l}. Then the problem of packing circles with nesting can be stated as follows:

subject to

In the problem (9) the weighting coefficients wik may be associated with the area of circles and/or represent the relative importance of subsets of the container.

Note that inequalities (7), (8) in general are not valid for the problem (9).

3

Computational results

A rectangular uniform grid was used in numerical experiments, such that all grid points are defined by the grid points on its edges. Let L be a horizontal dimension (length) and W be a vertical dimension (width) of the container; M be a number of the equidistant grid points on the horizontal edge of the container, while N be a number of the equidistant grid points on its vertical edge. Hence the grid has M × N node points (n = M × N).

All optimization problems were solved by the system CPLEX 12.5. The runs were executed on a PC Toshiba Satellite L735, Intel Core I-5, 2.5 Ghz and 8Gb RAM.

In the first part of our numerical experiment we add valid inequalities (7) or (8) or both to the problem (1)–(6) and compare corresponding LP-relaxations. Five different relaxations were studied corresponding to constraints used/droped:

• •

  LP1: only original constraints (2)–(5);

• •

  LP2: constraints (2)–(5) and (7);

• •

  LP3: constraints (2)–(5) and (8);

• •

  LP4: constraints (2)–(5), (7) and (8);

• •

  LP5: constraints (2)–(4), (7) and (8)

Ten instances with equal circles were used to (9) compare relaxations. The first 5 instances were the same as in [9, Table 3]: L = 3, W = 6 and radiuses 0.5, 0.625, 0.5625, 0.375 and 0.3125 correspondingly. The second 5 instances were from [6] with L × W, R defined as follows: 100 × 100, 13; 100 × 200, 25; 100 × 100, 18; 100 × 200, 31; 120 × 80, 21. In all instances the objective (1) was to maximize the number of circles packed.

The results of the numerical experiment are presented in Table 1. Here the second column presents the integer solution of the problem (2)–(5) while all the next columns give the optimal objectives of the corresponding relaxations.

Table 1.

LP bounds for packing equal circles.

	IP	LP1	LP2	LP3	LP4	LP5
1	18	2964.49	18.179	18.123	18.123	18.123
2	10	2722.493	10.049	10.003	10.003	10.003
3	13	4788.501	13.957	13.957	13.957	13.957
4	32	2768.501	34.659	34.535	34.535	34.535
5	45	4178.501	50.946	50.763	50.763	50.763
6	13	1799.996	14.462	14.425	14.425	14.425
7	8	1799.996	8	8	8	8
8	6	1799.996	6.633	6.632	6.632	6.631
9	3	1799.996	3.032	3.001	3.001	3.001
10	4	1799.996	4.367	4.359	4.359	4.359

As we can see form Table 1, valid inequalities improve significantly LP1, continuous relaxation of the original problem, and provide a very tight bound for the optimal objective of the original integer problem IP. In many cases rounding below the corresponding rational bound results in the optimal objective value. Note that if we drop the pair-wise non-overlapping constraints (5) and use both families of valid inequalities (relaxation LP5), the bound is still good. We see that the values of LP3-LP5 are very close to each over. From computational point of view the relaxation LP5 is less expensive since the pair-wise non-overlapping constraints (5) are relaxed.

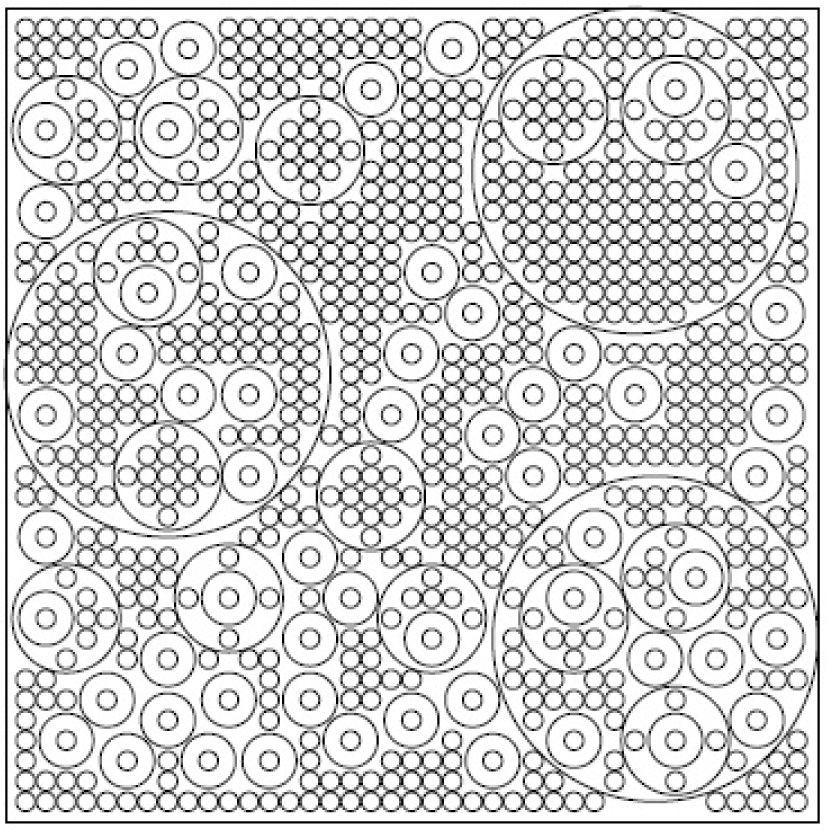
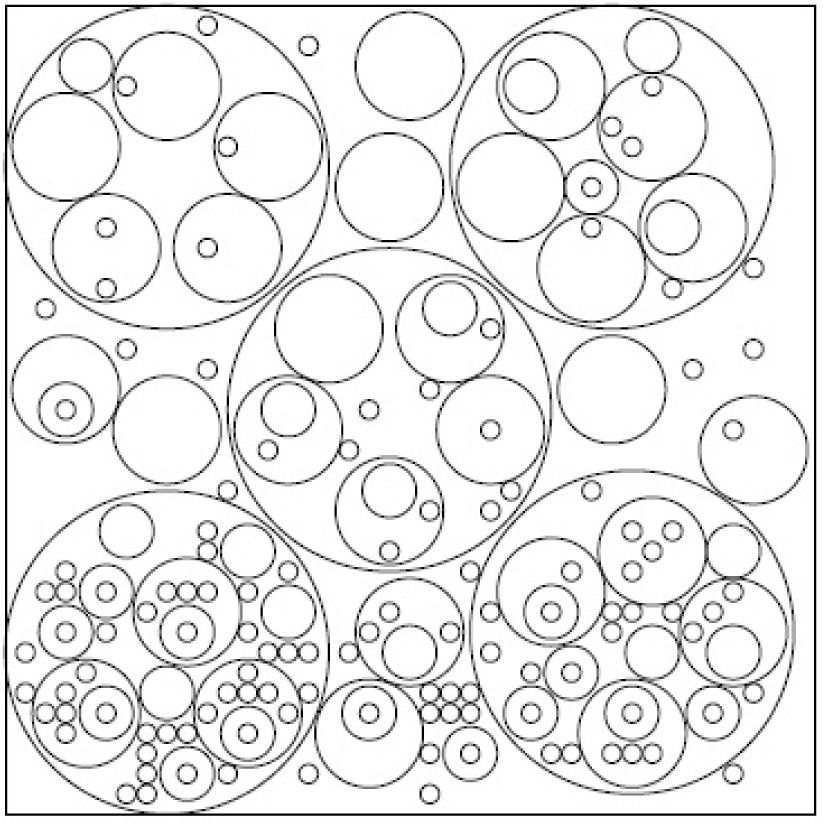
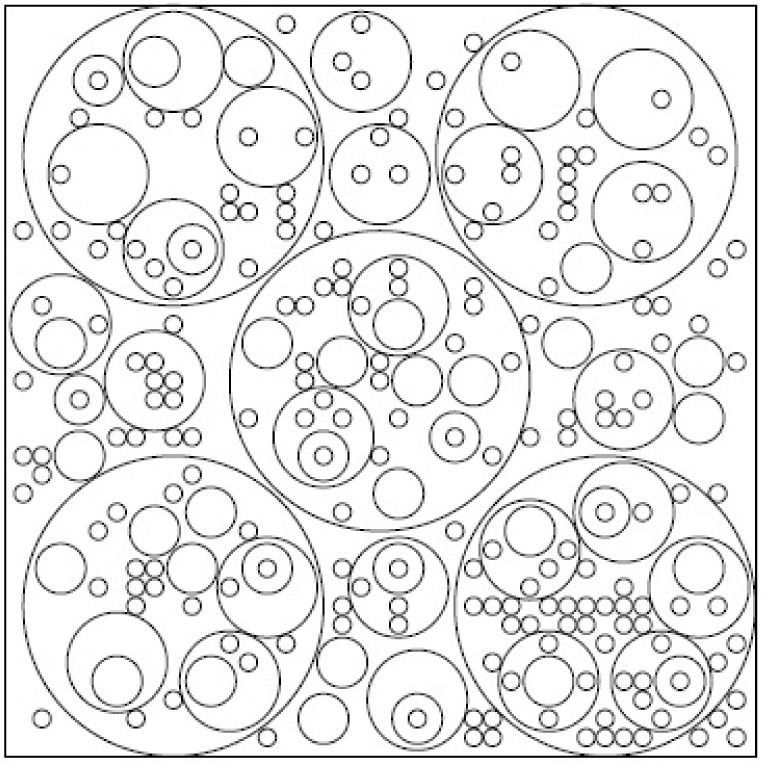
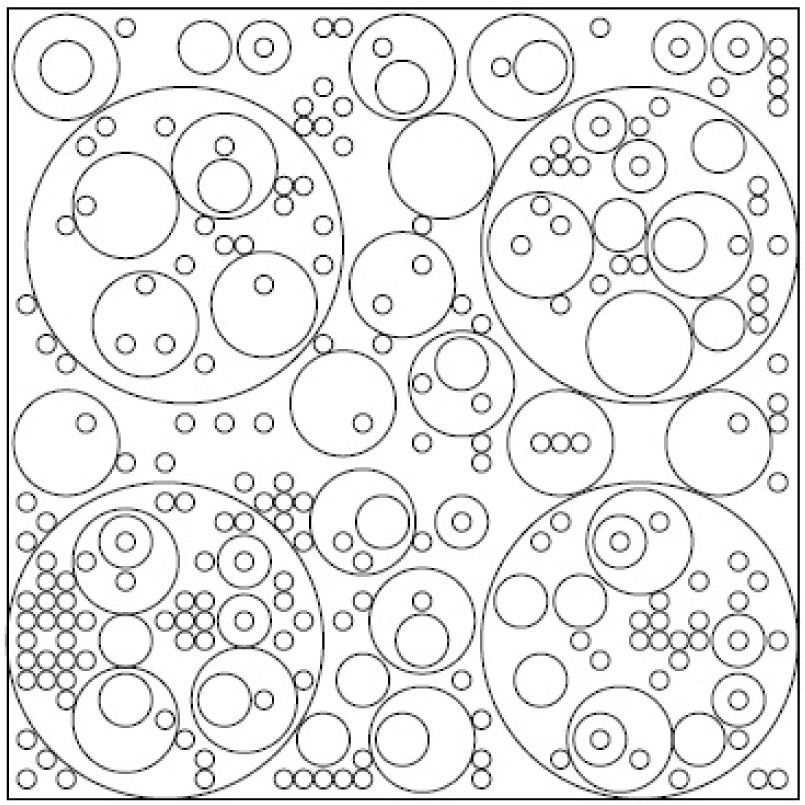
In the second part of the experiment packing of different circles with nesting was studied. We fixed the dimension of the container (L = W = 60), radiuses of the circles (R₁ = 12, R₂ = 2, R₃ = 4, R₄ = 0.7) and vary the bounds m_k, M_k for the circles to be packed.

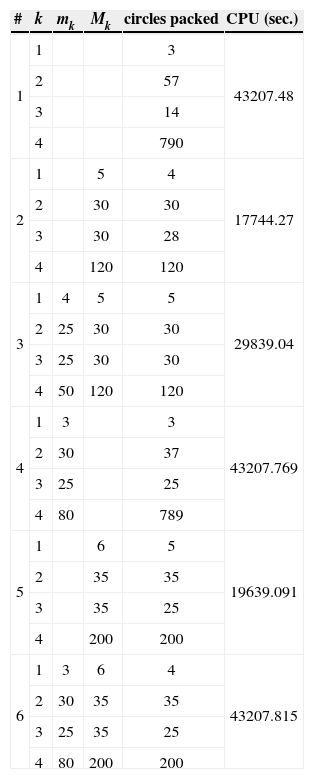
The data for 6 instances of the problem (9) considered in the experiment are presented in Table 2 together with the number of the circles packed and corresponding CPU time. Empty cells in this table correspond to the case with no lower/upper limits for the circles to be packed. All 6 problem instances were solved using the grid 41 × 41 and with mipgap = 15% for running CPLEX.

Table 2.

Problem instances and numerical results for packing with nesting.

#	k	mk	Mk	circles packed	CPU (sec.)
1	1			3	43207.48
	2			57
	3			14
	4			790
2	1		5	4	17744.27
	2		30	30
	3		30	28
	4		120	120
3	1	4	5	5	29839.04
	2	25	30	30
	3	25	30	30
	4	50	120	120
4	1	3		3	43207.769
	2	30		37
	3	25		25
	4	80		789
5	1		6	5	19639.091
	2		35	35
	3		35	25
	4		200	200
6	1	3	6	4	43207.815
	2	30	35	35
	3	25	35	25
	4	80	200	200

The objective was to maximize the total area of the circles packed.

As we can see from Table 2 the instances with lower bounds for the number of circles to be packed are mostly expensive computationally.

Figures 1–6 present packing configurations for the corresponding instances. We can see that varying the limits for the number of circles to be packed changes significantly the packing configuration.

Figure 1.

Packing pattern for instance 1.

Figure 2.

Packing pattern for instance 2.

Figure 3.

Packing pattern for instance 3.

Figure 4.

Packing pattern for instance 4.

Figure 5.

Packing pattern for instance 5.

Figure 6.

Packing pattern for instance 6.

4

Conclusions

The plane circle packing problem was approximated using integer formulation based on a grid approximation of a container.

The case of nesting circles inside one another was considered. This problem was mentioned in [10] in the context of packing pipes of different diameters into a shipping container and has not received much attention so far.

The presented approach can be easily generalized to three (and more) dimensional case and to different shapes of the container, including irregulars.

For the case without nesting two families of valid inequalities were introduced to strengthening the formulation. Numerical experiment was presented to demonstrate the efficiency of the proposed approach.

An interesting topic for the future research is to study the use of Lagrangian relaxation [14] or decomposition techniques [7] to cope with large dimension of the problem formulation. The other direction for future research is using metaheuristic approaches [13].