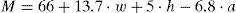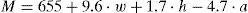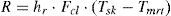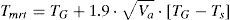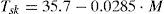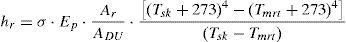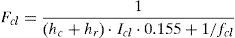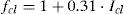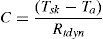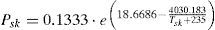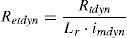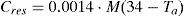Different materials have been used to fabricate summer (warm environment) clothing, such as cotton, nylon, neoprene, polyester and 100% synthetic fibers. However, because of their mechanical and thermal properties, nylon and polyester cloth has a tendency to rot and chafe in damp conditions. In addition, close-fitting synthetic fibers and neoprene make some wearers feel uncomfortable because of the rapidly occurring body skin sweat. However, bamboo and cotton have demonstrated to have low thermal conductivity. Hence, they are excellent materials to fabricate summer clothing. In this study, a theoretical analysis complemented with practical measurements of thermal properties of three different rib knitted structures produced from a 30 tex yarn of three blends of fibers (100% regenerated bamboo, 100% cotton and 50:50 regenerated bamboo: cotton) was realized to compare bamboo and cotton performance in warm environment. Obtained results show that garment thickness and heat storage rate in the human body can significantly be reduced by using 100% regenerated bamboo, without compromising comfort.
To maintain its temperature in a safety interval, the human body needs to eliminate excessive warmth. To eliminate the excessive warmth, it changes the amount of blood circulating through the body and it increases the amount of liquid transpiration on the body skin. These actions are commonly self-activated once its average internal temperature overpasses the 98.6°F (37°C) (Jessen, 2012; Hockey & Rew, 1996). Also, when the environmental temperature is close to the temperature of the body skin, the internal temperature regulation becomes more difficult. If the air temperature is equal to or higher than the temperature of the body skin, the blood that circulates close to the body skin cannot help to decrease the human body temperature (Widmaier, Raff, & Strang, 2013). In addition, if the environmental humidity increases, the evaporation of the liquid transpiration on the body skin decreases. Hence the effort of the body to maintain a safety temperature is affected, excessive blood arrives to the body skin and less arrives to the active muscles, the brain, and the other internal organs (Marieb & Hoehn, 2012). As a consequence, the body capacity to work decreases and a premature exhaustion due to the heat stress is experienced.
The previously described conditions are commonly found in seaside cities and also in many jobs in industrialized countries (Auliciems & Szokola, 2007). Different approaches have been used to prevent and minimize the effects of premature exhaustion due to heat stress in hot and warm environment. On the one hand, supplements such as drinks specially designed to replace body fluids and electrolytes have been used. They may be of benefit for workers who have very physically active occupations but they may add unnecessary sugar or salt to the diet (Jones, 1992). On the other hand, protective clothing has been used to reduce the effects of environmental stress factors. The materials used in clothing which has been designed for warm and hot weather must be able to give comfort and durability. It must allow air to circulate freely across the skin, which can help to keep the body cool. In addition, the material needs to resist the sun's rays in order to help delay the onset of sunburn.
Materials such as cotton, nylon 6, nylon 6.6, neoprene, polyester, and 100% synthetic fibers have been used for warm and hot environment clothing fabrication. However, pure nylon and polyester cloth have a tendency to rot and chafe in damp conditions. In addition, even a close-fitting and lightweight garment made of 100% synthetic fiber and neoprene make some wearer feel uncomfortable because of the rapidity of body skin sweat. On the other hand, cotton and bamboo are a tribe of flowering perennial evergreen plants in the grass family Poaceae (Das & Chakrabarty, 2008) which is an excellent candidate for warm environment clothing fabrication due to its mechanical and thermal properties (Mounika, Ramaniah, Prasad, Rao, & Reddy, 2012; Prakash, Ramakrishnan, & Koushik, 2013; Raimundo & Figueiredo, 2009).
In this study, the thermal properties of three different rib knitted structures produced from a 30 tex yarn of three blends of fibers (100% regenerated bamboo, 100% cotton and 50:50 regenerated bamboo: cotton) were used to compare the performance of regenerated bamboo and cotton in warm environment. Standardized values for metabolic rate, for different physical activities, were used in the calculations. The heat storage rate in the human body vs clothing insulation for the considered yarn blends was calculated. In addition, the relation of clothing thickness and clothing isolation was established. Theoretical results show that the garment thickness as well as the heat storage rate can significantly be reduced in the human body by using 100% regenerated bamboo, without compromising comfort.
2Heat balance and exchange modeling of human body and clothingThe interaction of heat with a dressed human body can be described from an arbitrary flux of heat impinging with the dressed body. Once the flux of heat is inside the front surface of the dressed body, the behavior of the flux of heat is determined by the rates of storage, production and losses. By conservation of energy, the net heat storage must balance the net production and losses within the unit volume of the dressed body. Using the nomenclature of Table 1, this can be written as: (Bartkevicius, Rackiene, & Virbalis, 2008; Holmer, 2006)
where S is the heat storage rate, M is the metabolic energy production rate, W is the external mechanical work, and R, C and E are the radiation, convective and evaporative heat loss from the skin, respectively. K is the conduction to the surfaces by direct contact with skin or clothing, Cres and Eres are the convective and evaporative heat losses from respiration, respectively. The units of the rate of storage, production and losses are energy per second, which are joules per second (Js−1) or watts (W). It is useful to standardize over persons of different sizes by using units of watts per square meter (Wm−2) of the body surface area.Nomenclature used in the theoretical modeling.
| ArADu | Fraction of skin surface involved in heat exchange by radiation | ArADu≈0.77 n.d. |
| C | Convective heat loss from skin | Wm−2 |
| CORR | Correction factor to clothing insulation | n.d. |
| Cres | Convective heat loss from respiration | Wm−2 |
| E | Evaporative heat loss from skin | Wm−2 |
| EP | Emissivity of the human body | Ep≈0.97 n.d. |
| Eres | Evaporative heat loss from respiration | Wm−2 |
| Fcl | Reduction factor for sensible heat exchange due to the clothes warm | n.d. |
| fcl | Clothing are factor | n.d. |
| hc | Convective heat transfer coefficient | Wm−2C−1 |
| hr | Radioactive heat transfer coefficient | Wm−2C−1 |
| Icl | Intrinsic insulation of the clothing | clo |
| imdyn | Dynamic permeability index for the clothing | n.d. |
| imst | Static permeability index of the clothing | imst≈0.38 n.d. |
| Lr | Lewis relation | Lr=1665°CkPa−1 |
| M | Metabolic rate | Wm−2 |
| Pa | Vapor pressure of the environment | kPa |
| σ | Stefan–Boltzmann constant | σ=5.67×10−8Wm−2K−4 |
| Psat | Saturation vapor pressure | kPa |
| Psk | Saturated vapor pressure at mean skin temperature | kPa |
| R | Radiation heat loss from skin | Wm−2 |
| Ra | Static insulation of boundary air layer | Ra≈0.11m2°CW−1 |
| Retdyn | Dynamic total water vapor resistance of the clothing system | m2kPaW−1 |
| RH | Relative humidity | (%) |
| Rtdyn | Dynamic thermal resistance of the clothing system | m2°CW−1 |
| Rtst | Static insulation of the clothing | m2°CW−1 |
| S | Rate of body heat storage | Wm−2 |
| Ta | Air temperature | °C |
| TG | Globe temperature | °C |
| Tmrt | Mean radiant temperature | °C |
| TS | Dry temperature | °C |
| Tsk | Skin temperature | °C |
| Va | Air velocity | ms−1 |
| W | Mechanical power | Wm−2 |
| WS | Walking speed | ms−1 |
The energy balance components, M and W, describe the heat production in the human body. The other components (R, C, E, K, Cres, and Eres) describe the heat consumption. Thermal energy balance is obtained when the heat storage rate is equal to zero (S=0). In addition, when the heat storage rate is positive (S>0) the body temperature increases and there exists a heat gain, hence the body needs to be cooled. On the other hand, when the heat storage rate is negative (S<0) the body temperature decreases and there exists a heat loss, hence the body needs to be heated.
2.1Heat production componentsIn heat production components, the metabolic rate M is defined as the rate at which the body utilizes food to produce energy. The unit of metabolic rate is the Met, where 1 Met=58.15 W m−2. An accepted approximation for the calculation of this component is the equation of Harris–Benedict (Horrocks & Anand, 2000) given by Eq. (2) for males and Eq. (3) for females.
Here, w is the human weight given in kg, h is the human height given in meters, and a is the human age given in years. In addition, standardized values for metabolic rates for different physical activities are given by the norm ISO8996 (ISO-8996, 2004). The other heat production component, the external mechanical work W is defined as the realized body mechanical work that does not add internal heat. For most activities it can be made equal to zero.2.2Heat consumption componentsThere is a difference in temperature between the environment and the surface of the body with cloth isolation participating in the heat interchange. The radiation heat loss from the skin R is given by Eq. (4)
where the mean radiant temperature Tmrt is given in °C and its value can be calculated using Eq. (5). The skin temperature Tsk is also given in °C and can be calculated using Eq. (6).The radioactive heat transfer coefficient hr and the reduction factor for sensible heat exchange due to the clothes Fcl are given by Eqs. (7) and (8), respectively.
Standardized values for the intrinsic insulation of clothing Icl are given by the norm ISO7730 (ISO-7730, 2005). The clothing area factor fcl which is dependent on Icl, and the convective heat transfer coefficient which depends on air velocity va are given by Eqs. (9) and (10), respectively.
The convective heat loss from the skin can be found using Eq. (11) and it is the heat loss due to air flowing by the skin and carrying away body heat.
Here, the ambient temperature Ta comes from real measurements and is given in °C. The dynamic thermal resistance of the clothing system Rtdyn that has units m2°C/W is dependent on the characteristics of the clothes worn and on environmental parameters. Rtdyn is obtained using Eq. (12).In Eq. (12) the static isolation of clothing is given by Rtst=Icl⋅0.155+Ra/fcl. The correction factor to clothing insulation CORR can be calculated using Eq. (13) where the walking speed can be found using WS=0.0052⋅(M−58).
Evaporative heat loss from the skin to the environment is proportional to the difference between the saturated vapor pressure at mean skin temperature Psk and the vapor pressure of the environment air Pa. This evaporative heat loss can be found using the next equation
In Eq. (14) the skin wittedness is found using w=0.001⋅M and the vapor pressure of the environment using Pa=Psat⋅Ta⋅RH, where the saturation vapor pressure at a given temperature Psat is calculated using equation (15) which is known as Antoine's formula. The saturated vapor pressure at mean skin temperature Psk and the dynamic total water vapor resistance of the clothing system Retdyn are calculated using Eqs. (16) and (17), respectively.
In Eq. (17) the dynamic permeability index for the clothing is given by imdyn=imst−6.5⋅CORR+2.6⋅CORR2. The conduction K is usually very small, relative to other terms, and can safety be neglected.
Heat loss from respiration combines the processes of evaporation of moisture from the lungs as well as convection due to displacement of warm air in the lungs by cold air from the outside environment. Both effects from respiration, convective heat loss Cres and evaporative heat loss Eres, can be quantified using Eqs. (18) and (19) respectively.
3Modeling resultsTo compare regenerated bamboo and cotton capacity for warm environment clothing, we used the warm environment characteristics shown in Table 2. These characteristics are found in seaside cities and in many jobs of industrialized countries. Three different rib knitted structures, as shown in Fig. 1, were produced from a 30 tex yarn of three blends of fibers (100% regenerated bamboo, 100% cotton and 50:50% regenerated bamboo: cotton). The 30 tex yarn of the three blends of fibers were spun in a spinning mill using twist multiplier of 3.8 and 15,500 spindle r.p.m. The regenerated bamboo fibers were produced in a wet-spun process in which natural cellulose was used as raw material in a hydrolysis–alkalization process obtaining a soft mass, from which the natural fibers are mechanically combed out and spun into yarn. The three fabric samples were prepared in a 1×1 rib machine. The parameters of the knitted machine are: number of feeders 24, diameter 30in. and machine gauge 18. The hairiness of yarns was measured by Zweigle G566 hairiness tester. For each yarn a cone of 1000m length was tested. The number of hairs longer than 3mm length per 1000m length of yarn was considered for analysis. The thermal conductivities, (W m−1 K−1), defined as the property of a material to conduct heat flow, were measured using an Alambeta instrument. Five readings were taken for each of the knitted fabric and then averages were calculated. Table 3 shows the calculated average values for the three fabric samples. The Alambeta instrument uses two measuring heads between which the test sample is placed. Both measuring heads are equipped with heat flow sensors (thermocouples). The lower measuring heads is adjusted to the ambient temperature by suitable cooling means; the upper, heated measuring head is adjusted to a controlled constant differential temperature. The heat flow sensors act up at the contact faces of both measuring heads. When upper measuring head is lowered on the measuring sample the heat flow at the upper surface and the underside of the test sample can be measured. The fabric thickness can also be measured by the instrument. The thermal resistance, R(m2 K W−1), defined as the property of a material to resist a heat flow, was calculated using Eq. (20) (Chidambaram, Govindan, & Venkatraman, 2012; Majumdar, Mukhopadhyay, & Yadav, 2010)
where h(m) is the garment thickness given in meters. In addition, from the norm ISO8996 (ISO-8996, 2004), we used four standardized values for metabolic rate. The four considered values for metabolic rate and their associated physical activities are: M=9.2 met for heavy construction, M=9 met for gardening, M=6.61 met for medium weight construction and M=4.46 met for light weight construction.Environmental characteristics used in calculations.
| Air temperature | Ta=41°C |
| Vapor pressure of the environment | Pa=143.5kPa |
| Relative Humidity | RH=45% |
| Air velocity | Va=3.63m/s |
| Mean radiant temperature | Tmrt=33.47°C |
| Stefan–Boltzmann constant | σ=5.67×10−8Wm−2K−4 |
| Emissivity of the human body | Ep=0.97 |
| Fraction of skin surface involved in heat exchange by radiation | Ar/ADU=0.77 |
| Static insulation of boundary air layer | Ra=0.11 |
| Static permeability index of the clothing | Imst=0.38 |
| Lewis relation | Lr=16.65°C/kPa |
Fig. 2, for different ambient temperatures, shows the heat storage rate that needs to be eliminated from the human body to reach thermal energy balance. Thermal energy balance that is given when the heat storage rate in the human body is equal to zero, (S=0), will be referred as thermal comfort in this study. The curves of Fig. 2 were obtained by using Eq. (1) and the parameters given in Tables 1–3. As expected, from Fig. 2 it is observed that as the temperature increases, the heat storage rate in the human body increases, and more heat needs to be eliminated from the body to reach thermal comfort. In addition, as the metabolic rate increases, more heat is stored in the body.
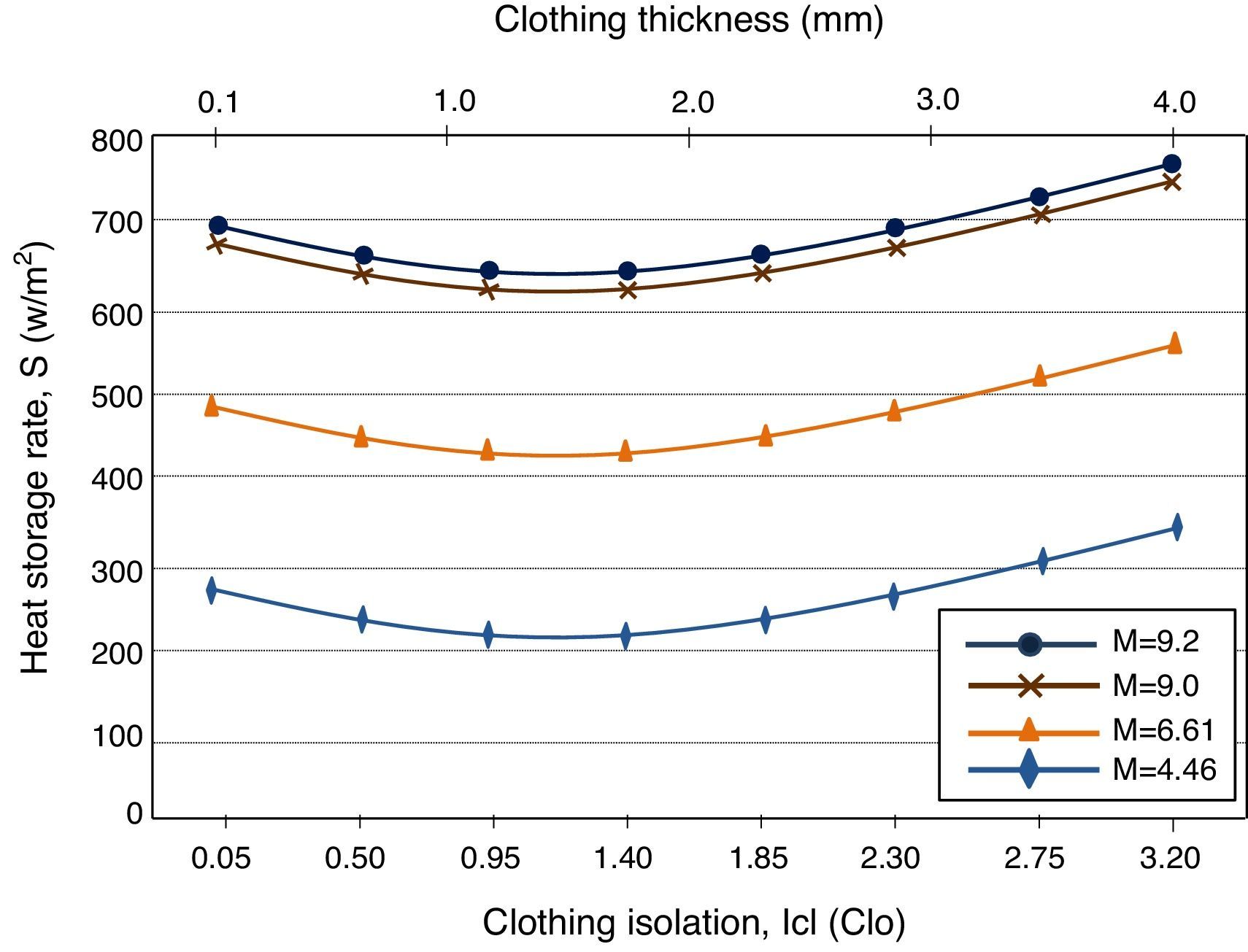
In order to compare the effect in heat storage rate by clothing isolation, the thermal properties of the three fabricated samples were evaluated in the heat balance and exchange models described in Section 2. Fig. 3, for four different metabolic rates, shows the heat storage rate in the human body vs clothing insulation for the rib knitted structure fabricated, using 100% regenerated bamboo. The curves of Fig. 3 were obtained using Eq. (1) and parameters shown in Tables 2 and 3. From Fig. 3, it is observed that for clothing isolation from 0.05 to 1.4clo, which is given by clothing thickness from 0.1 to 1.18mm, as the insulation increases less heat is stored in the human body. On the other hand, for clothing isolation greater than 1.4clo which is given by clothing thickness greater than 1.18mm, as the insulation increases the heat stored in the human body increases. This behavior is understandable because for clothing thickness less than 1.18mm the mechanical and thermal properties of 100% bamboo allows air to circulate freely across the skin, which helps to keep the body cool. On the other hand, increases in clothing thickness until reaching 3clo of isolation represents a thick and heavy garment such as winter wear; hence, for characteristics shown in Table 2, the heat storage rate increases. In addition, it is observed that as the metabolic rate decreases less heat is stored in the body. Hence, less heat needs to be eliminated from the body to reach thermal comfort.
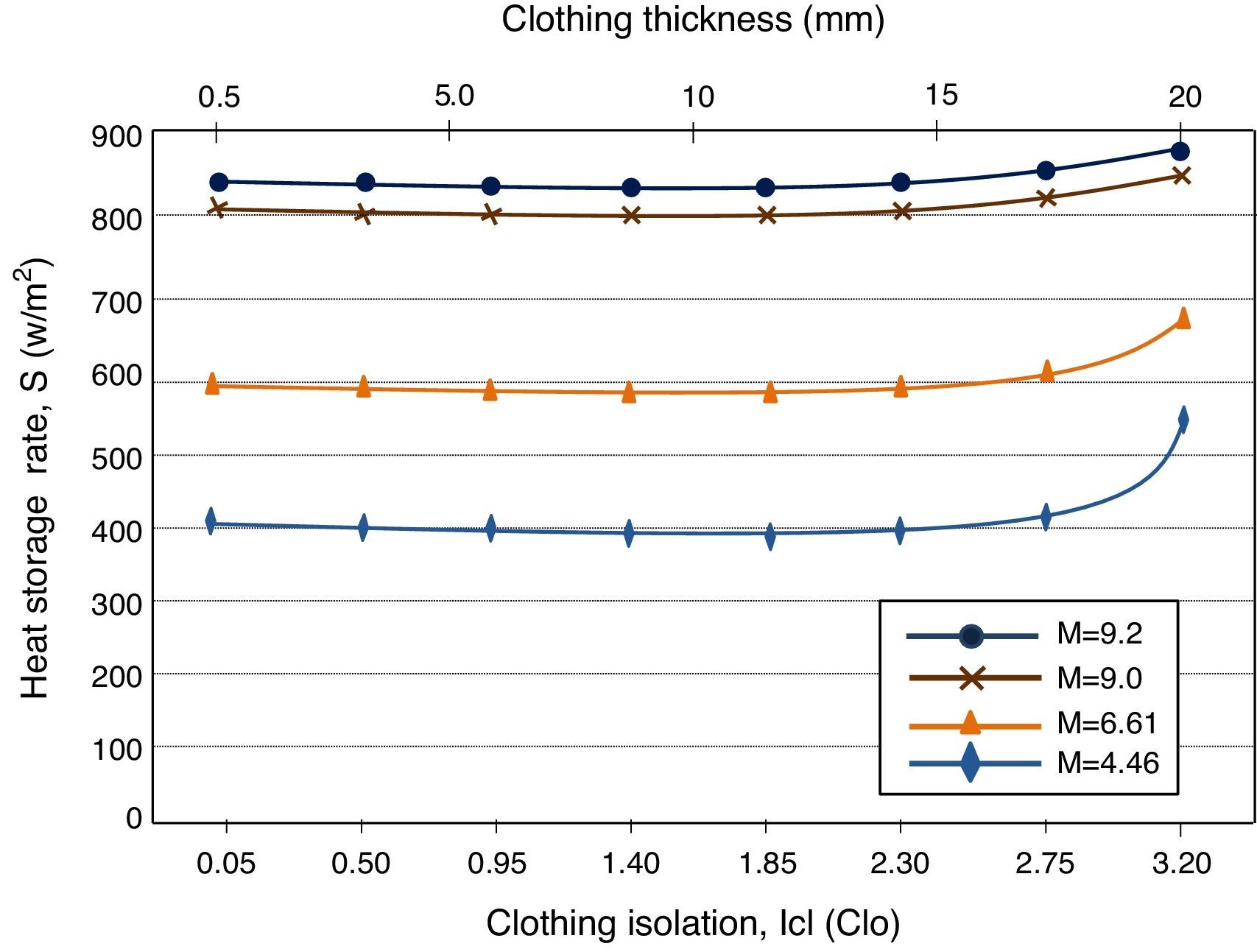
Fig. 4 shows the heat storage rate in the human body vs clothing insulation for the rib knitted structure fabricated using 100% cotton and the considered metabolic rates. In addition, Fig. 4 shows the relation of clothing thickness and clothing isolation. From Fig. 4, it is observed that as the clothing insulation increases from 0.05 to 2.75clo, no significant change on the amount of stored heat in the human body is obtained. However, for clothing isolation greater than 2.75clo the heat storage rate in the human body starts drastically increasing. Similar to 100% bamboo, cotton clothing thickness with isolation close to 3clo represents a thick and heavy garment such as winter wear. In addition, it is also observed that as the metabolic rate decreases due to decrease in physical activity, less stored heat needs to be eliminated from the body.
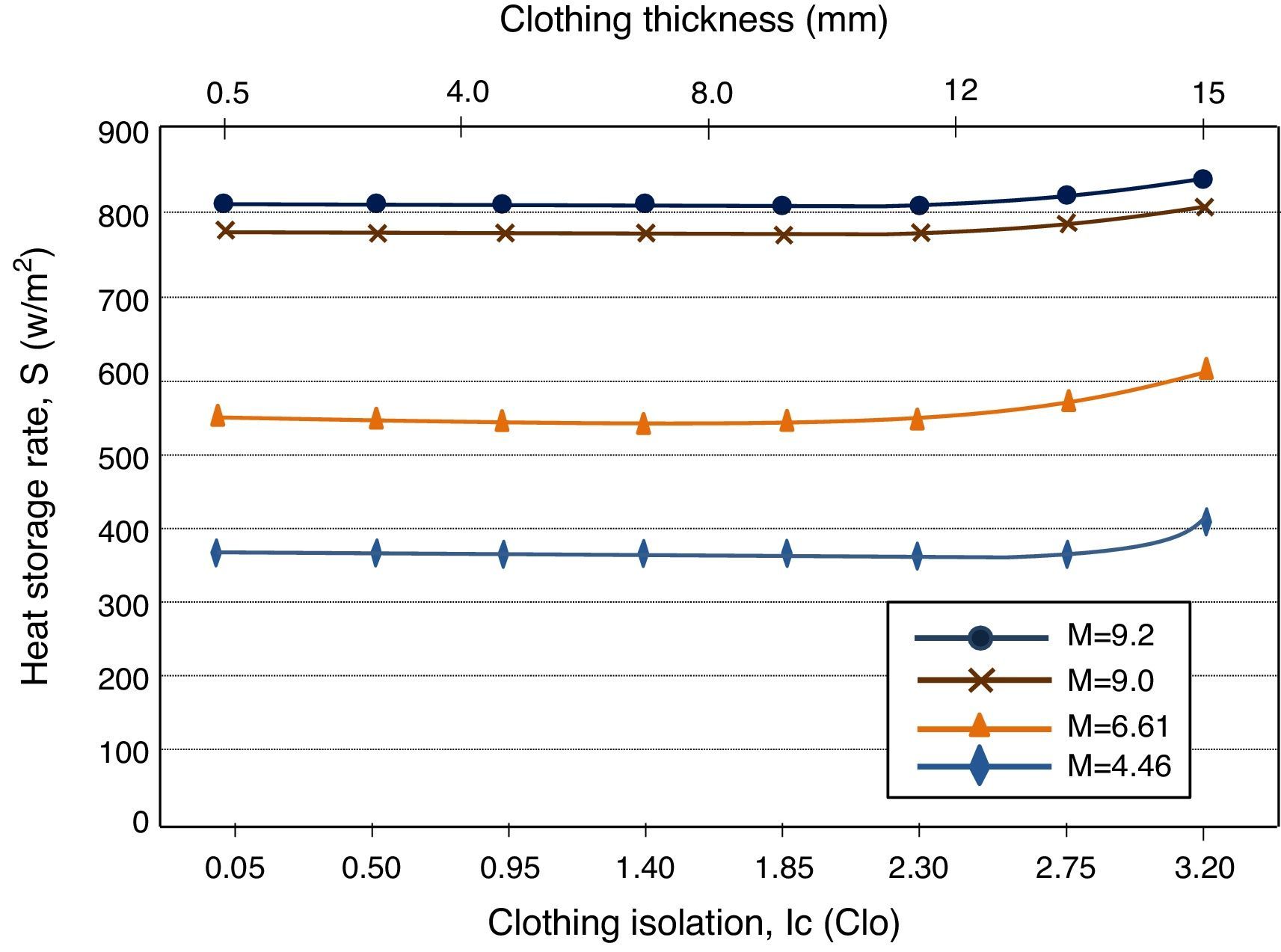
Fig. 5 shows the heat storage rate in the human body vs clothing insulation for the rib knitted structure fabricated using 50:50% regenerated bamboo-cotton. Fig. 5 also shows the relation of clothing thickness and clothing isolation. Similar to 100% cotton (Fig. 4), in Fig. 5 it is observed that as the clothing insulation increases from 0.05 to 2.75clo, no significant change on the amount of stored heat in the human body is obtained. However, for clothing isolation greater than 2.75clo, the heat storage rate in the human body starts drastically increasing. The observed difference between 100% cotton (Fig. 4) and 50:50% regenerated bamboo-cotton (Fig. 5) is that 50:50% regenerated bamboo-cotton can reach the same clothing isolation as 100% cotton with a half of clothing thickness. In addition, it is also observed that as the metabolic rate decreases, less stored heat needs to be eliminated from the body.
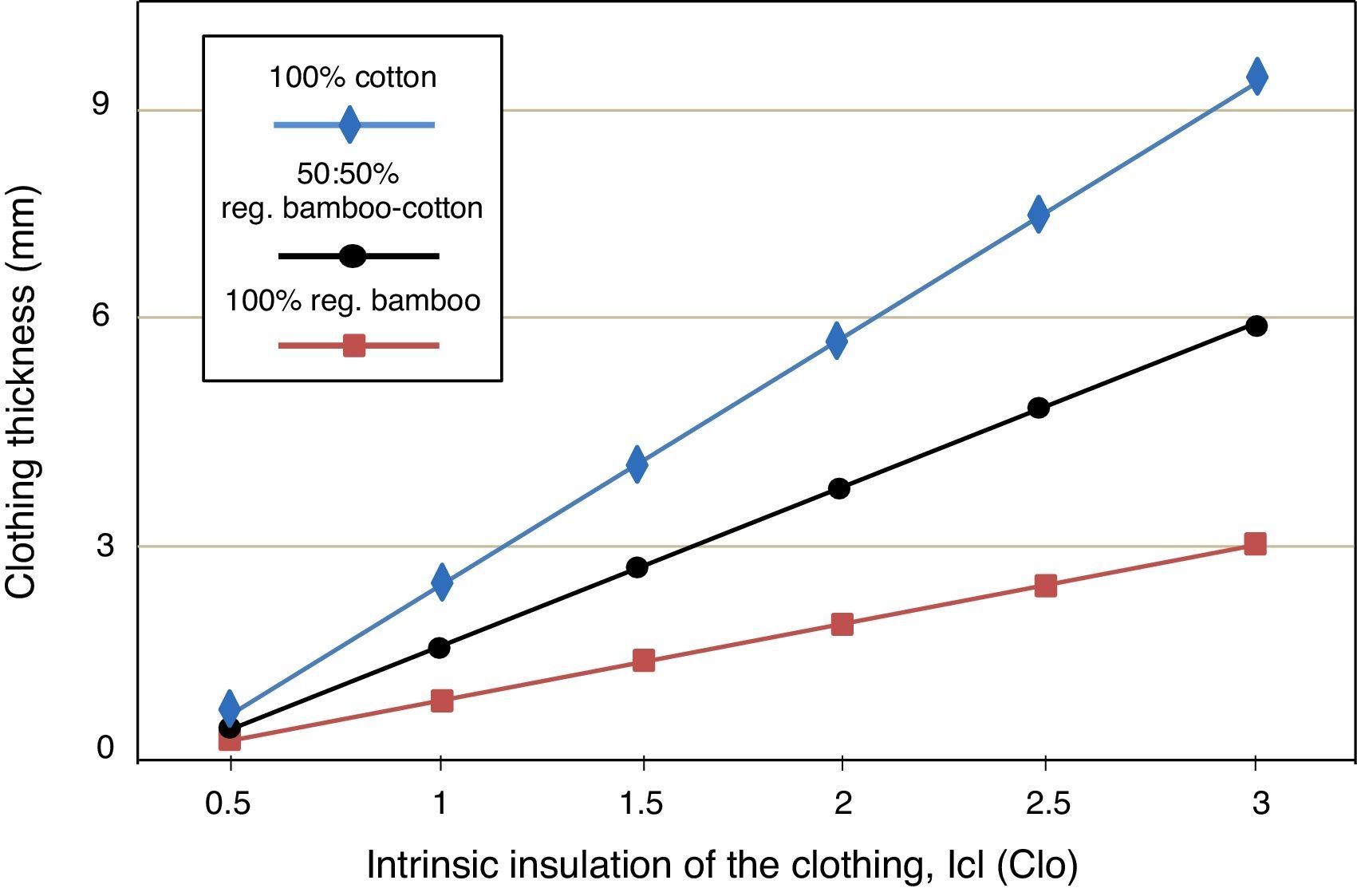
Fig. 6 shows clothing thickness vs intrinsic insulation of the clothing for 100% regenerated bamboo, 100% cotton and 50:50% regenerated bamboo-cotton yarn blends. As expected, from Fig. 6 it is observed that intrinsic insulation of the clothing increases when clothing thickness is increased. It is seen that 100% regenerated bamboo can reach isolation values using smaller clothing thickness than 100% cotton and 50:50% regenerated bamboo: cotton. For example, 3clo of isolation can be given by a 100% regenerated bamboo garment with a thickness of 3mm, while a garment of 100% cotton and 50:50% regenerated bamboo cotton need 5.9mm and 9.6mm of thickness, respectively. Hence, to reach intrinsic insulation of the clothing of 3clo, the garment thickness needed by using 100% regenerated bamboo is more than three times smaller as compared to 100% Cotton, and more than two times smaller as compared to 50:50% regenerated bamboo: cotton.
4Discussions and conclusionsIn this study, thermal properties of a 30 tex yarn from a blends of 100% fiber of regenerated bamboo, 100% fiber of cotton and 50:50% fiber of regenerated bamboo: cotton were used to compare bamboo and cotton performance in warm environment. Four physical activities, characterized by their metabolic rate, were used in the calculations. Theoretical results show that 100% regenerated bamboo has a better isolation performance in hot environment. The heat storage rate in the human body can significantly be reduced by using 100% regenerated bamboo. In addition, the garment thickness can also be significantly reduced by using 100% regenerated bamboo. This means that 3clo of thermal isolation can be given by a garment of 100% regenerated bamboo with a thickness of 3mm, while 5.9mm and 9.6mm of thickness are needed by 50:50% regenerated bamboo: cotton and 100% cotton, respectively. In summary, theoretical analysis, complemented with practical measurement of thermal properties of three different rib knitted structures produced from a 30 tex yarn of three blends of fibers, show that 100% regenerated bamboo can be used to reduce garment thickness and heat storage in warm environment clothing, without compromising comfort. Hence, a comprehensive understanding of theoretical models, will be of great importance to experimentalists, who are potentially interested in obtaining the numerical estimates and correlate the theoretical results with practical measurements.
Conflict of interestThe authors have no conflicts of interest to declare.
Peer Review under the responsibility of Universidad Nacional Autónoma de México.