Information acquisition and assimilation capacities as determinants of technological niche markets

Abstract

We present an equilibrium model where the demand side of the market determines the strategic incentives of firms when considering the introduction of technologically superior products (TSPs) and the subsequent dynamic evolution of the market configuration. Market demand is built on conventional features defining the behavior of decision-makers (DMs), who are required to acquire information sequentially about the characteristics describing the products. Firms may signal the introduction of TSPs, though only sufficiently experimental DMs update their beliefs when selecting a product from a firm. That is, technological habits and inertia condition the incentives of DMs to acquire information and select potential products within a market. In particular, the choices made by the DMs will be determined by their capacity to assimilate signals describing the introduction of TSPs and their attitude towards risk. We identify the conditions required for the emergence of technological niche markets allowing firms that signal the introduction of TSPs to thrive.

Introduction

This study analyzes the importance of different demand structures built on consumers’ information acquisition and assimilation capacities for technology dynamics. Our research is motivated by a major observation made by Malerba (2007), who stated that “... the insertion of demand in analyzing the relationship between industrial dynamics and innovation is still in its infancy”. He then went on to ask for a redefinition of the passive role played by demand in the industrial organization literature Sutton (1998). However, with a few exceptions (Di Caprio and Santos Arteaga, 2014; Tavana et al., 2016b), the literature has generally remained oblivious to this request, even when dealing with demand-related phenomena (Kahraman et al., 2007; Murarka et al., 2019; Shi and Shen, 2019; Wang and Lyu, 2020; Alhawari et al., 2021).

Malerba (2007) emphasized two main demand features as relevant to promoting innovation across industries: the behavior of consumers [endowed with imperfect information regarding novel technological products and habits and inertia towards the products and technologies composing the market] and their absorptive capabilities. We study these qualities in a sequential information acquisition environment that determines the optimal behavior of consumers/decision-makers (DMs) when choosing among distinct types of products comprising multiple characteristics.

The demand side of the market will be built on four conventional features defining the behavior of consumers and their absorptive capabilities.

• (i)

  DMs face an imperfect information environment and must acquire information about the main sets of characteristics defining the products. Information is acquired sequentially, and its total amount is limited to reflect cognitive and pecuniary information processing costs (Bearden & Connolly, 2007; Epstein & Robertson, 2015).

• (ii)

  Firms may signal the introduction of technologically superior products (TSPs). We will assume that only sufficiently experimental [perfect foresight] DMs update their beliefs when retrieving information and selecting products from the firms (van den Ende & Dolfsma, 2005; Harty, 2010; Gomez et al., 2016; Höflinger et al., 2018).

  • •

    Malerba et al. (2003, 2007) defined experimental DMs as those craving the incorporation of novel technologies in current products or searching for entirely new ones in novel demand segments.

  • •

    TSPs are products experiencing improvements in a subset of features defining their main characteristics, increasing the expected utility of perfect-foresight DMs. Credibly signaled improvements may be directly observable or require the purchase of the product to be evaluated. A similar intuition regarding the market introduction of technologically advanced products was put forward by Bender (1989) within a managerial environment.

• (iii)

  Inertia and habits about technologies and products constrain the capacity of DMs to shift across markets (Lin et al., 2015; Si and Chen, 2020; Wang et al., 2021). As stated by Malerba et al. (2003), “customers are very sophisticated and won't buy a new model computer unless it is as good as or better than the old model ones” (pg. 8). Thus, a DM's incentives to shift between product markets should be determined by the potential improvements defined upon the characteristics of the existing products.

• (iv)

  The preferences of DMs, together with their absorptive capabilities, determine their incentives to continue acquiring information within a given market (Eng and Quaia, 2009; Chung et al., 2012; Speier-Pero, 2019). The numerical simulations were performed to illustrate that risk-neutral DMs are more prone to retrieve information across market products than risk-averse ones.

We will illustrate how DMs condition the behavior of firms when proceeding sequentially through the different characteristics of the alternatives and deciding whether to focus on the products from a given firm or evaluate those of a direct competitor.

Intuitively, we will consider two firms offering various products comparable across different sets of characteristics. DMs may observe realizations from the products offered by one of the firms while deciding whether to continue checking the products from this firm or performing comparisons with the products offered by a competing firm. Two main strategic scenarios will be analyzed when formalizing the requirements for the emergence of technological niche markets.

• •

  The emergence of a niche market equilibrium within a Nash pre-commitment setting requires a demand composed of a sufficiently low proportion of perfect foresight DMs, a relatively low signal intensity, and a reasonably large consumer base on the side of the signaling firm.

• •

  Subgame perfection differs considerably, with the signaling firms also requiring a sufficiently low proportion of perfect foresight DMs and issuing signals of relatively low intensity. However, in this case, a reasonably small consumer base is needed for a niche market equilibrium to emerge.

The main differences between both strategic scenarios are substantial and relate directly to the interactions between the types of DMs composing the demand side of the market, the signaling strategies followed by the firms within the supply side, and the relative size of the consumer bases available to evaluate their products.

Information acquisition in online environments

The four features described above are also significant when analyzing the behavior of DMs in online shopping environments. Recent empirical studies based on questionnaires distributed among online consumers across North America and Europe deliver similar findings regarding their purchase intentions, which range from brand loyalty to the influence of third-party reviews. Thus, while firms may expect a proportion of consumers to form a loyal base, there is still ample room for variability and uncertainty in the expected behavior of DMs when facing novel products or substantial modifications to previously existing ones (Dimoka et al., 2012; Al-Samarraie et al., 2017; Lee et al., 2021).

In addition, DMs do not generally perform thorough searches or product comparisons, a feature emphasized by psychologists when analyzing compulsive consumption and regret (Schwartz, 2004; Chen et al., 2009; Tzini and Jain, 2018), and economists when incorporating bounded rationality into their models (Kreye et al., 2012; Lim, 2013). DMs’ intent to perform complex searches indicates their limited information processing and assimilation capacities, constraining the subsequent scope of their decisions.

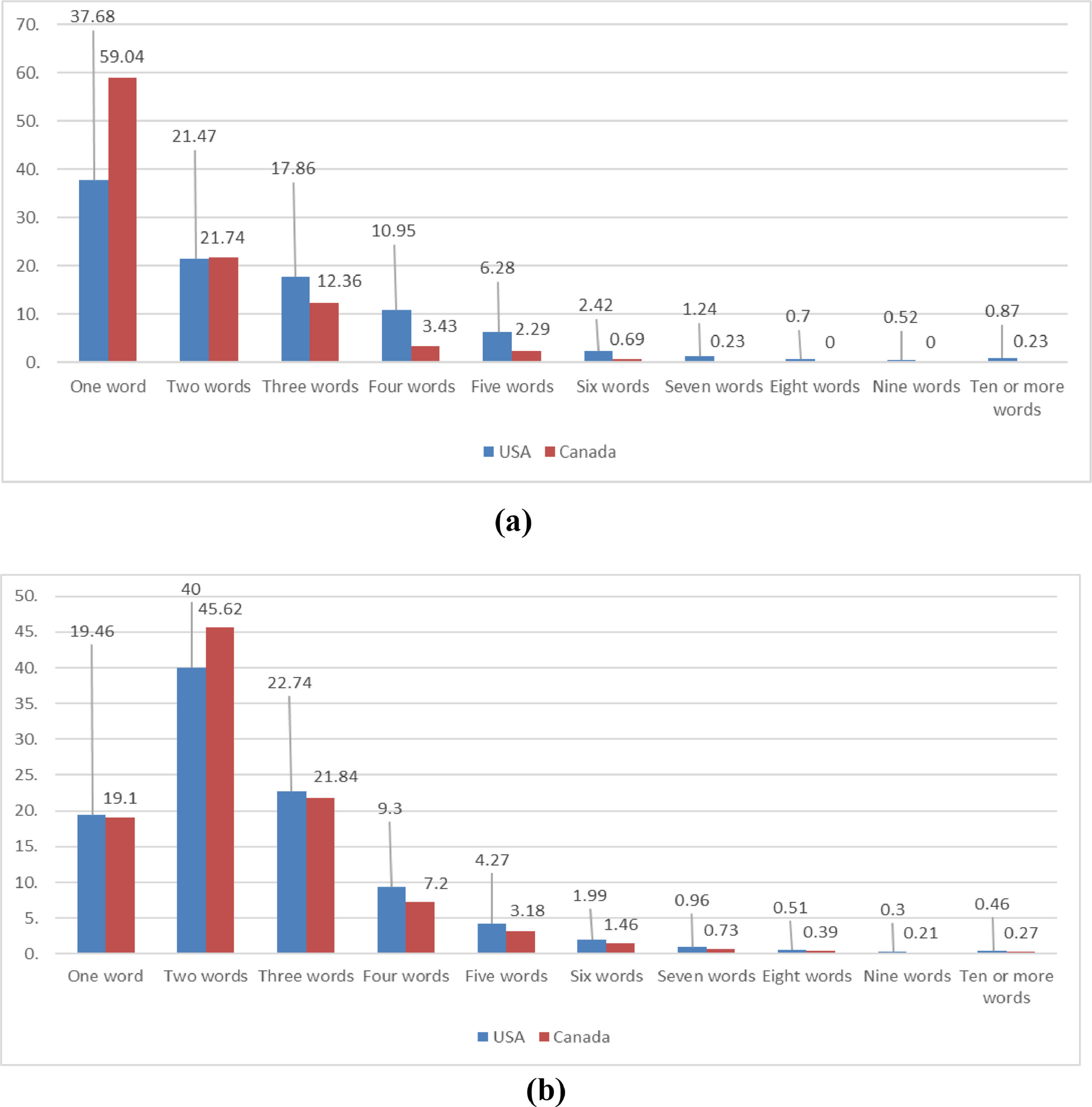
Fig. 1 describes the average number of keywords used per online search query in the United States and Canada in two different periods, 2017 and 2020. Even though most searches consisted of two words in 2020 – improving upon the dominance of one-word queries in 2017 – the three-word limit accounting for over 80% of total searches prevails in 2020. Because DMs click on two links per search query (Jansen et al., 1998; Baeza-Yates, 2005), this feature highlights the limited information acquisition process followed by consumers.

Fig. 1.

The average number of search terms for online search queries in the United States and Canada.

Thus, DMs may face considerable constraints when noticing the enhanced qualities of products or observing – or believing – the signals issued by a firm (Oghazi et al., 2021). In this regard, when incorporating into the analysis the choice volatility triggered by the anonymous reviews available online (Bae and Lee, 2011; Zimmer & Henry, 2017), firms cannot guarantee that their customer base will remain intact as they venture into the introduction of the novel or enhanced technological products.

The inherent subjectivity of the DMs’ decision processes can also be observed through their answers to different questionnaires describing their consumption habits. For instance, when asking United States consumers

• •

  Whose recommendations are they most likely to trust when choosing between different products online (and allowing for multiple answers)? Most consumers selected their friends, acquaintances, family members (61%), and other customers (53%), while only 39% selected independent review websites.¹

• •

  Which stage of the digital purchase process makes them happiest? Only 24% selected researching their options, namely, comparing items across sites, while 21% declared selecting products from their website of choice. On the other hand, over 50% chose to see their purchases confirmed and go through checkout.²

Thus, DMs are divided in their intent to acquire information and display tendencies to implement basic heuristic mechanisms or perform thorough searches. The volatility of their decisions can also be observed in their payment incentives. When asked what drives them to pay for a higher-priced option when facing similar products online, the answers range from a brand trust (23%) and sufficient product information (9%) to better reviews (35%) and reduced shipping costs (11%).³

We conclude by focusing on the behavior of younger consumer groups. When millennial internet users in the United States were asked the likelihood of purchasing products or services using chatbots, only 14% declared not being interested.⁴ A similar tendency could be observed among European consumers when asked about their main concerns regarding online purchases. The capacity to inspect the product and retrieve information directly increases in relevance with the consumer group's age sampled.⁵ The importance of directly verifiable information describing the main characteristics of products decreases among younger DMs.

Contribution

Given the previous features describing the type of DMs that compose the demand side of the market, we define a game-theoretical framework where duopolistic firms must decide whether or not to signal the existence of a TSP. We will analyze two different types of signaling equilibria determined by the information transmission framework assumed. A Nash equilibrium setting will be applied to oblige each firm to commit to its original signaling strategy. On the other hand, a subgame perfect equilibrium (SPE) will be defined to allow firms to observe the signaling strategy of their rivals and behave accordingly.

The resulting set of equilibria emphasizes the importance that perfect foresight on the side of DMs and the existence of monopolistic rents have for the formation of niche markets that allow firms to signal and introduce TSPs. Moreover, according to the classical findings of Ireland & Stoneman (1986), we will illustrate how the presence of perfect foresight DMs expecting swift technological developments hinders the adoption of the technology available within the market when compared to myopic ones.

The current framework improves upon both the game-theoretical models, mostly centering on the diffusion of technology (Beath et al., 1995; Chen et al., 2018; Zhang & Sun, 2020), and the traditional decision-theoretical ones where demand is based on stopping criteria that validate or dismiss the introduction of new technology (Jensen, 1982; McCardle, 1985). At a formal level, the lack of interaction between the strategic diffusion of innovations by firms and the subsequent emergence of demand by DMs represents a drawback that the equilibrium model developed in the current paper helps to solve (Kim Wang and Seidle, 2017; Li et al., 2020; Ren et al., 2021; Tiberius et al., 2021).

We describe the main results intuitively and highlight the requirements that need to be satisfied for the corresponding equilibria to exist. Technical analyses illustrating these requirements as a function of the set of parameters conditioning firms’ behavior through the pre-commitment and subgame perfection frameworks have been relegated to the Appendix sections.

Demand

We build on the models of Di Caprio et al. (2014, 2016) to introduce a demand evaluation and decision environment defined via two expected utilities. These functions are non-recursive and require DMs to redefine their behavior at each stage of the information retrieval process, preventing the implementation of standard dynamic programming techniques.

Product attributes: formalization and technical assumptions

Denote the set of available products as G. Assume that products are given by pairs of characteristics (x1,x2), whose values are defined within the Cartesian product of two nonempty sets, X1×X2.

Identifying and evaluating product attributes is a complex task even when the characteristics are directly observable (Lu et al., 2008; Arruda-Filho and Lennon, 2011). Given the coexistence of immediately observable (search) and time-consuming (experience) attributes within a product Nelson (1970), we will assume that both of them can be found in the sets of characteristics composing each Xi, i=1,2. These temporal requirements are reflected in the information acquisition capacity of DMs, who focus on either fully observing a product, which may or may not be purchased, or partially observing two products and deciding whether or not to purchase the best one.

Two important remarks follow. First, we must highlight that if we were to introduce the convolution of several random variables by assuming that multiple features are included within both X1 and X2, and normalizing the corresponding realizations, the main retrieval setting and analyses would remain qualitatively unchanged. An intuitively manageable analytical framework would require limiting the analysis to three features per characteristic, allowing for products to be defined by six main features categorized in two sets of characteristics of the same cardinality. Second, the order defining the sets of characteristics corresponds to the relative importance allocated by the DM. We will elaborate further on this second point in the next section.

A preference relation≻̲̲ on Xi, i=1,2, is a binary relation on Xi satisfying reflexivity, completeness, and transitivity. A function ui:Xi→R is a utility function representing≻̲̲onXi if

X1 and X2 will be identified with a closed real subinterval of [0,+∞), that is, for i=1,2:

with 0Wilde, 1980).

We assume Xi to be endowed with the standard Euclidean topology and the preference relation defined by the DM on Xi to be the standard linear order <. Therefore, ui can be assumed strictly increasing and continuous, implying that the function u(x1,x2)=u1(x1)+u2(x2), defined ∀(x1,x2)∈X1×X2, induces an additive preference on X1×X2 and is also increasing Wakker (1989).

Xi will also be interpreted as a continuous random variable and μi:Xi→[0,1] defined as its associated density function. Given Zi⊆Xi, μi(Zi) represents the subjective probability of the event “the i-th characteristic of a randomly observed product from G is described by a value xi∈Zi”. The support of μi is the set ξ(μi)=def{xi∈Xi:μi(xi)≠0}. The probability functions μi,i=1,2, will be considered independent, though the decision framework is designed to allow for correlations between both sets of characteristics.

Finally, the certainty equivalent defined by μi and ui will be used by the DM as the main point of reference for both sets of characteristics. For i=1,2, the certainty equivalent of μi and ui is defined as the value cei=ui−1(Ei), with Ei standing for the expected value of ui. The value cei exists and is unique since ui is assumed to be continuous and strictly increasing.

Expected utility functions from acquiring information

G consists of two potentially different types of products about which the DM can collect information. Let J and K denote the two types of products. Since we are assuming that the DM evaluates two sets of attributes, after the initial characteristic of J is observed, he must determine whether to continue acquiring information on J or to shift his attention to a different type of product K. This decision is based on the realization x1∈X1 retrieved from J. We follow Tavana et al. (2016a, 2016c) to introduce the next functions, whose values describe the utilities expected to be obtained from the information acquired on the first characteristic.

Let F:Xi→R and H:X1→R be given by:

such that ∀x1∈X1:

F(x1) [resp., H(x1)] describes the gain in expected utility relative to E1+E2 in the case when, after evaluating the initial characteristic x1 of J, the DM decides to observe the second characteristic of J [resp., the first characteristic of K].

Consider a standard evaluation interval framework defined on the characteristics of the products, such as the ones that can be found on online recommender websites such as Tripadvisor, Trivago, and Amazon. The relative importance assigned to the different characteristics can be incorporated into the analysis by assuming that one of the probability distributions provides a higher expected value. Thus, within a common upper limit reference setting, we increase the lower limit of the interval defining the domain so as to increase the expected value that the DM assigns to the potential realizations from the first characteristic. That is, given two probability distributions Γ(x1) and ξ(x2), and a nondecreasing function u: R → R, the domain of the relatively more important characteristic will be shrunk so that

where E1>E2, with x1M=x2M. Intuitively, given the relatively higher importance assigned to the first characteristic, we assume that the DM constraints the search to products that score higher than a minimum reference value while discarding the others.

The Appendix A section illustrates the behavior of the functions F(x1) and H(x1) within the evaluation intervals [x1m,x1M] and [x2m,x2M], such that x1M=x2M and E1>E2 as x1m>x2m, and discusses the natural conditions required for the existence of a crossing point between both functions located below the certainty equivalent value of the first characteristic, i.e., x1

This latter result constitutes an important contribution to the current paper. Consider two DMs, a standard one basing his information retrieval behavior on the certainty equivalent value assigned to the set of potential realizations of the characteristics and a forward-looking one formalized through Eqs. (3) and (4). Appendix A illustrates how forward-looking risk-neutral or risk-averse DMs are more willing to continue evaluating the initially observed alternatives than standard ones.

Signals and learning

Firms can issue credible signals regarding improvements implemented on X2, modifying the probability density and expected utility assigned to the corresponding set of products (Brockhoff & Rao, 1993). Note that signals are defined on characteristics that are not initially observable, requiring the consumption of the product to be verified. In this regard, the formal analyses performed throughout the paper can be expanded to analyze the effects of signaling improvements on either X1 or both characteristics simultaneously (Tavana et al., 2016b).

Improvements are not assumed to be completely radical but enhancements of the secondary characteristics defining the products. The main results described are independent of this assumption. They can also be obtained when considering enhancements of the first set of characteristics, as the analysis performed in Appendix B is emphasized.

We will assume that the DM does not have any initial information on the distribution of characteristics and, as a result, assigns uniform densities to X1 and X2, reflecting the highest information entropy faced by the DM. That is, for i=1,2, the DM defines an initial density function μi as μi(xi)=1xiM−xim, ∀xi∈Xi=[xim,xiM].

Suppose that, after checking the first characteristic, a positive signal is received. Then, the DM must update the density function μ2 initially defined on X2.

We will use the symbol θ to denote the fact that positive signals are received and write θ=1 to indicate that one positive signal is received. Receiving a positive signal, θ=1, modifies the initial density on X2, μ2(x2)=1x2M−x2m for x2∈[x2m,x2M], leading to the following conditional density function:

That is, half the probability mass from the lower half of the density is shifted to the upper half. The signal leads the DM to update his initial beliefs, μ2(x2), by implementing Bayes’ rule as follows

Equations (B1) to (B4) within the Appendix B section generalize the conditional density and subsequent Bayesian updating functions presented in Eqs. (10) and (11) so as to account for any potential probability mass shift defined on X2.

Tavana et al. (2014) illustrate that F(x1|θ=1)≥F(x1) and H(x1|θ=1)≥H(x1) if μ2(x2|θ=1) first-order stochastically dominates μ2(x2).

The framework of analysis just described allows us to categorize the DMs that comprise the market demand in two main groups.

Definition 2.1

We say that “signaling an improved characteristic is technologically neutral” whenever E(2|θ=1)=E2, while “signaling an improved characteristic is not a technologically neutral strategy” whenever E(2|θ=1)>E2.

We define as myopic those DMs whose E2 remains unchanged after observing a positive signal – from either credible online recommender systems or independent product reviewers –. As a result, the corresponding functions F(x1) and H(x1) remain unaffected whenever TSPs are introduced in the market. If DMs have perfect foresight, then observing a credible signal leads to an update of their expectations, such that E(2|θ=1)>E2, resulting in an upper shift of their functions F(x1) and H(x1).

Technological improvement

Two decision processes will condition the technological transition between coexisting markets. Each process determines the potential improvements that signaling firms can guarantee upon the initial characteristic observed by the DMs when deciding whether or not to shift markets.

Irreversible decision processes

Shifting to the signaled market constitutes an irreversible decision (ID) for the DM, who, after observing the initial characteristic of a product in the unsignaled market, must start over in the signaled one. As a result, his final choice, if any, is determined by the set of products composing the signaled market. The resulting H(x1|id) function provides the expected value from observing a product better than the certainty equivalent to one defined in the signaled market.

In the above equation and henceforth, the notation id refers to the ID setting.

If signaling is not a technologically neutral strategy, then ∂H(x1)∂E2>0, which implies H(x1|id)>H(x1), ∀x1≤ce1. We will illustrate numerically how this effect is not sufficient to guarantee a shift of the DM to the signaled market. The loss in utility derived from the irreversibility assumption eliminates the transition incentives that follow from a higher value of E2 for large x1 realizations.

Guaranteed improvement processes

In this setting, the signaling firm guarantees the DM a product whose first characteristic value is not inferior to the one from the product assessed within the unsignaled market, that is, x(1|θ=1)≥x1.If DMs trust the commitment of the firm, the function H(x1|gi) would be defined as follows:

In the above equation and henceforth, the notation gi refers to the GI setting.

Given E(2|θ=1)>E2, the value of H(x1|gi) is higher than the corresponding value of H(x1) defined in the unsignaled market ∀x1∈X1.

Numerical simulations

We simulate numerically both the ID and guaranteed improvement (GI) scenarios to study the behavior of the crossing points, i.e., incentive thresholds, defined by the corresponding functions F and H.

Through this section, X1=[5,10] and X2=[0,10] represent the domains on which both sets of characteristics are defined. These specific domains have been chosen to illustrate numerically the main results derived from the current decision theoretical framework. The results build on the natural conditions described in Appendix A, which are required to ensure the existence of a unique threshold value lower than ce1 within the unsignaled reference setting.

In particular, consider the framework of analysis defined by the evaluation intervals [x1m,x1M] and [x2m,x2M] with

• •

  identical upper limits x1M=x2M;

• •

  identical utilities defined on both characteristic spaces;

• •

  a uniform distribution assigned to each interval to reflect the uncertainty faced by DMs;

• •

  x1m>x2m, implying that the first set of characteristics delivers a higher expected utility than the second one;

• •

  x1m≤ce2, limiting the importance assigned to the first characteristic relative to the second one.

Two main constraints are imposed within the above evaluation framework to guarantee the existence of a unique crossing point located below ce1 when dealing with risk-neutral DMs

• •

  P−(x1M)≠∅: DMs must be willing to observe the second characteristic of a product; that is, the first one cannot guarantee a sufficiently high utility on its own relative to a random choice.

• •

  x2m=0: the lower limit value assigned to the second characteristic equals zero.

These requirements represent scenarios where the main characteristics of a product are evaluated within common reference intervals, and DMs focus on those alternatives whose preferred characteristics are distributed above a subjectively determined x1m value. Risk-averse DMs require additional formal constraints, restricting even the type of utility function assumed and its concavity.

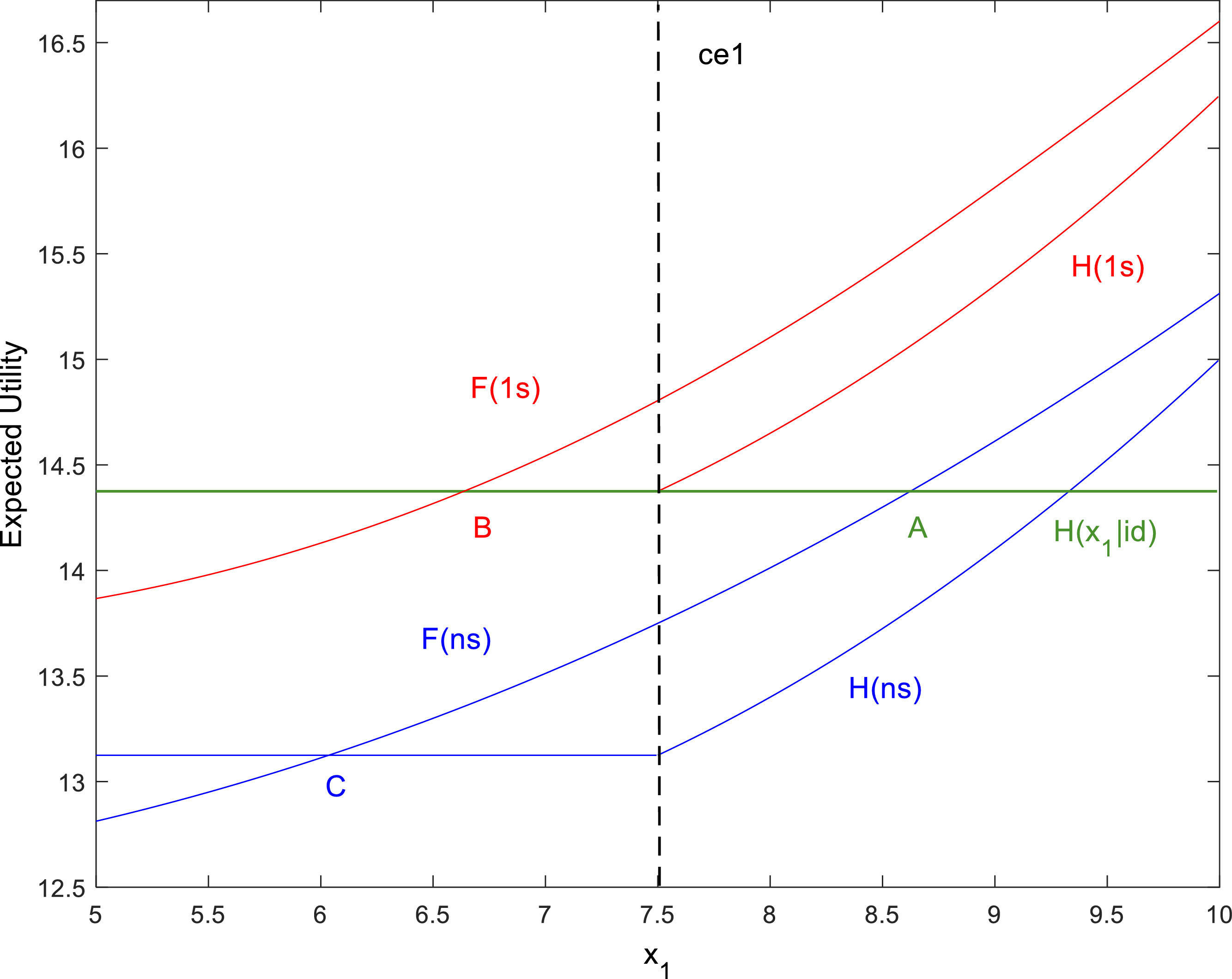
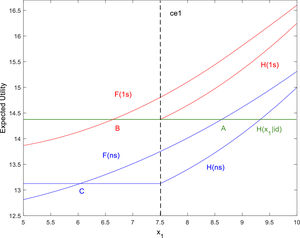
Fig. 2 describes the “1s” case where one signal indicating the existence of TSPs is issued by one of the firms within a risk-neutral framework, i.e., u1(x1)=x1, u2(x2)=x2. Points C and B represent the unsignaled and one signal threshold values, respectively. The definition of the Nash pre-commitment equilibria is based on these two reference points. We have used the notation F(ns) and H(ns) to emphasize the fact that the functions F(x1) and H(x1) refer to the unsignaled setting.

Fig. 2.

Optimal threshold values for risk-neutral DMs.

At the same time, when studying SPE, perfect foresight, DMs will be allowed to shift markets after retrieving information from the firms located in any of them. Similar to the Nash pre-commitment scenario, the cutoff value B defines a GI relative to C, while A accounts for the ID process. In this latter case, the observation forgone when shifting between markets leads H(x1|id) to a lower expected utility than H(x1|gi) for all x1>ce1 values.

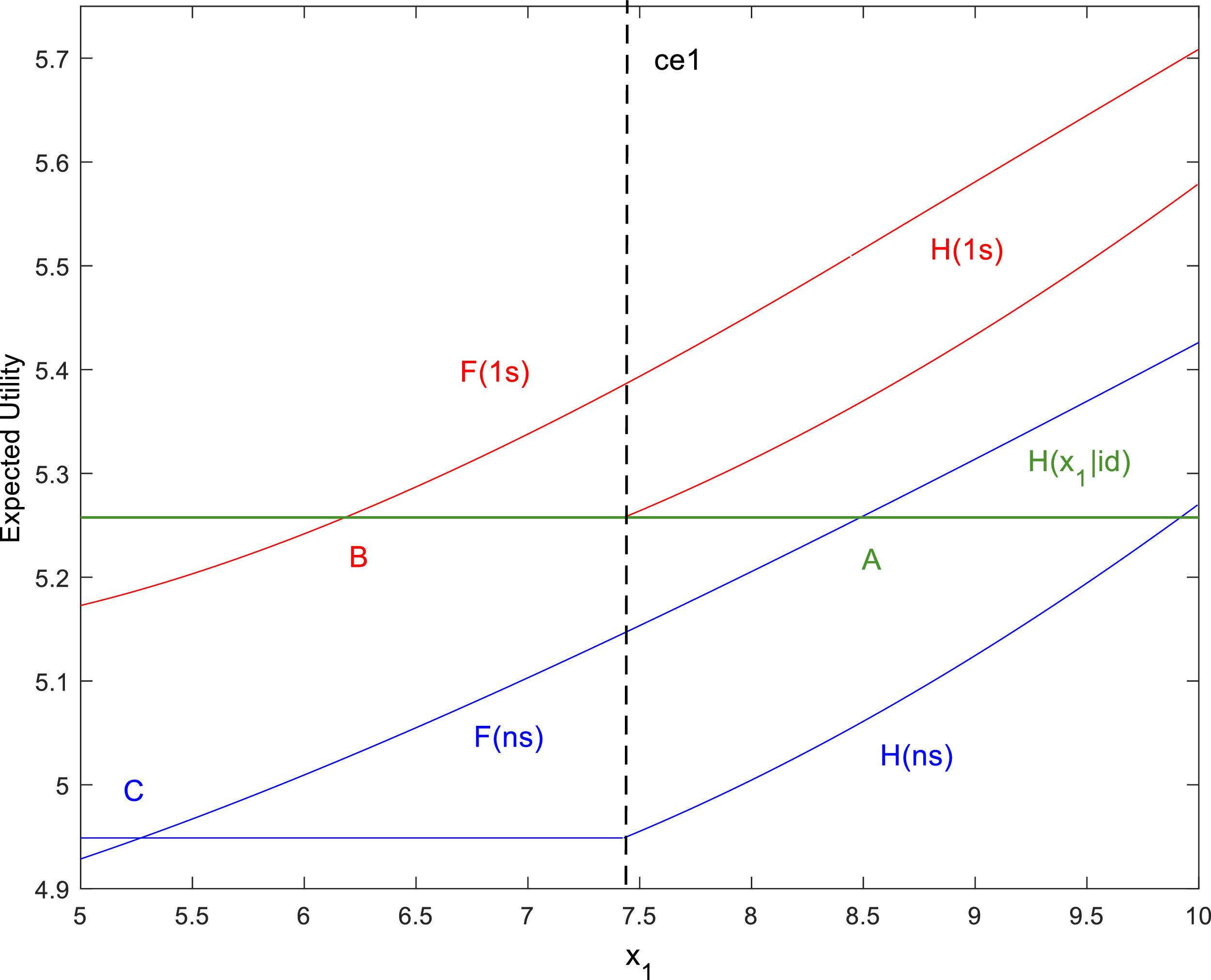
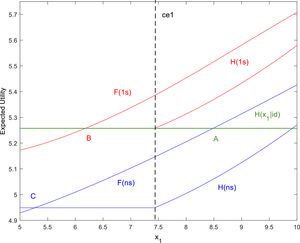
Fig. 3 shows the threshold points relative to the same environment as Fig. 2 when DMs are risk-averse, i.e., u1(x1)=x1, u2(x2)=x2. Note how risk-averse perfect foresight DMs require lower realizations of x1 than risk-neutral ones to continue acquiring information on the initial products. Moreover, in both the risk-neutral and risk-averse cases, GI does not imply faster adoption of the TSP, as can be inferred from the rightward shift of the corresponding threshold values, i.e., from point C to B.

Fig. 3.

Optimal threshold values for risk-averse DMs.

Supply

Through this section, we demonstrate that the strategic decision to signal the existence of a TSP is conditioned by the type of DMs composing the demand side of the market.

Technological transition

Consider a duopolistic environment with identical firms. Each firm must decide between either introducing a TSP and issuing the corresponding signal, S, or remaining in the unsignaled market, NS. The time sequence defining the strategic environment proceeds as follows. There are three time periods, t=0,1,2. Signals can only be issued at t=0 or t=1. The DM acquires information during periods t=1 and t=2. Thus, the strategies of the firms aim at modifying the information acquisition process of DMs at t=0 and t=1.

In order to avoid biases in the final choice made by the DM, we will assume that if the product(s) observed after completing the information acquisition process does(do) not provide him with an expected utility higher than E1+E2, then the DM rejects making a random choice (Christensen, 1997; Dedehayir et al., 2014; Di Caprio & Santos Arteaga, 2014).

As in Rahman & Loulou (2001), we will analyze two different strategic equilibria determined by a specific information transmission framework. A Nash pre-commitment equilibrium is considered whenever a firm cannot monitor the rival decisions and must therefore commit to the signaling strategy followed at t=0. Subgame perfection implies that a firm is allowed to monitor the interim signals issued by its rivals before deciding whether or not to issue a signal. As a result, firms should anticipate the signaling decision of the rival and incorporate it when defining their signaling strategies at t=0.

Nash pre-commitment equilibrium

Consider the threshold values described in Figures 2 and 3. For ε=B,C, denote by r(ε) and Revε the revenue and expected revenue per firm when both of them compete in a duopoly within the ε setting. Similarly, RevB|s and RevC|ns are the expected revenues of the unilaterally signaling and not signaling firm, respectively.

The signaling strategies that can be implemented by the firms within a pre-commitment environment give rise to a technological transition matrix (TTM) whose rows and columns represent the strategies of the firm and its rival, respectively. This matrix is defined as follows:

	S	NS
S	RevB, RevB	RevB|s, RevC|ns
NS	RevC|ns, RevB|s	RevC, RevC

Intuitively speaking, when both firms signal the introduction of a technological improvement, they must compete for DMs in the corresponding market. This yields an expected revenue, RevB, strictly smaller than the one derived by the signaling firm, RevB|s, in a monopolistic setting. Moreover, given the fact that perfect foresight DMs shift to the signaled market, the not signaling firm, which receives RevC|ns, would suffer a loss with respect to the revenue obtained in the not signaling equilibrium, RevC. Despite the decrease in competition induced, signaling unilaterally leads perfect foresight DMs to require a higher continuation value. Thus, the relative strength of these effects on the revenues expected to be obtained determines the signaling incentives of firms.

We refer to φ(f) as the probability that firms assign to DMs gathering information from any of their products within a duopolistic competing scenario. The corresponding probability assigned to the rival firm equals φ(fr)=1−φ(f). To simplify notations, we will use ε to denote both the value of the threshold and its projection on X1.

Given the threshold values described in the numerical simulations, the expected revenue of a firm when competing with a rival at ε, with ε=B,C, is given by the following expression:

where

• •

  γ(ε)=(x1M−ε)(x1M−x1m), with ε=A,B,C, is the probability that the DM continues acquiring information on the initial product observed;

• •

  rπ(ε)=σ(P+(x1))r, is the revenue expected by the firm when x1>ε, with ε=A,B,C;

• •

  σ(P+(x1))=∫x1x1M(x2M−x2(x1)x2M−x2m)dx1, represents the probability of the DM observing u2(x2)>E1+E2−u1(x1).

• •

  r is the revenue obtained by the firm from the sale of its product.

Remarks

. (1) Regarding the definition of σ(P+(x1)), the exact expression, accounting for the whole set of potential probability mass shifts defined on X2, is developed through Equations (B1) to (B11) within the Appendix B section.

(2) The case where ε=A is not considered in this section since it is not relevant within the current pre-commitment scenario. The analysis of this case requires further assumptions and explanations and will be examined in detail within the SPE setting. ■

Eq. (14) can be rewritten as

When describing the expected revenue derived from a unilateral signaling framework the presence of both DMs, perfect foresight and myopic within the set of potential consumers, must be explicitly incorporated into the analysis (Liu et al., 2017). As a consequence, the unilaterally signaling firm would receive an expected revenue given by:

where α stands for the percentage of myopic DMs composing the market demand. This expression follows from the fact that perfect foresight DMs search only within the signaled market. When a unique firm issues signals, it competes in terms of the threshold C for the α percentage of myopic DMs with the firm that does not signal. At the same time, the signaling firm serves alone the (1−α) proportion of perfect foresight DMs in terms of the threshold B.

Note that preserving a consistent equilibrium framework requires that the uniform density function defined on X2, which, at the same time, determines the value of σ(P+(x1)), remains unchanged when dealing with myopic DMs. Their inability to assimilate signals prevents myopic DMs from recognizing the superiority of the products introduced by the unilaterally signaling firm. This assumption could be modified, allowing myopic DMs to ascertain the superior quality of the products the signaling firm offers when retrieving information from the corresponding market. Clearly, this modification would foster the signaling incentives of firms. However, it also implies that firms would prefer to deal with myopic DMs when signaling since they would face a threshold value of C – increasing the acceptance probability of their products relative to the B value defined by perfect foresight DMs –. Thus, preserving consistency implies that myopic DMs either do not observe or remain unaffected by the features on which technological improvements are introduced when retrieving information.

On the other hand, when both firms issue signals and a signaling duopoly is defined, we will assume that both types of DMs acknowledge this fact and update the distribution of the second characteristic accordingly when retrieving information. Once all firms introduce a technological improvement within the market, the technology becomes standardized, and all DMs behave according to the updated distribution of characteristics. The model is designed to emphasize the risks the signaling firms face when issuing unilaterally, together with the resulting monopolistic gains. We could assume that both types of DMs prevail within the duopolistic signaling market, driving the expected revenues of the firms accordingly. However, this assumption would increase the complexity of the analysis considerably without adding any relevant insights.

Remark

. We will relax the assumption that perfect foresight DMs search only within the signaled market when studying the SPE version of the game. We will allow for consumption habits and inertia among perfect foresight DMs. Thus, even though perfect foresight DMs recognize the superiority of the products being signaled, they could still acquire information relative to the unsignaled market because of prevailing inertia and consumption habits. It must be emphasized that this assumption does not affect the qualitative results derived from the pre-commitment scenario. ■

The expected revenue received by the firm that remains in the unsignaled market equals

Clearly, RevB|s>RevB when α=0 and RevC|ns

with γ′(ε)<0. Exact comparisons between RevB and RevC are presented throughout the different scenarios analyzed within the Appendix B section, while an analysis of their behavior in an environment with multiple signals can be found in Tavana et al. (2016b).

Myopic decision-makers

Suppose that the whole set of DMs is myopic. As a result, the expected revenues derived by the firms do not depend on their signaling strategies. Indeed, by definition, all entries of the corresponding TTM would be given by RevC and random events would drive the transitions between technologies, resulting in identical Nash and SPE.

Furthermore, whenever frictions arise from signaling the introduction of a TSP (i.e., whenever quality decreases as the product is introduced), with a consequent decrease in the expected utility derived from the product (Malerba et al., 2003), any firm issuing signals would not be able to generate a niche market on which to thrive, leading to its eventual disappearance.

Theorem 3.1

Suppose that the whole set of DMs is myopic and frictions arise in the signaled market. Then, the subgame perfect and Nash's pre-commitment equilibria imply that technological transition does not take place.

Proof

. Consider the TTM that follows from a myopic scenario. If the frictions triggered lead to a signaling payoff lower than RevC, then both firms coordinate on NS, which constitutes a strictly dominant strategy. ■

Decision-makers with perfect foresight

Suppose that the whole set of DMs is endowed with perfect foresight, that is, α=0 and RevC|ns=0. In this case, the relative values of RevC and RevB|s determine the set of Nash pre-commitment equilibria.

Assume first that RevB|s>RevC. In this case, signaling at t=0 defines the only Nash pre-commitment equilibrium. The Nash pre-commitment scenario is equivalent to a classical prisoner's dilemma whenever RevB

Theorem 3.2

Suppose that the market is composed by perfect foresight DMs and RevB|s>RevC. Then, signaling constitutes an optimal strategy independently of the relative values taken by RevB and RevC.

Appendix B.1 illustrates the results described in Theorem 3.2. In particular, the incentives fostering technological transition weaken as myopic DMs are introduced in the market and firms become endowed with relatively higher φ(f) values. That is, the payoff incentives obtained from monopolizing the signaled market lose relative importance as firms expect DMs to evaluate their products with higher probability, increasing their capacity to compete in a duopolistic scenario.

Assume now that RevB|s=RevC. Analogously to the previous case, signaling becomes a weakly dominant strategy.

Finally, assume that RevB|s

Proposition 3.3

Suppose that all DMs have perfect foresight and RevB|s

Corollary 3.4

Suppose that all DMs have perfect foresight and RevB|s

where φ*(S) defines the probability of a firm signaling the introduction of a TSP, with φ*(NS)=1−φ*(S).

Note that ∂φ*(S)∂RevB|s<0 and ∂φ*(S)∂RevC>0. Thus, an increase in RevB|s or a decrease in RevC would expand the set of probability values for which signaling constitutes an equilibrium strategy.

A detailed analysis of the requisites guaranteeing that RevB|s

Perfect foresight and myopic decision-makers

Consider now the case where the market is composed of both types of DMs. Perfect foresight consumers, as well as a percentage of the myopic ones, defined via RevB|s for α∈(0,1), would select a product from the signaling firm. The expected revenue received by the not signaling firm equals αRevC>0. As a result, the set of Nash pre-commitment equilibria is determined by the relative values of RevC, RevB and RevB|s.

In this regard, note that RevB|s is obtained considering only the (1−α) proportion of perfect foresight DMs shifting their information acquisition processes to the signaled market. Thus, if operating within the signaled market would constitute an advantage for the signaling firm, i.e. RevB>RevC, the signaling incentives will be lower than in the perfect foresight scenario.

Note that, besides the Nash pre-commitment equilibria arising within the perfect foresight scenario, the proposed approach fosters the emergence of niche markets where the existence of TSPs is signaled by one firm.

Proposition 3.5

Suppose that the market is composed of both types of DMs – myopic and perfect foresight –, RevB|s>RevC and RevB

A sufficient condition for the equilibria of Proposition 3.5. to exist is that RevB|s>RevC>RevC|ns>RevB. This chain of inequalities holds true if we assume both the value of α to be sufficiently close to zero and the payoff difference between RevB|s and RevB through (1−φ(f)) to be large enough. These two assumptions require the market to be composed by a relatively low percentage of myopic DMs and the monopolistic rents received from signaling unilaterally to be sufficiently large compared to those obtained from competing within the signaled market. The relative intensity of (1−φ(f)) is indeed what guarantees that RevB|s is larger than RevC and RevB.

It should be emphasized that a small value of α is required for the exploitation of the monopolistic revenues relative to the duopolistic ones, RevB|s>RevB. At the same time, a relatively high value of α is required for RevC|ns>RevB. Appendix B.2.1 analyzes in detail the requisites that must be satisfied for the existence of the equilibrium described in Proposition 3.5. In addition to a relatively large proportion of myopic DMs, sufficiently low signal intensities and large consumer bases are also required to guarantee the existence of this equilibrium.

Note that, as in the perfect foresight setting, a relatively large value of RevB|s would lead both firms to try to signal first, due to the monopolistic rents delivering RevB|s>RevC|ns.

Subgame perfection

Consider the TTMs potentially faced by firms at t=1, just before DMs start acquiring information.

Guaranteed Improvement
	S	NS
S	RevB, RevB	RevB|s, RevC|ns
NS	RevC|ns, RevB|s	RevC, RevC

Irreversible Decision
	S	NS
S	RevB, RevB	RevA−C|s, RevC−A|ns
NS	RevC−A|ns, RevA−C|s	RevC, RevC

The GI setting bears a considerable resemblance to the Nash pre-commitment scenario. In fact, the set of GI equilibria are going to be defined by the relative values of RevB, RevC, RevB|s, and the α proportion of myopic DMs. However, subgame perfection enhances the capacity of firms to create niche markets at t=1 relative to the pre-commitment case.

Consider now the ID framework. The expected revenue received by the not signaling firm equals

To be consistent, we have required the observation acquired from the unsignaled market to be higher than A in order for the DM to purchase the subsequent product. Even if ce1 is taken as a reference point instead of A, we have that RevC−A|ns

Similarly, the expected revenue received by the signaling firm equals

Note that perfect foresight DMs shift to the signaled market provided that x1

Perfect foresight [α=0] decision-makers

Consider the expected revenues described in the previous section. Three potential TTMs can be defined at t=0.

If RevC>RevB|s and RevC>RevA−C|s, then a NS strategy from a firm at t=0 leads the rival not to signal at t=1. Similarly, α=0 leads to RevC|ns=0 and RevC−A|ns

	S	NS
S	RevB, RevB	-
NS	-	RevC, RevC