Edited by: Brij B. Gupta, Kwok Tai Chui
More infoDo cities with higher administrative hierarchies always enjoy higher intercity connections? Based on an innovation of twin cities (Chengdu-Chongqing) in China, this paper uses machine learning methods (linear model, support vector machines, neural network and random forest) to predict the innovation effect of a new administrative hierarchy on intercity connections. The key findings indicate the following. (1) The innovation effect of administrative hierarchy on intercity connections is asymmetric in twin cities. (2) For the city with a later-higher administrative hierarchy (LHC, Chongqing in this case), the innovation effect of the administrative hierarchy on intercity connections is initially negative (approximately 10 years for Chongqing) and then becomes positive. (3) For the city with an initially higher administrative hierarchy (IHC, Chengdu in this case), the innovation effect is continually positive. (4) The underlying mechanism of the reverse trend for LHC is due to more financial independence, investment in transportation infrastructure and less transaction cost of market access associated with the new administrative hierarchy, which have an innovative effect after a time lag (approximately 10 years for Chongqing). (5) However, IHC enjoys a continual net-positive innovation effect on the intercity connection due to its first-mover advantage on administrative hierarchy and the diffusion effect of LHC. These findings shed light on practical implications that for intercity connections, the primary concern and dominant strategy of innovation is cooperation with the trickle-down rather than the siphon effect. We should tailor different intercity connection strategies for the separate cities in a twin-city pair. This can provide new contributions to the innovation of intercity connections only if the twin cities see one another politically as “siblings” rather than as a “divorced couple”.
The urban administrative hierarchy, as described in central place theory, is linked to the provision of services and political resources (Chen & Partridge, 2013; Shi et al., 2020). The urban administrative hierarchy is also closely correlated with population size, urban function, financial independence, infrastructure investment and innovation (Fan et al., 2021). A study of the spatial structure of the urban administrative hierarchy identifies a down-filtering innovative phenomenon from more connected to less connected cities (Zhong & Wei, 2018). To take advantage of already high levels of innovation and connection, consulting firms and other knowledge-based industries prefer to cluster in highly connected cities (Campbell & Carayannis, 2016). Higher city ranks tend to be correlated with a stronger externalization and innovation of informational services (Zhong & Wei, 2018).
The urban administrative hierarchy may have a strong positive influence on intercity connections. When a city is higher in the urban hierarchy, it can attract more population mobility. When a city has a higher administrative position, it shows better social and economic innovation (Camagni et al., 2015). Intercity connections are influenced by many factors, including government policies, business services and geographical location (Lin et al., 2019; Taques et al., 2021; Kekezi & Klaesson, 2020). Provincial capitals are usually the dominant city in their respective provinces, and they can be better connected because of resources, business, accessibility, and geographical location (Liu & Zhang, 2018; Ferreira & Teixeira, 2019).
In addition to geographical factors, political factors, such as the urban administrative hierarchy, may influence intercity connections (H. Ma et al., 2018). For example, as the administrative centers of their provinces, provincial capitals are given more political resources and innovative opportunities to invest in transportation infrastructure (Albalate et al., 2012).
Some comparative analyses discuss the comprehensive understanding of administrative hierarchy and intercity cooperation (Wang, Du & Huang, 2020; Huang & Zong, 2022; H. Ma & Xu, 2022). Against the backdrop of the urban regionalization of urban jurisdictions, the two dominant typologies of intercity cooperation are divided by de facto (common) geopolitical aspects, diversifying mechanisms and concrete economic policy frameworks. In particular, administrative hierarchies help create internal market-driven cooperation and strong government commitment (Zhang, Shen & Gao, 2021).
However, there is also a paradox phenomenon in which, with the transition of the urban administrative hierarchy, intercity connections may become increasingly acute for small cities located in larger cities with higher administrative ranks (Chen et al., 2018; Boutillier et al., 2020). Such an unbalanced administrative hierarchy can generate new transaction costs for mutual market access (B. Yang et al., 2020). That is, cities with a higher administrative hierarchy are inclined to cause a siphon effect (polarization effect) on their neighboring cities with a lower administrative hierarchy and as a result, worsen intercity connections (Brakman et al., 2012). The restructuring and reform of the urban administrative hierarchy could induce the reallocation of governmental administrative power and innovation effects for cities with a higher administrative hierarchy.
Regarding the methodology of the existing works, most of them use an urban network analysis to measure connections based on intercity flow data. This is consistent with what seems to be an ongoing paradigm shift toward network thinking in urban system analysis (X. Liu, Derudder & Wu, 2016). In the conventional approach, urban systems are characterized based on the characteristics of cities in and by themselves (Neal, 2011). However, the emerging network paradigm suggests that the urban administrative hierarchy is increasingly associated with cities’ positions within intercity networks of people, information and goods (Y. Liu, Derudder & Wu, 2016). In light of this overall development, recent studies have increasingly emphasized and employed flow data to assess intercity connections.
Regarding the limitations of the existing works, the current analytical framework equally weighs different urban administrative hierarchies of intercity connections. Moreover, these analyses focus on the connection of tangible resources rather than the innovation and knowledge of intangible assets. Although innovation has intuitive meaning, the interpretation of the innovation effect of intercity connections is less straightforward and requires further research (H. Ma & Xu, 2022). As a result, the typology of administrative hierarchy has centered on transaction costs rather than on the identification of innovation effects among different cities (Ferraris, Santoro & Pellicelli, 2020).
Accordingly, it is unknown the extent to which and how administrative hierarchy influences the innovation effect of intercity connections. Due to the endogeneity of interaction and reflection problems (Mallipeddi et al., 2021), it is difficult to clearly distinguish the net effects of administrative hierarchy on intercity connections. Particularly if the administrative hierarchy of cities undergoes fundamental changes due to governmental intervention, could cities with higher administrative hierarchies still dominate in terms of innovation? A next step could therefore involve a causal inference of the relationship between administrative hierarchy and the innovation effect of intercity connections.
Taking China as an example, the association between cities’ political status, especially their administrative rank, and their economic growth rates tends to be self-evident (Li et al., 2015). However, the reshuffling of urban political power in Chinese cities is often treated as an elusive variable (Lin et al., 2015). Relatively few studies have been conducted to quantify the exact relationship between the urban administrative rank and the magnitude of intercity connections to better understand rapid urban innovation in China.
Once territorially integrated and presently separated twin cities can be used to answer such questions about the urban administrative rank and intercity connections. Twin cities were first considered complementary economic complexes (Marquez-Ballesteros et al., 2019). Since then, they have been widely used in the scholarly literature (mainly in geography and economics) to denote one type of urban agglomeration and sustainability innovation performance (Shen, 2014; Rauter et al., 2019). Twin cities are a special case of two cities that were founded in close geographic proximity that then grew together over time by losing most of their mutual buffer zone (Lei, Flacke & Schwarz, 2021).
We define twin cities by distinguishing them from other municipal units. Twin cities are adjacent geographically; they have a common history from a time when they were each a single entity. Despite the history of shared frontiers, at the present stage, twin cities are administratively divergent, institutionally independent but economically linked. The significant role of social, demographic, and economic inclusion in coordinating intercity innovation networks is a precondition for jointly carrying out the intercity connection of twin cities (Mervyn et al., 2014).
Our paper fills academic gaps and makes several contributions. First, we use a historical event of twin cities in China as an innovation to restructure the urban administrative hierarchy. Second, we apply machine learning to overcome the endogeneity of intercity connections due to changes in administrative hierarchies. Third, we choose Chengdu and Chongqing, twin cities, as our example to observe the intertemporal continual innovation and gradual adjustment of their intercity connection over 30 years.
Intercity connections have important linkages with innovation and knowledge management. On the one hand, innovation in a city is not only determined by local innovation activity but also facilitated when the city is deeply embedded in intercity innovation networks (Yao, Li & Li, 2020). This systematic view of cities and innovation suggests that the research on cities and innovation needs to go beyond regional interactions in independent innovation centers to explore extra-regional interactions in interdependent systems of cities (Cao, Derudder & Peng, 2018). On the other hand, intercity connections and networks support less resilient cities by sharing knowledge, expertise, best practices, and resources and by providing guidance and advice (Pribadi et al., 2021). There seems to be a lack of research that links innovation to intercity connections and knowledge management platforms.
Our results show that the innovation effect of the administrative hierarchy on intercity connections is asymmetric for twin cities. We split the twin cities into one city with a later-higher administrative hierarchy (LHC) and the other city with an initially higher administrative hierarchy (IHC). For LHC, the negative innovation effect of the administrative hierarchy predominates in the first few years; then, the positive innovation effect of the administrative hierarchy overwhelms the negative effect. However, for IHC, the net innovation effect of the administrative hierarchy on intercity connections is always positive, although frequent fluctuations exist.
Accordingly, the research contributions of this paper creatively build a theoretical framework to study the innovation effect of administrative hierarchy on intercity connections. Then, by using twin cities as the research objective, it uses the new setting of administrative hierarchy as the natural experiment and takes machine learning methods as the causal inference to predict and test the trend of the net innovation effect for the twin cities. Through the comparison of IHC and LHC, the underlying mechanism of the divergent trends for twin cities due to tangible resource agglomeration and intangible knowledge innovation is found.
In this paper, section 1 is the introduction, and section 2 discusses the theoretical hypothesis. Section 3 explains the methodology, including the data, variables, and model. Section 4 provides the empirical results, and section 5 contains the discussion and conclusion.
Theoretical hypothesisIn urban political power, cities with higher political status can enjoy a series of innovative priorities in resource allocation (Hong & Lee, 2018). They tend to have faster economic and social development, and their innovation in a region gradually increases over time. First, in terms of communication with central governments, cities with higher administrative hierarchies have more direct communication channels with central governments (Y. Liu et al., 2012), which generates innovation asymmetry between twin cities with different administrative statuses. Second, in terms of transportation infrastructure investment, cities with higher administrative hierarchies have greater autonomy in cost approval, which can reduce the innovation risks faced by enterprises (Campisi et al., 2021). Third, cities with higher administrative hierarchies often enjoy more financial independence (Cartier, 2016).
In twin cities, innovative decentralization is hierarchical and unequal (Li et al., 2015). Higher administrative ranks relate to a stronger policy-making ability and greater administrative territory for land conversion, which is also expressed by the amount of autonomy of their land innovation (Wang & Yeh, 2020). Furthermore, communities with better innovative rankings are more likely to receive federal government investment (Chen & Partridge, 2013).
Intercity connections refer to the reconfiguration, combination, integration, and coordination of two geographically adjacent cities in terms of population mobility, transportation infrastructure, industrial distribution, cultural exchange, economic development, policy interaction and innovation (X. Yang et al., 2020; Mao et al., 2020; B. Wang et al., 2020). The contradictory relation of the administrative hierarchy and intercity connection represents two different hypotheses for twin cities: competition or cooperation (Lundén, 2018).
On the one hand, the underlying innovation mechanism of the cooperation hypothesis is the trickle-down effect (or diffusion effect). In the urban generation discourse of the new city, large-scale investments in transportation infrastructure are supposed to have trickle-down effects on neighboring areas. This reflects the positive spillover effect of capital and human resource innovation, which has an intracity origin and then spreads to achieve a better intercity connection.
Beyond a general belief of the trickle-down effect is that if personnel and resources are attracted to an area, this will automatically create intercity mobility and innovation between twin cities. The trickle-down effect would build on and put into praxis the emphasis on the need for innovative regeneration to solve the intercity connection (Bauman, 2013). Therefore, the positive gains from transportation investment and innovative spillover due to the setting of another city may be beneficial to the intercity connection of twin cities despite the potential barrier of administrative hierarchy.
On the other hand, the underlying innovation mechanism of the competition hypothesis is the siphon effect (or polarization effect) of twin cities (P. Zhang et al., 2020). This is due to the synergetic imbalance of twin cities: IHC accelerates the innovation of resources by economic agglomeration, while LHC performs worse due to the new administrative barrier to the unified market, which aggravates the imbalance of resource mobility and innovation on both sides of the administrative hierarchy of twin cities.
Accordingly, the siphon effect of administrative hierarchy on intercity connections refers to the fact that IHC, with a dominant institutional and administrative advantage in the first stage, can attract more resource innovation than LHC. The reason is that IHC has a more mature infrastructure, better public services, a longer historical endowment, and a more favorable geographical location for attracting mobility and innovation (He et al., 2019).
Under the siphon effect, IHC continuously obtains resources, which boosts the mobility of capital and the population. Finally, the twin cities form a close network structure. At this stage, the division of innovation between the twin cities differs, but each provides indispensable functions that together form a dynamic and innovative metropolitan area (Zhang et al., 2019). This duality shows that the influence of the siphon effect of twin cities is complex, and it is not easy to judge whether it is good.
Based on these theories, this paper holds that twin cities face different trickle-down effects and siphon effects due to their various administrative hierarchies. This evolution trend may cause the interaction of tangible resource agglomeration and intangible knowledge innovation for the twin cities, which include market access to the counterpart, transportation infrastructure, financial independence and the first-mover advantage. In this way, we can link the background theories to practical hypotheses.
This paper assumes that the twin cities are not affected by all neighboring cities other than one another. The function of intercity connections is thought to be linear and correspond to a normal distribution. We assume that there is knowledge spillover due to the innovation of resource mobility between the twin cities. The administrative hierarchy can only be changed by governments.
Under these assumptions, to illustrate the underlying innovation mechanism of administrative hierarchy on intercity connection more clearly, we set the following function:
Connection is intercity connection, AH is administrative hierarchy,T is the time period, and Marketaccess is market access. Infrastructure is transportation infrastructure investment, Independence is financial independence, and Firstmoveris the first mover advantage. Thus, all five variables are functions of AH and T.On the one hand, for the LHC, the siphon effect of AH initially has a net-negative innovation effect on Marketaccess due to the new setting of institutional barriers and transaction costs, which means that Marketaccess(AH)<0. Additionally, as a newborn city, Firstmover(AH)=0; therefore, in the first time period, Connection(AH,T)<0 if T is small.
However, due to the greater fiscal autonomy, higher administrative level, and political independence of the LHC compared with its previous situation, which means that Independence(AH)>0, it has a stronger motivation to innovate in the intercity transportation infrastructure and achieve resource agglomeration, which means that Infrastructure(AH)>0.
The infrastructure construction and resource mobility of the LHC need time to finish and offset the negative effect, which means that the derivatives areMarketaccess′(T)〈0;Infrastructure′(T)〉0and eventually the comprehensive function Connection(AH,T)>0, if T is large enough. That is, for the LHC,
Inequality (2) means that for the LHC, the marginal effect of higher administrative hierarchy on intercity connection is not always beneficial: it is a curse in the short run but a blessing over time. Due to the sunk cost of time and knowledge, the innovation effect caused by financial independence and infrastructure connection will finally prevail over more transaction costs caused by the border effect.
Accordingly, we propose hypothesis 1:
H1: The net innovation effect of the administrative hierarchy on the intercity connection of the LHC in twin cities is initially negative and then becomes positive.
On the other hand, the IHC has a “first-mover advantage” due to its initially higher rank: Firstmover(AH)>0. The trickle-down innovation effect of the administrative hierarchy will take advantage of the intercity connection. Especially due to its earlier administrative advantage and better institutional endowment, the IHC will automatically encourage mobility and social learning to formalize a complementary division of innovation (Bursztyn et al., 2014).
In this way, although a market barrier still exists, that is, Marketaccess(AH,T)<0, it is difficult for the IHC to enjoy more financial independence after restructuring, that is, Independence(AH,T)≈0. The infrastructure investment of the LHC has a positive diffusion effect on the IHC compared with a single core city, that isInfrastructure(AH,T)>0. Therefore, Connection(AH,T)>0 for anyT, that is, for the IHC,
The inequality (3) tells another story. For the IHC, the marginal effect of administrative hierarchy on intercity connection is always positive. The first-mover advantage and related mature infrastructure can continually formulate the innovation effect caused by the trickle-down effect of tangible and intangible resources, which can always compensate for the new transaction cost caused by the new border effect.
Accordingly, we propose hypothesis 2:
H2: The net innovation effect of the administrative hierarchy on the intercity connection of the IHC in twin cities is continually positive.
Generally, a comparison of the net innovation effect of the administrative hierarchy on the intercity connection between LHC and IHC is shown below in Table 1.
Comparison of the Key Features between LHC and IHC.
Source: Drawn by the author.
Some cities have a greater administrative level than others, according to the Chinese hierarchical system (Wang & Loo, 2019). Beijing, Shanghai, Tianjin, and Chongqing are all municipalities (Zhixiashi) at the province level, according to this administrative system (Chan, 2010). They report directly to the central administration and hold the highest rank in the city hierarchy. Subprovincial cities are the second-highest level of urban administration. Although they are still governed by the provincial government, they have a higher administrative level than other prefecture-level cities (Chan, 2010). Chengdu, in Sichuan Province, is one of China's 15 subprovincial cities.
We chose Chongqing and Chengdu in China as our data sample of twin cities. Chongqing was the second capital of China in World War II. However, in 1954, it was incorporated into Sichuan Province and became a prefecture-level city under the jurisdiction of Sichuan Province, which means that its administrative hierarchy has been lower than that of its counterpart Chengdu since then. Chengdu, as the capital and a subprovincial city of Sichuan Province, is 308.41 km away from Chongqing. Chengdu and Chongqing share the same culture, customs, dialect, and cuisine (McDougall, 2021).
Sichuan's population surpassed 100 million by 1996, and the province had 221 county-level administrative entities (Liu, 2012). The central government considered disaggregating Sichuan Province due to the high administrative expense of so many administrative entities and the enormous population. Many migrants were relocated because of the construction of the Three Gorges Dam. Changing the administrative hierarchy was one way to address the enormous migratory movements. Chongqing serves as a transportation hub for southwestern China and the upper and middle sections of the Yangtze River since it is the largest metropolis in these areas (Notteboom, 2012; Bao, Li & Lizieri, 2019).
Chongqing was therefore detached from Sichuan Province and designated as a municipality by the Chinese central government in 1997 (higher administrative hierarchy than Chengdu). The old Chongqing, Wanxian (later renamed Wanzhou), Fuling, and Qianjiang regions are governed by the Chongqing municipality, which has 43 districts, cities, and counties that span an area of 82,402.95 km2 and a population of 30.02 million people.
The secession of Chongqing is treated as a quasi-natural experiment in administrative reorganization and innovation. We contend that the administrative hierarchy reversal between Chongqing and Chengdu as an LHC and IHC was an external innovation shift. The partition of Chongqing was debated before 1997, but the specific reorganization was not made public until March 14, 1997, when the central government authorized the partition. Although Chongqing was divided from Sichuan Province, Chengdu remains one of China's major subprovincial cities, but it is not as large as Chongqing. As a result, Chongqing can be considered the LHC, and Chengdu can be considered the IHC.
The Chongqing and Chengdu data are from the Chongqing Statistical Yearbook and Chengdu Statistical Yearbook, respectively. Due to data access restrictions and inconsistent statistical calibers, we chose the time span from 1988 to 2018.
VariablesThe key outcome variable of this paper is the intercity connection between Chongqing and Chengdu. The measurement of the intercity connection is based on Newton's gravity model based on economic radiation ability and the receiving ability of economic radiation. When the radiation force of the economic space is stronger, the connection is better between the economy and the transportation infrastructure, and the intercity connection is closer. Zipf first applied Newton's gravity model to the study of urban spatial interactions: the number, sizes, and locations of communities theoretically depend on minimizing the work of transporting mass over distance. Then, the Newton gravity model was also applied to other urban affairs, such as transportation connections (Ducruet et al., 2020), migration (X.N. Zhang et al., 2020), and hierarchical patterns (Han et al., 2018).
The gravity model is the most common example of spatial interaction modeling (Sen & Smith, 2012). It was the first spatial interaction model, and it uses different variables to predict or estimate the volume of spatial interaction between or among places, whether they are cities, counties, or regions (Wegener, 2021). It can also be used to analyze the spatial interactions of the core city with the periphery (Surya et al., 2020).
The standard gravity model is written as follows:
where Iij is the estimate of the volume of spatial interaction between place of origin i and place of destination j, k is a constant, Dij is the distance between i and j, b is the exponent of distance, and Pi and Pj represent the population sizes of the places of origin and destination, respectively. The values of k and b vary depending on the specific data set.Based on the spatial connection and mutual innovation between Chengdu and Chongqing, this paper adjusts the standard gravity model and constructs an economic spatial gravity model to measure the intercity connection of Chengdu and Chongqing as follows.
where Connectionijt is the intercity connection of Chongqing and Chengdu for year t, and Mit and Mjt are the mobility indices, including the population and transportation of Chongqing and Chengdu. In this paper, we use population as the main index and highway mileage as a robustness check. Git and Gjt are the total GDPs of Chongqing and Chengdu, respectively. Dijt is the straight-line distance between Chongqing and Chengdu. Due to the adjustment of the administrative divisions of Chongqing since 1997, the geographic center of Chongqing also needs to be adjusted.There are many data in the statistical yearbooks of Chongqing and Chengdu, which affect the connection and innovation of cities. We collected all of these data and defined them as variables that affect urban connections to a certain extent. In the data preprocessing, we first selected variables with missing values greater than 30% (from 1988 to 2018) and deleted them. The variables with missing values of less than 30% were interpolated by their median.
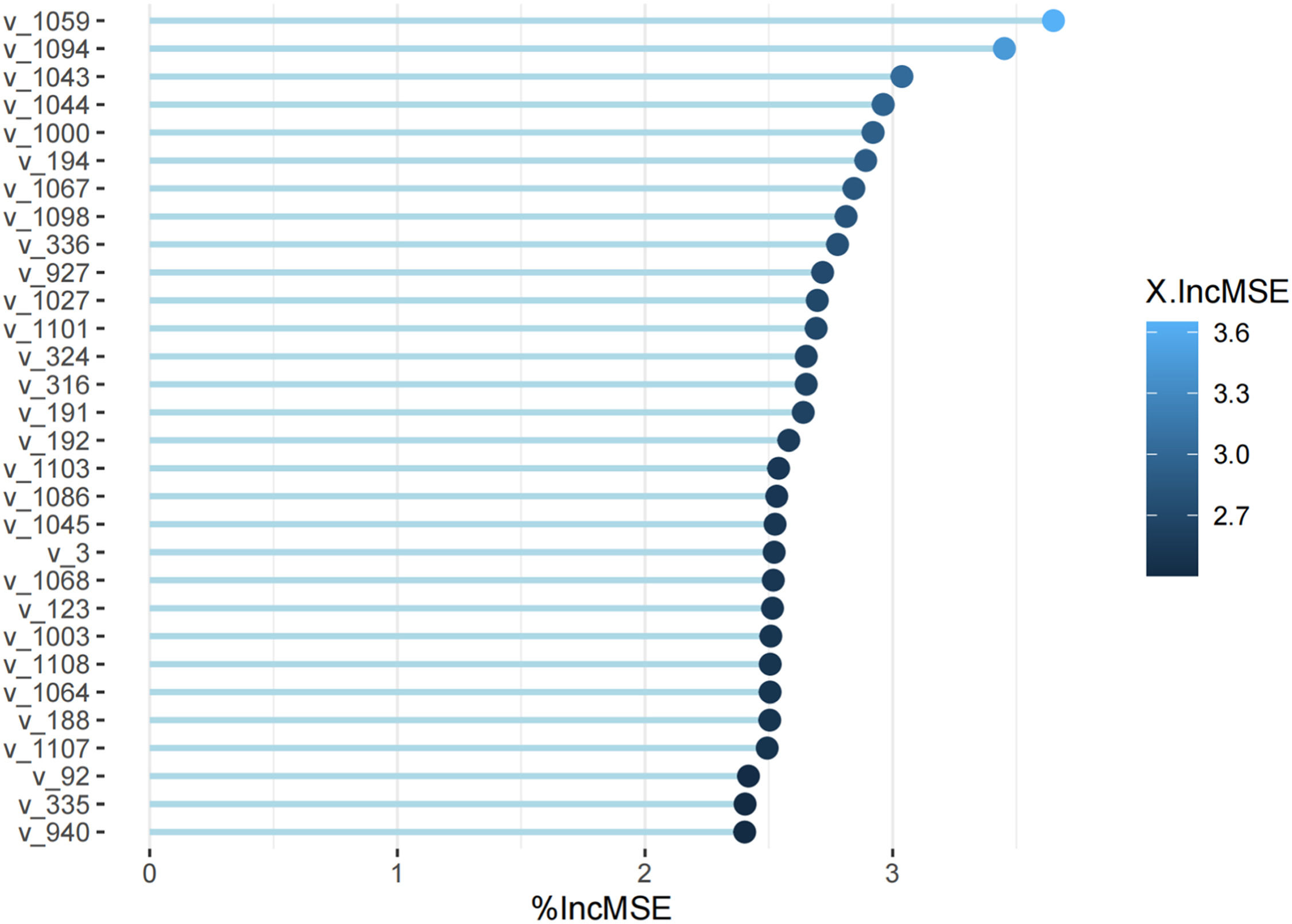
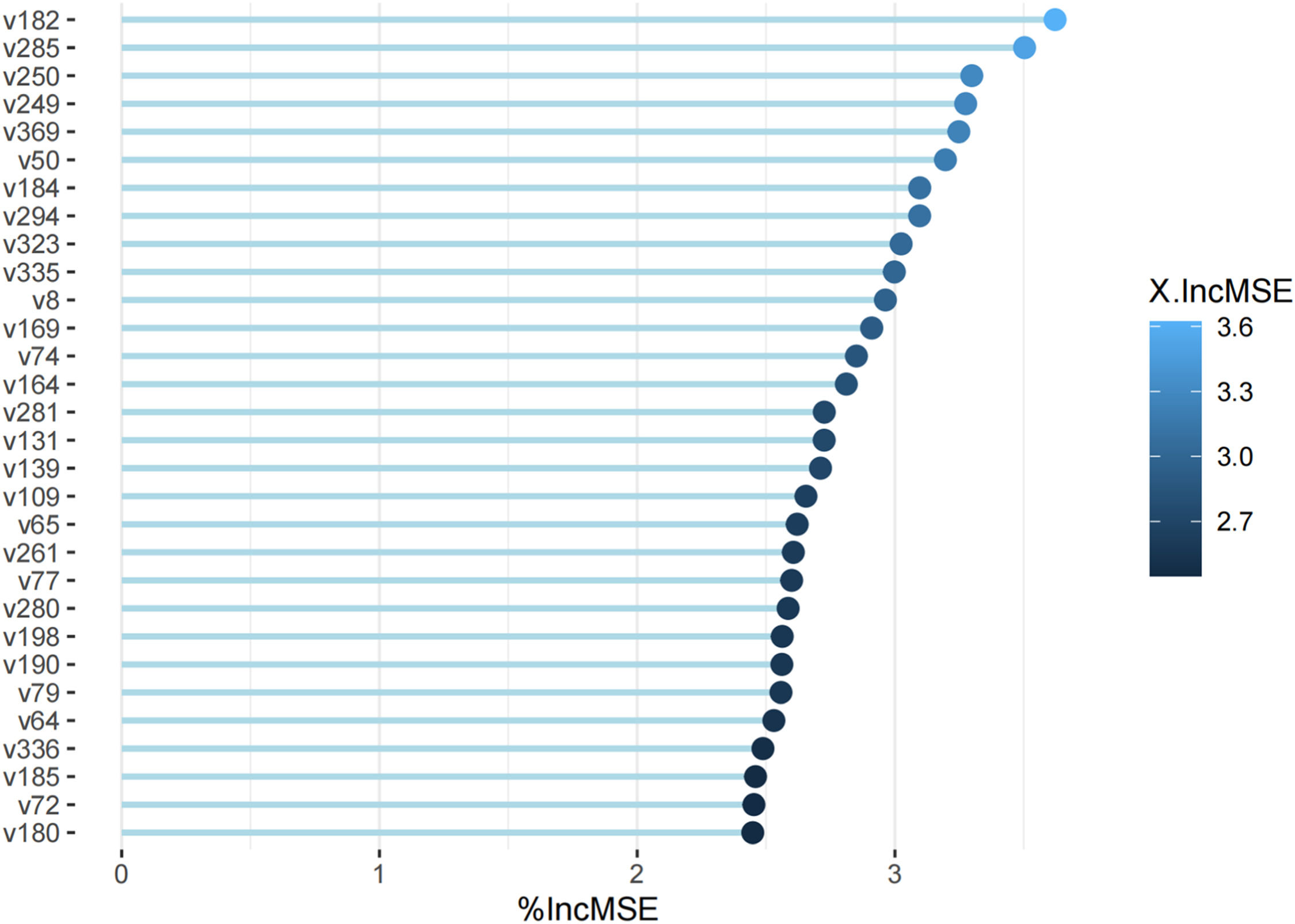
Then, using the random forest method, which is a machine learning method, we extracted important variables from the feature vectors. The rankings of the important variables are listed below (Figs. 1 and 2):
The top 30 features were extracted from large to small according to the importance ranking, and collinearity was checked. We found that once more than 4 variables were added to the model, the kappa value surpassed 100. Therefore, we chose the 4 most important variables as our feature vectors. They were the turnover of technical achievements, R&D output, the net value of fixed assets and the contribution rate of total assets of the automobile manufacturing industry for Chongqing and the number of university students, financial investment, innovative greening rate, and number of invention patent applications for Chengdu.
ModelNo counterfactual means that causal effects produced by observational methods do not correspond to true causal effects. This is a fundamental problem of causal inference rooted in individual differences, and a causal inference cannot be taken as the anti-reality of individual differences. The ultimate goal of all analytical tools developed by traditional econometrics is to construct a counterfactual treatment group, regardless of the research design employed (Luo et al., 2021).
We followed Luo et al. (2021) and used various machine learning algorithms to model the samples before the new setting of the administrative hierarchy for Chongqing in 1997 and constructed the counterfactual test. Assuming that the new setting of administrative hierarchy for Chongqing in 1997 does not occur, by training for the feature set, we calculated the respective predicted value of intercity connection (counterfactual) and compare it with the actual value of intercity connection.
To overcome the endogeneity of the intercity connection, we used several machine learning methods (support vector machines (SVMs) and linear models (LMs)) to calculate and predict the external impact of the restructuring of the new administrative hierarchy (T. Hastie et al., 2009) [1]. The reason for choosing these machine learning algorithms is that these methods are the most typical in training and predicting data.
An SVM is a type of generalized linear classifier that classifies data by supervised learning. Its decision boundary is the maximum margin hyperplane. SVM uses the hinge loss function to calculate empirical risk and adds a regularization term to the solution system to optimize structural risk (T. Hastie et al., 2009). The first four feature vectors were extracted. The data before 1997 were used for learning and testing, and the data after 1997 were used for prediction. We chose Chongqing as the treated group and Chengdu as the control group.
According to Luo et al. (2021), to construct the counterfactual test, we first randomly took 80% of the samples before 1997 (the restructure of Chongqing) as the training set and the other 20% as the test set and treated all other indicators in the statistical yearbooks of Chongqing and Chengdu as the feature set to test the model effect before implementation. We followed Chui et al. (2022) as an example of a 5-fold cross-validation to set the 5-fold cross-validation. Finally, the adjusted optimal hyperparameters and optimal model were tested in the test set, and the out-sample R-square coefficient of the prediction set was 0.91, which shows that the test effect is good. After 1997, the same procedure was also conducted to test the effect of the model after implementation. The out-sample R-square coefficient was 0.85, which again shows that the test effect is good.
Accordingly, the model can be shown as
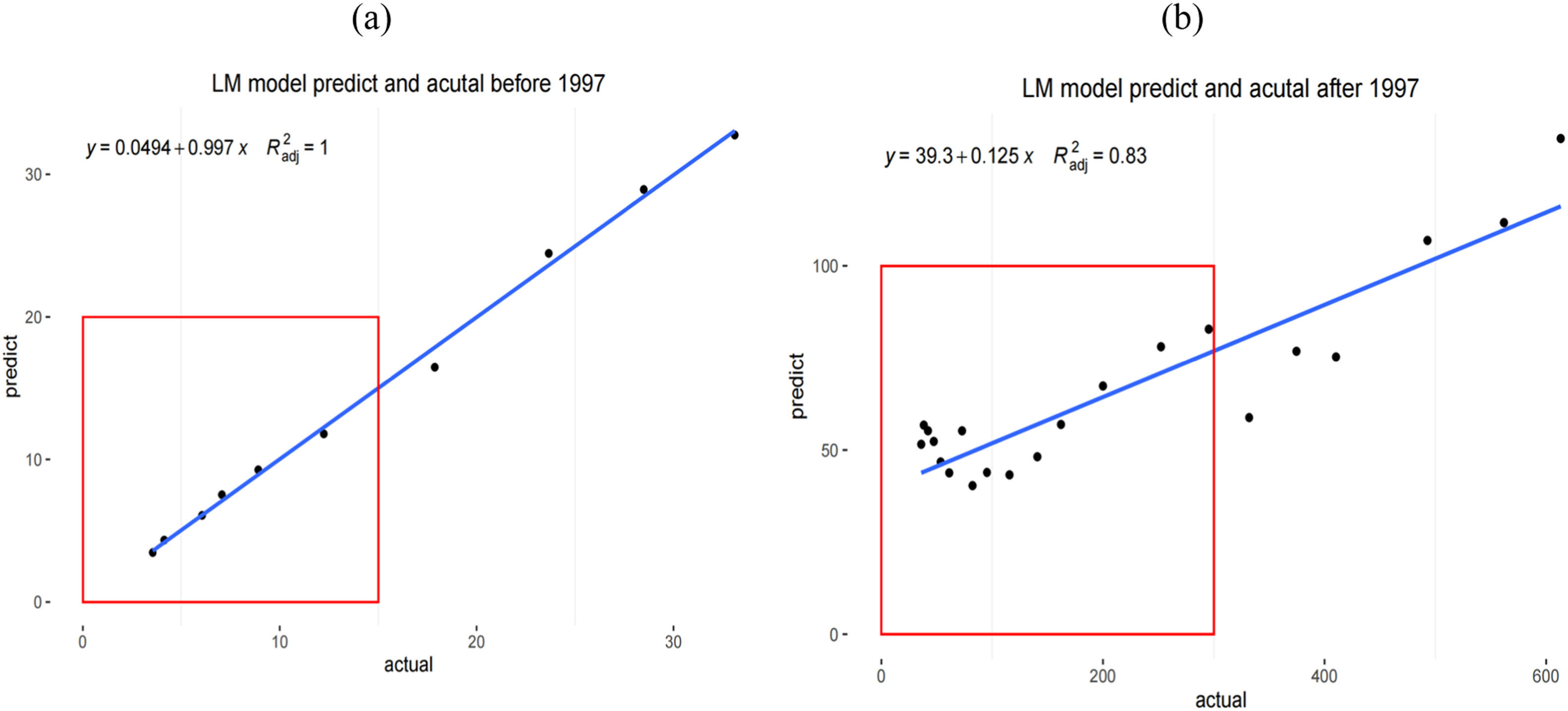
ResultsWe first used an LM for Chongqing before 1997. The empirical results showed that the adjusted R2 was 0.98. The coefficients of mineral output and the contribution rate of total assets of the automobile manufacturing industry were significant at the 5% level, and the net value of fixed assets was significant at the 10% level. Then, we used this LM from before 1997 to predict the value after 1997 and checked the fit of the actual value and predicted value as shown below (Fig. 3).
The results of the LM for Chongqing indicated that the adjusted R2 before and after 1997 decreased from 0.98 to 0.93. The predicted data, due to the impact of an external shock (new administrative hierarchy), reveal a large difference between the predicted value and the actual value in the first 10 years after 1997 (the lower-left corner of the right figure, the same below).
We also applied the LM to Chengdu before 1997 (Fig. 4). The empirical results showed that the adjusted R2 was 0.99. The coefficients of all feature vectors were significant at least at the 5% level.
The results of the LM for Chengdu indicated that the adjusted R2 before and after 1997 decreased from 0.99 to 0.83. The predicted data showed that there was also a large difference between the predicted value and the actual value in the first 10 years after 1997.
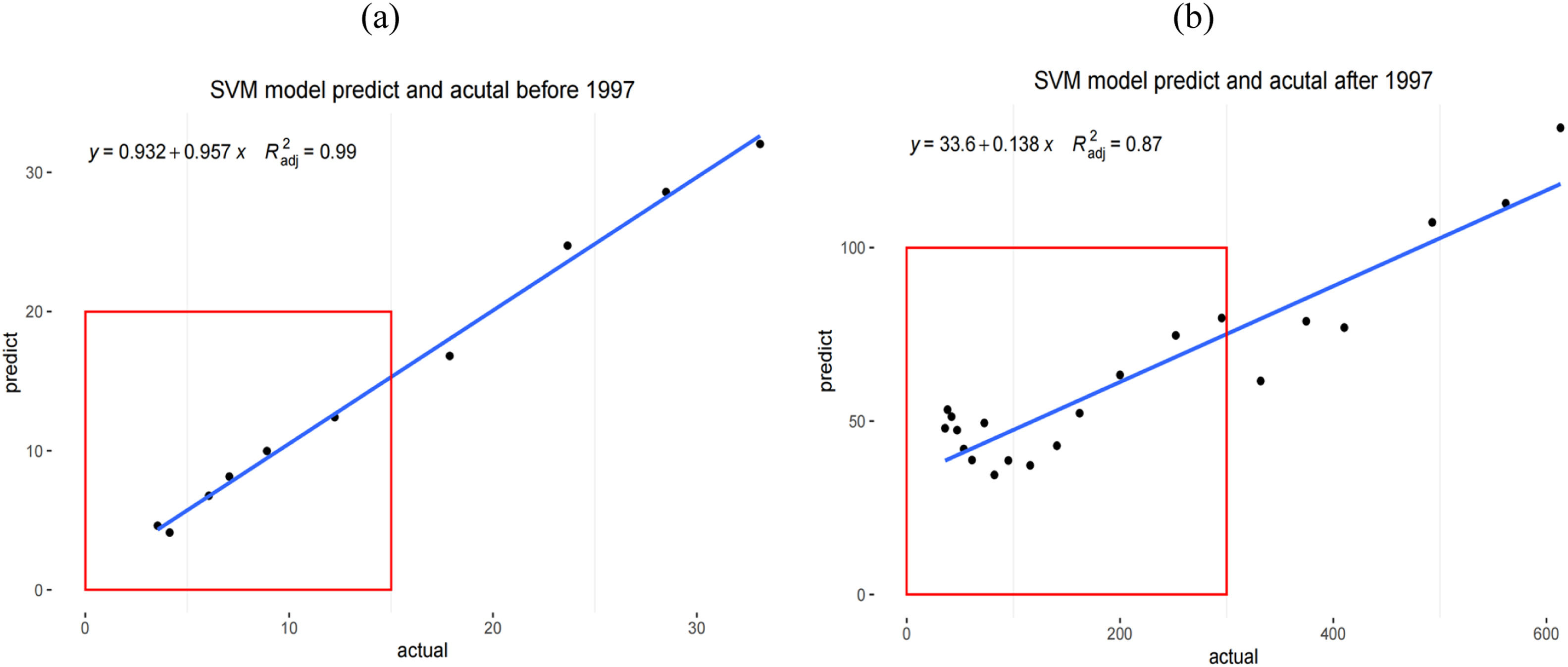
We then used SVM to fit Chongqing before 1997 and applied SVM before 1997 to predict the value after 1997 by checking the fit of the actual value and predicted value of Chongqing (Fig. 5).
The SVM results for Chongqing indicated that the adjusted R2 before and after 1997 decreased from 0.98 to 0.94. The predicted data revealed that there was also a large difference between the predicted value and the actual value in the first 10 years after 1997. We also obtained a significant difference in the SVM for Chengdu as follows (Fig. 6.).
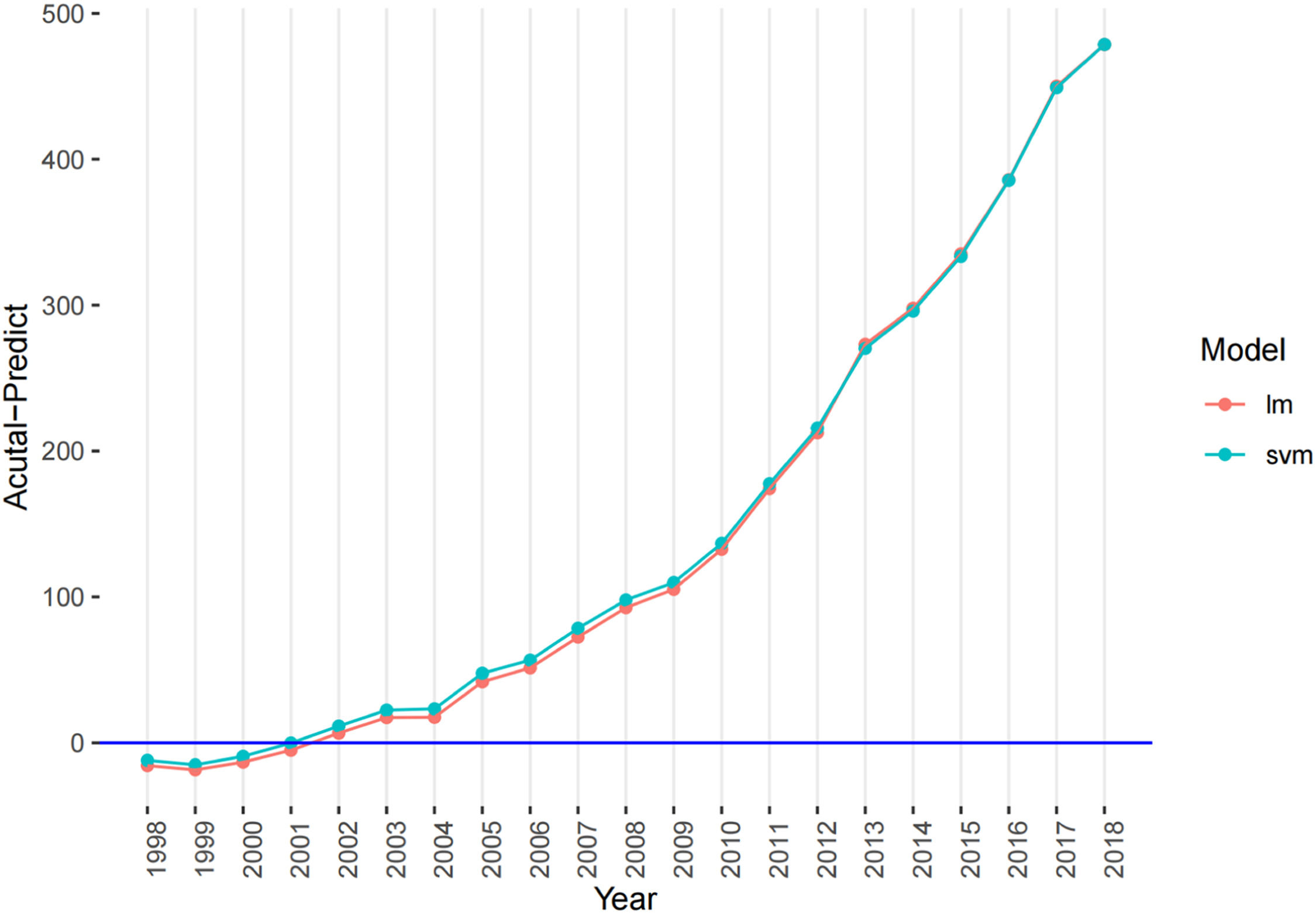
After showing the significant difference in the intercity connection due to the innovation of administrative hierarchy in 1997, to clearly show the specific time trend of this divergence, we set the difference in the actual and predicted values (actual value minus predicted value) as the y-axis and year as the x-axis for Chongqing and Chengdu, as shown below (Figs. 7 and 8):
We found that the intercity connection of Chongqing as the LHC and Chengdu as the IHC had a divergent trend in the value differences. For Chongqing, the value difference was negative from 1997 to 2007 for both the LM and SVM. This means that the actual intercity connection was worse than predicted due to the external shock in 1997. The underlying reason may be that the innovation of the administrative hierarchy between Chengdu and Chongqing could have hampered the personnel exchange and resource mobility of the LHC over the first ten years. When several neighboring counties coalesced into the new Chongqing in 1997, the newly merged counties (Wanxian, Fuling and Qianjiang) were located east of Chongqing and were thus geographically farther from Chengdu (Fig. 9). These counties are in the mountain valley of East Sichuan, with the Daba Mountains to the north and the Sichuan-Hubei Plateau to the south; thus, the precipitous terrain is an obstacle to innovation for connecting with a western plains area, such as Chengdu.
Therefore, the new geographical barrier and change in administrative hierarchy, which made the connection for the new Chongqing to Chengdu's market innovation more difficult, led to the net negative effect of the difference between the actual and predicted values between 1997 and 2007. Why has there been a turning point since 2008, and why has the net innovation effect become positive with sustained growth?
The underlying reason is the breakthrough of transportation investment since 1997. Before 1997, there was only one Chengdu-Chongqing expressway connected to the provincial capital. In terms of railways, Chongqing's railway network before 1997 was composed mainly of several railway trunk lines built in the early days of the founding of the People's Republic of China (PRC), such as the Chengdu-Chongqing line, Hunan-Guizhou line, and Xiangyang-Chongqing line.
Chongqing has long hoped to open an eastern passage with the Chongqing-Huaihua Railway. However, such a change could cause Chengdu, as the provincial capital, to view Chongqing as a potential competitor rather than as a cooperator. Since Chongqing will eventually become independent, there is no impetus for Sichuan's capital to help build the transportation infrastructure of “another province”.
Since the new setting of Chongqing with more independent government financing and a higher administrative level, Chongqing's railway network planning has entered a stage of accelerating innovation (Ren et al., 2019). The Chongqing-Huaihua Railway broke ground in 2001 and opened to traffic in 2007. It is one of the landmark projects of China's western development strategy and shoulders the great mission of innovating Chongqing's economy. The Suining-Chongqing Railway started construction in 2003 and officially opened to traffic in 2006. The construction of the Dazhou-Wanzhou Railway broke ground in 1997, and passenger trains were officially put into operation in 2004. The completion and operation of the Chongqing North Railway Station in 2006 indicated that the railway construction of Chongqing had entered a period of great innovation, and Chongqing was gradually established as a regional intercity connection hub with Chengdu.
For Chengdu (the IHC), the intercity connection has been continually positive and has maintained stable growth since 1997. Before 1997, Chengdu was an indisputable railway hub in Southwest China. In addition to the Chengdu-Chongqing expressway, Chengdu opened a total of five expressways to Mianyang, Dujiangyan and other surrounding cities. The Chengdu-Chongqing Railway was built very early in 1952 as the first line of the PRC, but its speed was only 80 km/h. On the one hand, Chengdu first built the Neijiang-Kunming Railway and then built the Chengdu-Dazhou Railway. On the other hand, Chengdu wanted to replace the Chongqing-Huaihua Railway with a Sichuan-Hankou Railway that completely bypassed Chongqing (but was not constructed because the Yichang-Wanzhou Railway was constructed instead).
If the new setting had not been established in 1997, then the booming population and limited financial funds would have made it difficult to balance regional innovation between these twin cities. After 1997, with the independence of Chongqing from Sichuan Province, Chengdu, as the provincial capital, was released from the heavy burden of administrative management. Chengdu could also share the spillover effect of more financial support for Chongqing as the LHC and as a municipality directly under the central government.
There are three main reasons for the sustained net-positive innovation effect of the administrative hierarchy on Chengdu. First, the administrative region was optimized, especially for the connection of southeastern and northeastern new Chongqing (Wanxian and Qianjiang) to Chengdu, due to the facilitation of transportation. Second, the industrial structure of Chengdu-Chongqing became complementary due to their respective advantages, which led to the trickle-down innovation effect. Third, the attractiveness of Chengdu and Chongqing as twin cities increased because of the more important political level and higher administrative hierarchy, which overcame the barrier of the transprovincial border.
For a robustness check, we chose another measurement of the intercity connection to emphasize the transportation infrastructure (as set in the Variables section). Then, we used the same models (LM and SVM) to calculate the actual difference value and predict the intercity connection since 1997. We found that the difference in the values for Chongqing was still initially negative, with a back-and-forth fluctuation, and eventually became positive. The difference in the values for Chengdu was continually positive, although fluctuations also occurred from 2011 to 2015. This evidence further supports hypotheses 1 and 2. Compared with the IHC, the LHC has a greater struggle to achieve bargain and a longer investment period in transportation innovation. However, once these adverse conditions are overcome, the institutional profit of financial independence and a higher administrative level will triumph over the border effect and lead to the trickle-down that results from innovation.
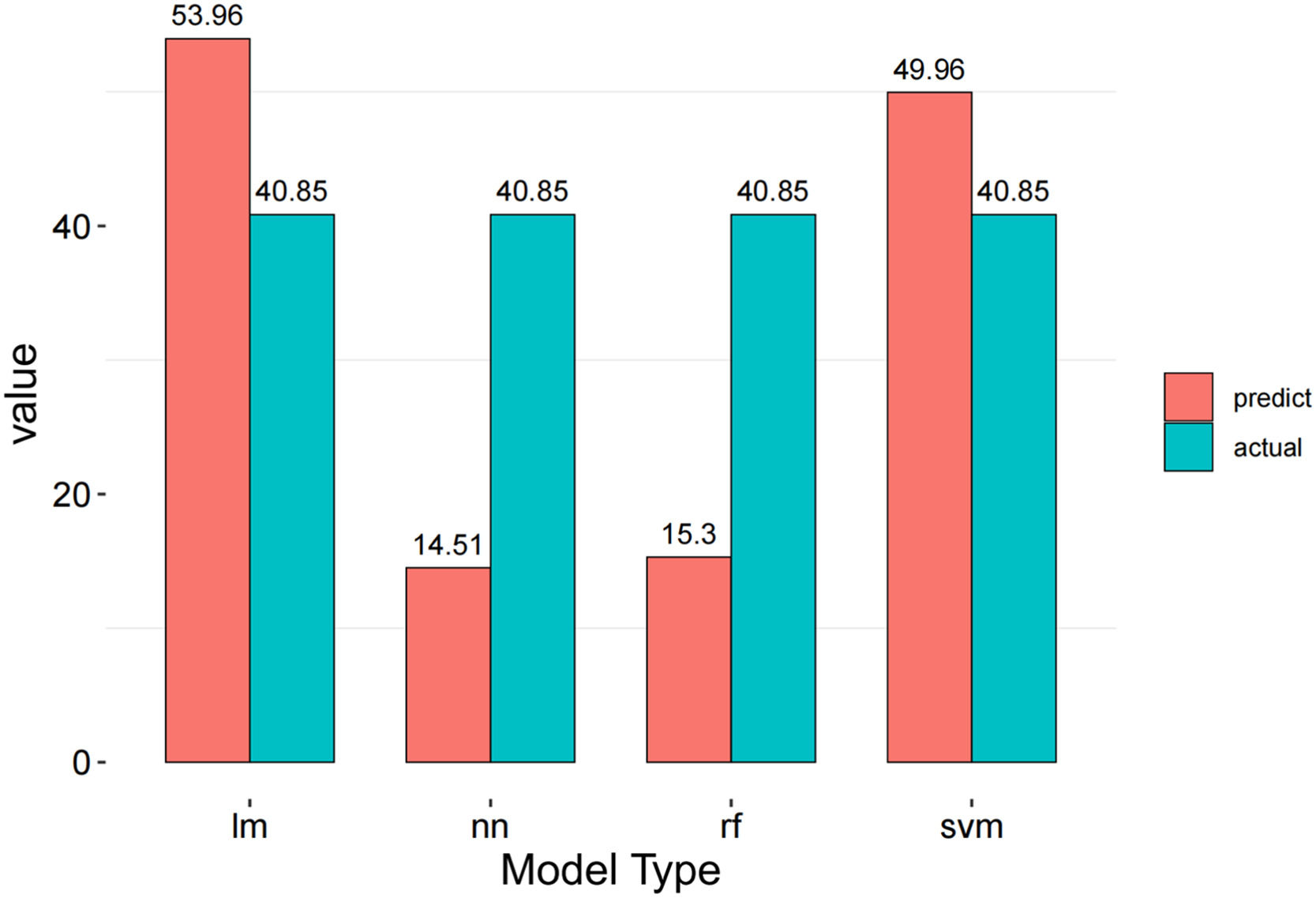
In addition, for another robustness check, we drew a comparison histogram of the predicted and actual values of intercity connections by using different machine learning methods (linear model (LM), neural network (NN), random forest (RF) and SVM) for Chengdu and Chongqing, as shown below (Figs. 10 and 11).
We found that Chongqing (LHC) and Chengdu (IHC) had divergent trends in the comparison histogram. For Chongqing, the predicted value and actual value have sharply opposite trends in different machine learning methods (such as LM/SVM vs. NN/RF). However, for Chengdu, the actual value is always higher than the actual value in the four machine learning methods, which means that the results are more stable and less fluctuating.
Moreover, considering the broadening of new Chongqing in geographical areas since 1997, we also split old Chongqing and the newly merged areas (Wanxian, Qianjiang, Fuling). We then set only old Chongqing (now the urban center since 1997) as the example of Chongqing and ran an LM and SVM prediction. The innovation trend is the same as that of new Chongqing: it has a turning point from negative to positive in the intercity connection with Chengdu.
Accordingly, the various empirical results obtained by using different machine learning models show that there is a significant divergence between the predicted value (counterfactual) and actual value for both the IHC and LHC. For the IHC, the actual value is always higher than the predicted value, which means that the net innovation effect is always positive. For the LHC, the actual value is first lower and then becomes higher than the predicted value, which means that the net innovation effect is from negative to positive.
However, this method may still have shortcomings. For example, the real world may not work as the machine learning predicted because of random contingency, city administrator's subjective preferences, and individual independence; however, this paper reports on exploratory research that can give rise to further in-depth studies.
Finally, to test the underlying innovation mechanism of the change in the net effect of administrative hierarchy on the intercity connection, we used railway turnover and cash mobility as the measurements of two contrary effects (investment in transportation infrastructure and the transaction cost of market access) on the turning point of net value change. We set the turning point of 2007 as the time node and ran a difference-in-differences (DID) model between Chongqing (as the treated group) and Chengdu (as the control group) (Table 2.).
DID Model of the Change in the Net Innovation Effect in 2007.
| Railway Turnover (100 million/km) | Cash Mobility (%) | |
|---|---|---|
| Chongqing*Post-2007 | 74.499⁎⁎⁎ | 0.362* |
| (3.065) | (1.886) | |
| Chongqing | −166.150⁎⁎⁎ | −0.279 |
| (−8.183) | (−1.602) | |
| Feature Vector | Yes | Yes |
| Year | Yes | Yes |
| N | 40 | 40 |
Note: t statistics in parentheses
⁎⁎p < 0.05.
We found that the coefficients of Chongqing*Post-2007 were significantly positive in railway turnover and cash mobility. After 2007, due to the comprehensive operation (even high-speed railway) of the railway network in Chongqing and nearby areas, the positive innovation effect of the new border finally totally compensated for the transaction cost of market access. On average, it takes approximately 10 years for this transition to occur, as the intercity connection for the LHC has a time-lagged positive effect.
Conclusion and discussionDo cities with higher administrative hierarchies always enjoy higher intercity connections? Existing studies have found that if twin cities are still subject to resource limitations within the same province and have similar administrative hierarchies, it is inevitable that they will be inclined to compete rather than cooperate, which results in the siphon effect of innovation (Deng et al., 2019). Especially in countries with governments that have strong political power to intervene in market access, relatively weaker capital cities have the impetus to generate more institutional borders and allocate less financial capital to their counterparts in the same provinces.
We tell the other side of the story. The reversal and innovation of administrative hierarchy for twin cities, especially regarding their relative comparison of city administrative ranks, is a good way to overcome such path dependence. In the case of Chongqing and Chengdu, even though the new administrative hierarchy could generate a barrier to market access in the short run, the positive spillover effect of more investment in transportation innovation and industrial agglomeration finally trumped the net innovation effect in the long run (approximately 10 years).
In addition, we found that the net innovation effect of administrative hierarchy on intercity connections was asymmetric in these twin cities. For the LHC (Chongqing in our case), there was a turning point for the divergent trend. At first, the barrier to market access had the upper hand, but later, more investment in transportation infrastructure and financial integration due to the higher administrative hierarchy had a diffusion effect, attracted more mobility, and finally caused a positive trickle-down effect to their neighboring areas. However, for the IHC (Chengdu in our case), the “first-mover advantage” allowed it to strategically enjoy the spillover effect of more financial resources and political support for innovation, which enabled the intercity connection to stabilize and grow.
Therefore, our paper makes marginal contributions to existing studies. First, it is consistent with Zhang et al. (2018), who found that the government-led administrative process has a strong intervention power in intercity connections, especially through changing political resources and infrastructure innovation. However, our findings differ from theirs in that we further discuss possible changes in the transaction costs of market access due to the revolution in the bargaining of twin cities. For intercity connections, the primary concern and dominant strategy of innovation is cooperation with the trickle-down rather than the siphon effect.
Second, our paper supplements the idea of Shen (2014) that the economic connection of twin cities necessitates institutional connections, which, in turn, attempt to facilitate economic connections. We tell this story from the other side of the coin: a well-designed administrative innovation for the twin cities can also generate economic connections from the effect of transportation infrastructure with diffusion effects and cash mobility with trickle-down effects.
Third, our paper supports the conclusion of Mikhailova and Wu (2017) that some city-twinning efforts are deliberately compartmentalized. We proved that such a “city-twinning phenomenon” can also happen with the popular slogan of metropolitan innovation. However, interestingly, it can “hit the mark by a fluke”: the recombination of Chengdu and Chongqing after administrative separation from the same “family (province)” attracted a stronger intercity connection with the existence of financial independence and the innovation effect.
Moreover, the nature of dispersion and asymmetry in the intercity connection of twin cities is the dual function of the new administrative hierarchy. If the new administrative hierarchy is the natural extension of the market division of innovation and endowment (Indraprahasta & Derudder, 2019), then the intercity connection could follow and match the evolution of the relative political power. However, if administrative innovation is a subjective governmental design and intervention, then how can it still inspire positive trickle-down effects to overcome the barriers to market access? This paper provides some answers in the findings that more transportation infrastructure and capital mobility, especially for the LHC, are possible ways to make twin cities act independently but reach the same innovative goal through different channels.
As Hesz and Joszkin (2019)) noted, fluctuations in the innovation of administrative hierarchy constantly reorder the settlement space around twin cities. The level of integration has shaped the urban fabric multiple times by creating periods of openness and closeness regarding settlement functional innovation. Therefore, we should tailor different intercity connection strategies for the separate cities in a twin-city pair. For the LHC in twin cities, more supporting innovative measures should be implemented to facilitate transactions and transportation, especially for newly merged areas. For the IHC in twin cities, the natural endowment and “first-mover advantage” can still make new innovative contributions to the intercity connection, but only if the cities see one another politically as “siblings” rather than as a “divorced couple”.
Future research directions should explore the underlying mechanism of the intangible knowledge spillover effect of the twin cities and how the innovation effect of intercity connections involves the formation of metropolitan areas and other socioeconomic indicators.
FundingsThis research was funded by the National Social Science Foundation of China, grant number 22AZD050, the National Natural Science Foundation of China, grant numbers 71721002, and Tsinghua University Initiative Scientific Research Program, grant number 2021TSG0820.
Note[1] Actually, we also test Random Forest, Neural Network and Boosting. But their goodness of fitting is worse. Hence, we didn't choose these algorithms.