Experimental validation of finite elements model in hip fracture and its clinical applicability

Abstract

Fracture of the proximal extremity of the femur is the subject of research interest. The complexity of the bone framework and the structural inefficiency associated with ageing leave many variables yet to be understood from an experimental perspective. However, there is no clearly defined structural and biomechanical research model for hip fracture.

The hypothesis of this paper is that it is possible to create a computational experimentation model that characterises the bone of the proximal extremity of the femur as a heterogeneous material from directly translating the mechanical parameters obtained from anatomical experimentation specimens.

Material and method

An experimental paper comparing real experimentation on cadavers and a numerical model based on finite element analysis (FEA). The variables uses were: the start point of the fracture, propagation of the fracture, progressive load and maximum load until fracture.

The real mechanical parameters obtained from the anatomical specimens were translated to the computational model based on the relationship between the Hounsfield units of the high resolution CAT scan and the bone mineral density of each virtual element, whereas the propagation of the fracture was modelled by the research team's own computational design, reducing the mechanical properties of the damaged elements as the fracture line advanced.

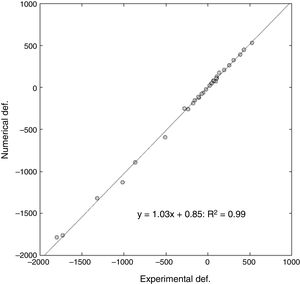
Results

The computational model was able to determine the start point of the fracture, with a slight tendency towards anatomical medialisation of this point compared to what happened experimentally. The degree of correlation was very high on comparing the real value of progressive deformation of the samples compared to that obtained by the computational model. Over 32 points analysed, a slope of 1.03 in lineal regression was obtained, with a relative error between the deformations of 16% and a Pearson's coefficient of R² = .99. The computational model slightly underestimated the maximum fracture load, with a relative error of approximately 10%.

Conclusion

The FEA computational model developed by this multi-disciplinary research team could be considered, as a whole, a complete FEA model of the proximal extremity of the femur with future clinical applicability since it was able to simulate and imitate the biomechanical behaviour of human femurs contrasted with a traditional experimental model made from anatomical specimens. On this basis, qualitative and quantitative interactions can be assessed which consolidate it as a powerful computational experimentation test bench for the human proximal femur.

Resumen

La fractura de la extremidad proximal de fémur es objeto de interés en investigación. La complejidad del entramado óseo y la ineficiencia estructural asociada al envejecimiento hacen que existan muchas variables todavía por comprender desde el punto de vista experimental, pero no existe un modelo de investigación estructural y biomecánico de la fractura de cadera claramente definido.

La hipótesis de este trabajo es que es posible desarrollar un modelo de experimentación computacional que caracterice el hueso de la extremidad proximal del fémur como un material heterogéneo a partir de la traslación directa de los parámetros mecánicos obtenidos de piezas anatómicas de experimentación.

Material y método

Trabajo experimental que compara la experimentación real en cadáver y un modelo numérico basado en análisis de elementos finitos (AEF). Las variables que se han empleado son: punto de inicio de la fractura, su propagación, carga progresiva y la carga máxima hasta fractura.

Al modelo computacional se trasladaron los parámetros mecánicos reales obtenidos de las piezas anatómicas basándose en la relación entre las unidades Hounsfield de la TAC de alta resolución y la densidad mineral ósea de cada elemento virtual, mientras que la propagación de la fractura se modeló mediante desarrollo computacional propio del equipo investigador, con disminución de las propiedades mecánicas de los elementos dañados conforme avanza la línea fractuaria.

Resultados

El modelo computacional fue capaz de determinar el punto de inicio de la fractura, con una discreta tendencia a la medialización anatómica de dicho punto respecto a lo ocurrido de manera experimental. El grado de correlación fue muy alto al comparar el valor real de deformación progresiva de las muestras frente al obtenido por el modelo computacional. Sobre 32 puntos analizados, se obtuvo una pendiente de 1,03 en regresión lineal, con un error relativo entre las deformaciones del 6% y un coeficiente de Pearson de R²=0,99. El modelo computacional infraestimó discretamente la carga máxima de fractura, con un error relativo aproximado al 10%.

Conclusión

El modelo computacional de AEF desarrollado por este equipo investigador multidisciplinar se puede considerar, en conjunto, un modelo completo de AEF de la extremidad proximal del fémur con aplicabilidad clínica futura al ser capaz de simular e imitar el comportamiento biomecánico de fémures humanos contrastado con un modelo experimental clásico realizado en piezas anatómicas. Sobre esta base podrán evaluarse interacciones cualitativas y cuantitativas que lo consoliden como un potente banco de ensayos de experimentación computacional sobre el fémur proximal humano.

Introduction

Fracture of the proximal end of the femur is interesting from both a clinical and a socioeconomic perspective. Its high associated mortality, the dependence it generates and the high cost of its care have focussed the interest of the scientific community almost exclusively on the study of fracture patients. However, intrinsic aspects (pathogenic and biomechanical) of fracture of the proximal end of the femur remain unknown: the start point of the fracture, propagation of the fracture, the variables affecting the different fracture patterns, etc. The complexity of the bone framework and ageing-related structural inefficiency that makes the bone a more fragile material to support loads and impact, mean that there are still many variables to understand from an experimental perspective, yet there is no clearly defined structural and biomechanical research model for hip fractures.^1–4

There is no consensus either on whether research using these real anatomical specimens should be performed on fresh or dry bone, or on any inherent structural changes they might have⁵ and this has resulted in the alternative of using synthetic bones for experimental field work with synthetic bones^5–9 which, simulating the micro-structural features of cortical and spongy bone, bring down the costs of the required investment. This study material provided by manufacturers that simulates human bone has enabled advances in the mechanical knowledge of healthy bone, but is difficult to extrapolate to the clinical setting. The industrial scale production of synthetic specimens only provides standard phantom models of healthy bone or standard phantoms of osteoporotic bone.

Therefore, numerical models based on finite element analysis (FEA) have been proposed as a valid alternative because, thanks to the current increase in computational power, researchers can subject “virtual” structures to loads without the need for physical material, with the advantage of being able to change the structural parameters that most affect bone as a weight-bearing structure: bone mineral density (BMD), section area, cortical thickness, cortical porosity, trabecular microstructure, etc.^1,8,10–12

FEA is based on the decomposition of a complex structure, of unknown biomechanical behaviour, in a series of geometrically simplified substructures termed finite elements. The individual behaviour of each of these substructures, termed “blocks”, is determined using mathematical equations that evaluate the loads or strain that they receive. From the individual analysis of each of these elements a global computational model is obtained of the structure analysed, which enables, on the one hand, its global resistance to be determined and, on the other, it to be “subjected to load” mathematically to determine the form, type and location of the biomechanical failure.

A major limitation of the FEA models published to date is that they view the bone as a homogenous material in terms of the biomechanical properties related to fracture, and nothing could be further from the reality.^6,13 A mathematical model that does not consider this fact would not be clinically applicable, which is the ultimate goal of biomedical research.

Due to all of the above, it is necessary to establish new FEA-based research models that combine the experimental knowledge of the latest mechanical studies with the potential offered by the current computational parameterisation capacities.

The hypothesis of this paper is that it is possible to create a computational experimentation model that characterises the bone of the proximal extremity of the femur as a heterogeneous material from directly translating the mechanical parameters obtained from anatomical experimentation specimens.

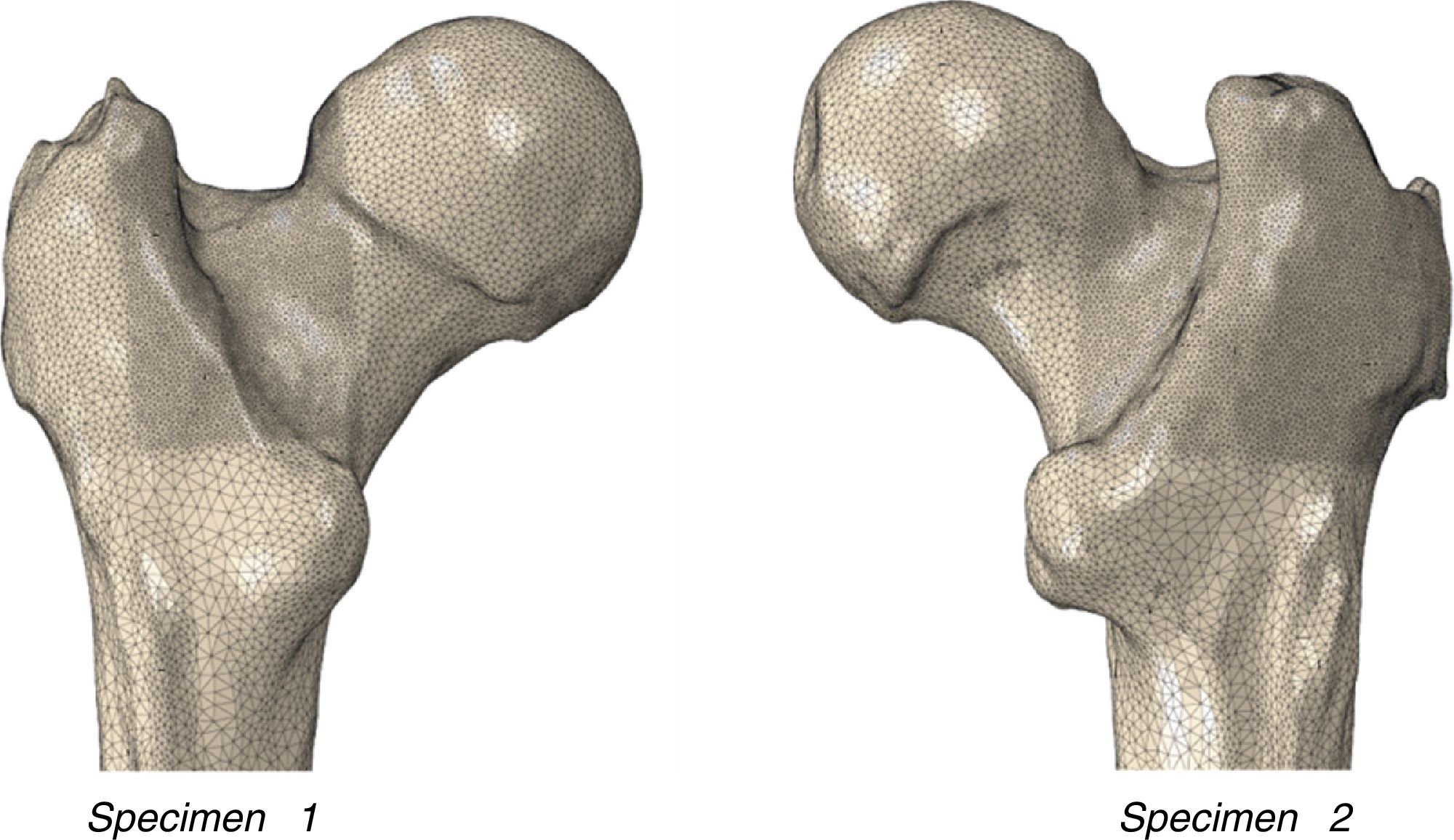
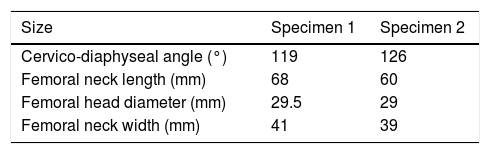
Material and method

Specimens

The experimental and numerical work was undertaken on 2 human femurs (specimen 1: 72-year-old female, left laterality, weight 78 kg, height 158 cm; specimen 2: 73-year-old male, right laterality, weight 88 kg, height 170 cm) donated by the Department of Anatomy of the Complutense University of Madrid, and that belonged to the university's body donation centre and dissection rooms. The subjects had no known musculo-skeletal disorders. The cadavers were preserved in a normal freezing chamber at −20 °C until the specimens were extracted.

The lower limbs of the cadavers were anatomically dissected with total disinsertion of all the capsuloligamentous coxofemoral structures and the knee until the complete femur was extracted with no osteotendinous insertions. A transverse osteotomy was performed of the proximal extremity of the femur at a distance of 35 cm from the most distal point of the lesser trochanter. The specimens were preserved fresh in saline-moistened cloth until high resolution computerised tomography (HR-QCT) was performed 12 h later.

Obtaining the 3D geometric model

HR-QCT was performed on each of the femoral specimens using a conventional Siemens Somaton clinical scanner. The femurs were placed horizontally secured at their most distal part, with the femoral neck parallel with the floor, and a free surface of 25 cm of bone material in the scanning arc. The study resolution was .44 mm on the transverse plane and 1.0 mm in the longitudinal direction of the femur, to obtain voxel sizes of .2 × .2 × .2 mm.³ The DICOM image obtained and its subsequent segmentation were performed using ScanIP software (Simpleware, Exeter, United Kingdom). This methodology enabled the generation of the geometric volume corresponding to the proximal femur, discrimination of its 2 main materials (cortical bone and trabecular bone), establishment of radiological densities, and the mechanical characterisation of each specimen.

Macroscopic morphology of the proximal femur

In order to characterise the femurs macroscopically, a digital measurement was made on the geometric model of the real morphology of each femur as shown in Table 1.

Table 1.

Descriptive measurements of the morphology of the proximal femur.

Size	Specimen 1	Specimen 2
Cervico-diaphyseal angle (°)	119	126
Femoral neck length (mm)	68	60
Femoral head diameter (mm)	29.5	29
Femoral neck width (mm)	41	39

Numerical finite element model of the proximal femur

A prior analysis of the mesh sensitivity enabled us to establish a mesh of 3 mm in the diaphyseal and 2 mm in the proximal area, with refinement in the femoral neck of 1 mm.

With these conditions, and using the finite element code Abaqus/Standard, the mesh of the proximal femur was generated comprising 500,000 tetrahedral quadratic elements and around 1,000,000 nodes. Fig. 1 shows the mesh obtained.

Figure 1.

3D virtual FEA model of the specimens studied.

The relationships established between the Hounsfield units (HU), MBD and mechanical properties (Young's modulus) of each voxel were established using the equations published by Morgan et al.¹⁴ The simulation of load and the distal fastenings of the virtual proximal femur were applied in a similar way to previous experimental trials.

The HU are the units extracted from the scanner, and comprise a grey scale. Their value depends on the attenuation of the material, defining 0 HU in distilled water in normal pressure and temperature conditions. This unit can be converted into mechanical properties based on the following series of relationships: −1000 HU for air, 10–40 HU in muscle, around 600 HU for trabecular bone and 1000 HU or more in cortical bone, its mechanical properties can be inferred according to the equations published by Morgan et al.¹⁴

Fracture propagation was modelled using the research team's own computational model,⁶ the mechanical properties of the damaged elements reduced and thus the separation between the different fractured parts was simulated. For calculating the maximum fracture load, the critical strain values in each element were considered according to their MBD.

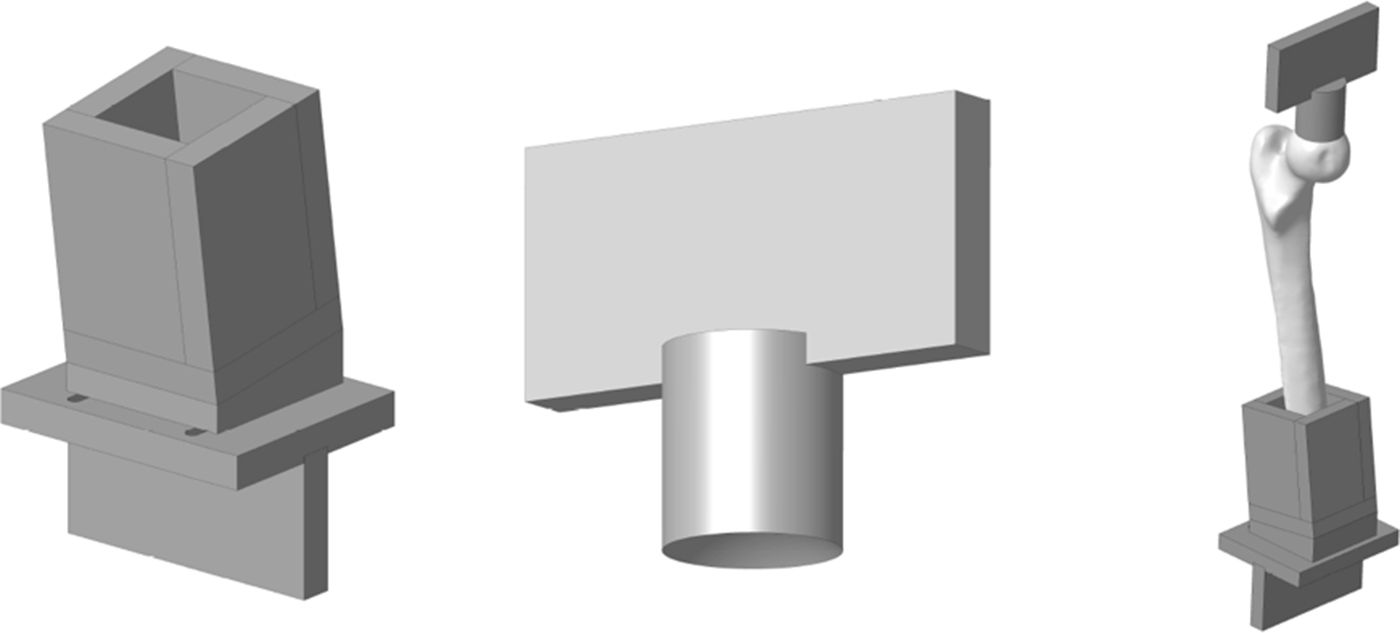
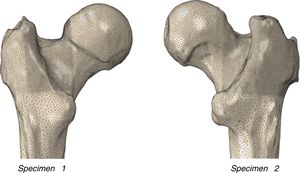
Experimental model of the proximal femur

In order to adapt the anatomical specimens to the test bench we designed a special tool comprising 2 sets of manufactured specimens in an aluminium alloy (AA 7075-T6). The upper set comprises a plate to attach the tool to the press and a cylinder with a concave end to adjust to the geometry of the femoral head with a radius of 25 mm. The lower set comprises a box in which the diaphysis of the femur is embedded using polymethylmethacrylate and a plate to secure it to the test machine. The box has a wedge so that the resulting geometry forms 8° with the femoral axis. Fig. 2 shows the specific designs we created.

Figure 2.

Tools manufactured by ourselves for the experimental field work.

Two consecutive experimental trials were performed on each anatomical specimen. The first comprised applying progressive loading forces on the frontal plane equalling 500, 1000, 1500 and 2000 N, with the load axis at 8° to that of the femoral diaphysis. Subsequently, the load on the femoral head was progressively increased until macroscopic fracture of the proximal limb.

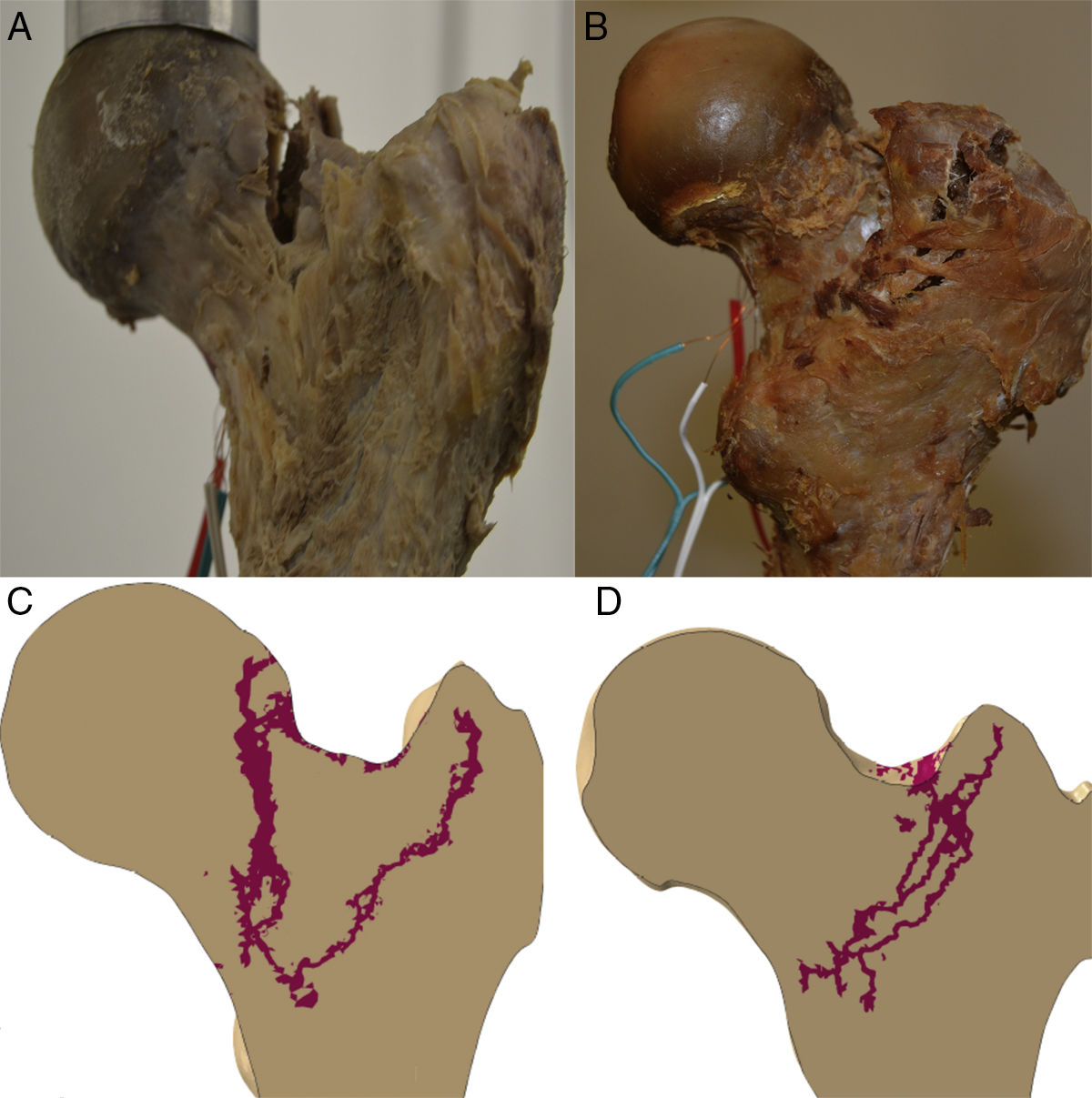
In order to quantify the deformations to the specimen during the abovementioned loads, strain gauges were placed on the femoral surface, 2 on the diaphysis and one on the femoral neck. Fig. 3 shows the specimens on the test bench.

Figure 3.

Specimen on experimental test bench with the gauges placed to record breaking forces.

Study variables

In order to validate the prediction capacity of the numerical model, 4 variables were considered to compare between the experimental model and the computational model:

• •

  Start point of the fracture.

• •

  Propagation of the fracture and correlation with the clinical pattern.

• •

  Deformations obtained at lower loads to the fracture.

• •

  Maximum fracture load.

Results

Start point of the fracture

The computational model was able to determine the start point of the fracture, with a slight tendency to anatomical medialisation of this point (Table 2).

Table 2.

Distance in millimetres between the fracture start point and the apex of the greater trochanter.

Specimen	Computational value	Experimental value
1	25	12
2	28	6

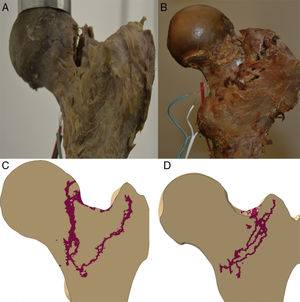
Propagation of the fracture

The propagation line of the computational model in the 2 specimens had a quasi-superimposable pattern to those obtained in the experimental models, as shown in Fig. 4.

Figure 4.

shows the propagation of the fracture comparing the real experimental model with the computational model (A and C; B and D). A double progression of the fracture can be seen in C, but with a single subcapital start point.

Deformations obtained with lower loads to the fracture

There was a very high degree of correlation on comparing the real value of deformations of the samples with that obtained by the computational model.

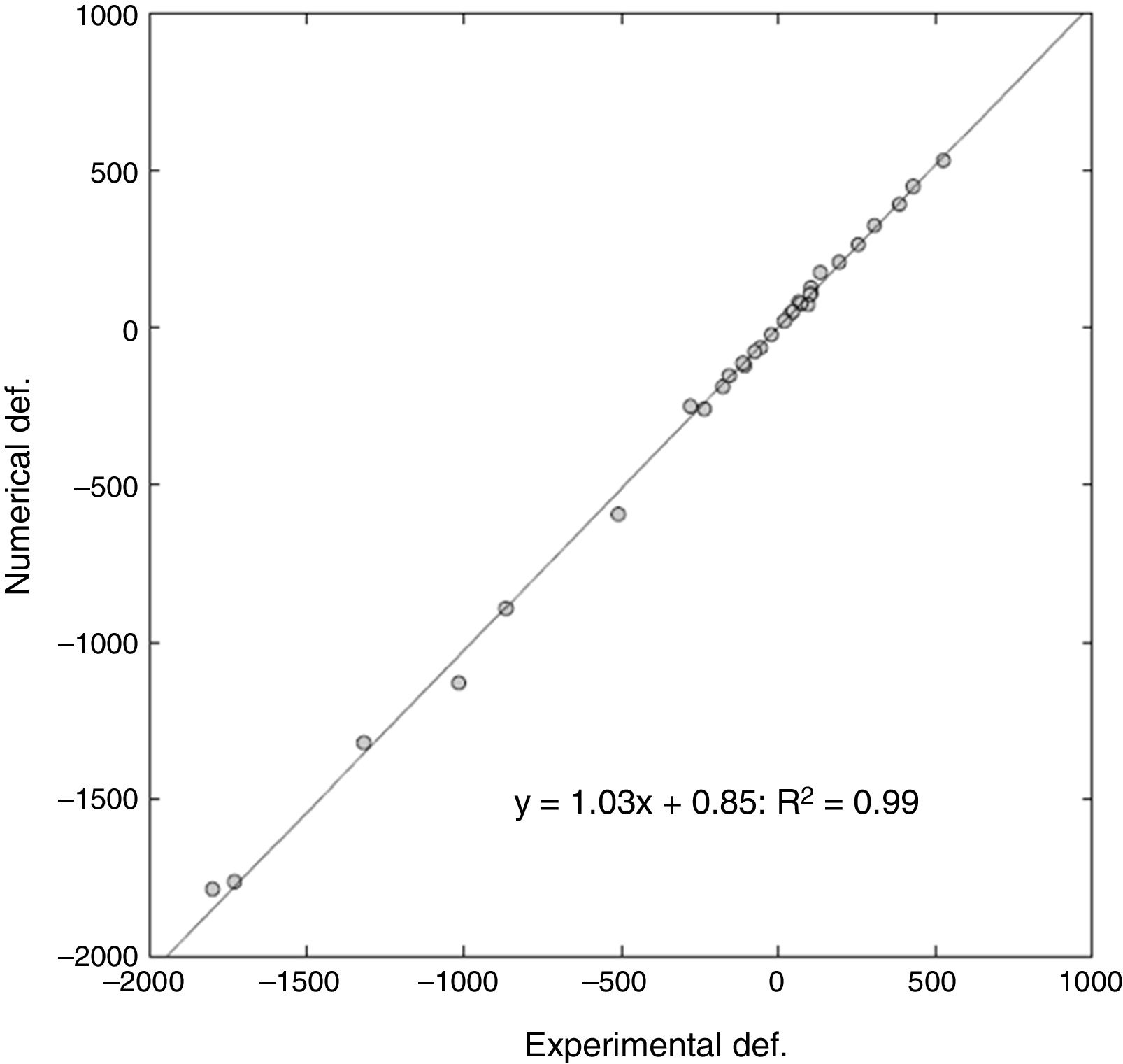
For a total of 32 points analysed (4 deformations per 4 cases of load on each femur), a slope of 1.03 on the linear regression was obtained, with a relative error between the deformations of 6%, and a Pearson's R² coefficient = .99 (Fig. 5).

Figure 5.

shows the comparison between the deformations in each subject.

Maximum fracture load

In both the computational and the experimental model, the maximum load value was higher in specimen 2, from a male, with an approximate difference of 1000 N between the 2 donors.

The computational finite element model slightly underestimated the maximum fracture load, with a relative error of approximately 10%. Table 3 shows the numerical fracture load values.

Table 3.

Value in Newtons of the load to achieve a fracture.

Specimen	Computational value	Experimental value	Differential error in %
1	6010	6572	8.55
2	7120	8178	12.93

Discussion

This paper's main achievement was to have developed a FEA computational model of the proximal femur capable of simulating and imitating the biomechanical behaviour of the human femur, for low loads as well as for fracture loads, which could be contrasted with a classical experimental model made from anatomical specimens on a test bench.

A multitude of qualitative and quantitative interactions could be evaluated by the research team: preload biomechanical conditions, load conditions, fracture models, osteosynthesis material, prosthetic implants, etc., which establishes it as a powerful computational experimentation test bench for the human proximal femur.

Vertebral¹⁵ and femoral^1,6,16 FEA models have been described from 3D slices of high resolution quantitative tomography-based finite element analysis (HR-QCT), even when low resolution scanner settings were used.¹⁷ A good correlation has been demonstrated between the biomechanical behaviour and the total bone resistance predicted by FEA^18,19 and those established experimentally in vertebral and femoral cadaver specimens.^1,17,20,21 Although these correlations are very interesting for the in vitro evaluation of a bone's total resistance, there is added difficulty in transferring these results to the clinical setting, especially in relation to ageing bone or senile osteoporosis.¹⁸

For the computational model of a proximal femur to be as realistic as possible, and especially when evaluating its behaviour in a fragility fracture, its mechanical properties must relate basically with BMD.^1,22 In our model, using specific software filters, we were able to differentiate the different areas of the femur according to the HU value of each voxel and secondarily, therefore, of its BMD. We used the method proposed by Morgan et al.¹⁴ to convert a grey scale (HU) into BMD values, and into mechanical properties in particular, to obtain the rigidity in each element in accordance with its BMD. Thus we were able on the one hand to differentiate trabecular bone from cortical bone and, on the other, to apply different mechanical properties to the model according to whether each micro area of the bone had a different BMD.

We followed the same system to calculate the maximum fracture load considering the critical strain values of each element until the break point was reached also according to its BMD. This strategy brings the model close to the mechanical conditions of senile osteoporotic bone, offers the most realistic possible numerical calculation values and, therefore, brings the mathematical model closer to the clinical problem of bone fragility faced daily by surgeons.

However, for the FEA computational model to be applied clinically it must be heterogeneous both in the rigidity of the materials and in the fracture properties,¹³ with different relationships between these parameters and the BMD.²³ Furthermore, the maximum load and the total fracture energy must be obtained from the load–displacement curve, as occurs in a real experimental trial.^1,12 Finally, it is crucial that the model should correlate well between the propagation of the fracture obtained in the experimental tests and the computational prediction.

In this regard, our model is the most complete that has been published to date, bearing in mind all the above-mentioned circumstances. We believe that the statistical correlation that is so important between deformities obtained at lower loads until fracture between the computational model and that obtained experimentally on the test bench, together with the similarity of the fracture propagation traces of specimens 1 and 2, clearly constitutes the robustness of the computational model, and validates our finite element model of the proximal femur.

We would like to highlight that the experimental work conditions for the 2 specimens were exactly the same and were monitored at all times by the research team (progressive load forces on the frontal plane forming 8° with the axis of the diaphysis of 500, 1000, 1500 and 2000 N). Therefore it is striking that there were 2 types of breaks that could be completely distinguished from each other, as shown in Fig. 4, and largely similar to what is found in routine clinical practice. In specimen 1 there was a fracture trace that could be classified as subcapital, whereas specimen 2 had a clearly extracapsular fracture. Yet more surprising, if possible, is that the computational prediction had the same findings. Therefore it is tempting to believe that there are material or nano-, micro- and macrostructural determining factors of a fracture pattern, regardless of the intensity of load or the direction it is applied. We must stress that specimen 2 had a greater cervico-diaphyseal angle, which made it tolerate the axial load it received better and therefore it required greater fracture force. But although neither the methodology used nor the number of specimens we analysed enabled us to establish a direct relationship between these variables, we believe that these findings further outline the accuracy of the computational model's prediction and, therefore, its future clinical application.

With regard to the latter point, the papers by Lenich^24,25 demonstrated that the first effect that occurs in the “cut-out” phenomenon is a moment of rotation of the bone fragment over the cephalic implant so that, subsequently, through a phenomenon of continuous micro-movements, the bone incurs increasing damage causing protrusion of the osteosynthesis material. The computational model that we created can help our understanding of this pathogenic model, in simulating the alterations that would occur if the apex of the circumference of the femoral head is considered a fixed point and simulating the flexo-extension micro-movements.

The main limitations of the computational model as a clinical support tool are those inherent to the FEA work. As we mentioned earlier, there is an entire process that includes the translation of a real physical element to a virtual element segmented into small geometric shapes, and how these elements fully interrelate is controlled by the conditions established by the research team.

It is also true that the anatomical, computational and experimental work was only carried out on 2 specimens. However, clearly the number of donors and the amount of physical and human resources necessary to enlarge the series would be huge, and in other production and research sectors, such as engineering, exclusively computational work is the standard in such circumstances where the traditional experimental models are unfeasible or economically unsustainable.^8,11,26

The role of the muscles, tendons and ligaments in absorbing the force of a fall and, therefore, the force of a fracture is undisputed.²² Age-related muscle weakening, which, together with the loss of elasticity of the ligaments and tendons, places individuals at risk of clinical fractures. Our model does not consider the action of these soft tissues because this would enormously increase the need for computational calculation, but above all because it is not possible to contrast the computational value with an experimental value. As far as we know there is no description of a cadaver model that reproduces the stabilising action of muscles and tendons in the event of a fall, let alone under conditions of senile osteoporosis. Nevertheless, despite the limitations mentioned, we believe this is a valid model to further our understanding of the proximal femur, not only as a weight-bearing structure, but how, in each specific point of the bone, the underlying microscopic parameters could affect the entire structure.

Translational research on the most relevant clinical aspects of this condition will only be possible if we have a clear understanding of the mechanical circumstances that dictate the onset of a fracture of the proximal extremity of the femur: the start point of the fracture and its subsequent progression throughout the bone surface typical of fracture, biomechanical predictors of fracture and its type, specific implant designs, predictors of osteosynthesis failure, etc.^1,10,16

In sum, this article was written by clinicians for clinicians. It was not our intention or desire to enter a deep discussion on the mathematical foundations that underpin the AEF method, or the mathematical formulae defining each element's relationships with each other. However, we did seek to highlight that the methodology that we used to obtain the “virtual” geometrical structure of the proximal femur, that the prior material and structural conditions of fracture contour and load were real, and that FEA is a valid method endorsed by the literature and used by research teams to evaluate different conditions relevant to our specialty.^{7,11,15,23,27–30}

The model that we present represents the consolidation of a line of work by a multidisciplinary group that comprised orthopaedic surgeons and engineers with a clear and convinced clinical focus.^6,13,23,31 The FEA computational model developed by this multidisciplinary research team can be considered, as a whole, a complete FEA model of the proximal extremity of the femur that can be applied clinically in the future.

Level of evidence

Level of evidence II.

Conflict of interests

The authors have no conflict of interest to declare.

Acknowledgements

The authors would like to thank Dr Teresa Vázquez, Professor at the Department of Anatomy of the Complutense University of Madrid for her help in completing the paper.