La fractura de la extremidad proximal de fémur es objeto de interés en investigación. La complejidad del entramado óseo y la ineficiencia estructural asociada al envejecimiento hacen que existan muchas variables todavía por comprender desde el punto de vista experimental, pero no existe un modelo de investigación estructural y biomecánico de la fractura de cadera claramente definido.
La hipótesis de este trabajo es que es posible desarrollar un modelo de experimentación computacional que caracterice el hueso de la extremidad proximal del fémur como un material heterogéneo a partir de la traslación directa de los parámetros mecánicos obtenidos de piezas anatómicas de experimentación.
Material y métodoTrabajo experimental que compara la experimentación real en cadáver y un modelo numérico basado en análisis de elementos finitos (AEF). Las variables que se han empleado son: punto de inicio de la fractura, su propagación, carga progresiva y la carga máxima hasta fractura.
Al modelo computacional se trasladaron los parámetros mecánicos reales obtenidos de las piezas anatómicas basándose en la relación entre las unidades Hounsfield de la TAC de alta resolución y la densidad mineral ósea de cada elemento virtual, mientras que la propagación de la fractura se modeló mediante desarrollo computacional propio del equipo investigador, con disminución de las propiedades mecánicas de los elementos dañados conforme avanza la línea fractuaria.
ResultadosEl modelo computacional fue capaz de determinar el punto de inicio de la fractura, con una discreta tendencia a la medialización anatómica de dicho punto respecto a lo ocurrido de manera experimental. El grado de correlación fue muy alto al comparar el valor real de deformación progresiva de las muestras frente al obtenido por el modelo computacional. Sobre 32 puntos analizados, se obtuvo una pendiente de 1,03 en regresión lineal, con un error relativo entre las deformaciones del 6% y un coeficiente de Pearson de R2=0,99. El modelo computacional infraestimó discretamente la carga máxima de fractura, con un error relativo aproximado al 10%.
ConclusiónEl modelo computacional de AEF desarrollado por este equipo investigador multidisciplinar se puede considerar, en conjunto, un modelo completo de AEF de la extremidad proximal del fémur con aplicabilidad clínica futura al ser capaz de simular e imitar el comportamiento biomecánico de fémures humanos contrastado con un modelo experimental clásico realizado en piezas anatómicas. Sobre esta base podrán evaluarse interacciones cualitativas y cuantitativas que lo consoliden como un potente banco de ensayos de experimentación computacional sobre el fémur proximal humano.
Fracture of the proximal extremity of the femur is the subject of research interest. The complexity of the bone framework and the structural inefficiency associated with ageing leave many variables yet to be understood from an experimental perspective. However, there is no clearly defined structural and biomechanical research model for hip fracture.
The hypothesis of this paper is that it is possible to create a computational experimentation model that characterises the bone of the proximal extremity of the femur as a heterogeneous material from directly translating the mechanical parameters obtained from anatomical experimentation specimens.
Material and methodAn experimental paper comparing real experimentation on cadavers and a numerical model based on finite element analysis (FEA). The variables uses were: the start point of the fracture, propagation of the fracture, progressive load and maximum load until fracture.
The real mechanical parameters obtained from the anatomical specimens were translated to the computational model based on the relationship between the Hounsfield units of the high resolution CAT scan and the bone mineral density of each virtual element, whereas the propagation of the fracture was modelled by the research team's own computational design, reducing the mechanical properties of the damaged elements as the fracture line advanced.
ResultsThe computational model was able to determine the start point of the fracture, with a slight tendency towards anatomical medialisation of this point compared to what happened experimentally. The degree of correlation was very high on comparing the real value of progressive deformation of the samples compared to that obtained by the computational model. Over 32 points analysed, a slope of 1.03 in lineal regression was obtained, with a relative error between the deformations of 16% and a Pearson's coefficient of R2=.99. The computational model slightly underestimated the maximum fracture load, with a relative error of approximately 10%.
ConclusionThe FEA computational model developed by this multi-disciplinary research team could be considered, as a whole, a complete FEA model of the proximal extremity of the femur with future clinical applicability since it was able to simulate and imitate the biomechanical behaviour of human femurs contrasted with a traditional experimental model made from anatomical specimens. On this basis, qualitative and quantitative interactions can be assessed which consolidate it as a powerful computational experimentation test bench for the human proximal femur.
La fractura de la extremidad proximal de fémur presenta interés desde cualquier punto de vista, ya sea clínico o socioeconómico. La alta mortalidad asociada, la dependencia que genera y el alto coste económico del proceso asistencial condicionan que el interés de la comunidad científica se haya centrado, casi exclusivamente, en el estudio del enfermo afecto de fractura. Sin embargo, se desconocen aspectos intrínsecos (patogénicos y biomecánicos) de la fractura de la extremidad proximal del fémur: el punto de inicio de la fractura, su propagación, qué variables condicionan los distintos patrones de fractura, etc. La complejidad del entramado óseo y la ineficiencia estructural asociada al envejecimiento, que convierten al hueso en un material más frágil para soportar cargas e impactos, hacen que existan muchas variables todavía por comprender desde el punto de vista experimental, pero no existe un modelo de investigación estructural y biomecánico de la fractura de cadera claramente definido1-4.
Tampoco existe consenso sobre si el estudio a través de estas piezas anatómicas reales debe realizarse sobre hueso fresco o hueso seco, ni sobre qué cambios estructurales puedan llevar implícitos5 y ello ha llevado a la alternativa de realizar el trabajo experimental de campo con huesos sintéticos5-9 que, simulando las características microestructurales de cortical y esponjosa, permitan abaratar las inversiones necesarias. Este material de trabajo proporcionado por fabricantes que simula el hueso humano ha permitido avanzar en el conocimiento mecánico del hueso sano, pero difícilmente es extrapolable al mundo clínico. La producción industrial a escala de los especímenes sintéticos solo permite elaborar fantomas estándar de hueso sano o fantomas estándar de hueso osteoporótico.
Por ello, los modelos numéricos basados en análisis mediante elementos finitos (AEF) se plantean como una alternativa válida, ya que gracias al aumento del poder computacional disponible en la actualidad el investigador puede someter a cargas a estructuras «virtuales» sin la necesidad de disponer de un material físico, con la ventaja que aporta el poder cambiar los parámetros estructurales que más afectan al hueso como estructura de soporte de cargas: densidad mineral ósea (DMO), área de sección, grosor cortical, porosidad cortical, microestructura trabecular, etc.1,8,10-12.
El AEF se basa en la descomposición de una estructura compleja, de comportamiento biomecánico desconocido, en una serie de subestructuras geométricamente simplificadas denominadas elementos finitos. El comportamiento individual de cada una de estas subestructuras, denominadas «ladrillos», se determina mediante ecuaciones matemáticas que evalúan las cargas o las tensiones que estas reciben. A partir del análisis individual de cada uno de estos elementos, se obtiene un modelo computacional global de la estructura analizada, que permite, por un lado, determinar su resistencia global y, por otro, ser «sometido a carga» matemáticamente para determinar la forma, el tipo y la localización del fracaso biomecánico.
Una limitación importante de los modelos AEF publicados hasta la fecha es que consideran al hueso como un material homogéneo en lo que se refiere a las propiedades biomecánicas relacionadas con la fractura, y no hay nada más alejado de la realidad6,13. Cualquier modelo matemático que no contemple este hecho nunca podrá tener aplicabilidad clínica, fin último de la investigación biomédica.
Por todo ello, es necesario determinar nuevos modelos de investigación basados en AEF que reúnan el conocimiento experimental de los últimos estudios mecánicos con la potencia que brindan las actuales capacidades de parametrización computacional.
La hipótesis de este trabajo es que es posible desarrollar un modelo de experimentación computacional que caracterice el hueso de la extremidad proximal del fémur como un material heterogéneo a partir de la traslación directa de los parámetros mecánicos obtenidos de piezas anatómicas de experimentación.
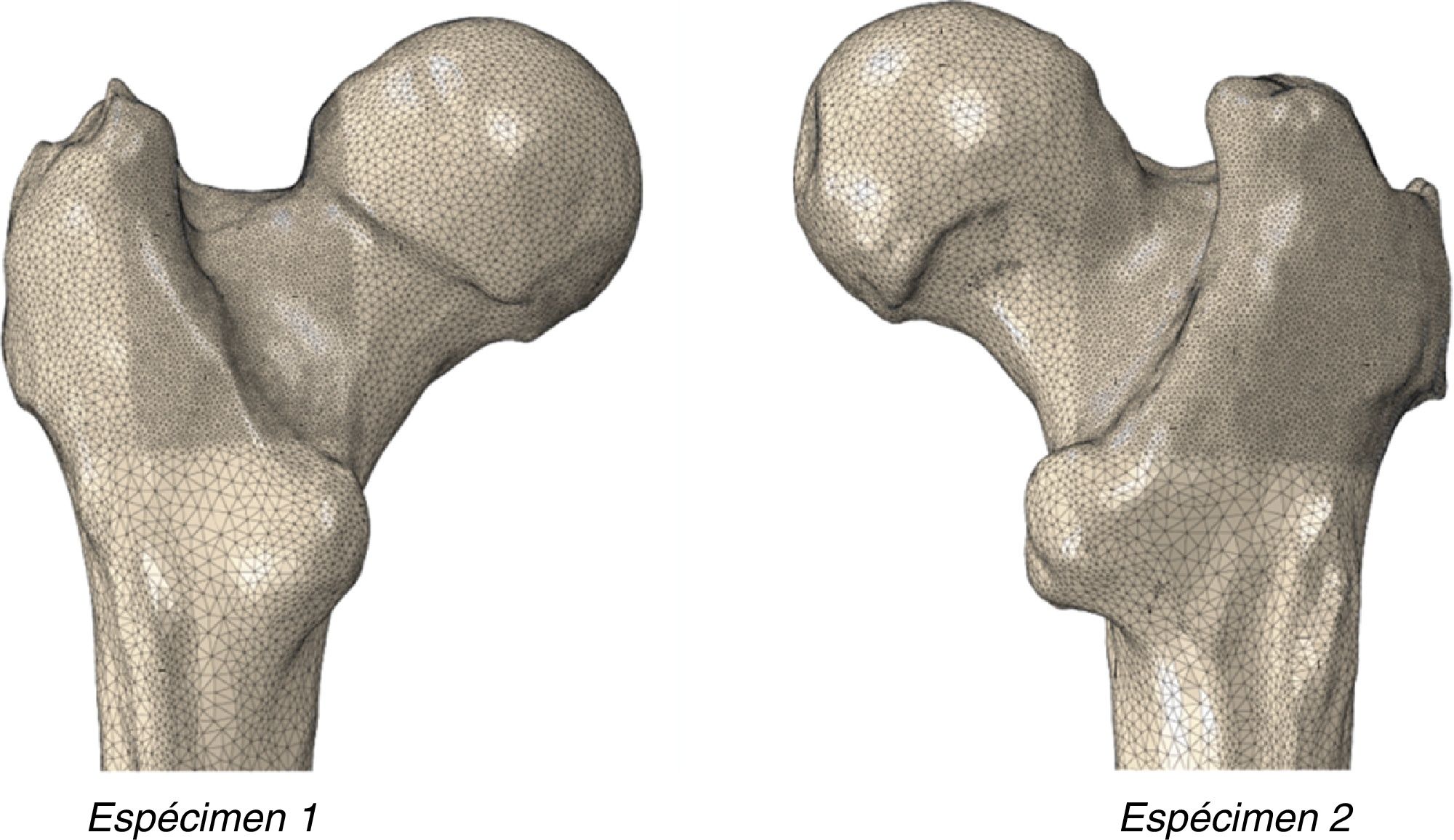
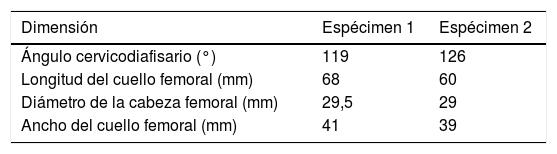
Material y métodoEspecímenesEl trabajo experimental y numérico ha sido llevado a cabo sobre 2fémures humanos (pieza 1: mujer de 72 años, lateralidad izquierda, peso 78kg, altura 158 cm; pieza 2: varón de 73 años, lateralidad derecha, peso 88kg, altura 170 cm) donados por el Departamento de Anatomía de la Universidad Complutense de Madrid, pertenecientes al Centro de Donación de Cuerpos y Salas de Disección de dicha universidad. Los sujetos no tenían dolencias músculo-esqueléticas conocidas. Los cadáveres se conservaron en cámara de congelación normal a −20°C hasta el momento de la extracción de las piezas.
Se efectuó disección anatómica del miembro inferior de los cadáveres con desinserción total de todas las estructuras cápsulo-ligamentosas coxofemorales y de rodilla hasta la extracción del fémur total sin inserciones osteotendinosas. Se realizó osteotomía transversa de la extremidad proximal del fémur a una distancia de 35cm del punto más distal del trocánter menor. Las piezas se conservaron frescas en material humedecido en suero salino hasta la realización de la tomografía computarizada de alta resolución (AR-QCT) 12 h más tarde.
Obtención del modelo geométrico en 3DSe realizó una AR-QCT a cada uno de los especímenes femorales mediante un escáner clínico convencional modelo Siemens Somaton. Los fémures se dispusieron en posición horizontal fijados por su parte más distal, con una orientación del cuello femoral paralela al suelo y una superficie libre de material óseo de 25cm en el arco de escaneado. La resolución del estudio fue de 0,44mm en el plano transversal y de 1,0mm en la dirección longitudinal del fémur, al objeto de obtener vóxeles con dimensiones de 0,2×0,2×0,2mm3. El tratamiento de la imagen DICOM obtenida y su posterior segmentación se llevó a cabo mediante el software ScanIP (Simpleware, Exeter, Reino Unido). Esta metodología permitió la generación del volumen geométrico correspondiente al fémur proximal, la discriminación de sus 2principales materiales (hueso cortical y hueso trabecular), la determinación de las densidades radiológicas y la caracterización mecánica de cada espécimen.
Morfología macroscópica del fémur proximalAl objeto de caracterizar macroscópicamente los fémures, se realizó medición digital sobre el modelo geométrico de la morfología real de cada fémur como expresa la tabla 1.
Modelo numérico de elementos finitos del fémur proximalUn análisis previo de la sensibilidad del mallado permitió establecer una malla de 3mm en la zona de la diáfisis y 2mm en la zona proximal, con un refinamiento en el cuello femoral de 1mm.
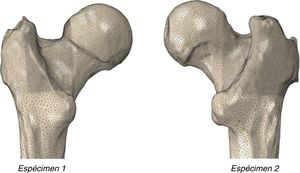
Con estas condiciones, y mediante el código de elementos finitos Abaqus/Standard, se generó la malla del fémur proximal formada por 500.000 elementos tetraédricos cuadráticos y alrededor de 1.000.000 de nodos. La figura 1 muestra la malla obtenida.
Las relaciones establecidas entre las unidades Hounsfield (UH), DMO y propiedades mecánicas (módulo de Young) de cada vóxel se establecieron mediante las ecuaciones publicadas por Morgan et al.14. La simulación de carga y las sujeciones distales del fémur proximal virtual se aplicaron de forma similar a lo realizado en los ensayos experimentales previos.
Las UH son las unidades extraídas del escáner, y consisten en una escala de grises. Su valor depende de la atenuación del material, estableciendo el 0 HU en el agua destilada a condiciones normales de presión y temperatura. Esta unidad puede ser transformada en propiedades mecánicas a partir de la siguiente serie de relaciones: −1.000 HU para el aire, 10-40 HU en el músculo, en torno a 600 HU para el hueso trabecular y 1.000 HU o superiores en el hueso cortical, y se pueden inferir sus propiedades mecánicas según las ecuaciones publicadas por Morgan et al.14.
La propagación de la fractura se modeló mediante desarrollo computacional propio del equipo investigador6, se disminuyeron las propiedades mecánicas de los elementos dañados y se simuló así la separación entre las distintas partes fracturadas. Para el cálculo de la carga máxima de fractura se han considerado los valores críticos de tensión en cada elemento en función de su DMO.
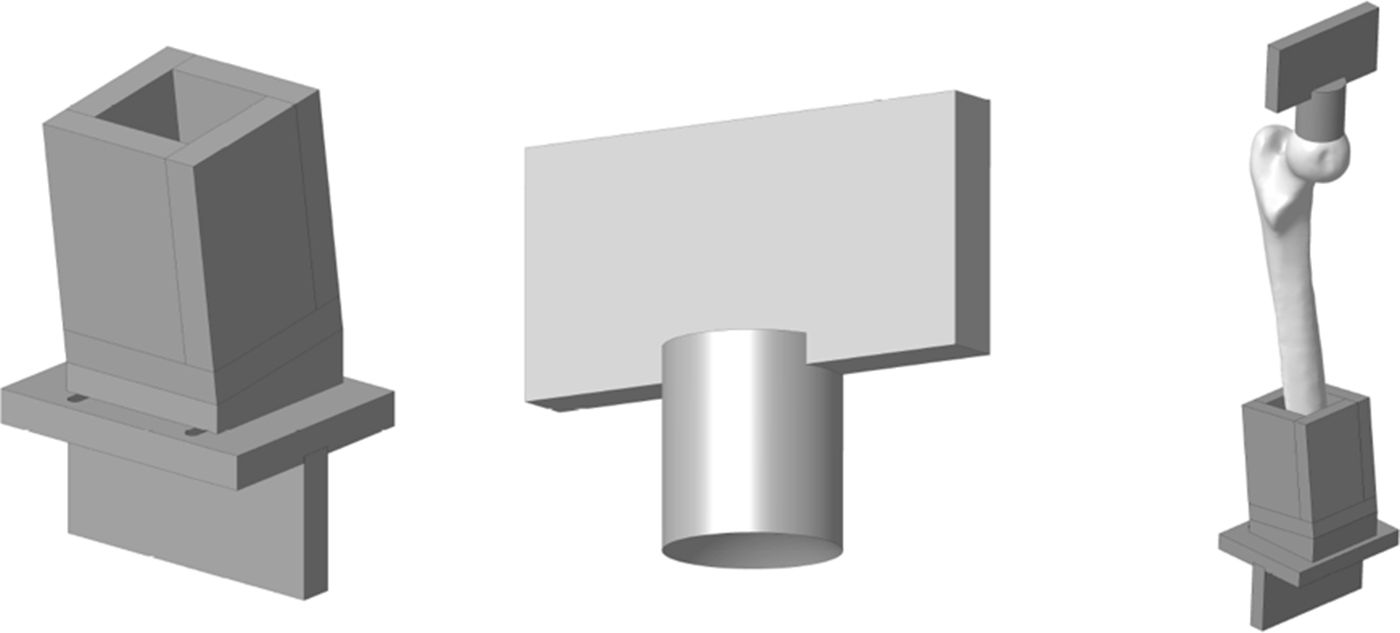
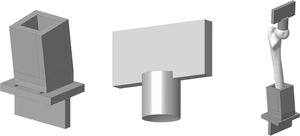
Modelo experimental de fémur proximalPara la adaptación de las piezas anatómicas al banco de ensayos se diseñó un utillaje especial formado por 2conjuntos de piezas fabricadas en una aleación de aluminio (AA 7075-T6). El conjunto superior estaba formado por una placa para sujetar el útil a la prensa y un cilindro con un extremo cóncavo para adaptarse a la geometría de la cabeza del fémur con un radio de 25mm. El conjunto inferior estaba formado por una caja en la que se embebe la diáfisis del fémur mediante polimetilmetacrilato y una placa para fijarla a la máquina de ensayos. La caja tiene una cuña para que la geometría resultante forme 8° con el eje del fémur. La figura 2 muestra los diseños específicos desarrollados.
Se realizaron 2ensayos experimentales consecutivos sobre cada pieza anatómica. El primero consistió en aplicar fuerzas progresivas de carga en el plano frontal iguales a 500, 1.000, 1.500 y 2.000N, con el eje de carga a 8° con respecto al de la diáfisis femoral. Posteriormente se realizó un aumento progresivo de la carga sobre la cabeza del fémur hasta que se produjo la fractura macroscópica de la extremidad proximal.
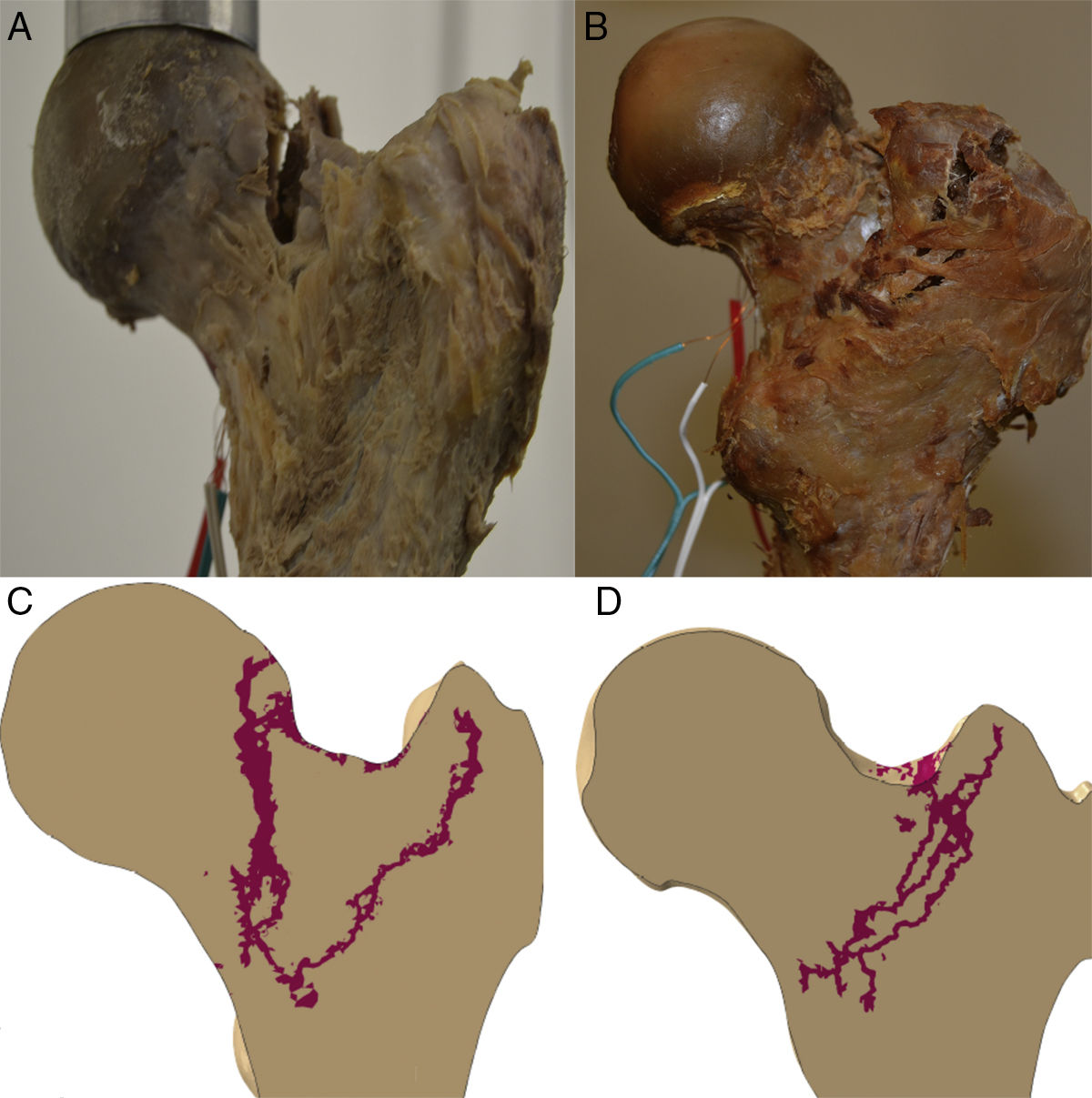
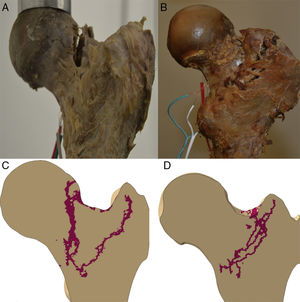
Para cuantificar las deformaciones experimentadas por la pieza durante las cargas mencionadas, se dispusieron galgas extensiométricas sobre la superficie del fémur, 2en la diáfisis y una en el cuello femoral. La figura 3 muestra los especímenes en el banco de ensayos.
Variables de estudioPara la validación de la capacidad de predicción del modelo numérico se consideraron 4 variables para comparar entre el modelo experimental y computacional:
- •
Punto de inicio de la fractura.
- •
Propagación de la fractura y correlación con patrón clínico.
- •
Deformaciones obtenidas en cargas inferiores a la fractura.
- •
Carga máxima de fractura.
El modelo computacional fue capaz de determinar el punto de inicio de la fractura, con una discreta tendencia a la medialización anatómica de dicho punto (tabla 2).
Propagación de la fracturaLa línea de propagación del modelo computacional en los 2especímenes tuvo un patrón cuasi superponible a los obtenidos en los modelos experimentales, como muestra la figura 4.
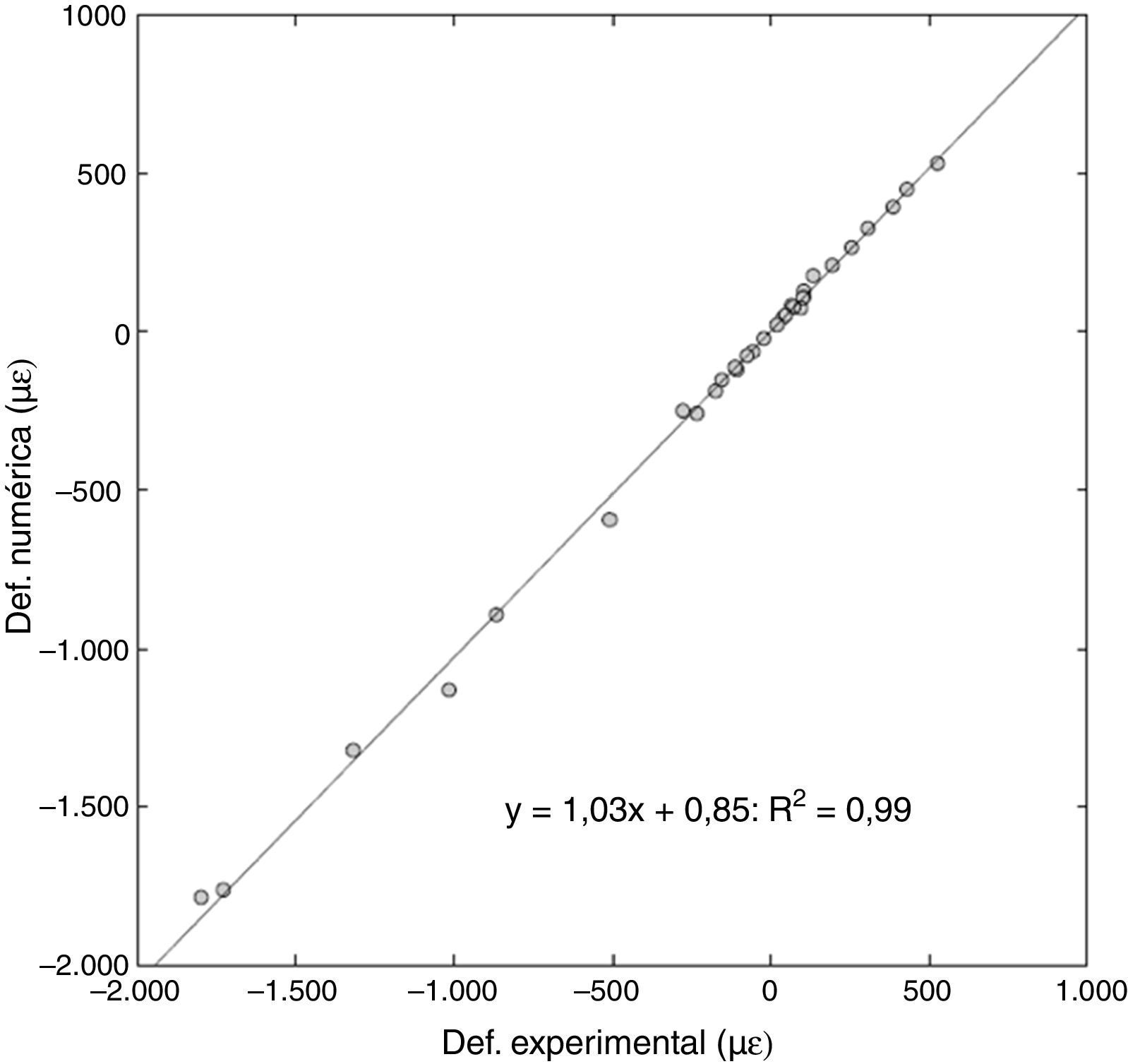
Deformaciones obtenidas en cargas inferiores a la fracturaEl grado de correlación fue muy alto al comparar el valor real de deformación de las muestras con el obtenido por el modelo computacional.
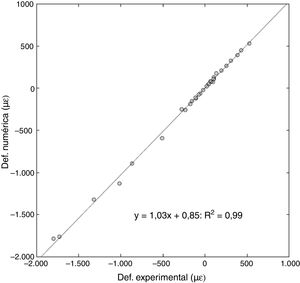
Para un total de 32 puntos analizados (4 deformaciones por 4 casos de carga en cada fémur), se obtuvo una pendiente de 1,03 en la regresión lineal, con un error relativo entre las deformaciones del 6% y un coeficiente de Pearson de R2 = 0,99 (fig. 5).
Carga máxima de fracturaTanto en el modelo computacional como en el experimental, el valor de carga máxima era mayor en el espécimen 2, correspondiente a un varón, con una diferencia aproximada de 1.000N entre los 2donantes.
El modelo computacional de elementos finitos infraestimó discretamente la carga máxima de fractura, con un error relativo aproximado al 10%. La tabla 3 muestra los valores numéricos de carga de fractura.
DiscusiónEl principal logro de este trabajo es haber desarrollado un modelo computacional de AEF del fémur proximal capaz de simular e imitar el comportamiento biomecánico de fémures humanos, tanto para cargas bajas como para cargas de fractura, que ha podido ser contrastado con un modelo experimental clásico realizado en piezas anatómicas sobre un banco de ensayos.
Sobre este modelo computacional podrán evaluarse infinidad de interacciones cualitativas y cuantitativas por el equipo investigador: condiciones biomecánicas de precarga, condiciones de carga, modelos de fracturas, material de osteosíntesis, implantes protésicos, etc., que lo consoliden como un potente banco de ensayos de experimentación computacional sobre el fémur proximal humano.
Están descritos modelos vertebrales15 y femorales1,6,16 de AEF a partir de cortes 3D de tomografía cuantitativa de alta resolución (AR-QCT), incluso cuando se emplean resoluciones de escaneado bajas17. Se ha demostrado que existe una buena correlación entre el comportamiento biomecánico y la resistencia ósea total predicha por AEF18,19 y los determinados experimentalmente en especímenes vertebrales y femorales de cadáver1,17,20,21. Si bien estas correlaciones resultan muy interesantes para la evaluación in vitro de la resistencia total de un hueso, existe una dificultad añadida para la transferencia a la clínica de estos resultados, especialmente en lo relacionado con un hueso envejecido o con osteoporosis senil18.
Para que el modelo computacional de un fémur proximal sea lo más realista posible, y especialmente en el momento de evaluar su comportamiento en un modelo de fractura por fragilidad, es necesario que sus propiedades mecánicas estén relacionadas básicamente con la DMO1,22. En nuestro modelo, mediante filtros de software específicos, se ha podido diferenciar las distintas zonas del fémur en función del valor de las UH de cada vóxel y, secundariamente, por tanto, de su DMO. La transformación de una escala de grises (UH) en valores de DMO y especialmente en propiedades mecánicas se realizó siguiendo la propuesta por Morgan et al.14 para obtener la rigidez en cada elemento en función de su DMO. De esta manera se pudo, por un lado, diferenciar hueso trabecular de hueso cortical y, por otro, se pudieron aplicar al modelo distintas propiedades mecánicas en función de si cada zona micro del hueso presentaba distintas DMO.
La misma sistemática se ha seguido para el cálculo de la carga máxima de fractura considerando los valores críticos de tensión en cada elemento hasta alcanzar el punto de rotura en función también de su DMO. Esta estrategia aproxima el modelo a las condiciones mecánicas que se dan en el hueso osteoporótico senil, ofrece unos valores numéricos de cálculo lo más realistas posibles y, por tanto, aproxima el modelo matemático al problema clínico diario de fragilidad ósea al que se enfrenta el cirujano.
Pero para que el modelo computacional de AEF tenga aplicación clínica es necesario que sea heterogéneo tanto en la rigidez de los materiales como en las propiedades de fractura13, con diferentes relaciones entre estos parámetros y la DMO23. Además, la carga máxima y la energía total de fractura ha de obtenerse a partir de la curva de carga-desplazamiento, tal y como ocurre en un ensayo experimental real1,12. Por último, resulta crítico que el modelo demuestre una buena correlación entre la propagación de la fractura obtenida en los test experimentales y la predicción computacional.
En este sentido, nuestro modelo es el más completo publicado hasta el momento, al tener en cuenta todas las circunstancias mencionadas. Creemos que la correlación estadística tan importante que existe entre deformidades obtenidas en cargas inferiores a la fractura entre el modelo computacional y lo obtenido experimentalmente en el banco de ensayos, junto con la similitud de los trazos propagación de fractura de los especímenes 1 y 2, constituye un claro elemento de solidez del modelo computacional y es un hecho validador de nuestro modelo de elementos finitos de fémur proximal.
Queremos llamar la atención sobre que las condiciones de trabajo experimental para los 2especímenes han sido exactamente las mismas y que han estado controladas en todo momento por el equipo investigador (fuerzas progresivas de la carga en el plano frontal formando 8° con el eje de la diáfisis de 500, 1.000, 1.500 y 2.000N) y, por ello, resulta llamativo que se produzcan 2tipos de rotura totalmente diferenciables entre sí, como muestra la figura 4, y con importante similitud con lo que ocurre en la práctica clínica habitual. En el espécimen 1 se produce un trazo de fractura que puede clasificarse como subcapital mientras que en el espécimen 2 se trata de una fractura claramente extracapsular. Más sorprendente es, si cabe, que en la predicción computacional encontremos los mismos hallazgos. Por ello, es sugestivo pensar que existen unos condicionamientos materiales o nano-, micro- y macroestructurales que condicionan un patrón de fractura, independientemente de la intensidad de la carga o de la dirección de aplicación. Hay que destacar que el espécimen 2 presentaba un mayor ángulo cervicodiafisario, que hace que tolere mejor la carga axial recibida y, por ello, que precise mayor fuerza de rotura. Pero, a pesar de que ni la metodología empleada ni el número de especímenes analizados nos permite establecer una relación directa entre estas variables, sí creemos que estos hallazgos refuerzan la exactitud de la predicción del modelo computacional y, por ello, su futura aplicación clínica.
En relación con este último punto, los trabajos de Lenich24,25 han demostrado que el primer efecto que ocurre en el fenómeno de «cut out» es un momento de rotación del fragmento óseo sobre el implante cefálico para, posteriormente, a través de un fenómeno continuo de micromovimientos, ir dañando el hueso hasta que se produce la protrusión del material de osteosíntesis. El modelo computacional que hemos desarrollado puede ayudar a entender este modelo patogénico, al permitir simular las alteraciones que se producirían al considerar como punto fijo el ápex de la circunferencia de la cabeza femoral y simular los micromovimientos de flexoextensión.
La principal limitación del modelo computacional para su utilización como herramienta de apoyo clínico son las inherentes al trabajo por AEF. Como hemos comentado, existe todo un proceso que incluye la traslación de un elemento físico real a un elemento virtual segmentado en pequeñas formas geométricas y que toda la relación de estos elementos entre sí está controlada por las condiciones que establece el equipo investigador.
También es cierto que se ha realizado el trabajo anatómico, computacional y experimental solo sobre 2especímenes, pero es innegable que el número de donantes y la cantidad de recursos físicos y humanos que se necesitan para ampliar la serie es ingente, y que en otros sectores productivos y de investigación, como la ingeniería, el trabajo exclusivamente computacional constituye el patrón estándar en aquellas circunstancias en las que los modelos experimentales clásicos son inviables o económicamente insostenibles8,11,26.
El papel de los músculos, tendones y ligamentos como elementos amortiguadores de la caída y, por ello, de la fuerza de rotura, es indiscutible22. Asociado a la edad existe un debilitamiento muscular que, junto a la pérdida de elasticidad de ligamentos y tendones, pone al individuo en situación de riesgo de fractura clínica. Nuestro modelo no tiene en cuenta la acción de estas partes blandas porque aumentaría enormemente la necesidad de cálculo computacional, pero, sobre todo, porque no se puede contrastar el valor computacional con un valor experimental. No existe descrito, que nosotros sepamos, un modelo cadavérico que reproduzca la acción estabilizadora de músculos y tendones ante una caída y mucho menos en condiciones de osteoporosis senil. No obstante, y a pesar de las limitaciones expresadas, creemos que el modelo es válido para avanzar en el conocimiento del fémur proximal, no solo como una estructura de carga, sino también en comprender cómo, en cada punto concreto del hueso, los parámetros subyacentes microscópicos pueden afectar a la totalidad de la estructura.
Únicamente con un conocimiento claro de las circunstancias mecánicas que condicionan la aparición de una fractura de la extremidad proximal de fémur estaremos en condiciones de hacer investigación traslacional hacia los aspectos clínicos más relevantes de esta dolencia: punto de inicio de la fractura y su posterior progresión a lo largo de la superficie ósea tipo de fractura, factores biomecánicos predictores de fractura y de su tipo, diseños específicos de implantes, factores predictores de fracaso de osteosíntesis, etc.1,10,16.
En resumen, este es un artículo escrito por clínicos para clínicos en el que no se pretende, ni se quiere, entrar en discusión profunda sobre los fundamentos matemáticos que sustentan el método de AEF, ni en las fórmulas matemáticas que definen cada una de las relaciones de los elementos entre sí, pero en el que queremos destacar que la metodología que hemos utilizado para la obtención de la estructura geométrica «virtual» del fémur proximal, las condiciones materiales y estructurales previas, de contorno y de carga de fractura son las reales y que el AEF es un método válido avalado en la literatura que viene siendo utilizado por equipos investigadores para la evaluación de distintas dolencias relacionadas con nuestra especialidad7,11,15,23,27-30.
El modelo que presentamos representa la consolidación de una línea de trabajo de un grupo multidisciplinar compuesto por cirujanos ortopédicos e ingenieros con una clara y convencida orientación clínica6,13,23,31. El modelo computacional de AEF desarrollado por este equipo investigador multidisciplinar se puede considerar, en conjunto, un modelo completo de AEF de la extremidad proximal del fémur con aplicabilidad clínica futura.
Nivel de evidenciaNivel de evidencia ii.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses en relación con el manuscrito y sus conclusiones.
AgradecimientosLos autores quieren agradecer a la Dra. Teresa Vázquez, profesora titular del Departamento de Anatomía de la Universidad Complutense de Madrid su ayuda para la consecución del trabajo.