Tras las evidencias acumuladas con el uso de dispositivos de asistencia circulatoria de flujo pulsante y continuo, surge la polémica sobre los efectos del tipo de flujo en el sistema circulatorio. Este artículo propone la caracterización del flujo pulsante en conductos elásticos, para analizar la influencia de la pulsación en el sistema y entender las peculiaridades del flujo en el lecho vascular.
MétodosUtilizando un dispositivo de bombeo tipo saco elástico de accionamiento neumático, se procedió a la observación visual e instrumental del flujo a través de conductos tanto flexibles (vaso venoso bovino) como rígidos (tubo plástico), y se analizaron las características biomecánicas de la pulsación en ambos.
ResultadosBasado en la observación experimental y el análisis biomecánico del flujo pulsante en un conducto elástico, se caracterizó el patrón de la pulsación y se planteó un modelo que explica la influencia de la pulsación en el sistema vascular y los efectos de su ausencia. El modelo propuesto incluye la condición general de flujo (componente mecánico) y su aplicación al sistema vascular (componente fisiológico).
ConclusionesEl modelo planteado permite determinar la relación entre las condiciones del flujo y la reacción de la pared, así como unificar la interpretación de factores fluido-dinámicos involucrados a la vez, que advierte sobre los efectos del cambio de flujo y su significado en lo que sería la operación de dispositivos de asistencia circulatoria.
The evidence accumulated on the use of pulsatile and non-pulsatile flow-dependent devices raises a controversy concerning the effects of the flow type on the Circulatory system. This paper proposes to characterize the properties of pulsatile flow in elastic conduits in order to determine how the pulse affects the system and to determine the specific details of the flow in the vascular bed.
MethodsThe biomechanical properties of pulsatile flow were measured on flexible (calf venous vessel), and rigid (plastic pipe) conduits in which the flow was implemented using a pneumatic elastic sack-like pumping device.
ResultsThe experimental data and the biomechanical analysis of the pulsing flow was used to determine the flow pattern in order to develop a mechanical model explaining the effects of the pulse on the vascular system. The resulting model includes the flow's general condition (mechanical component) and its effects on the vascular system (biological/physiological component).
ConclusionsThe model proposed here allows determining the relationship between the flow conditions and the reaction on the wall; it also allows unifying the interpretation of fluid-dynamic factors affecting these phenomena and represents a warning system about the effects of flow changes on the operation of circulatory assistance devices.
Luego de utilizar por varios años las máquinas de circulación extracorpórea y los dispositivos de asistencia circulatoria, surge la polémica por los efectos del tipo de flujo tanto pulsante1,2 como continuo3,4 en el sistema vascular5, con el fin de identificar las consecuencias de reemplazar temporal o permanentemente la función de bombeo del corazón, y sacar el mejor provecho de este tipo de ayudas terapeúticas6.
Aunque varias investigaciones muestran la conveniencia de mantener el flujo pulsante, no sólo por su condición natural, sino por los beneficios que representa en los procesos de recuperación del paciente; algunas investigaciones sobre asistencia circulatoria con dispositivos de flujo continuo, sugieren que se presentan alteraciones mínimas metabólicas y funcionales2,4.
Una opción para esclarecer los efectos de la pulsación del flujo -dilucidando las características de la corriente sanguínea-, y comprender su interacción con el sistema vascular7, son los datos clínicos obtenidos durante el soporte con máquinas de circulación extracorpórea; aunque son datos difíciles de aplicar para tal propósito, porque se obtienen bajo condiciones no controladas, que involucran múltiples factores: recirculación pulmonar, oxigenación extracorpórea, hipotermia, suministro de agentes farmacológicos, entre otros; además de que sólo es posible evaluar tales condiciones en un corto tiempo de aplicación8, a la vez que tampoco pueden ser manipuladas experimentalmente por los peligros que implicaría en el sujeto de estudio.
Para superar las limitaciones impuestas por la verificación directa en el organismo humano, se ha recurrido a modelos físicos y a modelos animales, analizados mediante conceptos biomecánicos. Schneck et al.9–11 desarrollaron un modelo para analizar el flujo pulsante en un conducto rígido de sección divergente; considerando la interacción entre los efectos viscosos y los efectos inerciales convectivos y transitorios. Por su parte, Kiser et al.12 realizaron un estudio en un modelo animal para analizar la onda de flujo en la aorta.
El propósito del presente trabajo es analizar la formación de un flujo pulsante en conductos elásticos13, por medio de una bomba pulsante de saco14, para comprender la interacción de los fenómenos subyacentes en la corriente y así plantear un modelo que caracterice dicho flujo en conductos flexibles, que permita describir el efecto de la pulsación en el sistema vascular. El modelo de flujo propuesto permite además dilucidar los efectos del cambio de flujo pulsante a continuo, según se deriva de algunos de los procedimientos de asistencia circulatoria.
El modelo de flujo se plantea con base en modelos experimentales in vitro que reproducen el flujo pulsante a través de 2 tipos de conductos: uno biológico (yugulares de bovinos) y otro mecánico (conductos elásticos). Los resultados obtenidos fueron interpretados mediante conceptos biomecánicos y fluido-dinámicos, de acuerdo con la caracterización del sistema vascular y circulatorio9–11,15.
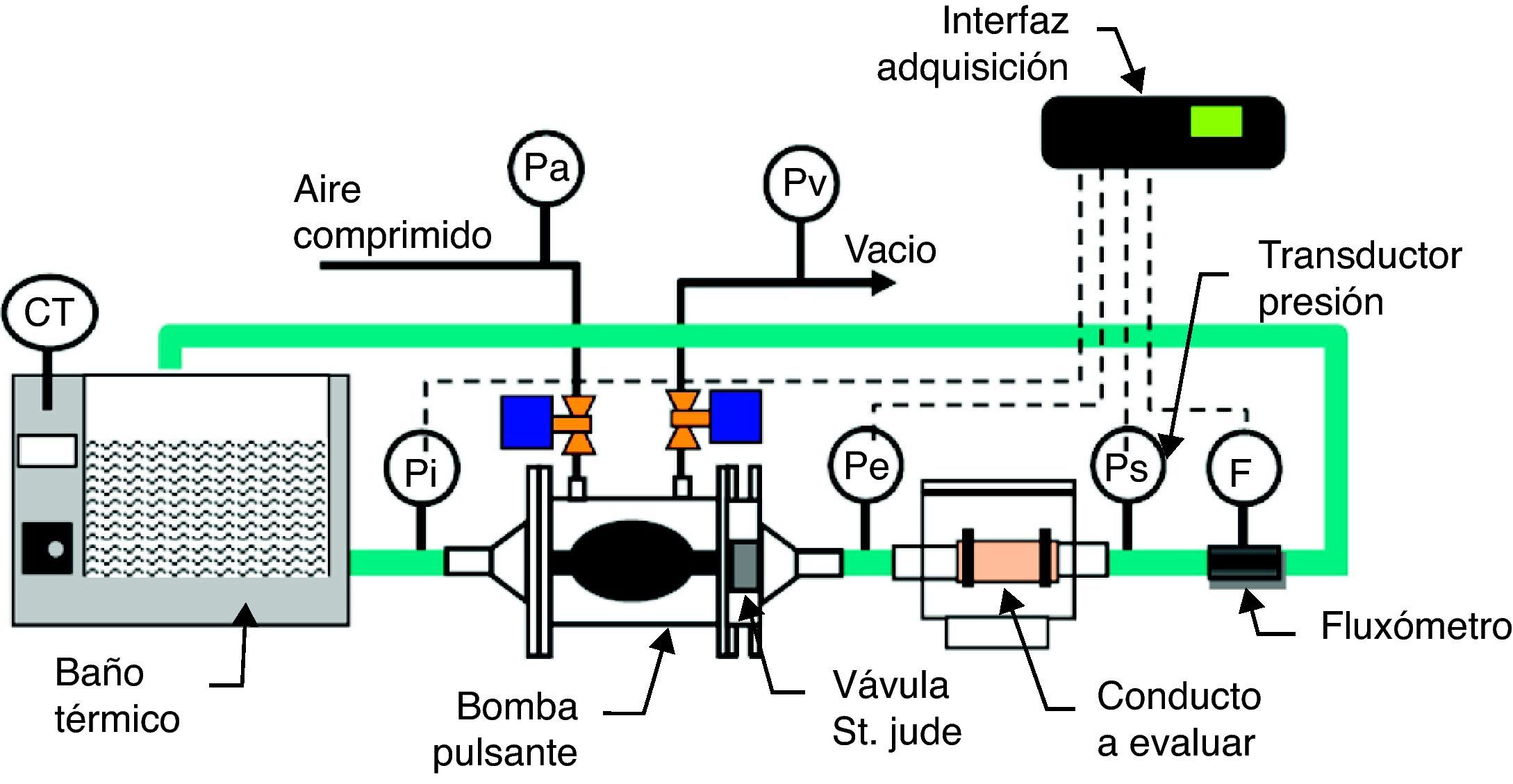
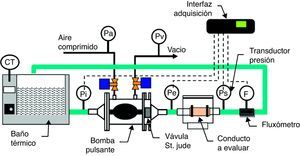
MétodosMediante un dispositivo mecánico de bombeo de saco elástico (fig. 1) conectado a una cámara de visualización14, se analizó el patrón de un flujo pulsante. Se generó un flujo entre 2 y 3.2 L/min, con una frecuencia de 50-70ppm, mediante la aplicación intermitente de una presión entre 150 y 160mmHg dentro de una carcasa rígida, para la compresión del saco elástico de bombeo. Como fluido de trabajo se usó una solución acuosa de carboximetil-celulosa con 5 cPo de viscosidad, teñida con colorante rojo. Las propiedades de la solución se midieron así: la viscosidad de la solución acuosa con una copa Ford, con la solución precalentada a 37°C, y la densidad con un pignómetro y una báscula gramométrica. Por su parte, las variables de proceso se midieron así: el caudal con un fluxómetro electromagnético y las presiones en la salida del dispositivo, en la descarga de la cámara de visualización y en los conductos, con transductores de presión Ohmeda®. Las 4 variables se capturaron con un recolector16 de datos Datataker® a una frecuencia de 250 muestras/min, es decir, 4.2 muestras/seg que equivale a 3 veces la frecuencia del fenómeno observado, como lo exige el teorema de Nyquist; y por tanto, se descarta el riesgo de submuestreo y distorsión de la señal capturada. La tensión de pared, como la fuerza de reacción a la presión de flujo, se calculó con la presión medida en el conducto dividida entre el área de pared donde se aplica.
Banco de pruebas para flujo pulsante. Consta de bomba de flujo pulsante (cámara rígida, saco elástico y válvula bivalva St. Jude® en la salida), baño térmico con control de temperatura, fluxómetro y transductores de presión (en la entrada de la bomba y en la entrada y salida del conducto). Modificada de Bustamante J et al.14.
El procedimiento de pruebas de los conductos fue el siguiente: se varió la frecuencia de operación de la bomba, y se midieron el caudal resultante en la salida del banco de pruebas y las presiones en la entrada y la salida del conducto evaluado. Además, el flujo pulsante fue observado en una cámara de visualización de vidrio, a una frecuencia determinada.
Para evaluar la interacción entre la pulsación del flujo y el comportamiento mecánico de la pared del conducto, se conectaron al dispositivo de bombeo conductos de diferente composición y elasticidad (biológicos e inertes). Un grupo de conductos lo conformaron segmentos de venas yugulares frescas de bovinos, las cuales se mantuvieron sumergidas en solución salina isotónica a 37°C, para conservar la viscoelasticidad de la pared, y con ellas representar la respuesta de pared flexible; se midieron el diámetro interno en reposo y el diámetro exterior una vez alcanzada la continuidad del flujo durante la prueba. El otro grupo lo conformaron tubos inertes con diferente módulo de elasticidad: silicona, con una expansión excesiva ante la presión de trabajo, y Tygon®, con una expansión despreciable. Por su poca expansión en las condiciones de la prueba, el Tygon® fue seleccionado para evaluar la respuesta de pared rígida.
El modelo propuesto consta de 2 criterios: el primero, describe la condición general de flujo basada en las características del flujo pulsante y los resultados obtenidos en conductos flexibles y rígidos, o componente físico; y el segundo, plantea su aplicación conceptual al sistema vascular, basado en la interpretación biomecánica del sistema cardiocirculatorio11,15 y los resultados observados en conductos vasculares frescos (yugulares de bovinos), o componente fisiológico.
Considerando que la pared vascular reacciona con una respuesta viscoelástica ante la presión de expulsión ventricular, las condiciones fijadas para modelar el sistema vascular fueron: flujo pulsante, fluido incompresible y viscoso, conducto flexible (viscoelástico), e interacción entre el pulso de flujo y el pulso de la pared. Estas condiciones específicas se representan con los números adimensionales de Reynolds (Re) y Womersley (Wo)9–11,17,18. El número de Re establece las condiciones de flujo relacionando la densidad (ρ) y viscosidad (μ) de la sangre, la velocidad de la corriente (V) y el diámetro del vaso (D), mediante la expresión (Re=ρVD/μ); por su parte, el número de Wo determina el efecto de la frecuencia (f) en el flujo, mediante la expresión (Wo=ρfD2/μ). Se ha encontrado que Re puede alcanzar valores de 6000 en la aorta proximal durante la expulsión ventricular, y entre 1 y 1600 en los demás segmentos vasculares; mientras que Wo puede tener valores de 13 en la aorta, entre 4.5 y 6.6 en las arterias medianas y entre 0.2 a 5.6 en vasos pequeños y arteriolas.
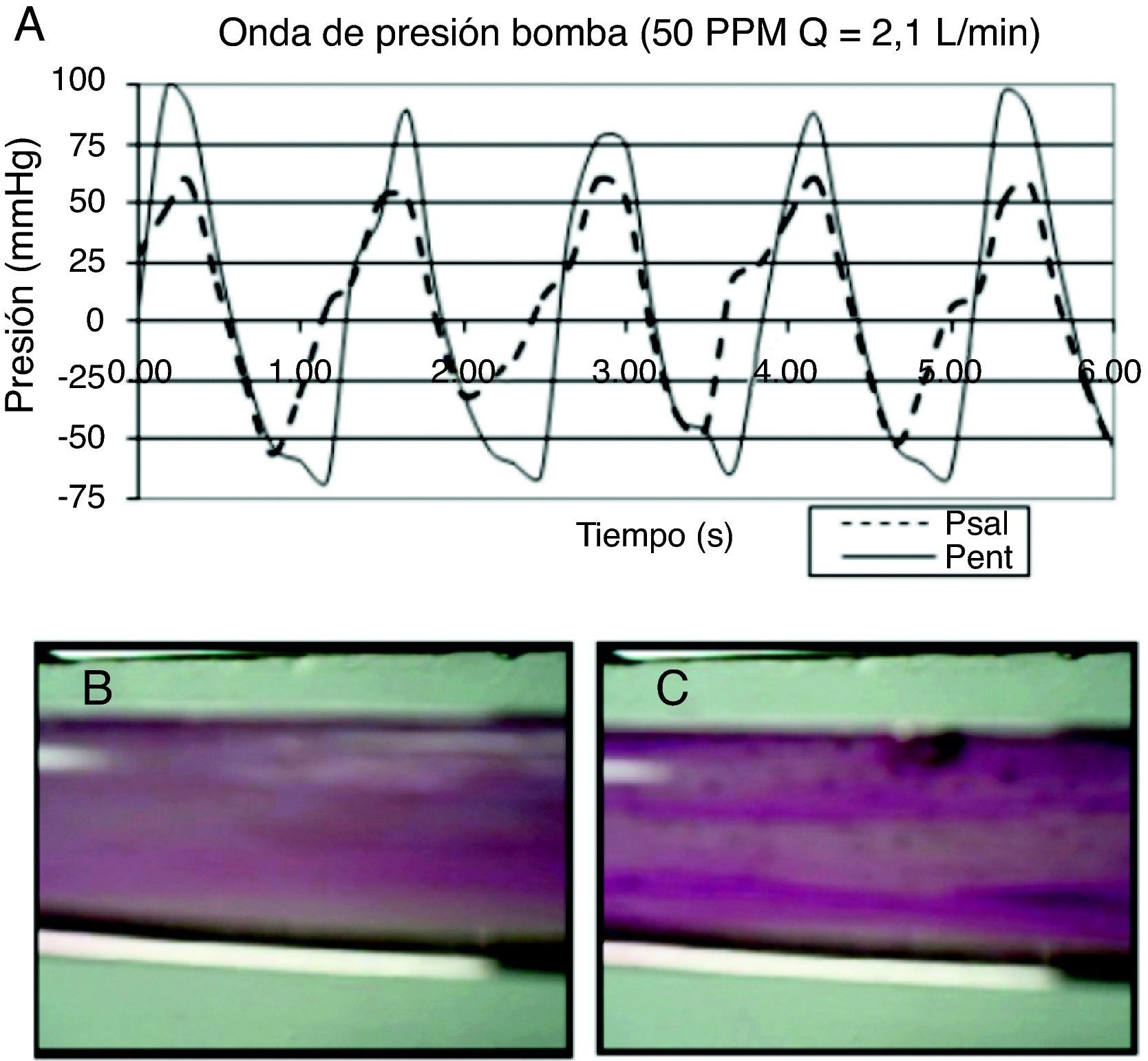
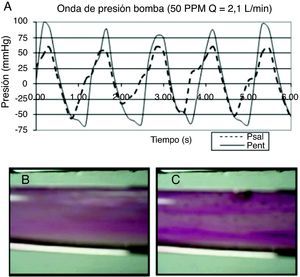
ResultadosLa onda de presión registrada durante la visualización (fig. 2 A) tiene un contorno ondulatorio complejo (como el de la onda de pulso vascular); también se pueden apreciar las muescas de apertura y cierre de la válvula, que mantienen el flujo unidireccional. Con las condiciones de trabajo fijadas en la visualización del flujo, la amplitud de la onda de presión en la entrada de la bomba de saco fue de 150-160mmHg (Pent) (fig. 2 A), y la salida de la cámara de visualización fue de 80-90mmHg (Psal) (fig. 2 A). Los valores negativos de presión en el registro se deben al vacío que se aplica para distender el saco elástico.
Visualización del flujo pulsante. A) Registro de presión generada por la bomba pulsante. La curva de presión en el interior del saco (línea continua, Pent) es la presión de bombeo del sistema, que correspondería a la del ventrículo izquierdo; mientras que la curva de presión en la descarga (línea punteada, Psal) es la presión de flujo en el conducto, que correspondería a la del sistema vascular. B) Observación de la fase activa del flujo pulsante en cámara de visualización: el flujo es ordenado y con velocidad constante. C) Observación de la fase pasiva: el flujo es desordenado y se forman 2 corrientes: una delgada en el núcleo y otra radial cerca a la pared.
Mediante un trazador aplicado al flujo pulsante durante la visualización14, se pudo observar que al aplicar la presión de bombeo se genera una corriente en la que el trazador muestra líneas de flujo definidas, que avanzan de manera organizada en la dirección del flujo, especialmente en el centro donde el efecto de la viscosidad es menor (fig. 2 B); al suspender el bombeo aparecen 2 corrientes: una en el centro del conducto, donde el trazador muestra tendencia al reposo pero conservando el orden de la fase anterior, y otra en la periferia, en la que el trazador se dispersa con movimientos rápidos y localizados, en mayor grado hacia la pared (fig. 2 C).
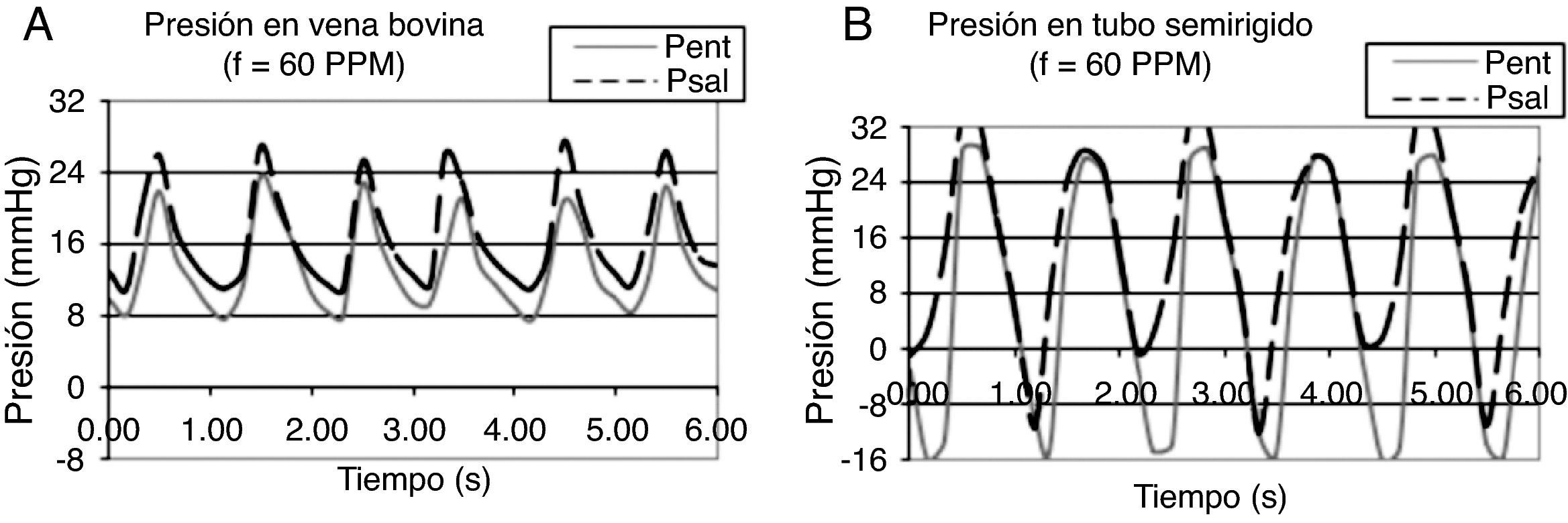
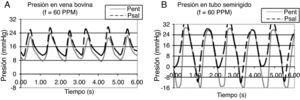
En los registros de presión a través de las venas yugulares bovinas (con presión de bombeo de 40mmHg) se encontró que la onda de presión resultante es asimétrica, con un valor máximo de 23mmHg y mínimo de 8mmHg (fig. 3 A). Durante el bombeo, la presión predomina sobre la tensión de pared, conformando el flujo anterógrado, como se advierte en el ascenso rápido de las curvas; pero es amortiguada por la elasticidad de la pared, que acumula gran parte de la presión de bombeo (17mmHg), dándole a la onda de presión poca amplitud y al área bajo la curva una leve concavidad (debido al tiempo que tarda la expansión del vaso). El equilibrio entre la presión de flujo y el amortiguamiento de la pared determinan la amplitud de la onda de pulso, que en este caso se ve afectada por el efecto de la viscoelasticidad del vaso.
Registro de presión de flujo en conductos. A) Conducto de pared flexible (vena yugular): la curva es asimétrica porque la elasticidad del conducto permite la recuperación de la energía acumulada en la pared; y el gradiente de presión permanente (curvas separadas) indica que hay flujo durante todo el ciclo. B) Conducto de pared rígida (Tygon®): la curva es simétrica porque la rigidez del material impide la deformación de la pared, y no hay gradiente de presión durante la fase pasiva, por lo que sólo hay flujo durante la fase activa.
Durante la suspensión del bombeo, la relajación del vaso conlleva la recuperación viscoelástica de la pared, que se manifiesta por un descenso gradual de la presión, dándole a la onda de presión mayor duración y al área bajo la curva una convexidad pronunciada; evento que además de generar el flujo retrógrado, atenúa los efectos transitorios de la pulsación: sostiene la reducida corriente en el núcleo y previene la separación del flujo, como se advierte de la eliminación de los valores negativos de presión en el conducto vascular.
La recuperación viscoelástica de la pared mantiene un gradiente de presión positivo, con la energía suficiente para propiciar la superposición de la reducida corriente del núcleo de la fase pasiva con el flujo anterógrado de la siguiente fase activa, como lo indica el paralelismo entre la curva de entrada al conducto (Pent) (fig. 3 A) y la de salida (Psal) (fig. 3 A), conformando una corriente que avanza permanentemente durante el ciclo, dándole al flujo el aspecto de continuo. Este fenómeno depende de la frecuencia del pulso13, que se advierte con las variaciones de Wo.
En contraste, en el registro de presión de un tubo rígido se encontró que la onda de presión generada es simétrica, con un valor máximo de 30mmHg y mínimo de −16mmHg (fig. 3 B). Durante el bombeo, como no hay expansión del conducto, se invierte casi toda la energía en la formación del flujo anterógrado, como lo muestra el ascenso rápido de la onda de presión, con apreciable amplitud porque no hay acumulación de energía en la pared; la otra parte de la presión (8mmHg) se pierde en aceleración del flujo y rozamiento con la pared. Durante la suspensión del bombeo, la presión se disipa rápidamente porque no hay acumulación de energía, como lo indica el descenso súbito de la curva, dándole a la onda la forma simétrica. Como el área de flujo es constante (conducto que no se expande), se propicia la aparición de los efectos transitorios: reduciendo la corriente continua del núcleo y provocando la separación, como se advierte por los valores negativos de presión, que son persistentes y de magnitud apreciable. Dado que la pared no se deforma no hay acumulación de energía, entonces tampoco se libera energía al flujo para mantener el gradiente de presión durante la fase pasiva: la presión en la entrada del conducto (Pent) (fig. 3 B) y en la salida (Psal) (fig. 3 B) son casi iguales, como lo indica el traslapo de las 2 curvas durante el descenso, por lo que tampoco hay flujo de una fase a otra durante un ciclo; provocando una corriente segmentada en el tiempo. Además, la poca atenuación de la pared provoca la superposición de las fases activas, propiciando resonancia en el sistema; como se advierte del adelanto del ascenso de presión en la curva de salida.
Planteamiento del modelo de flujo pulsante vascularEl modelo propuesto para caracterizar el patrón general de flujo de una corriente pulsante y su interacción con la elasticidad de pared, así como su consecuente aplicación conceptual al sistema vascular, se plantea en los siguientes términos.
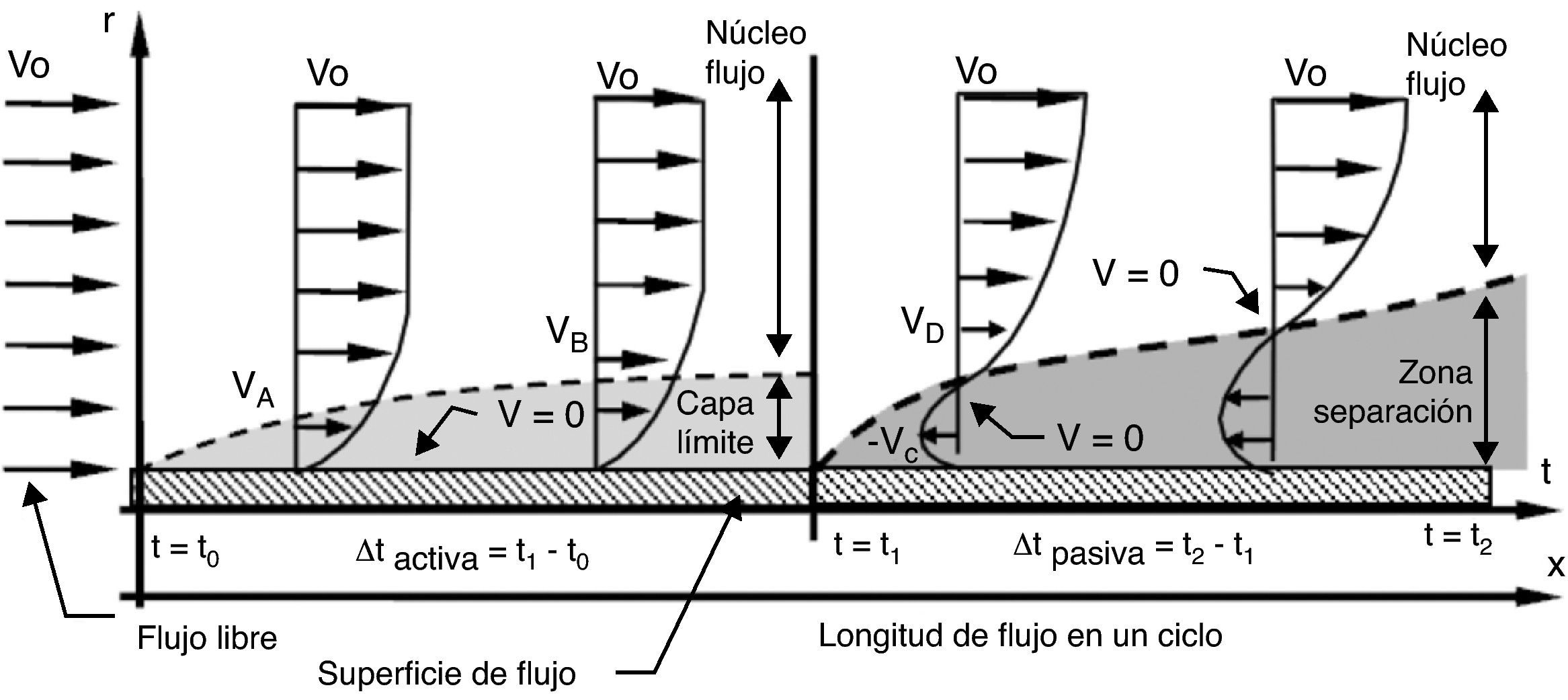
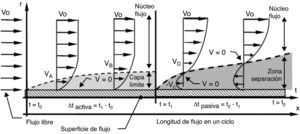
Cuando el fluido es impulsado por una presión periódica (pulsante), se desarrolla un patrón de flujo en cada fase del ciclo. Durante la aplicación de presión (fase activa), el flujo es dominado por las fuerzas inerciales convectivas, produciendo una corriente central en dirección axial que ocupa casi toda el área de flujo, y formación de capa límite (fig. 4). En cambio, cuando cesa la aplicación de presión (fase pasiva), el desequilibrio súbito entre las fuerzas inerciales convectivas y las viscosas genera fuerzas inerciales transitorias, que a su vez provocan la aparición de una corriente secundaria caracterizada por tener dirección radial y velocidad en sentido contrario a la dirección de la corriente principal. Esta corriente secundaria frena el avance del fluido, causando la separación de la corriente aún en presencia de un gradiente de presión favorable. Así, la corriente secundaria frena el fluido tanto en el núcleo de flujo como en la capa límite. Como el flujo axial se va desvaneciendo en la fase pasiva, la velocidad llega a 0 en un punto entre el centro de flujo y la pared del conducto, y no sobre la pared, propiciando la separación de la corriente (ver puntos con velocidad 0 [V=0] en fase pasiva) (fig. 4). El efecto de las fuerzas inerciales transitorias en la fase pasiva es entonces, el de la formación de 2 corrientes: una axial residual en el centro, que continua avanzando por el impulso acumulado en la fase activa anterior, y otra radial dominante en la periferia del conducto, que retarda el flujo y provoca la separación.
Estructura de flujo pulsante cerca de la pared de un conducto elástico. Durante la fase activa se forma capa límite y la velocidad es 0 (V=0) sobre la pared; en cambio, durante la fase pasiva es 0 en un punto entre el centro y la pared. Vo: velocidad de entrada; Vi: velocidad del flujo en el punto i; r: radio del conducto; t: tiempo transcurrido del ciclo.
La separación de la corriente en un flujo pulsante es más temprana que en uno continuo, es decir, para las mismas condiciones (con Re semejantes) la distancia que recorre un flujo pulsante sin separarse de la pared del conducto durante la fase activa es menor que la que puede alcanzar el continuo. La magnitud en la cual se anticipa la separación depende de la proporción de las fuerzas inerciales convectivas (representadas por la velocidad en Re) y las fuerzas inerciales transitorias (representadas por la frecuencia en Wo): a medida que aumenta la frecuencia13 se incrementan las fuerzas inerciales transitorias (Wo es más alto), aumentando la influencia de los efectos transitorios de la fase pasiva, y se adelanta la separación de la corriente; pero si Re es alto y Wo es bajo la separación se retarda. Así, hay un Wo a partir del cual no hay corriente radial secundaria, y la separación ocurre en el mismo punto en el que se presenta en un flujo continuo11.
Cuando el flujo pulsante tiene lugar a través del conducto de pared rígida, los efectos transitorios de la fase pasiva son realzados: el gradiente de velocidad negativo frena el avance de la corriente del núcleo, y la separación de corriente se adelanta, generando una presión negativa cerca de la pared (fuerza de arrastre). Además, la corriente secundaria desarrollada por las fuerzas inerciales transitorias de la fase pasiva es absorbida por el flujo que genera las fuerzas inerciales convectivas de la fase activa siguiente, dándole al flujo un aspecto fragmentado a lo largo del conducto.
Si el flujo pulsante tiene lugar a través del conducto de pared flexible, los fenómenos transitorios son atenuados: el gradiente de presión negativo es reforzado por la recuperación elástica de la pared, dándole a la corriente secundaria suficiente energía para generar un flujo reverso; y la separación es retardada por la recuperación del diámetro del conducto, previniendo la aparición de fuerzas de arrastre. Además, la corriente del núcleo avanza a lo largo del conducto dependiendo de la frecuencia del pulso (Wo) y la relación entre la presión y la tensión de pared, dándole al flujo un aspecto casi continuo.
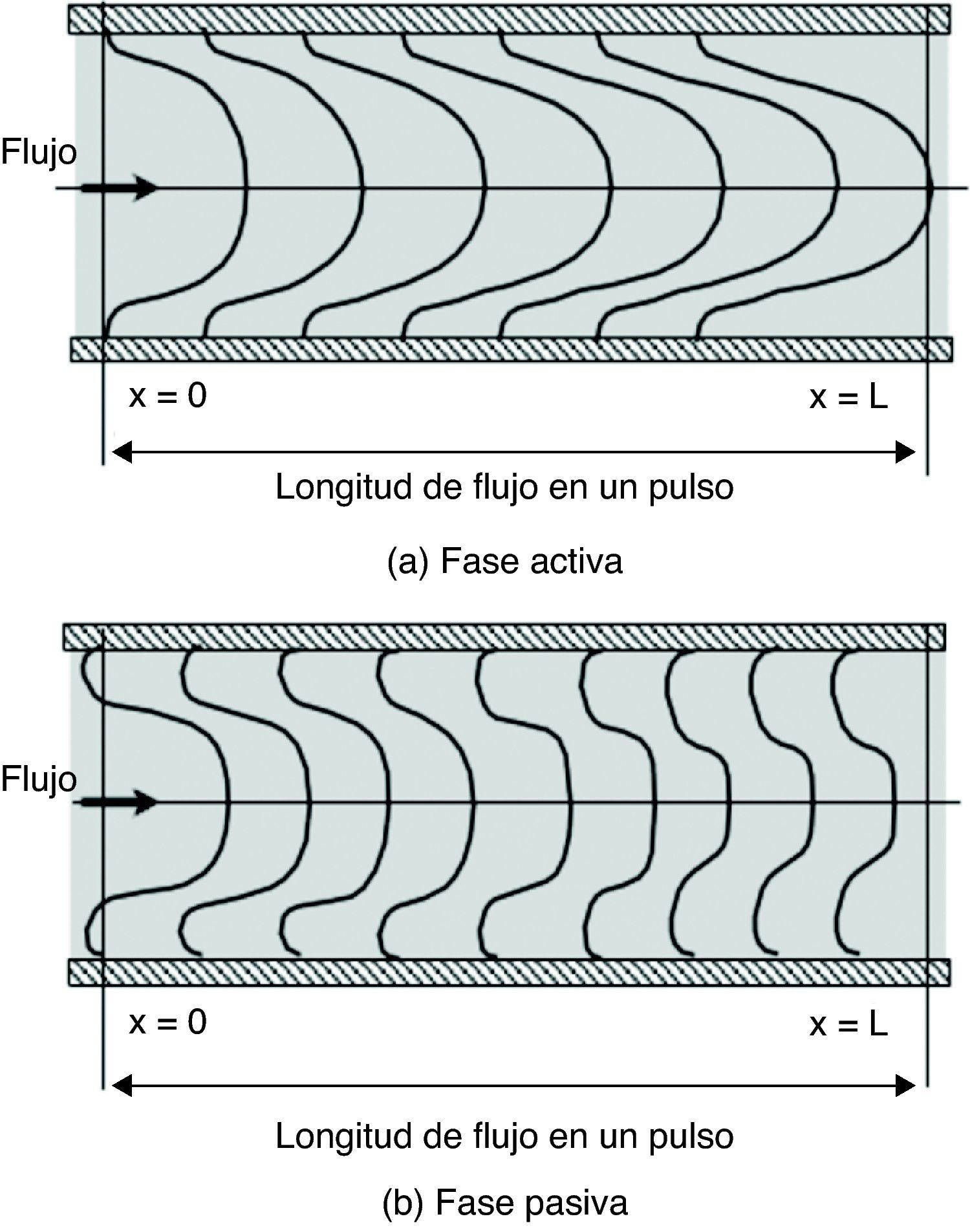
Aplicando el modelo planteado, el patrón de flujo vascular se interpreta así: en la fase activa el pulso de presión produce una corriente sanguínea que ocupa gran parte del área del vaso, conformando el flujo anterógrado, mientras que en las cercanías de la pared se forma la capa límite debido a la viscosidad sanguínea (fig. 5 A), modificando el esquema según Fung Y. propuesto en 199619.
Estructura del flujo pulsante. A) Fase activa: la corriente avanza con velocidad de perfil parabólico, conformando el flujo anterógrado. B) Fase pasiva: hay 2 corrientes, una que se mantiene en el núcleo con un perfil achatado, y otra con velocidad negativa en dirección radial, la cual conforma el flujo retrogrado. Modificada de Fung Y19.
Durante la fase pasiva, la suspensión súbita de presión produce fuerzas inerciales transitorias que generan la corriente secundaria, causante de que la velocidad sea 0 en el campo de flujo y no sobre la pared (fig. 4), propiciando la separación de la corriente, conformando así el flujo retrógrado (fig. 5 B).
La magnitud en la cual se reduce la corriente del núcleo y se favorece la separación depende de las condiciones de flujo (Re y Wo) y del estado de la pared vascular. Cuando el flujo tiene un Re alto (3000 a 6000) y un Wo medio (3 a 7), el punto de separación se retarda. Manteniendo el Re constante, un flujo con Wo>10 se caracteriza por un perfil de velocidad aplanado en la fase activa y con propensión a la separación en la fase pasiva; mientras que un flujo con Wo≤1 tiene un perfil más parabólico y baja tendencia a la separación. Cuando Wo aumenta se reduce el Re requerido para que ocurra la separación.
La respuesta biomecánica vascular permite que las 2 fases de flujo interaccionen: la recuperación elástica de la pared sostiene la corriente en el núcleo aún durante la fase pasiva12,20, la cual avanza a lo largo del vaso dependiendo de la frecuencia de pulsación (Wo) y la distensibilidad de la pared; situación que no se presenta en el conducto de pared rígida. Esta interacción de las fases es la causa que la velocidad inicial en el vaso no sea siempre 0, y por la cual el perfil de velocidad es alargado durante la fase activa (fig. 5 A) y achatado en la pasiva (fig. 5 B), confiriéndole al flujo sanguíneo un perfil de velocidad aplanado12, aunque tenga un Re bajo.
El balance entre un Re medio (1800-3000) y un Wo alto (7-14) en el flujo a través del vaso atenúa los efectos transitorios, por lo que se sostiene la corriente del núcleo durante la fase pasiva y se empalma con el flujo anterógrado de la siguiente fase activa; confiriéndole a la corriente el aspecto de flujo continuo y desordenado, pero sin entrar en régimen turbulento (que disipa más energía) y sin propensión a la separación (que lesiona los elementos formes de la sangre).
DiscusiónEl modelo propuesto coincide con el concepto de capa límite en el flujo pulsante de Schlichting10,21, según el cual en un flujo pulsante no aplica el criterio de separación de Prandlt, porque la separación se da entre las capas del fluido, y la ubicación donde ésta se inicia depende de la relación entre los valores Re y Wo.
De la aplicación del anterior criterio de separación, se infiere que10: 1) la separación en un flujo pulsante ocurre con un Re menor que en uno continuo; 2) la separación en un flujo pulsante es más sensible a los cambios de geometría del conducto que un flujo continuo, debido a la corriente secundaria; 3) la corriente secundaria es la causante de la elongación del perfil de velocidad axial.
Adicionalmente, para caracterizar el efecto de la pulsación del flujo en el sistema vascular hay que considerar el carácter viscoelástico del vaso15, evaluando la tensión que desarrolla la pared (generando la onda de pulso) ante el esfuerzo de flujo aplicado (durante la generación de la onda de flujo).
Implicaciones del modelo propuestoConsiderando que el sistema circulatorio cumple las funciones de: transportar el fluido sanguíneo por el lecho vascular y la de distribuir los eritrocitos en órganos y tejidos22; un flujo pulsante no sólo es la condición natural, sino una adaptación acertada que cubre estas peculiaridades fisiológicas con menor consumo de energía: durante la sístole aumenta la velocidad transportando eficientemente los eritrocitos en el núcleo de flujo de un segmento vascular a otro, y en la diástole, reduce la velocidad distribuyéndolos hacia las ramificaciones, porque la corriente secundaria propicia la dispersión de los eritrocitos, perfundiendo adecuadamente los tejidos. Por su parte, el lecho vascular aporta el componente viscoelástico que se requiere para atenuar la pulsación: el vaso sanguíneo se expande durante la sístole para soportar la tensión producida por el incremento súbito de presión, con el beneficio implícito de reducir la resistencia hidráulica; y se relaja durante la diástole disipando la energía de deformación acumulada, y contrarrestando la separación de la corriente, este último fenómeno lesivo tanto para eritrocitos como para la pared misma.
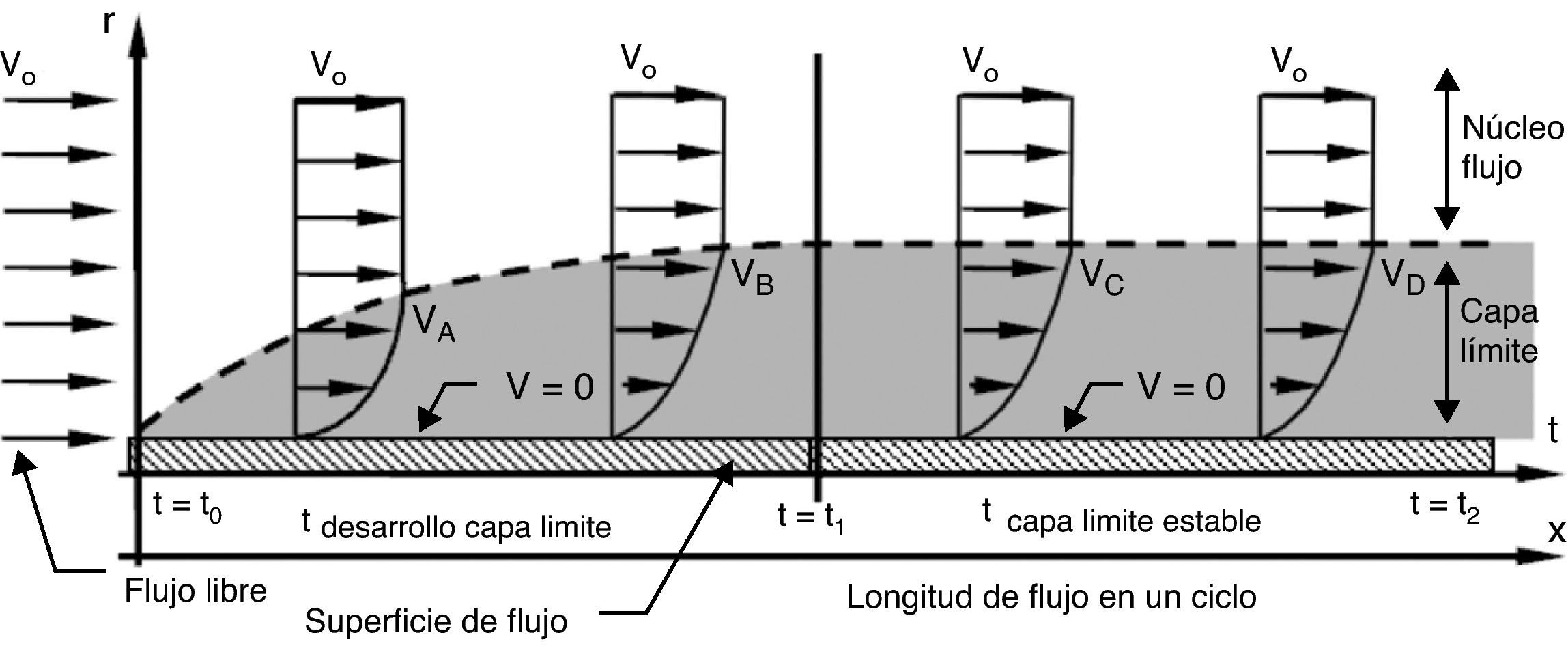
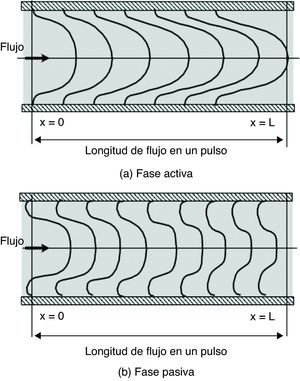
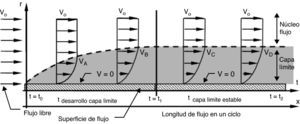
En contraste, un flujo continuo (fig. 6) aunque transportaría eficientemente los eritrocitos en el núcleo de la corriente, dificultaría el proceso de perfusión. La mayor parte de los eritrocitos serían arrastrados por la corriente principal que se desplaza por el centro del vaso, mientras que los restantes serían atrapados en la capa límite, que restringiría el movimiento radial de los eritrocitos, permaneciendo allí por un tiempo indeterminado, según el régimen de flujo. En una corriente continua laminar la capa límite es gruesa y estable, mientras que en una turbulenta es delgada e inestable; de manera que los eritrocitos quedan atrapados más tiempo en una laminar y escapan aleatoriamente en una turbulenta. Esto implica, en ambos casos, una distribución heterogénea de eritrocitos en cada segmento vascular tanto en el tiempo como a lo largo del lecho vascular2,8,23.
Estructura de flujo continuo. Al iniciar el flujo empieza a formarse la capa límite que continua desarrollándose hasta que se equilibran las fuerzas inerciales y viscosas, después de lo cual permanece estable. La velocidad siempre es 0 (V=0) sobre la pared. Vo: velocidad de entrada; Vi: velocidad del flujo en el punto i; r: radio del conducto; t: tiempo transcurrido del ciclo.
En un flujo pulsante el eritrocito enfrenta 2 esfuerzos: los inerciales transitorios (moderados) cuando está en la zona marginal de plasma, y los inerciales convectivos (altos) cuando se desplaza con la corriente principal. En cambio, en un flujo continuo enfrenta esfuerzos inerciales convectivos permanentes, con diferente magnitud, dependiendo de la sección de flujo donde quede atrapado en la corriente central o en la capa límite. Al permanecer sometido al mismo esfuerzo, el eritrocito puede alterar su morfología dinámica, desencadenando consecuencias reológicas derivadas de dicho evento. Además en el flujo continuo la aplicación permanente de presión, sumada a un mayor esfuerzo de flujo para sostener la corriente, mantiene el vaso distendido, por lo que la pared acumula tensión permanentemente.
El modelo propuesto permite vincular otros 2 aspectos de la mecánica del flujo sanguíneo: uno, según el cual el flujo sanguíneo es laminar aunque presente valores de Re más altos que el crítico en un flujo continuo, y otro, que describe el perfil de velocidad como achatado aunque el flujo sea laminar.
Un flujo pulsante no es ni laminar ni turbulento en el mismo sentido del concepto aplicado al flujo continuo24, ya que los efectos de la corriente secundaria pueden frenar el movimiento durante la fase pasiva, provocando un flujo fragmentado o no; es decir, el flujo puede quedar en reposo o en movimiento dependiendo de la energía de flujo (definiendo Re), la frecuencia de pulsación (definiendo Wo) y la elasticidad de pared (definida por el índice de reflexión). Cuando un flujo pulsante tiene alta frecuencia (Wo alto)11,19, la separación es temprana y la corriente del núcleo no acumula momentum suficiente para avanzar durante la fase pasiva; por lo que el flujo tiene aspecto fragmentado (como si se tratase de turbulencia). En contraste, cuando tiene baja frecuencia aumenta el valor de Re al cual ocurre la separación, por lo que la corriente del núcleo queda con energía suficiente para permanecer en movimiento durante la fase pasiva, de manera que el flujo tiene un aspecto continúo (como si fuese laminar).
La siguiente etapa experimental, más allá del estudio en el sistema ex vivo desarrollado en el presente trabajo, será llevada a cabo en un sistema in vivo (modelo animal), con el fin de observar las respuestas bajo la homeostasia propia del sistema circulatorio.
ConclusionesCon base en la observación experimental de modelos biomecánicos y el análisis conceptual del flujo pulsante en conductos elásticos, se caracterizó el patrón de una pulsación con el fin de plantear un modelo que explica la influencia del pulso de flujo en el sistema vascular y los efectos de su ausencia. El modelo propuesto considera simultáneamente la pulsación del flujo (sangre) y la reacción elástica del conducto (vasos), para explicar la relación de fenómenos como la poca energía requerida por el flujo sanguíneo, la baja tensión sobre las células hemáticas y la adecuada distribución de eritrocitos por las distintas ramificaciones del árbol vascular. Asimismo, el modelo explica a priori la reacción del lecho vascular cuando la sangre es bombeada por un dispositivo de asistencia cardiocirculatoria mecánico de flujo pulsante o continuo25. La interpretación de las evidencias acumuladas con la aplicación de estas terapias de asistencia, mediante el modelo propuesto permitirá redefinir las bondades de los diferentes tipos de dispositivos cardiovasculares y orientar las tendencias de su desarrollo en los próximos años.
FinanciamientoNo se recibió patrocinio de ningún tipo para llevar a cabo este artículo.
Conflicto de interesesLos autores declaran no tener conflicto de intereses.