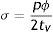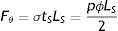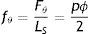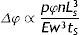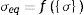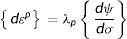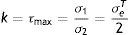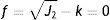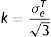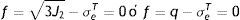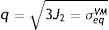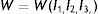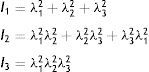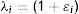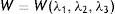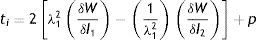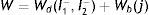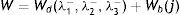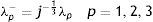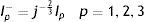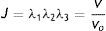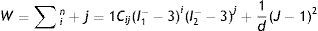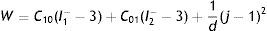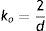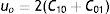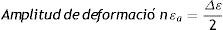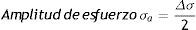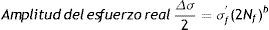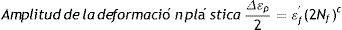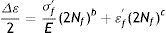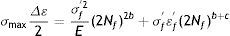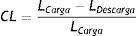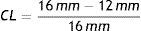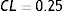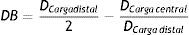Tras las evidencias acumuladas mediante el uso de técnicas de angioplastia con stents, surge la polémica sobre los factores que inciden en la respuesta final, ya que hay estudios que reportan reestenosis de la luz en el 30-40% alrededor de 6 meses luego de ser implantados, vinculándose como una de las causas al diseño del dispositivo. Este artículo propone la caracterización funcional de stents endovasculares, analizando su influencia mecánica en el sistema vascular y prediciendo los factores de trauma implícitos en el lecho de los vasos.
MétodosUtilizando modelos computacionales de prótesis endovasculares tipo stents, mediante técnicas Finite Elements Analysis, se procedió al análisis estructural de dichos dispositivos con el fin de predecir el comportamiento mecánico y el trauma vascular. Para ello, las prótesis fueron consideradas estructuras tubulares compuestas por múltiples eslabones que están sometidos a cargas de presión, que se reflejan como concentradores de esfuerzos.
ResultadosEl estudio permitió visualizar cómo se ajusta la geometría del stent a las diferentes cargas, obteniéndose una aproximación a la respuesta de interacción «sólido-sólido» entre el stent y la pared arterial. Así, se caracterizó el patrón de esfuerzos y se planteó un modelo conceptual que explica su incidencia mecánica en la interacción stent-vaso, para inferir en la funcionalidad del diseño del dispositivo.
ConclusionesEl modelo conceptual planteado permite determinar la relación entre las condiciones de interacción mecánicas del stent, y advierte sobre los efectos en lo que sería la operación del dispositivo en el ambiente vascular.
The accumulated evidence on angioplasty techniques with stents has raised a controversy about the factors that influence the final vascular response. Indeed, several studies have shown there might be re-stenosis between 30% to 40% about 6 months after placement, relating to the design of the device as one of the main causes. This paper proposes the functional characterization of endovascular stents, analyzing its mechanical influence in the vascular system and predicting implicit traumatic factors in the vessel.
MethodsA structural analysis was made for several computational models of endovascular stents using Finite Element Analysis in order to predict the mechanical behavior and the vascular trauma. In this way, the stents were considered as tubular devices composed of multiple links under radial pressure loads, reflecting stress concentration effects.
ResultsThe analysis allowed to visualize how the geometry of stents is adjusted under several load conditions, in order to obtain the response of “solid-solid” interaction between the stent and the arterial wall. Thus, an analysis was performed in order to calculate stress, and a conceptual model that explains its mechanical impact on the stent-vessel interaction, was raised, to infer on the functionality from the design of the devices.
ConclusionsThe proposed conceptual model allows to determine the relationship between the conditions of mechanical interaction of the stents, and warns about the effects in what would be the operation of the device on the vascular environment.
Luego de utilizar por varios años los stents vasculares como una opción terapéutica en el tratamiento de la estenosis vascular y a sabiendas de su gran impacto en la morbimortalidad, muy especialmente en la enfermedad coronaria y cerebrovascular, surge la polémica por los efectos mecánicos, que se traducen en causales aún no del todo identificados en la estimulación de la reestenosis. Esta gira el curso de una exitosa recanalización inicial del vaso, que ayuda a restablecer el flujo sanguíneo normal, para tornarse en un instigador de respuesta agresiva que culmina en la reoclusión, de la que estudios reportan reestenosis de la luz hasta del 30-40% alrededor de los 6 meses después de ser implantado el stent1–5, vinculándose como una de las causas, entre otras, al diseño del dispositivo6–9.
Si se intuye que durante la proliferación neointimal que deriva en la reestenosis, factores mecánicos involucrados van de la mano de factores histoquímicos en el sistema vascular, estos son aspectos aún no del todo considerados e incluidos en una terapia conjunta que propenda por hacer del procedimiento menos traumático10–13. Así, aunque múltiples investigaciones han buscado la llave para obtener el prototipo ideal, tanto en materiales como en el diseño, ninguno cumple enteramente las limitaciones que impone la condición natural, y han evidenciado que predisponen a algún tipo de disfunción a nivel local14–18.
Una opción para esclarecer los efectos de esta terapia y dilucidar las condiciones de interacción mecánica stent-vaso, como soporte nominal de la luz arterial, es llevar a cabo un análisis estructural de las prótesis endovasculares. Esto se lograría mediante datos obtenidos durante ensayos experimentales que aproximen a identificar los efectos mecánicos de uno u otro, sin embargo son datos difíciles de aplicar para tal propósito, porque in vivo se obtienen bajo condiciones no controladas, que involucran múltiples factores, a la vez que tampoco pueden ser manipuladas experimentalmente por los peligros que implicaría en el sujeto de estudio.
Con este fin, en el presente trabajo se ha recurrido a modelos computacionales, planteados mediante conceptos biomecánicos19–21, con el propósito de analizar la respuesta mecánica de distintos prototipos de stents vasculares. Así, se espera comprender la interacción de los fenómenos subyacentes ante las cargas durante la implantación y la liberación en el vaso arterial, y de ello deducir un modelo que caracterice dichas respuestas en el sistema vascular22. Para el caso se emplearon técnicas computacionales mediante elementos finitos, una técnica numérica con la que se pueden simular un sinnúmero de escenarios para entender el comportamiento de las prótesis en las condiciones fisiológicas de un tramo arterial23 y determinar su incidencia en el trauma local, situación clave para sacar el mejor provecho de este tipo de dispositivos terapéuticos.
MétodosRepresentación del stentEl modelo de esfuerzos se plantea con base en datos experimentales que reproducen la dinámica del dispositivo tipo stent y los resultados obtenidos son interpretados mediante variables biomecánicas de acuerdo a la caracterización del lecho vascular. Para el estudio se utilizó el software SolidWorks® y la teoría basada en análisis por Finite Elements Analysis (FEA). Se elaboró una malla no estructurada, buscando una relación de aspecto 1:3 garantizando uniformidad; y aplicando el método Repeat Unit Cell (RUC), se trabaja con celdas con el fin de optimizar la convergencia24. La malla se realiza con elementos triangulares, para ello se utilizó el procedimiento de malla tipo shell, con una curva de carga variable en el tiempo, para analizar esfuerzos durante la expansión y relajación con el balón de angioplastia, así como durante la pulsación natural del vaso.
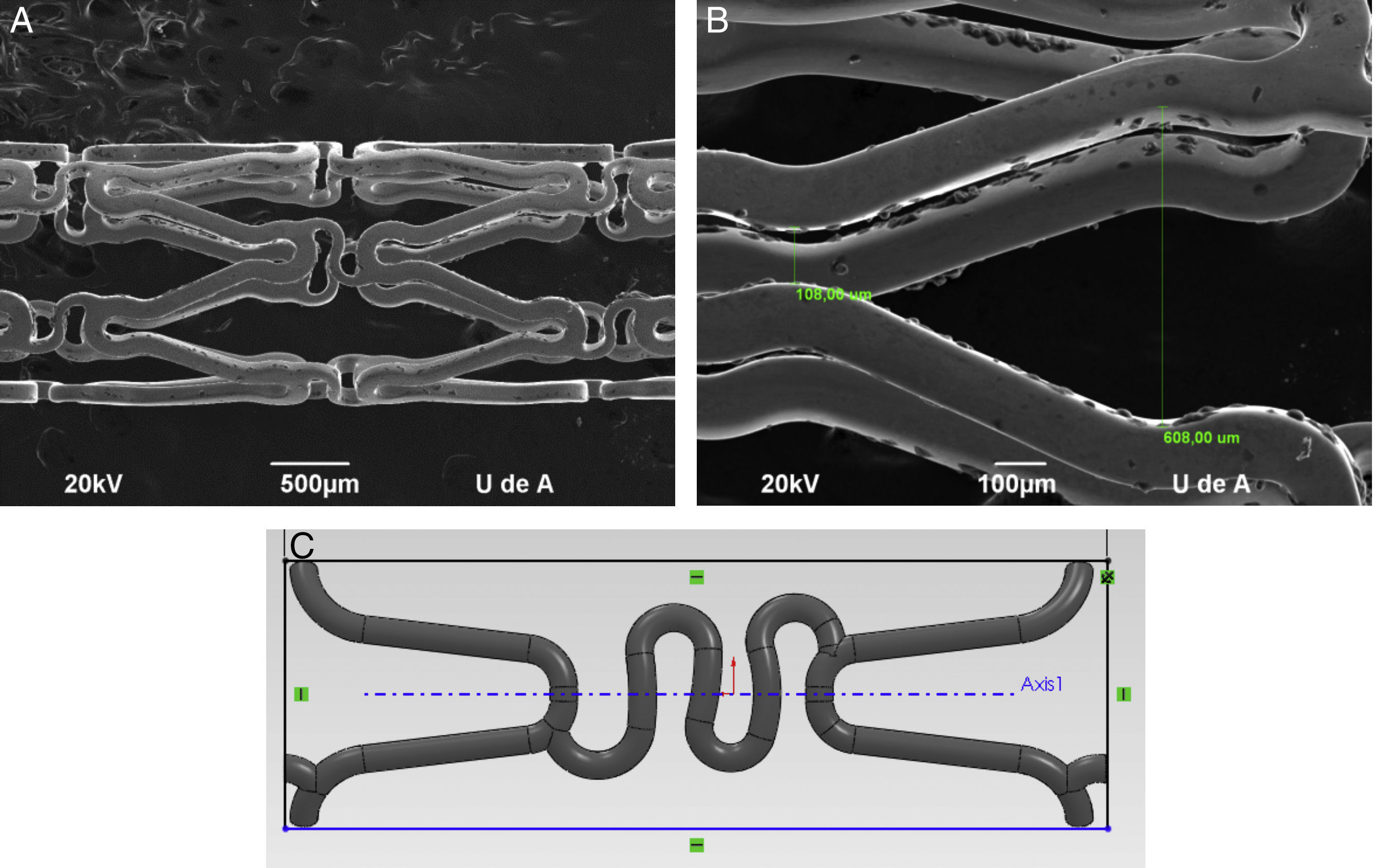
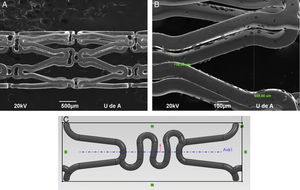
Para la construcción de modelos Computer Aided Design (CAD) más representativos, se utilizaron imágenes de microscopia de escaneo electrónico de donde se tomaron las dimensiones de la geometría y sección estructural de los dispositivos (fig. 1).
Los modelos fueron sometidos a una presión incremental hasta 1MPa, provocando deformaciones plásticas, lo cual lo circunscribe en un análisis no lineal. Los esfuerzos obtenidos son evaluados por el criterio de plasticidad de von Mises, que hace referencia a una magnitud física proporcional a la energía de distorsión o deformación, los cuales son comparados respecto a los rangos de elasticidad del material. En primera instancia se estudia un stent en acero inoxidable 316L y se hace una caracterización por el método Mooney Rivlin de 5 constantes, que hace referencia a la razón modelizable de una función de densidad de energía de deformación o energía almacenada. Seguidamente, se plantea una etapa de verificación y calibración con un stent tipo Palmaz-Schatz®, contrastando con un estudio de referencia, con el fin de generar un modelo CAD, base que sirve de guía para el análisis de una geometría más compleja como la del stent tipo Cypher®.
En el protocolo de pruebas se consideró el comportamiento mecánico durante el proceso de implantación a través de la angioplastia, cuando se retira el balón de expansión y cuando queda sometido a las cargas del flujo pulsátil propias del vaso. Se generaron esfuerzos relacionados con la funcionalidad del stent, considerando que la pared vascular reacciona con una respuesta mecánica ante la presión del stent; así las condiciones fijadas para modelar el sistema fueron: conducto flexible (viscoelástico), flujo pulsante, fluido incompresible, e interacción entre el stent y la pared del vaso.
Sobre las propiedades exhibidas en el comportamiento del material se tuvieron en cuenta: el módulo de Young, que hace referencia a la razón o cambio en el incremento de los esfuerzos dados por una deformación unitaria; el módulo de Poisson, que hace referencia a cambios como el alargamiento y disminución del área transversal que se sufre cuando el elemento está sometido a diversas fuerzas; la resistencia a la fluencia, relacionada con la capacidad del material para soportar una fuerza constante sin deformarse ni cambiar sus propiedades mecánicas; y el límite de elasticidad, como la máxima tensión que puede soportar el material sin alcanzar deformaciones permanentes.
En este entorno se probaron los criterios de calidad recomendados para dichos dispositivos por la Food and Drug Administration de EE. UU., tales como: flexibilidad, acortamiento durante la expansión (foreshortening), deformación en la expansión (dogboning), contracción radial (radial recoil) y contracción longitudinal (longitudinal recoil); para lo cual, hubo de considerarse el dominio del complejo stent-placa-pared arterial, tanto en el estado estacionario como en el transitorio. Otros parámetros considerados fueron las propiedades de caracterización del material, así como las condiciones fisiológicas del tramo vascular donde es implantado.
Usando el análisis computacional, se calculan los esfuerzos, deformaciones y desplazamientos del dispositivo partiendo de las condiciones máximas y mínimas obtenidas en los diferentes escenarios de trabajo, como se detalla a continuación:
Los esfuerzos circunferenciales se deducen de las cargas radiales en el vaso en función del área de la sección transversal y la presión según
donde: σ es el esfuerzo circunferencial, p es la presión, ϕ es el diámetro y tV el espesor de pared vascular, y donde la fuerza circunferencial se puede describir comodonde: F¿ es la fuerza circunferencial, tS el espesor de pared y LS la longitud del stent.Calculando la fuerza circunferencial por unidad de longitud, basado en (1) y (2) se obtiene
siendo fθ la variable que representa la fuerza que describe el fenómeno de cargas circunferenciales del vaso.
La rigidez del stent se determina por la respuesta elástica de los elementos ante las cargas que se aplican, traduciéndose en la resistencia para mantener su forma geométrica. El cambio radial de las prótesis se da en función de diferentes parámetros de la geometría. La representación de este cambio viene dada por la ecuación
donde: Δφ es el cambio radial, Ls es la longitud de un strut, n el número de struts alrededor del radio, tS el espesor del stent, E el módulo elástico del material, w el ancho del strut.Para su análisis se emplea el modelo de plasticidad de von Mises. En este caso de tensión producida por cargas multidireccionales, se representa por la tensión equivalente (σeq), que se da en función de las componentes individuales, según
La dirección de estas deformaciones está regida por la regla de flujo, expresada por
donde: λp es la constante de proporcionalidad de deformación plástica y ψ es la función de esfuerzos, en la que su gradiente muestra la dirección de la deformación.Se emplea además el criterio de Tresca, cuyo planteamiento se basa en las tensiones tangenciales aplicadas en un punto de magnitud crítica para la plastificación. En el caso del ensayo uniaxial el esfuerzo máximo está dado por
donde: τmax es tensión de plastificación o cortante pura, σ1 y σ2 son los esfuerzos principales, σeT es el límite elástico del material sometido a tracción.El criterio de von Mises está dado por la ecuación
donde: f es la superficie de plastificación, J2 es el segundo invariante del desviador y k es la tensión de plastificación o cortante puro.La constante k se expresa en función del límite elástico en el ensayo de tracción, según la ecuación
mientras la expresión de la superficie de plastificación en función del límite elástico se representa en la ecuacióndonde: q es el esfuerzo equivalente de von Mises, de acuerdo a la expresiónEn la representación del criterio de von Mises en el stent, la superficie de plastificación es un cilindro y el eje que lo rige está en dirección del esfuerzo hidrostático. Los vértices del hexágono que rige Tresca involucran la circunferencia que define dicho cilindro.
Representación de la pared vascularEl modelo que rige el comportamiento elástico de los vasos incluye los términos relacionados con los fenómenos experimentados en la fase de expansión y contacto entre el stent y la pared, y las cargas restrictivas que ello representa en el vaso. El análisis general de la relación esfuerzo-deformación del stent y pared se representa con el modelo de Mooney Rivlin, suponiendo que el material en estado natural es isotrópico e incompresible. Este análisis se fundamenta en la ecuación de la densidad de energía de deformación, que relaciona la cantidad de energía almacenada elásticamente en una unidad de volumen, bajo un estado deformado. Es expresada en términos de las invariantes de deformación, según la ecuación
donde la mecánica del medio continuo se utiliza para conocer las invariantes I1, I2 y I3; por consiguiente las diferencias geométricas debido a las deformaciones pueden medirse independientemente del eje de referencia elegido. De esa forma, las invariantes se definen comodonde las constantes λ1, λ3 y λ3 son las proporciones entre los alargamientos longitudinales y las longitudes no deformadas de un volumen diferencial en reposo. Los valores que toma esta contante están dados por la ecuacióndonde: ¿i corresponde a la deformación principal y los valores de Ii son cero en reposo, ya que todas las constantes serán iguales.Otra manera de presentar la ecuación de densidad de energía de deformación unitaria es en términos de los alargamientos principales, quedando de la siguiente forma
Cuando ti corresponde a un esfuerzo en la dirección i, la densidad de energía de deformación unitaria relacionando esfuerzos y deformaciones, queda así
Con esta función se determina la relación no lineal entre los esfuerzos y las deformaciones del material. La cantidad p corresponde a la presión, resultado de que los elastómeros son casi incompresibles y por lo tanto favorecen dicha generación de presión.
El análisis para la caracterización a través de la ecuación de densidad de energía de deformación se realiza asumiendo los materiales incompresibles, lo que reduce el término I3 a cero. Para el planteamiento de dichos modelos, se presentó la necesidad de separar esta ecuación en un elemento deviatórico (Wd) y un elemento volumétrico (Wb), según las expresiones
donde: λp es un término necesario para la separación y J representa la razón de cambio de volumen.Con la siguiente expresión se representa el modelo de Mooney Rivlin, basado en las invariantes de deformación. La respuesta de este modelo depende del número de coeficientes del grado del polinomio, según la expresión
y el modelo Mooney Rivlin de 2 contantes, que representa la forma polinómica de N igual a uno esIndependiente de la forma del modelo, se define el módulo de rigidez volumétrica inicial presentado con la ecuación
y también el módulo cortante inicial con la ecuaciónEste método es preciso para rangos de deformaciones hasta del 100% para un modelo de N igual a 2 (siendo N el grado polinómico del modelo) y hasta un 300% con N igual a 3. Esta forma también es indicada para caracterizar esfuerzos cortantes puros con deformaciones máximas entre el 70% y el 90%, debido a que el módulo cortante utilizado es constante.
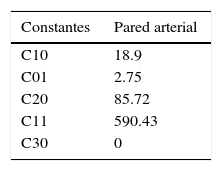
Este método fue utilizado para la caracterización del material del vaso sanguíneo, que cumple con la descripción de un material hiperelástico, según datos utilizados de la literatura. La tabla 1 presenta los valores de las constantes que se aplican al modelo de pared arterial.
ResultadosAplicado el modelo de plasticidad de von Mises para caracterizar los stents, y el modelo de hiperelasticidad de Mooney Rivlin para el material de la arteria, se aplica sujeción en un extremo del stent para analizar el comportamiento ante el pandeo y flexión a la que está sujeto el dispositivo, cuando es forzado a adquirir la forma del vaso. Esta sujeción proporciona movilidad paralela al plano, permitiendo simular una deformación longitudinal y diametral, con lo que se encuentra que las prótesis expandidas por medio de balón presentan importante capacidad de deformación plástica; siendo fabricadas a partir de una forma no expandida, una vez retirado el balón, estas mantienen una tensión contra la pared vascular.
Comportamiento de deformación ante esfuerzos cíclicosLas pruebas relacionan las fallas del material que se presentan en el tiempo, debido a cargas fluctuantes y cíclicas, que se encuentran incluso por debajo de la resistencia última. Aunque las estructuras desarrolladas están diseñadas para que su carga nominal permanezca elástica, las concentraciones de esfuerzos causan deformaciones plásticas las cuales se desarrollan en las secciones más críticas de la estructura.
Están fijadas en términos de amplitud de deformaciones y esfuerzos que definen el ciclo, y se relacionan en las ecuaciones
El área dentro del lazo significa la energía por unidad de volumen disipada durante el ciclo, la cual representa una medida de trabajo de deformación dado en el material.
Curva vida de deformación: usando la amplitud del esfuerzo real la gráfica se linealiza de la siguiente forma
donde: σf' es el coeficiente de fuerza a la fatiga, 2Nf son las reversiones al fracaso (1rev=1/2 ciclo), b es el exponente de Basquin (puede variar entre −0.05 y −0.12).La deformación plástica se linealiza como
donde: εf' es el coeficiente dúctil de fatiga, 2Nf son las reversiones al fracaso, c es el exponente dúctil de fatiga (puede variar entre −0.5 y −0.7).Luego, la deformación total se interpreta de la manera que se expresa a continuación
Dicha ecuación muestra que tanto la relación elástica como la plástica son líneas rectas en el gráfico y que la amplitud de la deformación total puede ser graficada sumando ambas relaciones. Con una amplitud de deformación prolongada, la curva se acerca a la línea plástica. Con una amplitud de deformación baja, la curva se acerca a la línea elástica.
Se hicieron modificaciones a las ecuaciones esfuerzo-deformación para considerar los efectos del valor del esfuerzo. Por lo tanto, para el cálculo de fatiga se utiliza la ecuación
2Nf≈N / Número de ciclos
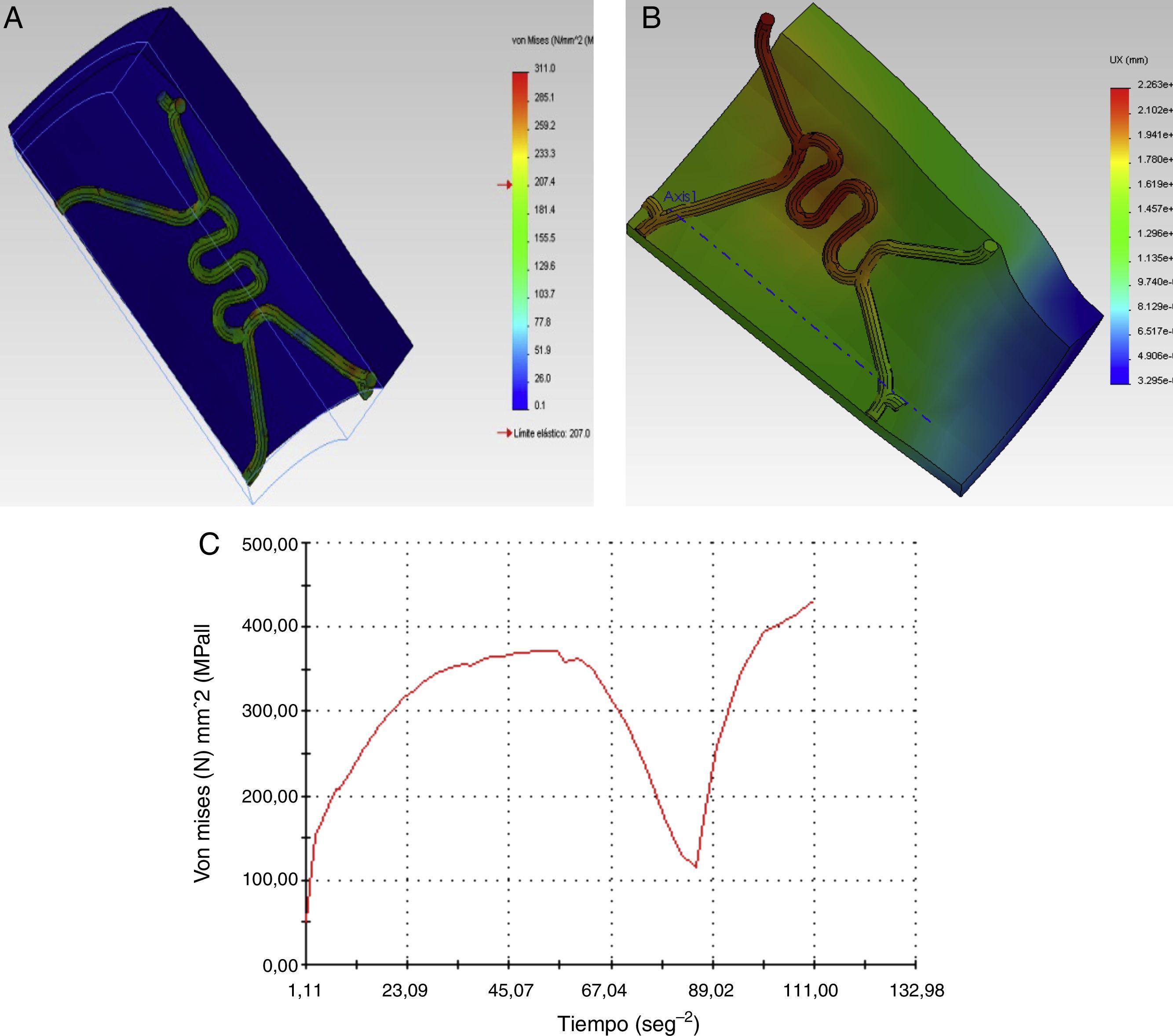
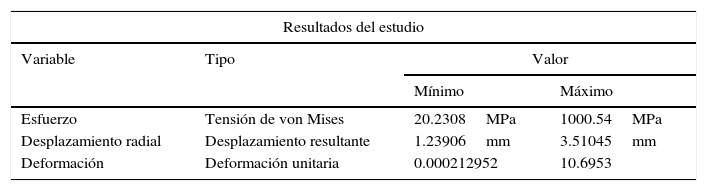
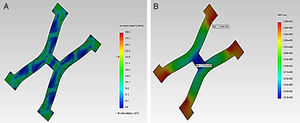
En la figura 2 se visualiza los esfuerzos y desplazamientos en un strut del stent Palmaz-Schatz®, durante la acción de inflado del balón en la expansión. En el gráfico se puede observar que los puntos críticos coinciden con las aristas donde se presentan la concentración de esfuerzos, más relevantes en los cambios de sección.
La tabla 2 presenta un resumen de los resultados obtenidos para el RUC del Palmaz-Schatz®. La prótesis se deforma en el primer momento debido a la aplicación de la carga; al inicio se encuentra una constante donde la estructura se resiste a la deformación hasta posteriormente ceder, presentándose una gran deformación plástica, al completarse el tiempo se retira la carga y solo se produce una mínima recuperación.
Se relaciona los esfuerzos de von Mises en el stent tras la deformación plástica del material ante las fuerzas aplicadas, en donde dichos esfuerzos son mayores en las zonas de conexión entre los diferentes struts, que conforman las zonas críticas. Se determinan las condiciones de máximos y mínimos durante las pulsaciones vasculares, para encontrar la amplitud de los esfuerzos y deformaciones, creando la curva de histéresis. Se resalta que el esfuerzo mínimo se alcanza antes que la presión de inflado llegue a cero y se observa posteriormente cómo se incrementa nuevamente por la pulsación.
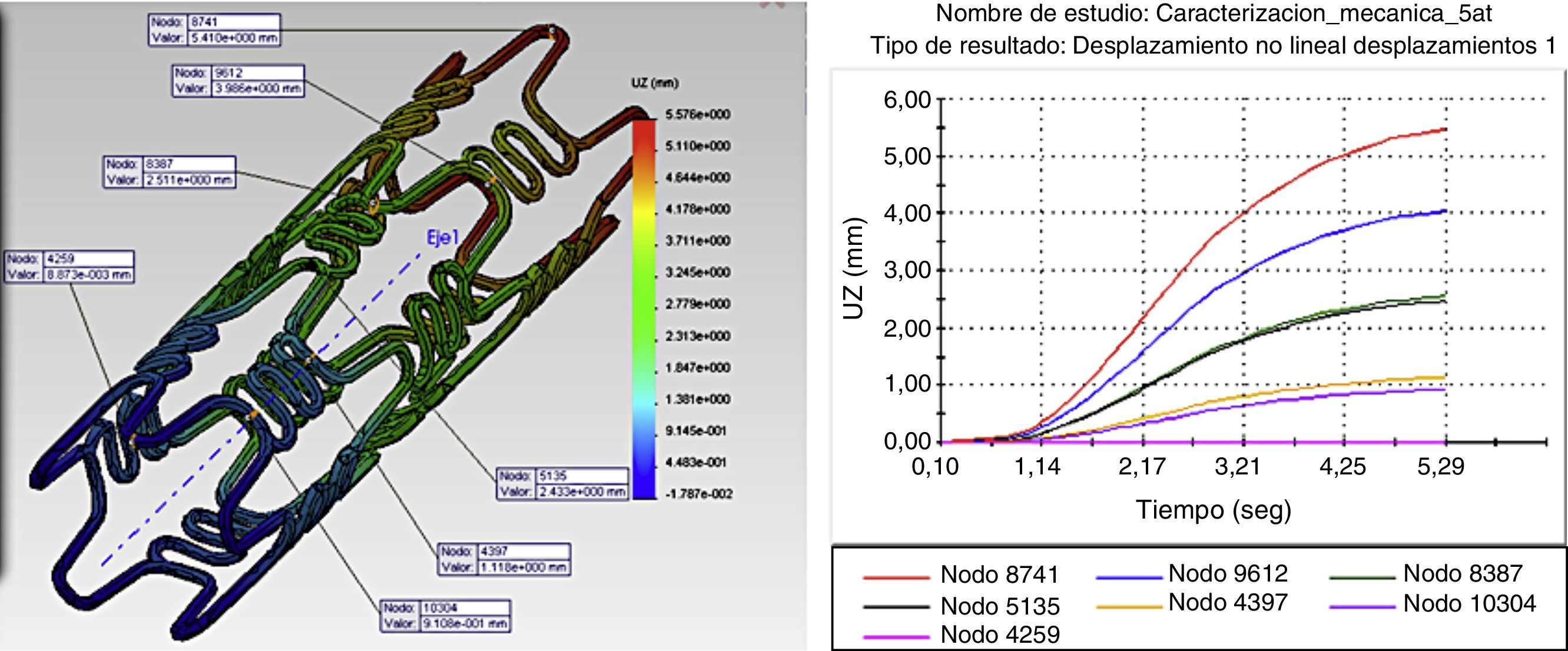
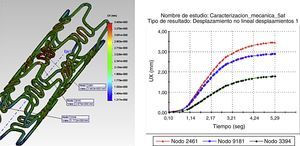
La figura 3 muestra la deformación radial del stent (dogboning), en un desplazamiento no lineal de la prótesis ante las fuerzas aplicadas en un stent tipo Cypher®, generando variaciones en las medidas radiales a lo largo de su sección longitudinal, resultando un mayor diámetro en el centro de la misma que en los extremos. Ver resultados obtenidos en tabla 3.
Los resultados obtenidos son utilizados para el análisis de parámetros, mediante la ecuación (cálculo de la longitud radial), donde la longitud inicial del stent Lo=16mm
donde:De acuerdo a la deformación plástica que presenta la estructura, se hace un análisis geométrico en función de los diámetros finales obtenidos, permitiendo hacer un cálculo del dogboning, el cual representa el grado máximo de deformación entre las secciones de la estructura (extremo y centro), mediante la ecuación
donde RUC central:- •
DB=72−117
- •
DB=1.9
RUC del extremo:
- •
DB=72−97
- •
DB=2.2
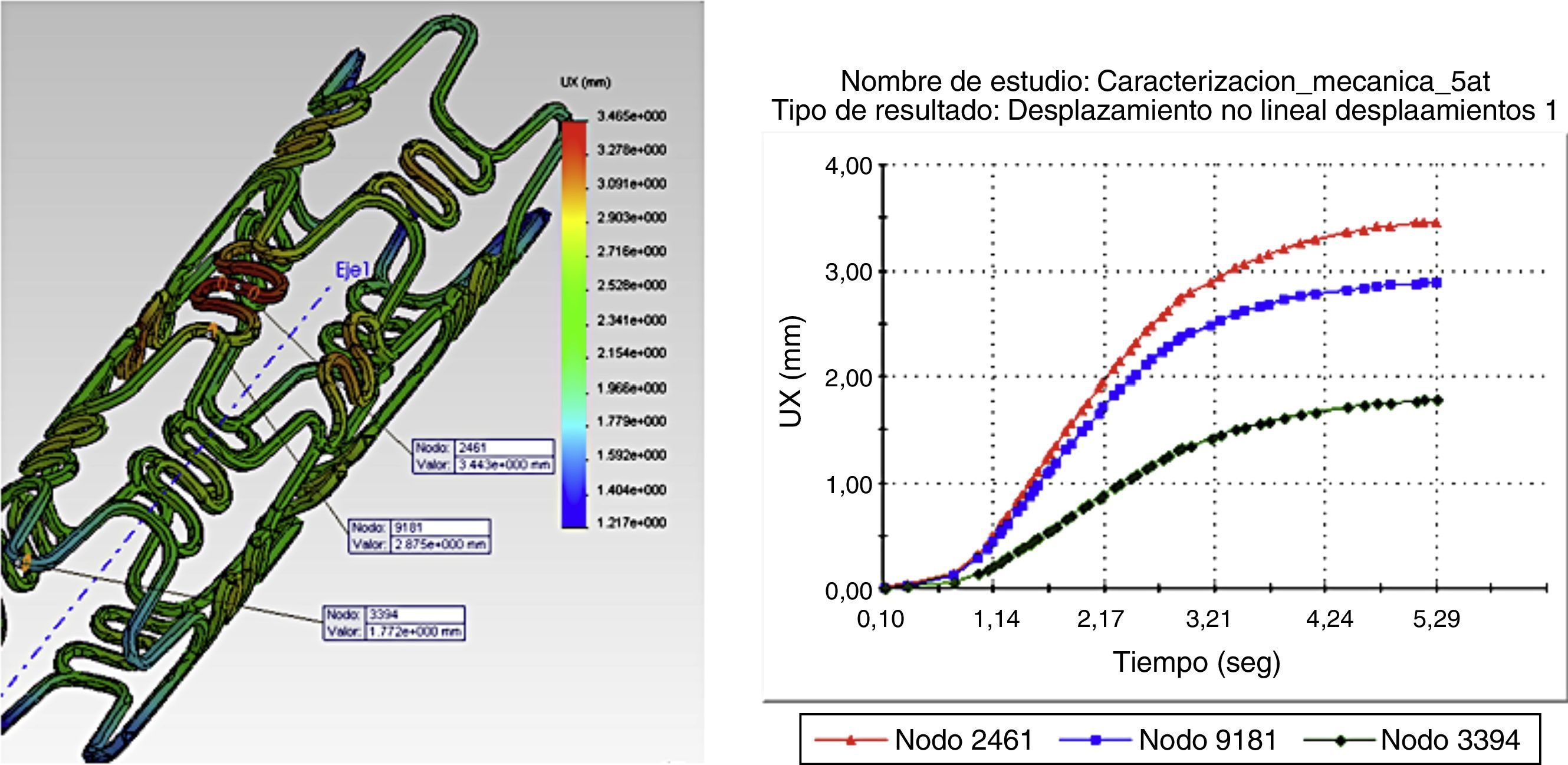
La figura 4 ilustra la variación longitudinal en presencia de una presión máxima en diferentes puntos de interés, donde se aprecia un cambio en la longitud del stent (foreshortening) cuando este se expande. Las magnitudes de las distancias entre los nodos varían de igual forma.
Las restricciones utilizadas para esta prueba son la sujeción fija en un punto, con restricción de movilidad y rotación a lo largo del eje de referencia, como se explica en la sección de comparación usando el stent tipo Palmaz-Schatz®. Las condiciones de frontera de la pared arterial tienen como restricción la movilidad longitudinal con respecto al eje de referencia, así como restricciones de rotación con respecto a los planos de corte, permitiendo deformaciones y desplazamientos en sentidos radiales para simular la expansión.
Se estableció una carga de presión de inflado de 1MPa, que es alcanzada durante el primer segundo y durante el otro segundo se presenta el desinflado, completando así el ciclo.
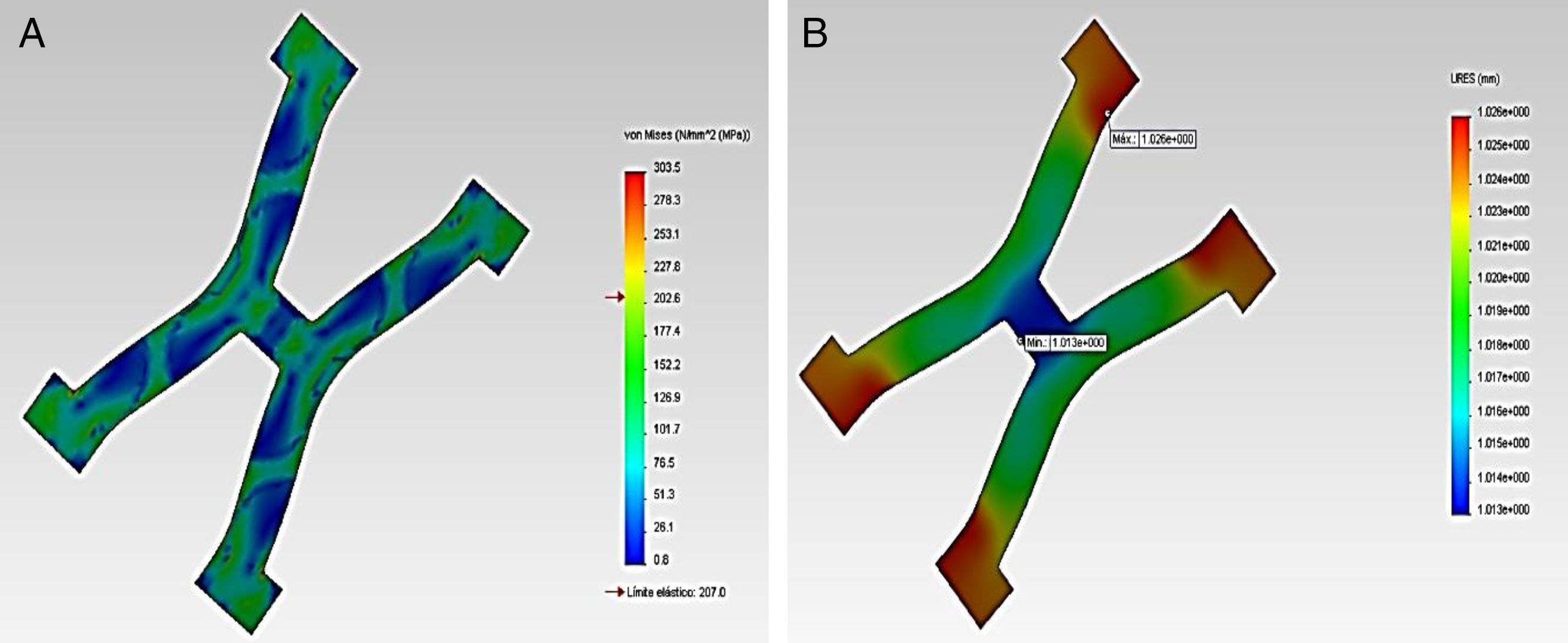
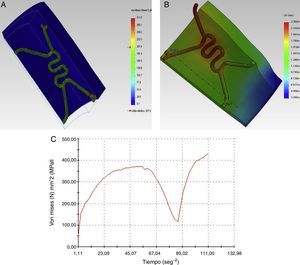
Los resultados gráficos arrojados por SolidWorks® en la figura 5 representan los esfuerzos y deformación presentes en una RUC de la prótesis tras la fuerza aplicada, y la reacción del vaso a la misma.
En los gráficos de desplazamiento se puede observar cómo en la unión stent-vaso se presenta mayor fricción en el puente de la estructura (strut), debido a su alto grado de deformación; es aquí en donde la pared arterial presenta una mayor reacción generando puntos de contacto que pueden incidir en el trauma local.
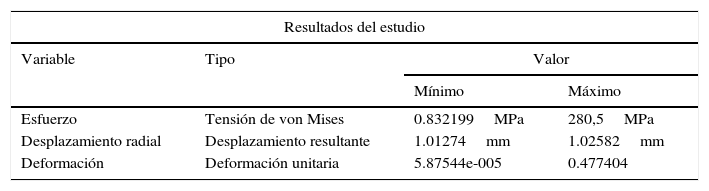
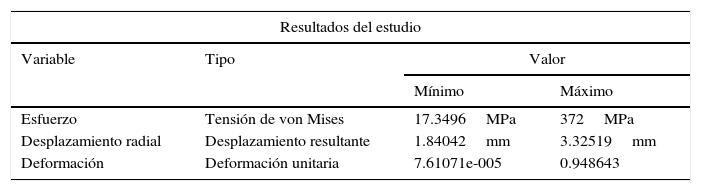
En la tabla 4 se puede observar los valores máximos y mínimos encontrados para la RUC del stent Cypher® y la pared del vaso. Con base en los datos arrojados en el estudio, se puede observar un comportamiento irregular en el extremo del stent, el cual es producido por la respuesta ejercida por la arteria. Debido a esta presión son afectados diferentes parámetros geométricos como la contracción radial, longitudinal y el dogboning.
Dicha presión del vaso sobre el stent cuyos valores son aproximados a 0.14MPa es tomada de estudios implementados en la simulación del ciclo completo (análisis mediante elementos finitos para el RUC sin arteria del stent tipo Cypher®) luego de hacer la descarga de presión.
Con base en los resultados obtenidos, es evidente que la RUC que presenta mayores deformaciones y esfuerzos es la central, corroborando así el análisis del dogboning, en donde su valor es mayor en dicha zona.
Como paso final, se hace el mismo análisis con la RUC durante la etapa de pulsación, y se observa un incremento del esfuerzo máximo hasta de 372MPa. De acuerdo con los resultados obtenidos bajo los parámetros de funcionamiento, se obtiene la gráfica que muestra la evolución del esfuerzo en el punto de interés durante un ciclo cardiaco completo (fig. 5C). El esfuerzo mínimo no es obtenido durante la descarga del balón, sino en un punto intermedio entre la relajación y la carga del vaso arterial.
DiscusiónPlanteamiento del modelo de traumaEl análisis del comportamiento de los stents, determinando cómo se ajusta la geometría a diferentes cargas y obteniendo la respuesta de interacción «sólido-sólido» en el área de cobertura stent-pared arterial, se lleva a cabo basándose en el análisis biomecánico de las prótesis. El modelo propuesto a partir de caracterizar el patrón esfuerzo-deformación y su interacción con la pared, con su consecuente aplicación al sistema vascular, se plantea en un modelo conceptual que explica su incidencia mecánica en la interacción stent-vaso, para inferir en la funcionalidad derivada del diseño del dispositivo y prever su relación con la predisposición al trauma.
Evaluando la tensión que desarrolla el stent implantado sobre la pared, caracterizando el efecto de la pulsación del flujo en el sistema vascular y considerando el carácter viscoelástico del vaso (onda de pulso), se determina unas condiciones no naturales con incidencia local, en la que la onda de pulso se verá afectada en un segmento, con un patrón de amortiguamiento completamente irregular. La velocidad de desplazamiento y la amplitud de la onda variarán, con un pérdida de la energía acumulada desde la contracción ventricular, y con un desplazamiento trasimplante forzado por unas condiciones biomecánicas restrictivas ante el esfuerzo de flujo aplicado (durante la generación de la onda de flujo).
Las implicaciones del modelo propuesto se relacionan con los efectos sobre la pared del vaso, considerando las respuestas tisulares dentro de un equilibrio de fuerzas-tensión-deformación y una relación de respuesta elástica. La falta de amortiguación durante la pulsatilidad transmite mayores esfuerzos sobre la misma pared, y la respuesta en relación con el trauma local.
ConclusionesCon base en la evaluación de modelos biomecánicos y el análisis de fuerzas aplicadas por los stents vasculares mediante métodos numéricos, se caracterizó el patrón de esfuerzos sobre la pared con el fin de plantear un modelo conceptual que explique la influencia del dispositivo en el trauma intimal. En la literatura se han reportado trabajos donde se evalúan los esfuerzos y deformaciones sobre el stent, pero en este trabajo el haber incluido la reacción de la pared vascular ha permitido valorar nuevos elementos en la funcionalidad de dichos dispositivos.
De lo anterior, como de la interpretación de las evidencias acumuladas con la aplicación de múltiples modelos de stents, puede decirse que se está en la construcción de un entorno terapéutico preliminar, en el cual se avizora a los stents actuales en un futuro muy cercano como dispositivos anecdóticos. Mientras el diseño con nuevos modelos propuestos y la introducción de materiales nanoestructurados permitirán seguramente redefinir las bondades de los diferentes tipos de dispositivos endovasculares, orientando las tendencias de su desarrollo en los próximos años.
Responsabilidades éticasProtección de personas y animalesLos autores declaran que para esta investigación no se han realizado experimentos en seres humanos ni en animales.
Confidencialidad de los datosLos autores declaran que en este artículo no aparecen datos de pacientes.
Derecho a la privacidad y consentimiento informadoLos autores declaran que en este artículo no aparecen datos de pacientes.
FinanciaciónEl apoyo para la realización de este trabajo se recibió de parte de la Universidad Pontificia Bolivariana, Centro de Investigación para el Desarrollo y la Innovación-CIDI, Colombia, para la cual se expresa un agradecimiento.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses con el desarrollo del presente trabajo.
| ¿ | Módulo de Poisson |
| E | Módulo de Young |
| σ | Esfuerzo circunferencial |
| P | Presión |
| Φ | Diámetro del vaso |
| tV | Espesor de la pared del vaso |
| Fθ | Fuerza circunferencial |
| fθ | Fuerza circunferencial por unidad de longitud |
| LS | Longitud del stent |
| Ls | Longitud del strut |
| tS | Espesor del stent |
| w | Ancho del strut |
| Δφ | Cambio radial del stent |
| φ | Diámetro del stent |
| ρeq | Tensión equivalente |
| λp | Constante de proporcionalidad de deformación plástica |
| ψ | Función de esfuerzos |
| ρ1, ρ2 | Esfuerzos principales |
| τmax | Tensión de plastificación o cortante puro |
| σeT | Límite elástico |
| J2 | Segundo invariante del desviador |
| f | Superficie de plastificación |
| q | Esfuerzo equivalente de von Mises |
| W | Densidad de energía de deformación unitaria |
| λ1, λ2,λ3 | Proporción entre alargamiento longitudinal y longitud no deformada |
| I1, I2, I3 | Invariantes |
| ¿i | Deformación principal |
| ti | Esfuerzo en la dirección i |
| Wd | Componente deviatórico |
| Wb | Componente volumétrico |
| J | Razón de cambio de volumen |
| σf′ | Coeficiente de fuerza a la fatiga |
| b | Exponente de Basquin |
| 2Nf | Reversiones al fracaso |
| C | Exponente dúctil de fatiga |
| εf′ | Coeficiente dúctil de fatiga |