Halos and multifocal intraocular lenses: Origin and interpretation

Abstract

Objective

To present the theoretical and experimental characterization of the halo in multifocal intraocular lenses (MIOL).

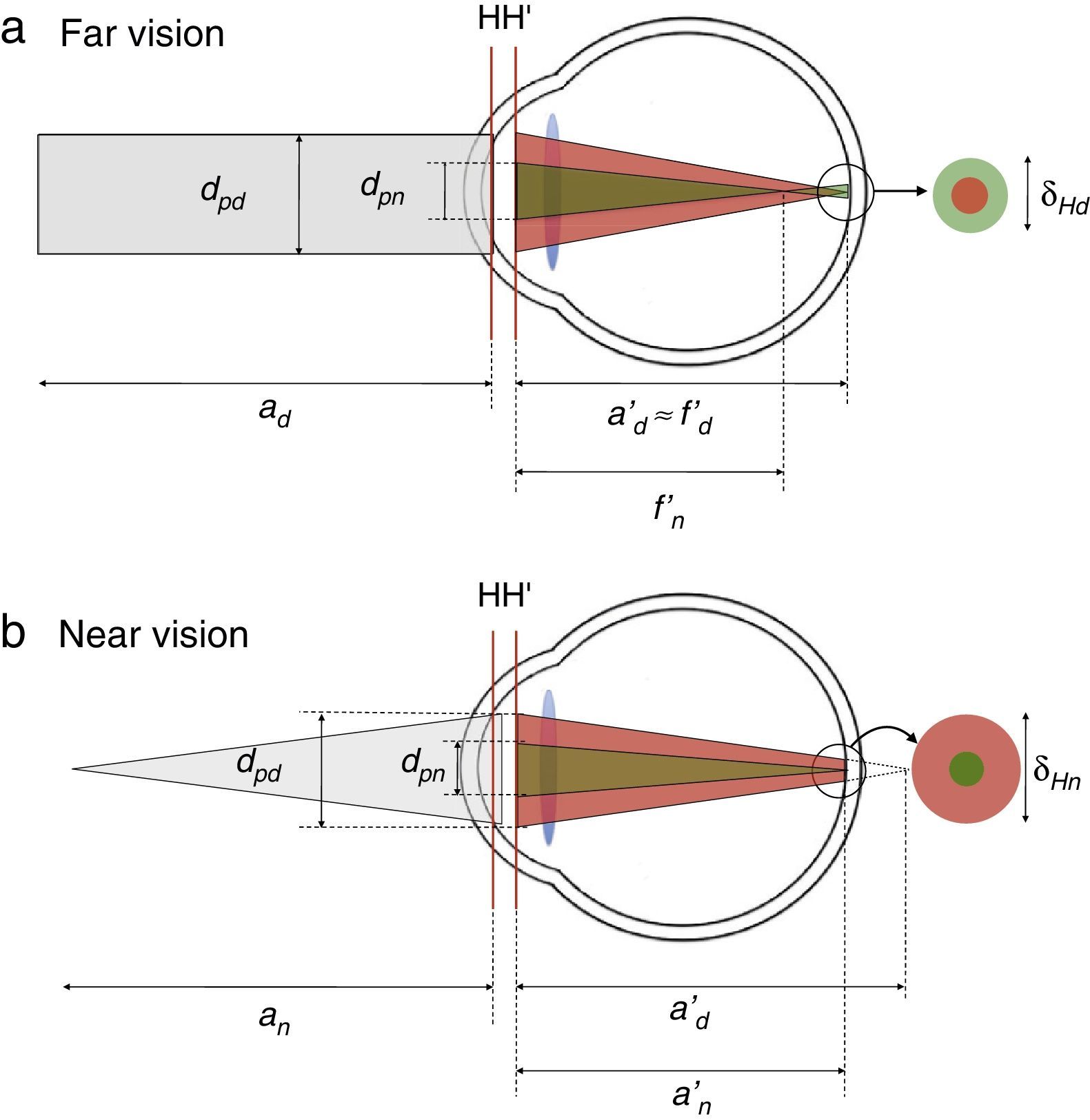
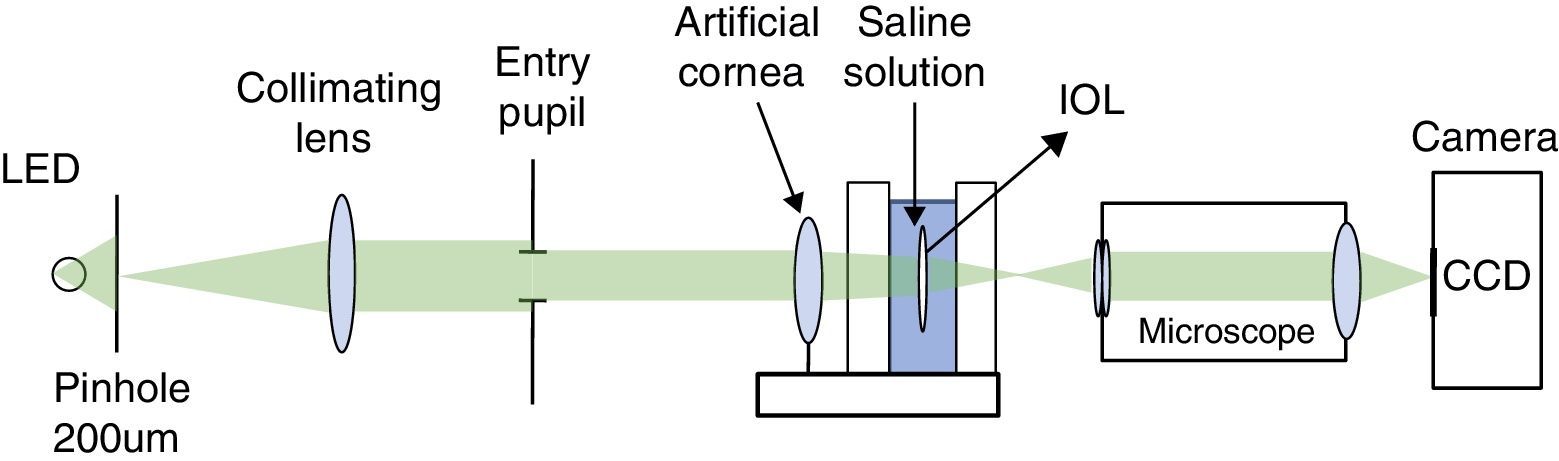
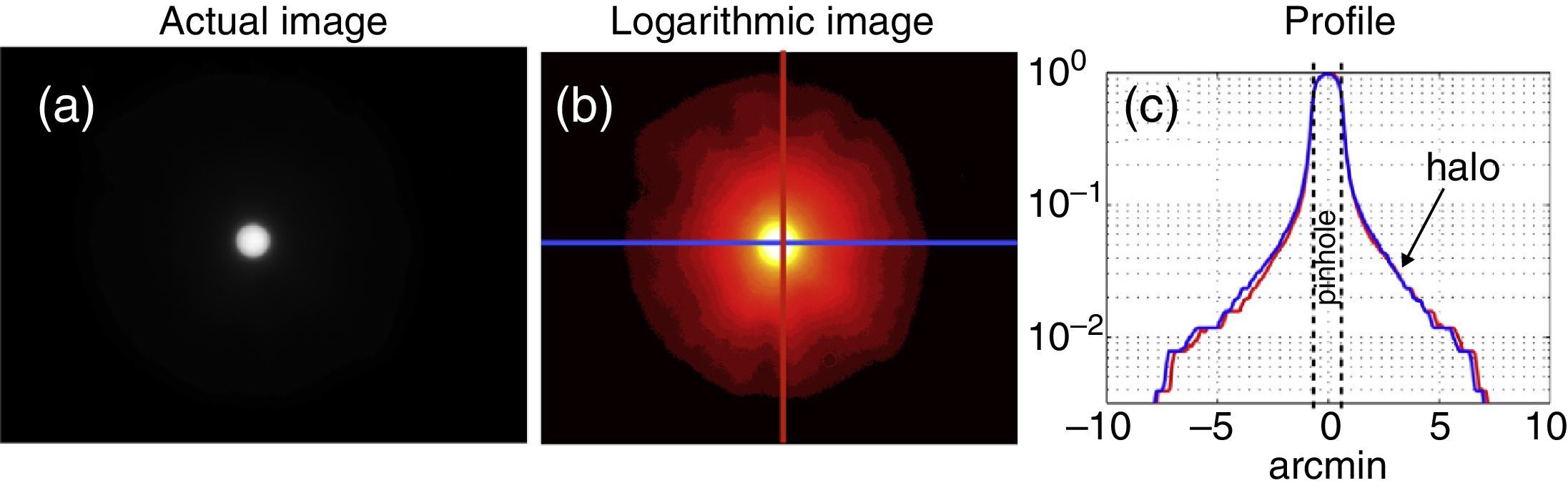
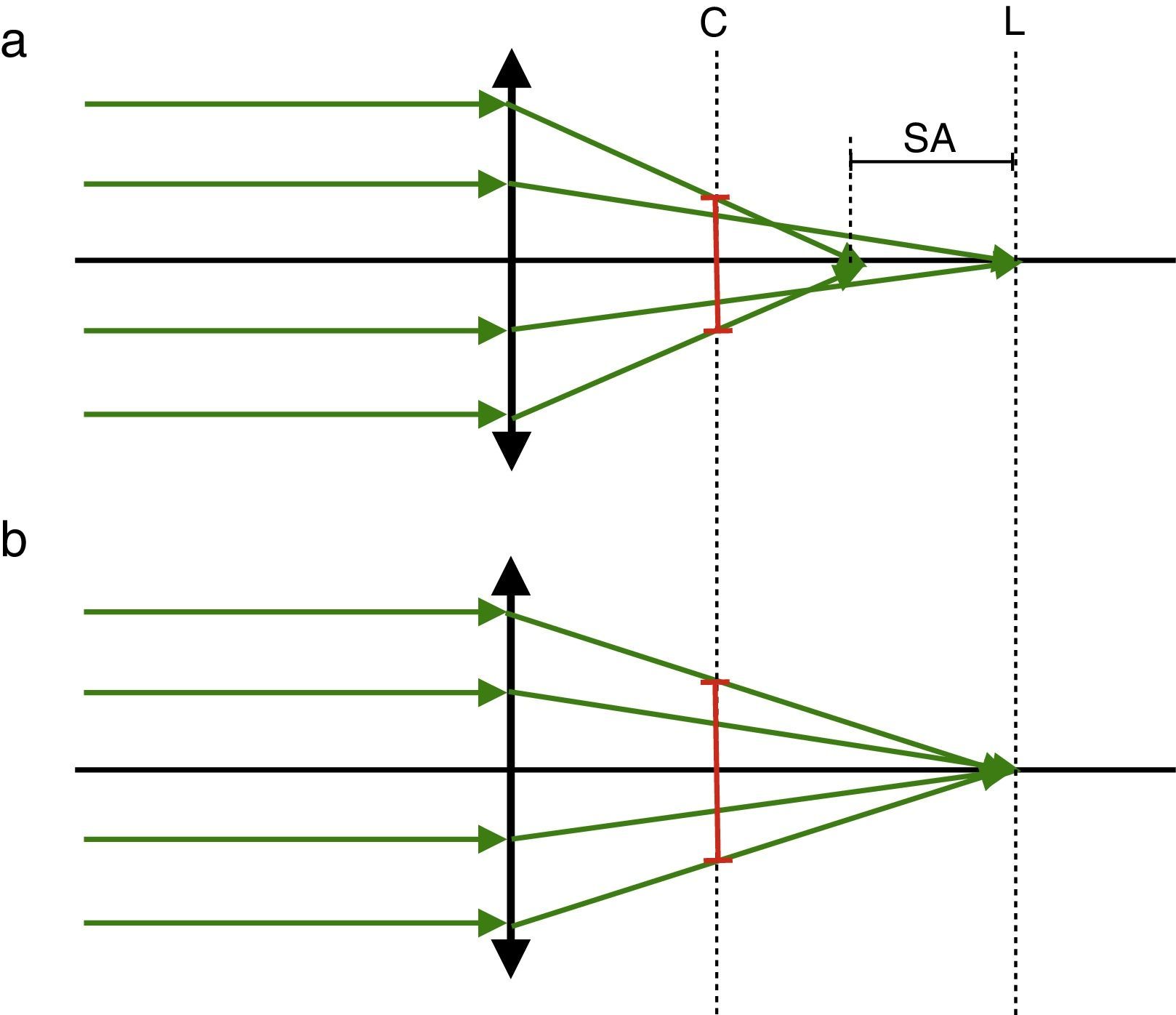
Method

The origin of the halo in a MIOL is the overlaying of 2 or more images. Using geometrical optics, it can be demonstrated that the diameter of each halo depends on the addition of the lens (ΔP), the base power (P_d), and the diameter of the IOL that contributes to the “non-focused” focus. In the image plane that corresponds to the distance focus, the halo diameter (δH_d) is given by: δH_d = d_pn ΔP/P_d, where d_pn is the diameter of the IOL that contributes to the near focus. Analogously, in the near image plane the halo diameter (δH_n) is: δH_n = d_pd ΔP/P_d, where d_pd is the diameter of the IOL that contributes to the distance focus. Patients perceive halos when they see bright objects over a relatively dark background. In vitro, the halo can be characterized by analyzing the intensity profile of the image of a pinhole that is focused by each of the foci of a MIOL.

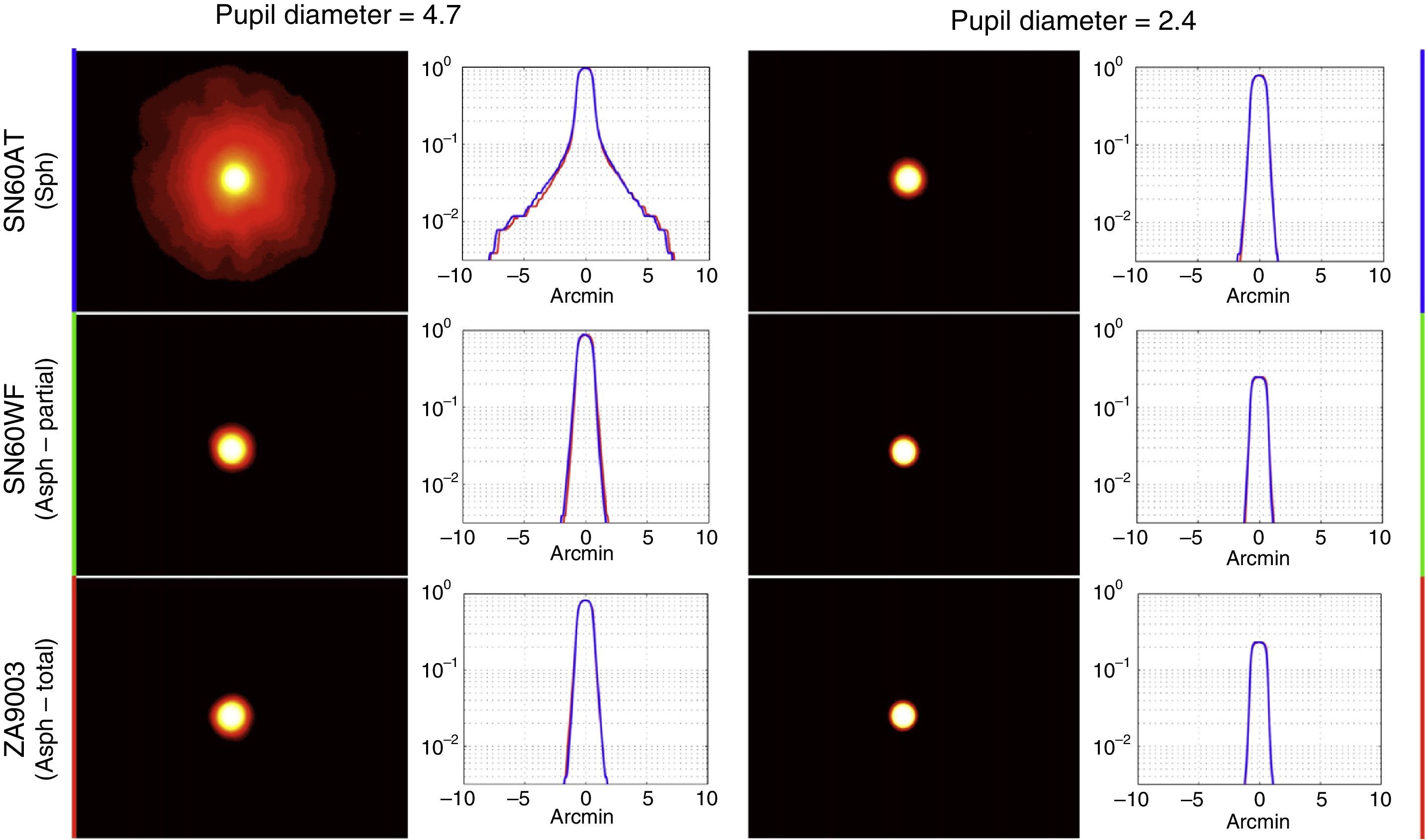
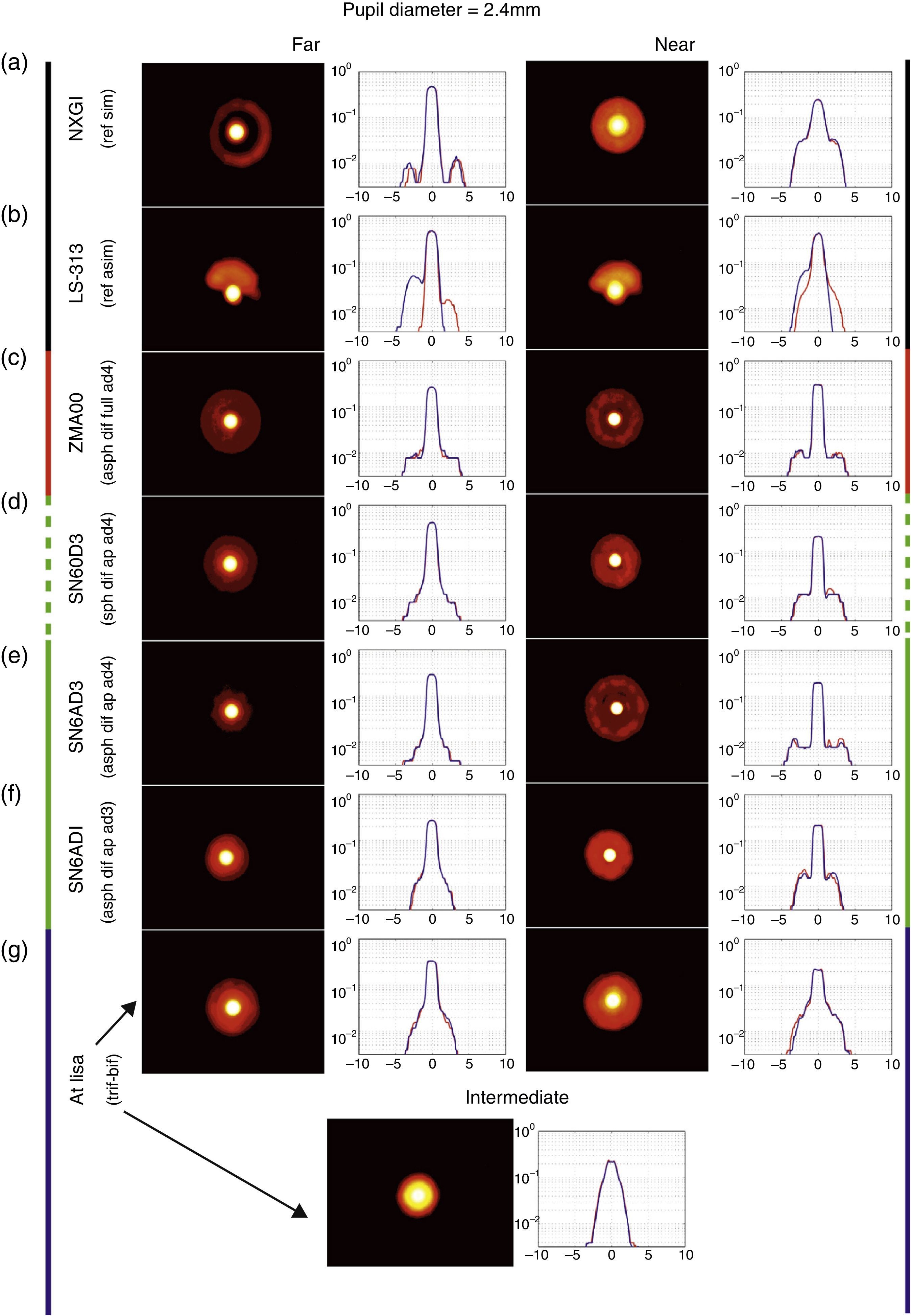
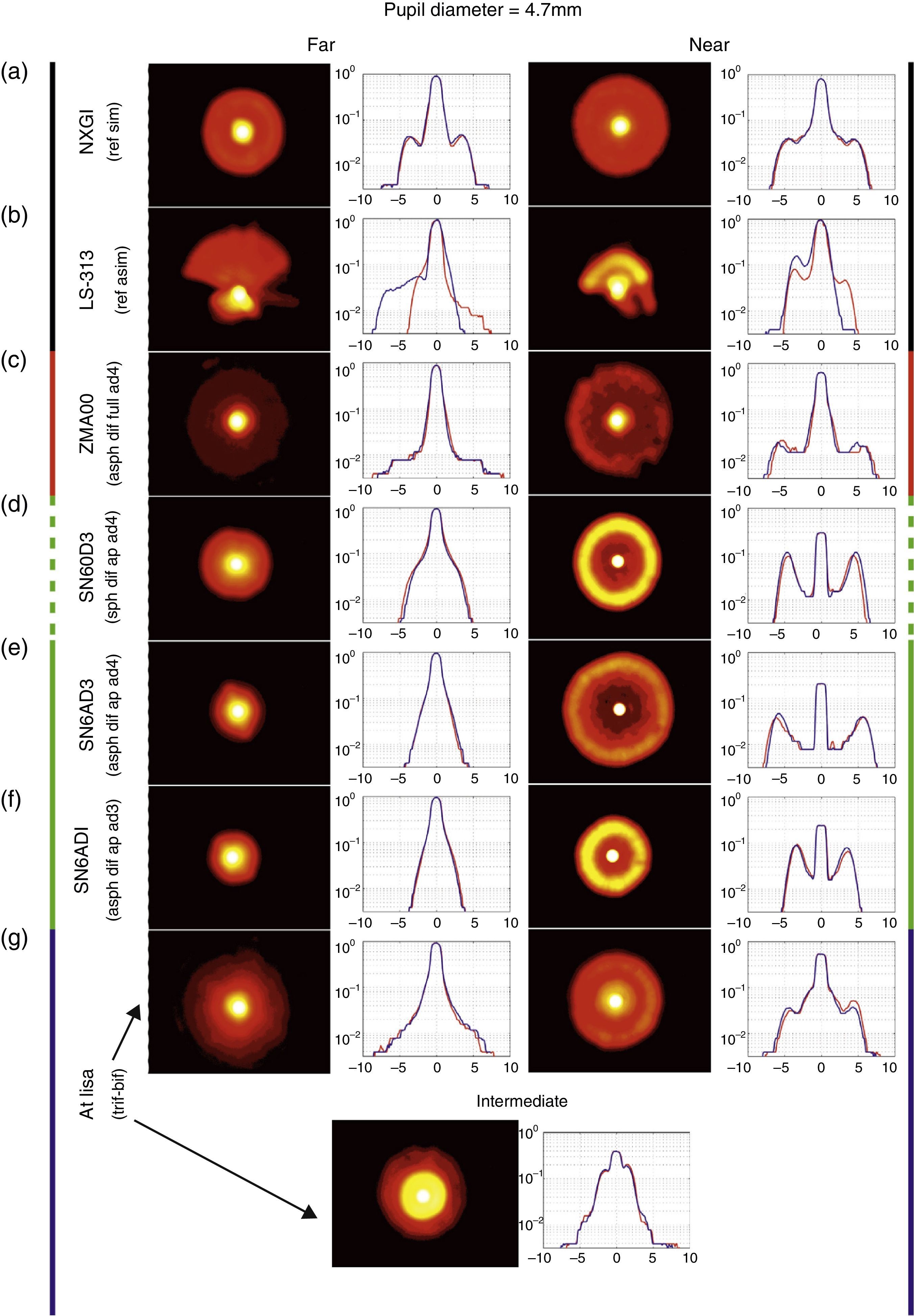
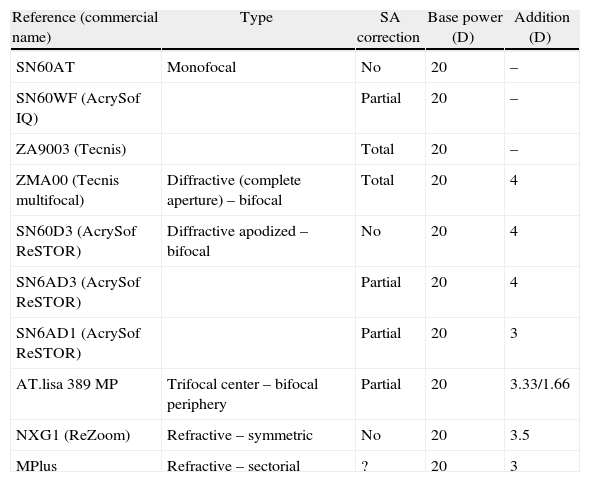
Results and conclusions

A comparison has been made between the halos induced by different MIOL of the same base power (20D) in an optical bench. As predicted by theory, the larger the addition of the MIOL, the larger the halo diameter. For large pupils and with MIOL with similar aspheric designs and addition (SN6AD3 vs. ZMA00), the apodized MIOL has a smaller halo diameter than a non-apodized one in distance vision, while in near vision the size is very similar, but the relative intensity is higher in the apodized MIOL. When comparing lenses with the same diffractive design, but with different spherical-aspheric base design (SN60D3 vs. SN6AD3), the halo in distance vision of the spherical MIOL is larger, while in near vision the spherical IOL induces a smaller halo, but with higher intensity due to the spherical aberration of the distance focus in the near image. In the case of a trifocal-diffractive IOL (AT LISA 839MP) the most noticeable characteristic is the double-halo formation due to the 2 non-focused powers.

Resumen

Objetivo

Caracterización teórica y experimental del halo en lentes intraoculares (LIO) multifocales.

Método

El halo producido por una LIO multifocal (LIOM) se origina cuando sobre una imagen enfocada se superpone otra desenfocada. Mediante óptica geométrica se demuestra que el diámetro de cada halo depende de la adición de la lente (ΔP), de la potencia base (P^d) y del diámetro de la lente iluminada que contribuye al foco «no-enfocado». En plano imagen que corresponde al foco de lejos, el diámetro del halo (δH^d) viene dado por: δH^d = d^pn ΔP/P^d donde d^pn es el diámetro de la LIO que contribuye al foco cercano. Análogamente, en el plano imagen del foco de cerca del diámetro del halo (δHⁿ) viene dado por δHⁿ = d^pd ΔP/P^d, donde d^pd es el diámetro de LIO que contribuye al foco lejano. Los pacientes perciben halos cuando observan objetos luminosos sobre un fondo relativamente oscuro. In vitro, el halo se puede caracterizar analizando el perfil de intensidad de la imagen de un pinhole que forma cada uno de los focos de una lente multifocal.

Resultados y conclusiones

Hemos comparado los halos producidos por varias LIOM de la misma potencia base (20 D) en un banco óptico. Tal y como predice la teoría, cuanto mayor es la adición de la LIOM de diseños asféricos (SN6AD3 vs. ZMA00), las lentes apodizadas presentan un halo de menor diámetro que las no-apodizadas en visión lejana, mientras que en visión cercana el halo es del mismo tamaño pero la intensidad relativa es mayor en el caso de las apodizadas. Comparando lentes esféricas y asféricas con igual diseño difractivo (SN60D3 vs. SN6AD3) el halo en visión lejana en la lente esférica es mayor, mientras que en visión cercana la lente esférica produce un halo de menor tamaño pero de mayor intensidad debido a la aberración esférica del foco lejano en el plano imagen del foco cercano. En el caso de una lente trifocal (AT LISA 839MP) la característica más distintiva es la aparición de un doble halo debido a los focos lejano e intermedio de la LIO, sobre la imagen enfocada en visión cercana.