La estadística es la ciencia que permite tomar decisiones en situaciones de incertidumbre1. Estas decisiones se basan con frecuencia en inferir a partir de muestras, tanto para estimar valores en las poblaciones como para realizar pruebas de contraste de hipótesis. Básicamente, el propósito de las pruebas de hipótesis es obtener conclusiones sobre los parámetros de la población (media, proporción u otros) basándonos en los resultados obtenidos en muestras aleatorias2. La estadística ha desarrollado dos grupos de pruebas para tomar decisiones de este tipo: pruebas paramétricas y pruebas no paramétricas.
Las pruebas paramétricas tienen en cuenta los parámetros en las poblaciones. Para su utilización es necesario que se de una serie de requisitos o supuestos que, en caso de no cumplirse, impiden su utilización3,4: la escala de medida debe ser de intervalo o razón; las observaciones deben ser independientes unas de otras; las variancias poblacionales de las variables en estudio deben ser similares (homocedasticidad); la relación entre las variables debe ser de tipo lineal, y la distribución de las variables en la población debe seguir una ley normal.
Las pruebas no paramétricas no necesitan estas condiciones previas de aplicación. Pueden utilizarse para analizar variables nominales y ordinales. La distribución poblacional puede ser cualquiera y no es necesario conocer ni suponer nada acerca de las variancias poblacionales. La mayoría no requiere el supuesto de linealidad.
Cuando se dan las condiciones de aplicación, las pruebas paramétricas tienen más potencia que las no paramétricas, pero, cuando esto no es así, el riesgo alfa puede ser mayor que el especificado de antemano5, es decir, se aumenta la probabilidad de afirmar una diferencia entre grupos que no existe, que podríamos traducir como que se incrementa la probabilidad de cometer un falso positivo6.
Una estrategia posible sería utilizar siempre pruebas no paramétricas ya que, si se dan las condiciones de aplicación, la pérdida de potencia no es muy grande y, si no se dan, son los métodos que deben emplearse. Es conocido que los métodos no paramétricos tienen una alta potencia cuando se dan las condiciones de aplicación de las paramétricas y tienen muy pocas probabilidades de conducir a una conclusión distinta de la obtenida por los métodos tradicionales paramétricos7.
Otra alternativa es la utilización de los llamados métodos robustos. Estos métodos son menos potentes que los paramétricos, pero se muestran superiores a los no paramétricos clásicos. Entendemos por potencia o poder de un test la probabilidad de elegir la hipótesis alternativa cuando es cierta, es decir, la capacidad para encontrar diferencias significativas cuando es cierto que existen8,9.
La principal de sus ventajas es que no se afectan por la existencia de datos anómalos, como, por ejemplo, algunos datos muy extremos (outliers), y que no requieren los supuestos de aplicación de las pruebas paramétricas.
Cuando una distribución cualquiera presenta datos anómalos, existe el hábito generalizado de eliminarlos, proceso eufemísticamente llamado de limpieza o depuración, antes de realizar inferencias con ella. Esta actitud asume que los datos extremos son erróneos, lo cual no es admisible. Otras opciones que se utilizan son las de su sustitución por el valor promedio, por la interpolación de un dato con respecto a los adyacentes u otros métodos similares a los empleados cuando existen datos ausentes (missing) en una base de datos10,11. Sin embargo, un enfoque más adecuado es comprobar la veracidad de los datos. Si el dato extremo está equivocado debe corregirse. Si es correcto, eliminarlo o sustituirlo puede modificar las inferencias que se realicen a partir de esa información, debido a que introduce un sesgo que es difícil de cuantificar12 y a que disminuye el tamaño muestral. Este último aspecto es crucial cuando la muestra estudiada es pequeña.
Los métodos robustos pueden ser de utilidad para la realización de inferencias sin tener que «depurar» los datos extremos, ya que están diseñados para realizar inferencias sobre el modelo, reduciendo la posible influencia que pudiera tener la presencia de datos anómalos13.
Métodos robustos para estimar medidas de centralización
Un problema conocido en el cálculo de medidas de posición o centralización es aquel en el que una distribución de datos no sigue una ley normal; en esta circunstancia la media no es un buen estimador del promedio de los datos. La media es particularmente sensible cuando la serie de datos es pequeña y existe algún valor extremo. Por ejemplo, en la serie 2, 3, 4, 5, 100, la media es 22,8, que no refleja bien el valor promedio de la serie. La alternativa que suele proponerse a esta situación es utilizar la mediana y los percentiles para describir la distribución14,15, ya que estas medidas no se ven afectadas, generalmente, por la existencia de valores extremos. La mediana de la distribución es 4. Sin embargo, en algunas circunstancias la mediana tampoco estima bien el promedio de la distribución. Esto ocurre cuando en una muestra la mediana y los valores superiores a ella están muy cercanos entre sí y, a su vez, muy alejados de los valores que se sitúan por debajo de la mediana, o viceversa. Por ejemplo, en la muestra 1, 2, 98, 99, 100, la mediana es 98, que no es un índice de resumen apropiado. El porcentaje máximo de valores extremos que soporta un estimador antes de no ser válido se llama punto de ruptura (breakdown point)16.
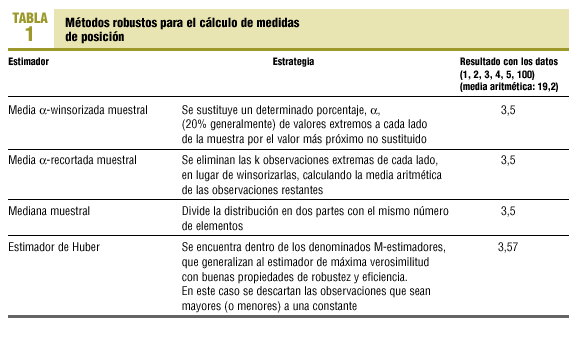
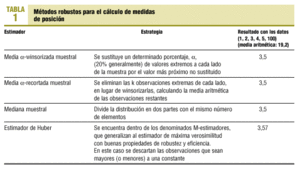
En estas circunstancias, tamaño muestral pequeño y presencia de valores extremos, pueden utilizarse métodos robustos para el cálculo de estadísticos de centralización o localización (tabla 1).
Como parámetros de localización se recomienda en primer lugar, el de Huber y, en segundo lugar, la media α-recortada muestral (con α = 0,2).
Métodos robustos para estimar medidas de dispersión
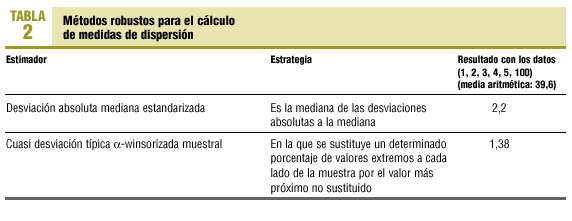
Las medidas de dispersión clásicas (variancia y desviación típica) se ven afectadas por las mismas limitaciones que las medidas de posición. La desviación típica sólo es un buen estimador del promedio de la desviación del conjunto de los datos con respecto al valor central, cuando la distribución es normal (gaussiana). Las alternativas robustas para el cálculo de medidas de dispersión se resumen en la tabla 2.
Se recomienda la utilización de la desviación absoluta mediana estandarizada.
Métodos robustos para el contraste de hipótesis
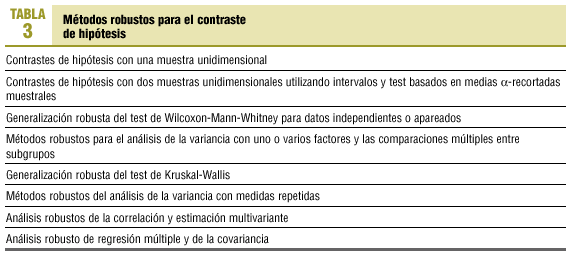
Con los parámetros antes referidos, se pueden construir intervalos de confianza robustos y realizar contrastes de hipótesis13. Las principales pruebas de contraste de hipótesis basadas en métodos robustos se presentan en la tabla 3.
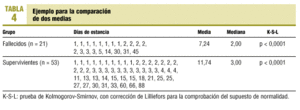
Ejemplo para la comparación de dos medias
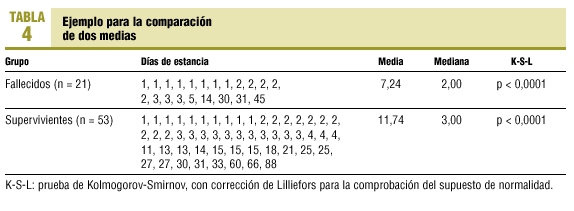
Disponemos de 74 pacientes ingresados en una unidad de cuidados intensivos (UCI) y queremos comparar las estancias generadas en dicha unidad entre un grupo de pacientes fallecidos y otro grupo de supervivientes (tabla 4).
La variable estancia, como casi todas las que se refieren al tiempo, es una variable conocida por su distribución alejada de lo normal. Si el tamaño de los grupos que se estudian es pequeño menor de 30, no sería adecuada la utilización de métodos paramétricos (t de Student) y deberíamos recurrir a los clásicos no paramétricos (U de Mann-Whitney). Sin embargo, en este caso concreto ninguna de estas dos opciones tiene potencia suficiente para detectar diferencias significativas. La potencia es la capacidad para encontrar diferencias significativas cuando es cierto que existen8. Sin embargo, el test robusto de Yuen, que utiliza medias α-recortadas muestrales, es capaz de detectar diferencias significativas entre ambos grupos (tabla 5).
Por tanto, el test de Yuen es una alternativa a las pruebas de la t de Student y U de Mann-Whitney para tamaños muestrales pequeños y distribuciones no normales.
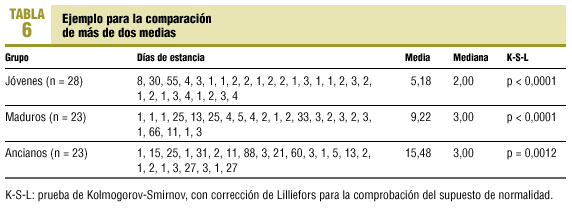
Ejemplo para la comparación de más de dos medias
Como ejemplo de la utilidad de los métodos robustos para el análisis de la variancia continuamos utilizando a otros 73 pacientes ingresados en una UCI y queremos comparar las estancias generadas en dicha unidad entre tres grupos de pacientes clasificados en función de la edad (jóvenes, maduros y ancianos). Las características que los describen se resumen en la tabla 6.
Por otro lado, el test de Levene para valorar la homogeneidad de las variancias (homocedasticidad) muestra que existen diferencias entre ellas (p = 0,027). Por lo tanto, existen varios incumplimientos (ausencia de normalidad y homocedasticidad, y existencia de valores anómalos outliers) que impiden la utilización de métodos paramétricos (ANOVA clásico) en este ejemplo y deberíamos recurrir a los clásicos no paramétricos de Kruskal-Wallis o, mejor, a métodos robustos como la generalización robusta del test Welch, que utiliza medias α-recortadas muestrales y es capaz de detectar diferencias significativas entre los grupos (tabla 7).
Ejemplo para el análisis de correlación y regresión lineal
Por último, para comparar los distintos métodos en los análisis de correlación y regresión utilizaremos también a 22 pacientes ingresados en una UCI. En este caso deseamos valorar la relación entre la edad de los mismos y sus estancias generadas en dicha unidad (tabla 8).
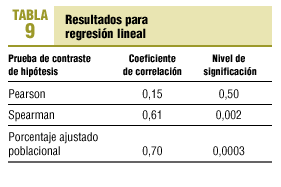
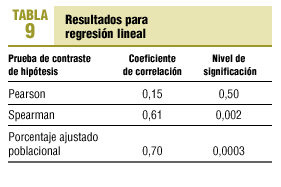
De nuevo observamos la ausencia de normalidad en las dos variables que invalida la utilización de métodos paramétricos (correlación de Pearson y regresión lineal), por lo que deberíamos recurrir a métodos no paramétricos (Spearman) o, mejor, a métodos robustos como el coeficiente de porcentaje ajustado poblacional y el estimador robusto de regresión medio biponderado (tabla 9).
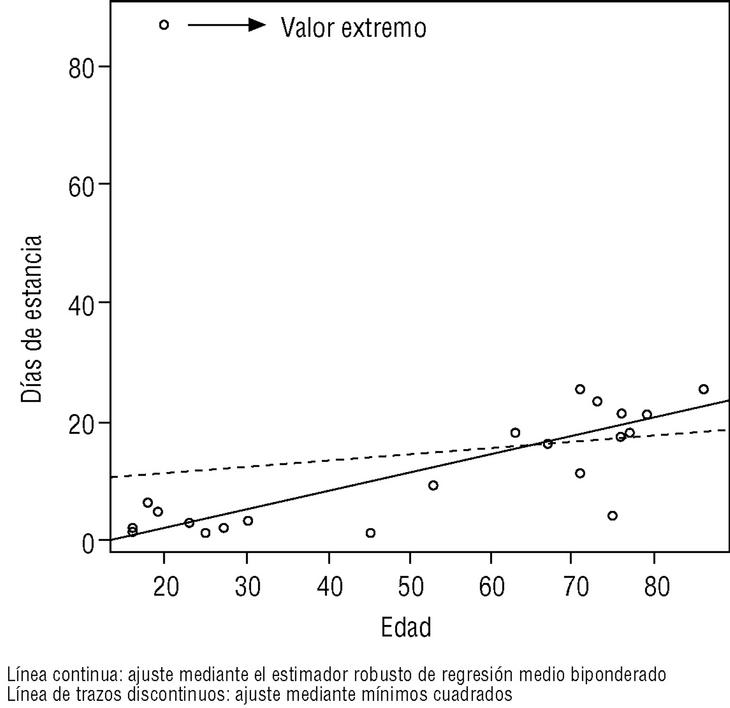
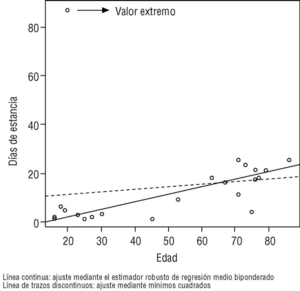
En la figura 1 podemos apreciar la diferencia entre la recta de regresión obtenida por el método de mínimos cuadrados y la obtenida por el estimador robusto de regresión medio biponderado, y cómo afecta la existencia de un valor extremo.
Figura 1. Rectas de regresión obtenidas por mínimos cuadrados y por el estimador robusto de regresión medio biponderado.
Como puede comprobarse en la figura 1, el ajuste es mejor con el estimador robusto que con la estimación por mínimos cuadrados. El valor extremo apenas afecta a la estimación robusta.
La realización de cualquiera de estas estimaciones requiere un programa estadístico apropiado. Entre ellos puede utilizarse el programa R, que añade al hecho de facilitar estos cálculos el de ser de libre distribución, por lo que no está sometido a derechos de copyright y se obtiene gratuitamente en Internet17.
Correspondencia: Enrique Ramalle-Gómara. Servicio de Epidemiología. C/ Villamediana, 17. 26071 Logroño. La Rioja. España. Correo electrónico: ramalle@larioja.org
Manuscrito recibido el 22 de julio de 2002.
Manuscrito aceptado para su publicación el 22 de julio de 2002.