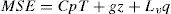A simple mechanism for the climatological midsummer drought along the Pacific coast of Central America

Resumen

Se investigan la distribución mundial, la evolución estacional y los mecanismos subyacentes de la sequía de medio verano (MSD, por sus siglas en inglés) mediante un conjunto de observaciones realizadas en estaciones climatológicas y datos de reanálisis con resolución espacial y temporal relativamente alta, con especial énfasis en la costa del Pacífico centroamericano y el sur de México. Aunque la MSD de Centroamérica destaca por su coherencia y escala espacial, no es exclusiva de la región del Gran Caribe ni necesariamente la más intensa del planeta, como lo demuestra un análisis objetivo de varios conjuntos de datos globales de precipitación. Se propone un mecanismo para la MSD que relaciona la dependencia latitudinal de los dos máximos climatológicos de precipitación con el cruce semestral de la declinación solar, lo cual determina la presencia de dos picos de inestabilidad convectiva y por lo tanto de lluvias. Además de este mecanismo local subyacente, una serie de procesos remotos tiende a alcanzar su punto máximo en el vértice de la MSD. Dichos procesos incluyen el monzón de Norteamérica, la corriente en chorro de bajo nivel del Caribe y el anticiclón subtropical del Atlántico Norte, que también puede suprimir las lluvias a lo largo de la costa del Pacífico centroamericano y generar variabilidad interanual en la fuerza o el momento de la MSD. Sin embargo, los hallazgos de este estudio contradicen el paradigma existente de que la MSD debe su existencia a un mecanismo supresor de la precipitación. Por el contrario, a partir del análisis de registros temporales de mayor resolución de precipitaciones y variaciones que toman en cuenta la latitud, se sugiere que la MSD es básicamente el resultado de un mecanismo de reforzamiento de la precipitación que ocurre dos veces.

Abstract

The global distribution, seasonal evolution, and underlying mechanisms for the climatological midsummer drought (MSD) are investigated using a suite of relatively high spatial and temporal resolution station observations and reanalysis data with particular focus on the Pacific coast of Central America and southern Mexico. Although the MSD of Central America stands out in terms of spatial scale and coherence, it is neither unique to the Greater Caribbean Region (GCR) nor necessarily the strongest MSD on Earth based on an objective analysis of several global precipitation data sets. A mechanism for the MSD is proposed that relates the latitudinal dependence of the two climatological precipitation maxima to the biannual crossing of the solar declination (SD), driving two peaks in convective instability and hence rainfall. In addition to this underlying local mechanism, a number of remote processes tend to peak during the apex of the MSD, including the North American monsoon, the Caribbean low-level jet, and the North Atlantic subtropical high which may also act to suppress rainfall along the Pacific coast of Central America and generate interannual variability in the strength or timing of the MSD. However, our findings challenge the existing paradigm that the MSD owes its existence to a precipitation-suppressing mechanism. Rather, aided by the analysis of higher-temporal resolution precipitation records and considering variations in latitude, we suggest the MSD is essentially the result of one precipitation-enhancing mechanism occurring twice.

1

Introduction

A successful growing season is aided by the ability to rely on regular or predictable seasonal rainfall. Throughout the tropics, the timing and intensity of the rainy season are governed by monsoon dynamics, which are driven by local ocean-atmosphere-land interactions, the migration of the Intertropical Convergence Zone (ITCZ), and interactions thereof. The climatological seasonal cycle of precipitation in the Greater Caribbean Region (GCR) spans roughly May through October, although the exact beginning and end dates vary significantly by location. Long known to agriculturally based societies across the global tropics, within the rainy season there is a temporary break from monsoon rains. This so-called midsummer drought (MSD), known colloquially by “veranillo” or “canícula” in Central America, is such a regular feature of the climatological rainy season that seeding and growing practices of many farmers have been tailored specifically to leverage a biannual monsoon (McLaurin et al, 2008). Previous studies have suggested that the GCR is home to the strongest MSD on the planet (e.g., Curtis, 2002).

The MSD was first reported in the scientific literature by Portig (1961). Drawing on the observation by Alpert (1945,1946) that the ITCZ in the eastern Pacific makes a brief equatorward excursion from its northernmost position during July-August, Hastenrath (1967) asked whether the regular seasonal cycle of the ITCZ can explain the MSD. With precious little meteorological data. Hastenrath (1967)also discussed the potential role of the North Atlantic subtropical high (NASH), which happens to strengthen and extend westward into the Caribbean during July-August. He later showed that modern reanalysis data supports the role of the eastern Pacific ITCZ (Hastenrath, 2002). Following the publication of Hastenrath’s early ideas, nearly three decades passed before interest in the MSD was renewed. These three decades were also a period during which climate observations throughout the GCR, both ground-based and space-borne, were improving and expanding.

Magaña et al. (1999) proposed that the MSD can be explained in terms of a local mechanism involving lagged feedbacks between sea surface temperature (SST), convection, and surface insolation. The argument is as follows: seasonal insolation causes SST in the east Pacific warm pool (EPWP) to warm in early summer, which drives convection and produces the first peak in precipitation; at the height of convective activity, surface insolation is reduced due to cloud cover, thereby cooling SST, which reduces convection and produces the midsummer precipitation minimum; finally, while convection is at a minimum, increased insolation again warms SST, which results in convection and the second peak in precipitation. It follows that if seasonal forcing was constant (or summer was indefinite) with no remote influences, this feedback cycle would imply a perpetual oscillation of rainfall peaks and troughs (or MSDs) amidst a general rainy season, with a timescale determined by the SST-convection-radiation feedback and governed by the thermal response timescale of the ocean mixed layer.

Following Magaña et al. (1999), the most recent decade has seen a multitude of theories for the MSD. In the most general terms, the biannual structure of the seasonal cycle we refer to as the MSD could be the result of one or more precipitation-enhancing processes occurring twice per year: once during early summer (May-June) and once during late summer (September-October). The relevant processes in early and late summer need not be the same. Alternatively, the MSD could be due to one or more precipitation-inhibiting processes occurring once per year: in July-August. The MSD may also be the result of local nonlinear air-sea interactions such as those described by, e.g., Hastenrath (1967) or Magaña et al (1999). Finally, there may be multiple processes at work, any of which may alone be capable of producing a brief annual reduction of precipitation in the GCR resembling the MSD.

Many have recently argued for a dominant role of the westward intensification of the NASH, similar to ideas envisaged by Hastenrath (1967). Mapes et al. (2005)used a “slowed-calendar” simulation of an atmospheric general circulation model to show that thermal disequilibrium in the land-atmosphere system results in a less pronounced westward intensification of the NASH and therefore a less pronounced MSD. The model results show that if summer was long enough for the land surface temprature to reach equilibrium with seasonal forcing, the NASH would be stronger in midsummer and the rainfall reduction would be larger and begin ~1 month earlier.In addition to the intrusion of high pressure into the GCR, the NASH may be linked to the MSD through its associated easterly trade winds, which are regionally manifestas low-level easterlies, the Caribean low-level jet(CLLJ), and the central American gap winds.for example, Mestas-Nuñez et al.(2007)argued that the MSD is the result of a midsummer strengthening of the CLLJ, which cools SST in the Caribbean Sea and reduces convection. Wang et al. (2007,2008), Muñoz et al. (2008), Small et al. (2007), and Xie et al. (2008)have presented arguments that the NASH and associated CLLJ moisture transports partially explain the MSD. Romero-Centeno et al. (2003,2007) argued that the Tehuantepec and Papagayo gap winds, which exhibit a secondary maximum in midsummer, cause the MSD by preventing the southerly trade winds over the EPWP and convection from reaching the Central American coast. Similarly, Xie et al. (2005) theorized that the Tehuantepec and Papagayo gap winds play a role, but that their direct impact on the EPWP SST field—especially the Costa Rica dome—modulates convection and may explain the MSD. Some have argued that the seasonality of tropical cyclone frequency helps explain the MSD (e.g., Curtis, 2002; Inoue et al, 2002; Small et al. 2007; Liebmann et al, 2008), while others have suggested the Madden-Julian Oscillation (MJO) is involved in producing the MSD (e.g., Molinari and Vollaro, 2000). Suppression of precipitation by Saharan dust has also been proposed as a mechanism for the MSD (González et al., 2007). Looking to the future, Rauscher et al. (2008) assessed how current coupled GCMs capture the MSD and how the MSD is projected to change in response to global warming. They found that the MSD is fairly well represented in coupled GCMs despite overall biases, and that the MSD is projected to become stronger, including an earlier onset. The long-term changes appear to be accompanied by a westward expansion and intensification of the NASH (including the associated low-level easterlies) and an equatorward-displaced eastern Pacific ITCZ.

The body of work on the MSD to date has implicated several climate processes capable of producing interannual variability and/or long-term trends in characteristics of the MSD such as its strength and onset. However, it remains unknown what are the basic causal mechanisms for the midsummer drought in the GCR. In order to ultimately improve predictions of the seasonal cycle of rainfall in the GCR, the causal mechanisms of the MSD, as well as those that contribute to its variability must be better understood. Focusing on the Pacific coast of Central America and southern Mexico, here we analyze a suite of relatively high spatial and temporal resolution observations and propose a simple underlying mechanism for the climatological midsummer drought. The remainder of the paper is organized as follows: the various data sets analyzed are described briefly in section 2, observational results are presented in section 3, and the conclusions along with a discussion of future research directions are given in section 4.

2

Data and methods

A useful characterization of the MSD phenomenon in terms of precipitation requires balancing the strengths and limitations of multiple observational data sets, i.e., record length, temporal resolution, spatial domain (including whether the ocean is included), spatial resolution, and platform (satellite, gauge, blend, etc.). To this end, we acquired and analyzed the following gridded monthly observed precipitation data sets: National Oceanic and Atmospheric Administration Land Precipitation (NOAA PREC/L; Chen et al, 2002); National Aeronautics and Space Administration Global Precipitation Climatology Project (NASA GPCP; Adler et al., 2003); NASA Tropical Rainfall Measuring Mission (NASA TRMM; Huffman et al, 2007); NOAA Climate Prediction Center Merged Analysis of Precipitation (CPC CMAP; Xie and Arkin, 1997); Microwave Sounding Unit (MSU; Spencer, 1993); University of East Anglia-Climate Research Unit (UEA-CRU) Global (Hulme, 1992) and v.TS2.1 (Mitchell and Jones, 2005); University of Delaware (UDEL; Willmott and Matsuura, 1995); Universidad Nacional Autónoma de México (UNAM) v.0605 and v.0705; German Climate Research Program (DEKLIM; Beck et al, 2005); NOAA Climate Anomaly Monitoring System (CAMS; Janowiak and Xie, 1999); and NOAA CPC Morphing Technique (CMORPH; Joyce et al., 2004). For brevity, we do not show the results from all data sets in this paper.

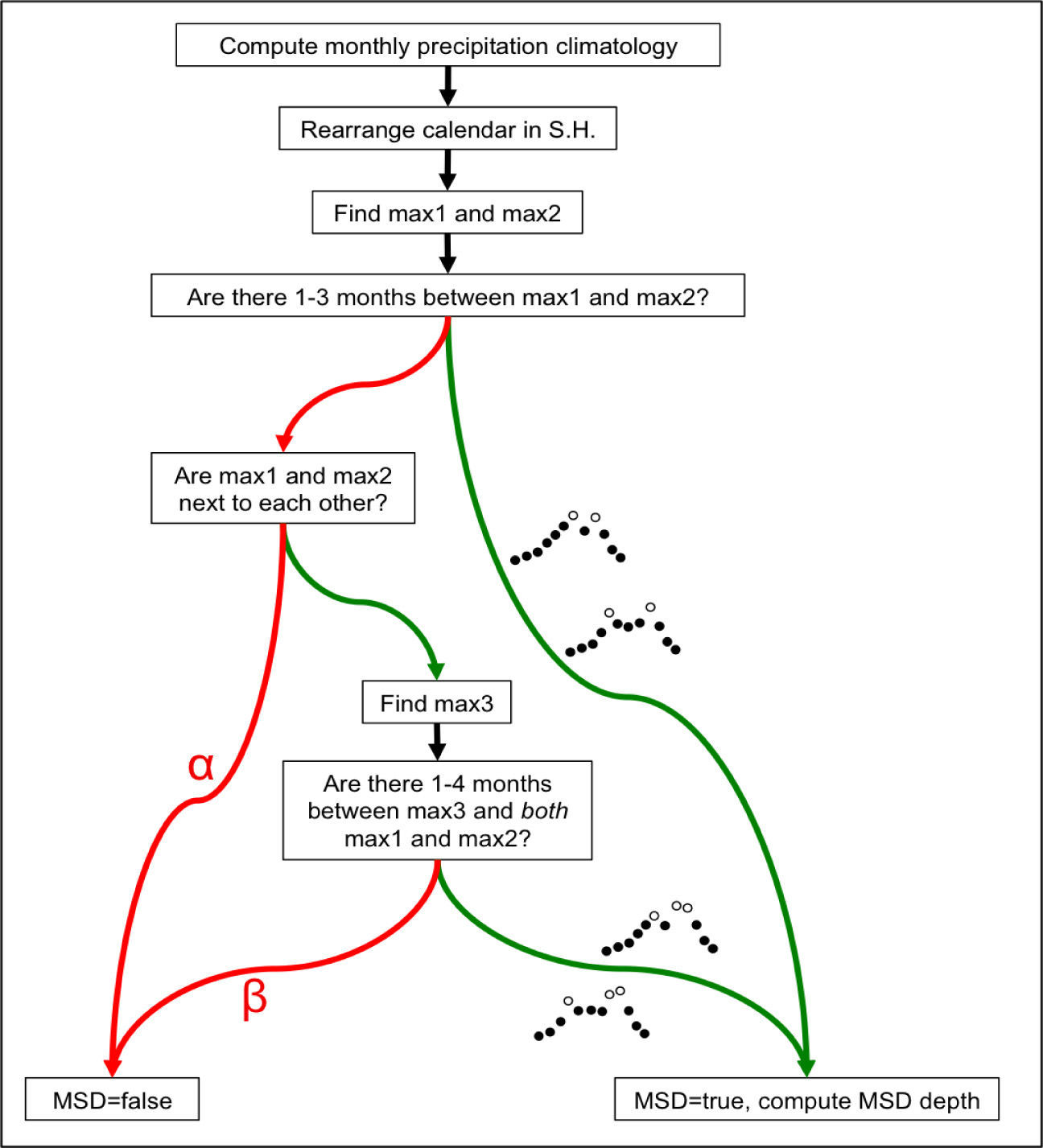
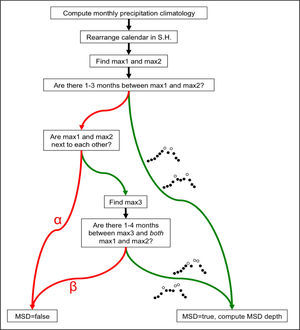
Beginning with each of the monthly gridded observed precipitation data sets, we developed an algorithm to objectively map the global distribution of the MSD existence and strength. The essence of the MSD existence/strength algorithm (MESA) is as follows: for every point on the globe (or every point in the domain in the case of regional data sets such as UNAM), the algorithm tests for the existence of the MSD in the monthly precipitation climatology and, if the MSD is present at that point, quantifies the strength of the MSD. Strength in this case is considered to be the reduction of rainfall during the minimum relative to the mean of the two rainfall maxima. The algorithm is flexible as it does not a priori assume the months of the two climatological precipitation maxima, the month(s) of the minima (i.e., the MSD), or a parametric shape of the seasonal cycle. The precipitation climatology is evaluated objectively at every location, and “peaks” (relative maxima) that are separated by 1-3 months are searched for. The MESA considers peaks that are separated by four or more calendar months to be two distinct rainy seasons, and considers three consecutive months containing the three rainiest months of the year to be a single, complete rainy season without a MSD. Furthermore, the southern hemisphere calendar is shifted such that at any location on the globe, the only season during which a precipitation minimum between two maxima would not constitute a MSD is local winter. A schematic illustration of the MESA is provided in Figure 1.

Fig. 1.

Diagram illustrating the MSD existence/strength algorithm (MESA) applied to several global, gridded precipitation data sets in this study. If “yes” (“no”) is the response to a test, then the green (red) arrow is the next step. The implication of reaching the red arrow marked a is that the duration of the would-be MSD ≥ 4 months, which is arguably too long to be a break in a rainy season; rather, it indicates that there are two distinct climatological rainy seasons. The implication of reaching the red arrow marked (3 is that the three wettest months of the year comprise a single peak thus completing a single rainy season without a break, or the duration of the would-be MSD ≥ 4 months.

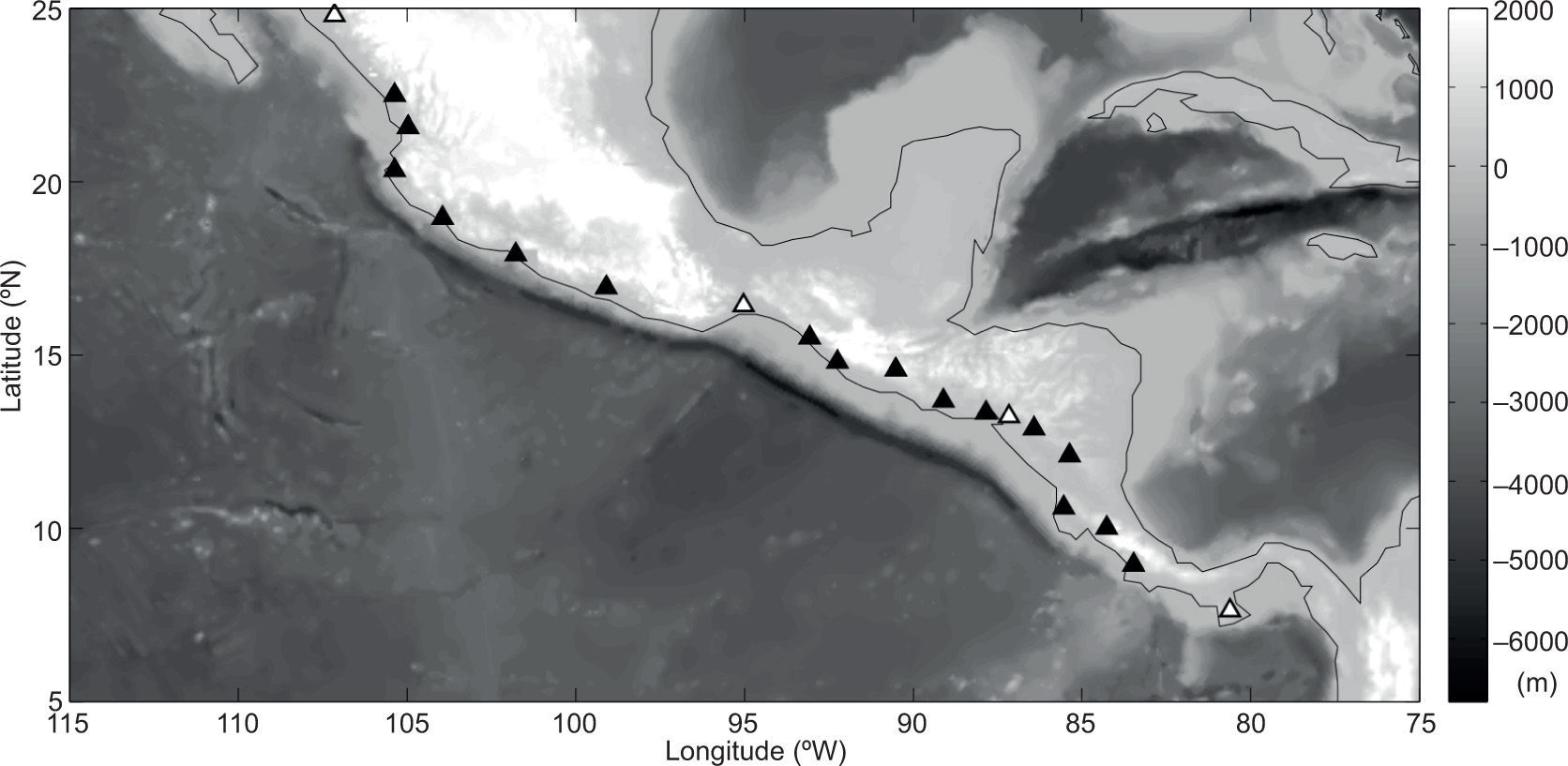
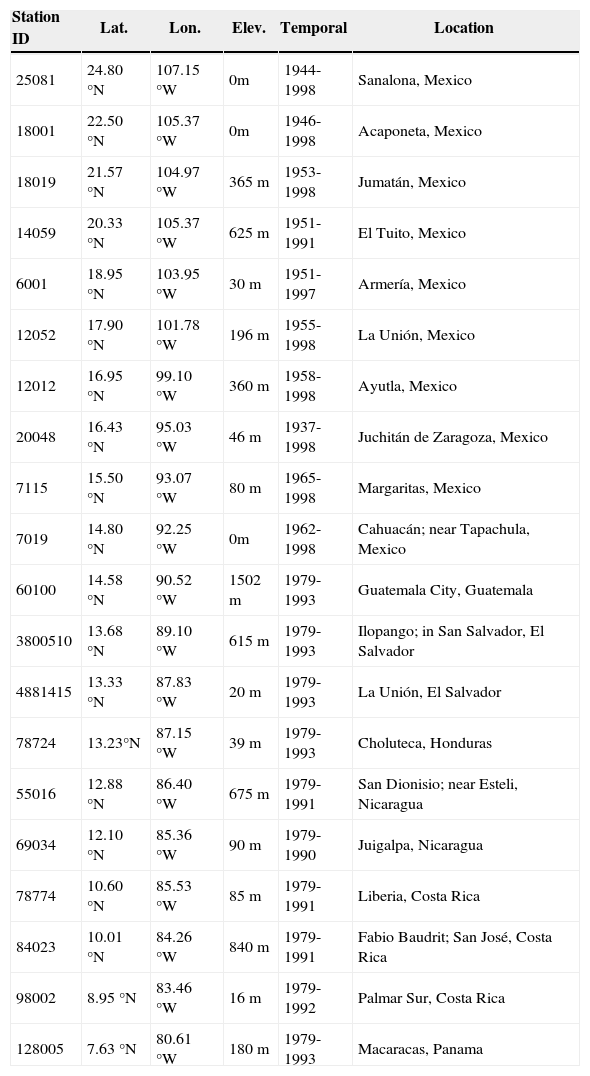
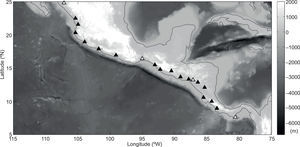
For detailed analysis of precipitation within the GCR, particularly our focus on the Pacific coast of Central America and southern Mexico, we acquired daily meteorological data from 20 stations along the Pacific coast of Central America from the IPJ/LDEO Climate Data Library. Station records of precipitation and surface air temperature analyzed in this study are from the NOAA NCDC Global Historical Climatology Network (GHCN) Daily v.l (Vose et al, 1992). Table I provides some details on each station, and Figure 2 shows the geographic distribution of the 20 stations. These stations were chosen because they have similar, overlapping temporal records spanning at least one decade, they are all coastal stations on the Pacific side of the cordillera, and they span the entire latitude band of Central America from Panama into southern Mexico. The period of overlapping temporal coverage shared among all stations (save for sporadic periods of missing data), and therefore the period for analysis of station data in this study, is 1979-1990 (12 years). Our method of averaging was carefully chosen; we first apply a 31-day running mean to the full 12 years of daily data, and then compute the daily climatology. This is distinct from computing a monthly climatology by averaging discrete calendar months or computing a noisy daily climatology without prior smoothing. The result is effectively a monthly climatology at daily resolution.

Table I.

List of stations along the Pacific coast of southern Mexico and Central America used in this study, from the GHCN Daily v.l (Vose et al, 1992). Stations are listed in descending order of latitude (Sanalona, Mexico through Macaracas, Panama). See Figure 4 for the geographic distribution of these stations. The period of overlapping temporal coverage shared among all stations (save for sporadic missing data), and therefore the period for analysis of station data in this study, is 1979-1990 (12 years). Surface air temperature records for stations south of Mexico (14.8° N) were not available.

Station ID	Lat.	Lon.	Elev.	Temporal	Location
25081	24.80 °N	107.15 °W	0m	1944-1998	Sanalona, Mexico
18001	22.50 °N	105.37 °W	0m	1946-1998	Acaponeta, Mexico
18019	21.57 °N	104.97 °W	365 m	1953-1998	Jumatán, Mexico
14059	20.33 °N	105.37 °W	625 m	1951-1991	El Tuito, Mexico
6001	18.95 °N	103.95 °W	30 m	1951-1997	Armería, Mexico
12052	17.90 °N	101.78 °W	196 m	1955-1998	La Unión, Mexico
12012	16.95 °N	99.10 °W	360 m	1958-1998	Ayutla, Mexico
20048	16.43 °N	95.03 °W	46 m	1937-1998	Juchitán de Zaragoza, Mexico
7115	15.50 °N	93.07 °W	80 m	1965-1998	Margaritas, Mexico
7019	14.80 °N	92.25 °W	0m	1962-1998	Cahuacán; near Tapachula, Mexico
60100	14.58 °N	90.52 °W	1502 m	1979-1993	Guatemala City, Guatemala
3800510	13.68 °N	89.10 °W	615 m	1979-1993	Ilopango; in San Salvador, El Salvador
4881415	13.33 °N	87.83 °W	20 m	1979-1993	La Unión, El Salvador
78724	13.23°N	87.15 °W	39 m	1979-1993	Choluteca, Honduras
55016	12.88 °N	86.40 °W	675 m	1979-1991	San Dionisio; near Esteli, Nicaragua
69034	12.10 °N	85.36 °W	90 m	1979-1990	Juigalpa, Nicaragua
78774	10.60 °N	85.53 °W	85 m	1979-1991	Liberia, Costa Rica
84023	10.01 °N	84.26 °W	840 m	1979-1991	Fabio Baudrit; San José, Costa Rica
98002	8.95 °N	83.46 °W	16 m	1979-1992	Palmar Sur, Costa Rica
128005	7.63 °N	80.61 °W	180 m	1979-1993	Macaracas, Panama

Fig. 2.

Topographic map of Central America, southern Mexico, and surrounding region (ETOP05) indicating the locations of the 20 GHCN Daily v. 1 stations used in the present study. The four stations marked by white triangles are highlighted in Figure 6. See Table 1 for additional details on each station.

We also analyzed satellite-derived SST and diagnostic fields from global and regional reanalyses at pseudo-stations corresponding to the nearest grid point to and just offshore of each of the 20 GHCN stations described above and in Table I / Figure 2. The SST data we used are from the NOAA Optimal Interpolation (OI) v.2 weekly 1° product (Reynolds et al., 2002). We utilize reanalysis fields from the global NCEP/NCAR Reanalysis Daily T62 product (Kalnay et al, 1996) and, especially, the precipitation-assimilating NCEP North American Regional Reanalysis (NARR) Daily ~0.3° product (Mesinger et al., 2006). Similar conclusions based on diagnostic calculations were reached with both the NCEP/NCAR and NARR reanalyses, save for fundamental differences due to spatial resolution; for brevity, we show results from NARR only. A careful evaluation of NARR fields and discussions of its quality and limitations can be found in Nigam and Ruiz-Barradas (2006) and Shafran et al. (2005). For consistency with the GHCN daily station precipitation records, the period 1979-1990 is used throughout all analyses, and the same method of computing the monthly climatology from daily data was used.

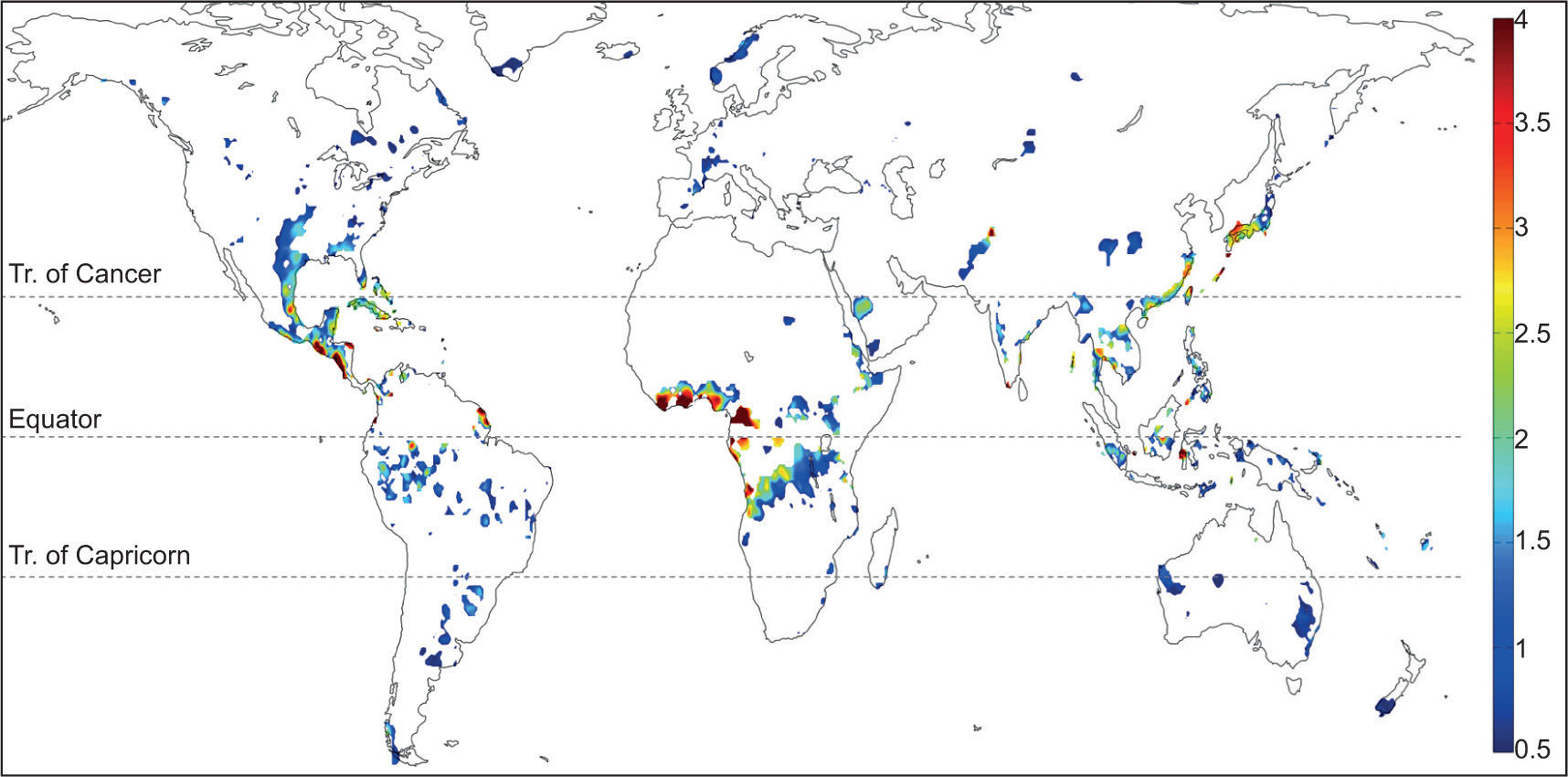
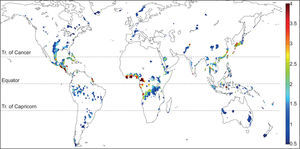
3

Results

3.1

Global distribution

Given the multitude of global, gridded land precipitation data sets available, a worthwhile starting point for understanding the basic mechanism(s) for the MSD is its global distribution based on the objective MESA algorithm described in the previous section. The resulting map from one such data set, NOAA PREC/L (Chen et al, 2002), is shown in Figure 3. Even in this land-only data set, the global prevalence of the MSD is quite surprising, including South America, south/central US, Japan, the east coast of China, central Africa, and coastal Australia. The flexible nature of our MSD algorithm (MESA) enables illuminating regions that experience a biannual seasonal cycle of rainfall without the constraint that the mean climatology be parametrically identical to that of the GCR. The distribution of biannual precipitation over Africa is rather interesting, with a strong biannual signal on either side of the equator, which is probably related to the seasonal migration of the ITCZ. The biannual signal hugging the Gulf of Guinea in west and central Africa indeed appears to be the strongest on the planet. Despite the fact that the MSD is a more globally prevalent feature than previously thought, the MSD over the GCR stands out especially in spatial scale and coherence.

Fig. 3.

Global distribution of locations objectively determined to exhibit a mean biannual cycle of precipitation based on the NOAA PREC/L data set (gridded station and satellite blend, land only, 0.5° resolution, 1948-2007). Plotted is the difference between the mean of the two relative maxima and the relative minimum (mm/day), calculated according to the MESA algorithm illustrated in Figure 1.

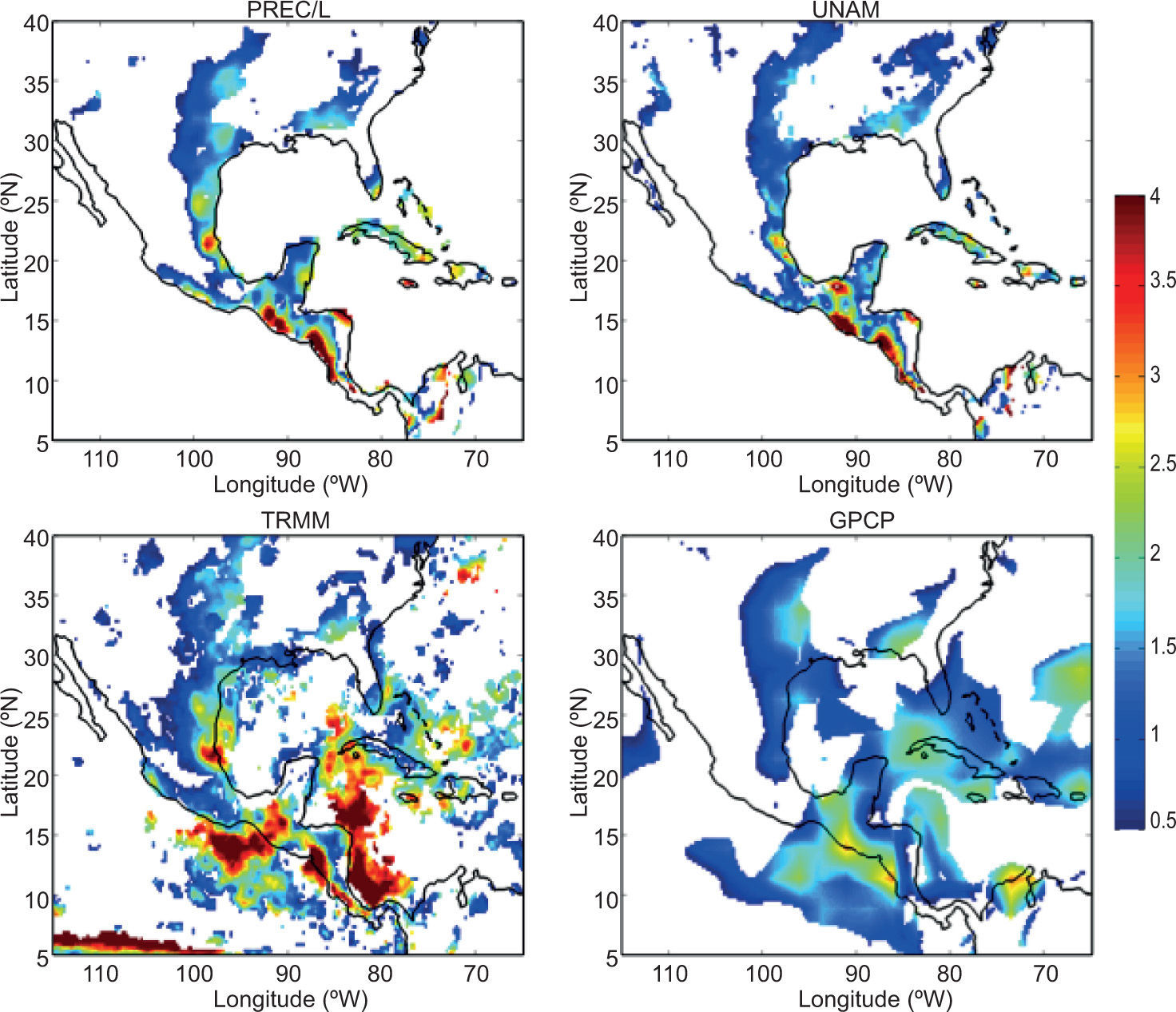
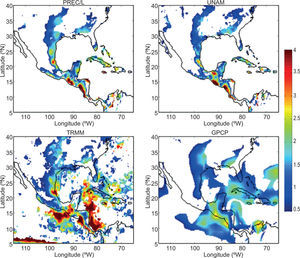
Focusing on the GCR, shown in Figure 4 are equivalent MSD distributions from PREC/L and three additional precipitation data sets (UNAM, TRMM, and GPCP). Throughout the GCR. the MSD stands out as a robust feature of the seasonal climate, especially Central America. Cuba, Hispaniola, south Florida and the Bahamas, and the Gulf coast of Mexico and Texas. There is remarkable agreement among the four data sets shown regarding the distribution and magnitude of the MSD, particularly the > 4 mm/day MSD along the Pacific coast of Guatemala and Nicaragua. The TRMM and GPCP results confirm the strongest MSD along the Central American coastline as well as just offshore in both the eastern Pacific and western Caribbean. Throughout the remainder of this paper, we focus our analysis on the Pacific coast of Central America and southern Mexico.

Fig. 4.

As in Figure 3, but focused on the GCR in four gridded precipitation data sets. including PREC/L (land only, gauge-satellite blend), UNAM (land only, gauge only), TRMM (land and ocean, satellite only), and GPCP (land and ocean, gauge-satellite blend).

3.2

Seasonal evolution

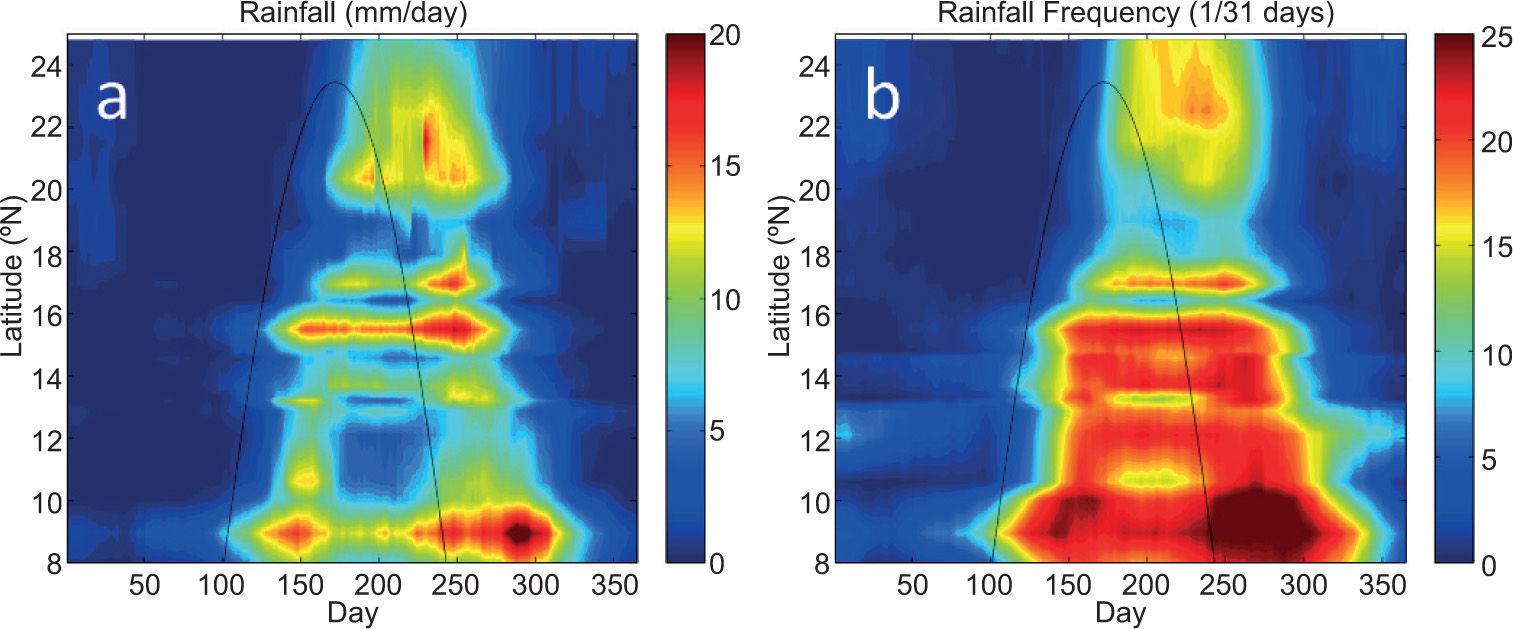
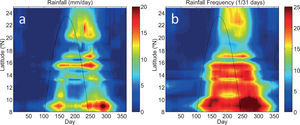
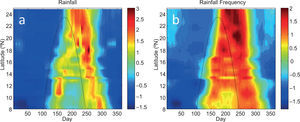
To explore the spatiotemporal evolution of the MSD, we present in this and the following subsections a series of analyses that view stations along the Pacific coast of Central America and southern Mexico ideally as a function of latitude. Using the high temporal resolution (daily) station precipitation records from locations indicated in Table 1 and Figure 2, shown in Figure 5 are time-latitude plots of mean climatological 31-day running mean precipitation and rainfall frequency. Despite differences in total precipitation over the year, nearly all stations in this domain experience a biannual cycle of precipitation and therefore an MSD. Total annual rainfall does not depend in an obvious linear fashion on latitude, which can be contrasted to rainfall frequency. Maximum rainfall frequency during the rainy season(s) decreases from > 25 days per month in Costa Rica (9° N) to ~15 days per month in Sinaloa, Mexico (24° N). However, based on either rainfall or rainfall frequency, it is clear that the timing and duration of the MSD is a strong function of latitude. The general rainy season arrives first in the southern latitudes, propagates northward through Central America and well into Mexico, and then southward, leaving in between a relative minimum of rainfall rate and frequency that decreases in duration with latitude. However, it can also be seen that the duration of the MSD (i.e., the time between the first and second precipitation maxima) is inversely related to latitude, approaching zero at ~23° N.

Fig. 5.

Time-latitude plots of mean climatological (1979-1990) 31-day running mean (a) rainfall (mm/day) and (b) rainfall frequency (1/31 days) along the Pacific coast of Central America and southern Mexico, i.e., all 20 stations shown in Figure 2. The solar declination angle is denoted by a black line.

The solar declination angle (SD hereafter) is a convenient seasonal pace-keeper with which to compare since it is equivalent to the latitude at which the sun is directly overhead at its zenith, and therefore represents the latitude at which the most solar radiation is incident upon the top of the atmosphere. When compared with the SD, also shown on both panels of Figure 5, both the total rainfall and rainfall frequency follow the seasonal march of the sun, but with a 30-50 day lag. To highlight a few stations representative of the range of latitudes shown in Figure 5, time series of climatological precipitation rate and frequency are provided in Figure 6.

Fig. 6.

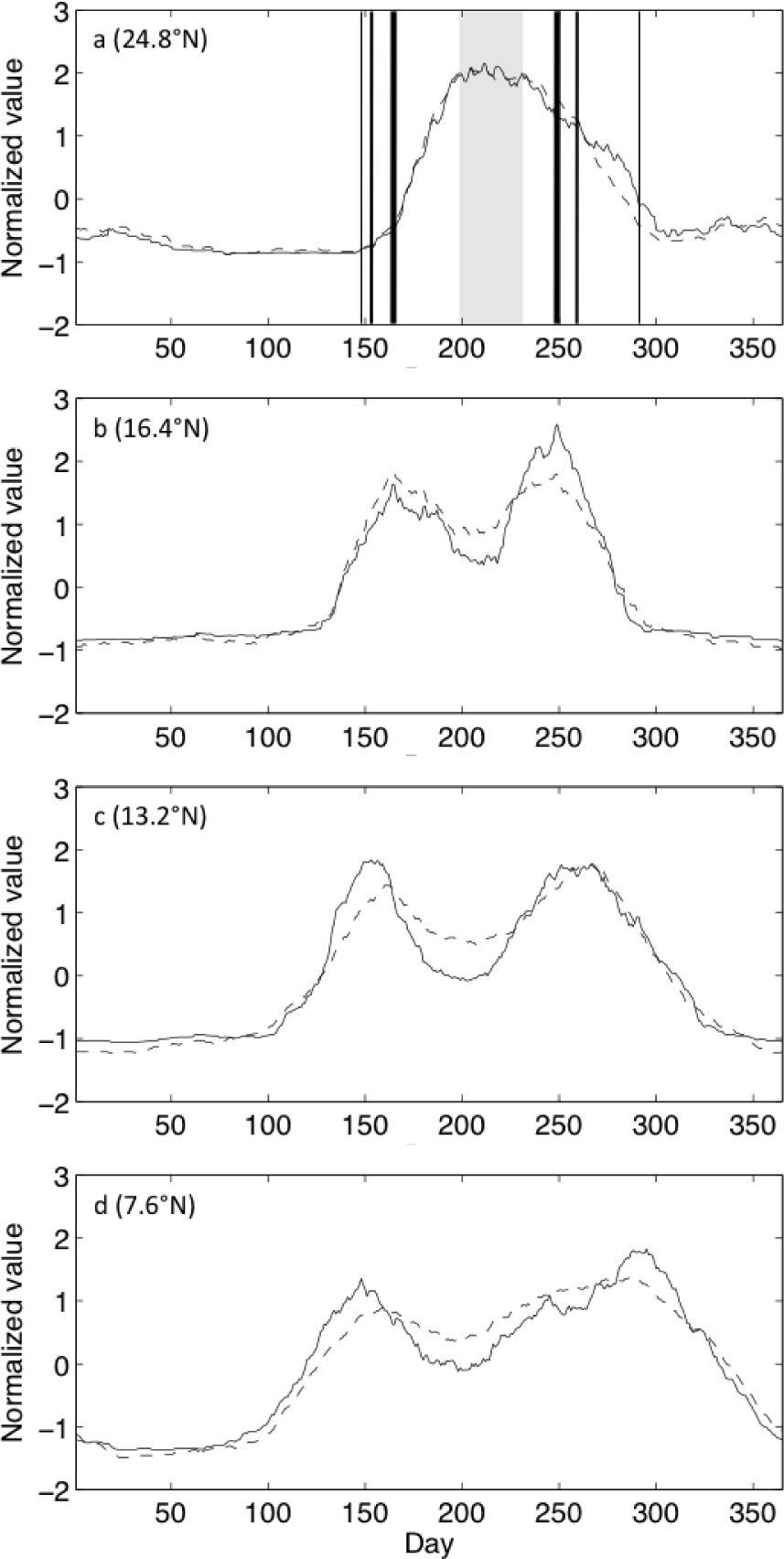
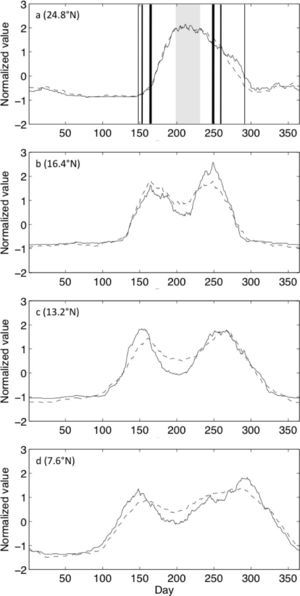
Mean climatological 31-day running mean rainfall (solid lines) and 31-day running sum of rain days (dashed lines) at four representative stations (denoted as white triangles in Fig. 2). All time series are normalized by the local annual mean and seasonal standard deviation to facilitate comparison. Vertical lines in (a) denote the timing of maxima in (b-d) with thickness corresponding to station latitude.

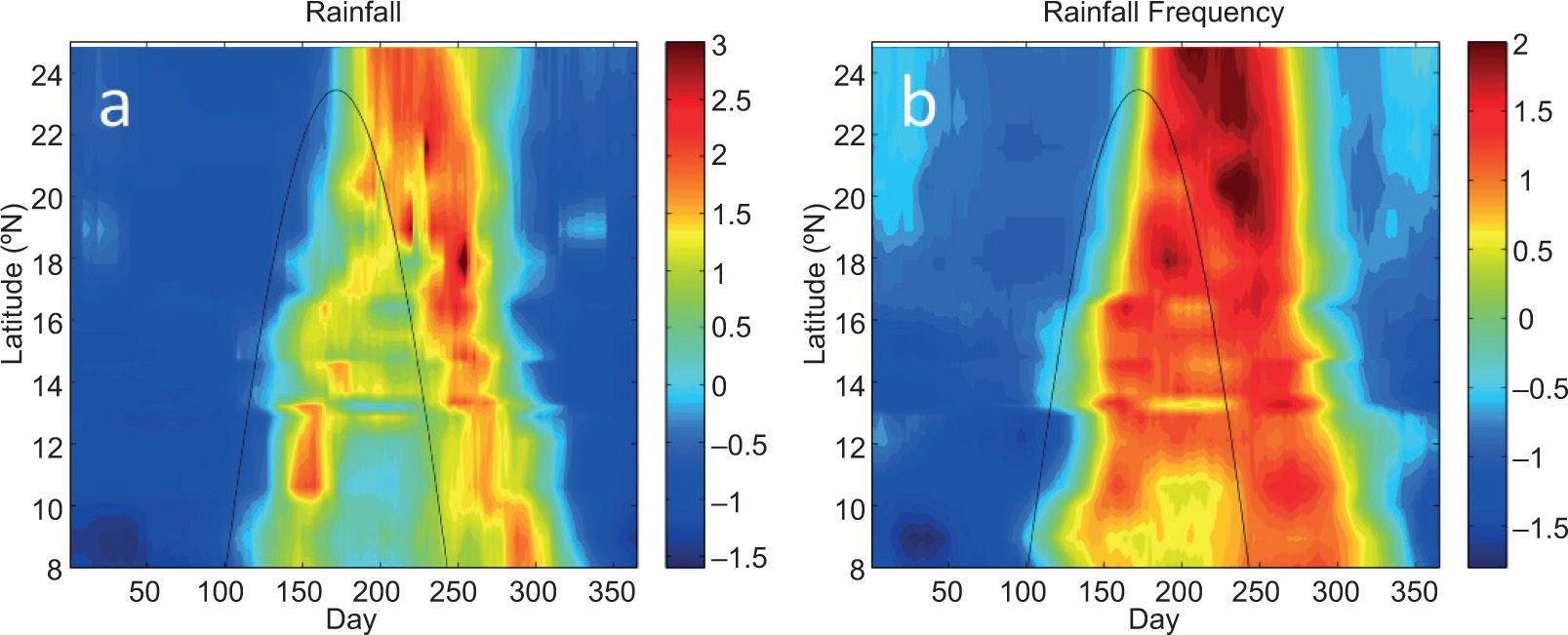
At 7.6° N, the duration between the first and second maxima in rainfall rate and frequency is ~150 days. This duration decreases to ~120 days at 13.2° N, and to ~90 days at 16.4° N. At Sanalona, Mexico (24.8° N), there is only a single maximum in rainfall rate and frequency, i.e., no MSD. Clearly, the duration of the MSD at each of these locations is a simple function of how early (late) the first (second) precipitation maximum arrives. Since total rainfall rates at different stations along the coast will be influenced by several factors, Figure 7 shows time-latitude plots of precipitation rate and frequency where the values at each station are normalized by the local annual mean and seasonal standard deviation. Along with the strong correspondence between seasonal rainfall and the SD, one can also see that, at most locations, the second maximum in precipitation rate appears stronger than the first, and the second maximum in precipitation frequency appears to last longer than the first. It is also interesting to identify the deepest midsummer minimum in normalized precipitation within the latitude range ~10-14° N which, by virtue of being directly adjacent to the western Caribbean basin, may be related to the maximum seasonal strength of the CLLJ as implicated by several previous studies.

Fig. 7.

As in Figure 5, but data at each station are normalized by the local annual mean and seasonal standard deviation.

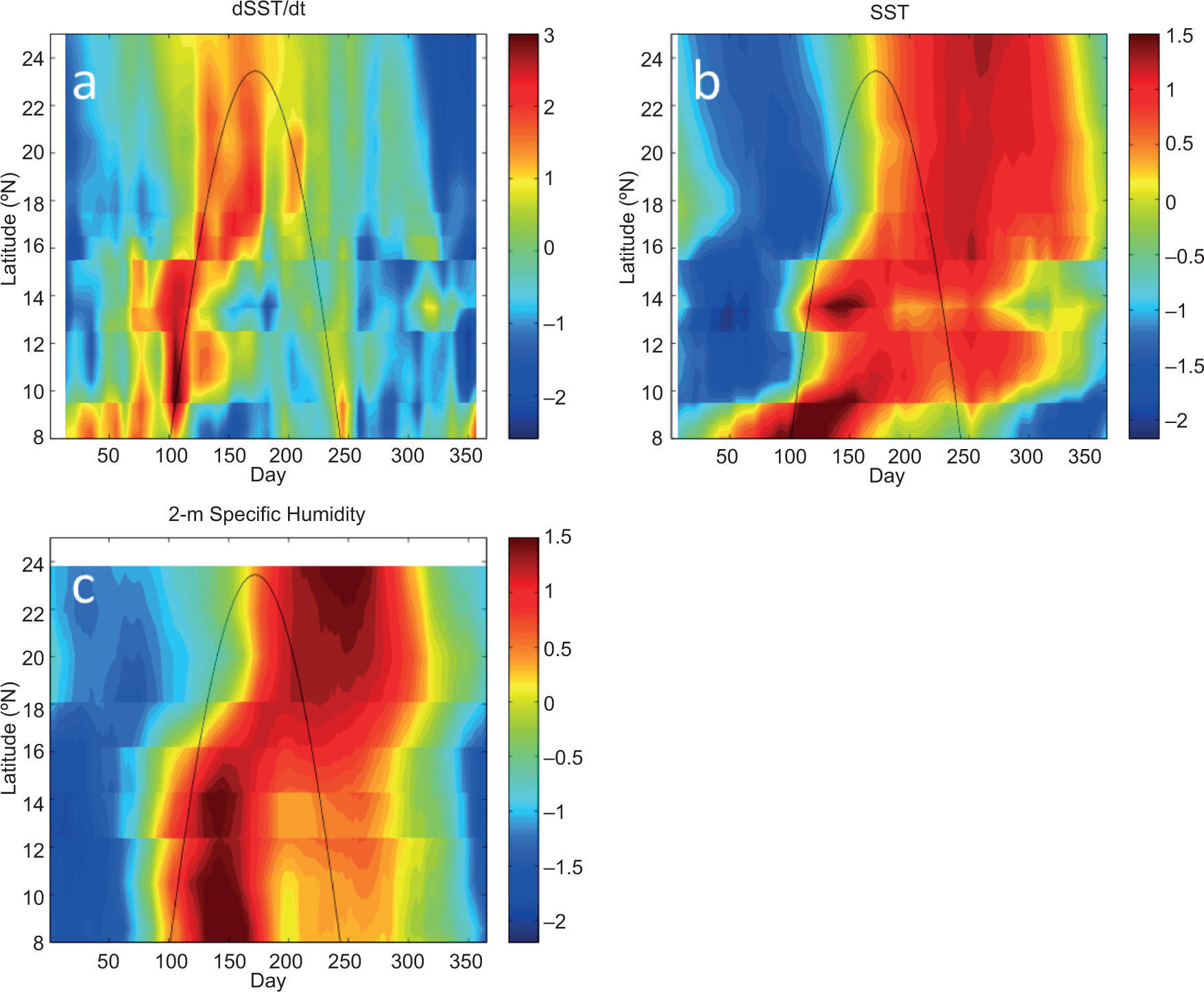
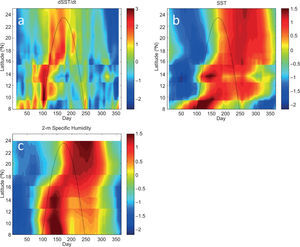
The time lag of 30-50 days between the maximum solar radiation (for which we use SD as a proxy) and the seasonal maxima in rainfall suggest a possible role for solar heating of the ocean off the coast of Central America, i. e., in the EPWP, as well as the land surface. Previous numerical modeling has shown that the dominant term governing the seasonal and interannual variability of the mixed layer heat budget in the EPWP is surface shortwave radiation (\ Karnauskas and Busalacchi, 2009). Moreover, seasonal analysis of moored measurements from the EPWP indicates that the maximum SST in the EPWP lags maximum shortwave radiation by ~2 months (Karnauskas, 2007). With this in mind, Figure 8 illustrates that the first (ascending) pass of the solar declination angle corresponds to the greatest rate of increase of SST (Fig. 8a) at pseudo-stations along the Pacific coast of Central America and southern Mexico nearest to the aforementioned GHCN stations, leading to maximum SSTs that, like precipitation, are lagged by 30-50 days (Fig. 8b). Also lagging the solar declination angle, and coincident with maximum SST, is maximum near-surface specific humidity (Fig. 8c), in this case from the lower-resolution global reanalysis. In late summer and early fall, neither SST nor humidity has returned to lower wintertime values, and the second (descending) pass of the SD only results in modest SST warming and a relatively minor late-seasonal maximum in absolute SST. The biannual seasonal cycle of absolute SST is only evident south of ~14° N; further north, the time interval between the ascending and descending SD passes is too short relative to the response time of the ocean mixed layer (1-2 months) for SST to cool down in between and hence the seasonal maximum absolute SST persists throughout the summer.

Fig. 8.

As in Figure 7, but for (a) ∂SST/∂t, (b) SST, and (c) 2 m specific humidity for offshore pseudo-stations. SST observations are from the NOAA OI v. 2 weekly 1° resolution data set, and humidity data are from the NCEP/NCAR reanalysis daily T62 resolution data set. All values are normalized by the local annual mean and seasonal standard deviation. Locations used from each data set were those offshore points nearest to the GHCN stations indicated in Table I and Figure 2.

3.3

Seasonal thermodynamic energy budget

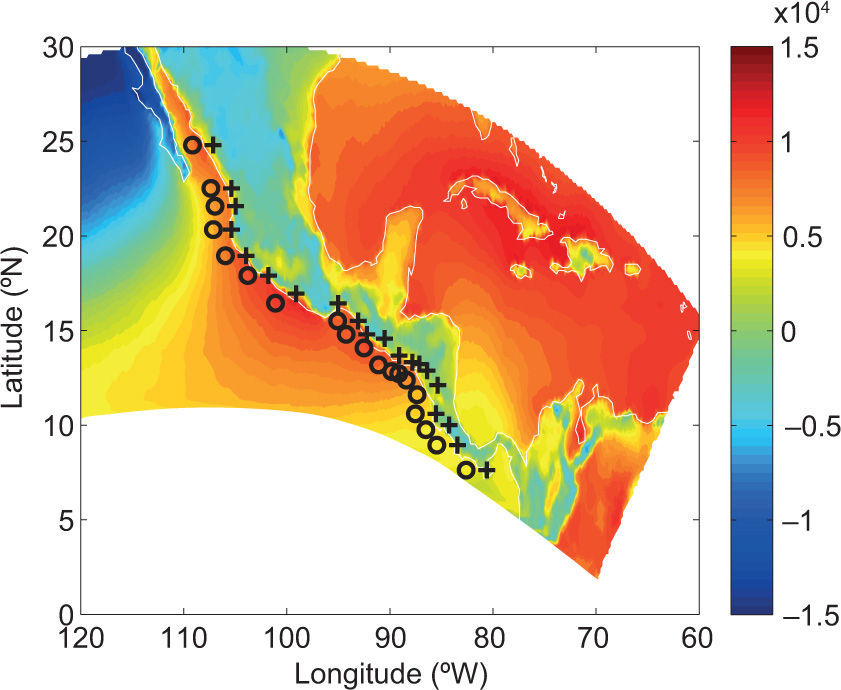
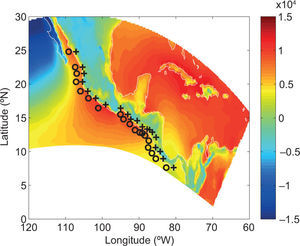
To better understand the thermodynamic processes giving rise to the observed biannual seasonal cycle of precipitation (and associated MSD) along the Pacific coast of Central America and southern Mexico and how they relate to the SD, we examine daily diagnostic fields from the higherresolution NARR reanalysis data set. Similar to the above analyses of SST and surface humidity, we analyze time-latitude depictions at pseudo-stations closely corresponding to the twenty GHCN stations listed in Table 1, and offshore counterparts. Due to the complex topography of the GCR region, which can only approximately be represented by a model with 32 km spatial resolution, and our hypothesis that the seasonal migrations of precipitation following the SD is related to warm pool SST, we focus on both coastal (onshore) and offshore pseudo-stations. A map of the southernmost extent of the NARR domain and the locations of the pseudo-stations analyzed in this subsection is given in Figure 9.

Fig. 9.

Area within the domain of the NorthAmerican Regional Reanalysis (NARR) encompassing southern Mexico and Central America. Coastal and offshore pseudo-stations corresponding to GHCN stations are indicated by + and o signs, respectively. Plotted in the background is the mean climatological (1979-1990) moist static stability (MSS; J/kg) averaged from April 10-November 21 (Julian days 100-325) from the NARR, with positive values indicating instability.

While convective available potential energy (CAPE) is perhaps the most precise measure of tropical convective potential and is a standard output of the NARR reanalysis product, moist static stability (MSS) readily lends itself to decomposition into intuitive terms. The moist static energy (MSE) of an air parcel is defined as the sum of its internal, geopotential, and latent energy. MSE is thus given by the expression

where C_p is the specific heat for dry air at constant pressure (1004 J kg^-1 K^_1), T is temperature, g is the acceleration due to gravity (9.81 m s^-2), z is height, L_v is the latent heat of vaporization for water (2.5 10⁶ J kg”¹), and q is specific humidity. Note that the internal and geopotential energy terms (C_p T + gz) together constitute the parcel’s dry static energy. Saturation MSE is the same as MSE except that q is replaced with the saturation value, q_sat(T, p), a function of temperature and pressure alone. The MSS is the saturation MSE at a reference level (600 hPa) minus the surface MSE, and the air column is unstable if this is negative. The mean climatological moist static stability averaged from April 10-November 21 from the NARR is shown as background to the map in Figure 9. Over the oceanic regions, MSS is strongly a function of surface air temperature, which is in turn strongly a function of SST Hence, areas with strongest moist static instability are found over the warmest mean annual SST, such as along the Pacific coast of southern Mexico and in the central Caribbean region.

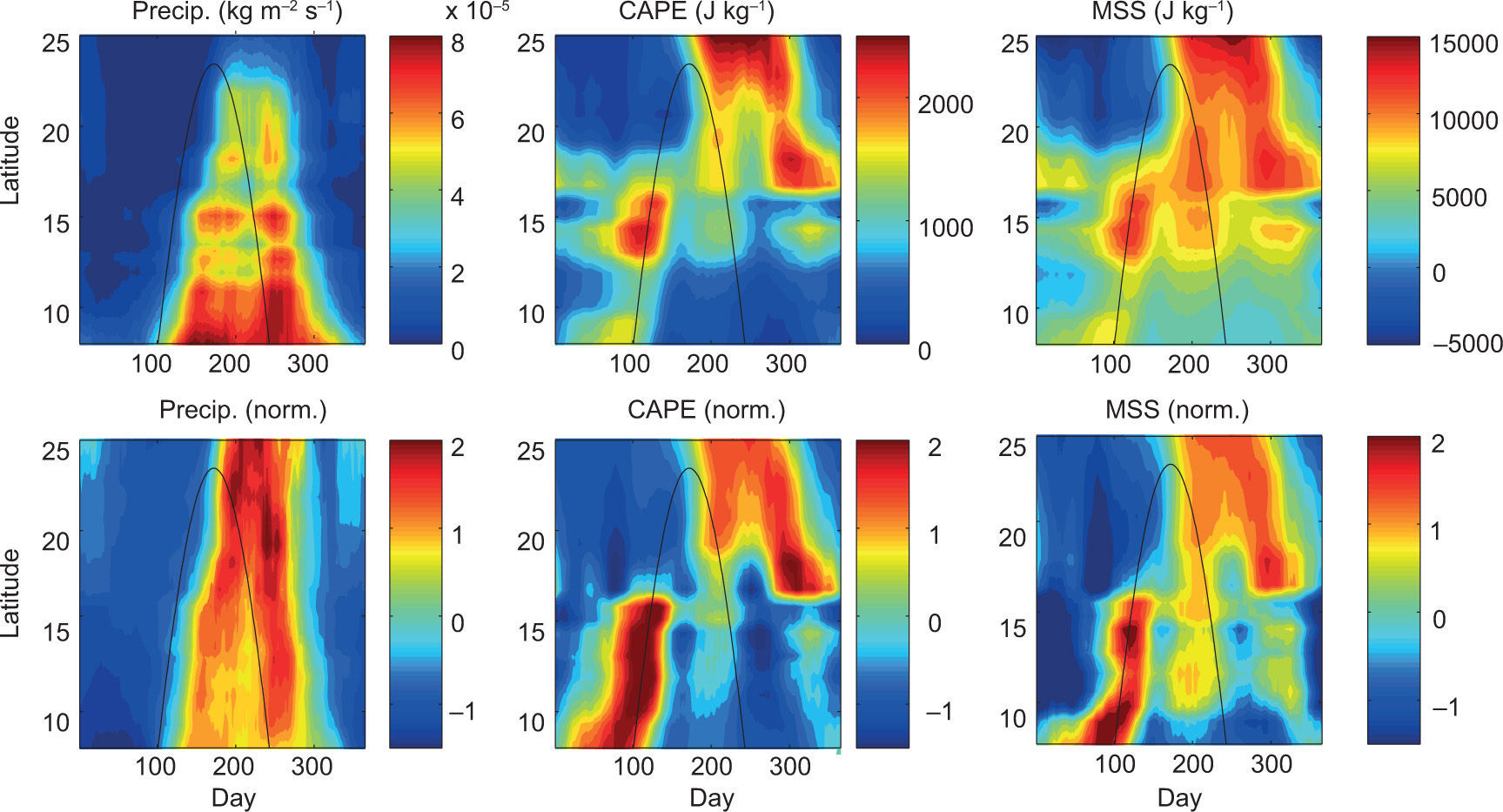
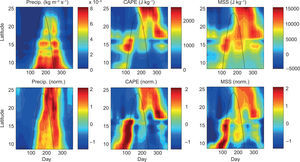
Before dissecting the terms involved in the thermodynamic energy budget, it is necessary to ensure that (a) the NARR captures the observed seasonal evolution of precipitation in the region of interest, and (b) MSS is a good surrogate for CAPE. Shown in the left panels of Figure 10 are precipitation and normalized precipitation from the NARR. (Results from coastal and offshore pseudo-stations are very similar; for brevity we only show the offshore pseudo-station results.) Comparing these time-latitude plots with those generated from the daily GHCN station records (Figs. 5a and 7a), the NARR indeed offers a very realistic rendition of the MSD along the Pacific coast of Central America and southern Mexico. Furthermore, our calculated MSS using a reference level of 600 hPa closely mirrors the CAPE fields from the NARR product (Fig. 10; the seasonal structure of MSS is examined further below).

Fig. 10.

Top row: Time-latitude plots of climatological (1979-1990) precipitation (kg m^-2 s^-1), convective available potential energy (CAPE; J kg^-1), and moist static stability (MSS; J kg^-1) from the NARR offshore pseudo-stations. Bottom row: as in top row but data at each pseudo-station are normalized by the local annual mean and seasonal standard deviation. Note that 1 mm/day ~10^-5 kg m^-2 s^-1

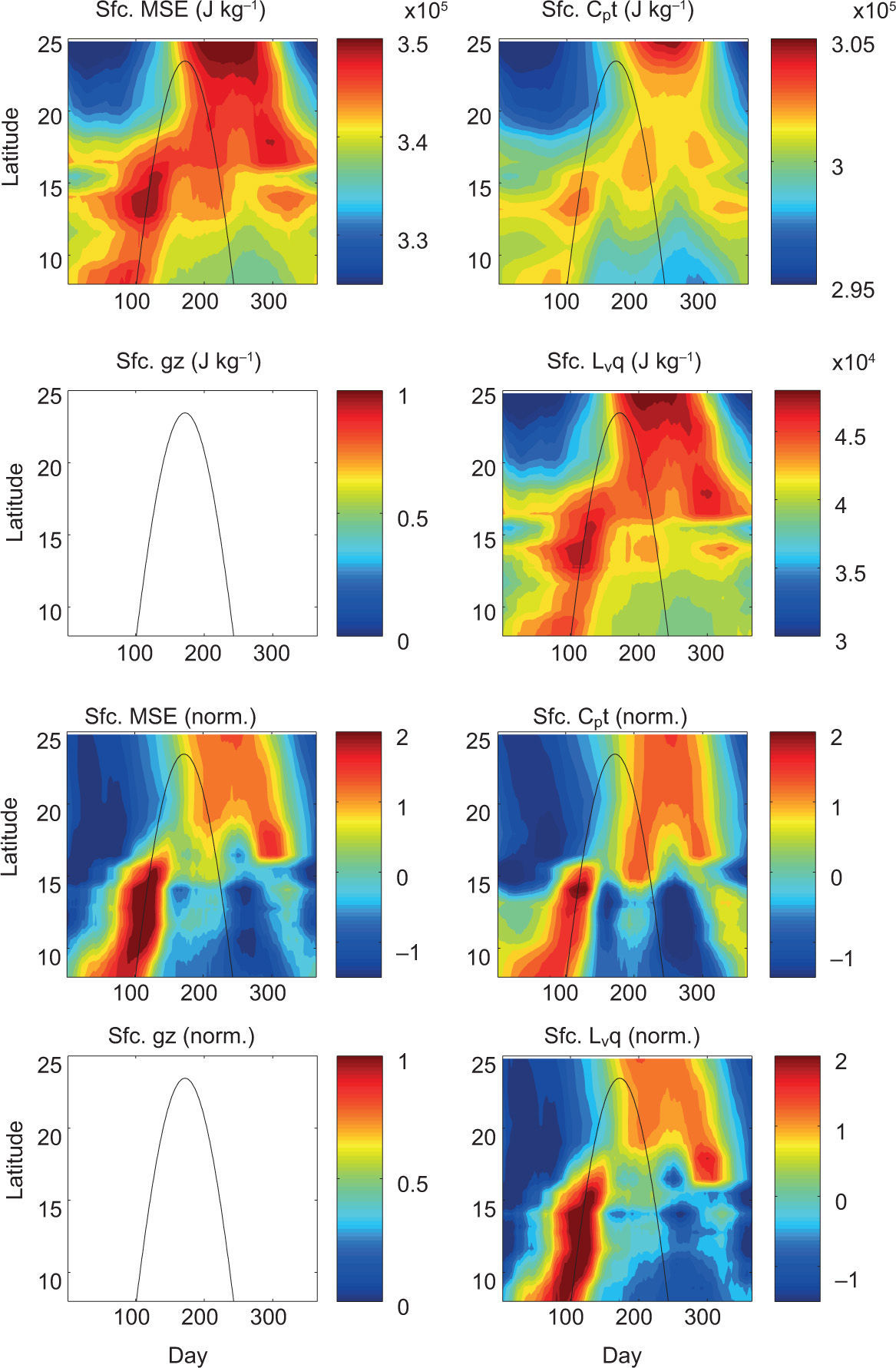
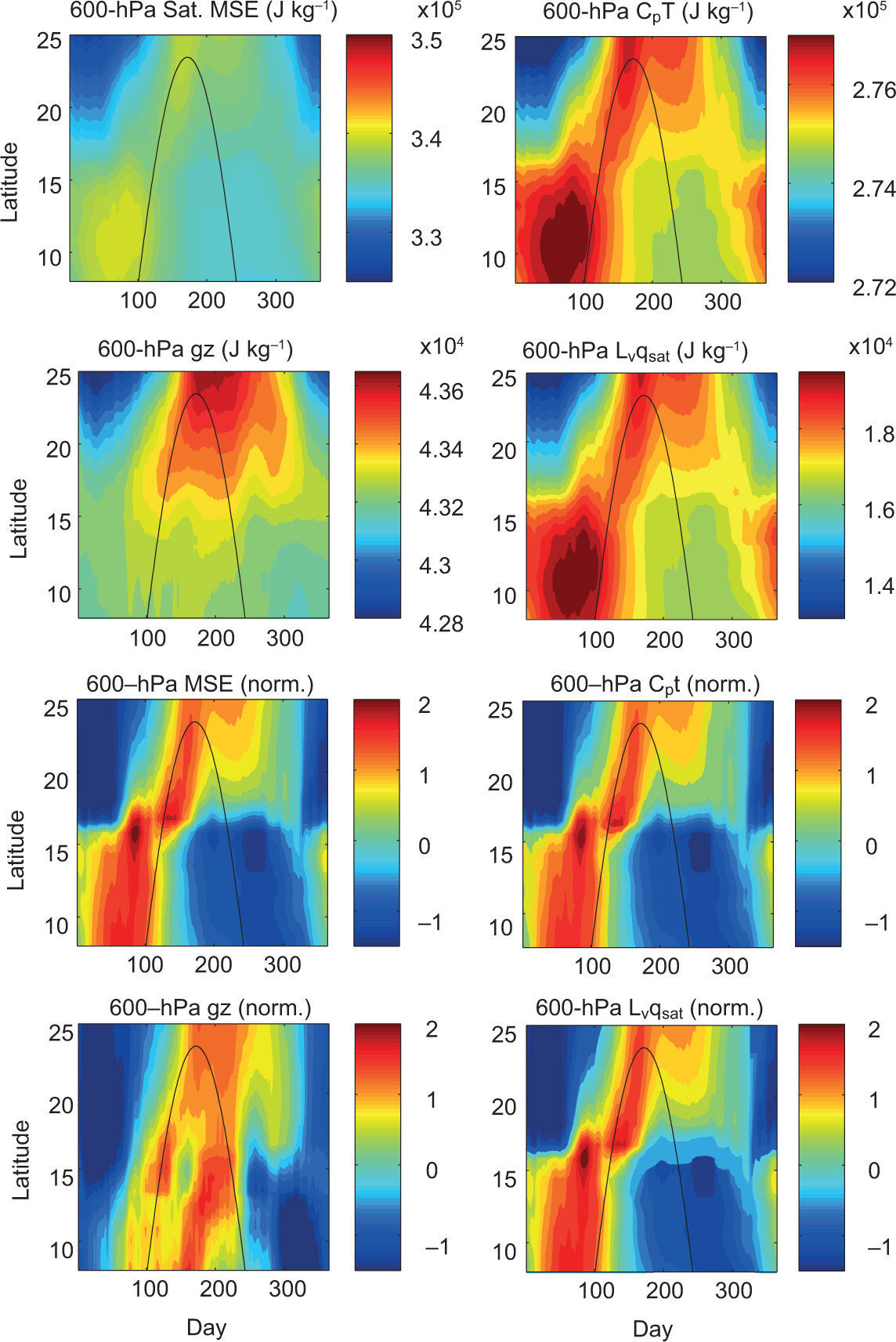
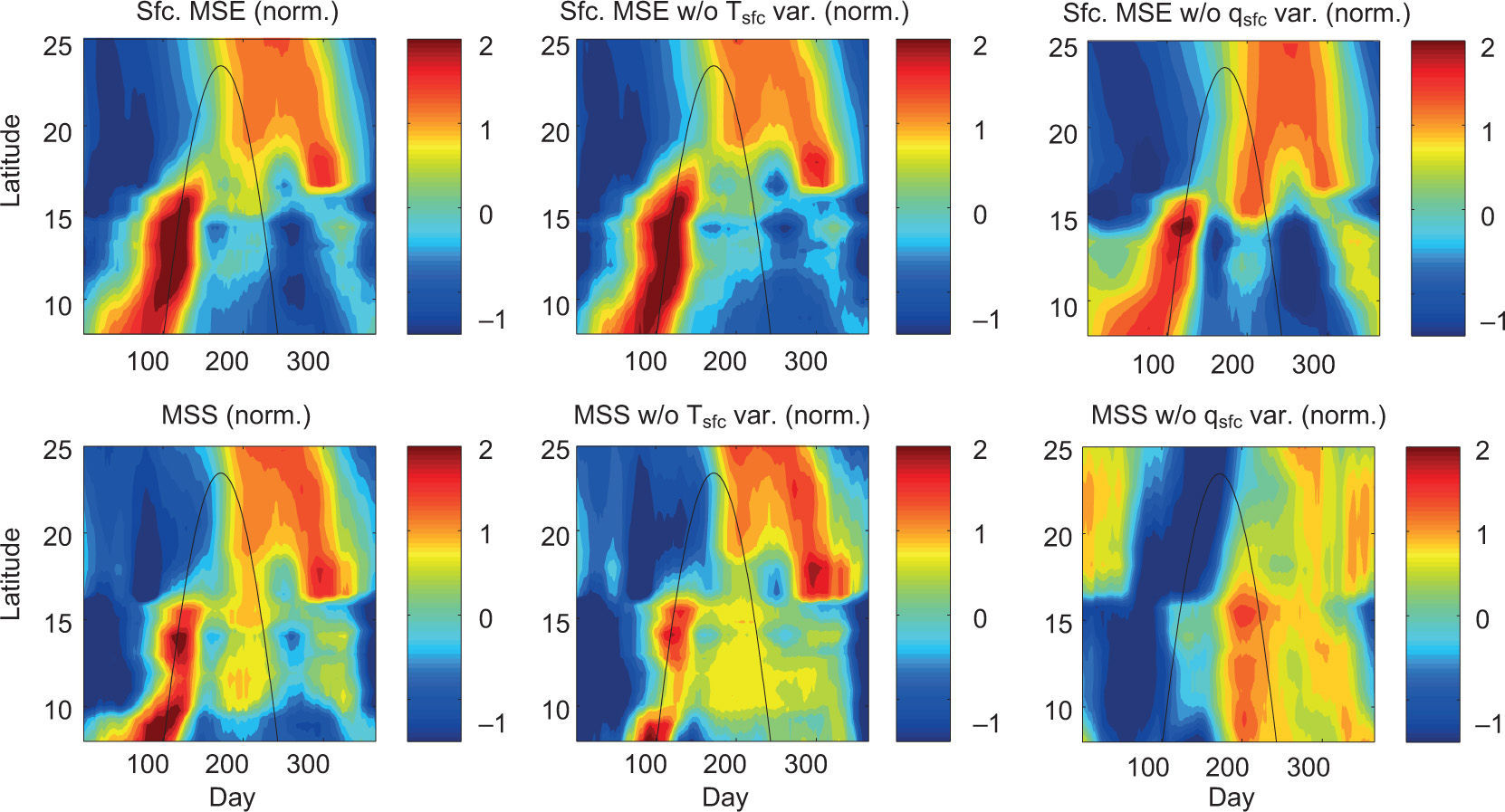
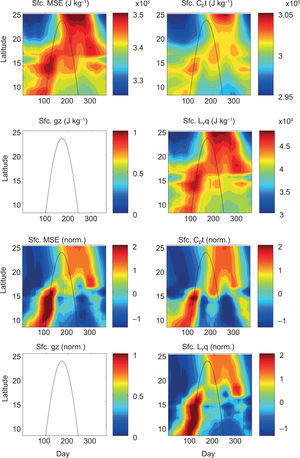
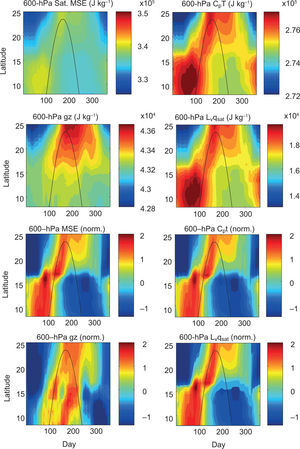
Surface MSE and 600 hPa saturation MSE are decomposed into their three component terms and presented in time-latitude format in Figures 11 and 12, respectively. At the surface, the internal energy term is nearly an order of magnitude larger than the latent energy term (Fig. 11, top row), meaning the relatively warm temperature of the surface is providing the bulk of the surface MSE. However, as is evident in the normalized series of plots (Fig. 11, bottom row), both the dry static energy and latent energy contribute strongly to the seasonality of the surface MSE. This is reasonably intuitive since the water vapor pressure is an exponential function of temperature according to the Clausius-Clapeyron relation. As indicated in the upper-left panel of Figure 12, the 600 hPa saturation MSE is overall less than the surface MSE throughout the majority of the latitudinally-dependent rainy season. As with the surface, the saturation MSE at 600 hPa is also dominated by the internal energy term. The geopotential energy term approaches ~15% of the amount contributed by internal energy in the northern latitudes, and the latent energy term again mirrors the internal energy term but only at ~7% thereof. Examining the second half of the year, there is a particularly striking lack of saturation MSE at 600 hPa (Fig. 12, left panels), during which a second, albeit weaker, equatorward-propagating signal in surface MSE arrives with the SD.

Fig. 11.

First and second rows: Time-latitude plots of climatological (1979-1990) surface moist static energy (Sfc. MSE; J kg^-1) and its three component terms including C_p T (J kg¹), g z (J kg^-1), and L_v q (J kg^-1) calculated for the NARR offshore pseudo-stations. Third and fourth rows: As in top row but data at each pseudo-station are normalized by the local annual mean and seasonal standard deviation. Note that 1 mm/day ~10^-5 kg m^-2 s^-1.

Fig. 12.

First and second rows: Time-latitude plots of climatological (1979-1990) 600 hPa saturation moist static energy (Sat. MSE; J kg^-1) and its three component terms including C_p T (J kg^-1), g z (J kg^-1). and L_v q_sat (J kg^-1) calculated for the NARR offshore pseudo-stations. Third and fourth rows: as in top row but data at each pseudo-station are normalized by the local annual mean and seasonal standard deviation.

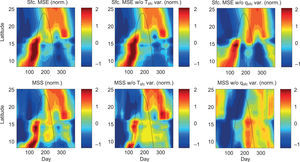
Despite the fact that the mean annual MSE budgets both at the surface and aloft are dominated by the internal energy terms, the seasonal variation as a function of latitude is fundamentally influenced by the variation of surface specific humidity. This is likely due to the larger seasonal range of specific humidity than surface air temperature, which is again a property owing to the nonlinear nature of the Clausius-Clapeyron relation. For example, the first peak in MSS (day ~100) is primarily a result of the increase in surface specific humidity (Fig. 13, bottom right). Furthermore, the relative maximum of MSS found near the middle of the year (day ~200), which precedes the second precipitation maximum propagating equatorward along the coast, is the only salient feature of the seasonal structure of normalized MSS that would exist without the seasonality of the latent energy term.

Fig. 13.

Top row: Time-latitude plots of climatological (1979-1990) surface MSE, surface MSE without seasonal variation of T_sfc, and surface MSE without seasonal variation of q_sfc (all values normalized by the local annual mean and seasonal standard deviation). Bottom row: as in top row but for moist static stability (MSS).

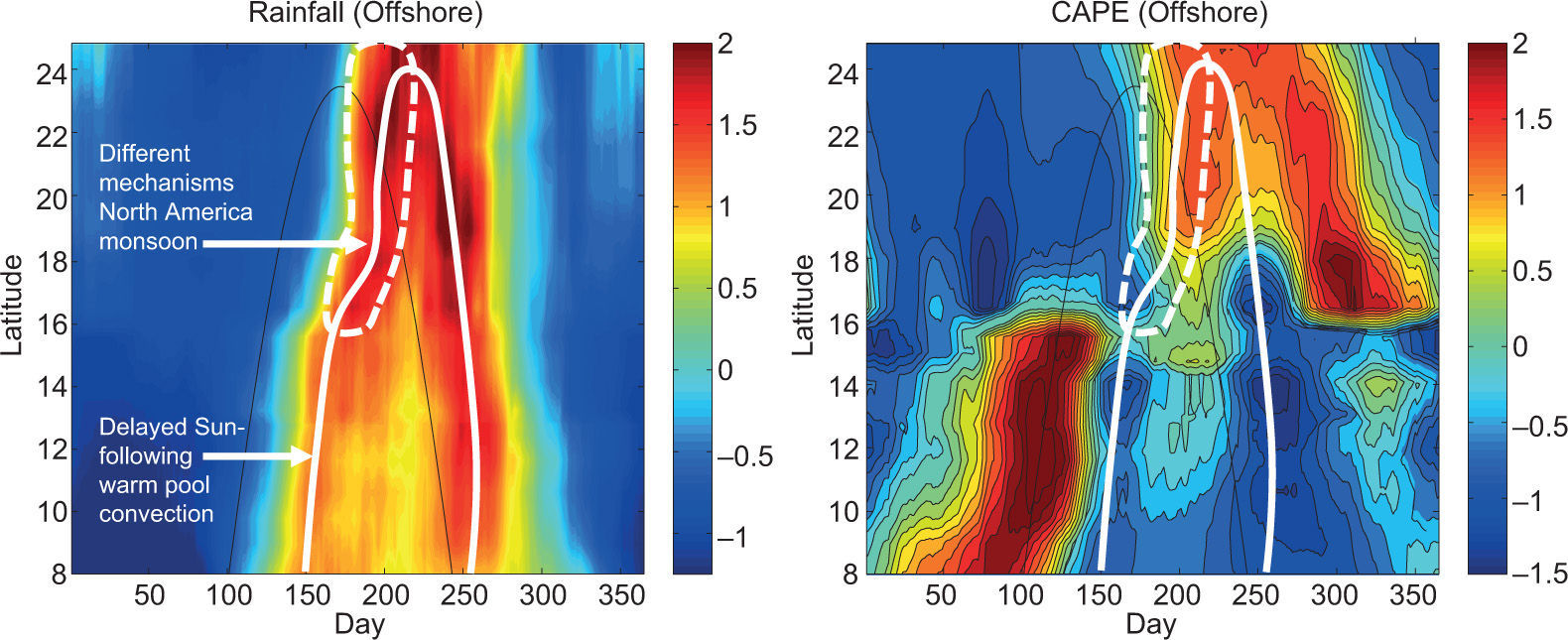
Having a better understanding of the dominant terms in the seasonal thermodynamic energy budget, we return to the juxtaposition of rainfall, SD, and CAPE (Fig. 14). Along the Pacific coast of Central America and southern Mexico, there is a clear biannual precipitation signal that squeezes toward a single annual maximum at or very near the Tropic of Cancer (23.4° N). Between the two maxima is a relative minimum we know as the MSD. In general, this structure is very closely aligned with the SD but with a distinct time lag of less than two months. This time-latitude evolution of precipitation can be well explained by SD-following maxima in CAPE, but with one obvious exception.

Fig. 14.

Time-latitude plots of climatological (1979-1990) precipitation (left) and CAPE (right) along the Pacific coast of Central America and southern Mexico at the NARR offshore pseudo-stations (all values normalized). As in all previous figures, the thin black line indicates the solar declination angle. The heavy white line on the left panel follows the meridionally propagating precipitation maxima and is reproduced on the right panel. The region outlined by the dashed heavy white line indicates seasonal precipitation that is related to the North American monsoon and, as discussed in the main text, is mechanistically distinct from the remainder of the meridionally propagating precipitation maxima.

The only precipitation maximum that is not preceded by a CAPE maximum is the precipitation occurring north of 16° N during the first half of the year, which is related to the initiation of the North American Monsoon System by a large-scale thermally-driven low over continental Mexico and propagating northward and out of the analysis domain (Vera et al., 2006 and references therein). All other local relative precipitation maxima are found subsequent to local relative maxima in CAPE. that is, large values of CAPE destabilize the atmosphere and initiate convection and precipitation, which, in turn, removes humidity and re-stabilizes the atmosphere, until CAPE builds again with the equatorward-passing SD, leading to the second precipitation maximum.

4

Summary and conclusion

In this paper, we have presented a novel, objective analysis of the global distribution of the MSD phenomenon, and focused on diagnosing its basic underlying mechanism with observations. Although there is a robust MSD in the GCR, it is not necessarily the strongest in the world as compared to other tropical regions (e.g., the Gulf of Guinea). Furthermore, several extratropical coastal regions also exhibit a robust MSD (e.g., China and Japan). Our analyses of daily precipitation and diagnostic reanalysis fields point to a relatively simple underlying mechanism for the climatological MSD along the Pacific coast of Central America and southern Mexico. Critical in the mechanism is the solar declination angle, which drives a strong seasonality in both surface temperatures and surface humidity. The extent of the seasonal poleward excursion of the ITCZ at any longitude is likely influenced by the land surface, with Central America and Mexico having optimal characteristics for a large northward excursion during summer. Along the descending SD, the exaggerated ITCZ excursion returns equatorward at the same pace and with appropriate lag to the solar declination. Meanwhile, the still-warm SSTs continue to supply enhanced moisture to the daytime thermal circulation and further enhance coastal rainfall by virtue of being on the periphery of widespread increased maritime convection and tropical storms.

The mechanism proposed here is essentially an extension of Magaña’s et al. (1999) hypothesis for the first peak to the full biannual cycle, however, the descending pass of the solar declination angle is also responsible for the second precipitation maximum. We consider this mechanism to be the simplest possible one, since it also should theoretically occur in a world without the influence of complex continental geometry and requires only that the Earth be tilted. However, this mechanism cannot explain the MSD everywhere in the world, since (a) there are some locations outside of the tropics (poleward of 23.5° N latitude, where there is only one annual pass of the solar declination angle) that experience an MSD-like seasonal cycle of precipitation (Fig. 2), and (b) there are some regions within the tropics that do not experience an MSD. Moreover, the mechanism proposed here can only account for how the climatological MSD unfolds as approximately a function of latitude; a rich set of mechanisms for longitudinal variations in the MSD within the GMR was explored by Curtis and Gamble (2007). Other regular features of the climatology such as tropical cyclone activity may account for a biannual monsoon in some of these regions. However, for the Pacific coast of Central America and southern Mexico, “remote” mechanisms such as the NASH are not essential to explain the existence of the climatological MSD and its interannual variability. One hypothesis is that the appearance of a westward-extended NASH during the MSD is actually a manifestation of the reduced convection associated with the MSD rather than a remote cause of the MSD. Nonetheless, our results challenge the existing paradigm that the MSD is the result of a distinct precipitation-suppressing mechanism. Rather, we suggest that the MSD is essentially the result of the same precipitation-enhancing mechanism occurring biannually.

The characterization of the MSD as a latitudinally-dependent climatological feature related to the SD was made possible by the use of high temporal resolution data; the meridional propagation of the monsoon and its lagged correlation with the solar declination angle could easily be missed in monthly and even perhaps fixed-pentad data. Future research will address the contribution of other processes that also tend to peak during the apex of the MSD as they may be essential to understanding interannual variability and predictability by modulating rainfall along the Pacific coast of Central America.

Acknowledgements

The authors gratefully acknowledge funding from the NOAA Climate Program Office (CPO) Modeling, Analysis, Predictions, and Projections (MAPP) Program, under awards NA10OAR011023 9 to the Woods Hole Oceanographic Institution, NA10OAR4310253 to the University of Maryland, and NA10OAR4310252 to Columbia University. The IRI/1DEO Climate Data Library (http://iridl.ldeo.columbia.edu/) was an invaluable tool for acquiring the observational data sets used in this study. A special thanks to Henry Diaz and Víctor Magaña for organizing the special issue oí Atmósfera on the climate of the greater Caribbean region.