El objetivo de este estudio es determinar la probabilidad de ocurrencia de estaciones lluviosas o secas a lo largo de la costa oeste de Centro y Sudamérica, mediante la construcción de perfiles latitudinales para la asociación entre el fenómeno El Niño-Oscilación del Sur (ENOS) y la precipitación a lo largo de la región indicada. El análisis se realizó mediante modelos de regresión lineal multinomial y de regresión logística multinomial. Se usaron series de tiempo mensuales de la temperatura superficial del mar en el pacífico ecuatorial (SST) y el Índice de Oscilación del Sur (SOI) para la presión atmosférica a nivel del mar. Las anomalías de lluvia corresponden a series de tiempo sobre una retícula de 2.5×2.5° grados, a lo largo de la costa oeste de América Central y América del Sur desde 25° N hasta 45° S de 1951 a 2011. Definimos un índice para el ENOS que se usó como predictor y la lluvia como respuesta. Los datos se agruparon en trimestres y luego se categorizaron en terciles para construir tablas de contingencia no simétricas de 3×3. Como resultado, se generaron perfiles latitudinales de la probabilidad de ocurrencia de las distintas condiciones de lluvia, dadas las distintas fases de ENOS.
The objective of this study was to determine the probability of occurrence of wet or dry season events, by means of estimating latitudinal profiles for the association between El Niño Southern-Oscillation and the rain-fall along the west coast of Central and South America. The analysis was performed using multinomial linear regression and multinomial logit regression models. We used monthly time series of the Pacific equatorial sea surface temperature (SST), the Niño 3.4 index, a sea level pressure index (SOI) and rainfall anomalies over a 2.5×2.5° grid along the west coast of Central and South America, for latitudes starting at 25° N through 45° S, from 1951 to 2011. We defined an ENSO index (NSO) as predictor and rainfall as response. Data was grouped into seasons and then categorized into terciles to construct 3×3 non-symmetrical three way contingency tables. As results, we generated latitudinal profiles of the predictability (association) of rainfaíl for the west coast of Central and South America, using the ENSO phases as predictor.
Interest in useful climate predictions for various regions of the Americas has developed substantially over the past two decades given its recognized impacts in socioeconomic and geological issues, as well as in ecosystems (Katz and Murphy, 2000; Viles and Goudie, 2003). Over recent decades, efforts have increased toward improving forecast techniques for seasonal climate (Goddard et al., 2001).
In dealing with the ocean/atmosphere interactions of El Niño-Southern Oscillation (ENSO), most statistical forecasting studies focus on time series modeling and/or spatial fields for predicting the time of arrival and strength of an event. Time series modeling is done by fitting univariate or multivariate auto regressive moving average models (ARMA) to the target variable data (Box et al., 1994; Alfaro and Cid, 1999; Alfaro and Soley, 2001) in the time domain, Fourier-derived methods for the frequency domain, and neural networks (Goddard et al., 2001). The spatial fields approach is done by using multivariate techniques such as principal components or derivations thereof (Zwiers and von Storch, 2004; Maldonado et al., 2013). However, common practice has shown that in many cases the primary interest is not to measure the exact magnitude of an ENSO associated event, but simply to assess the “chances of occurrence” of events such as El Niño or La Niña. In that case, the main interest is to determine if a given year will or will not be an El Niño or La Niña year instead of predicting its strength or timing. Consequently, one could be interested in knowing if, given an El Niño or La Niña event, a specific season (winter, spring, etc.) will be dry or wet.
At present we have some deterministic prediction ability, although the spring barrier effect (significant prediction failures between lead times of six to 12 months) limits the predictability of warm/cool anomalous temperatures in the equatorial Pacific (Latif et al., 1998). We know from statistical analysis that ENSO is related to these “warm/cool events” and that they are also associated with climate anomalies around the globe (e.g., Ropelewski and Halpert, 1987, 1989), allowing us to make qualitative statements about expected climate effects given a warming (or cooling) event. But this is not nearly good enough. The economic and social sectors (agriculture, fisheries, health, etc.) need more concrete information (Katz and Murphy, 1997). A farmer needs specifically to know if a given year will be “dry” or “wet” to plan his crops and fishermen need to know if a warm or cool event will affect the fisheries. However, the occurrence of an ENSO event is no guarantee of a given impact because these “teleconnected” consequences—good or bad—do not always materialize. The deleterious effect of a false positive, normally called false alarm, which results when the expected teleconnection does not occur, may be worse than the direct effects when it does occur and was not expected. Because observations and models usually warn us when an ENSO event is imminent or beginning, one strategy is to assume the El Niño or La Niña event as given, and to project probabilities for far-field climatic and societal impacts around the globe based on the observed history (“hits” or “misses”) of such impacts. When an educated public or economic sector is informed of the relative likelihood of a consequence, contingency plans can be made for either possibility (García and Ramírez, 2012).
1.1The ocean-atmosphere interaction perspectiveMany studies have been conducted over the last two decades linking climatic variability and ENSO, focusing on the tropical Pacific and its interactions with the atmosphere (e.g, Philander, 1990; McCreary and Anderson, 1991; Weisberg and Wang, 1997; Goddard et al., 2001; Lee et al., 2010, 2013). According to Rassmusson (1985) these large-scale interactions between ocean and atmosphere over the tropical Pacific can greatly influence the weather patterns around the world.
Many ofthese investigations have been undertaken through the study of ocean-atmosphere indices, such as the Southern Oscillation Index (SOI), the difference in atmospheric pressure between Tahiti and Darwin, or the El Niño indexes based on sea surface temperature (SST) (Enfield, 1989; Enfield and Mayer, 1997). The statistical modeling of ocean-atmosphere interaction from a perspective of discrete possibilities implies a completely different approach vis-à-vis the traditional models based on a time domain approach, in which only continuous time series are modeled according to their auto-correlative structure, in the simpler case, or using cross-covariance arrays in the case of multivariate analyses.
There are only few cases in which such an approach has been attempted, or where this type of analysis seems to be an obvious need. For example,Mason and Mimmack (2002) compared different statistical techniques, including logit models, for predicting ENSO, but did not investigate the strength of the method for associating ENSO events and their worldwide climatic impact. Akin to the idea of the present paper and therefore its precursors, Enfield et al. (1999) used contingency tables to establish the relationships between extreme dipole configurations of the tropical Atlantic SST, using the north and south areas (NA and SA, respectively) of the intertropical convergence zone (ITCZ) for a 136- year period, recording the occurrence frequencies for which these indexes fall into their respective quartile ranges, and then comparing them against the frequencies expected by chance. This analysis concluded that such dipole configurations are due only to chance, the NA and SA classes being stochastically independent.
The main purpose of this study is to introduce the analysis of contingency tables into the study of the relationships between the variables most commonly used to evaluate ocean-atmosphere interaction, such as the Southern Oscillation Index (SOI) or equatorial SST-related time series indices (e.g., Niño 3 or Niño 3.4) and the distribution of rainfall along the west coast of South America, using rainfall data for latitudes between 22.5° N and 45° S. We expect to establish the usefulness and practical need of this analytic tool, which will provide a simple quantitative measure of rainfall modulation by ENSO within the framework of the terciles categorization. Finally, an advantage of this method is that it gives the results in terms of probabilities for the different terciles, which is the most common output of the actual Regional Climate Outlook Forums in Latin America (e.g., IRI, 2001; García and Ramírez, 2012).
2Data and methodsMonthly sea surface temperature (SST), sea level pressure (SLP) anomalies (SOI) and rain data for different latitudes were classified into three categories. This classification was then converted into threeway non-symmetric contingency tables, including a predictor and a response variable (Lauro and Balbi, 1999). Using predictive generalized linear models (Agresti, 2002) we estimated the odds of classifying a single event in each of the three predefined categories, based on the marginal probability distribution of a number of the “predictive” processes.
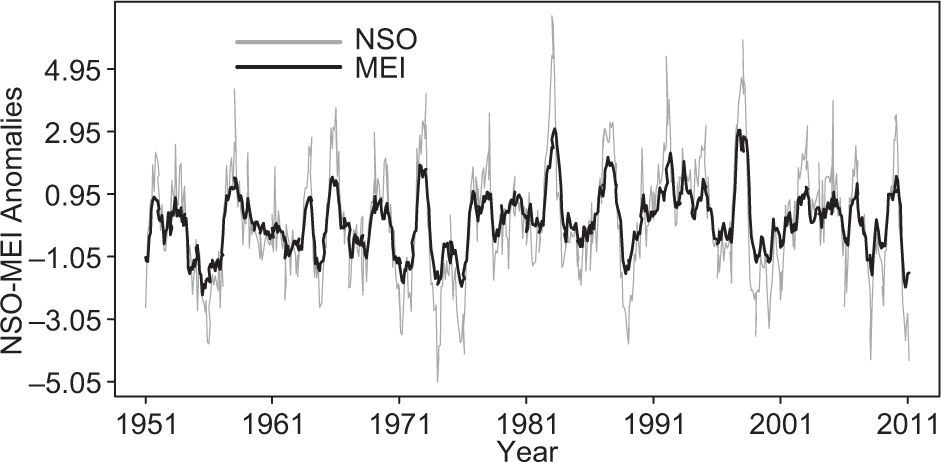
To construct contingency tables for evaluating the relationship between rainfall and the warm/neutral/ cool events, we considered monthly time series from 1951 through 2011 for the Southern Oscillation Index (SOI) and for equatorial SST represented by the series Niño 3.4 (N34, monthly SST averaged over 5° N-5° S and 150-160° W). We summarized both into an index that we call Niño Southern Oscillation or hereafter NSO (to distinguish it from the conventional ENSO acronyms), which considers both the atmospheric and oceanic contributions ofthe coupled phenomena. NSO is defined as the difference N34-SOI of standardized contemporaneous monthly values. The purpose ofthis index is to focus the analysis on the events in which there is a coupling between the atmosphere and the ocean. The relationships between ENSO events and the NSO index are clear, since during the warm (cool) phase of ENSO, SST has positive (negative) anomalies and SOI has negative (positive) anomalies, so that the NSO has its maximum (minima) for El Niño (La Niña) events. As such, the NSO index has the advantage of summarizing in a more simple and straightforward manner the information given by both indices. When NSO is compared, for example, with Wolter's MEI index (Wolter, 1987; Wolter and Timlin, 1993) a good correspondence is found (Fig. 1). The NSO index emphasizes extreme events, which helps in the differentiation of terciles for this analysis.
The NSO time series was then summarized into seasons, taking the standard average of three months (DJF, MAM, JJA or SON) as a way to reduce the noise and the autocorrelation of contiguous observations, and associated with boreal (austral) winter (summer), spring (autumn), summer (winter), and autumn (spring). All the analyses were performed independently for each season.
Monthly rainfall (R) data were obtained from the National Centers for Environmental Prediction (NCEP) of the National Oceanic and Atmospheric Administration (NOAA), corresponding to the anomalies of worldwide rainfall measures over a 2.5×2.5° latitude-longitude grid from 1951 to 2011 (Chen et al., 2002). From the database we selected 28 grid points located along the west coast of South America from 25° N through 45° S (Fig. 2). Chen et al. (2002) describe that their global analyses are defined by interpolation of gauge observations over land. Their analyses are derived from gauge observations from over 17 000 stations collected in the Global Historical Climatology Network (GHCN), v. 2, and the Climate Anomaly Monitoring System (CAMS) datasets. To determine the most suitable objective analysis procedure for gridding, the analyses generated by four published objective analysis techniques (those of Cressman, Barnes, and Shepard, and the optimal interpolation [OI] method of Gandin) were compared. Based on their results, the OI technique was used to create monthly gridded analyses of precipitation over the global land areas. In addition, the mean distribution and annual cycle of precipitation observed in their data set showed good agreement with those in several published gauge-based datasets, and the anomaly patterns associated with ENSO resemble those found in previous studies (Chen et al., 2002).
Rainfall data were also summarized into seasons as indicated above, so we obtained 61 data points for each season along the 28 different grid point latitudes for the west coast of South America. However, due to the scarce rainfall over the Atacama Desert in Chile, the corresponding two grid points were not included in the analysis.
2.1Contingency tablesConsider two categorical variables X and Y, with I and J categories, respectively, where Y is the dependent variable and X the predictive variable. These variables generate a two-way contingency table of order I × J.
For the purpose of this study, we define a two-way (R × NSO) contingency table of order 3×3. The column and row of the table are divided into three classes, each of them defined by the corresponding tercile of their distribution. Data in the upper tercile of R correspond to wet periods and those in the first tercile to dry periods. For NSO, the first tercile defines the cool events for SST (La Niña) and the third defines the warm events (El Niño). The cell (i,j) corresponds to the i-th tercile of the NSO and the j-th tercile of the response R. Normally the categories in the second tercile are called neutral.
For the statistical analysis of the contingency tables we used generalized linear models, which is a common statistical methodology to study how the cell counts are related to the levels of the categorical variables (Agresti, 2002), analyzing the association and interaction patterns between the variables, and the response is multinomial for variables categorized into ordinal classes. We also fit multinomial response logit regression models when the predictors were used in their original continuous expression.
2.2Interpretation of response probabilitiesTable I shows the probabilities Pij associated with each cell, to be estimated through the logit model. In this table, the probability Pij corresponds to the probability of any given trimester to be classified into the (i,j) cell of the contingency table, in the absence of any expectation for ENSO.
3×3 contingency table for the rainfall (R) as response and the NSO index as predictor. Rows and columns correspond to the terciles of the series, Pij is the probability that a given observation, being classified in the row i of the predictor, is classified into the column j of the response.
| Rainfall terciles | |||
|---|---|---|---|
| NSO Terciles | R1 | R2 | R3 |
| NSO1 | P11 | P12 | P13 |
| NSO2 | P21 | P22 | P23 |
| NSO3 | P31 | P32 | P33 |
Pi,j probabilities can be interpreted as follows:
P11 is the probability that the first tercile of NSO induces rainfall in the first tercile of the rainfall distribution, so it measures the association of cool events and dry years.
P13 is the probability that the first tercile of NSO induces rainfall in the third tercile of the rainfall distribution, so it measures the association of cool events and wet years.
P31 is the probability that the third tercile of NSO induces rainfall in the first tercile of the rainfall distribution, so it measures the association of warm events and dry years.
P33 is the probability that the third tercile of NSO induces rainfall in the third tercile of the rainfall distribution, so it measures the association of warm events and wet years. We expect this probability as well as P11, to be higher than 1/3.
P21, P22, P23, P12 and P32 are the probabilities for the central terciles that are supposed to be determined by the climatology, i.e. they will be always close to 1/3.
Logit models were fit to estimate the expected values for the cells of the contingency tables, when one of the classifications is used as causal and the other as dependent. In this study, we used the NSO index as causal and rainfall as the response variable. According to Wilks (2011), systems for producing probability forecasts are developed in a regression setting by first transforming the predictand to a binary (or dummy) variable, taking on the values zero and one. In a sense, zero and one can be viewed as probabilities of the dichotomous event not occurring or occurring, respectively, after it has been observed.
3Results and discussionAlthough most of our results are very consistent with the physical models for rain patterns in the region, it is likely that some of the results present some local discrepancies. This is probably due to the fact that, given the size of the cells (2.5×2.5°), in some regions located from the coast to the Andes mountains—which present different climates—the enclosed area comprises heterogeneous rain patterns. We also include areas with very scarce rainfall—just a few millimeters/year—such as the Atacama Desert in Chile. In those cases, a small amount of rainfall could result in large deviations from de mean, with large variances.
3.1Contingency tablesBelow, we will analyze the results of the response to logit models, which will associate an event (cool, neutral, warm) to a rainfall situation (dry, neutral, wet). The association between warm and cool events and dry and wet phases will be emphasized, unlike the association between or with neutral phases, which is less pertinent. Therefore, we will mostly investigate the direct relationships, cool-dry, cool-wet, warm-dry, and warm-wet (the P11, P13, P31 and P33 probabilities, respectively), i.e. the corners ofthe contingence tables.
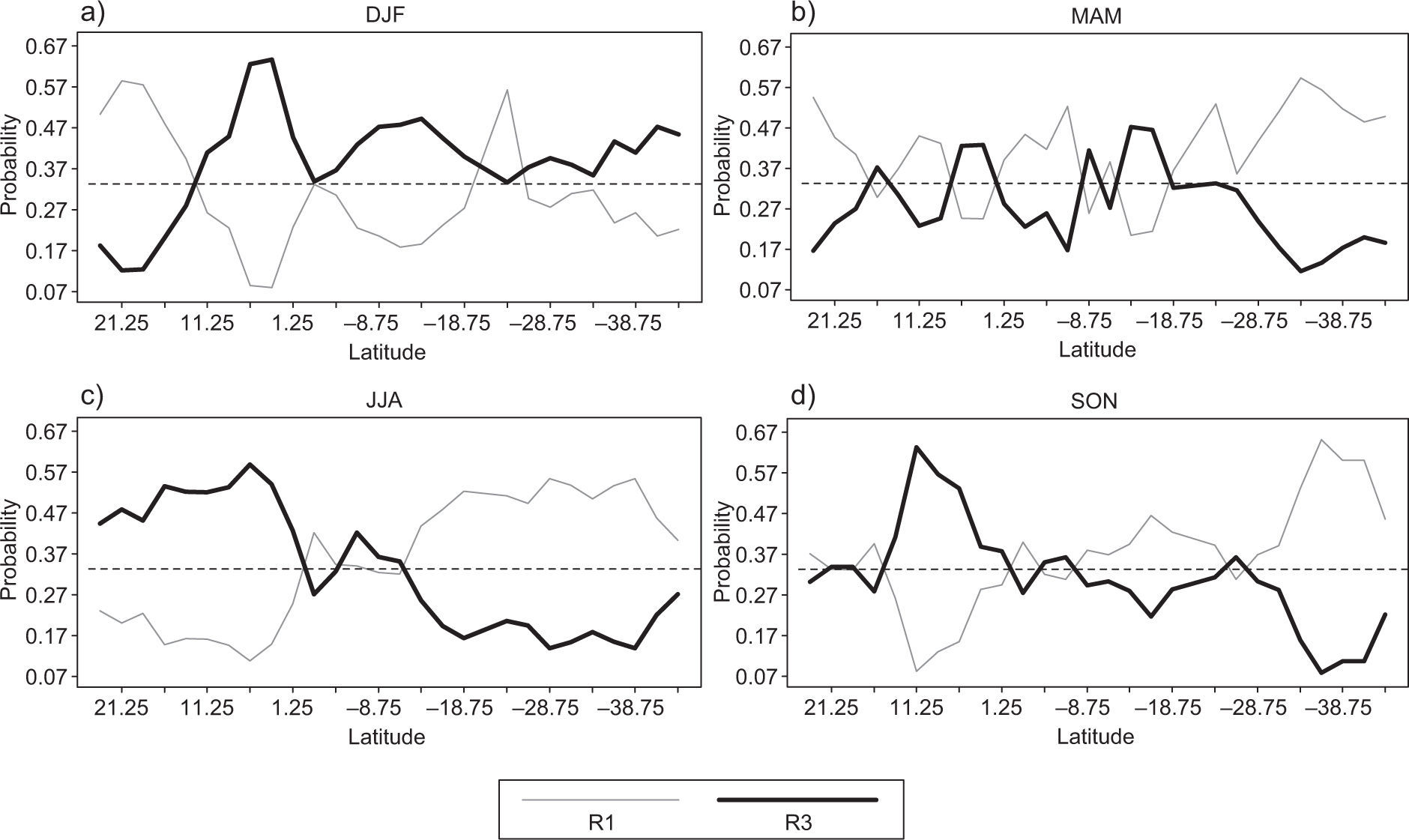
Analyses by season are shown in Figs. 3 and 4. We consider that events with probabilities along the 0.333 line are not predictable, events associated with values below the 0.333 line are less probable, and values well above this line represent the most likely events.
For the boreal winter (austral summer), Figure 3a shows that from 22.5 to 13 °N, the most likely association during La Niña is R1|NSO1, which corresponds to cool-dry associations, while from Costa Rica through south Chile, it corresponds to a cool-wet condition, which is particularly true for Panama and Colombia. For most latitudes, El Niño is R3|NSO3, which corresponds to warm-wet associations (Fig. 4a) except for the coast of Mexico, Guatemala and El Salvador, dominated by warm-dry conditions.
The results of Figures 3a and 4a are consistent with the following previous studies. During the warm (cool) phases of ENSO, an increase in the occurrence of cold outbreaks or cold fronts is observed in the north Pacific coast of Mexico, associated with more (less) precipitation in that region (Magaña et al., 1999a). Gershunov and Barnett (1998) observed and added that typical El Niño patterns (e.g., low pressure over the northeastern Pacific, dry northwest, and wet southwest, etc., in North America) are strong and consistent only during the high phase of the North Pacific Oscillation (NPO), which is associated with an anomalously cold northwestern Pacific. The SLP and precipitation patterns during La Niña winters are consistent only during the low NPO phase. They also explain that a deeper Aleutian low shifts the storm track southward while El Niño provides an enhanced eastern tropical Pacific moisture source for the storms. Alternatively, a weaker Aleutian low during the low phase of the NPO paired with La Niña steers cyclonic storms farther north, increasing precipitation in the northwest while the less frequent storms passing over the southwestern United States tend to be drier than normal because less moisture is available from the eastern tropical Pacific. This paradigm is also observed with precipitation anomalies in the western United States. Over Central America, results of Figures 3a and 4a are consistent with Amador (2008), who found that the Caribbean low level jet (CLLJ) core is weaker (stronger) than normal during warm (cold) ENSO phases in winter. It means that zonal easterlies decrease (increase) over the isthmus, increasing (decreasing) the precipitation over the Pacific slope by two mechanisms, decreasing (increasing) the Foehn effect (Oliver, 2005) and enhancing (reducing) the mesoscale system formation over that slope. Drier summers over most of Peru and Chile have been associated over most of the last 60 years with cool situations in the ENSO index, and abnormal wetter summers in central Chile have been associated with warm situations in the ENSO index.
For the austral autumn (boreal spring), figures 3b and 4b show the predicted probabilities for rain ter- ciles given the cool and warm phases of ENSO. Note that for this season, the patterns are irregular, and only few regions show a noticeable association, except for central-south Chile, which shows a strong wet-cool and wet-warm association. For the north coast of Mexico, this season could replicate the same explanations given by Gershunov and Barnett (1998) and Magaña et al. (1999a), meaning that during the warm (cool) phases of ENSO, an increase in the occurrences of cold outbreaks or cold fronts is observed in that region, associated with more (less) precipitation. For Central America, this is the season associated with the beginning and first peak of the rainy season (Taylor and Alfaro, 2005). Rainfall in this region is mainly dominated by deep cumulonimbus formations and the northward migration of the intertropical convergence zone (ITCZ). Philander (1990) describes that this migration is delayed (favored) during warm (cool) ENSO phases. This situation could inhibit (potentiate) the deep convection, resulting in drier (wetter) conditions in the Central American Pacific slope. From this it can be inferred that during the MAM trimester, we cannot clearly discriminate the effect of the warm and cool phases of ENSO over rainfall, except in the zones above described. In addition, it could reflect the influence of other climate variability sources that obscure or potentiate the ENSO signal. For example, Enfield and Alfaro (1999), Giannini et al. (2000), Taylor et al. (2002) and Gouirand et al. (2013) observed that during this season the Caribbean and Central America are highly influenced by the tropical North Atlantic variability.
For the austral winter (boreal summer), Figures 3c and 4c show the predicted probabilities for rain terciles given the cool and warm phases of ENSO. For this season, except for 2° N-14° S, there exists a very clear pattern of association. Figure 3c shows that in the region from 22.5 to 5° N, there is a clear wet-cool association, while from 15 through 45° S, there is a dry-cool association. The opposite association—i.e., dry-warm and wet-warm—is evident for the same regions, respectively, as shown in Figure 4c. The result for 22.5-5° N agrees with the work of Magaña et al. (1999b), who showed drier (wetter) conditions along the Pacific coast of Mexico and Central America during warm (cool) ENSO phases. Such a relationship is very important because the midsummer drought (Magaña et al., 1999b; Karnauskas et al., 2013) is observed in Mesoamerica during July-August as a reduction in rains in the eastern tropical Pacific. As for the MAM season, Magaña et al. (1999a) explained that this could be due to a southern (northern) position of the ITCZ during the warm (cool) ENSO phases. In addition, Amador (2008) explained that in contrast to winter conditions, the CLLJ core is stronger (weaker) than normal during warm (cold) ENSO phases in summer, meaning that zonal easterlies increase (decrease) over Mesoamerica, decreasing (increasing) the precipitation over the Pacific slope by the two mechanisms already mentioned for winter.
Much of the rainfall in central Chile happens during the winter season. Therefore, most of the agricultural economy is based on weather conditions during this season, being of particular interest to determine if winter will be drier than normal. As shown in Figures 3c and 4c, seasonal association with the ENSO index increases with latitude, particularly in central Chile, where it reaches its highest value at roughly 38° S. For most of central Chile, wetter than normal conditions are associated with warm situations. The opposite can be concluded for some latitudes in the Northern Hemisphere (Figs. 3c and 4c), where wetter situations are found for the cool phase of El Niño.
Since drier conditions are associated with cool events (more than 1/3), there are high probabilities of a dry situation occurring in most of central Chile in presence of a cool event. The analysis performed here does not preclude a warm-dry association at specific latitudes. Elsewhere, from Ecuador to most of Peru (1-10° S), wetter-drier than normal winters are associated particularly to cool-warm events. Instead, for most of southern Peru and northern Chile the warm-wet and cool-dry association dominates, although less strong than for central Chile.
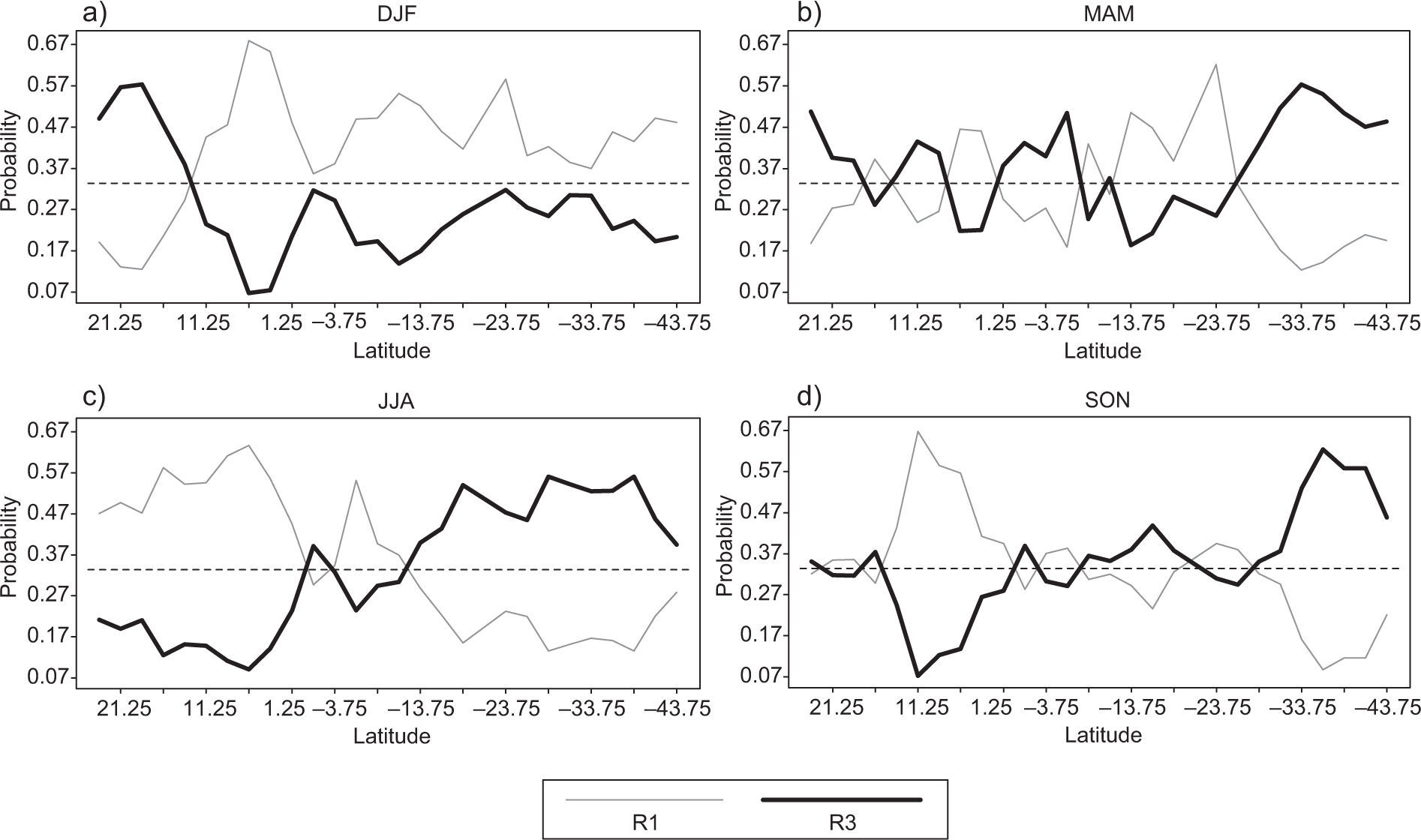
Predicted probabilities for rain terciles given the cool and warm phases of ENSO for the austral spring (boreal autumn) are shown in Figures 3d and 4d, where we can observe the same patterns than for the JJA term, except for narrower regions. In fact, Figures 3d and 4d show two regions, one for 22.5 to 10 °N, plus a wider region, 5° N to 30 °S), with no clear predominance of an association between NSO and rainfall, while for Ecuador there is a clear wet-cool association and for central-south Chile the association is wet-cool (Fig. 3d). Figure 4d shows strong dry-warm and wet-warm conditions for the same regions, respectively.
The analysis of austral spring on Figures 3d and 4d shows the latitudes for which the probabilities of cool-dry and wet-dry association reach their maximum (i.e., Costa Rica through Colombia) and those for which the cool-wet and warm-wet associations are maximum (central-south Chile).
During this season, which correspond to boreal autumn, the Pacific slope of Central America presents the second peak of the rainy season, when most of the extreme events are observed, especially during September-October. Results of Figures 3d and 4d show that in Central America, when equatorial eastern Pacific SST anomalies tend to be warmer (cooler), the precipitation response over land tends to be associated with drier (wetter) anomalies over the Pacific slope, consistent with the results of Enfield and Alfaro (1999) and with the results for rainfall anomalies and extreme events of Maldonado et al. (2013). Enfield and Alfaro (1999) noticed that the end of the rainy season in lower Central America tends to be delayed when the eastern equatorial Pacific is cool at the end of autumn. This means that zonal easterlies increase (decrease) over the isthmus, reducing (enhancing) the mesoscale system formation over that slope. During this trimester, the Atlantic Ocean shows also its peak in tropical cyclone occurrences near Central America, which are the main cause of floods associated with the so-called “indirect effect” of a low pressure system located either in the Caribbean Sea or in the Central America Pacific slope (Peña and Douglas, 2002). However, warm (cool) ENSO phases reduce (increase) the occurrence of cyclones in the Caribbean Sea increasing (reducing) the wind shear over the basin (Gray, 1984), which is also consistent with Figures 3d and 4d.
Amador (2008) describes that near the South American coasts (north of the equator) the southerly trade wind regime becomes westerly, except during February, due to a change of sign of the Coriolis force and to the land-sea temperature gradient, among other factors. In western Colombia near 5° N these winds form a low-level westerly jet, the Chocó jet (CJ) (October-November). At lower levels, warm air and moisture convergence associated with the CJ, low surface pressure, and topographically induced vertical motion on the western Andes contribute to deep convective activity organized as mesoscale convective complexes. Amador (2008) adds that during cold (warm) ENSO phases, the boreal autumn CJ shows stronger (weaker) than normal wind speeds, enhancing (diminishing) precipitation in that region, which is consistent with Figures 3d and 4d.
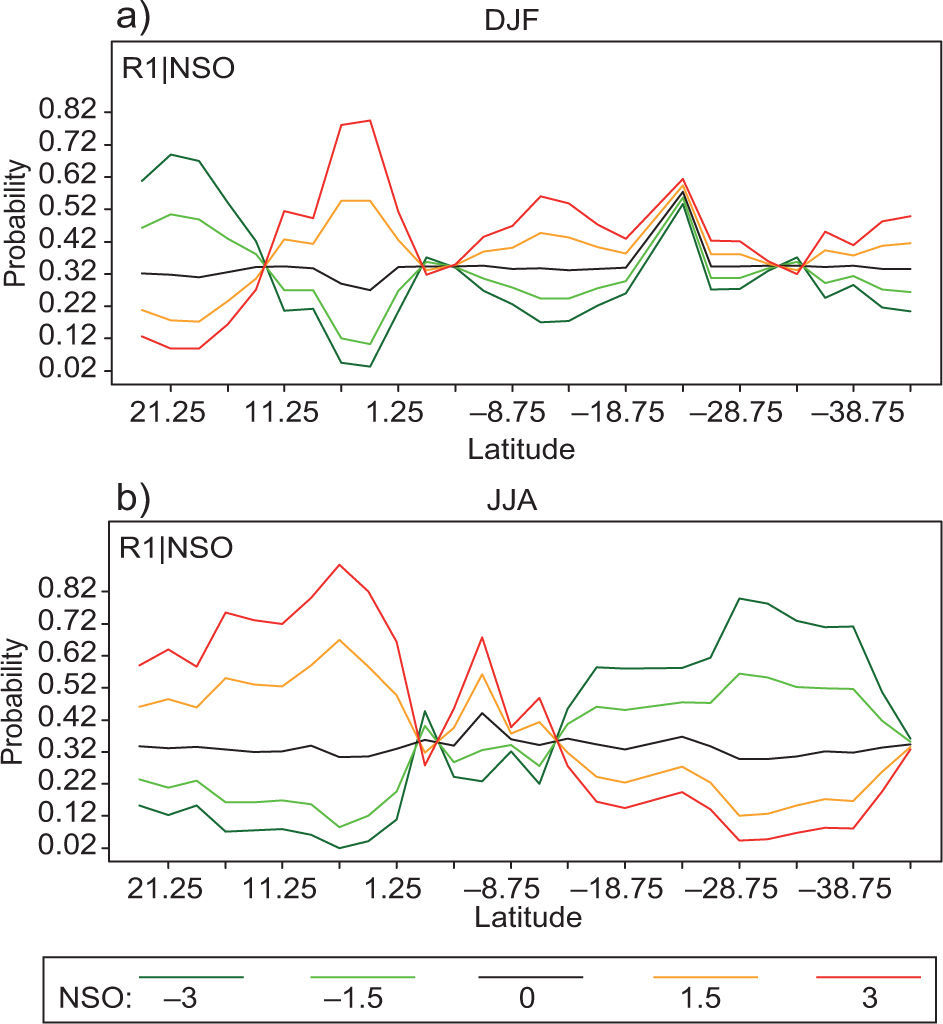
Similar results were found when applying regression models with multinomial response, and using the NSO index as independent variable in its continuous form. We used five different values of NSO, namely –3, –1.5, 0. 1.5 and 3.0. Some of the results, which confirm the results of the contingency table analysis, are shown in Figure 5. Figure 5a shows the latitudinal probability of dry season profiles for the austral summer season, given five different values of the NSO index, and the results for extreme values of NSO (NSO1 and NSO3). Figure 5b shows the latitudinal probability of dry season profiles for the austral spring season given five different values of the NSO index.
Interestingly, the highest correlation found between the ENSO index and rainfall in central Chile is related to the spring season roughly between 35 and 40° S (Fig. 5b). There, the seasonal warm-wet and cool-dry association is particularly clear and meaningful. Therefore, if a warm-cool ENSO related variability takes place, most probably during the following autumn, rainfall must experience a wetter-drier than normal situation. Ecuador experiences also the same situation, whereas central Peru appears to be slightly dominated by a cool-wet association. Elsewhere, from southern Peru to most of northern Chile the association is irregular, which is probably meaningful for local or other remote influences. Figure 5a shows that for DJF, which correspond to austral summer, the highest probabilities are for P11 and P33 for the region of Arica through Valdivia, in Chile, indicating a strong association between the warm-cool events and rainfall in the region.
Considering the probabilities of association between warm-cool events in an ENSO index as given by a logit model and dry and wet situations as given by monthly rainfall data over most of the western side of South America (from southern Ecuador to southern Chile), categorized into seasonal values, we can conclude based in the analysis of the last 60 years that there are high probabilities that warm and cool events within the ENSO variability may give rise to drier and wetter than normal situations in Chile, particularly along the central region. Interestingly, the best probabilities of association (in central Chile) are given equally for both cause-effect relationships in the autumn season. The spring season appears to be dominated by a cool-dry situation and the winter season by a warm-wet situation, even if in both cases the other direct association (respectively warm-wet and cool-dry) is also meaningful though less intense. It is of particular interest for agriculture that there are much higher probabilities of a cool event in ENSO being followed or accompanied by a dry season than by a neutral or wet season. Summer presents interesting differences with the other three seasons, which are of particular interest for the tourism sector (and for any person interested in sunny summers), wetter than normal summer seasons will be most probably associated to cool events in ENSO. Instead, drier than normal summer seasons are associated to warm events along the tropical Pacific.
The relationships along northern Chile and the desert are most probably contaminated by noise due to scarce pluviometry therein, although a warm-wet association in winter is illustrative of the rare rainfall occurrences after a very strong El Niño event. However, results for latitudes associated with desert regions need to be more carefully analyzed. In fact, since there are only a few rain episodes and the amount of precipitation is very small, anomalies could be rather large, i.e. the distribution could be highly skewed and rainfall accumulation over the period may not differ significantly from the common observed values.
The probabilities of association found for Ecuador and Peru are also very interesting. For Ecuador, represented here only by two grid points, the yearly average association interestingly resembles that observed along central Chile. Warm conditions in ENSO will be most probably associated with wetter than normal rainfall and cool conditions with drier ones. It appears that all seasons show the same pattern favoring the strong cool-dry and warm-wet association, but excluding the winter season, when no association is favored. For central Peru the cool-wet and warm-dry relationship appears to dominate the yearly average association. The cool-wet association is supported in all seasons, particularly during winter and spring, whereas the warm-dry situation in central Peru is confirmed mostly for summer and winter.
From the analysis presented here it can be inferred that warm and cool phases of ENSO in the above-described zones are clearly discriminated in the austral spring. In contrast, over much of northern Chile and part of southern Peru (16-30° S) a nonlinear association is shown. Therefore, for most latitudes analyzed here (from Mexico to Chile), drier and wetter than normal spring seasons were associated with cooler and warmer situations in the ENSO variability. In central Peru, spring situations wetter than normal were associated with cooler conditions related to ENSO.
Although our results are very coherent with the meteorological background, we decided to crosscheck them using a different data base. For this purpose, we used data from the Global Precipitation Climatology Project (GPCP) (Adler et al., 2003), v. 2.2, provided by the Earth System Research Laboratory ofNOAA (http://www.esrl.noaa.gov/psd/). Adler et al. (2003) explain that these data are combinations of satellite and rain-gauge sources, available from January 1979 to December 2014. Using this new data set, although much shorter, we consistently found almost the same results as with Chen et al. (2002) data.
4ConclusionsPrecedent studies, beginning with Pittock (1980), established the relationship between Southern Oscillation variability and drier and wetter climate for western South America, particularly for Chile. Numerous studies have followed. We cite here those by Rutllant and Fuenzalida (1991) and Montecinos et al. (2000), which include an appropriate and complete review of literature as well as a deeper insight into the causes, time delay and particular cases of relationship. The research described here was intended to be methodological rather than theoretical, and aims to provide a tool for analyzing cause-effect relationships by way of generalized linear logit models, providing the reader with the probability of occurrence of a wetter or drier than normal season given the phase of an ENSO event. Our studies confirm, though differently and with a dissimilar insight, precedent studies on the region (e.g., Ruttlant and Fuenzalida, 1991; Enfield and Alfaro, 1999; Montecinos et al., 2000).
Although criticism for this type of analysis focuses in the fact that there is an obvious loss of information, since a continuous variable is allocated into a few categories, it needs to be noticed that this loss of information allows to focus the analysis on the occurrence of events. In a way, this highlights the specific categories of the event in which we are interested. In a first stage, this means that our main interest is not the strength of an upcoming event but whether it will occur or not. Such information is instead emphasized using the categorization procedure. Only in the second stage of the study we will focus on the intensity of the event and on determining how strong (or weak) it will be if it eventually occurs.
Although the probabilities in the corners of the contingency table, P11, P13, P31, P33 (cool-dry, cool-wet, warm-dry and warm-wet, respectively), seem to be more interesting and have a more straightforward interpretation, the center row and column are also interesting, since they show that there is no basis to expect any extreme condition (warm or cool events), which therefore corresponds to a probability close to 1/3. However, the results herein presented are viewed as a preliminary study on cause-effect relationships based on the introduction of logit models. We did not, for example, discriminate associations between strong, moderate and weak events to rainfall statistics, neither did we study a particular event impact as, e.g., Curtis et al. (2001) for the 1997-1998 event. It will be necessary to extend this research to higher density estimations for rainfall along the Latin American west coast. For example, the analysis of high density Ecuadorian rainfall data (more than 210 rain gauges) by Rossel et al. (1998) revealed that although coastal rainfall is highly associated to ENSO events, this association in near-Andean regions like Puyo or Cuenca is weaker. Therefore, our analysis, based in 2.5×2.5° latitude-longitude grids (roughly over 250 kilometers), does not discriminate between coastal and near-Andean regions, therefore mixing or most probably mitigating the ENSO influence. Also, our investigation constructed an ocean-atmosphere ENSO index through the mixing of Niño 3 and SOI indices, which is practical, but it did not take into account the reality of the tropical Pacific SST evolution through longitude.
Most probably, other indices such as Niño 1.2 SST could have been more meaningful for regions from Ecuador to northern Chile. In this regard, Coelho et al. (2002) analyzed the correlation between the South America rainfall variability (poorly gridded) and six regions along the tropical Pacific, and showed the need for a better specification of variability sources (i.e., Niñol, 2, 3 and 4 regions may be not enough). It is worth noting that using logit models with regional specifications for tropical variability and higher resolution precipitation grids may probably yield very useful results.
We must, as well, focus this research on some particular time scales. For example, in this study we did not discriminate between different modes of ENSO, i.e., interannual from decadal time scales (Zhou and Lau, 2001); neither did we differentiate ENSO from non-ENSO variabilities (Mestas and Enfield, 2001). These ENSO modes, which could be focused on the types of relationships found in this paper, need a different study, particularly for the effects of decadal time scales or even lower frequencies, like the global warming effect on rainfall. Finally, we might also extend our results to rainfall prediction based on the precedent season variability (see Montecinos et al., 2000). The following years will be fruitful in this regard, given the practical benefits of this kind of models on agriculture, epidemiology and at large in all economic activities associated with climate. As mentioned earlier, an advantage of this method is that it gives the results in terms of probabilities for different terciles, which is the most common output of current Regional Climate Outlook Forums in Latin America (e.g., IRI, 2001; García and Ramírez, 2012), and it could be extended to other variables considered in these forums like extreme events, number of rainy days or the midsummer drought (e.g. Maldonado et al., 2013; Alfaro, 2014).
This research was funded by grants from the Universidad del Bío Bío, Chile (DIUBB 120808 2/R), the Pontificia Universidad Javeriana seccional Cali, Colombia (research group EMAP, project “Aspectos metodológicos del análisis categórico en la predictibilidad de la precipitación en la costa oeste de Centro y Sudamérica a partir de ENSO-020100256”), the Panamerican Institute of Geography and History (GEOF.02.2013). E. A. also received funds through the following grants: IAI-CRN2-050, UCR-VI-805-A7002, B4227, B3413, B3600, A9532 and B0065.