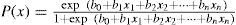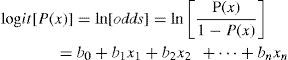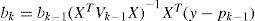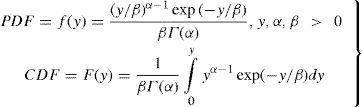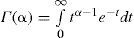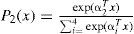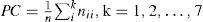Downscaling standardized precipitation index via model output statistics

Resumen

El presente estudio analiza los posibles impactos futuros del cambio climático sobre los eventos meteorológicos de sequía en Turquía, utilizando para ello una nueva técnica estadística de reducción de escala (downscaling) basada en regresión logística politómica. Esta técnica, conocida como “estadísticas de salida del modelo” (model output statistics, MOS), está diseñada para la reducción de escala de las categorías de sequía del índice estandarizado de precipitación (SPI, por sus siglas en inglés). El principal objetivo de un procedimiento de reducción de escala es determinar la influencia de la variabilidad climática de gran escala y los cambios proyectados en las variables a nivel regional y local. Los predictores de gran escala utilizados en este estudio se obtuvieron a partir de simulaciones del modelo canadiense de circulación general acoplado de segunda generación (CGCM2, por sus siglas en inglés), las cuales abarcan de 1940 a 2100 e incluyen tres escenarios socioeconómicos: control, con los límites de la concentración atmosférica de gases de efecto invernadero en el siglo XX, y los escenarios A2 y B2 del Informe especial sobre escenarios de emisiones del Panel Intergubernamental de Cambio Climático. Se utilizaron observaciones de 96 estaciones meteorológicas para calcular los valores anuales del SPI para el periodo 1940-2010, dejando los últimos 10 años para validación contra los resultados simulados por el CGCM2. Los resultados del MOS derivados de la simulación del clima denominada control coincidieron con los patrones observados en el clima actual. Los resultados del MOS derivados de escenarios climáticos futuros llevan a concluir que hay una probabilidad disminuida de que se presenten condiciones muy húmedas o extremadamente húmedas. Adicionalmente, las probabilidades de que las condiciones sean cercanas a lo normal disminuirán en la costa del Mar Negro, y aumentarán en la transición del Mármara y en Anatolia oriental.

Abstract

This study investigates the possible impacts of future climate change on meteorological drought events in Turkey by using a new statistical downscaling technique based on polytomous logistic regression, denoted as the model output statistics (MOS) technique. It is designed to downscale the drought classes of the 12-month Standardized Precipitation Index (SPI). The main goal of a downscaling procedure is to determine the influences of large-scale climatic variability and the projected changes on the local scale-regional variables. The large-scale predictors used in this study were obtained from the output of the Second Generation Canadian Coupled General Circulation Model (CGCM2) simulations, run from 1940 to 2100 for three socioeconomic scenarios, namely control, with the constraint of the 20th century atmospheric concentration of greenhouse gases, and the SRES A2 and B2 scenarios. Observations from 96 meteorological stations were used to estimate 12-month SPI values for the period 1940-2010, leaving the last 10 years for validation against the results simulated by the CGCM2. The MOS results derived from the control climate simulation agree with the observed patterns for present climate. The MOS results derived from future climate scenarios lead to conclude that there is a decreased probability of very wet and extremely wet conditions. In addition, the probabilities of near-normal conditions will decrease in the Black Sea coast and will increase towards the Marmara Transition and continental eastern Anatolia regions.

1

Introduction

Droughts in any form in the meteorological, hydrological and agricultural fields are the anticipated results of climate change, particularly in subtropical regions including the Mediterranean countries. Droughts will become more prevalent and thus, more complex water management and drought monitoring tools will be required (IPCC, 2001, 2007). The impacts of climate change on future weather and climate are generally evalauted by running general circulation models (GCMs) based on various scenarios.

The Mediterranean region, including Turkey, is one of the areas in which GCMs simulate decreases in precipitation. For instance, Ozturk et al. (2012) have investigated the annual time-scale performance of the regional climate model RegCM4.0 in simulating annual change of dry-spells and extreme-precipitation in the central Asian region by running the model for two 30-yr. periods (1971-2000 and 2071-2100). They used the ERA40 reanalysis as boundary conditions of the regional climate model for the present period (control) and global datasets of EH5OM for the future with the IPCC SRES A1B scenario. They concluded that the southern part of Central Asia will be most vulnerable for droughts in the future, and there will be an increase in extreme drought conditions over almost the whole region.

However, simulations of the GCMs at coarse resolution may contain inherent inconsistent variability in climate variables. In view of that, a downscaling process is necessary to reduce uncertainty. For example, in a water management plan, the possible impacts of climate change on precipitation are remarkably important for local-scale studies, but the resolution of the GCMs is not suitable; hence, the scale-gap should be bridged with the local-scale variables (i.e., precipitation). This can be achieved either by empirical-statistical downscaling (which also includes probabilistic weather generators, etc.), or by physical-dynamical downscaling (e.g., Karl et al., 1990; Wilby et al., 1999; Easterling, 1999; Timothy and Hulme, 1999; Tatli et al., 2004, 2005; Coulibaly et al., 2005; Fowler et al., 2007; Tolika et al., 2007; Anandhi et al., 2008; Radu et al., 2008; Hertig and Jacobeit, 2008; Tatli, 2013).

Many useful techniques have been suggested in traditional statistical-downscaling procedures, such as linear and nonlinear regression, artificial neural networks (ANNs), canonical correlation analysis (CCA) and weather generator, which are are examples of methods for deriving relationships between large-scale predictors and local-scale predictands (Semenov and Barrow, 1997; Conway and Jones, 1998; Wilby et al., 1998; Kocak et al., 2004; Tatli et al., 2004, 2005; Dibike and Coulibaly, 2006; Loukas et al., 2008; Schmith, 2008; Mishra and Singh, 2009; Mishra et al., 2009; Vasiliades et al., 2009Tatli, 2013).

Additionally, other studies have proposed are dealing with new methods, concepts, comparative studies and modeling, and have been applied in many fields (e.g., Wilby and Wigley, 1997; Huth et al., 2000, Hay and Clark, 2003; Fowler et al., 2007; Mascaro et al., 2008).

Monitoring drought via the standard precipitation index (SPI) was first introduced by McKee et al. (1993, 1995), and found immediate applications in many fields (e.g., Guttman, 1998, 1999; Hayes et al., 1999; Wilhelmi and Wilhite, 2002; Steinemann, 2003; Wu et al., 2005; Türkeş and Tatli, 2009; Vasiliades et al., 2009). The SPI approach has several advantages including its simplicity and temporal flexibility, which allow its application to water resources on all timescales. For instance, Hayes et al. (1999), based on a case study of drought in Texas, concluded that the SPI method is an important tool that could be operationally used in a local, state, regional, or national drought monitoring system in the United States.

In this study, a statistical-downscaling model based on the logistic regression technique is suggested for downscaling 12-month SPI values using large-scale precipitation series on the four nearest grid points around the selected station. The large-scale simulated precipitation values are used as predictors, and logistic regression is suggested as a downscaling technique for projecting future SPI values. The paper proceeds as follows: Section 2 describes the employed methods. Results are given in Section 3. Finally, Section 4 comprises the conclusions.

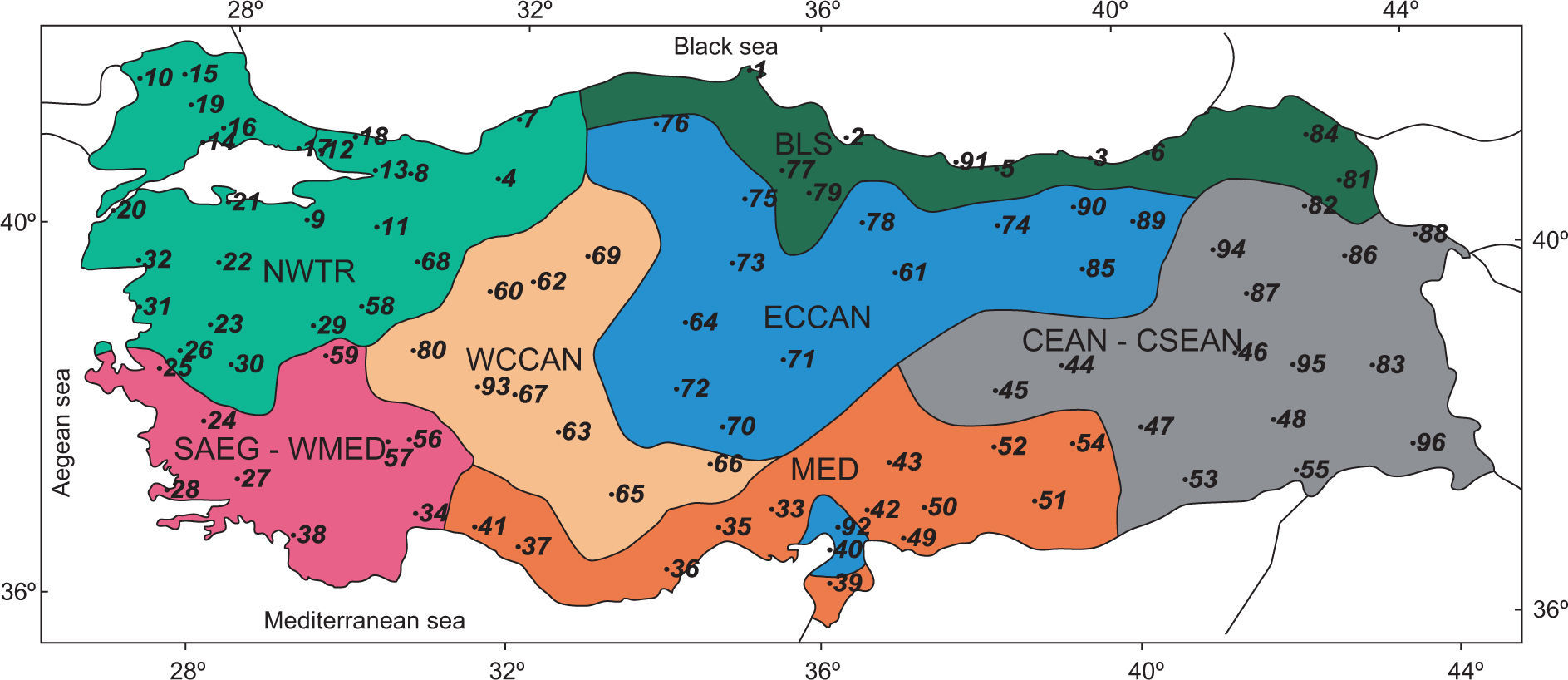
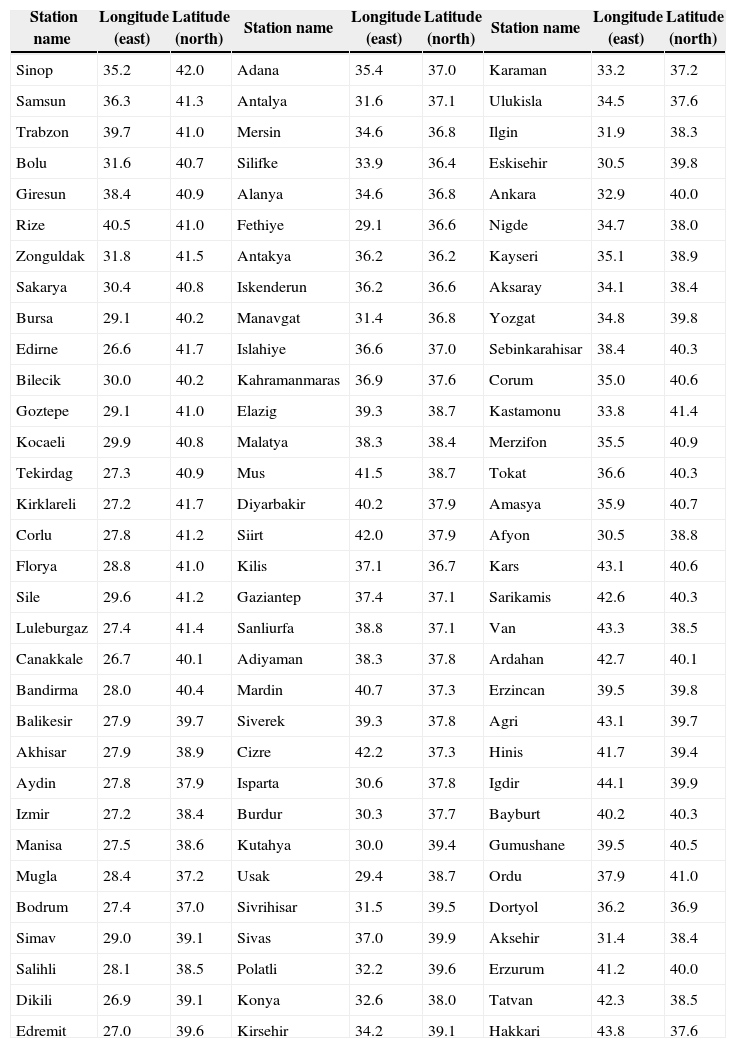
2

Data and methodology

2.1

Data and study area

The dataset of local-scale variables used in this study is the monthly precipitation records of the Turkish State Meteorological Service. The selected meteorological stations provide a suitable spatial distribution of the rainfall regions (Fig. 1, Table I) of Turkey.

Fig. 1.

The rainfall regions of Turkey according to Türkes and Tatli (2011). The stations used in this study are numbered on the map, and their identifier can be found in Table I. BLS: Black Sea; NWTR: northwest Turkey; SAEG-WMED: southern Aegean and western Mediterranean; MED: Mediterranean; W-CCAN: west continental Central Anatolia; E-CCAN: east continental Central Anatolia; CEAN-CSEAN: continental eastern and southeastern Anatolia.

Table I.

Meteorological stations of Turkey used in this study, arranged according to the sequence numbers of the map in Figure 1.

Station name	Longitude (east)	Latitude (north)	Station name	Longitude (east)	Latitude (north)	Station name	Longitude (east)	Latitude (north)
Sinop	35.2	42.0	Adana	35.4	37.0	Karaman	33.2	37.2
Samsun	36.3	41.3	Antalya	31.6	37.1	Ulukisla	34.5	37.6
Trabzon	39.7	41.0	Mersin	34.6	36.8	Ilgin	31.9	38.3
Bolu	31.6	40.7	Silifke	33.9	36.4	Eskisehir	30.5	39.8
Giresun	38.4	40.9	Alanya	34.6	36.8	Ankara	32.9	40.0
Rize	40.5	41.0	Fethiye	29.1	36.6	Nigde	34.7	38.0
Zonguldak	31.8	41.5	Antakya	36.2	36.2	Kayseri	35.1	38.9
Sakarya	30.4	40.8	Iskenderun	36.2	36.6	Aksaray	34.1	38.4
Bursa	29.1	40.2	Manavgat	31.4	36.8	Yozgat	34.8	39.8
Edirne	26.6	41.7	Islahiye	36.6	37.0	Sebinkarahisar	38.4	40.3
Bilecik	30.0	40.2	Kahramanmaras	36.9	37.6	Corum	35.0	40.6
Goztepe	29.1	41.0	Elazig	39.3	38.7	Kastamonu	33.8	41.4
Kocaeli	29.9	40.8	Malatya	38.3	38.4	Merzifon	35.5	40.9
Tekirdag	27.3	40.9	Mus	41.5	38.7	Tokat	36.6	40.3
Kirklareli	27.2	41.7	Diyarbakir	40.2	37.9	Amasya	35.9	40.7
Corlu	27.8	41.2	Siirt	42.0	37.9	Afyon	30.5	38.8
Florya	28.8	41.0	Kilis	37.1	36.7	Kars	43.1	40.6
Sile	29.6	41.2	Gaziantep	37.4	37.1	Sarikamis	42.6	40.3
Luleburgaz	27.4	41.4	Sanliurfa	38.8	37.1	Van	43.3	38.5
Canakkale	26.7	40.1	Adiyaman	38.3	37.8	Ardahan	42.7	40.1
Bandirma	28.0	40.4	Mardin	40.7	37.3	Erzincan	39.5	39.8
Balikesir	27.9	39.7	Siverek	39.3	37.8	Agri	43.1	39.7
Akhisar	27.9	38.9	Cizre	42.2	37.3	Hinis	41.7	39.4
Aydin	27.8	37.9	Isparta	30.6	37.8	Igdir	44.1	39.9
Izmir	27.2	38.4	Burdur	30.3	37.7	Bayburt	40.2	40.3
Manisa	27.5	38.6	Kutahya	30.0	39.4	Gumushane	39.5	40.5
Mugla	28.4	37.2	Usak	29.4	38.7	Ordu	37.9	41.0
Bodrum	27.4	37.0	Sivrihisar	31.5	39.5	Dortyol	36.2	36.9
Simav	29.0	39.1	Sivas	37.0	39.9	Aksehir	31.4	38.4
Salihli	28.1	38.5	Polatli	32.2	39.6	Erzurum	41.2	40.0
Dikili	26.9	39.1	Konya	32.6	38.0	Tatvan	42.3	38.5
Edremit	27.0	39.6	Kirsehir	34.2	39.1	Hakkari	43.8	37.6

The large-scale predictors needed for the study were extracted from the precipitation series simulated by the Second Generation Canadian Coupled General Circulation Model (CGCM2) of the Canadian Centre for Climate Modeling and Analysis (CCCma). For more details about the CGCM2 one may refer to the website of the CCCma (http://www.cccma. ec.gc.ca/models/models.shtm), Flato et al. (2000), or the IPCC data distribution center (http://www. mad.zmaw.de/IPCCDDC/html/ddcgcmdata.html). The atmospheric component of CGCM2 is a spectral model with triangular truncation at wave number 32 and a surface grid resolution of roughly 3.75 × 3.75° with 10 vertical levels

2.2

Methodology

A logistic regression technique is used in this study to statistically downscale results from simulations of a global climate model with coarse resolution. Some definitions are needed for clarifying the question of how a logistic regression can be used as a downscaling technique. In simple logistic regression, the dependent variable (i.e., predictand) is usually dichotomous or binary, that is, the predictand can assume the value of 1(one) with a probability of P for ^{success and} the value of 0 (zero) with a probability of 1-P for failure. However, the logistic regression can also be extended to cases where the dependent variable can take more than two values, known as multinomial or polytomous (Aldrich and Nelson, 1984; Menard, 1995; Tabachnick and Fidell, 1996; Kleinbaum and Klein, 2002; Preisler and Westerling, 2007; Prasad et al., 2010). The logistic regression is more powerful than other linear regression models, and it makes no assumption on the probability distribution of the predictors. The probability distribution in question needs not to be normally distributed, linearly related or have an equal variance within each group; these restrictions are needed in the traditional linear regression applications. The relationships are derived from the so-called logit-transformation by the success probability of:

where x_i(i = 1,2,…,n) is the predictor and b_i (i = 0,1,2,…,n) is the coefficient of logistic regression. Since logistic regression estimates the probability of success over the probability of failure, the results of the analysis could be put as odd ratios in the following expression:

The logistic regression is structurally similar to the well-known multivariate linear regression, where the logits act as predictors and the predictands are natural logarithms of the success probabilities (i.e., the odds).

The coefficients are generally obtained by using the weighted Newton-Raphson algorithm. This method is attractive, because the response variables can be naturally arranged as a sequence of binary choices. For this reason, it is a very suitable approach to categorize drought events. The application steps of this method are briefly summarized below according to Tabachnick and Fidell (1996), and Kleinbaum and Klein (2002):

• 1.

  Choose initial estimates of the regression coefficients, b^{T =} 0.

• 2.

  At each iteration step k, update the coefficients,

where X and y are treated as large-scale predictors and predictands (containing zeros and ones), and V_k-1 is the weight matrix where the diagonal entries p_i,k-1(1-p_k-1) represent the occurrence probability. Step 2 is repeated until b_k is close enough to b_k-1. The estimated asymptotic covariance matrix of the coefficients is given by (XTVX)–1. The Newton-Raphson algorithm can be extended to a higher dimensional version (polytomous), and its parameters are illustrated with the vector of p_k-1 in Eq. 3. The method is a multivariate regression model of the so-called conditional multinomial logistic regression.

The predictors illustrated with the matrix X are selected from the output of the simulation with the CGCM2, which is used to produce ensemble climate change projections using the IPCC's older IS92a forcing scenarios, as well as the newer SRESA2 and SRESB2 scenarios (IPCC, 2000). Note that the results of the CGCM2 are also used in the third assessment report of the IPCC (IPCC, 2001), and in the Arctic climate impact assessment.

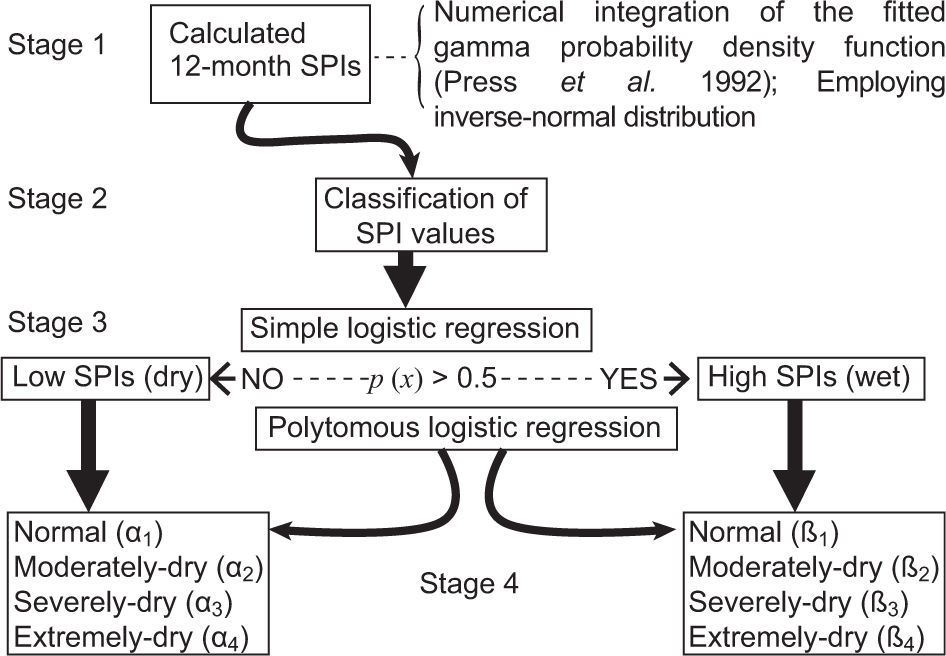
The suggested procedure is schematically given in Figure 2. Its source code is developed in Fortran 95, and it accounts for the missing values in the data. A test based on the index, namely the accuracy or proportion of correct predictions (Murphy, 1996; Livezey, 2003), was applied for measuring the performance of the logistic models. This test is commonly used to evaluate the performance of weather forecasting in meteorology.

Fig. 2.

Schematic description of the suggested downscaling model based on polytomous logistic regression. Alpha and beta vectors shown in parentheses are the coefficients of the regression model in question.

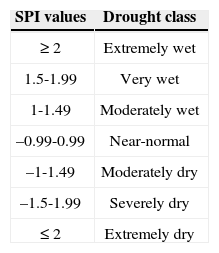
The drought and wet classes of 12-month SPI values are calculated from the observed precipitation values as a first stage. The probability density function (PDF) of precipitation values is the first step to estimate SPI values (one may refer to Türkeş and Tatli [2009] for a discussion on SPIs and modified-SPIs). The gamma function approach is widely used to estimate the PDF of precipitation values (e.g., Thom, 1966; McKee et al., 1993, 1995; Wilks, 1995; Guttman, 1998, 1999). In this study the cumulative distribution function (CDF) of the precipitation series is estimated by the numerical integration of fitted gamma PDF by the incomplete-gamma approach (Press et al., 1992). Twelve-month SPI values are used, but the suggested algorithm can be easily applied to other time slices of the SPI values, such as 1, 3, 6,…, -month, or more. The gamma PDF and CDF can be written as follows:

where y indicates the precipitation value, and α and β are the shape parameter and the scale parameter of the distribution, respectively. The quantity Γ(·) is the gamma function defined by

An improved method suggested by Bowman and Shenton (1988) was applied for estimating the shape parameter resulting from the use of an iterative sixth order polynomial. The scale parameter is then calculated by dividing the long-term mean of precipitation values by the shape parameter, β=y¯/α

At the second stage, SPI values are classified according to Table II. At the third stage, the dichotomous classes of drought and wet conditions are grouped into two classes, namely high and low SPIs treated as binary values (ones and zeros) represented by wet and dry classes in Figure 2. This stage involves a simple logistic regression which classifies the occurrence probabilities of wet and dry cases.

Table II.

Classification of the standardized precipitation index (SPI).

SPI values	Drought class
≥ 2	Extremely wet
1.5-1.99	Very wet
1-1.49	Moderately wet
–0.99-0.99	Near-normal
–1-1.49	Moderately dry
–1.5-1.99	Severely dry
≤ 2	Extremely dry

Finally, the fourth stage involves a polytomous logistic regression. In Figure 2, the vectors given in the parentheses represented by alphas and betas indicate the coefficients of the specific logistic regression. The dependent variable can take four dichotomous values numbered as (k = 0, 1, 2, 3), representing the drought classes as shown on the left and right sides of Figure 2. To further clarify this step, assume we wish to estimate the occurrence probability of a moderately dry class. By applying the vector of coefficients, the occurrence probabilities are calculated as:

where P₂(x) represents the occurrence probability of a moderately dry class (the subscript 2 indicates the second drought class), and the vector x illustrates the large-scale precipitation series simulated by CGCM2 in surrounding grid points to compare with non-uniformly distributed station data.

After calculating the occurrence probabilities of the entire dry classes by using Eq. 6, the drought class of maximum probability is selected as the downscaled-class for the specific station.

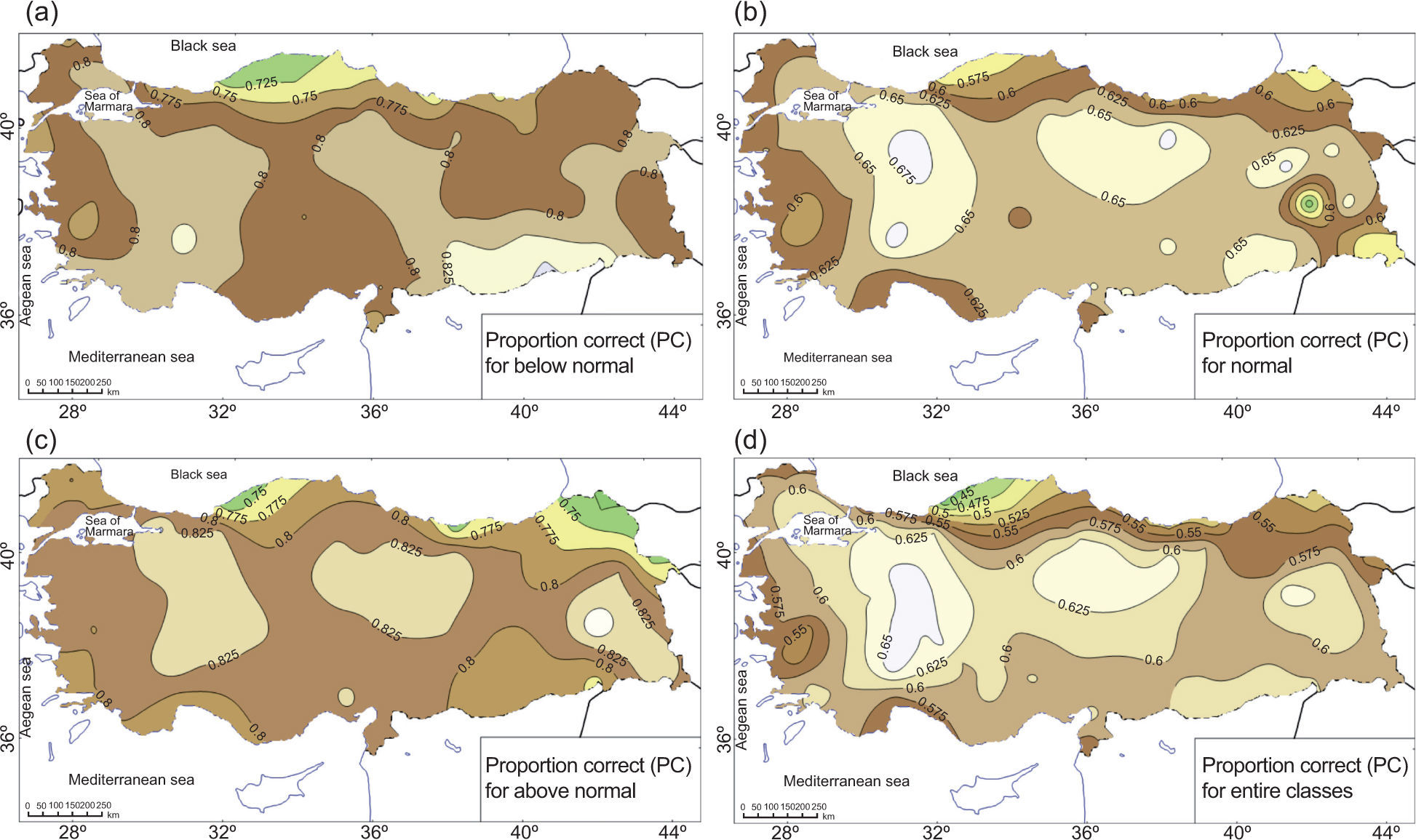
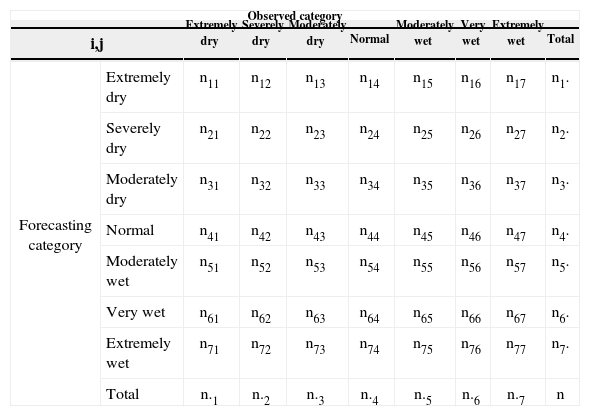
In order to measure the performance of the suggested model, the index of forecast accuracy or proportion of correct predictions (PC) was calculated between the output of the downscaling model-based control and the observed SPI classes for the period 1970-2000. For verifying multi-category forecasts, the method starts with frequencies of the forecast and observations in various bins, as given in Table III. A perfect forecast system should have values of non-zero elements only along the diagonal, and values of 0 (zero) for all entries off the diagonal. The off-diagonal elements give information about the specific nature of the forecast errors (Murphy, 1996; Livezey, 2003). The value of PC for the selected station is calculated as:

Table III.

Contingency table of the multi-categories of SPI values. The frequencies are used to calculate the proportion of correct (PC) prediction values as a criterion of performance for the suggested downscaling models.

^Observed category
i,j		^Extremely dry	^Severely dry	^Moderately dry	^Normal	^Moderately wet	^Very wet	^Extremely wet	^Total
Forecasting category	Extremely dry	n11	n12	n13	n14	n15	n16	n17	n1.
	Severely dry	n21	n22	n23	n24	n25	n26	n27	n2.
	Moderately dry	n31	n32	n33	n34	n35	n36	n37	n3.
	Normal	n41	n42	n43	n44	n45	n46	n47	n4.
	Moderately wet	n51	n52	n53	n54	n55	n56	n57	n5.
	Very wet	n61	n62	n63	n64	n65	n66	n67	n6.
	Extremely wet	n71	n72	n73	n74	n75	n76	n77	n7.
	Total	n.1	n.2	n.3	n.4	n.5	n.6	n.7	n

PC ranges from 0 to 1. If it assumes a value, close to 1, this indicates a high forecasting performance.

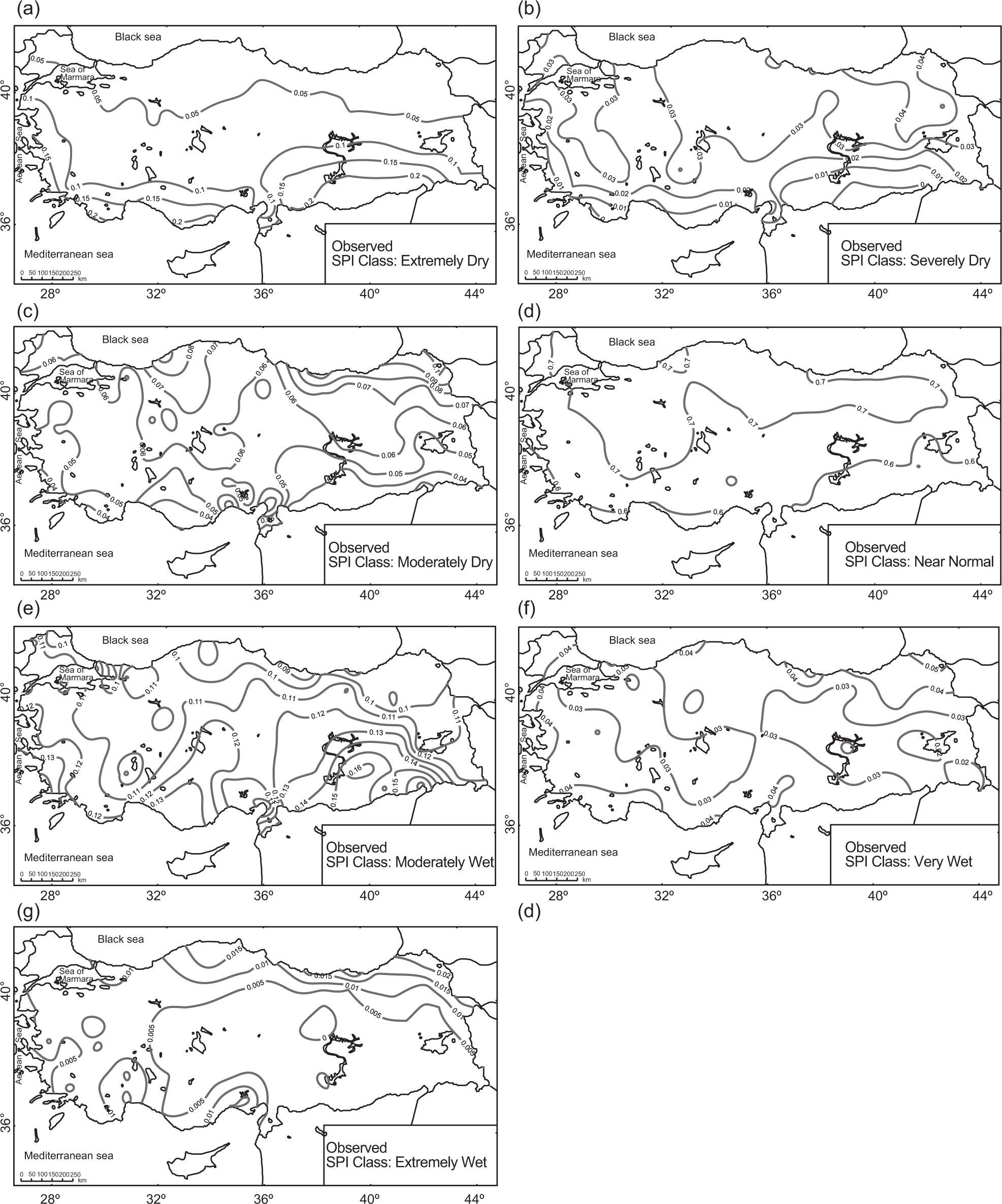
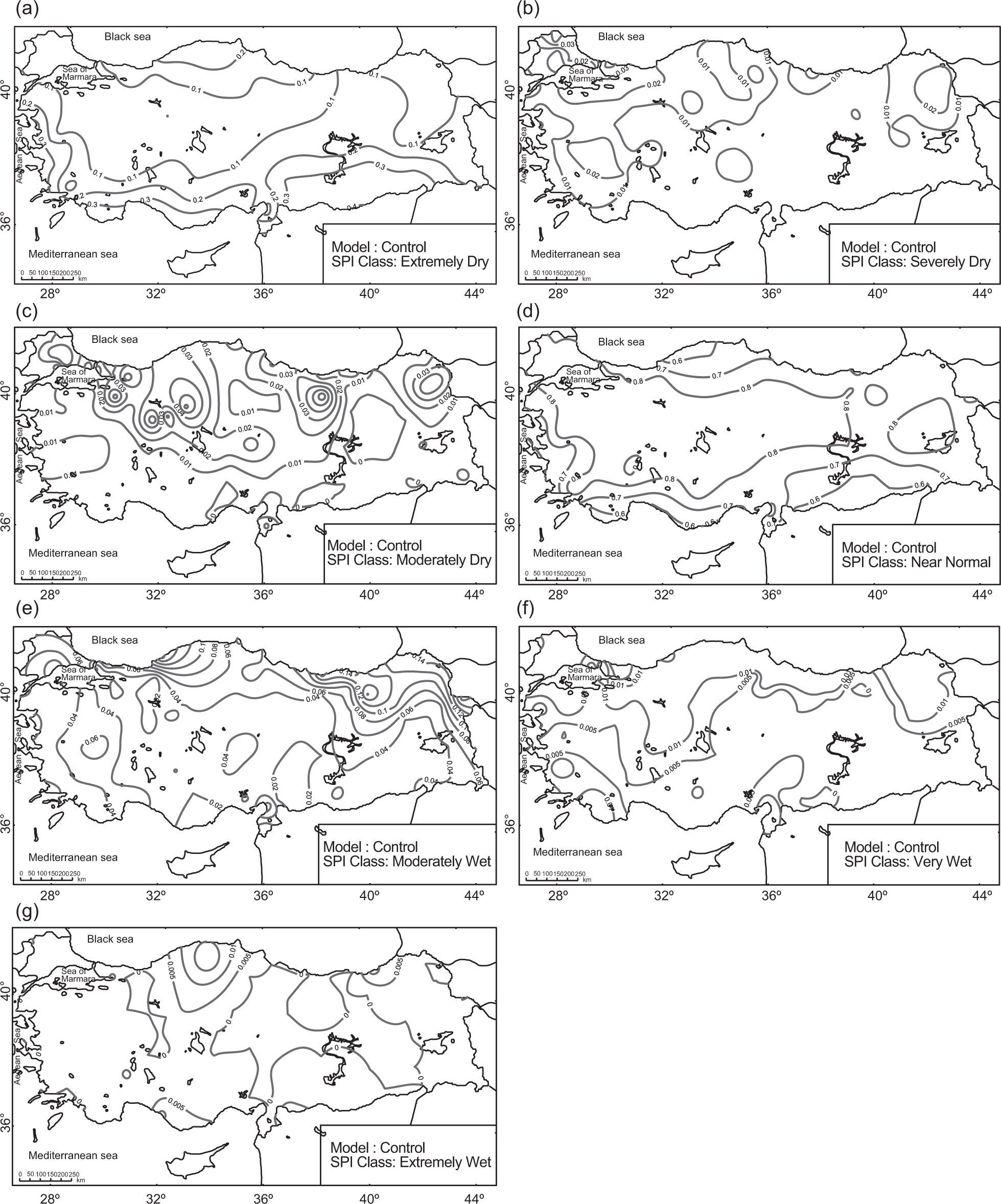
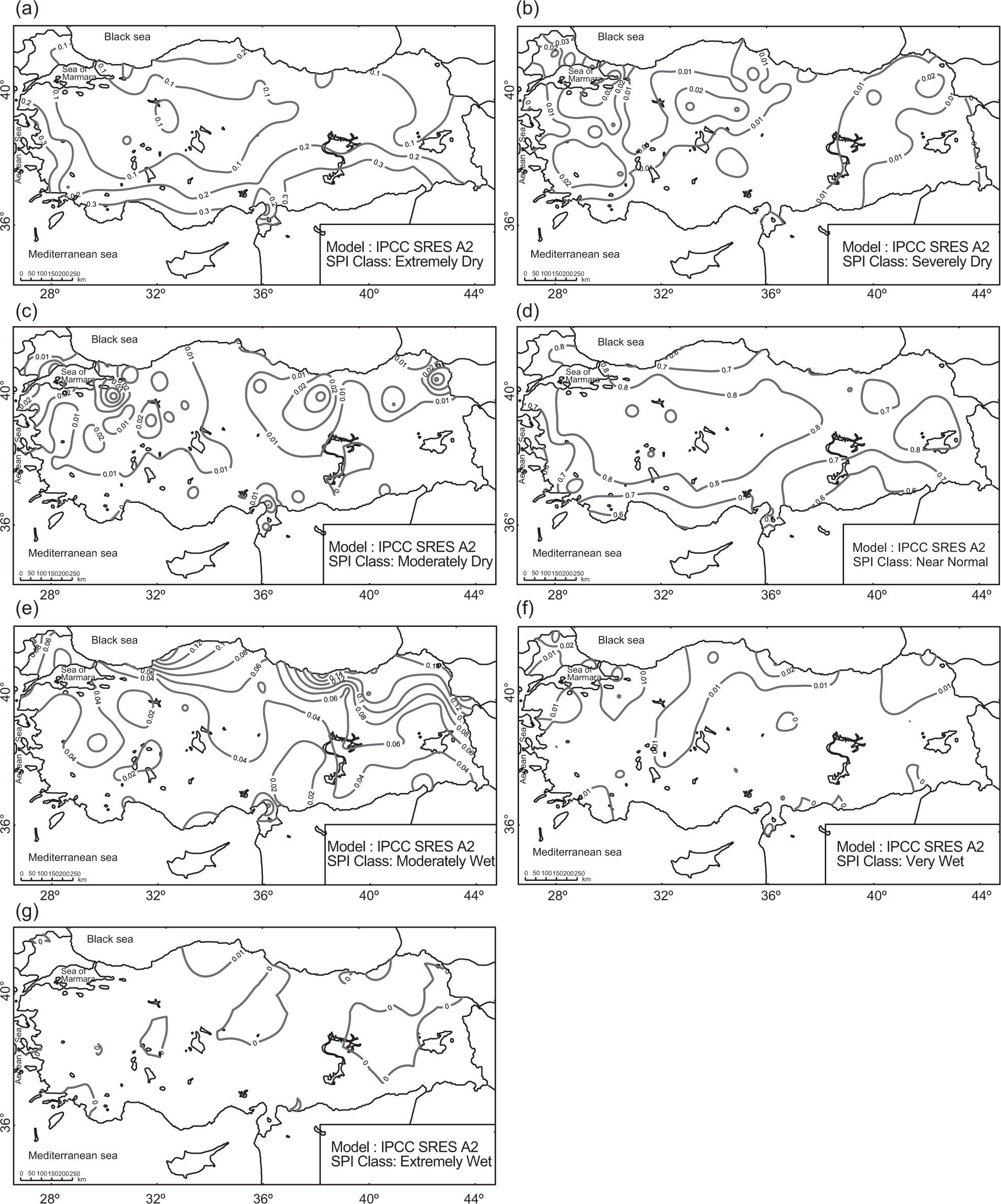
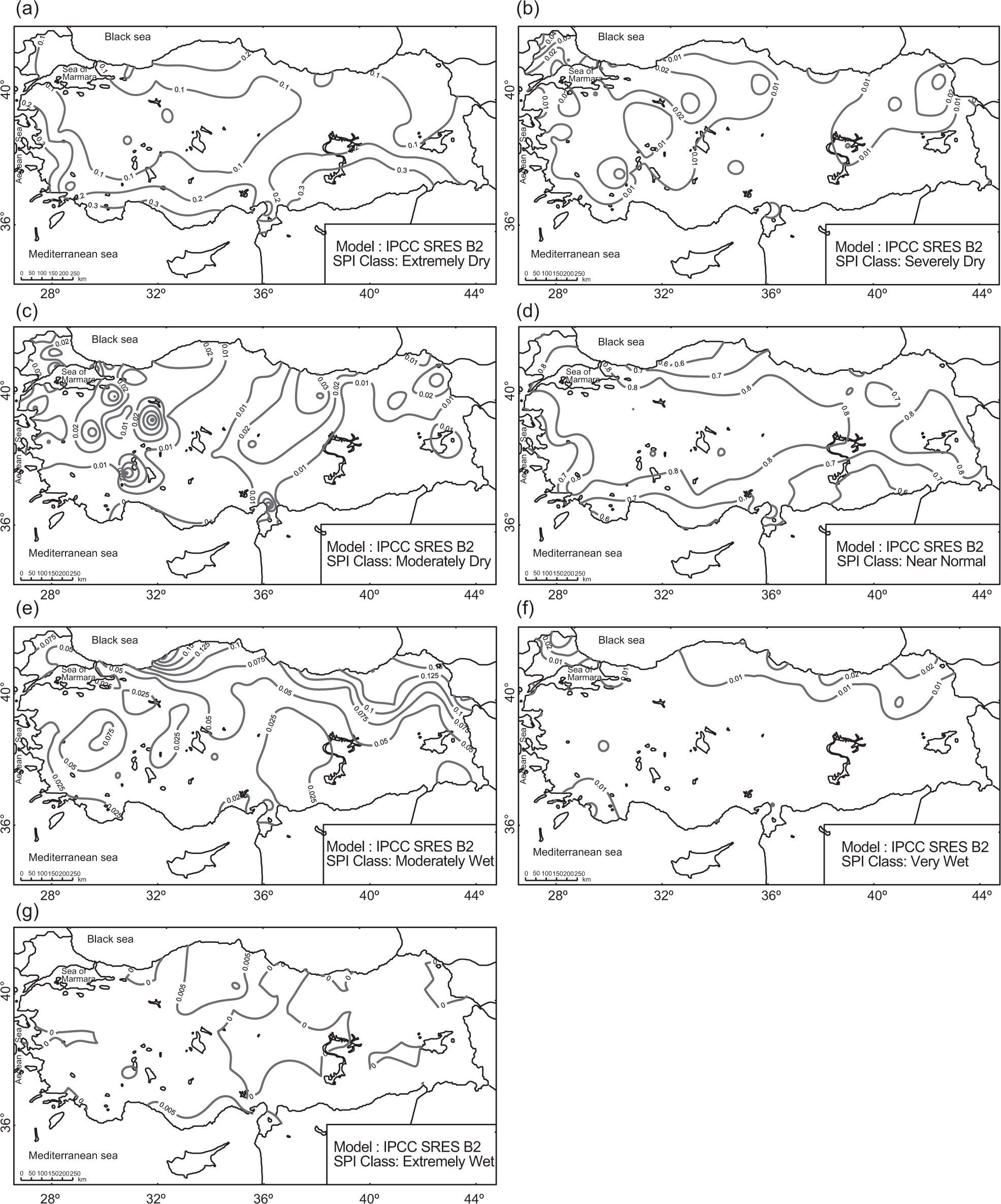
3

Discussion and results

The performance and results of the suggested downscaling models are compared with SPI values obtained from the observed precipitation series by covering each of the dry and wet event classes for the 12-month SPIs calculated over Turkey. The performance of the suggested downscaling model based on the values of PC is given in Figure 3. As shown in this figure, seven drought classes are first transformed into three major drought classes; for example, “extremely wet, very wet and moderately wet” drought classes are merged and renamed as above normal. Likewise, “extremely dry, severely dry and moderately dry” classes are merged, and renamed as below normal. The spatial patterns of the long-term (climatological) occurrence probabilities are shown in Figure 4 and those extracted from the downscaling model are given in Figures 5 through 7.

Fig. 3.

Spatial distribution of the proportion of correct (PC) prediction values obtained by comparing the downscaling-model of the IPCC control scenario and observations. For more information, please refer to the text.

Fig. 4.

Spatial distribution of the long-term probabilities of SPI values obtained by using the observed monthly precipitation totals.

Fig. 5.

Spatial distribution of the long-term probabilities of SPIs obtained from the suggested logistic downscaling model based on the control scenario.

The level of long-term probabilities of downscaled drought classes generally shows a zonal gradient from the rainfall regimes of the Mediterranean to the Black Sea basins. Maximum probabilities of a dry class regime are found near the border of Syria-Turkey, where the warmest and driest land of Turkey is located (Tatli and Türkeş, 2011). The results of downscaled drought classes and their relationships with the synoptic-climatological situations are discussed in the following sub-sections.

3.1

Extremely dry conditions and projections

According to the extremely dry conditions obtained from the observed rainfall totals, the long-term (climatological) probabilities display a zonal-pattern gradient from the Mediterranean to the Black Sea basins. Maximum probabilities are found in the warm and dry southern parts of the continental Mediterranean (CMED) rainfall regions, in which the areas of the Turkish-Syrian border are located (Fig. 4a).

According to the logistic model constructed by the predictors from the control climate simulations (Fig. 5a), the probabilities of extremely dry conditions will increase in approximately 10% of the cases. These downscaling results for the Mediterranean (MED) and CMED rainfall regions agree well with the observations, as seen in Figure 4a. The probabilities of extremely dry conditions obtained from the observed values are around 1%, in spite of the results of the logistic model based on the control scenario indicate around 20% in the country's sub-regions of the western Black Sea basin (Fig. 5a). Additionally, the results show that the probabilities do not change sharply in the regions of the Marmara Transition (MRT) and the Mediterranean Transition (MEDT).

The probability patterns of downscaling models based on the IPCC SRESS A2 and B2 (Figs. 6 and 7, respectively) resemble each other. Furthermore, the estimated probabilities of extremely dry conditions in the Black Sea (BLS) region seem similar to the probabilities obtained by the downscaling-model based on the control simulations. However, the estimated probabilities of extremely dry conditions in the MED and CMED regions are 10% higher than the values obtained from the control simulation (Figs. 6a and 7a). The estimated probabilities for the eastern sub-regions of the BLS and northeastern Anatolia are similar in magnitude and spatial distribution.

Fig. 6.

Spatial distribution of the long-term probabilities of SPIs of the downscaling model based on the IPCC SRES A2.

Fig. 7.

Spatial distribution of the long-term probabilities of SPIs of the downscaling model based on the IPCC SRES B2.

3.2

Severely dry conditions and projections

Although the observed probabilities of severely dry conditions are relatively low (about 2%), they increase from the MED and CMED to the northern part of the country. Furthermore, the probability values reach 4% in the eastern BLS and northern Anatolia sub-regions of the Anatolian Peninsula, even though the probability values of extremely dry conditions are low (Fig. 4b).

The logistic control model produces somewhat different patterns of probabilities when compared to observations, except for the MRT rainfall region (Fig. 5b). Conversely, results of the logistic model based on the IPCC SRES A2 and B2 scenarios show patterns similar to the observed probabilities obtained from the severely dry scenario (Figs. 6b and 7b).

The probabilities of a severely dry scenario obtained from the observations have a 2-4% interval, with some exceptions as seen in the MED and CMED rainfall regions (Fig. 4b), where the probabilities of a severely dry scenario show a negative trend. The results of the logistic model based on the IPCC SRES A2 have somewhat higher probabilities than those obtained from the IPCC SRES B2 (Figs. 6b and 7b).

3.3

Moderately dry conditions and projections

The probabilities of having 12-month SPI values of moderately dry class increase in rainfall regions MED and BLS, where the probabilities observed are about 4-5% (Fig. 4c). The probabilities observed in the western and eastern BLS sub-regions vary from 7 to 9%, respectively.

The results of the logistic model based on the control scenario show that the pattern of higher probabilities has detailed spatial features, though some small probabilities are also observed (Fig. 5c). According to the logistic model with predictors from the IPCC SRES A2 and B2 scenarios, the patterns of probabilities of moderately dry conditions have a positive trend (Figs. 6c and 7c).

3.4

Normal conditions and projections

The 12-month SPI values from observations in Turkey are mostly in the near normal class, since the climatological probabilities are generally changing from 60 to 70% (Fig. 4d). As a result, this class could be referred to as reference class, which has a probability of being observed at least in 60% of the meteorological stations.

The probabilities of the logistic model based on the control scenario are in the near normal class, partially decreasing in the BLS basin. However, the patterns show that probabilities increase in the regions of the MRT and continental eastern Anatolia (CEAN) (Fig. 5d), where the probabilities observed are around 80% or more.

The results obtained from the logistic model based on the IPCC SRES A2 and B2 scenarios are significantly similar, and related to the results obtained from the control scenario (Figs. 6d and 7d). According to the downscaling results, it can be expected that the near normal class probability will increase about 10% as compared to its present values.

3.5

Moderately wet conditions and projections

In Figure 4e, the probabilities of moderately wet conditions have a negative gradient from the sub-rainfall regions of MED, MEDT and CMED to the BLS basin. Some of the minimum probabilities are observed on the coasts of the BLS basin, whereas the maximum values are only obtained in the CMED regions. The sub-regions of western and eastern BLS and CEAN are exceptions, since the logistic model based on the control scenario simulates very small probabilities of moderately wet conditions (Fig. 6e). The maximum probabilities are generally observed in the rainfall regimes of the MED and CMED, whereas the probabilities of the logistic model based on the control scenario decrease here and increase in the eastern BLS basin and north-eastern Anatolia.

The results of the logistic model based on the IPCC SRES A2 and B2 show similarities with the control scenario (Figs. 6e and 7e). These similarities may be seen in the probability patterns of moderately wet conditions, which decrease in the southern and western regions of the country.

Accordingly, it can be expected that the probabilities of moderately wet conditions will increase in the BLS basin and in the northeastern continental regions of the country. Furthermore, the maximum probabilities of moderately wet conditions are found in the eastern BLS basin for the logistic model based on the IPCC SRES A2, and in northeastern Anatolia for the model based on the IPCC SRES B2.

3.6

Very wet conditions and projections

The probabilities of the very wet class range from 3% in the CEAN region to 4% in the Aegean, Mediterranean and Black Sea regions (Fig. 4f). The maximum probabilities of very wet conditions are about 5% in northeastern Anatolia. The probabilities are smaller for the logistic model based on the control scenario (Fig. 5f). The probabilities in the Black Sea basin, middle-northern parts of the CCAN and northeastern Anatolia are nearly 1% and close to 0% for the rest of the country.

The results obtained from logistic models based on the IPCC SRES A2 and B2 are consistent with the control simulations, in which the probabilities of very wet conditions are expected to be below 1% in the majority of the country (Figs. 6f and 7f). Both models show that the maximum probabilities are seen in parts of the northern Thrace, and in the sub-regions of the eastern and middle Black sea basin.

3.7

Extremely wet conditions and projections

The probabilities of extremely wet conditions from observations are small in magnitude and vary from 0 to 2%. Maximum probabilities are evident over some limited areas of the eastern Black Sea basin, northeastern Anatolia and western Mediterranean coasts (Fig. 4g). According to the results of the logistic model based on the control scenario, except in the sub-regions of the western Black Sea basin, the probabilities are very small (Fig. 5g). In addition, the results of logistic models based on the IPCC SRES A2 and B2 agree with the results of the logistic model based on the control scenario, indicating that in the future, probabilities of extremely wet conditions will decrease in the entire country (Figs. 6g and 7g).

4

Conclusions

Climate change impacts on future weather and climate are traditionally evaluated by running general circulation models in the various socio-economic scenarios. However, simulations of the GCMs at coarse grids may yield large uncertainties in climate variables. For instance, changes in global climate give rise to large uncertainties when determining its impacts on regional precipitation regimes, such as drought and wet conditions and their variability (Tatli, 2014). Downscaling techniques can provide an answer to these problems.

At country level, downscaling drought and wet conditions is a very important challenge, especially in management plans of water resources, energy, natural disasters, agriculture and forestry. Drought conditions often cause serious damage and negatively affect various socio-economical activities. For example, they can lead to decreased crop yields and reduced fresh water resources.

Traditionally, downscaled precipitation is used to estimate the SPI. However, it is easier to downscale the drought classes than precipitation itself. In addition, one may employ much more sophisticated downscaling processes for selecting the appropriate predictors (e.g., Tatli et al., 2004; Pryor et al., 2005; Tatli, 2007, 2013).

Since the downscaling model based on logistic regression suggested in this study uses the large-scale predictors directly from the GCMs, it should be regarded as model output statistics.

In this study, the risks of drought and extreme wet conditions under climate change scenarios are assessed by means of statistical downscaling. According to the logistic models applied, the results are more sensitive to the predictors obtained from large-scale GCMs, while boundary conditions coming from these are sensitive, as in the dynamical-downscaling procedure. The applied logistic models produce satisfactory statistical results when compared with observations. The probabilistic patterns of the results are statistically acceptable, since they capture the main features of the local-scale climate. Since the main goal of downscaling is to determine the effects of large-scale climatic changes on the local-scale variables, the proposed model based on logistic regression produces acceptable statistical results.

Additionally, the results reveal that the downscaled-probabilities of very wet and extremely wet conditions will decrease in the future for almost all three scenarios. However, there are some exceptions. In the future, the probabilities of near-normal conditions will decrease in the BLS basin and relatively increase in rainfall regions of the MRT and CEAN.

Acknowledgments

The author acknowledges the anonymous referees for their valuable and constructive suggestions.