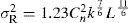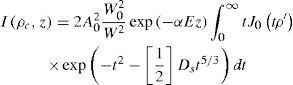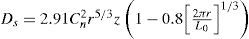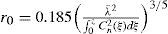Experimental verification of the turbulent effects on laser beam propagation in space

Resumen

En este trabajo se modificó un diseño experimental preexistente para clasificar íntegramente los efectos térmicos de un rayo láser que se propaga en el aire. Las mejoras incorporadas al diseño previo incluyeron un láser más potente, un sistema de formación de turbulencias de alta precisión, un sensor de presión integrado, y una plataforma para ajustar la altura entre el rayo láser y el modelo de turbulencia. Este diseño no sólo puede reproducir resultados previos con exactitud, sino que además permitió la medición exitosa de nuevos datos sobre la intensidad de la turbulencia Cn2, la varianza de Rytov (cintilación) y el diámetro de coherencia (parámetro de Fried). Los interferogramas resultantes se analizaron utilizando transformadas rápidas de Fourier. Los resultados confirman, dentro del régimen de Kolmogorov, que las fluctuaciones en fase e intensidad se incrementan en relación con la temperatura. La región turbulenta mostró perturbaciones muy intensas, en el rango de 1.1 × 10^-12 m^-2/3 a 2.7 × 10^-12 m^-2/3. A pesar de la intensidad de la turbulencia, con relación a la cintilación se demostró algo diferente, ya que la condición para un entorno de turbulencia débil se determinó en el laboratorio y se esperaba un bajo índice de cintilación. Esto es resultado de las distancias de propagación relativamente cortas obtenidas en el laboratorio. En la atmósfera abierta las trayectorias cubren grandes distancias y, para determinar los efectos de la turbulencia, el modelo debe generar turbulencias de mayor intensidad. De esta manera, el modelo demostró su capacidad para cuantificar y determinar plenamente los efectos térmicos de la turbulencia en un rayo láser en propagación.

Abstract

In this work, we have modified an existing experimental setup to fully classify the thermal effects on a laser beam propagating in air. Improvements made to the setup include a new, more powerful laser, a precision designed turbulence delivery system, an imbedded pressure sensor, and a platform for height adjustability between the laser beam and the turbulence model. The setup was not only able to reproduce previous results exactly but also allowed new data for the turbulence strength Cn2, the Rytov variance (scintillation) and the coherence diameter (Fried’s parameter) to be successfully measured. Analysis of the produced interferograms has been discussed using fast Fourier transforms. The results confirm, within the Kolmogorov regime, that phase and intensity fluctuations increase relative to temperature. The turbulent region exhibited very strong disturbances, in the range of 1.1 × 10^-12 m^-2/3 to 2.7 × 10^-12 m^-2/3. In spite of the strong turbulence strength, scintillation proved otherwise, since the condition for a weak turbulence environment was determined in the laboratory and a low scintillation index was to be expected. This is as a result of the relatively short propagation distances achieved in the laboratory. In the open atmosphere, path lengths extend over vast distances and in order for turbulent effects to be realized, the turbulence model must generate stronger turbulence. The model was, therefore, able to demonstrate its ability to fully quantify and determine the thermal turbulence effects on a propagating laser beam.

1

Introduction

Theories relating to atmospheric turbulence have been studied over many decades in order to better understand the impact of turbulence on the propagation of a laser beam through the atmosphere (Tatarskii, 1961). Turbulence can be described as the random mixing of air particles in the atmosphere due to either rapid or small-scale spatial and temporal refractive index fluctuations in temperature (Ishimaru, 1981; Shaik, 1988). Although slight variations in temperature can cause changes in the refractive index of air (of the order 0.1-1.0 K), the accumulative effect of such inhomogeneities expanding over vast distances poses significant challenges for laser beam propagation (Baak, 1969; Prod’homme, 1969). Research has shown that refractive index fluctuations of the atmosphere are significant near the surface of the earth and negligible at higher altitudes (Andrews and Phillips, 1988). These refractive index fluctuations cause random phase perturbations of the laser beam that can lead to beam distortion (Chatterjee and Fathi, 2014). In addition, laser propagation through turbulent media can result in scintillation (Federico etal., 2004), beam wander (Berman etal., 2007) and beam spreading (Weichel, 1990). The extent to which these factors affect the beam depend largely on the varying nature of the turbulent eddies that exist at several altitudes. Knowledge of these effects, attained over the years, has been used notably in the domains of military (Titterton, 2005), radar (Mead, 1990), remote sensing (Shin, 1989), satellite communications (Ojo et al., 2008) and medical diagnostics (Ibrahim, 2007; Lonappen, 2007). This paper presents new modifications to a model used by Ndlovu (2013), as it has proven to be robust, cost efficient and stable in detecting and fully quantifying the effects of thermal turbulence on laser beam propagation in air. The previous method used a cigarette lighter as a turbulence source but this led to non-uniform heat distribution over a very small area (Ndlovu, 2013). In this work we have thus employed an automated heating plate for the turbulence re-creation. The design of the turbulence generator incorporates an aluminum panel with multiple high-powered resistors arranged on the underside to provide consistent heating above. In addition, a pressure sensor was positioned within the turbulent region to determine any phase fluctuations resulting from a change in pressure. The high sensitivity of the device allowed only slight variations in pressure change to be detected between the turbulent and non-turbulent regions. The primary light source used in this work was a green continuous wave He-Ne 532 nm laser. To determine the effect of thermal turbulence on laser beam propagation, a complete analysis of the produced interferograms at various temperatures has been discussed using image analysis software. Furthermore, the turbulence strength Cn2, the Rytov variance (scintillation) and the coherence diameter (Fried’s parameter) have been determined in the laboratory and shown to coincide well with published values.

2

Theory

Random fluctuations in the refractive index of the atmosphere alter the propagation pathway of light beams, which in turn effects their initial phase fronts. Once light propagates through a turbulent atmosphere, the phase fronts become distorted and experience random changes in the beam direction (beam wander) as well as random intensity fluctuations (scintillation) (Berman et al., 2007). Scintillation can be classified as the fluctuations experienced in the received irradiance when light beams propagate through a turbulent atmosphere (Churnside and Lataitis, 1990). Measuring certain observations in the laboratory allows the scintillation to be calculated from (Andrews and Phillips, 1988)

where Cn2 is the refractive index structure coefficient, k is the wavenumber and L is the propagation path length. The wavelength and path length are measured in the laboratory and Cn2 is thereafter inferred.

Propagation of the beam through turbulent conditions has shown that it undergoes a loss of coherence, focus and beam spread (Chernov, 1967; Esposito, 1967). The extent to which scintillation and beam wander occur depends largely on the combination of temperature, wind velocity and convection factors (Titterton, 1973). The key to obtaining information about the way in which beams are affected by turbulence is to determine the refractive index structure coefficient Cn2 given by (Andrews and Phillips, 1988)

with

where p is the atmospheric pressure in millibars and < > represents the ensemble average. CT2 is a measurable quantity defined by temperature differences T₁ and T₂, between two reference points separated by a distance r. Cn2 is a parameter which changes as a function of altitude and alters the behavior of the aberrations. The following characterizes the optical energy of the turbulence and measures the atmospheric turbulence contributions for a wave that propagates through it. As Cn2 increases, so does the effect of the aberration. Typically, Cn2 decreases in relation to altitude (Andrews and Phillips, 1988). The refractive index structure coefficient alone provides adequate information about the turbulent region and typically ranges from 10^–17 m^–2/3 or less for weak turbulences to 10^–13 m^–2/3 or more for strong turbulence (Andrews and Phillips, 1988; Weichel, 1990).

Advances made by Strohbehm (1978) have shown methods of determining the phase structure function D_s, beam size W and the coherent intensity of the beam. These expressions are useful for modeling the intensity of the laser beam propagating through an inhomogeneous medium and incident on a distant target. As the laser beam propagates through turbulent media, there is a redistribution of its intensity, which may be determined according to Strohbehm (1978), as

where A₀ is the uniform amplitude of the plane laser wave, W₀ the Gaussian beam size, J₀ the first-order Bessel function, ρ the transverse distance from the beam, W the beam size at z, and where z lies within the domain

Particular emphasis is placed on the phase structure function as it represents a measure of the phase correlation between two points in a plane traversing perpendicularly to the direction of propagation. The phase structure function D_s and atmospheric coherence diameter r₀ are given by Strohbehm (1978) and Magee (1993),

and

with r being the separation between the inner and outer scales, z the propagation path length, and λ¯ the wavelength of the laser beam. The coherence diameter is a measure of the quality of the optical signal through the atmosphere (Magee, 1993). Typical values of r₀ at a good observatory range between 5 to 20 cm and depend largely on the visibility conditions. The highly stochastic nature of the atmosphere determines the seeing strength (Magee, 1993). At high altitude, turbulent effects are relatively weak, which results in unaffected optical imaging effects. Such conditions infer good visibility conditions. However, closer to the ground, visibility conditions worsen and can be attributed to weather conditions, as well as the highly turbulent atmosphere.

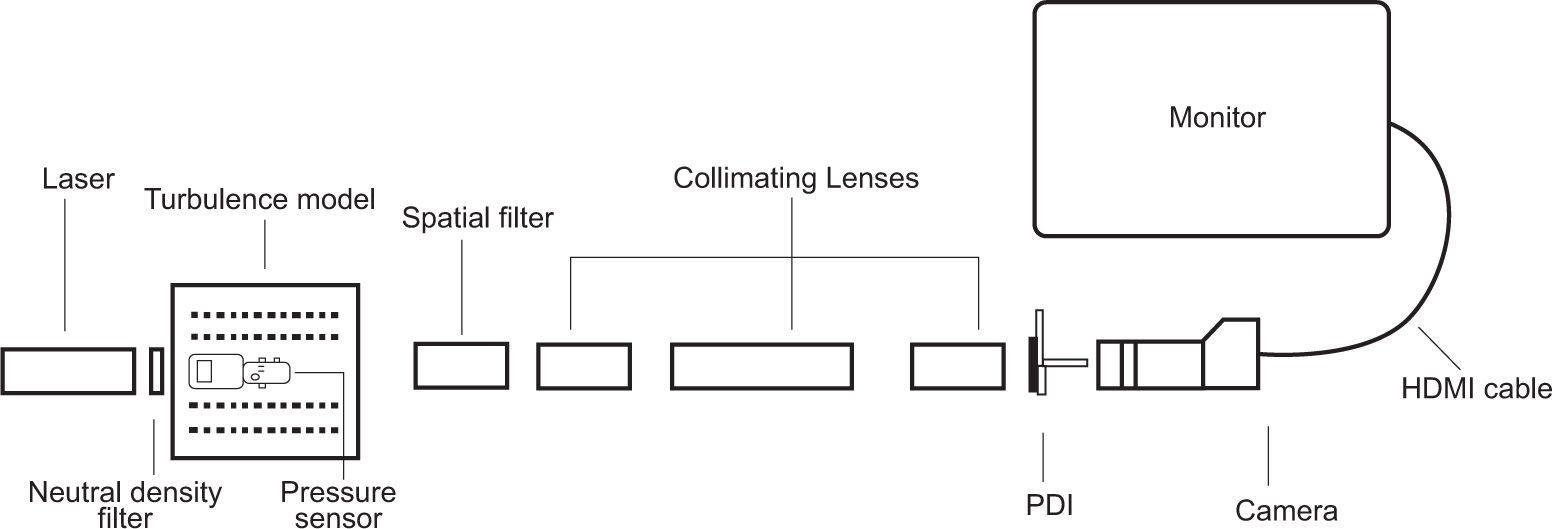
3

Description of the components

We consider a laser beam propagating through an inhomogeneous medium. The laser beam propagates through the following optical components: a microscope objective lens, the turbulence model and pressure sensor, a series of collimating lenses, a spatial filter, a point-diffraction interferometer and finally is captured on a camera. The camera acts as a detector to take photographs of the interferograms and display the interference pattern on a monitor. The entire setup is mounted on height-adjustable rails to vary the separation between the laser beam and the turbulence generator. The lowest height setting has been used in this work, corresponding to a separation of 28 mm between the laser beam and the turbulence source. Figure 1 presents a schematic diagram of the apparatus showing the complete optical train.

Fig. 1.

Two-dimensional side view of the complete optical train with height-adjustable rails.

3.1

The laboratory, granite table and optical bench

The experiment was assembled on a 1.2 × 2.5 m granite tabletop which presented a stable platform that protected the components from bumps and knocks as well as internal and external vibrations caused by the local environment. The experiment took place in a 5 × 5 m dark room and was structurally closed off from the outside environment as there were no windows or ventilation outlets.

3.2

The dovetail rail

A 91.44 cm Edmund dovetail v-block rail (model No. 54-402) was used for the main receiver train. The rail was divided into three sections to allow better alignment of the optical components and, more importantly, to provide space for the inclusion of the turbulence model. A 60.96 cm rail was used to hold the collimating lenses and two 15.24 cm sections, one for the light source assembly and the other for the camera assembly. All the rails were supported by and screwed down onto five 150 × 150 mm bench plates manufactured by Edmund (model No. 53936). These bench plates had a 13 mm thickness. Each bench plate was drilled with M6 holes arrayed on a pitch of 25 mm. This helped in aligning the optical components with the light source.

3.3

The light source and neutral density filter

A 5 mW laser with a 532 nm wavelength was mounted in conjunction with a microscope objective and collimating lens of 160 mm focal length. The microscope objective reduces the beam diameter to 1/20 of its original size. The collimating lens adjusts the beam diameter to 25 mm. The light source assembly consisted of a laser diode, a plastic aspheric collimator and a holographic diffuser. The plastic collimator and the holographic diffuser were mounted in separate 25 mm T-mount cells. The light source assembly was mounted on a micro-optical bench, which was glued onto a 6” dovetail rail to avoid movements and vibrations from the surroundings. A 3.0 reflective neutral density filter of 50 × 50 mm optical density with 1.5 mm thickness manufactured by Edmund optics (model No. 46126) was placed just in front of the light source. This reflective filter helped in reducing the laser beam intensity and eliminated stray-light artifacts so that clear and bright interferograms were produced for analysis. The automated turbulence model was introduced within a 200 mm gap between the light source assembly and the main receiver train.

3.4

The collimators

Three collimating lenses of 200 mm focal length were housed inside a 121.5 mm-long collimator holders and placed on a 60.96 cm dovetail rail. The collimating lenses were moved back and forth that the laser beam was focused, and this also served the purpose of reducing the effects of beam wander and beam spreading. The focus was adjusted by noting the size of the beam formed on the point-diffraction interferometer (PDI) plate. A focused beam is necessary as the PDI plate presents on its surface a point discontinuity in the form of a pinhole through which the laser beam enters.

3.5

The point-diffraction interferometer

A PDI manufactured by Astro Electronics was used in this work. It consisted of 55 pinholes, which were distributed on an array of 1 mm pitches. The PDI was mounted on an Edmund XYZ stage together with the carrier cell. There were three adjustments on the XYZ stage that were used to locate the laser beam so that it could pass through the PDI pinhole. The PDI was mounted between the third collimator and the camera assembly so that the beam could pass through the pinhole and form interferograms that would be detected by the camera.

3.6

The camera

While it may be necessary to use a monochrome video camera with a substantial frame-rate, a much more feasible alternative is to use an ordinary digital single lens reflex (DSLR) camera such as the Nikon D3100. The DSLR camera features a live view mode with a very high resolution, which was necessary for this work. An external power supply was added since the Nikon batteries run down fairly quick. The camera was mounted on a 15.24 cm dovetail rail and held down by a strap-down bar. It was modified to accommodate an Edmund lens holder, which in turn housed a double lens of 150 mm focal length.

3.7

The display monitor

A Samsung 23 inch high definition (HD) monitor was used to display the live video feed since it allowed a direct HD connection from the Nikon D3100. An HD monitor is necessary since the displays are crisp and allow easier visual inspection of the produced interferograms.

3.8

The height adjustable rails

The design incorporated two 1 cm thick aluminum sheets with lengths of 30 and 170 cm. Along either side of the sheets vertical strut bars were welded, each having a height of 32 cm. Holes were drilled along the height of the bars, spaced at 5 cm intervals. The aluminum sheets were also tapped with threads, allowing the optical components to be fastened down. The manufacture of the design was precision engineered in house by the mechanical instrument workshop (MIW at UKZN). Initial experimental runs were conducted at the lowest setting, which corresponds to no height adjustment.

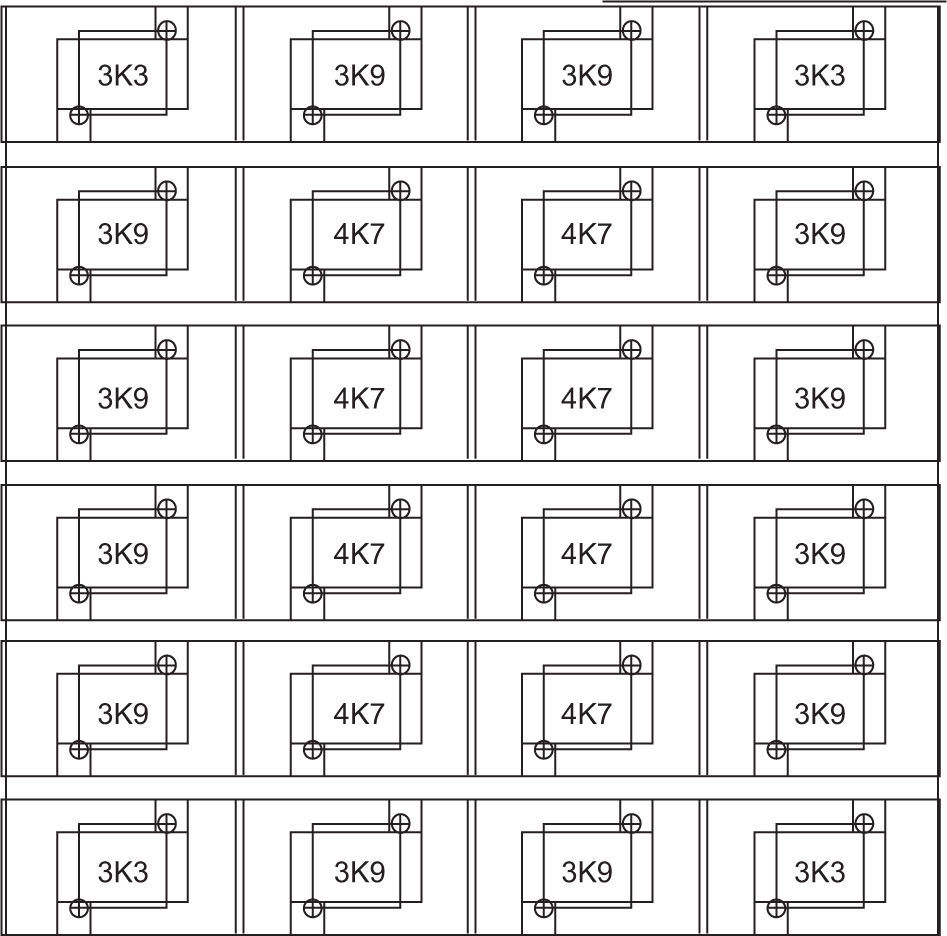
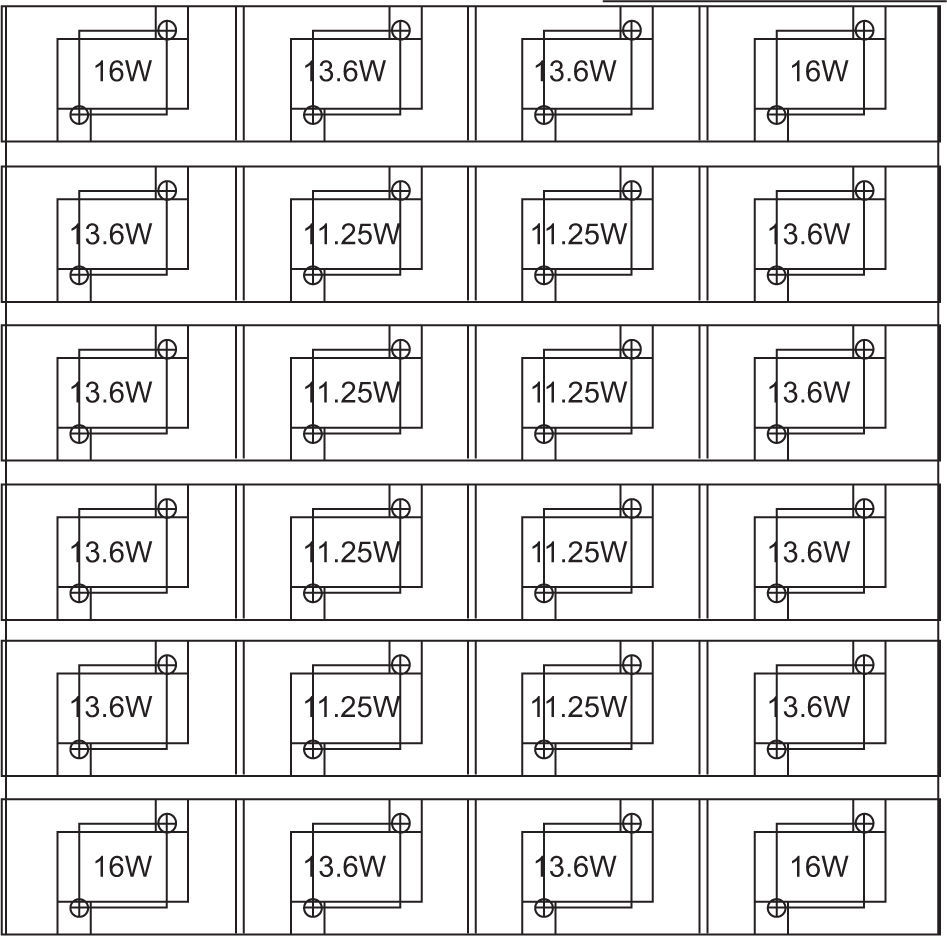
3.9

The turbulence model and thermocouple

Turbulence was created by a specially manufactured 20 × 20 × 1 cm heated aluminum panel. Arranged on the underside of the panel was an array of high-powered resistors that were fixed into position using steel nuts and bolts. The electronics department carefully constructed an arrangement of resistors such that consistent heating existed above the panel. This was achieved using a surface temperature probe to measure the temperature at different points on the panel, and thereafter placing appropriate resistors to accommodate their position. The aluminum panel was snugly placed in a case on a bed of fire blanket, which insulated it from external factors. The resistors varied in their resistances, according to Figure 2 (which presents resistance values in ohms, Ω), with the corresponding power values represented in Figure 3. Both figures explicitly show the arrangement of the resistors on the panel.

Fig. 2.

Schematic resistance diagram of the turbulence panel.

Fig. 3.

Schematic power diagram of the turbulence panel.

The resistances shown in Figure 2 are written in standard form, where 3 K3 = 3300 Ω, etc. So, naturally, according to P=V2R, a smaller resistance corresponds to a larger power. Figure 3 presents the power values associated with the resistors in watts (W). Intuitively, the largest powered resistors are on the corners since they are exposed on two of their four sides to natural elements. Thus, more power is needed to maintain the heat on the corners as opposed to the center of the panel, namely 29.7% more power.

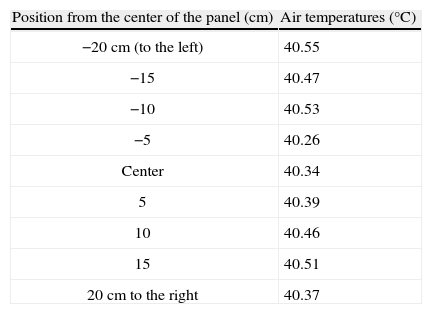
The temperature range was controlled between 0 and 180 °C using a proportional integral derivative (PID) controller. The device served the purpose of setting, monitoring and controlling the temperature of the panel. Temperature measurements were taken using a sensitive J-type thermocouple with a two-decimal precision. Table I shows the results obtained from the experiment for temperature vs. the position from the center of the panel, with the center point represented by 0 cm. Negative values represent a position to the left of the center and positive values represent a position to the right. The temperature of the PID was set to a value of 100 °C, which corresponds to the temperature of the panel as determined by using a surface temperature probe. Sufficient time was given for the air temperature to stabilize before readings were taken.

Table I.

Relation between air temperature and the position from the center of the panel.

Position from the center of the panel (cm)	Air temperatures (°C)
−20 cm (to the left)	40.55
−15	40.47
−10	40.53
−5	40.26
Center	40.34
5	40.39
10	40.46
15	40.51
20 cm to the right	40.37

Clearly from Figure 4, the heated panel is successful in maintaining a uniform heat distribution along the surface of the panel with a standard deviation of 9.7 × 10^–2 °C. The turbulence generated by the model was, therefore, effective in modeling an inhomogeneous and isotropic environment within an area of 0.04 m².

Fig. 4.

Temperature of the turbulence model plate at various positions.

4

Experimental procedure

4.1

Layout

A schematic layout of the design with the turbulence model included is presented in Figure 5.

Fig. 5.

Two-dimensional top view of the complete optical train.

As described in section 3.2, the Edmund optics rail was divided into three sections. The laser was mounted on the first 15.24 cm rail. The longer 60.96 cm rail supported the three collimators and the PDI. The second 15.24 cm rail supported the camera.

A crucial step in the setup of the apparatus was to reduce dust in and around the laboratory. Minimal levels of dust are extremely detrimental to the produced interferograms, as light is scattered by the dust particles leading to stray light artifacts falling upon the detectors. This in turn causes inconsistent intensity profiles, which cannot be characterized. To ensure that the optical components were free from dust, a commercial dust cleaner (Dust-Off) and methanol were periodically used to clean the surfaces of the optical lenses with lens tissue. In addition, the apparatus was always covered when not in use.

4.2

Description

The turbulence model was used to generate a uniformly heated panel that could be varied by the user. The heat emanating from the panel randomly influences the refractive index of air, which results in random fluctuations of the phase fronts of the laser beam. A wide range of temperatures could be tested as the model used a sophisticated PID algorithm control unit. Further measures were taken for precision purposes: a surface temperature probe was used to verify air temperature just above the panel.

Modification of the turbulence model involved the inclusion of a pressure sensor, which monitored the pressure in and out of the turbulent region. The differential of pressures existing between the regions was measured on the device’s most sensitive setting, i.e. 0-100 Pa.

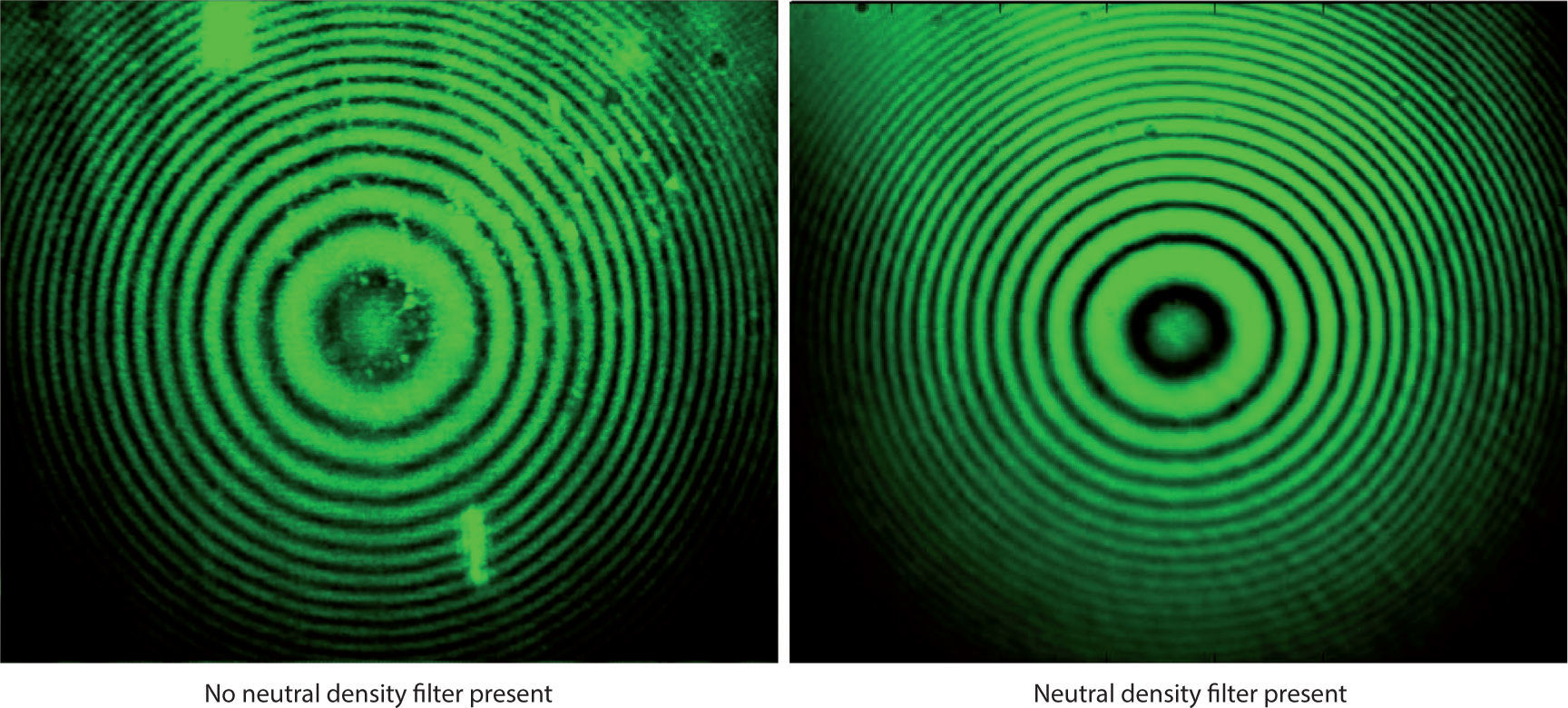
A reflective 50 × 50 mm 2.5 OD neutral density filter of 2.0 mm thickness was positioned immediately after the laser, since it served the purpose of reducing any stray light in the produced interferograms. Some filters considerably reduced the intensity of the light falling upon the PDI, hence numerous tests were conducted to determine the most effective filter whilst ensuring bright, clear interferograms that could be characterized. Examples of interferograms are presented in Figure 6. One of them (in the left panel) does not have an neutral density (ND) filter, while the other one (in the right panel) has it. The interferogram to the left shows random light artifacts that are not filtered out by the spatial filter and collimators. The interferogram to the right used the abovementioned ND filter to produce a flawless image, clearly depicting a Gaussian form profile for an unperturbed laser beam. A more descriptive discussion of the profile is provided in the results section. With the correct ND filter chosen and in place, the proceeding collimators were moved back and forth to yield a focused beam at the PDI pinhole. By doing so, a Gaussian form intensity profile was produced which provided stable and clear interferograms. At all times, alignment was perilous and utmost care was taken in ensuring a centralized beam. The final component in the optical train was the DSRL camera, which was positioned to receive the laser beam at the center of its aperture.

Fig. 6.

Comparison of a non-present ND filter with a present ND filter.

An HDMI cable transferred the captured image onto a 23-inch HD screen. Interferograms were then used to study the effect of thermal turbulence on a propagating laser beam. This was done by extracting the wavefront information from the phase shifts that formed on the interferograms due to thermal perturbations on the propagating laser beam. The wavefronts were analyzed using ImageJ and Matlab. A description of the findings will be discussed later.

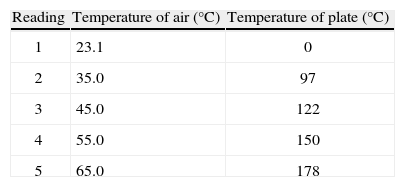
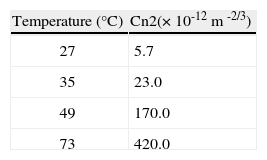
5

Results, analysis and discussion

Data analysis began at a room temperature of 23.1 °C. Temperature of the air was measured using a thermocouple positioned in close proximity to the laser beam. However, the value of air temperature did not correlate with the apparent temperature of the heated panel. This could be due to heat being transferred only through convection. Table II shows the temperature of the heated aluminum panel against the temperature of the air 28 mm above the heated panel.

Table II.

Comparison between actual air temperature and temperature of the heated panel.

Reading	Temperature of air (°C)	Temperature of plate (°C)
1	23.1	0
2	35.0	97
3	45.0	122
4	55.0	150
5	65.0	178

Numerous experiments were performed over a number of days and the consistency of the interferograms was analyzed. The averaged results are reflected on the following pages, split into five categories. Five interferograms are depicted on the subsequent pages. Section 5.1, corresponding to the first reading, includes the data for the unperturbed laser beam at a room temperature of 23.1 °C (Figure 7). Sections 5.2 to 5.5 (corresponding to readings 2 to 5) present the data for the perturbed laser beam, which was subjected to thermal turbulence of 35, 45, 55, and 65 °C, respectively.

Fig. 7.

Unperturbed interference pattern.

5.1

Reading 1 (at 23.1 °C)

To determine the extent to which the thermal turbulence affected the propagating laser beam, it was necessary to compare readings 2-5 with reading 1. A fast Fourier transform (FFT) was used, since it resolves an image into its magnitude and phase domains. The magnitude is useful for image processing since all the frequencies that compose the image are specified. Due to the fact that phase images do not provide sufficient new information to describe the image any further, we will focus on the frequency domain. In Figure 8, the image is formed on a two-dimensional plane in polar representation and contains various components whose magnitudes decrease with larger frequencies. The central bright spot is known as the zero frequency zone or direct current zone and represents the average color value of the entire image. Additionally, the image does not contain imaginary components, thus the magnitude at the center has a zero phase resulting in a grey spot. The large concentration around the central point indicates a lower spatial frequency. Numerous adjustments can be made to the transformed image to either improve the focus or decrease blurriness, which can be achieved by applying a low pass filter to preserve the low frequency regions, or a high pass filter to preserve the sharpness and defined edges. Intermittent filters known as band pass filters can be applied. In subsequent readings we will compare the FFT’s to Figure 8 by image subtraction. If the subtraction yields a completely grey image it is implied that the two images coincide completely, hence there is no change in beam position or phase. Figure 9 shows that the intensity profile of an unperturbed beam resembles that of the laser Gaussian laser beam (i.e., no change in intensity).

Fig. 8.

Magnitude of the FFT.

Fig. 9.

Intensity profile of the unperturbed interferogram.

5.2

Reading 2 (at 35 °C)

Reading 2 was taken at a measured air temperature of 35 °C. Within the turbulent region, the laser beam is exposed to a temperature increase of 11.9 °C above room temperature. The interferogram in Figure 10 does not display signs of distortion or defocus but it does have some signs of image blurring. The large localization around the centroid of Figure 11 describes a larger lower spatial frequency distribution. The intensity distribution in Figure 12 implies some energy redistribution occurring between 50 and 150 units, as well as between 300 and 400 units. In the analysis ofFigure 13, the image subtraction describes an almost completely greyed-out result, although there are black specs scattered randomly over the image. The image subtraction data shows a vague outline of the centroid in black Figure 13. According to Banish et al. (1990) this can be attributed to minor image blurring.

Fig. 10.

Perturbed interference partera

Fig. 11.

Magnitude of the FFT.

Fig. 12.

Intensity profile at 35 °C.

Fig. 13.

Image subtraction of reading 2 from 1.

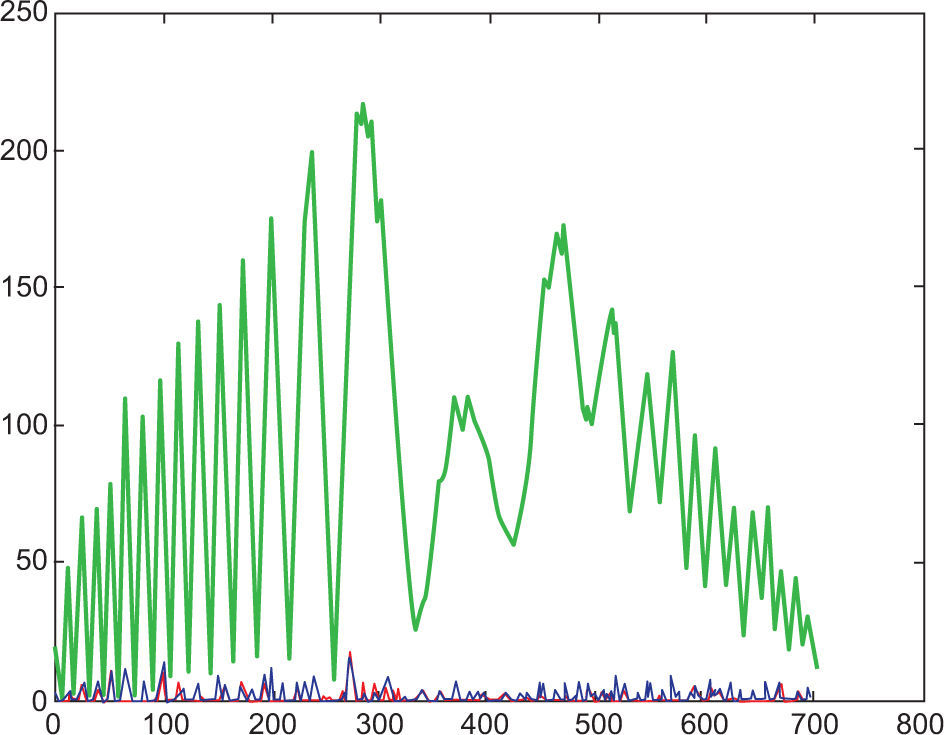
5.3

Reading 3 (at 45 °C)

Reading 3 was conducted at 45 °C, 21.9 °C above room temperature within the turbulent region. The interferogram in Figure 14 shows signs of distortion, defocus and blurring. The intensity profile still assumes a Gaussian profile in Figure 15 with minor energy redistribution between 100 and 150 units. The lower spatial frequencies in Figure 16 are beginning to darken, which indicates that phase shifts are becoming more distinct with the increasing temperature. The darker line running down Figure 17 shows a redistribution of the spatial domain in the interferogram, which corresponds to both image blur and image defocus. Banish et al. (1990) describe a similar scenario, which has been inferred in this work.

Fig. 14.

Perturbed interference pattern.

Fig. 15.

Intensity profile at 45 °C.

Fig. 16.

Magnitude of the FFT.

Fig. 17.

Image subtraction of reading 3 from 1.

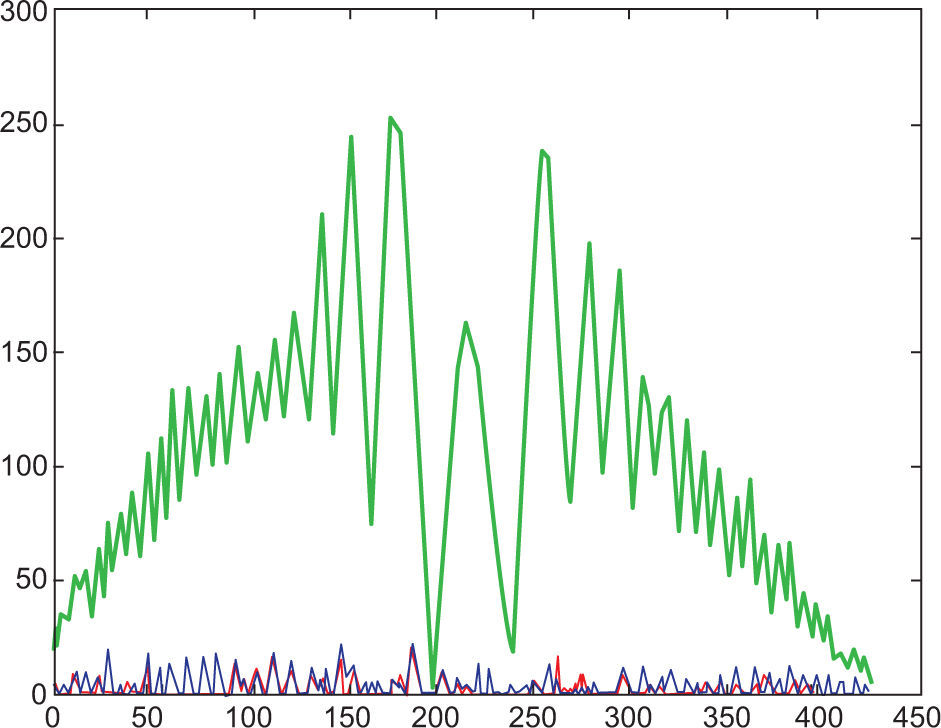
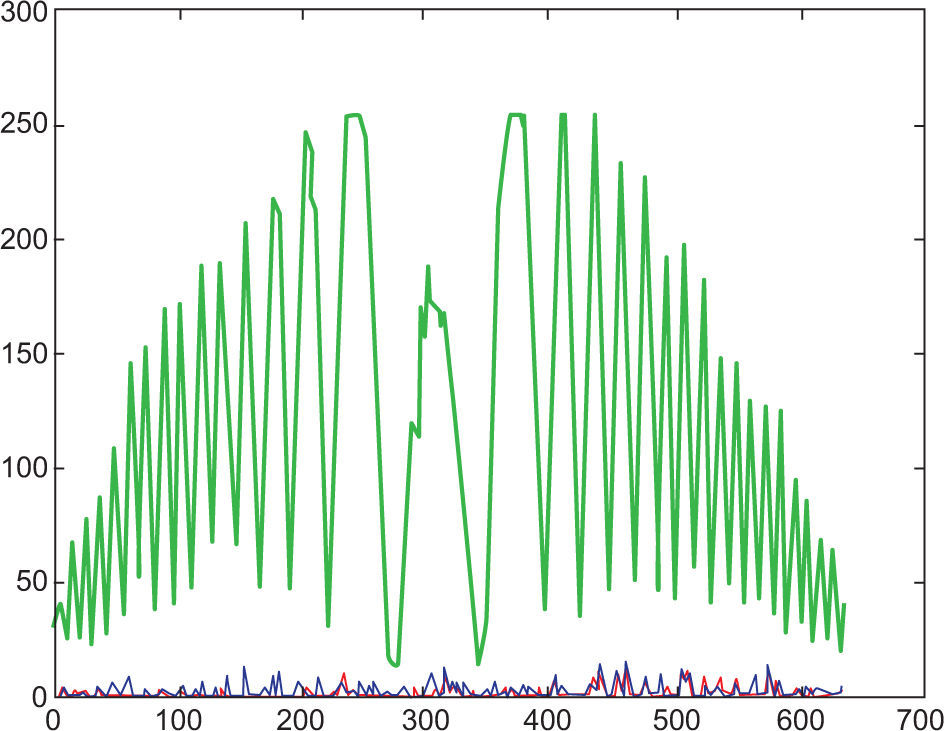
5.4

Reading 4 (at 55 °C)

Reading 4 is 31.9 °C above room temperature inside the turbulent region. The interferogram shows signs of deformity at the centroid and non-uniformity between the spacing of the nodes and anti-nodes. A phenomenon described by Andrews et al. (2005) known as beam jitter, which describes the movement of the beam around the unperturbed region, is evident here. The lower spatial frequencies in Figure 19 do not coincide well with the original unperturbed FFT. This implies defocus and image blurriness (Banish, 1990), which can be directly seen from the interferogram, possibly resulting from redistribution of power spatially in time due to the thermal fluctuations (Shaik, 1989). Energy redistribution over the beam in Figure 20 is severe over the 500 to 700 units region, with an overall maximum energy peak of less than 250 units. This redistribution of beam energy is known as beam spread (Andrews et al., 2005). The image subtraction data in Figure 21 shows signs of darkening around the centroid. The severity of the image distorsion and image blur are becoming more evident.

Fig. 19.

Magnitude of the FFT.

Fig. 20.

Intensity profile at 55 °C.

Fig. 21.

Image subtraction of reading 4 from 1.

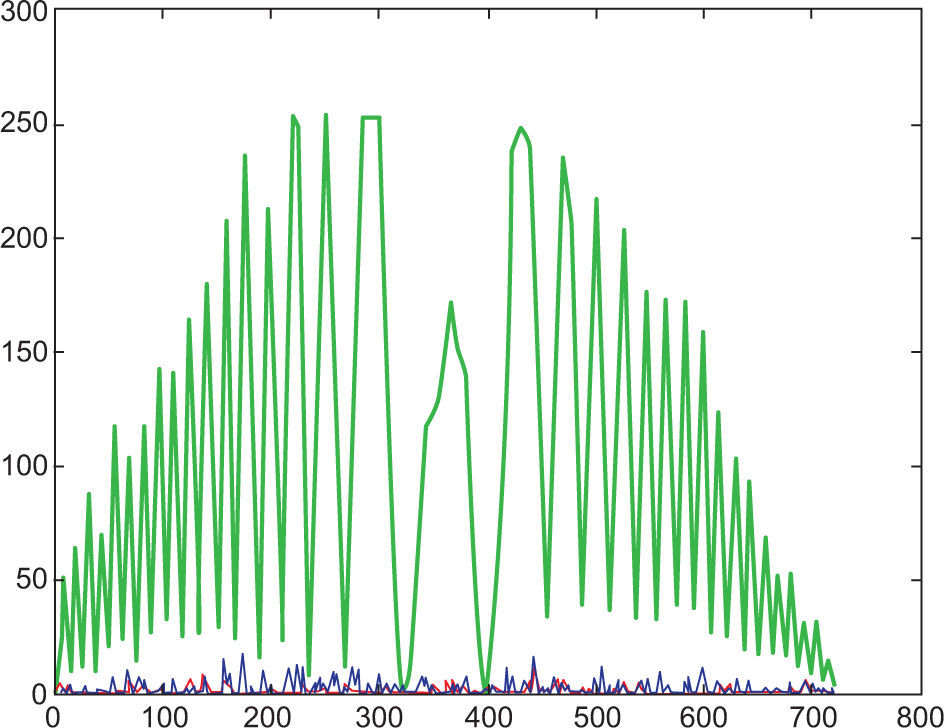
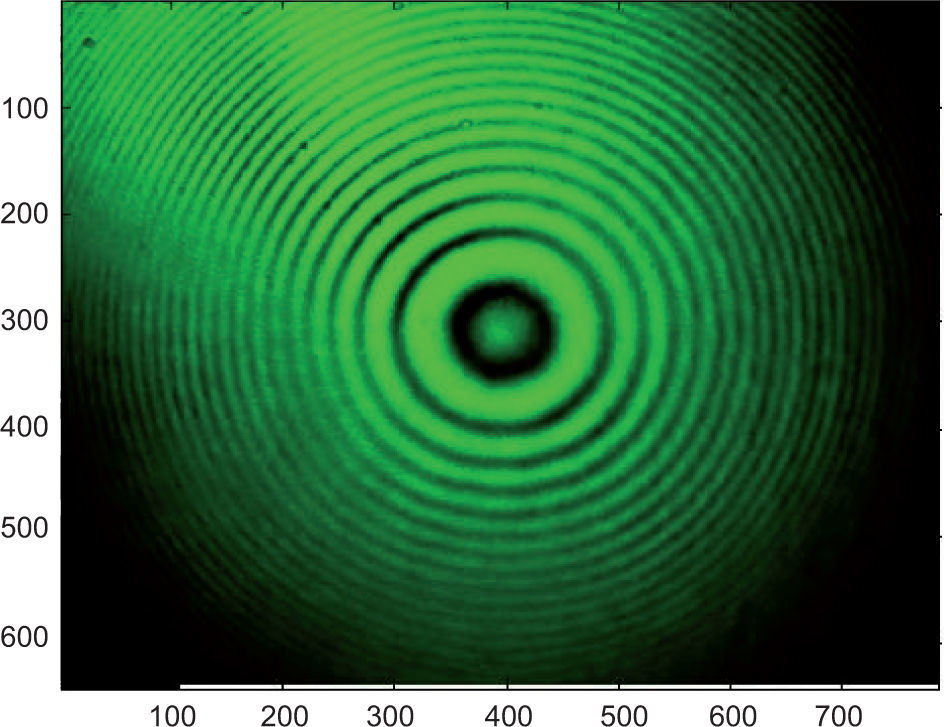
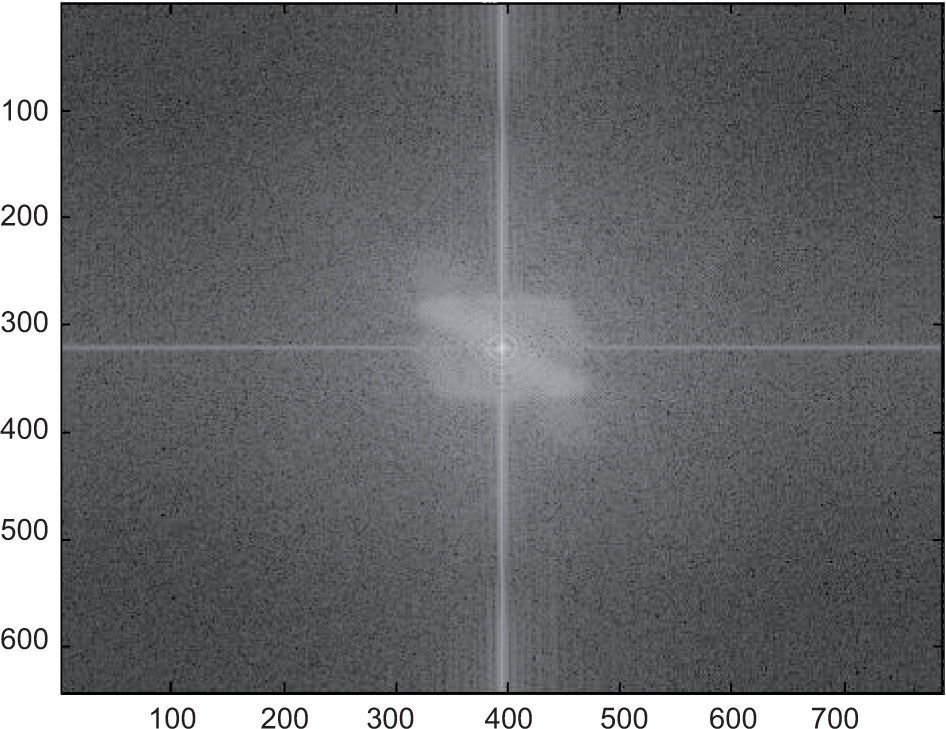
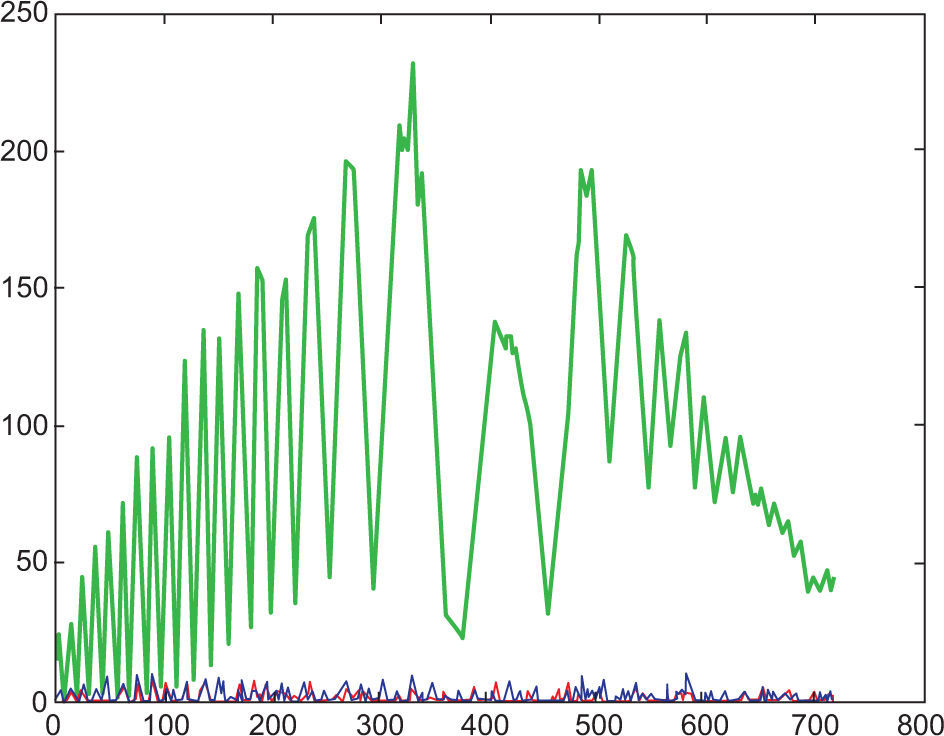
5.5

Reading 5 (at 65 °C)

Reading 5 presents the results of the most extreme temperature achievable using the heated panel. At 65 °C, the laser beam is exposed to thermal heat radiating at 41.9 °C above room temperature. The interferogram in Figure 22 shows signs of image blurring, defocus and shape distortion (beam jitter). The intensity profile (Fig. 23), however, provides a clearer understanding of energy redistribution over the beam. The maximum energy peak has decreased from a possible 250 units to an approximate value of 220 units. The energy redistribution (beam spreading) is considerable over the region of 400 and 700 units, and displays random non-uniform energy peaks. An explanation for this could be described through the use of the image subtraction data. A darker region around the center is evident when compared to previous data, which implies larger lower spatial frequency redistribution (Fig. 24). This implies that it leads to increased defocus and image blur, which has already been determined visually from the interferogram analysis (Banish et al., 1990). To classify the turbulence effect at various temperatures, the refractive index structure function was calculated and the results displayed in Table III. Figure 25 displays the image subtraction data of reading 5 from 1.

Fig. 22.

Perturbed interference pattern.

Fig. 23.

Intensity profile at 65 °C.

Fig. 24.

Magnitude of the FFT.

Table III.

Results of the turbulence strength for r = 0.2 m.

Reading	CT2(K^2 m^-2/3)	Cn2(x10^-12 m^-2/3)
1	1.35	1.11
2	1.73	1.42
3	2.37	1.94
4	2.81	2.29
5	3.29	2.69

Fig. 25.

Image subtraction of reading 5 from 1.

6

Determination of Cn2

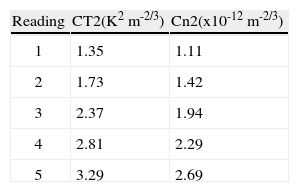
From Eq. (2) we can determine the turbulence strength due to a variation of temperature. A series of five readings were taken with a separation of r = 0.2 m. Readings 1-5 were taken at temperature values starting at approximately 30 °C and ending at approximately 60 °C with 5 °C intervals. Before Cn2 can be determined, the temperature structure function CT2 is required. This may be determined by invoking Eq. (3). Table III describes the temperature structure function CT2 and the turbulence strength Cn2 with separation r = 0.2 m. The data obtained for Cn2 ranges in magnitude from 1.1 × 10^–12 m^–2/3 to 2.7 × 10^–12 m^–2/3, which can be classified under the strong turbulence regime (Banish et al., 1990). Previous work by Ndlovu (2013) described an environment of very weak turbulence within the turbulent region using a similar experimental setup. His results are undoubtedly due to a fractional area being heated by the cigarette lighter source (Ndlovu, 2013). Although the flame produces intense temperatures, the focus of the heat is over a minuscule area. The turbulence generator used in our experiment provided a more consistent temperature delivery over a much larger region. Additionally, in our work slight variations in pressure were recorded, which allowed for the precise calculation of CT2, the temperature structure function. Ndlovu (2013) neglected to account for this in his work, and it seems to have contributed to his lower values.

Typical values of Cn2 for the atmosphere are four to five orders of magnitude larger than those obtained by Ndlovu (2013) and compare more favourably to the values determined in our work (Gochelashvili and Shishov, 1974; Gamo, 1978). Previously published values of Cn2 vary drastically from one source to another and are debatable (Gochelashvili and Shishov, 1974; Gamo, 1978). In the open atmosphere path lengths extend over vast distances, and in order for turbulent effects to be realized the turbulence model must generate stronger disturbance. This fact is evident as shown by the Rytov variance with σR2=1.4×10−3). For short propagation distances, as achieved in the laboratory, Gaussian beam propagation requires the condition of σR2≤1 for weak turbulence effects. The achieved scintillation therefore describes a weak turbulent environment despite the strong refractive index coefficient and this discrepancy can be attributed to the relatively short propagation paths. Figure 26 presents a graph of Cn2 vs. temperature for a separation distance of r = 0.2 m.

Fig. 26.

Graph of Cn2 vs. temperature with a separation distance of r = 0.2 m.

6.1

Comparison of Cn2 data from various publications

Table IV presents the refractive index structure constants Cn2 from various published data. As previously explained, the values vary from one source to the other and their relevance is highly interpretive for specific conditions. Numerous factors, such as wind speed, humidity and mean temperature need to be considered before the data can be directly compared to our work. However, we are able to immediately ascertain a common trend in this work and all comparative data: Cn2 is temperature dependent. To graphically analyze and verify this trend, it may be necessary to plot a few scenarios of Cn2 vs. temperature from various sources.

Table IV.

Comparison of results for Cn2 vs. temperature.

Cn2(m^-2/3) range	Reference
1.1 × 10^-12 – 2.6 × 10^-12	This work
1.0 × 10^-9 – 1.8 × 10^-7	Wright and Schutz, 1967
6.0 × 10^-16 – 3.0 × 10^-15	Weichel, 1990
5.7 × 10^-12 – 4.2 × 10^-10	Magee, 1993
2.0 × 10^-16 – 4.5 × 10^-14	Tunick et al., 2005
2.5 × 10^-19 – 1.1 × 10^-17	Ndlovu,2013
(3.3 ± 0.15) × 10^-18	Ngo Nyobe et al., 2014

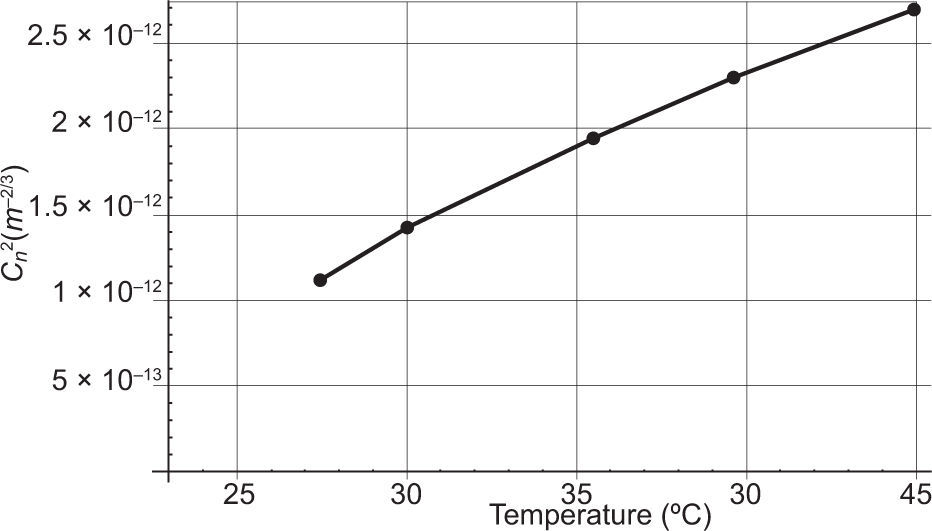
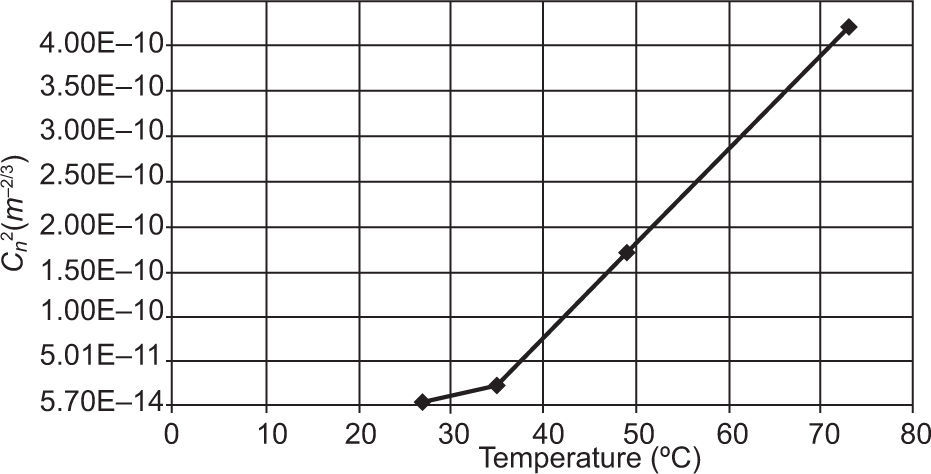
Varying values of Cn2 are tabulated in Table IV. The higher values of Cn2, as described by Ngo Nyobe et al. (2014), describe a highly turbulent atmosphere and predict a high level of visual blurring such as the wavy lines one may encounter when looking at a hot metal surface. Lower values of Cn2 as described by Ndlovu (2013), indicate more adiabatic conditions such as in windy or cloudy conditions. Figure 27 is a plot of Cn2 versus temperature as obtained experimentally by Magee (1993), who introduced a turbulent environment within a turbulence chamber in the laboratory and measured the perturbed wavefront using a shearing interferometer, which allows direct comparison with our own results. Table V presents the data for the plot in Figure 27.

Fig. 27.

Graph of Cn2 vs. temperature (Magee, 1993).

Table V.

Results of Cn2 compared with temperature.

Temperature (°C)	Cn2(× 10^-12 m ^-2/3)
27	5.7
35	23.0
49	170.0
73	420.0

Figures 26 and 27, although having different measurement scales, display similar patterns at higher temperatures. The differences in scales are attributed to the large turbulence chamber used by Magee (1993), which provided consistent heating over a much larger path length than ours, and it fully surrounded the beam whilst ours did not. The different scales could also be due to pressure and humidity fluctuations, which contribute to the temperature structure function. Our results are very pleasing when considering that the equipment used by Magee (1993) was highly specialized and very expensive. The major advantage of our work is the ability to reproduce equivalent results but still remaining robust and highly cost-efficient.

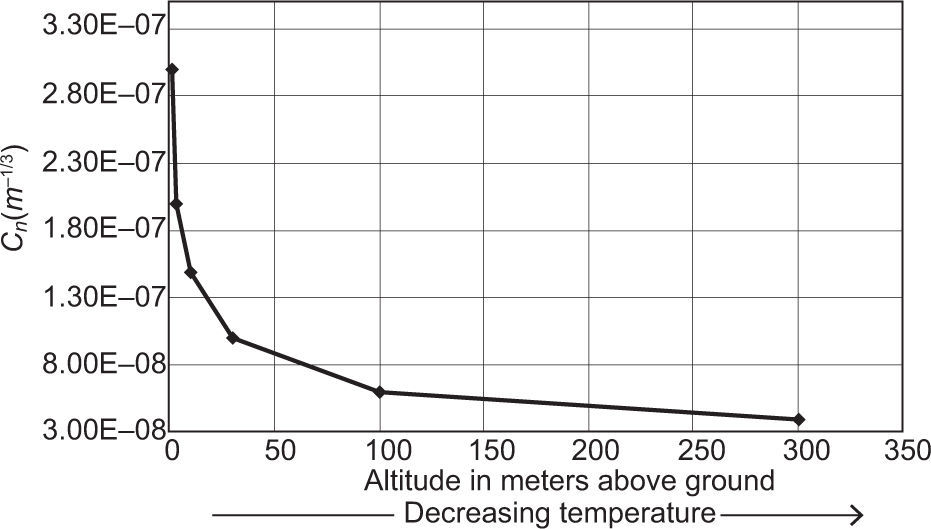
Another interesting set of comparative results is that of Weichel (1990), in which the refractive index structure constant was determined at varying altitudes. Measurements were made from ground level to a height of approximately 3 km, while we restricted ours to a region of 300 m within the troposphere for analysis reasons. See Table VI for the data of altitude vs. temperature vs. Cn2. A plot of Cn2 vs. altitude is presented in Figure 28. Data provided by Weichel (1990) does not include temperature values in relation to altitude; therefore a standard atmosphere calculator (Kroo, 1997) was used to compute approximate temperatures. Although our results differ from those presented in this work, the comparison is useful since the troposphere represents our region of interest. It is the most active in terms of wind sheer and humidity, and displays a decrease in temperature with respect to altitude. Figure 28 describes an increase in Cn2 related to altitude. This is expected, since a decrease in Cn2 is also predicted for decreasing values of temperature.

Table VI.

Comparison of Cn2 results with temperature and altitude.

Altitude (m)	Temperature (°C)	Cn2 (× 10^-15 m ^-2/3)
1	14.99	3.0
3	14.98	2.0
10	14.94	1.5
30	14.80	1.0
100	14.35	0.6
300	13.05	0.6

Fig. 28.

Graph of Cn2 vs. altitude (Weichel, 1990).

6.2

Error analysis

The statistical error in our work has been minimized by averaging results for Cn2 (approximately 500 values were averaged for a single Cn2, as stated in Table III). The values for Cn2 varied by less than 0.5% and thus may be neglected. Some experimental error analysis is also necessary. The accuracy of the PDI controller is quoted at 95%, hence a maximum error of 5% can be expected for the turbulence generator. The pressure sensor quotes a maximum possible error of 0.1 Pa (1%). The thermocouple states a precision of 0.1 °C, which is approximately a 1% error. The total experimental error can be estimated at approximately 7%, hence a new Cn2 range can be rewritten as (1.89 ± 0.64) × 10^–12 m ^–2/3.

6.3

Phase structure function D_s(r)

Figure 29 presents the phase structure function as a function of the outer scale L₀. The separation of the inner and outer scales is represented by r, which typically varies between 1 mm ≤ r ≤ 10 mm (Kerr, 1972). An increase in the outer scale directly relates to an increase in the geometric structure function. This relation was proved by Kerr (1972) and shown by Ndlovu (2013) to have a similar trend.

Fig. 29.

Graph of the phase structure function D_s (r) as a function of L₀.

The atmospheric coherence diameter was also determined to be r₀ = 22 cm, which falls within the 10% of accepted published values (Magee, 1993). For the high atmosphere observatories and in the presence of good seeing conditions, a value of r₀ = 20 cm can be achieved. Due to the ground level positioning of the laboratory, optical seeing conditions are much weaker as a result of the high convective nature of the atmosphere. Thus, optical perturbations of the laser beam increase causing an enlargement of the optical coherence diameter.

7

Conclusions

Unique modifications have been applied to an existing system to measure the effects of thermal turbulence on a laser beam. The laboratory experiment used a PDI to measure the thermal turbulence effects on a propagating laser beam in the air. Analysis of the produced interferograms required the use of fast Fourier transforms to decompose them into their constituent magnitude and phase regimes.

It has been previously discussed that the magnitude regime is of great importance, since it reveals the majority of the analysis data from the image. The data stated for the laser beam at a room temperature of 23.1 °C represents the baseline for all comparisons. The data analysis revealed that an increase of 11.9 °C provided substantial evidence that the laser beam experienced, although minor, directional fluctuations as well as image blur. Subsequent data at higher thermal turbulence showed that the severity of intensity and directional fluctuations increased in accordance with temperature increases. This result agrees well with the Rytov approximation, which indicates that for weak turbulence an increase in temperature leads to intensity fluctuations.

The laboratory measured data (namely temperature structure function, refractive index structure function, scintillation and Fried’s parameter) were also determined and are comparable to numerous published data. Each source varies drastically, which is acceptable since small changes in the path length or temperature affect calculated data drastically. According to data of Cn2, the turbulence strength resembles very strong conditions but, due to the short propagation length, the scintillation contradicts this result. The environment falls within the very weak turbulence regime, since σR2≤1. A coherence diameter of 22 cm determined in the laboratory does not fall within the range of 5-20 cm, since the seeing conditions at ground level are bad due to various factors, such as weather and the highly turbulent nature of the atmosphere.

Thus, we have effectively setup and tested a robust, inexpensive, highly accurate experiment to detect the effect of thermal turbulence on a propagating laser beam in air using a point diffraction interferometer. Future research should focus on changing the turbulent source to include a heated wind stream, which provides heat through a high velocity medium. Also of interest will be to move the entire setup to longer propagation distances in an open environment. A different choice of laser may also be necessary to examine the extent to which other lasers are affected. Such results are useful in defense technology and are therefore sought after by many researchers.