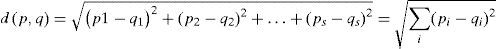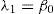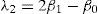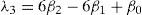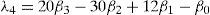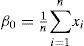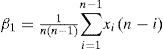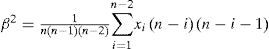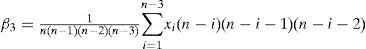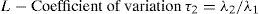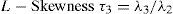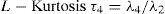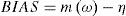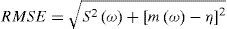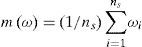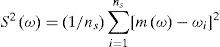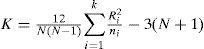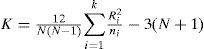Multivariate delineation of rainfall homogeneous regions for estimating quantiles of maximum daily rainfall: A case study of northwestern Mexico

Resumen

La escasez de información en el análisis de frecuencias de lluvias máximas diarias puede generar estimadores inefcaces para propósitos de diseño. Una forma de reducir estos errores es la aplicación de técnicas regionales, las cuales requieren que las estaciones involucradas pertenezcan a la misma región homogénea. En este trabajo se realiza una delimitación de regiones homogéneas de precipitación empleando un método multivariado basado en las técnicas de análisis de componentes principales y de agrupamiento jerárquico ascendente. La metodología propuesta se aplicó a una región del noroeste de México. Se concluyó que sólo se requieren los coefcientes de variación de los momentos-L y de la latitud, longitud y altitud de cada estación climatológica para definir las regiones homogéneas de precipitación, y que la inclusión o exclusión de información en las técnicas regionales tiene un impacto directo en la estimación de eventos asociados a diferentes periodos de retorno.

Abstract

Lack of data in maximum daily rainfall frequency analysis can generate ineffcient estimates for design purposes. An approach to diminish these errors is to apply regional estimation techniques, which require that all stations be located at the same homogeneous region. In this paper, a delineation of homogeneous precipitation regions was made based on the multivariate methods of principal component analysis and hierarchical ascending clustering. A region in northwestern Mexico was selected to apply this methodology. It was concluded that only the coeffcients of variation of the L-moments, along with latitude, longitude and altitude at each climatological station are sufficient to define the homogeneous rainfall regions, and that either the inclusion or exclusion of information in the regional techniques has a direct impact on the estimation of events associated to different return periods.

1

Introduction

The North American Monsoon System (NAMS) is defined as a pronounced increase in rainfall from an extremely dry June to a rainy July over large areas of the southwestern United States and northwestern Mexico (Adams and Comrie, 1997). The occurrence of NAMS is associated to atmospheric dynamics conditions and topographic characteristics, which interact with each other to cause a convective environment. This phenomenon can generate a high potential danger of flooding to residents in the country. In order to protect their lives and goods, it is very important to have a mathematical tool that may reduce the uncertainties in estimating design events for different return periods, which are needed in many hydraulic studies and projects such as food plain delineation or drainage works in cities.

In maximum daily rainfall frequency analysis, when information exists but not with the length of record required to provide accurate parameter estimates, the error of the estimated value for some return periods can be very large and inefficient for design purposes. A way of reducing this error is by applying a joint estimation model where information from nearby sites in the same region may be combined with the record of inadequate length. This approach will increase the amount of information and will provide a regional at-site estimate. An example of these regional models is the station-year technique, which is used to obtain a regional at-site estimate of the maximum daily rainfall for different return periods (Cunnane, 1988). These events are necessary to shape the intensity-duration-frequency curves (IDF) whose intensities i (mm/h) associated to certain duration d (h) and return period T (years) are used for designing hydraulic works.

The regional analysis correlates hydrological variables with the physiographical and climatological characteristics. Through these regional relations it is also possible to obtain flow estimates in rivers, as it can be seen in Wiltshire (1985), Stedinger (1983), Gingras and Adamowsky (1993), Burn (1988), Robinson (1997), Gutiérrez-López (1996), Escalante and Reyes (1998,2000), Pandey and Nguyen (1999), Ouarda et al. (2001), Gómez (2003), Skaugen and Vaeringstad (2005), and Ouarda et al. (2008).

The regional techniques require that the involved stations belong to the same homogeneous region. Since the inclusion or exclusion of information has a direct impact on the estimation of events associated to different return periods, adequately establishing that such homogeneity is achieved is an essential step to reduce the associated uncertainties.

A homogeneous region can be delineated by using geographical characteristics or statistical tests. Some works also have proposed indexes to evaluate the uncertainty and applicability of these methods: Nouh (1987), Cunnane (1988), Rosbjerg and Madsen (1995), GREHYS (1996a, b), Campos (1999), and Lin and Chen (2003).

In this work, the delineation of homogeneous regions is based on multivariate methods: principal component analysis (PCA) and hierarchical ascending clustering (HAC).

2

Materials and methods

2.1

Principal component analysis

PCA is a multivariate statistical technique highly descriptive, which is used to identify patterns on data in such a way as to highlight their similarities and differences. PCA can reduce the dimensionality of the data, transforming the set of r original variables or attributes in another set of s uncorrelated variables called principal components. The r variables are measured on each of the m sites. The order of the initial matrix of data is mr and it is restricted to m > r. After applying the PCA technique, the order of the resulting matrix is ms. This reduction of dimensionality is achieved with a little loss of information, which is considered non-significant to preserve the principal components.

PCA allows using either the correlation matrix or the covariance matrix. The first option gives the same importance to all and each of the variables. This can be convenient when the researcher considers that all the variables are equally relevant. The second option can be used when all the variables have the same units of measure.

The s new variables (principal components) are obtained as linear combinations of the r original variables. Components are arranged according to the percentage of variance that can be explained. In this sense, the first component will be the most important since it explains the largest percentage of the variance of data. Each researcher will decide how many components will be elected in the study.

PCA is performed in the space of the r variables and, in dual form, in the space of m sites. Variables and sites can be graphically represented by considering the first and second component as coordinate axes. A point-variable is represented by the coordinate corresponding to that variable in each of these components. The cloud of points-variables is located in a circular area of radius 1. The proximity between the point-variables indicates the degree of correlation between them. When the correlation is equal to one, the points coincide.

When the r variables are uncorrelated, r equally important components will be obtained. In contrast, when all variables have a perfect correlation, a simple component is generated. This component is a linear combination of the r equally weighted variables and explains 100% of the total variation.

The cloud of points-sites is not enclosed in a circle of radius 1. A point-site located at the extreme of one axis means that such station is closely related to the respective component. The opposite case indicates that the site has no relation with the two components. Proximity between sites is interpreted as similar behavior.

When there are several clouds of points that indicate the presence of a sub-population, and since the purpose of the study is to detect groups, the PCA achieves that aim.

2.2

Hierarchical ascending clustering

Hierarchical clustering is a method for grouping clusters, and seeks to build a hierarchy of these. There are two types of hierarchical clustering:

• a.

  Agglomerative: This is an ascending approach where each observation starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy.

• b.

  Dissociative: This is a descending approach where all observations start in one cluster, and splits are performed recursively as one moves down the hierarchy.

In order to decide which clusters should be combined (for the agglomerative approach), or where a cluster should be split (for the dissociative approach), a measure of dissimilarity between sets of observations is required. In most methods of hierarchical clustering, this is achieved by using an appropriate measure of distance between pairs of observations, in addition to a linkage criterion which specifies the dissimilarity of sets as a function of the pairwise distances of observations in them.

The choice of an appropriate metric will influence the shape of the clusters, as some elements may be close to one another according to a distance but farther away according to another distance. In this work the Euclidean distance will be the measure of distance between pairs.

If p = (p₁, p₂,..., p_s) and (q₁, q₂,..., q_s) are two points in Euclidean m-space with s-attributes (uncorrelated variables), the Euclidean distance from p to q is:

where p₁ and q1 could be the average number of days with rainfall per year at sites p and q; p₂ and q₂ could be the average annual maximum of daily rainfall at sites p and q, and so on. In fact, Eq. (1) represents a distance among the different attributes of precipitation at two sites and not a physical distance between them.

The linkage criterion determines the distance between sets of observations as a function of the pairwise distances between observations. The linkage criteria used will be the Ward’s minimum variance method. Ward (1963) suggested a general agglomerative hierarchical clustering procedure, where the criterion for choosing the pair of clusters to merge at each step is based on the optimal value of an objective function. Ward’s criterion minimizes the total within-cluster variance. The pair of clusters with minimum cluster distance is merged at each step. To implement this method, the pair of clusters that leads to minimum increase in total within-cluster variance after merging is found at each step. This increase is a weighted squared distance between cluster centers. At the initial step, all clusters contain a single point. To apply a recursive algorithm under this objective function, the initial distance between individual objects must be proportional to the squared Euclidean distance.

2.3

Delineation of homogeneous regions

2.3.1

First scenario: Chaos simulation

All available variables are used without any prior consideration to build the site-variable matrix, and clusters are obtained based on HAC. In this first approach to grouping it is very common to observe that clusters present intersections among them.

2.3.2

Representative simulation

A robust data matrix containing a set of variables with a high physical meaning by using HAC is formed. PCA is applied to obtain groups of variables associated with the four quadrants (principal components).

2.3.3

Quadrants simulations (QS)

In this stage, site-variable matrices are formed for each quadrant and HAC is applied to each of them.

2.3.4

Fit and testing of sites clusters (F&T)

PCA has to be applied to those variables whose quadrants presented the best spatial significance; then, groups containing the variables that explain 70 and 80% of the variance are gathered together. With these variables a new set of site-variable matrices is formed, which are analyzed with HAC.

2.3.5

Final groups

This step consists on the identification of optimal simulation based on scenarios and ratings from the previous phase. The procedure is applied by using:

• 1.

  Some conventional moments of data (mean and standard deviation, among others).

• 2.

  The L- coefficients of variation.

• 3.

  The L-coefficients of variation plus the latitude, longitude and altitude at each climatological station.

2.3.6

Linear moments

L-moments are analogous to conventional moments but differ in that they are calculated using linear combinations of the ordered data (Hosking, 1990).

L-moments offer some advantages in comparison with conventional moments. As an example consider a dataset with a few data points and one outlying data value. If the ordinary standard deviation of this data set is taken it will be highly influenced by this point; however, if the L-scale is taken it will be far less sensitive to this data value. Consequently, L-moments are far more meaningful when dealing with outliers in data than conventional moments. Another advantage of L-moments over conventional moments is that their existence only requires the random variable to have a finite mean. Therefore, L-moments exist even if the higher conventional moments do not exist. L-moments are statistical quantiles derived from probability weighted moments. The first four L-moments are:

For a sorted sample x₁, x₂,..., x_n in decreasing order, the values of the probability weighted moments β₀, β₁, β₂ and β₁ can be estimated by:

Additionally, a set of L-moments ratios or scaled L-moments can be defined by:

2.3.7

Reliability of estimated quantiles

Once homogeneity is achieved and regions are defined, it is necessary to show whether or not the regional at-site estimate of the maximum daily rainfall for different return periods is more reliable than those computed using only a short sample (at-site estimate). This reliability can be quantified by several measures such as bias, root mean squared error and variance.

Let η be a quantile to be estimated; ω_i, i= 1,...,n_s the estimates obtained from each sample and n_s the number of samples used in the experiment. Then, the bias and root mean squared error (RMSE) of the estimator ω may be computed as:

where m(ω) and S²(ω) are the mean and variance obtained from generated samples:

When estimating the parameters and quantiles of a distribution, it is convenient to have unbiased and minimum RMSE estimators. The RMSE involves both the variance of the estimator and the squared bias.

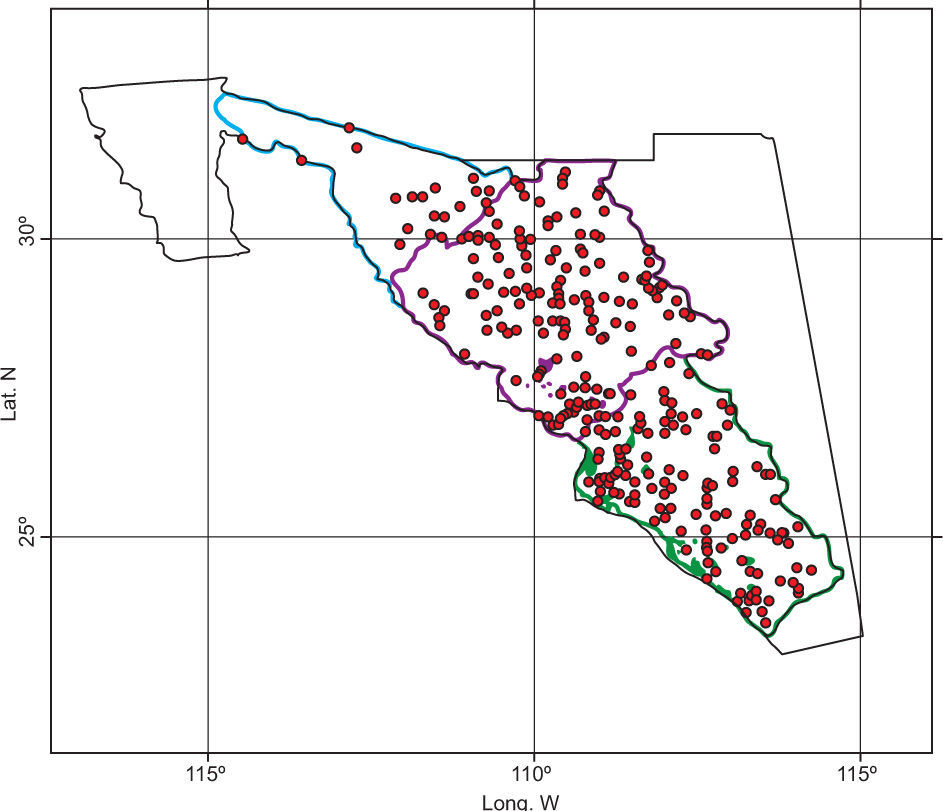
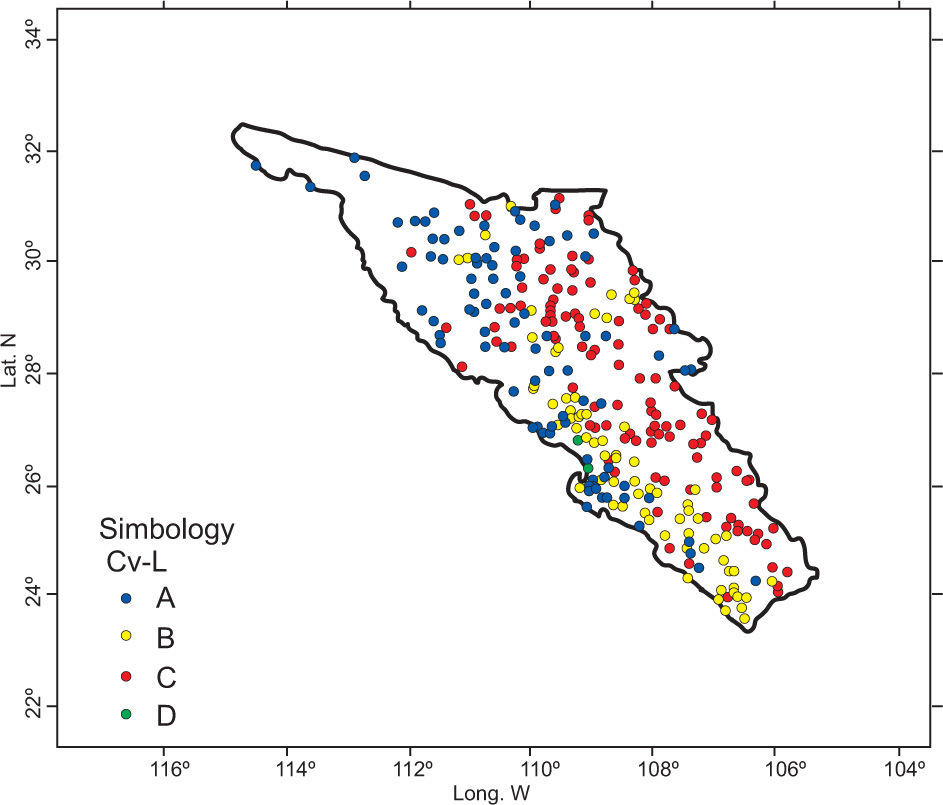
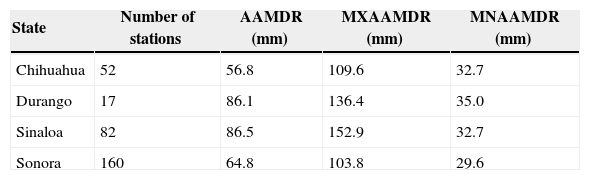
3

Case study

A region located in northwestern Mexico, with a total of 311 climatological stations was selected to apply the proposed methodology (Fig. 1). Records of annual maxima for daily rainfall were gathered for the period 1965 to 2006 from the Rapid Extractor of Climatological Information version 3 (ERIC-III, by its initials in Spanish) database (IMTA, 2012). This period of time was selected because we had 88% of the available information. The inverse distance weighting (IDW) interpolation analysis was chosen for estimating missing data. The number of stations used and its average annual maximum of daily rainfall (AAMDR) by each Mexican state are presented in Table I (MXAAMDR and MNAAMDR stand for the maximum and minimum value of AAMDR, respectively).

Fig. 1.

Location of the climatological stations used in the case study.

Table I.

Some characteristics of stations used in the case study.

State	Number of stations	AAMDR (mm)	MXAAMDR (mm)	MNAAMDR (mm)
Chihuahua	52	56.8	109.6	32.7
Durango	17	86.1	136.4	35.0
Sinaloa	82	86.5	152.9	32.7
Sonora	160	64.8	103.8	29.6

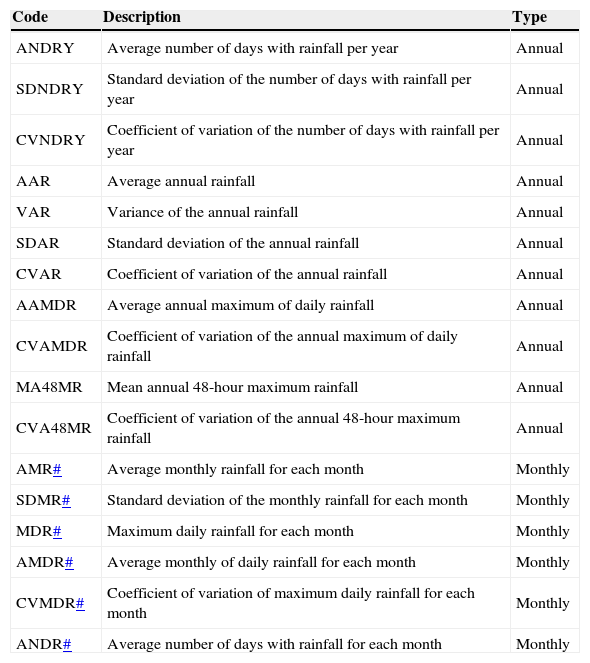
A first step to apply the PCA and HAC multivariate methods is the selection of variables to be analyzed. In order to achieve this, two sets of data were considered: The first one containing 11 annual variables and the second one consisting of 72 monthly variables, all of them from precipitation data (Table II). With this information a total of 83 variables were defined for each one of the 311 climatological stations. So, the first matrix of this analysis has 311 sites with 83 variables.

Table II.

List of variables used in the delineation process.

Code	Description	Type
ANDRY	Average number of days with rainfall per year	Annual
SDNDRY	Standard deviation of the number of days with rainfall per year	Annual
CVNDRY	Coefficient of variation of the number of days with rainfall per year	Annual
AAR	Average annual rainfall	Annual
VAR	Variance of the annual rainfall	Annual
SDAR	Standard deviation of the annual rainfall	Annual
CVAR	Coefficient of variation of the annual rainfall	Annual
AAMDR	Average annual maximum of daily rainfall	Annual
CVAMDR	Coefficient of variation of the annual maximum of daily rainfall	Annual
MA48MR	Mean annual 48-hour maximum rainfall	Annual
CVA48MR	Coefficient of variation of the annual 48-hour maximum rainfall	Annual
AMR#	Average monthly rainfall for each month	Monthly
SDMR#	Standard deviation of the monthly rainfall for each month	Monthly
MDR#	Maximum daily rainfall for each month	Monthly
AMDR#	Average monthly of daily rainfall for each month	Monthly
CVMDR#	Coefficient of variation of maximum daily rainfall for each month	Monthly
ANDR#	Average number of days with rainfall for each month	Monthly

#

stands for 1 to 12 months (January,…, December).

3.1

Chaos simulation

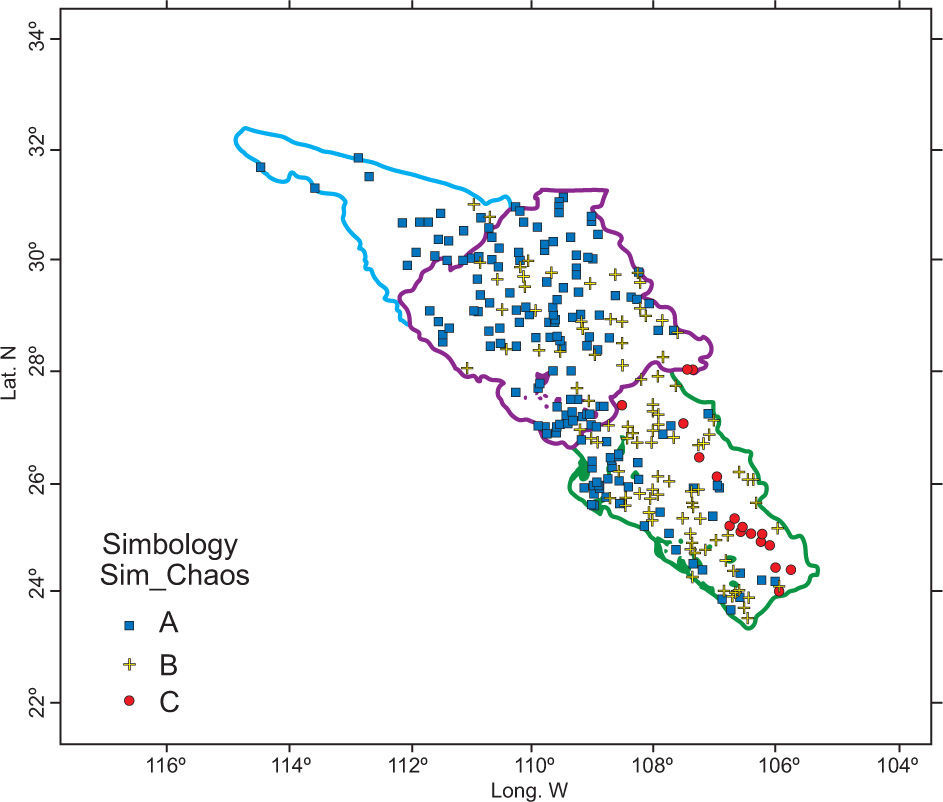
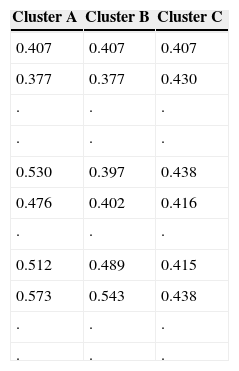
Using the 311 sites-83 variables matrix, clusters are obtained based on HAC. The behavior of the spatial distribution of the three groups of stations (A, B, and C) showed a high intersection among them (Fig. 2). These results led to the next stage of the study.

Fig. 2.

Regional distribution based on the first scenario (chaos).

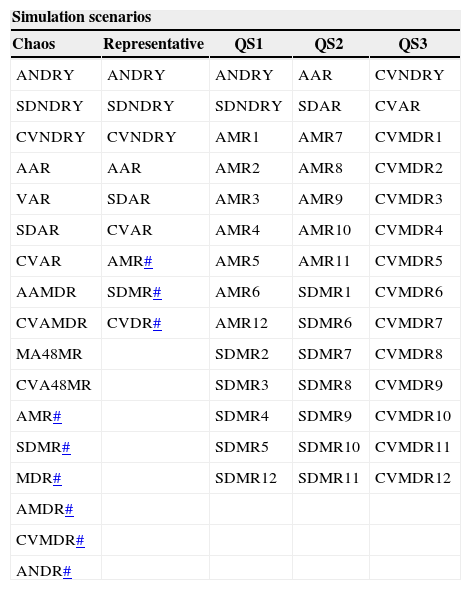
3.2

Representative simulation

In this stage it is necessary to create a matrix containing a set of 42 variables with high physical meaning at 311 sites. The variables are presented in the column tagged as “Representative” (Table III).

Table III.

List of variables used in each scenario of simulation.

Simulation scenarios
Chaos	Representative	QS1	QS2	QS3
ANDRY	ANDRY	ANDRY	AAR	CVNDRY
SDNDRY	SDNDRY	SDNDRY	SDAR	CVAR
CVNDRY	CVNDRY	AMR1	AMR7	CVMDR1
AAR	AAR	AMR2	AMR8	CVMDR2
VAR	SDAR	AMR3	AMR9	CVMDR3
SDAR	CVAR	AMR4	AMR10	CVMDR4
CVAR	AMR#	AMR5	AMR11	CVMDR5
AAMDR	SDMR#	AMR6	SDMR1	CVMDR6
CVAMDR	CVDR#	AMR12	SDMR6	CVMDR7
MA48MR		SDMR2	SDMR7	CVMDR8
CVA48MR		SDMR3	SDMR8	CVMDR9
AMR#		SDMR4	SDMR9	CVMDR10
SDMR#		SDMR5	SDMR10	CVMDR11
MDR#		SDMR12	SDMR11	CVMDR12
AMDR#
CVMDR#
ANDR#

#

stands for 1 to 12 months (January,…, December).

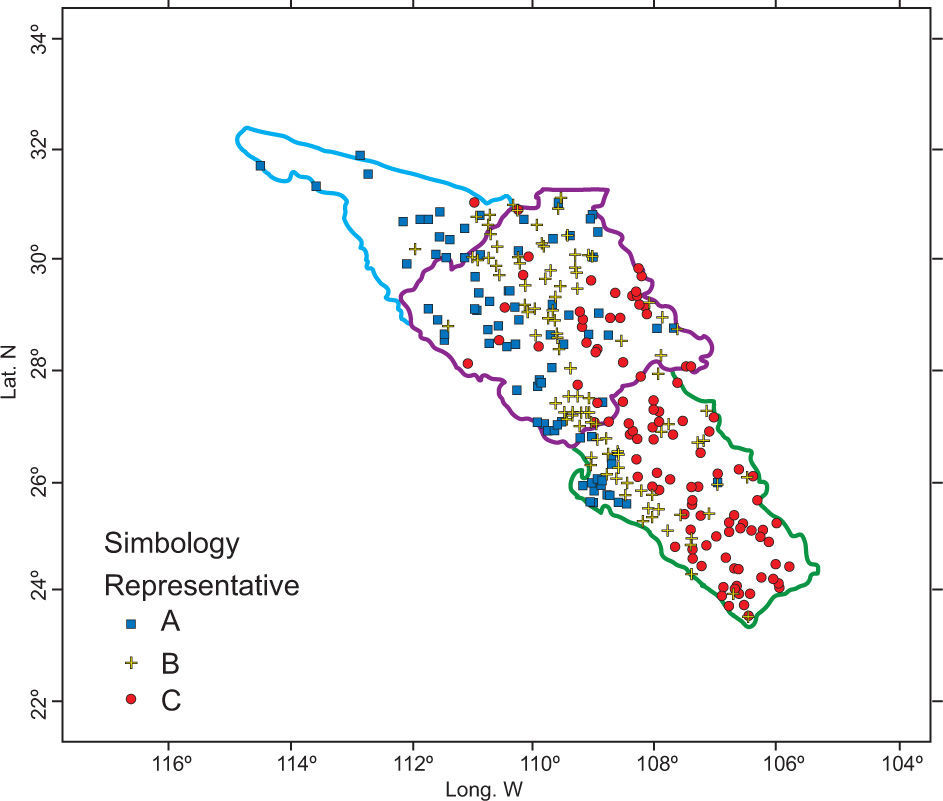
Before the HAC analysis, a correlation analysis is applied to identify variables with a high degree of interdependence that could be eliminated. However, no variable was really inadequate, so this matrix was kept. The HAC analysis defined three regions that also presented intersections (Fig. 3). It was not possible to obtain a good independence among the three regions, so a new combination of variables was proposed.

Fig. 3.

Regional distribution based on the second scenario (representative).

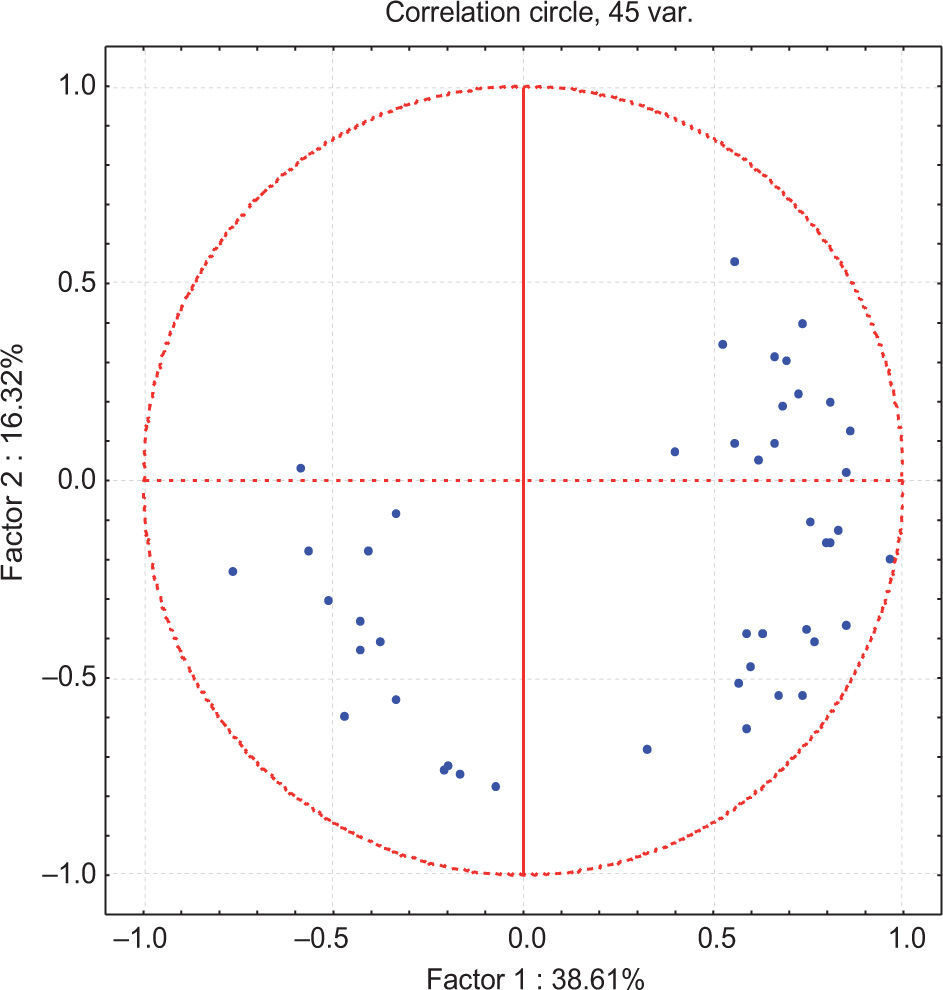
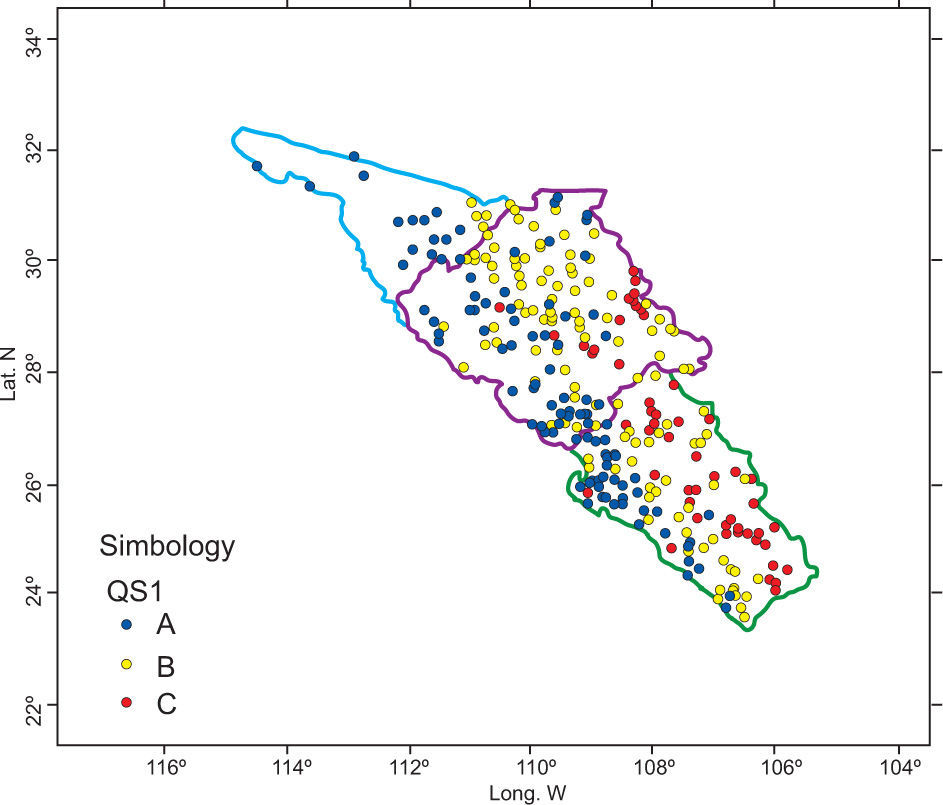
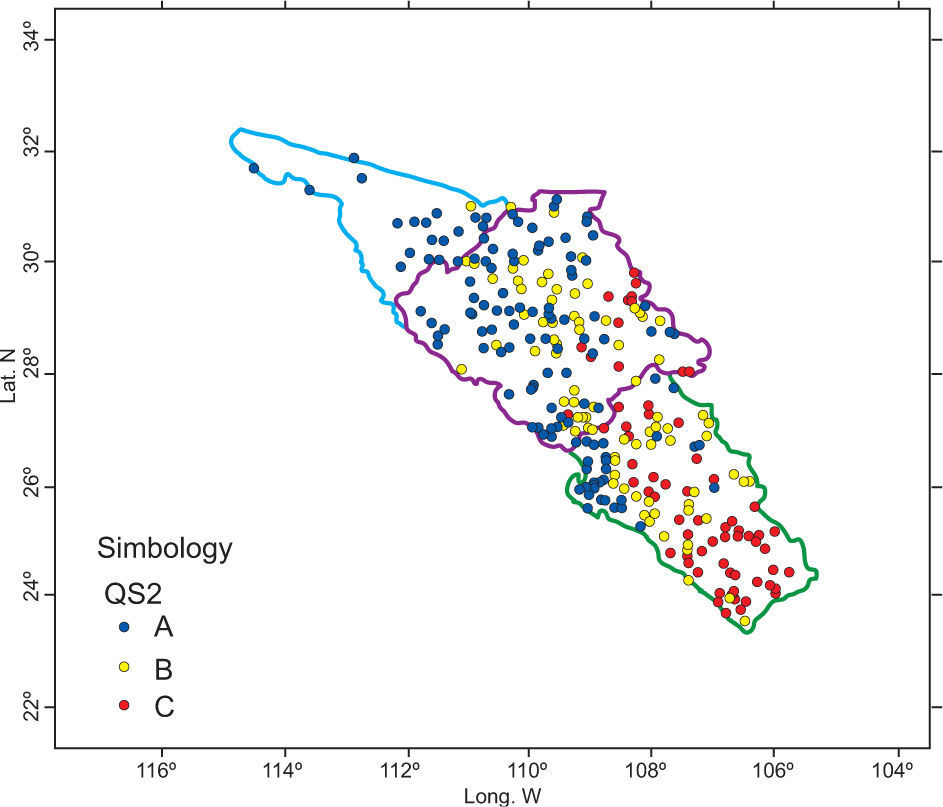
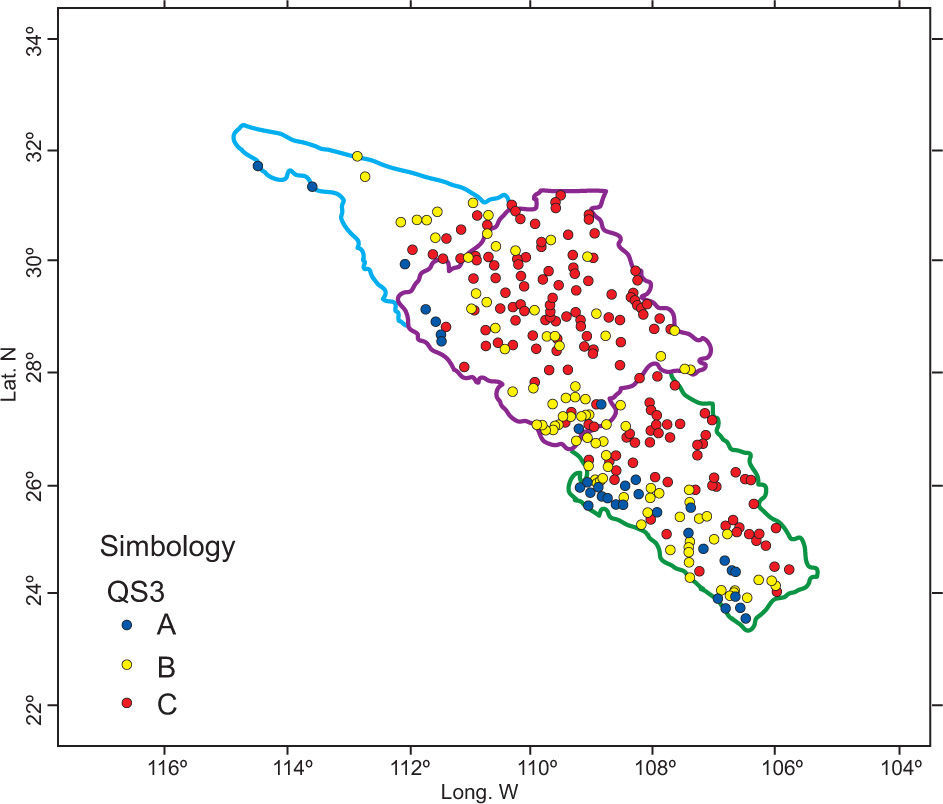
3.3

Quadrants simulations: Scenarios QS1, QS2, and QS3

After PCA was applied to the 311 × 42 matrix, it was concluded that the first component explains 38.61 % of the population variance and the second one 16.32%. According to Figure 4, only a site-variable matrix could be constructed for the first, second, and third quadrant. It was not possible to construct the fourth quadrant because there was only one variable available. The variables created for dry season months fell into the first quadrant (QS1); the variables in the second quadrant (QS2) mostly correspond to rainy season months, and finally the third quadrant (QS3) comprises the coefficients of variation (Table III).

Fig. 4.

Correlation circle for the first two principal components.

Once the site-variable matrices are constructed for each quadrant, the HAC procedure is applied for each of them. The resulting clusters are shown in Figures 5-7.

Fig. 5.

Clusters obtained based on the quadrant simulation process QS1.

Fig. 6.

Clusters obtained based on the quadrant simulation process QS2.

Fig. 7.

Clusters obtained based on the quadrant simulation process QS3.

The groups obtained for the first (QS1) and second (QS2) quadrants do not have a defined pattern, because stations still continue to present some intersections among clusters (Figs. 5 and 6).

A better definition of clustering is achieved with a simulation process in the third quadrant (QS3). Intersections among groups significantly decreased (Fig. 7). Group A is located in the strip along the coast, with a short penetration inland and bounded by an imaginary line 40 km inland, meaning this is a coastal region. Group C corresponds to a mountain region; meanwhile group B is located in the central belt between groups A and C. These variables were considered for the last part of the study.

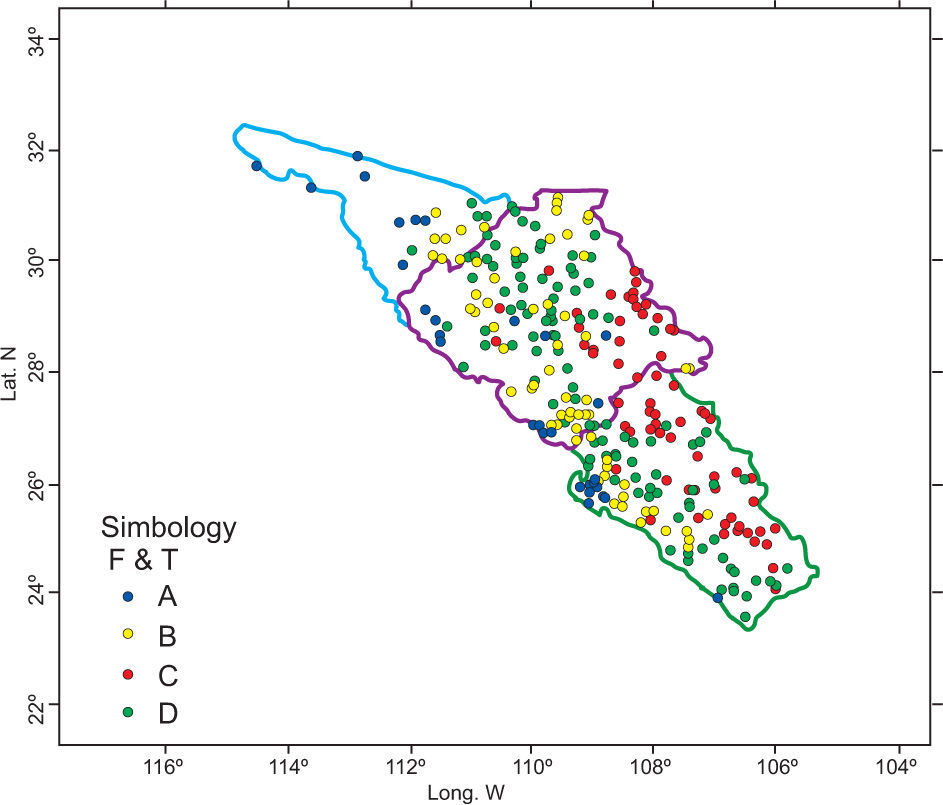
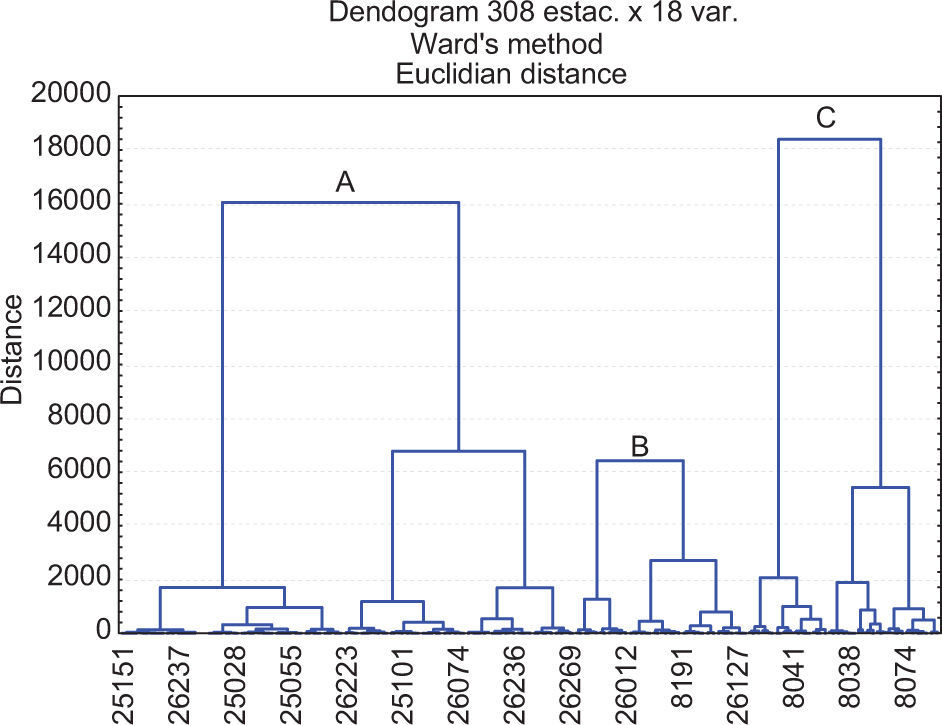
3.4

Fit and testing of clusters of individuals (F&T)

PCA was applied to variables from the third quadrant, which explained 70% of the variance. With this information a new site-variable matrix was created. This matrix is analyzed with HAC. Results (Fig. 8) show that groups A (coastal region) and C (mountain region) are stabilized; however, region B was divided into two parts (regions B and D).

Fig. 8.

Clusters obtained based on the fit and testing simulation process.

3.5

Final groups

This phase of the study was conducted in order to achieve the optimization of homogeneous regions. Until this point, it was observed that the most important variables to define a homogeneous region were CVN-DRY, CVAR and CVMDR#. In order to improve the imulation process, these coefficients were substituted by the Z-coefficients of variation (L-cv) obtained by using Eq. (10). In this step some intersections among regions can be found (Fig. 9), however the formed clusters present a better definition than the F&T case.

Fig. 9.

Clusters obtained by substituting the coefficients of variation by their L-cv version.

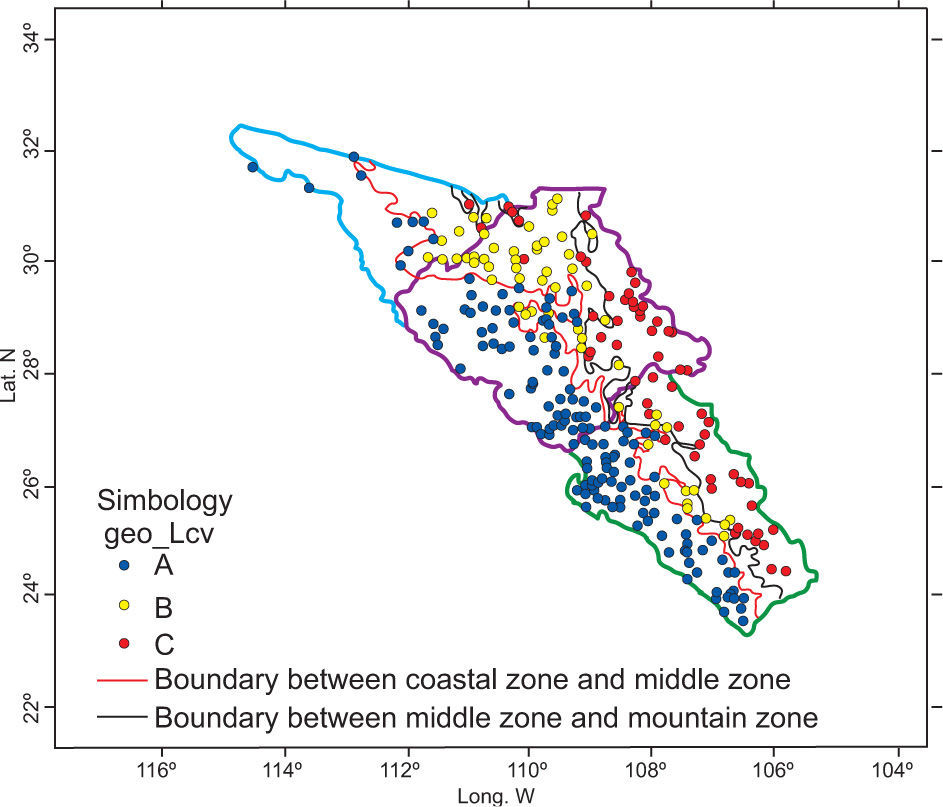
Finally, the geographical characteristics of latitude, longitude and altitude of each climatological station are added to the L-cv values from the former step. With this group of variables a new matrix is formed. The HAC analysis generated three well-defined clusters. A very important result was the migration of stations from the middle zone to the coastal region. So, group A would be located in the strip along the coast, bounded by an imaginary line 120 km inland. Group C corresponds to a mountain region; meanwhile, the middle zone was narrowed within both regions but extended along them. Figures 10 and 11 present the dendogram and clusters of the final simulation process.

Fig. 10.

Dendogram obtained based on the final simulation process (geo-L-cv).

Fig. 11.

Clusters obtained based on the final simulation process (geo-L-cv).

3.6

Comparison of k independent samples

Some statistical tests can be used to show the independency of the chosen groups. For instance, Kruskal-Wallis test is used to find if k samples come from the same population or populations with identical properties as regards a position parameter. If M¡ (median) is the position parameter for sample i, the null H₀ and alternative H_a hypotheses for the test are as follows:

• H₀: M₁ = M₂ = … = M_k

• H_a: there is at least one pair (i, j) such that M_i ≠ M_j

Calculation of the K statistic from the Krus-kal-Wallis test involves the rank of observations once the k samples or groups have been mixed. K is defined by:

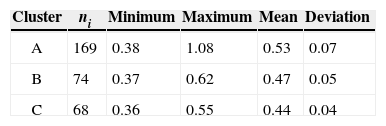
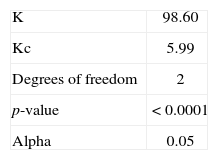
where n_i is the size of sample i, N is the sum of n_i variables, and R_i is the sum of the ranks for sample i. The distribution of the K statistic can be approximated by a chi-square distribution with (k-1) degrees of reedom. In this case, into each of the three groups only the average of the L-cv involved is considered to apply the Kruskal-Wallis test (Table IV). Results are presented in tables V and VI.

Table IV.

Average of the L-cv for each final cluster.

Cluster A	Cluster B	Cluster C
0.407	0.407	0.407
0.377	0.377	0.430
·	·	·
·	·	·
0.530	0.397	0.438
0.476	0.402	0.416
·	·	·
0.512	0.489	0.415
0.573	0.543	0.438
·	·	·
·	·	·

Table V.

Statistical characteristics of the three clusters.

Cluster	ni	Minimum	Maximum	Mean	Deviation
A	169	0.38	1.08	0.53	0.07
B	74	0.37	0.62	0.47	0.05
C	68	0.36	0.55	0.44	0.04

Table VI.

Kruskal-Wallis test (observed and tabulated).

K	98.60
Kc	5.99
Degrees of freedom	2
p-value	< 0.0001
Alpha	0.05

As K > Kc, then H₀ is rejected and the three regions can be considered independent from each other.

3.7

Comparison between at-site and regional at-site estimates of quantiles

Once homogeneity is achieved and regions are defined, it is necessary to show the effects of the inclusion or exclusion of information in the regional analysis. For this purpose, at-site and regional at-site estimates of the maximum daily rainfall for different return periods were obtained for the illustrative case of station number 25 036 (Fig. 12). For this station, the annual maxima of daily rainfall for the period from 1965 to 2006 were collected.

Fig. 12.

Station used in the stage of reliability of estimated quantiles.

The reliability of these estimates was quantified by obtaining the RMSE values, following this procedure:

Case 1

The at-site estimates of the maximum daily rainfall for return periods of 2-, 5-, 10-, 20-, 50- and 100-years are obtained by fitting the data to the normal (N), two-parameter lognormal (LN2). three-parameter lognormal (LN3), two-parameter gamma (GM2), three-parameter gamma (GM3), log-Pearson type 3 (LP3), Gumbel (G), and mixed Gumbel (MXG) distributions. The parameter estimation methods are moments (M), maximum likelihood (ML), L-moments (LM), maximum entropy (ME) and probability weighted moments (PWM). The best fit is selected according to the criterion of minimum standard error of fit (SEF), as defined by Kite (1988):

where g_i, i = 1,..., n are the recorded events; h_i, i = 1,..., n are the event magnitudes computed from the probability distribution at probabilities obtained from the sorted ranks of g_i, i = 1,..., n; mp is the number of parameters estimated for the distribution, and n is the length of record.

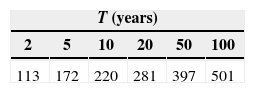
For this sample, the minimum value of SEF was obtained by fitting the MXG (ML) distribution. The maximum daily rainfall for each return period is presented in Table VII. These values are considered as the “true values” for long samples “η” in Eqs. (13) and (14).

Table VII.

Maximum of daily rainfall h (mm) for different return periods at station number 25 036.

T (years)
2	5	10	20	50	100
113	172	220	281	397	501

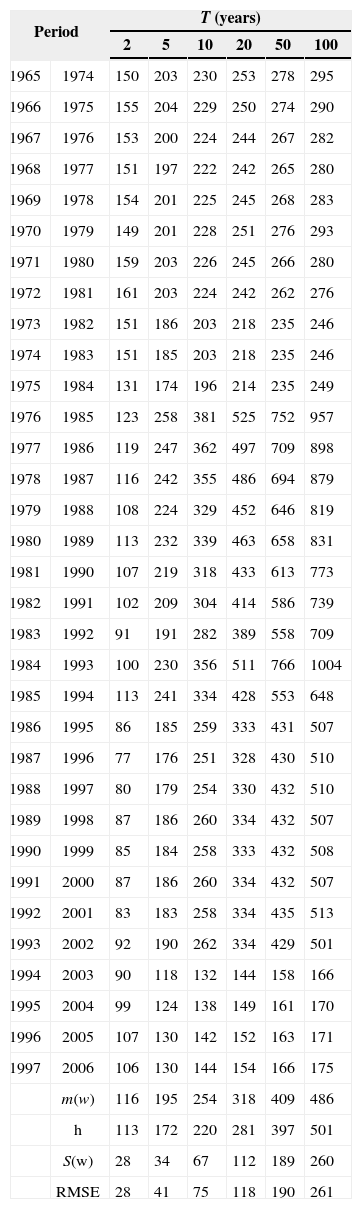
Case 2

The at-site estimates of the maximum daily rainfall for station number 25 036 are obtained by considering a set of 33 sub-samples of length n = 10 years (short samples). So, the record of annual maximum of daily rainfall for the periods 1965-1974, 1966-1975,…, and 1997-2006 are grouped. For each of them, at-site estimates of maximum daily rainfall are obtained by fitting the same distributions of the former case. These values are considered as the “estimated values” for short samples. The corresponding RMSE values are presented in Table VIII.

Table VIII.

Maximum daily rainfall ω (mm) and RMSE for each of 33 sub-samples at station number 25 036 (case 2).

Period		T (years)
		2	5	10	20	50	100
1965	1974	150	203	230	253	278	295
1966	1975	155	204	229	250	274	290
1967	1976	153	200	224	244	267	282
1968	1977	151	197	222	242	265	280
1969	1978	154	201	225	245	268	283
1970	1979	149	201	228	251	276	293
1971	1980	159	203	226	245	266	280
1972	1981	161	203	224	242	262	276
1973	1982	151	186	203	218	235	246
1974	1983	151	185	203	218	235	246
1975	1984	131	174	196	214	235	249
1976	1985	123	258	381	525	752	957
1977	1986	119	247	362	497	709	898
1978	1987	116	242	355	486	694	879
1979	1988	108	224	329	452	646	819
1980	1989	113	232	339	463	658	831
1981	1990	107	219	318	433	613	773
1982	1991	102	209	304	414	586	739
1983	1992	91	191	282	389	558	709
1984	1993	100	230	356	511	766	1004
1985	1994	113	241	334	428	553	648
1986	1995	86	185	259	333	431	507
1987	1996	77	176	251	328	430	510
1988	1997	80	179	254	330	432	510
1989	1998	87	186	260	334	432	507
1990	1999	85	184	258	333	432	508
1991	2000	87	186	260	334	432	507
1992	2001	83	183	258	334	435	513
1993	2002	92	190	262	334	429	501
1994	2003	90	118	132	144	158	166
1995	2004	99	124	138	149	161	170
1996	2005	107	130	142	152	163	171
1997	2006	106	130	144	154	166	175
	m(w)	116	195	254	318	409	486
	h	113	172	220	281	397	501
	S(w)	28	34	67	112	189	260
	RMSE	28	41	75	118	190	261

Case 3

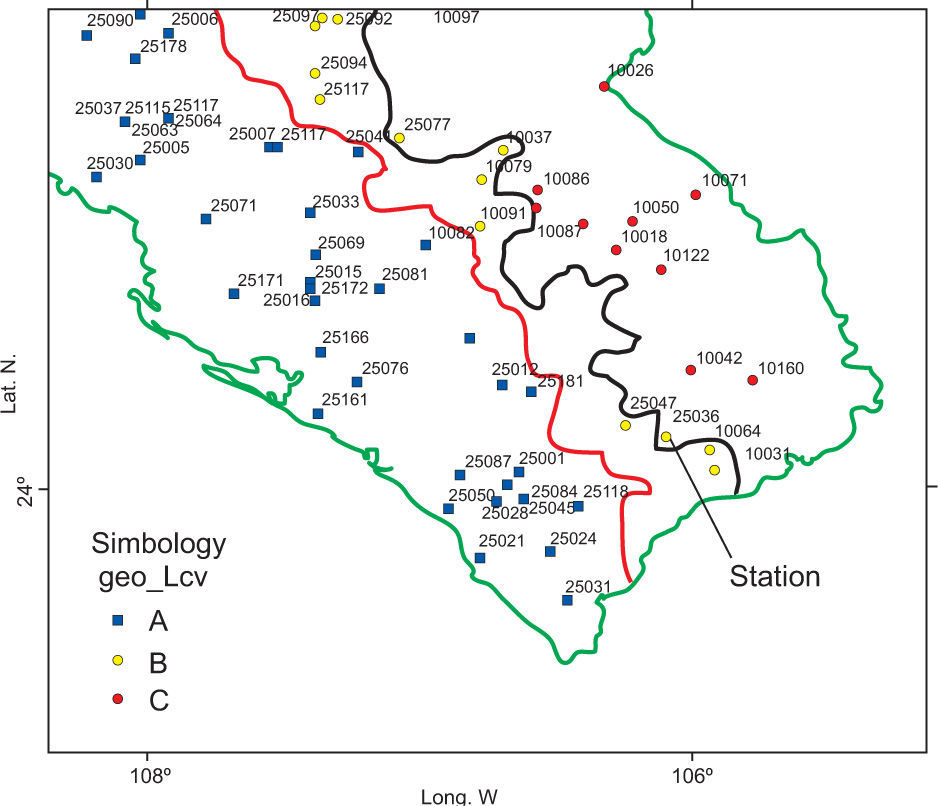
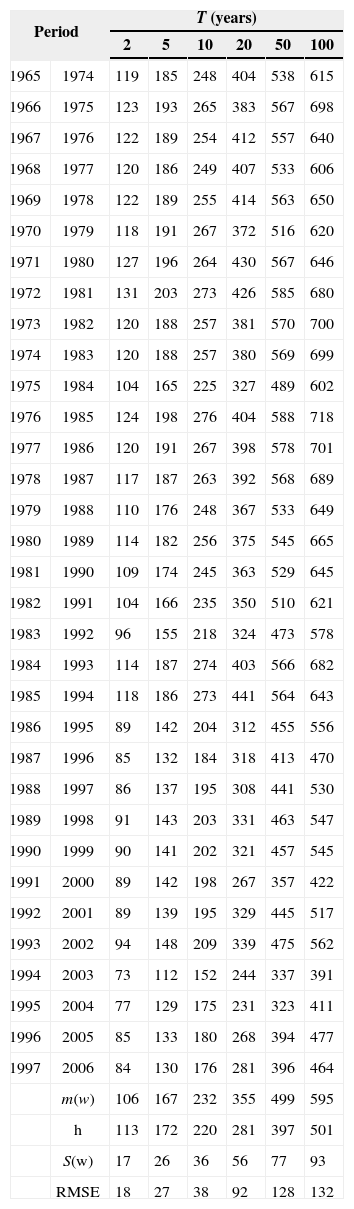
In the samples of case 2, differences among estimates “ω” can be considered very large. In order to improve them, it is possible to form a station-year record by adding information of stations belonging to the same homogeneous region. Again, as an illustrative case, only three neighboring stations are added to each of the 33 sub-samples of case 2. These stations are numbers 10 064, 10 081 and 25 047 (region B from Fig. 11). As already mentioned, each station has 42 years of available information (1965-2006), so the station-year records are formed by 136 values of annual maximum daily rainfall. These 33 station-year records are fitted to different distributions and regional at-site estimates of maximum daily rainfall are obtained. These values are considered as “regional estimates” for short samples with the inclusion of information coming from the same homogeneous region ω. The corresponding RMSE values are presented in Table IX.

Table IX.

Maximum daily rainfall ω (mm) and RMSE for each of the 33 station-year samples at station number 25 036 (case 3).

Period		T (years)
		2	5	10	20	50	100
1965	1974	119	185	248	404	538	615
1966	1975	123	193	265	383	567	698
1967	1976	122	189	254	412	557	640
1968	1977	120	186	249	407	533	606
1969	1978	122	189	255	414	563	650
1970	1979	118	191	267	372	516	620
1971	1980	127	196	264	430	567	646
1972	1981	131	203	273	426	585	680
1973	1982	120	188	257	381	570	700
1974	1983	120	188	257	380	569	699
1975	1984	104	165	225	327	489	602
1976	1985	124	198	276	404	588	718
1977	1986	120	191	267	398	578	701
1978	1987	117	187	263	392	568	689
1979	1988	110	176	248	367	533	649
1980	1989	114	182	256	375	545	665
1981	1990	109	174	245	363	529	645
1982	1991	104	166	235	350	510	621
1983	1992	96	155	218	324	473	578
1984	1993	114	187	274	403	566	682
1985	1994	118	186	273	441	564	643
1986	1995	89	142	204	312	455	556
1987	1996	85	132	184	318	413	470
1988	1997	86	137	195	308	441	530
1989	1998	91	143	203	331	463	547
1990	1999	90	141	202	321	457	545
1991	2000	89	142	198	267	357	422
1992	2001	89	139	195	329	445	517
1993	2002	94	148	209	339	475	562
1994	2003	73	112	152	244	337	391
1995	2004	77	129	175	231	323	411
1996	2005	85	133	180	268	394	477
1997	2006	84	130	176	281	396	464
	m(w)	106	167	232	355	499	595
	h	113	172	220	281	397	501
	S(w)	17	26	36	56	77	93
	RMSE	18	27	38	92	128	132

Case 4

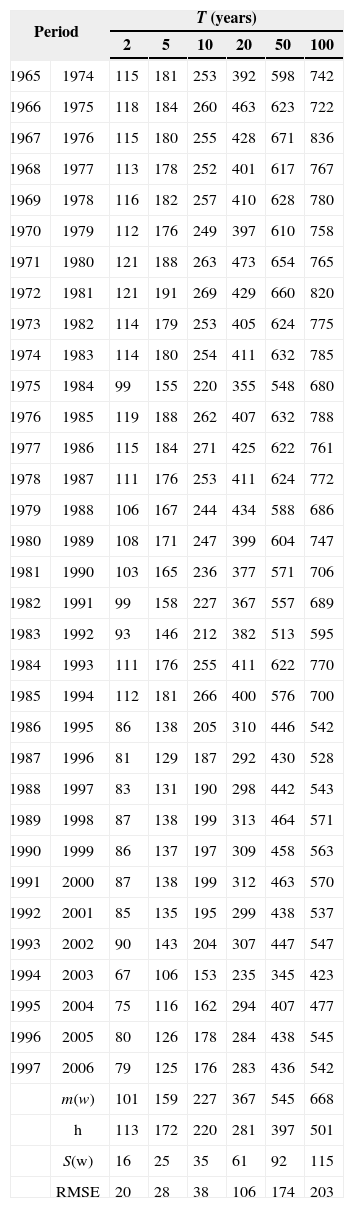
As it can be seen in Table VIII, a substantial gain is achieved by including some additional information to short samples. Additional information of stations 10 042 and 10 160 was added to each of the 33 station-year samples from case 3. These stations are located in a different homogeneous region (region C from Fig. 11). Each sample has a set of 220 values and after a frequency analysis the estimates of maximum daily rainfall were obtained. These values are considered as “regional estimates” for short samples with the inclusion of information coming from the same homogeneous region and from a different homogeneous region ω. The corresponding RMSE values are presented in Table X.

Table X.

Maximum daily rainfall ω (mm) and RMSE for each of the 33 station-year samples at station number 25036 (case 4).

Period		T (years)
		2	5	10	20	50	100
1965	1974	115	181	253	392	598	742
1966	1975	118	184	260	463	623	722
1967	1976	115	180	255	428	671	836
1968	1977	113	178	252	401	617	767
1969	1978	116	182	257	410	628	780
1970	1979	112	176	249	397	610	758
1971	1980	121	188	263	473	654	765
1972	1981	121	191	269	429	660	820
1973	1982	114	179	253	405	624	775
1974	1983	114	180	254	411	632	785
1975	1984	99	155	220	355	548	680
1976	1985	119	188	262	407	632	788
1977	1986	115	184	271	425	622	761
1978	1987	111	176	253	411	624	772
1979	1988	106	167	244	434	588	686
1980	1989	108	171	247	399	604	747
1981	1990	103	165	236	377	571	706
1982	1991	99	158	227	367	557	689
1983	1992	93	146	212	382	513	595
1984	1993	111	176	255	411	622	770
1985	1994	112	181	266	400	576	700
1986	1995	86	138	205	310	446	542
1987	1996	81	129	187	292	430	528
1988	1997	83	131	190	298	442	543
1989	1998	87	138	199	313	464	571
1990	1999	86	137	197	309	458	563
1991	2000	87	138	199	312	463	570
1992	2001	85	135	195	299	438	537
1993	2002	90	143	204	307	447	547
1994	2003	67	106	153	235	345	423
1995	2004	75	116	162	294	407	477
1996	2005	80	126	178	284	438	545
1997	2006	79	125	176	283	436	542
	m(w)	101	159	227	367	545	668
	h	113	172	220	281	397	501
	S(w)	16	25	35	61	92	115
	RMSE	20	28	38	106	174	203

Results indicate that there is a reduction in RMSE values when estimating the quantiles of a short sample (n = 10 years, case 2), taking into account the information from additional climatological stations oming from the same homogeneous region (case 3). However, when information belongs to different regions, RMSE values increase (case 4).

4

Conclusions

The delineation of homogeneous regions is based on multivariate methods: principal component analysis (PCA) and hierarchical ascending clustering (HAC)

A delineation procedure of rainfall homogeneous regions based on the multivariate methods of principal component analysis and hierarchical ascending clustering was presented. A region in northwestern Mexico was selected to apply this methodology.

The indiscriminate use of a large set of variables does not secure a robust result in cluster analysis. This study showed that the most important variables to define a rainfall homogeneous region were the coefficients of variation for series of number of days with rainfall per year, annual rainfall, and maximum daily rainfall for each month, which can be used as initial variables.

When coefficients of variation were substituted by their corresponding L-moments versions and the geographical characteristics were included into simulation, the HAC analysis allowed to obtain homogeneous regions that effectively preserve meteorological and orographic relationship (physical representation). So, three regions were settled, the first one from 0 to 500 masl, the second from 500 to 1500 masl, and the last one over 1500 masl.

The Kruskal-Wallis test was applied to prove that the chosen clusters are independent from each other, and they can be considered as different homogeneous regions.

Data-based results indicate that the inclusion or exclusion of information in the regional techniques has a direct impact on the estimation of maximum daily rainfall associated to different return periods. These differences could increase either the costs of hydraulic works or the risk of flooding, both of which affect people and their properties. Thus, it is very important to make a correct delineation of homogeneous regions.

Acknowledgments

The authors wish to express their gratitude to anonymous reviewers whose comments improved this paper.