Este trabajo explora el flujo zonal en forma de polinomios de Legendre. El flujo básico se divide en un flujo zonal simétrico y una onda de Rossby-Haurwitz (RH). Varias características (más realistas) de este flujo zonal lo hacen particularmente interesante, como las corrientes en chorro con dirección oeste en latitudes medias y un viento con dirección del este alrededor del ecuador, muy similar al flujo medio horizontal del periodo diciembre-enero a 200 mb. El flujo zonal se combina con la onda RH para evaluar las etapas tempranas del mecanismo de acciones de bloqueo en el Pacífco nororiental. Se llevó a cabo una simulación numérica utilizando un modelo barotrópico lineal con forzamiento tropical y disipación para analizar la respuesta extratropical del mecanismo de reforzamiento de torbellinos en los sistemas de alta presión a lo largo de la costa occidental de Norteamérica.
This study explores the zonal flow in the form of Legendre polynomials. The basic flow is divided into a zonally symmetric flow and a Rossby-Haurwitz (RH) wave. Several features of this (more realistic) zonal flow make it particularly interesting, such as the midlatitude westerly jet streams and an easterly wind around the equator, which closely resembles the mean horizontal flow at 200 mb of the December-February period. The zonal flow is combined with the RH wave, in order to test the blocking formation mechanism on early stages for the northeastern Pacific. A numerical simulation has been performed using a linear barotropic model with tropical forcing and damping to check the extra-tropical response of the mechanism of eddies reinforcement of the ridge along the western coast of North America.
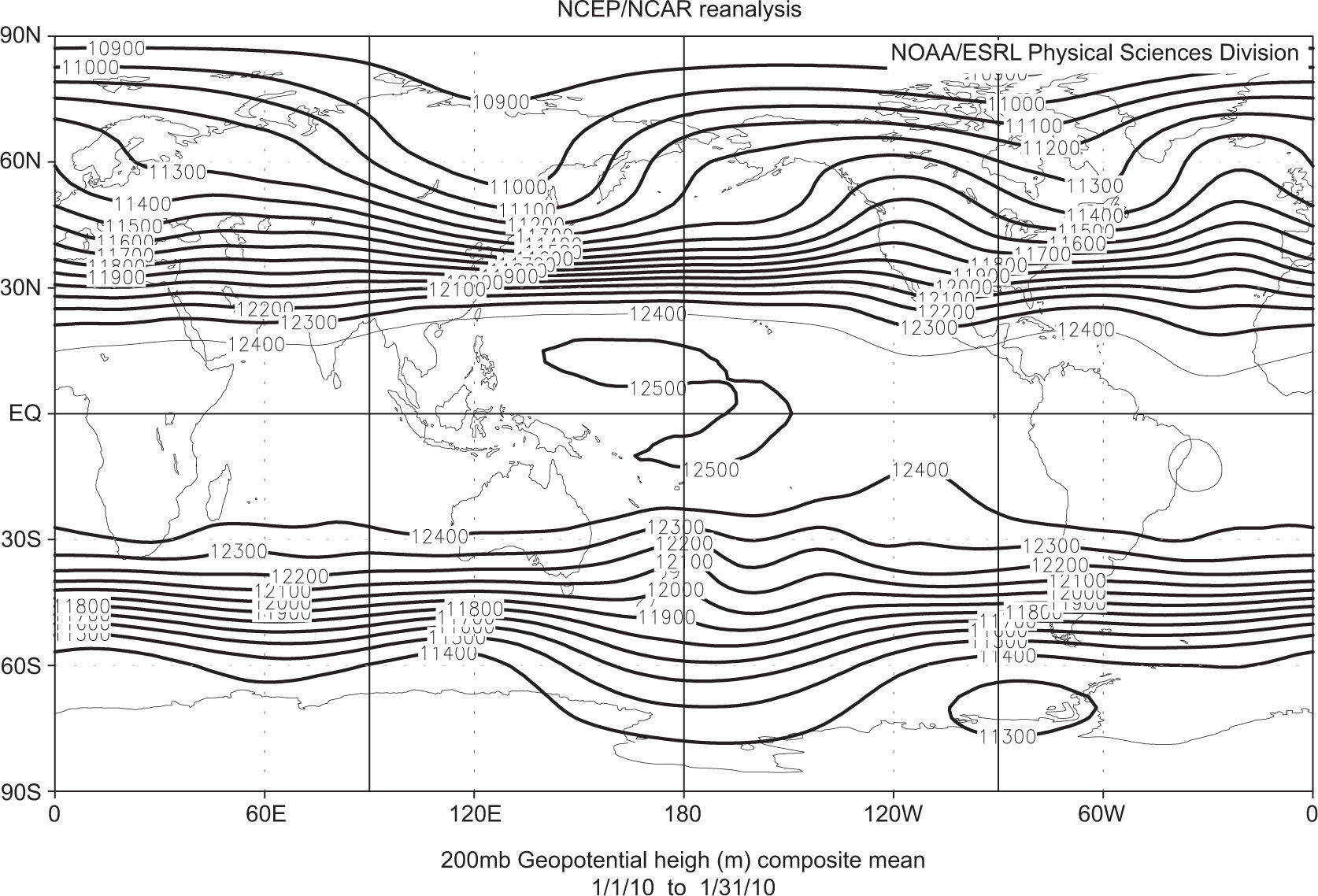
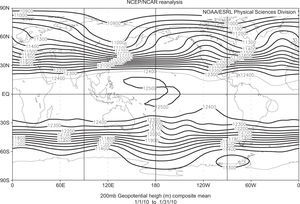
During the period from December 2009 to February 2010, the sea surface temperature (SST) in the central Pacific was anomalously warm. The Northern Hemisphere winter of 2009-2010 was notable for its low-frequency anomalous behavior because it was extremely cold in many places (Pérez-García et al., 2010; Wang et al., 2010; Kim et al., 2011; Ratnam et al., 2012). Figure 1 shows the 200-hPa geopotential height, a meridional dipole-like structure in its incipient stages that extended from the western North America to the southwest of Mexico on January 27, 2010. A convective heating over the tropical central and eastern Pacific linked to a teleconnection called the Pacific-North American pattern (PNA) (Wallace and Gutzler, 1981), is known to have influenced the extratropical circulation over the northeastern Pacific, Canada, and the southeastern USA.
Many theories have been proposed to understand the onset and maintenance of the teleconnection patterns and the synoptic blocking events in the atmosphere (Hoskins and Karoly, 1981; Haines and Marshall, 1987). The PNA manifests itself as a warm ridge (southerly flow) along the western coast, and a cold trough over eastern North America (Rex, 1950; Lejenas and Okland, 1983). The use of a one-level barotropic model to simulate the extra tropical response to a fixed tropical heating has been reported in several studies (Simmons, 1982; Branstator, 1983; Held and Kang, 1987; Sardeshmukh and Hoskins, 1988; Grimm and Silva-Dias, 1995), which found that the remote response to (steady) tropical forcing has an equivalent barotropic structure, and that energy propagation is influenced by both zonal and meridional variations of the basic-state flow. Simmons et al. (1983) show structures similar to the observed PNA when the barotropic model is linearized about the zonally varying flow (300 hPa mean of January flow). These flow patterns are related to the more unstable normal mode associated with barotropic instability. Hoskins and Ambrizzi (1993) examine the most frequent trajectories of the Rossby waves in a longitudinally varying flow, and found that the jet stream can act as waveguides in the atmosphere.
This study aims to increase the understanding of the northeastern Pacific blocking formation mechanism in its incipient stages, in connection with the Rossby-Haurwitz (RH) wave. Due to its importance, numerical simulations were performed with a barotropic model on a basic flow regarded as the sum of a zonally symmetric flow and an RH wave component. Midlatitude westerly jet streams are embedded within the zonally symmetric flow. In addition, linearized barotropic models through the zonally symmetric state are easier to simulate than those observed in the zonally asymmetric flow, because time-averaged basic flows generally do not satisfy the steady barotropic vorticity equation (BVE). Section 2 of this paper highlights some previous research related to the BVE on the sphere with forcing and damping, and also a brief description of the up-to-date solutions to the normal mode instability. In Section 3, the basic flow is constructed analytically; the selection of such basic flow allows for the application of analytical methods, which increase its potential use in persistent anomalies and low-frequency variability studies. The non-divergent vorticity equation for the vorticity perturbations, which is numerically time-integrated and has a steady tropical divergence forcing and damping, is addressed in Section 4. In order to test the extra-tropical response to tropical forcing, we explore the mechanism in which eddies can reinforce the warm ridge along the western coast of North America.
2Barotropic vorticity equation and linear instability on a sphereA viscous two-dimensional incompressible rotating fluid on a unit sphere is governed by a non-linear BVE with forcing S and damping F, whose non-dimensional form can be written as:
where Ψ(λ, μ, t) is the stream function; μ = sinϕ; ϕ and λ are the latitude and longitude; ς = ΔΨ + 2μ is the absolute vorticity; Δ is the Laplace operator;
is the Jacobian; vΨ=k×∇Ψ={uΨ,vΨ}={−1−μ2∂Ψ∂μ,11−μ2∂Ψ∂λ} is the horizontal with eastward and northward components uΨ and vΨ, respectively; and k is the normal vector to unit sphere. The term F = −σΔΨ + v(−Δ)s+1Ψ, σ is the Rayleigh friction coefficient, where v is the viscous dissipation constant, and s ≥ 1 must be a real number (Skiba, 1989).
Eq. (1) captures many features of the large scale dynamics of the barotropic atmosphere while providing a deeper understanding of the teleconnection patterns (Hoskins and Karoly, 1981; Simmons, 1982; Branstator, 1985; Sardeshmukh and Hoskins, 1985, 1988; Held and Kang, 1987; Haarsma and Opsteegh, 1989; Lau and Peng, 1992), and also the synoptic blocking events in the atmosphere (Shutts, 1983; Buizza and Molteni, 1996; Nakamura et al., 1997; Nascimento and Ambrizzi, 2002). Another well-known mechanism for the generation of low-frequency variability is the instability of non-zonal basic flow as proposed by Simmons et al. (1983).
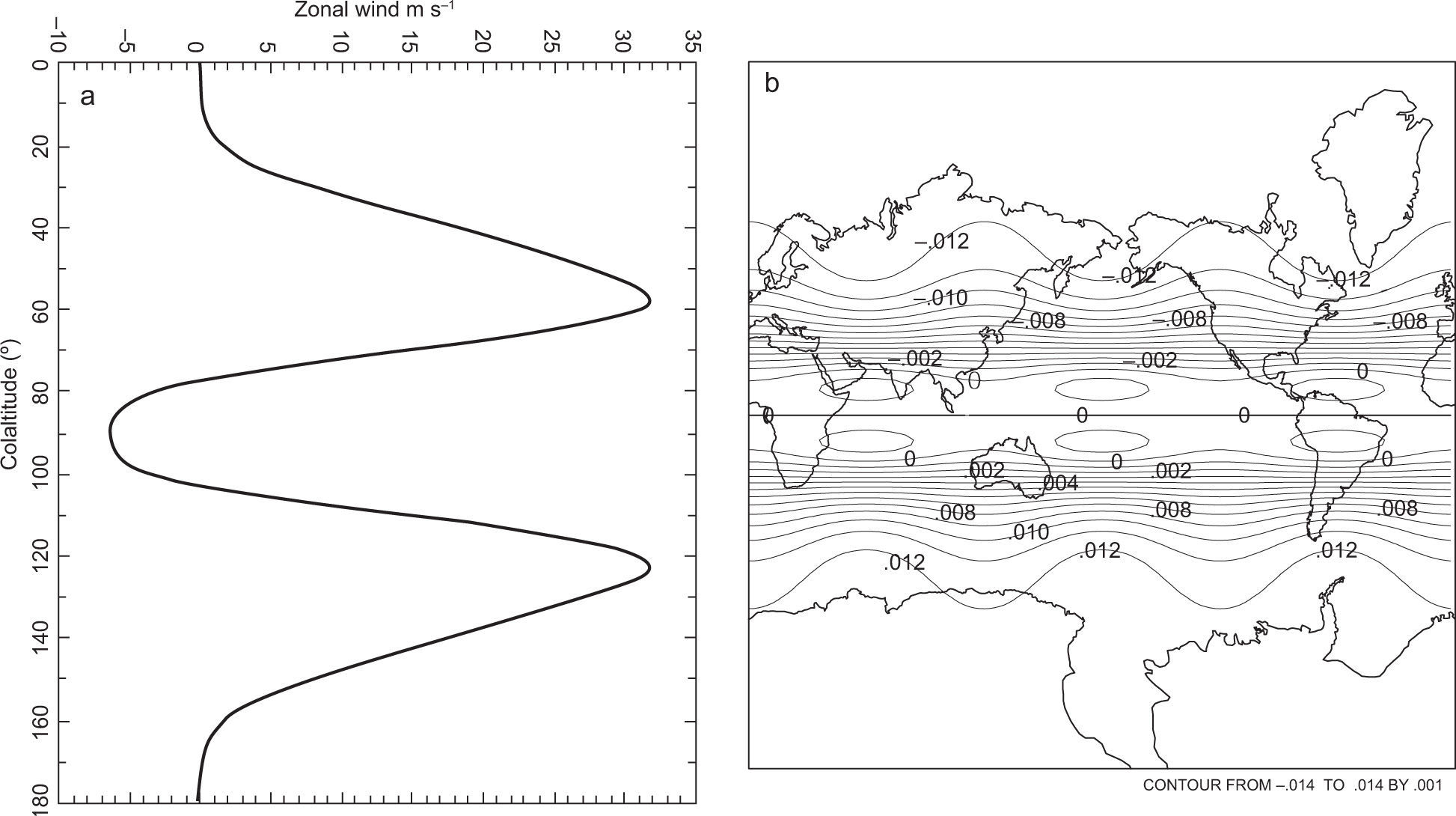
There are four widely-accepted solutions of BVE (for the ideal flow): the simple zonal flows Ψ(μ), more complicated flows called RH waves, the Wu-Verkley (WV) wave (Wu and Verkley, 1993) and modons (Tribbia, 1984; Verkley, 1984, 1987, 1990; Neven, 1992). RH waves are very useful for interpreting the large-scale wave structures in the atmospheric circulation of midlatitudes. Nevertheless, in tropical latitudes these structures cannot easily be described in terms of RH waves. Therefore, RH waves are still far from real atmospheric conditions in these regions, because the primary store of atmospheric kinetic energy is the zonal mean flow, and the growth of perturbations most often results from transfer of mean energy to the perturbations. This study explores how the change in the mean flow alters the evolution of the perturbations to the flow. Thus, the total flow was divided into a zonal symmetric flow Ψo(μ) and a wavy flow. It is in the interest of this study to observe the zonal symmetric flow, with the midlatitude westerly jet streams and a weak easterly wind around the equator (Fig. 2a). These zonal flows Ψo(μ) are assumed in the form of a linear combination of Legendre polynomials.
The basic model used in the present study was the non-divergent vorticity equation for the vorticity perturbations linearized about the basic flow Ψ˜;:
where ς′ = ξ′ + 2μ and ξ′ are the absolute and relative vorticities of the perturbation, respectively,
is the BVE operator linearized about the basic flow, ṽψ is the non-divergent component of the basic wind, the tilde represent basic flow, and primes are referred to infinitesimal perturbation, which in the form of a normal mode
leads to the spectral problem
for the linearized operator LG=J(G,˜;Δ−1G)−J(Ψ˜;,G)−[σ+v(−Δ)s]G, where ω =ωr + iωi, is the eigenvalue and G the eigenfuction. In the normal mode (linear) stability analysis, the basic state must be regarded as a steady state. Eq. (3) is then solved by representing all variables as series of spherical harmonics and using a triangular truncation TM for some M, reducing Eq. (3) to a discrete spectral problem
for a matrix L with elements
where Bβαγ=χβ−1−χγ−1
is the complex element of a diagonal matrix D. We used here the complex index α= (mα, nα) by Platzman (1962) and Skiba (1989), the Kronecker delta δαγ, and χβ = nβ (nβ + 1). It follows from Dαγ, that the linear drag (σδαγ) shifts the spectrum of L along the real axis to the left by value σ (Zhang, 1988). Indeed, for a k th eigenvalue with a linear drag ó can be represented as ((ωr)k − σ + i(ωi)k) and the stream function of a normal mode is
Thus, the instability (if ωr > 0) decreases with σ, where θ(λ,μ)=argΨˆ(λ,μ) is the initial phase of the mode. The diagonal term vχγS rised with v, and nγ increasing the distance between eigenvalues and the net effect of horizontal diffusion is the damping of small scale motion for a large power s.
3Zonal circulation and superimposed Rossby-Haurwitz perturbationIn this section the interaction between a zonal flow and an RH wave is addressed. This interaction is of particular importance to the theory of the general circulation of the atmosphere. As a representative of the mean zonal wind profile and also appropriate to the BVE, the distribution of the climatological zonal wind at 500 mb is analyzed after Kasahara (1980). Figure 1 in Kasahara (1980) (not shown) shows the four mean zonal wind distributions of the four different seasons corresponding to December, January, February (DJF); March, April, May (MAM); June, July, August (JJA); and September, October, November (SON). Over the regions of the subtropical NH jet stream, zonal wind speed decreased from DJF to JJA. However, from JJA to DJF, zonal wind increased with time. Within the NH the expected zonal wind pattern is that zonal wind will increase with time, due to the seasonal changes from JJA to DJF, and also an increment in the temperature gradient between the North Pole and the equator. The zonal wind behavior in the SH is the opposite. As the seasonal transition from winter to summer develops, the temperature gradients should decrease between the South Pole and the equator, and zonal wind should diminish as well. Therefore the zonal wind profile is directly related to the evolution of the lower level temperature field. Consequently, a zonally symmetric flow with horizontal shear can be constructed analytically. The simplest example is a flow defined by Ψo(μ) = aPn(μ), if n is odd, in which Pn(μ) is a Legendre polynomial, with a as an arbitrary constant. The zonal symmetric flow is then analytically formulated so that the midlat-itude westerly jet streams are preserved with a weak easterly wind around the equator. Not only should the zonal wind profile be consistent with climatology, but attention must also be given to the vorticity of the zonal flow in the equatorial region as noted by Wu (1993). The effect of the zonally symmetric flow, given by a linear combination of two Legendre polynomials, P1(μ), and Pn(μ) on the Rossby wave distribution was studied by Karunin (1970) and Wu (1992) for n = 3.
Observational evidence indicates that the zonal flow pattern can be approximately represented by a linear combination of seven Legendre polynomials of odd parity (Baer, 1968):
where N = 7 and b0 = −0.2677, b1 = 8.20 × 10−2, b2 = −5.95 × 10−2, b3 = 1.067 × 10−2, b4 = 2.1981 × 10−3, b5 = −3.71 × 10−3, b6 = 2.57 × 10−3 and b7 = −6.475 × 10−4. The zonal flow has the maximum westerly of 33 ms−1 at 35° north and south, and an easterly wind of 5 ms−1 at the equator. This zonal wind field resembles the upper troposphere during the northern winter (Fig. 2a).
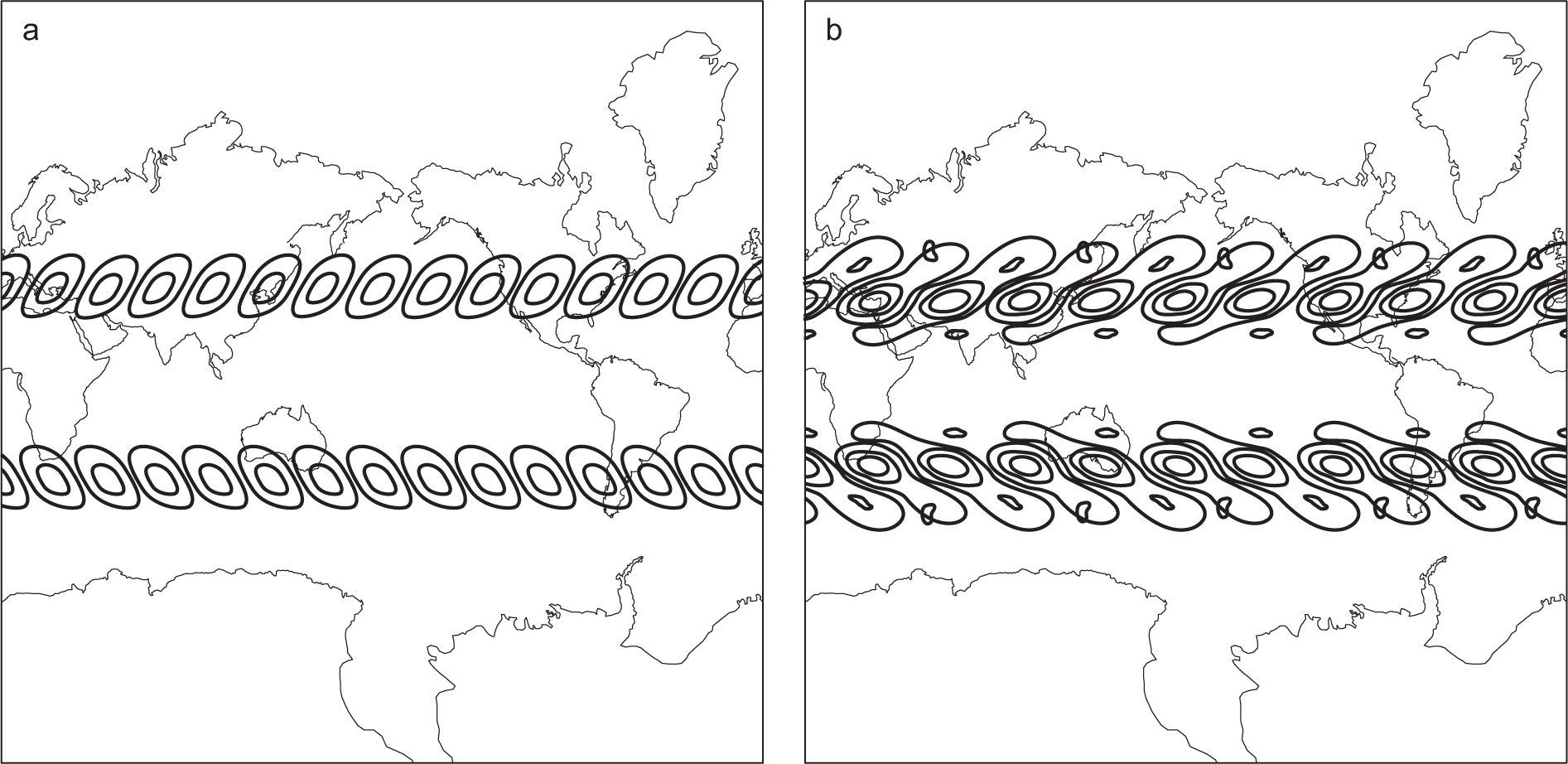
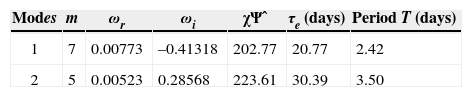
Several papers have been devoted to the linear instability of the zonal flows since Rayleigh (1880). We used the Rayleigh-Kuo necessary condition for the instability (Kuo, 1949): If Ψo(μ) is let to be a zonal flow on the sphere, then a normal mode may be unstable only if the derivative ∂ςo∂μ of the absolute vorticity ςo = ΔΨ0(μ) + 2μ, of flow Ψ0(μ) changes its sign at least in one point of the interval (−1, +1). Then ∂ςo∂μ=2−∑j=1Nχ2j+1bj∂P2j+10∂μ changes its sign at least in one point of the interval (−1, +1). Thus Eq. (5) may have an unstable normal mode (Pérez-García, 2001), being almost the only useful instability condition known for zonal flow described by a linear combination of Legendre polynomials. The numerical algorithm developed for the normal mode instability of arbitrary steady flow (Pérez-García and Skiba, 2001) has been previously tested for the zonal flow with a linear combination of two Legendre polynomials (zonal RH waves), P1(μ) and Pn(μ). Now, if the same numerical algorithm is tested for the zonally symmetric flow (Eq. 5), where 2j+1 is odd, the amplitude of modes can be symmetric or antisymmetric around the equator. There are few unstable modes; a mode ψ′ is unstable if ωr > 0, decaying if ωr < 0, neutral if ωr = 0 and stationary if ωi = 0. The main parameters of the first two most unstable modes are given in Table I, and the isolines of the real part of the amplitudes Ψr (λ, μ) are presented in Figure 3a, b. The e-folding time τe=12π|ωr|, period T=1|ωi|, and the spectral number χΨˆ (Skiba, 2000; Skiba and Pérez-García, 2004) are also given in Table I. Unstable perturbations are observed in the neighborhood of subtropical jets, and the dominant zonal wavenumber of the modes are m = 7 and m = 5.
The most unstable mode of the zonal flow described by Eq. (5).
| Modes | m | ωr | ωi | χΨˆ | τe (days) | Period T (days) |
|---|---|---|---|---|---|---|
| 1 | 7 | 0.00773 | –0.41318 | 202.77 | 20.77 | 2.42 |
| 2 | 5 | 0.00523 | 0.28568 | 223.61 | 30.39 | 3.50 |
The RH wave has proved to be very useful for interpreting the large-scale wave structures in the atmospheric circulation of midlatitudes. On the tropical latitudes these structures cannot easily be described in term of RH waves. Assume at a moment t that a basic wave is the sum of a zonal symmetric flow Ψ0(μ) and an RH wave, then the basic flow can be written as:
where
and
is a constant denoting the angular phase speed of the RH wave, wo is the strength of solid-body rotation flow, and Pnm(μ) is the Legendre function of degree n and the am wave amplitude. The RH wave RH(m, n) is steady when cnRH = 0, and wo=2χn−2. One may also consider the homogeneous spherical polynomials of the degree n:
as a perturbation of the basic flow Ψo(μ) - woμ. This perturbation is a linear combination of the 2n + 1 spherical harmonics, moving in the λ− direction with the speed c=−2χn.
When the basic stream function is Ψ(λ, μ, t) = Ψo(μ) − woμ + Ψn(λ, μ, t) at time t, Eq. (1) for the ideal flow (σ = v = 0) and without any external forcing leads to
Let the zonal-mean zonal wind U0(μ)=−1−μ2∂Ψ0∂μ, and the zonal-mean angular velocity that relates to the zonal-mean stream function (Chen, 1993) and zonal-mean wind by
in which Ynm is an eigenfunction of the Laplace operator with eigenvalue −χn; i.e ΔYnm=−χnYnm, so using
one shows easily that
from which it follows that a zonally propagating solution can be generally expressed in the form Ψn(λ, μ, t)=F (λ−ct, μ) where
is the phase speed. Then, by noting that ∂ΔΨ0μ∂μ=−∑j=1Nbj χ2j+1∂P2j+1o(μ)∂μ, the following assertion is valid:
Proposition. Letting , Ψo(μ) be the linear combination of the LP flow (Eq. 5), for any N, and −woμ + Ψn(λ, μ, t) the basic RH wave, then the Ψ(λ, μ, t) = Ψo(μ) − woμ + Ψn(λ, μ, t) flow is a wave propagating zonally with angular velocity c (u) given by
As ΔΨ0μ=−∂∂μcosϕU0μ, its latitudinal derivative
The pattern of the phase velocity (Eq. 7) for an RH wave embedded within a zonal flow is then analized:
On one hand, the second term of Eq. (9) when compared with the observed zonal flow increases about 30% within the jet stream regions, while the increment in different latitudes is of the same order as Uo(μ) On the other hand, the third term of Eq. (9) shows values of the same order as Uo(μ) within the jet stream regions. In accordance with the RH wave theory and also using Eq. (9), without zonal-mean zonal wind Uo(μ) long RH waves propagate more quickly than short RH waves against the direction of the zonal flow. When the zonal-mean zonal wind Uo (μ) is added to the situation, short RH waves move faster in the direction of the zonal flow because of their initial small speed against this flow. RH waves embedded in the zonal flow exhibited decreasing speed as the RH wave number decreased.
The wave Ψ is steady when c = 0, and
The horizontal structure of the steady wave
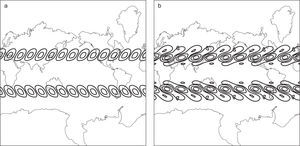
with a = 5 × 106, n = 6, and m = 3 is shown in Figure 2b. The scheme developed above is particularly interesting because it replicates some of the most important features of the zonal flow, e.g. the midlatitude westerly jet streams that closely resemble the mean horizontal flow at the upper troposphere during the boreal winter (Fig. 1). These basic waves are also frequently called planetary waves due to their known global structures.
The numerical normal mode stability of the RH (3,6) wave has been studied by Pérez-García (2001). The skill of the (normal mode stability) algorithm of this study has been checked by comparing it with the numerical stability results (Skiba and Pérez-García, 2006, 2009) using the analytical solution obtained by Skiba (2000).
4The extratropical response to tropical forcingWe now consider the barotropic model of the extra-tropical response to tropical forcing. The forcing at Eq. (2) associated with divergence is expressed as S′, specifed by
where vχ is the irrotational wind. The Rossby wave source (S′) contains contributions from both the vortex stretching effect and the advection of absolute vorticity by the divergent flow. Eq. (2) is numerically integrated (similarly to Pérez-García and Skiba, 1999) in the sphere using the spectral transform technique by representing all variables in a series of spherical harmonics truncated at T42. The case s = 2 at F = −σΔΨ + ν(−Δ)s+1Ψ has been considered, being σ a linear damping with a time scale of 14.7 days so that linear instability is inhibited, v is a biharmonic diffusion, and v = 2.338×1016m4 s−1 (Sardeshmukh and Hoskins, 1988).
Numerical simulations are performed with linear barotropic models with a tropical divergence forcing and damping. This scheme was chosen in order to test the extratropical response to tropical forcing that includes a hypothetical mechanism by which eddies can reinforce the ridge along the western coast of North America. Some models that linearized about a zonally symmetric flow have shown important differences from those that linearized about the zonally asymmetric climatological flow, as reported by Borges and Sardeshmukh (1995). In the present study we used Eq. (10) as the basic flow, because climatological basic flows are not maintained only by barotropic processes.
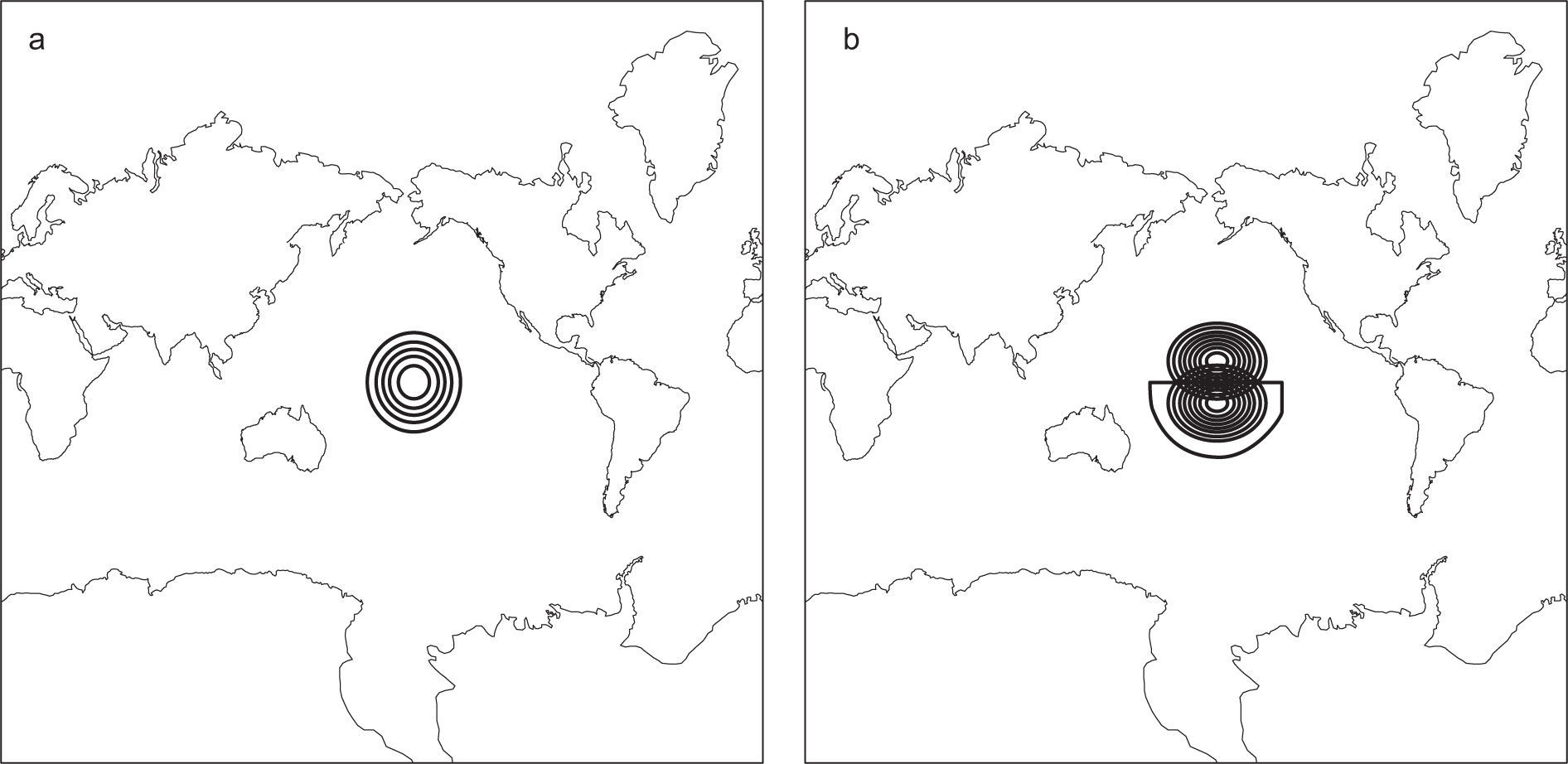
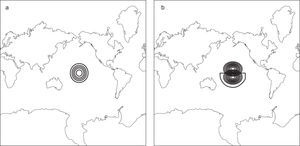
In order to examine the propagation of stationary Rossby wave trains in the model, a circular region of steady divergence (Hoskins and Karoly’s blob [1981]) on the equator is introduced (Fig. 4a) and the resulting steady perturbation on this longitudinally varying basic flow is determined by integrating the model based on Eq. (2) to a steady state. The source S is approximated to be S′=−∇·vχ′ς˜;−ς˜;D′ and is shown in Figure 4b, being similar to the model of Sardeshmukh and Hoskins (1988). The response on day 35, when a steady state is almost reached, can be observed in Figure 5b. The wave activity emanates from the region of the divergence and propagates eastwards and polewards in almost great-circle paths.
Isolines of the stream function Ψ˜;λ,μ+Ψ′λ,μ,t (a), and isolines of the stream function perturbation ψ′ (λ, μ, t) on day 35 (b) predicted by the linear model (Eq. [2]).
Dramatically, the numerical simulations reinforce the warm ridge along the western coast of North America, as seen in Figures 5a and 1. The magnitude of the extratropical response exhibits more sensitivity, as seen in Figure 5b. Finally, there is no wave propagation between both hemispheres because the equatorial region is controlled by easterly winds.
5ConclusionsThis paper has explored a basic flow for the BVE with a more realistic zonal flow. The selection of the basic flow allows the application of analytical methods, which increase its potential use in persistent anomalies and low-frequency variability studies. These basic waves form a different set from RH waves, WV waves, and modons. Their global structures closely resemble the mean horizontal flow at the upper troposphere during the boreal winter. Such basic waves compose an RH wave embedded within a zonal flow, clearly different from the known RH wave solution. RH waves are useful for interpreting the large-scale wave structures in the atmospheric circulation of midlatitudes. Nevertheless these structures cannot easily be described in terms of RH waves on the tropical regions.
Numerical experiments were performed using the non-divergent vorticity equation for the vorticity perturbations using the basic wave, with linear damping, diffusion and a tropical forcing included. In order to examine the propagation of stationary Rossby wave trains in the model, a circular region of steady divergence was introduced on the equator, located at 195° E, and the resulting steady perturbation on this basic flow was determined by integrating the model based on Eq. (2) to a steady state. The wave activity emanates from the region of the divergence and propagates eastwards and polewards in almost great-circle paths, and the magnitude of the extratrop-ical response exhibited more sensitivity. A dramatical reinforcement of the ridge along the western coast of North America was observed, very similar to the Pacific-North American (PNA) pattern. In the near future we will test the numerical normal mode stability algorithm with the basic flow.
I want to acknowledge Alejandro Aguilar and Marco A. Salas for their suggestions on the original manuscript of this paper and Alfonso Salas for his assistance in the computer graphics used in the preparation of this text. The author is also grateful to Claudio Amescua and Alberto Alazraki for their helpful suggestions for improving the manuscript.




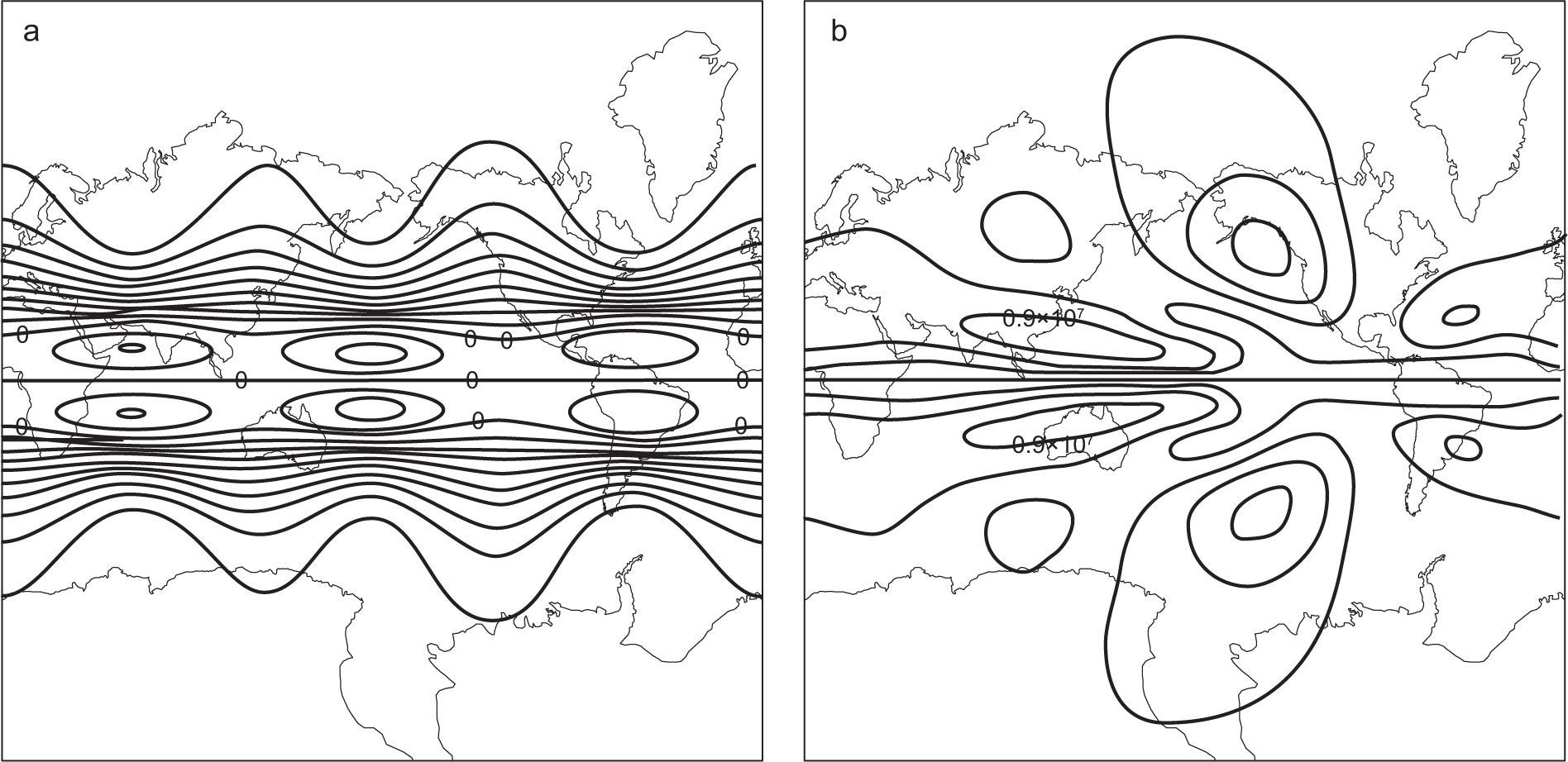
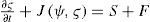
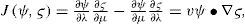
![Wind zonal of linear combination of Legendre polynamials (Eq. [5]) (a), and basic flow stream function from Eq. (10) (b). Wind zonal of linear combination of Legendre polynamials (Eq. [5]) (a), and basic flow stream function from Eq. (10) (b).](https://static.elsevier.es/multimedia/01876236/0000002700000003/v2_201505081718/S0187623614711130/v2_201505081718/en/main.assets/thumbnail/gr2.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
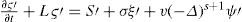
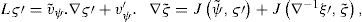
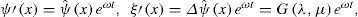
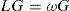
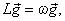
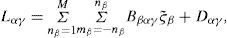
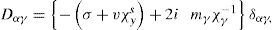
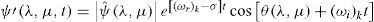
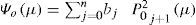
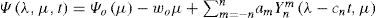
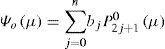
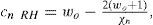
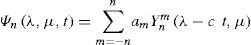
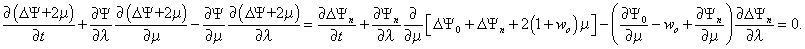
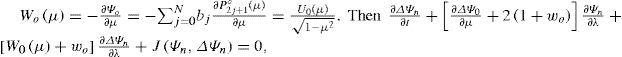
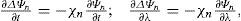
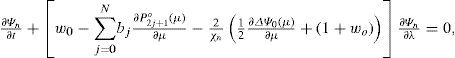
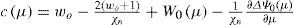
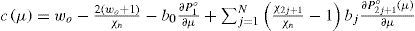
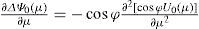
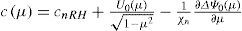
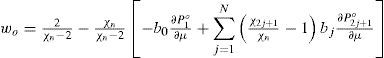

![Isolines of the stream function Ψ˜;λ,μ+Ψ′λ,μ,t (a), and isolines of the stream function perturbation ψ′ (λ, μ, t) on day 35 (b) predicted by the linear model (Eq. [2]). Isolines of the stream function Ψ˜;λ,μ+Ψ′λ,μ,t (a), and isolines of the stream function perturbation ψ′ (λ, μ, t) on day 35 (b) predicted by the linear model (Eq. [2]).](https://static.elsevier.es/multimedia/01876236/0000002700000003/v2_201505081718/S0187623614711130/v2_201505081718/en/main.assets/thumbnail/gr5.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)