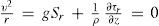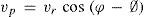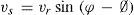Secondary currents: Measurement and analysis

Resumen

La dinámica de fluidos tiene como propósito entender el movimiento de líquidos y gases por medio de funciones que describen la distribución de velocidades. Algunos fenómenos naturales que presentan estas funciones son los huracanes, los cuales son generados por las diferencias de presión; los ciclones, cuya fuente primaria de energía es el gradiente horizontal de temperatura, y los remolinos, que están ligados al gradiente de presión hidrostático. En el caso particular de los remolinos, éstos generan velocidades secundarias, las cuales son flujos que se forman por la existencia de fuerzas desiguales entre el gradiente de presión hidrostático y las fuerzas centrífugas, o debido a esfuerzos cortantes tal como sucede en la unión de dos o más flujos. Este fenómeno también se observa en tornados, donde la fuerza centrífuga es mayor en la parte superior y luego va disminuyendo hacia el fondo, mientras que en los ríos se detecta particularmente en curvas y uniones (confluencias). Entender cómo se desarrollan estas velocidades secundarias es de interés, debido a que el comportamiento de los flujos está en función de la magnitud de dichas velocidades, de modo que su caracterización es fundamental. El objetivo de este estudio fue estimar las velocidades secundarias en la unión de dos ríos, a partir de mediciones de campo realizadas con medidores acústicos Doppler. Un segundo objetivo fue graficar las velocidades secundarias y, en consecuencia, apreciar las líneas de corriente y los mecanismos de rotación de flujo. Estos mecanismos están relacionados con los procesos de erosión y sedimentación, por lo que su entendimiento ayudará a pronosticar cambios morfológicos en los ríos.

Abstract

Fluid dynamics has the purpose of understanding the movement of liquids and gases by functions that describe the distribution of velocities. Some natural phenomena that present these functions are hurricanes, generated by pressure differences; cyclones, developed by the horizontal temperature gradient; and eddies, associated with a hydrostatic pressure gradient. In the particular case of eddies, they generate the so-called secondary velocities, which are flows formed by the presence of unequal forces between a hydrostatic pressure gradient and centrifugal forces, or by shear stresses at the joining of two flows. In addition, this phenomenon is observed in tornados, where the centrifugal force is greater in the upper layer and decreases towards the bottom, whereas the pressure gradient moves from a high to a low pressure; while in rivers it is detected particularly in bends or joins. Understanding the development of secondary currents is important for the reason that flow behavior is a function of the magnitude of these currents; hence their characterization is fundamental. The objective of this study was to obtain the secondary velocities developed as an effect of the union of two water currents, based on data acquired from Doppler acoustic recorders. A second objective was to draw the secondary velocities and to show the rotation flow effect, a kind of results that are difficult to obtain in any other way. The flow mechanisms are related with erosion and sedimentation processes; therefore, understanding them might help to evaluate and predict morphological changes in rivers.

1

Introduction

Unequal forces generate velocity components on a direction transverse to the flow, which produces a circulation named secondary current. This flow, coupled with the longitudinal movement, causes a helical flow that forms or models the section into the curves (Perkins, 1970). Furthermore, it is stated that it is not possible to reach an adequate description of the flow in curves or shallow water from one-dimensional models and even from classical two-dimensional models, such as the Saint-Venant equations, due to the essentially three-dimensional nature of the flow (Weber, 2007). Given these facts, a better understanding of hydrodynamics presented in curves and junctions, characterized mainly by the secondary flow, is necessary. The velocity on these areas is not uniformly distributed (Odgaard, 1982); rather, it is logarithmic due to the flow resistance produced by the bottom when turning on the same radius.

Hydrometric windlasses are used in traditional measurements of currents in channels (Priego et al., 2012); however, these are only able to measure the magnitude of the velocity vector in the main flow direction. In recent years, in order to experimentally characterize the velocity field and flow discharge in river environments, acoustic Doppler current profilers (ADCP) have been developed. However, its use in Mexico is still incipient, mainly due to lack of knowledge about its use and capabilities. In most of the documented cases, its use in Mexico is limited for flow measurement purposes, which results in high costs since these devices are expensive and require skilled personnel for its operation. These devices base their functioning on sound, in order to measure the particles suspended in water and obtain velocity compounds of the flow in three directions. From this kind of data and applying the Rozovskii development (1957), it is possible to estimate the secondary currents through the following equation:

where v is the velocity, ρ is the water density, r the curvature radius, S_r the cross slope, τ_r the transverse shear force, and g the acceleration of gravity. The first term in Eq. (1) is the centrifugal acceleration, the second is related to the slope of water on a transverse surface, and the third is the turbulent shear force.

Rozovskii (1957) and Kikkawa et al. (1976) indicated that the magnitude of the secondary flow is directly related to the water depth for the curvature's radius and the vertical profiles of transverse velocity, which vary significantly with the flow resistance of the bottom. However, secondary currents in the confluences are characterized by complex hydrodynamic conditions and which knowledge is essential for the development of a general theory; however, at present few field data are available (Best, 1987;Bridge, 1993;Weerakoon et al., 1991). Some conceptual models, based on experimental work (Lane et al., 1998;Roberts, 2004;Song et al., 2012) indicated that the hydrodynamic characteristics of the confluences include an area of stagnant flow upstream, which generates a shear layer or section (abrupt change on direction of velocities) between the junction of the two flows. The surface of this convergence generates a helical cell on each side of the shear layer, and flow separation occurs immediately downstream of the confluence (Mosley, 1976;Best, 1987).

Rozovskii (1957) and Bathurst et al. (1977) used electromagnetic flow meters in determining the transverse and longitudinal components of the velocity vector. Other authors such as Rhoads and Kenworthy (1995) proposed to identify separately the contributions of the uneven flow and the helical motion for the velocity field of cross currents; as a first approximation, primary and secondary velocities were calculated, and the components of the cross currents were determined.

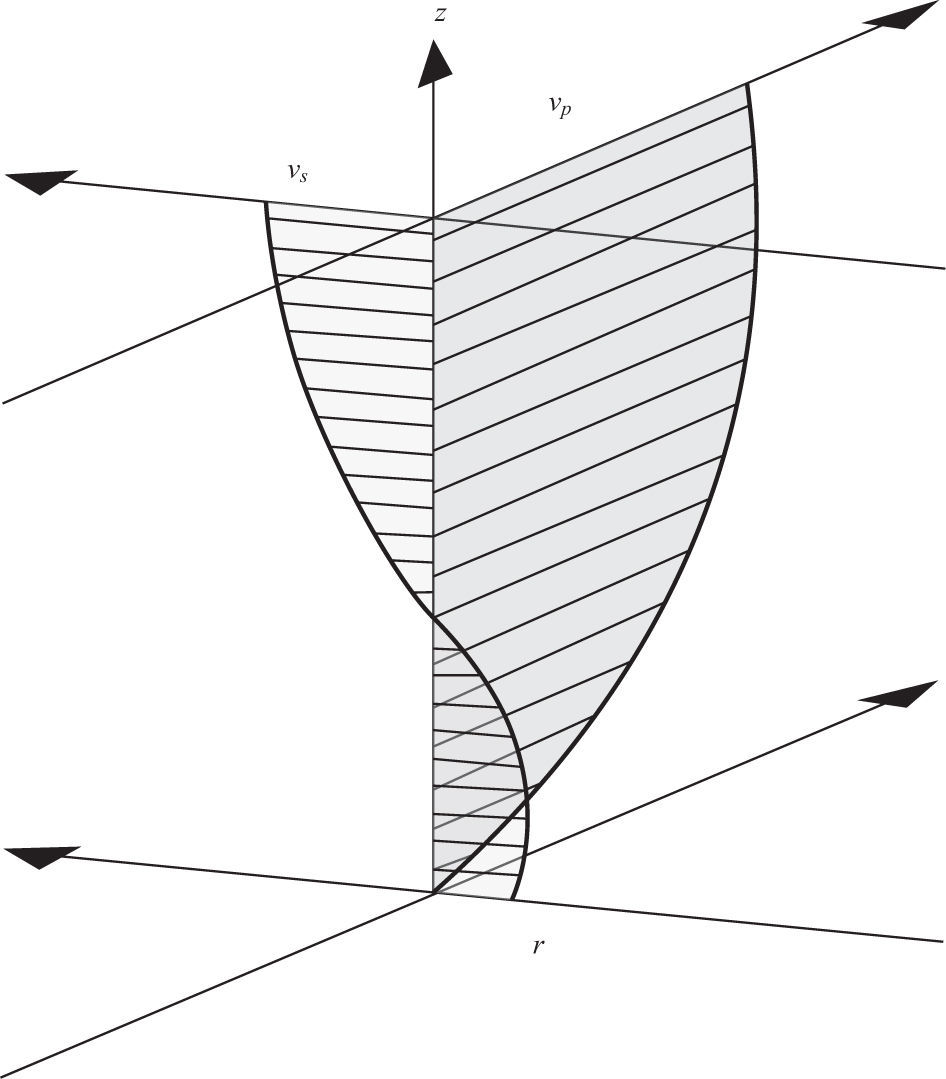
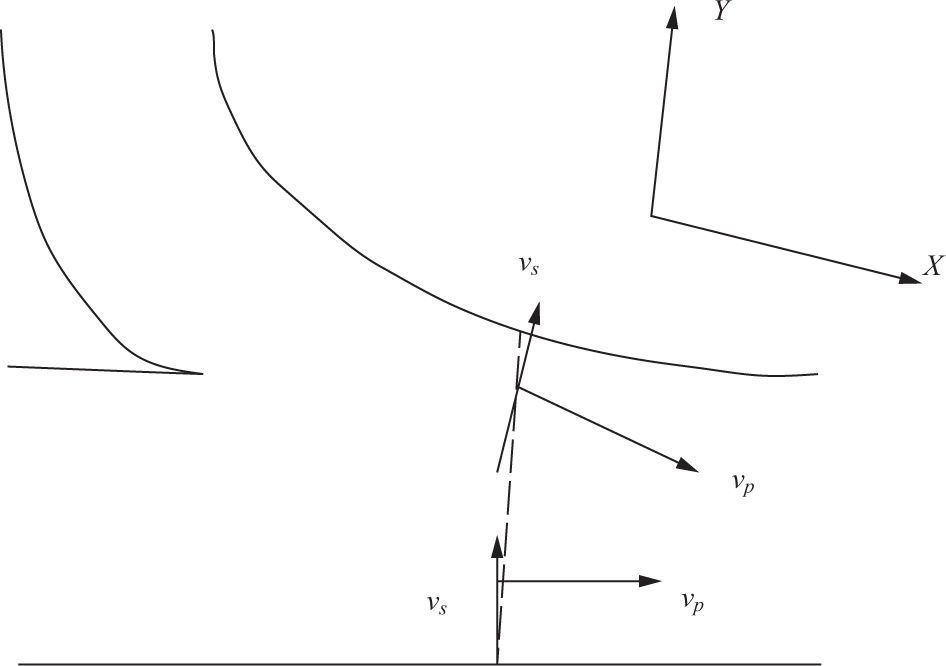
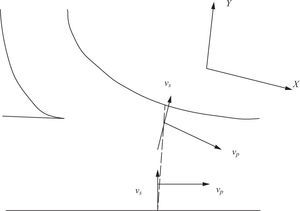
Primary (v_p) and secondary (v_s) velocities, defined by Bathurst et al. (1977) were the components of the resulting velocity (v_r) at some depth on the flow column (Fig. 1), which was oriented in a direction parallel and orthogonal to the average depth of the velocity vector on the vertical (Fig. 2). These velocities were calculated as:

Fig. 1.

Velocity vector components on a water column (adapted from Winterwerp et al., 2006)

Fig. 2.

Secondary velocity perpendicular to the primary velocity going downstream (adapted from Lane et al., 2000).

where vr = vx2+ vy2, φ = tan^–1 (v_x / v_y), and Ø = tan^–1 (V_x / V_y). V_y was the averaged cross-flow velocity on the depth, V_x the average velocity in the main direction, v_x the velocity measured in the downstream direction of the flow on each point of the water column, and v_y was the transverse velocity measured at each point of the water column. The orientation of the velocity vector's average (Ø) on different verticals through the channel defines the asymmetric flow pattern over the cross section, considering that individual v_p values for each vertical define an uneven flow intensity at particular locations of the water column. The secondary velocity v_s defines the average circulation on the normal plane of the velocity vector at each vertical; thus, it indicates the intensity of the helical movement within the asymmetric flow (Ashmore et al., 1992).

The specific objective of this study was to characterize the behavior and measurement of the secondary flow in two sites where transverse velocities were fully developed. The second objective was to represent the secondary circulation in river confluences, based on the results showed by Rozovskii (1957) and Bathurst et al. (1977).

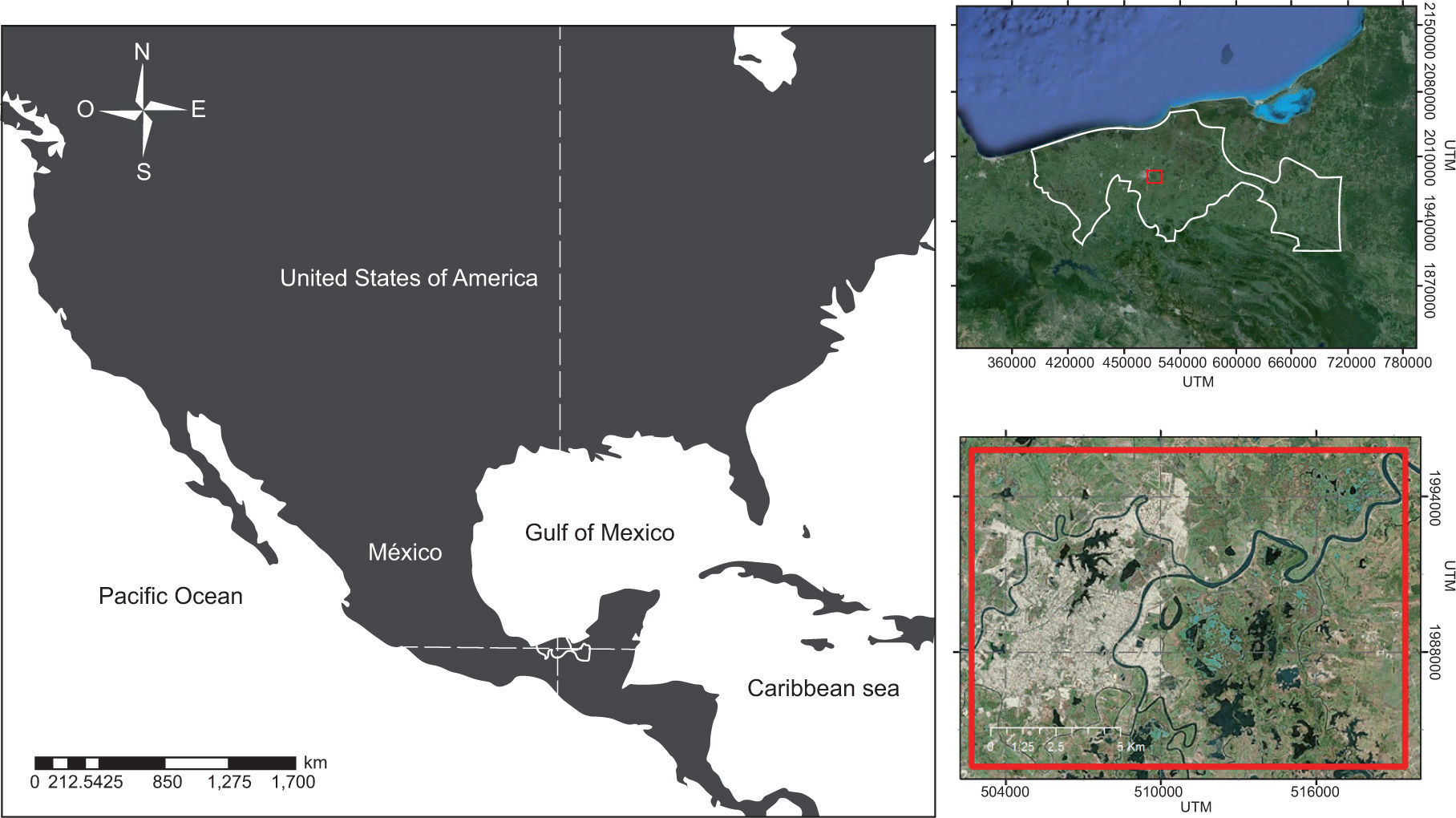
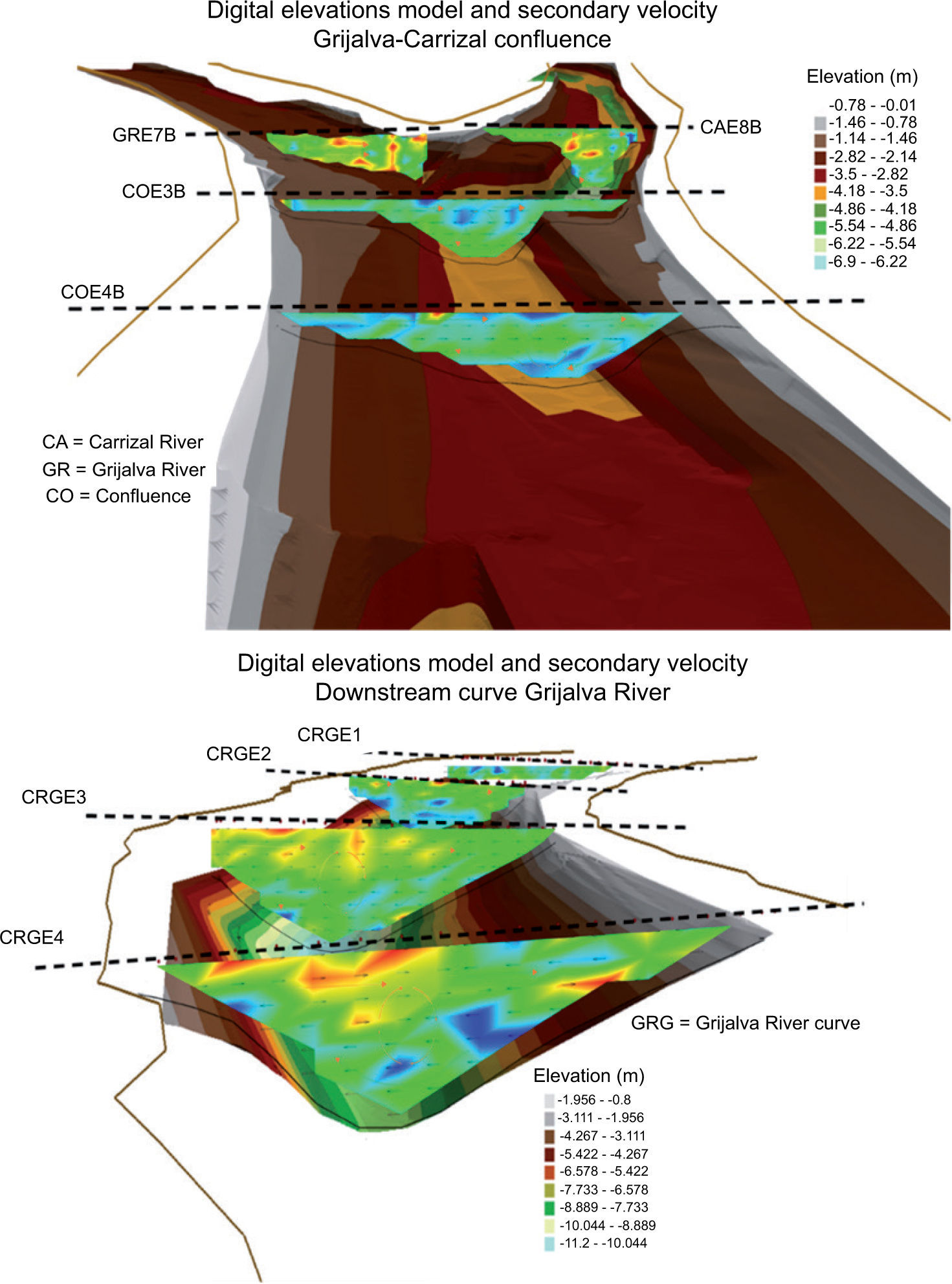
2

Methodology

2.1

Location

The selected measurement areas were located in the municipality of Centro, Tabasco, Mexico (Fig. 3), considering: (a) the confluence of the Grijalva-Carrizal rivers (18° 0’ 38” N, 92° 53’ 49” W; and (b) a curve downstream of the confluence (18° 0’ 18” N, 92° 51’ 24” W).

Fig. 3.

Location of the study area.

2.2

Measurement techniques

The measurements were performed using an ADCP RiverCat from Sontek®, model M481 (Fig. 4), mounted on a boat (Fig. 5). Seven cross-sections on the confluence of the river were selected, as well as eight sections on the curve. These measurements were carried out by traveling from the left to the right bank, having approximately 20 m of space between each transverse, as shown in Fig. 6a, b, respectively. In each cross-section, three measurements were made and an average discharge was obtained.

Fig. 4.

RiverSurveyor M481 system.

Fig. 5.

ADCP, RiverCat and GPS on the boat.

Fig. 6.

Measurement sections: (a) confluence; (b) curve.

2.3

Data processing

Data were collected with the RiverSurveyor software (Sontek, 2007), and ViewADP software (Sontek, 2007) was used to obtain three-dimensional velocities data. The software permits exporting data that are already processed in four files: three are the components of flow velocities (v_x, v_y, v_z) and the fourth contains the depths (h). From these, and based on Eqs. (2) and (3), secondary and primary rates velocities at the junction and the curve were identified by determining the hydrodynamics for each case.

2.4

Bathymetry and cross-section

Using the fields that correspond to the geographic position and depth of the stations, level curves were graphed using the softwares AutoCAD2007 and Tecplot 360 (Tecplot, 2013).

2.5

Digital elevation model (DEM)

ArcMap 10.1 software and a vector model (triangle irregular network, TIN) were adapted to identify the surface with varying degrees of detail, depending on the complexity of the relief, in order to have a clear idea of the river channel's shape.

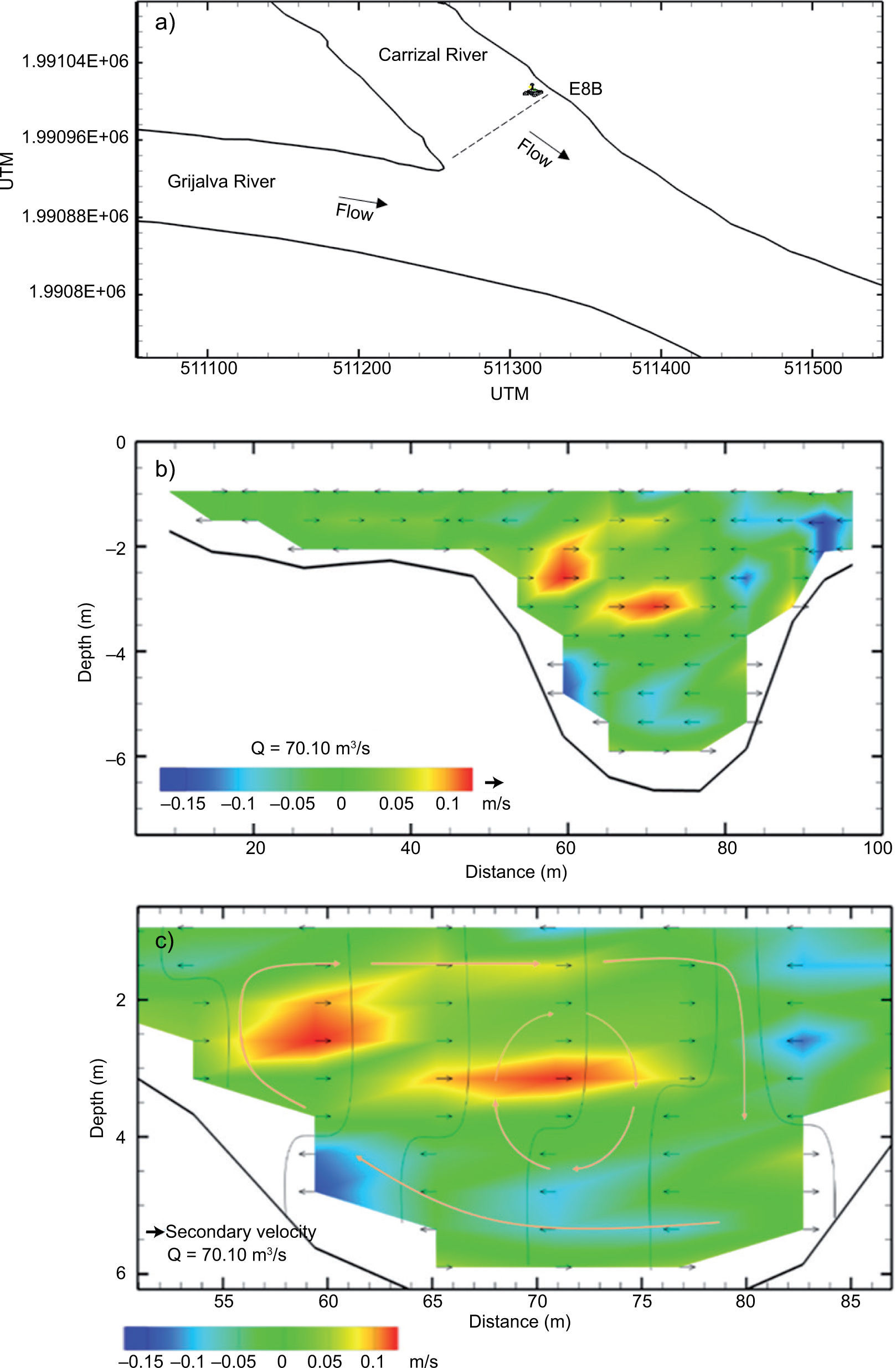
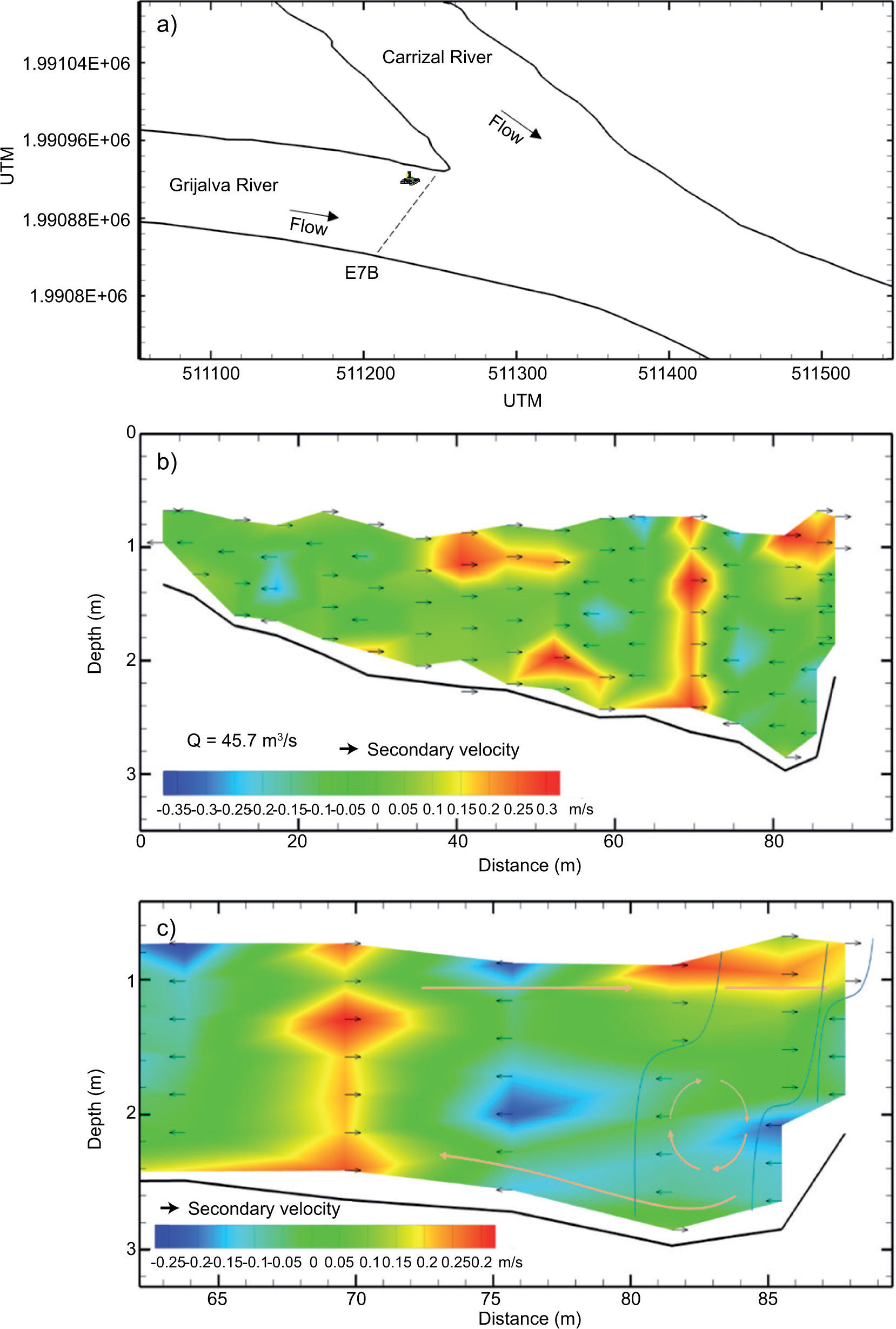
3

Results

3.1

Confluence

The secondary velocities of water in one of the branches of the Carrizal River confluence are shown in Figure 7a. In Figure 7b it is notorious that secondary velocities are not fully developed on the right side (distance 0); while, on the left side these velocities are clearly developed. This effect is due to the hydraulic pressure force exerted on the bank. Finally, the secondary currents circulation (orange arrows) is revealed in more detail in Figure 7c, as well as the undermining of the river as an effect of these velocities.

Fig. 7.

(a) Measurement section (left branch); (b) secondary velocities; (c) cross-circulation (secondary currents).

Regarding the other branch forming the junction, which corresponds to station 7 on the Grijalva River (Fig. 8a), secondary velocities are displayed. Figure 8b shows that secondary velocities on this section are developed in the right side due to the shear layer (abrupt change on the direction of velocities) between the junction of the two flows. Figure 8c shows that a secondary flow was only present on the right side of the section, and there was an over-elevation ofwater's surface due to the radial pressure force, known as the cross slope in the curve phenomenon (Falcón, 1984).

Fig. 8.

(a) Measurement section (right branch); (b) secondary velocity; (c) cross-circulation (secondary currents).

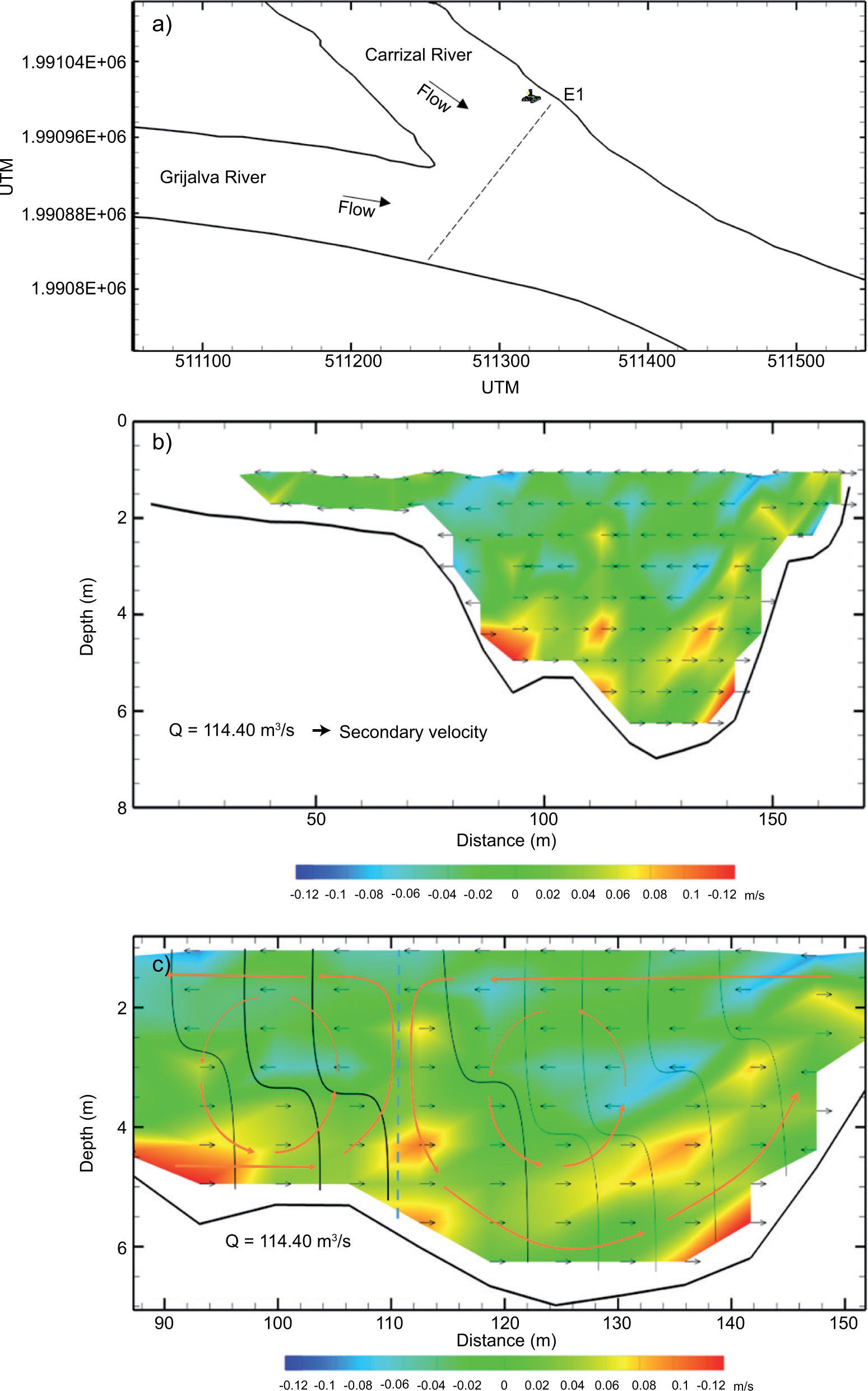
Regarding the measurement of the Grijalva-Carrizal confluence at station 1 (Fig. 9a), the completely developed secondary currents are exposed in Fig. 9b, c. Figure 9b also shows the fully developed secondary velocity throughout the cross-section of the junction; in addition, the cross slope phenomenon can also be observed. Figure 9c shows the secondary circulation caused by the shear layer. An interesting point to emphasize is that the effect produced is the result of the secondary flows of both branches.

Fig. 9.

(a) Confluence measurement section; (b) secondary velocity; c) cross-circulation (secondary currents).

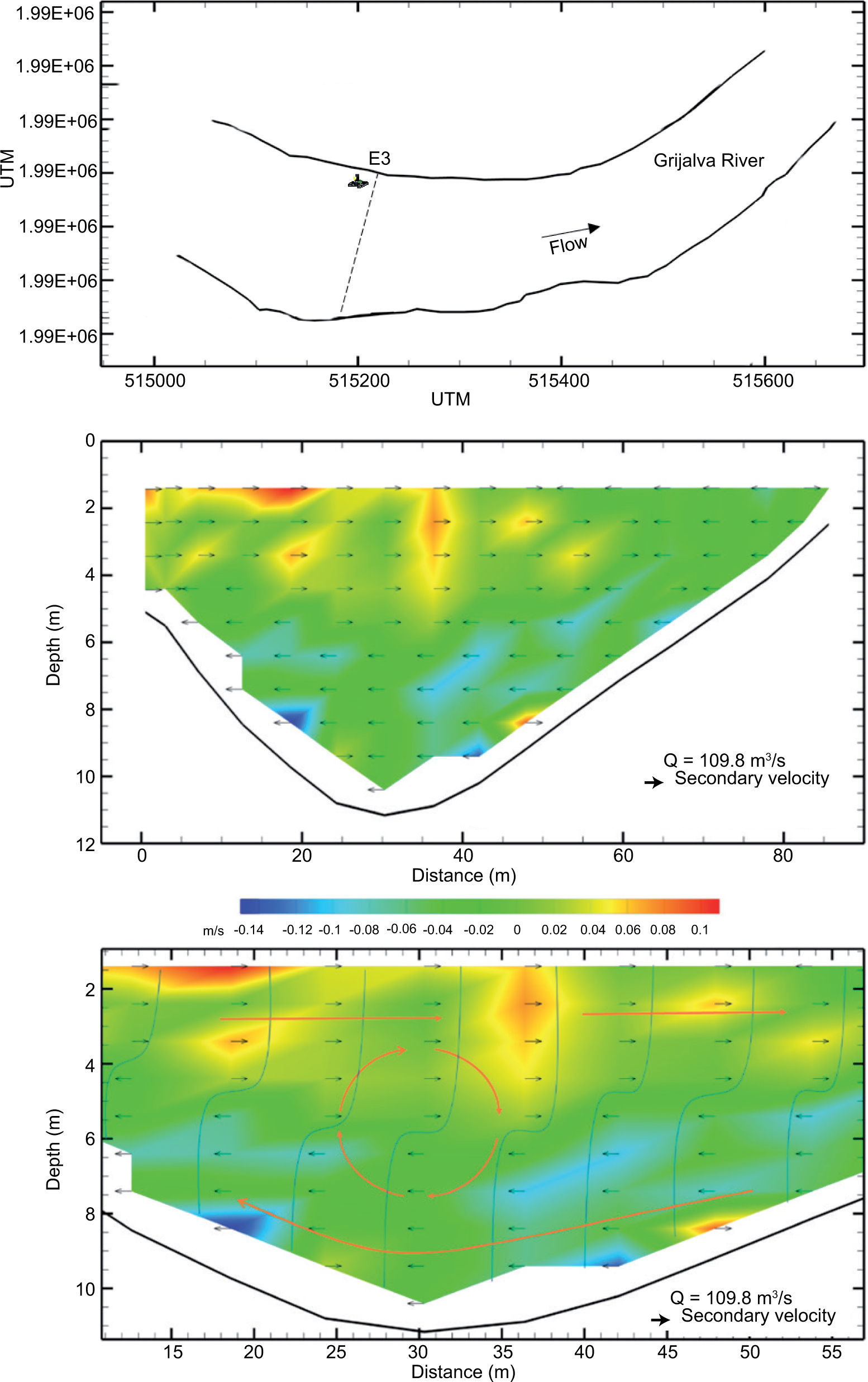
3.2

Curve

The secondary velocity for a transverse section in the downstream curve of the Grijalva-Carrizal confluence (Fig. 10a) is shown in Figure 10b, c. Figure 10b shows the secondary velocities caused by the centrifugal force due to the channel curvature. The secondary circulation developed on the left side, where the undermining is found, can be observed in Figure 10c.

Fig. 10.

(a) Transverse section on a curve; (b) secondary velocity; (c) cross-circulation (secondary currents).

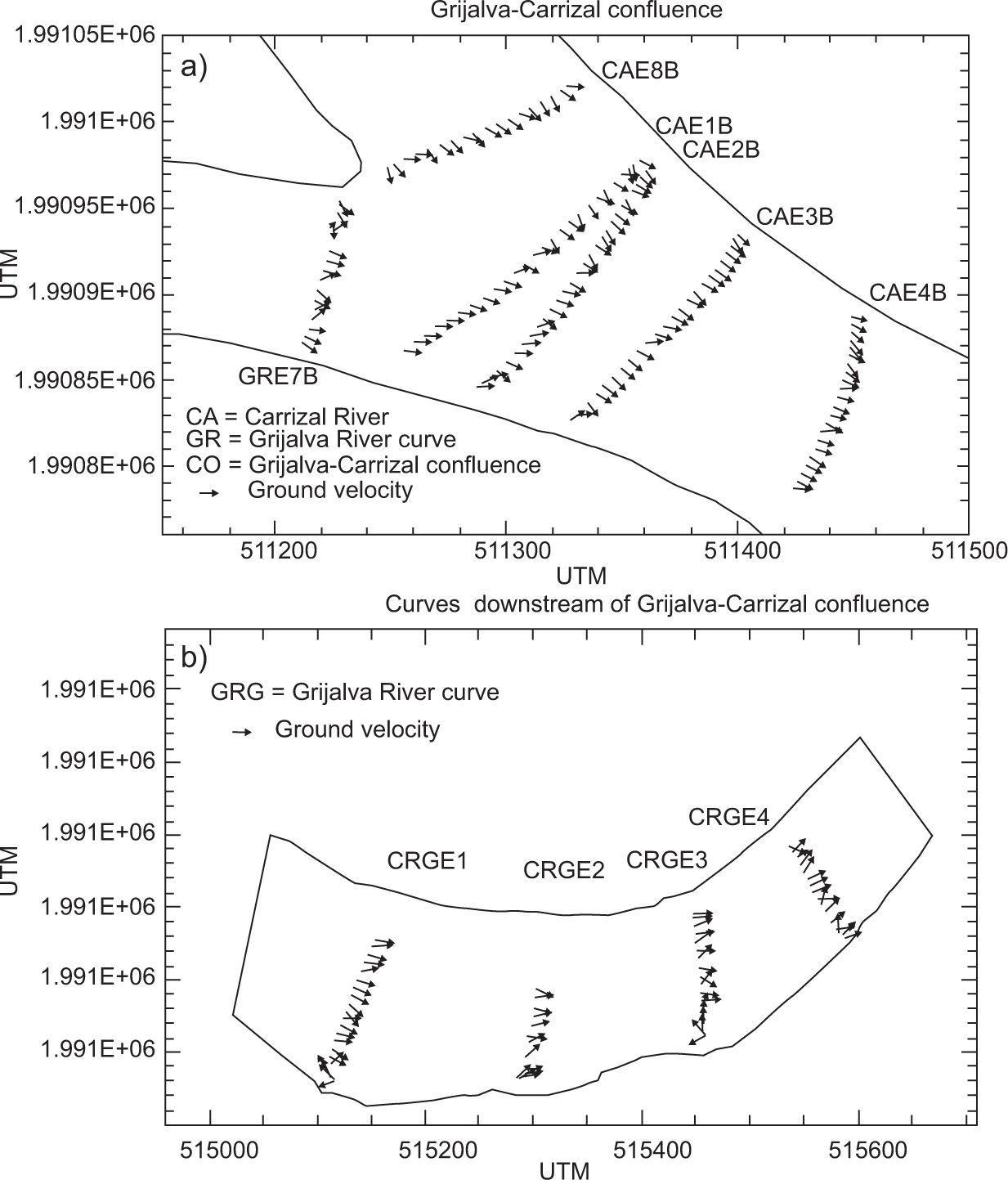
3.3

Plan view of velocities

Figure 11 depicts the velocity field in the main flow direction, in order to identify flow patterns with the secondary currents in the hydrodynamic operation of the confluence (Fig. 11a, b). Here, ADCPs can generate these velocity vectors, and by interpolation they allow to generate main current lines, which are linked to complex processes; for example, the transport of sediment or contaminants.

Fig. 11.

Plan view of velocities.

3.4

Digital elevation model

DEMs of the Grijalva-Carrizal confluence and a curve downstream, as well as the combination of secondary velocities obtained in different measured transverse sections, are shown in Figure 12a, b. This representation allows carrying out a comprehensive analysis of the hydrodynamic effect of these secondary velocities on the river channel.

Fig. 12.

Secondary velocities on the DEM.

4

Conclusions

The behavior of secondary currents shows a rotational effect that rarely is measured and drawn. The methodology proposed by Rozovskii (1957) and Bathurst et al. (1977) to estimate the secondary currents, works well compared to theoretical predictions.

We drew the secondary currents and their developments over the bed bottom. Although it needs to be confirmed, we found that over the right side of the confluence secondary currents are totally developed, while on the left branch they can not be fully developed due the geometry.

These kinds of results and procedures are useful for researchers interested in studying secondary currents, and it also provides the basis for making changes and developments in order to improve the knowledge of hydrodynamic processes and their relationship to morphodynamic processes in rivers.

Acknowledgments

This research was carried out within the project CB-2011-166068 of the CONACyT.