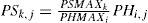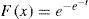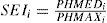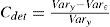Storms Generator Method That Preserves Their Historical Statistical Characteristics. Application To Mexico City Basin Daily Rainfall Fields

Resumen

En este trabajo se aplicó un procedimiento para generar tormentas sintéticas que preserva las características estadísticas de los eventos históricos de precipitación diaria registrados en 49 estaciones ubicadas en la cuenca de la Ciudad de México. Este procedimiento (variante del método de Svanidze) supone implícitamente que la correlación entre la lluvia máxima y su distribución espacial no es significativa; sin embargo, los resultados no validaron dicha hipótesis, lo que motivó la propuesta de un segundo procedimiento que permite considerar la correlación entre el valor máximo registrado durante una tormenta y su distribución espacial. Con esto se logra mejorar sustancialmente la forma en que las tormentas sintéticas reproducen las características estadísticas de las históricas.

Abstract

A first procedure to generate synthetic storms, which preserves the statistical characteristics of the historical daily precipitation events registered in 49 stations located within the basin of Mexico City is presented. This procedure (a variation of the Svanidze method) implicitly supposes that the correlation between the maximum rainfall and its spatial distribution is meaningless. However, the obtained results did not validate that hypothesis. For this reason a second procedure was developed, which allows to consider the correlation between maximum rainfall and spatial distribution. This second procedure allowed reproducing the statistical characteristics of the daily rainfall for each station and also its spatial distribution, as shown in this work.

1

Introduction

Synthetic generation of hydrological time series longer than the historical ones, is very useful because such series provide information about possible scenarios in the long term of the behavior of the hydrologic variable in the study area.

Arnaud et al. (1999) consider that the synthetic storm generation allows a new approach to study the asymptotic behavior of the probability distribution for the maximum rainfalls and to define design storms. Mehrotra and Sharma (2006) consider that the generated synthetic storms could be used in the reliability and risk analysis used for design and operation of hydraulic structures.

Among the synthetic storm generation models in literature, the work by Delleur and Kavvas (1978) can be cited. They used autoregressive models of integrated mobile averages (ARIMA) for series of monthly average precipitation of 15 watersheds in Illinois and Kentucky, USA, for synthetic generation and forecast.

Geng et al. (1986) proposed a method for synthetic generation of daily rainfall data at a station with a model whose parameters were derived from monthly data instead of daily data, considering, on the one hand, that the transition probabilities between dry and wet days could be estimated from the fraction of wet days per month and, on the other hand, that the precipitation magnitude on a rainy day can be modeled with a gamma distribution, whose parameters can be related with the average rainfall of rainy days. It is pertinent to mention that their studies were applied to agricultural models. Bogárdi et al. (1988) proposed a method for storm generation applied to daily rainfall records from semi-arid climates, using the concept of annual climate cycle, and generating random numbers with different probability distributions.

Coles (1993) supposed that spatial variability of storm types can be adequately described by variability within a subset of data sites. This leads to a two-stage estimation procedure. Firstly, a multivariate extreme value model is fitted to data from the subset, the appropriate dependence measure being identified as a parameter. Then the model is extended smoothly through suitable functions as a max-stable process, on the basis of information from the remaining data sites.

Wilks (1998) presents the extension of a widely used empirical-statistical precipitation climate model, which also includes the precipitation portion of a larger number of stochastic weather generators, for simulation at multiple locations simultaneously; the extension discussed is accomplished by driving each of a collection of individual single-site models with temporally independent but spatially correlated random numbers. Cisneros et al. (1998) developed a model that attempts to preserve the spatial structure of historical storms.

Arnaud et al. (1999) applied a stochastic generation model to data from the French coast, using a two-step scheme for the generation: the first step is a study of the variables that describe the phenomenon and its definition by probability distribution functions fitted to the observations, and the second is the creation of a rainfall time series using values of the descriptive variables generated randomly from their law of probability. When the model was extended to a larger area, it showed some limitations in the results; therefore, they developed an adaptation to the generation model, by fitting an exponential distribution to the values smaller than four times the mean of the variable. Then, they made a second amendment to develop a model that preserves the dependence of the storm intensity and duration variables, using a parameter that characterizes the cumulative frequency curve of the sum of the probabilities of the two variables. Finally, they studied the modeling of the persistence of the storm in the same event to generate episodes of maximum precipitation in 24 hours.

Cisneros (2001), like Salsón and García-Bartual (2003), simulated the origin of the storms. Bouvier et al. (2003) sought to preserve the spatial structure of storms with an analysis of main components. Srikanthan and McMahon (2001) reviewed several methodologies developed from the late 1960s to the year 2000, in order to generate annual, monthly and daily climate data, highlighting their advantages and disadvantages. They describe models of the Markov chain type, models of disaggregation fragments, auto regressive moving-average models (ARMA), and two-parts applied models (one for wet periods and one for dry periods), among others. In their study they indicate that the parameters of the generation model should be variable in time.

Fowler et al. (2005) combined Monte Carlo simulations and sampling techniques to generate long series of synthetic rainfall at multiple sites in areas with different properties of precipitation, but based on the same climate, in Yorkshire, UK. The coupling of a weather generator to a multisite stochastic model (regional) for the generation of precipitation gave them significant results, since it allows research on the impacts of changes on type, persistence or frequency of the climate, as in their internal properties, such as changes in precipitation intensity. Guichard-Romero et al. (2009), successfully used the multidimensional stochastic model of precipitation Raingen, created by Salsón and García-Bartual (2003), to obtain rainfall fields associated with maximum convective episodes in a Spanish basin.

In this paper two procedures for the generation of daily storms in 49 stations in the basin of Mexico City are compared. The former uses the fragments method of Svanidze (1980) that has been successfully used to generate simultaneous monthly runoff volumes in various basins with a certain degree of auto-correlations between consecutive months and cross-correlations between basins (Arganis-Juárez et al., 2008). This first procedure did not preserve adequately the distribution function of the average rainfall of historical storms. Thus, a detailed analysis of the correlation between the maximum rainfall over the 49 stations and the spatial average values was performed, by means of the spatial extension index concept (SEI). When using this index, it was found that it is correlated with the maximum value of the storm, therefore a second procedure, which takes into account this correlation, was developed. With this second procedure it was possible to generate synthetic storms that reproduce properly the distribution function of the spatial mean and the main statistics of the precipitation station by station.

2

Problem statement

Mexico City and its suburbs have grown at an exponential rate over the decades, increasing the problems in the drainage system during the rainy seasons. Therefore, it became necessary to study both the point rainfall storms of great magnitude (although concentrated in relatively small areas) and the storm events of great extension that have caused serious problems for the main flood control and drainage system. The historical experience has shown that punctual precipitations exceeding 25 mm/day or mean spatial precipitations of 2.5 mm/day may produce local or general flood problems (Domínguez, 1997).

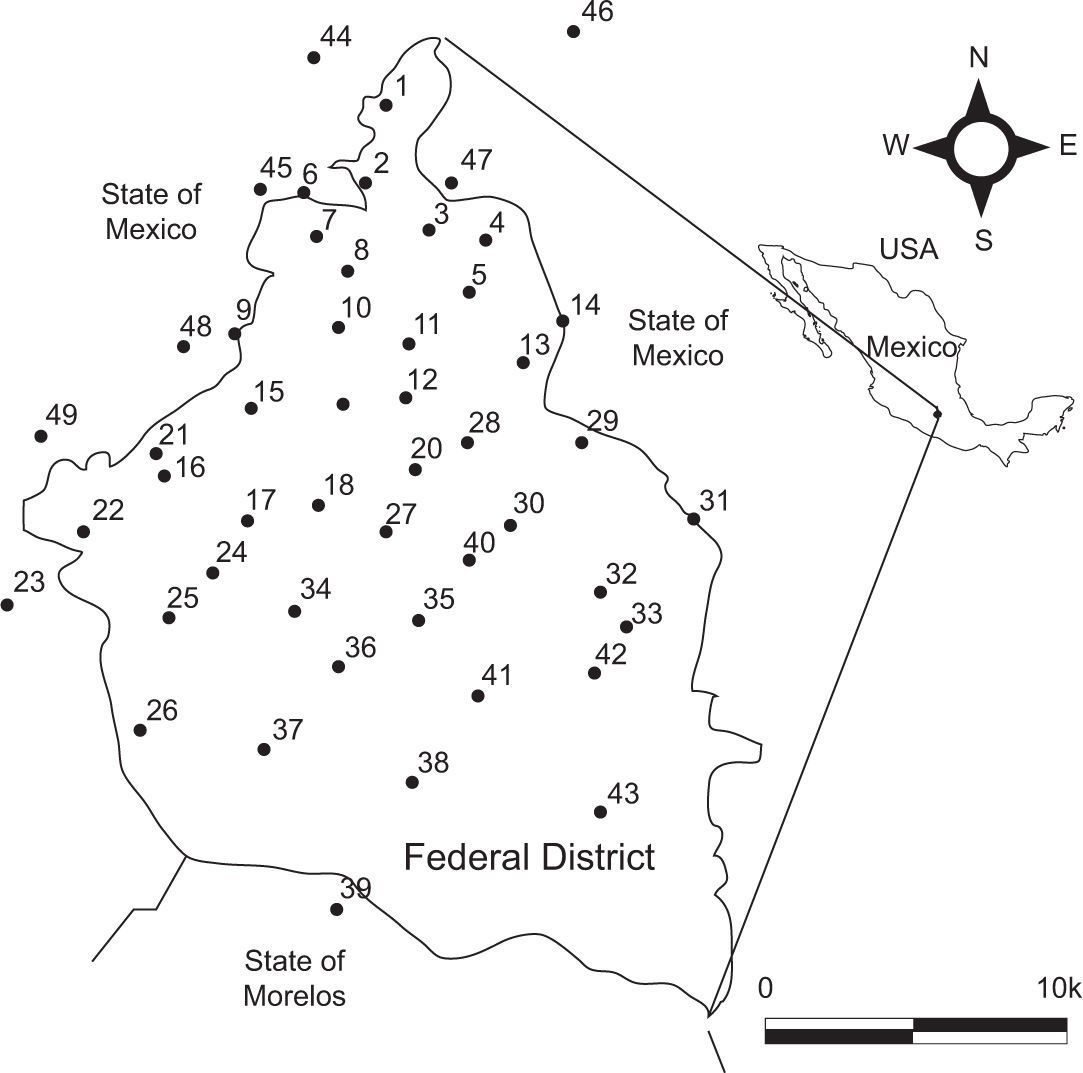
There is a network of 49 pluviometers (Fig. 1) operated by the Sistema de Aguas de la Ciudad de México (SACM) (a local government agency) at the basin. Each pluviometer transmits a pulse every time it registers a rainfall equivalent to 0.254 mm. Official records of daily rainfall are given.

Fig. 1.

Network of 49 pluviometers for the basin of Mexico City.

In order to analyze the performance of the alternative operation policies for the very complex main flood control and drainage system, it becomes convenient to develop a large number of different possible scenarios of storm events that preserve the statistical characteristics of the historical storms.

3

Methodology

To address this issue, 177 daily storms that occurred between 1988 and 1999 were selected. It was carefully reviewed that the data met one of the following criteria:

• a.

  Total daily precipitation in any of the 49 stations exceeded a threshold of 23 mm (i.e., storms with a high point value).

• b.

  And/or the arithmetic average of the daily rainfall in the 49 stations exceeded 2.3 mm in 24 hours (i.e., storms with large spatial extent).

3.1

Procedures to generate synthetic storms

3.1.1

First procedure

In order to apply the fragments procedure, historical storms were characterized, on the one hand, by the peak of the storm (i.e., the maximum daily precipitation recorded in the 49 stations); and, on the other hand, by the spatial shape of the storm, expressed in terms of the relationship between the rainfall registered at each pluviometer and the peak of the storm.

Assuming that the peak or maximum total precipitation for each storm and its spatial shape are independent, the synthetic generation procedure is applied by generating independently the maximum precipitation for each synthetic storm, according with its distribution function, and the spatial shape of a randomly selected historical storm. The steps in this first procedure were:

• 1.

  For the selected historical storm the following values were obtained: total daily precipitation recorded in each of the 49 stations, maximum of the former values and average rainfall over the 49 stations, as follows:

  • •

    PH_i,j. precipitation recorded for the storm i at station j.

  • •

    PHMAXi, maximum over j of PH_i,j.

  • •

    PHMEDi average for each storm i of the PH_i,j values.

• 2.

  The cumulative distribution function F(p-max) of the maximum, PHMAX_i, corresponding to the selected historical storms is obtained by means of an extreme values analysis; in this case a Gumbel distribution function gave the best fit.

• 3.

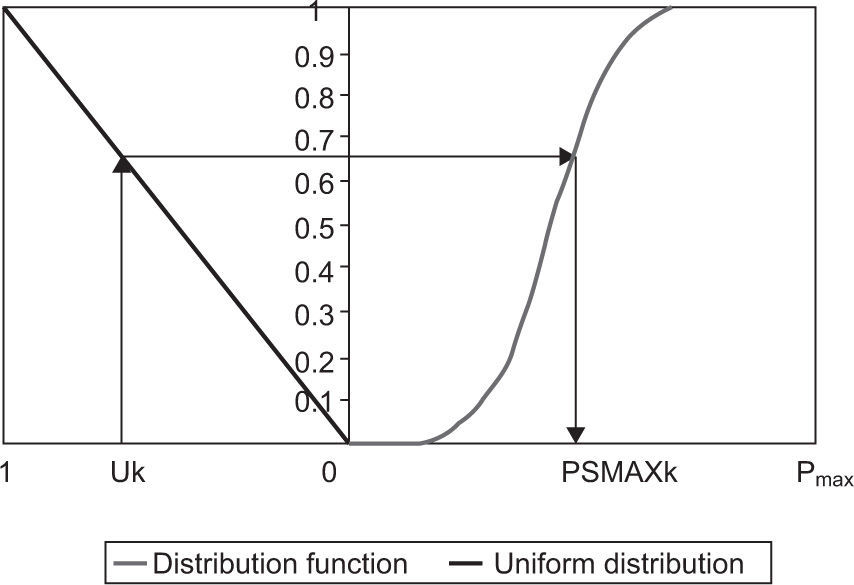
  A random number Uk with uniform distribution [0,1] is generated; then, the inverse of the distribution function F(p-max) is obtained to estimate the corresponding synthetic value (PSMAX_k) as shown in Figure 2.

  
  

  Fig. 2.

  Random generation of maximum rainfall.
• 4.

  On the other hand, a random integer between 1 and 177 is generated to achieve a random selection of an historical storm, i.

• 5.

  The generated daily precipitation at the 49 stations is obtained by multiplying the historical rainfall recorded in each one, PH_i,j, that corresponds to the storm i selected in step 4, by the relationship between the synthetic value of the maximum precipitation obtained in step 3 and the maximum recorded precipitation for the historical storm selected in step 4:

  

where PS_k,j is the precipitation for the synthetic storm k at station j, obtained according to the relationship between the maximum synthetic precipitation PSMAX_k and the maximum historical precipitation PHMAX_i corresponding to the randomly selected storm in step 4. Steps 3, 4 and 5 are repeated for k = 1, 2… ns (number of synthetic storms to be generated).

3.1.2

Validation procedure

In order to validate the procedure, it is proposed to compare at first the distribution functions of the mean and the maximum of the storms generated with the corresponding distribution functions of the historical storms. Once the distribution functions of maximum and average values of historical storms are adequately reproduced, it would be necessary to check whether the statistical parameters of recorded rainfall in each of the stations are also reproduced.

It is worthwhile to point out that the described procedure uses the adjusted distribution function of the maximums (and therefore the comparison of the empirical distribution functions of those maximums is not really a validation); nevertheless the reproduction of the empirical distribution functions of the spatial means and of the statistical parameters of the recorded rainfall for each of the stations depends on the hypothesis used to generate the synthetic storms, so that the proposed comparisons constitute a real validation.

4

Results and discussion

4.1

First procedure of generation (whole group analysis)

Maximum and average precipitations, for each of the 177 historical storms, were calculated.

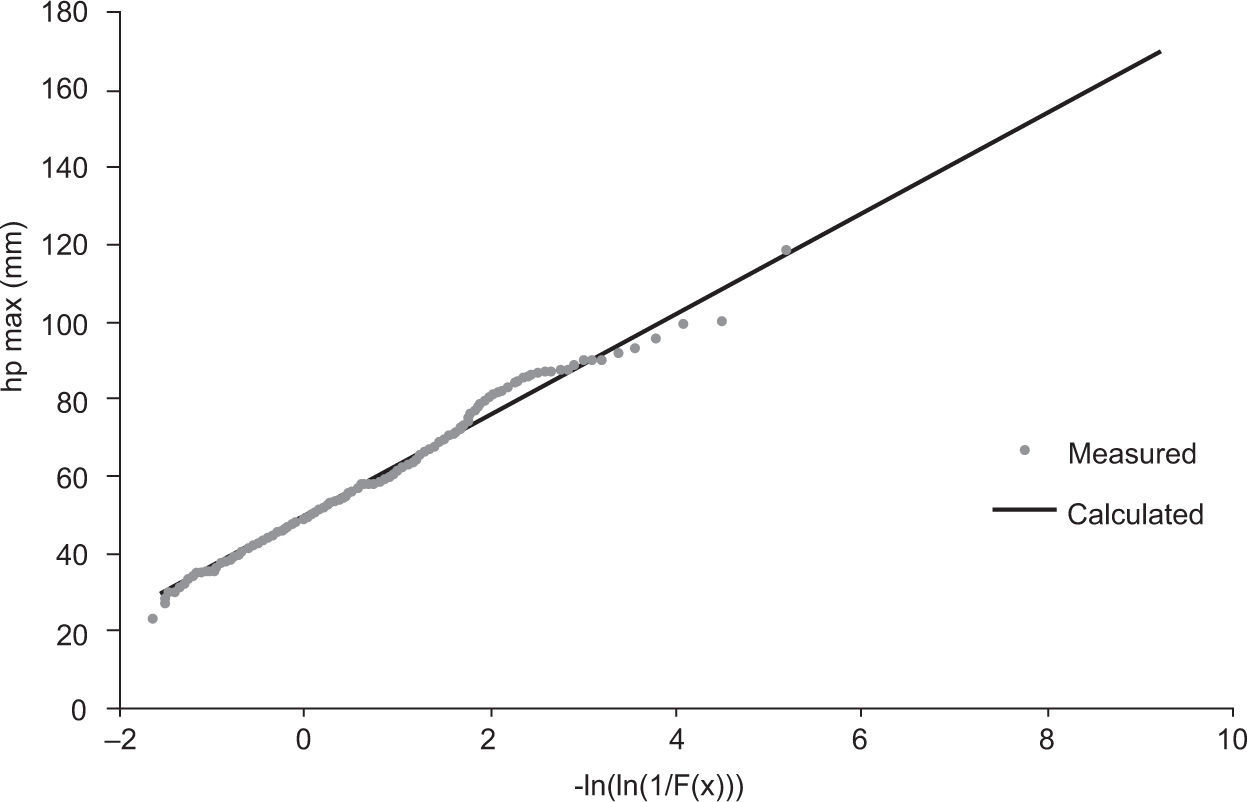
An extreme value analysis was performed for the maximum rainfall data at the 177 historical storms. By testing several distribution functions (i.e., normal, exponential, lognormal, gamma, Gumbel and Gumbel of two population) their parameters were estimated with moments and maximum likelihood methods; finally, it was determined that the best fit, in terms of the standard error (i.e., differences between theoretical and empirical cumulated distribution functions) was obtained with the Gumbel distribution function, adjusted by the method of moments. The distribution function obtained was:

where t = α (x-β) withα = 0.019786, β =195.8799, Figure 3 shows the obtained distribution function with Gumbel scale on the horizontal axis.

Fig. 3.

Distribution function of maximum historical values.

Using the distribution function given by Eq.(2), 1000 random numbers (PSMAX) were generated, and independently 1000 storms were generated by a random selection, with replacement, from the 177 historical storms. Finally the precipitation recorded in each station was scaled by applying Eq. (1).

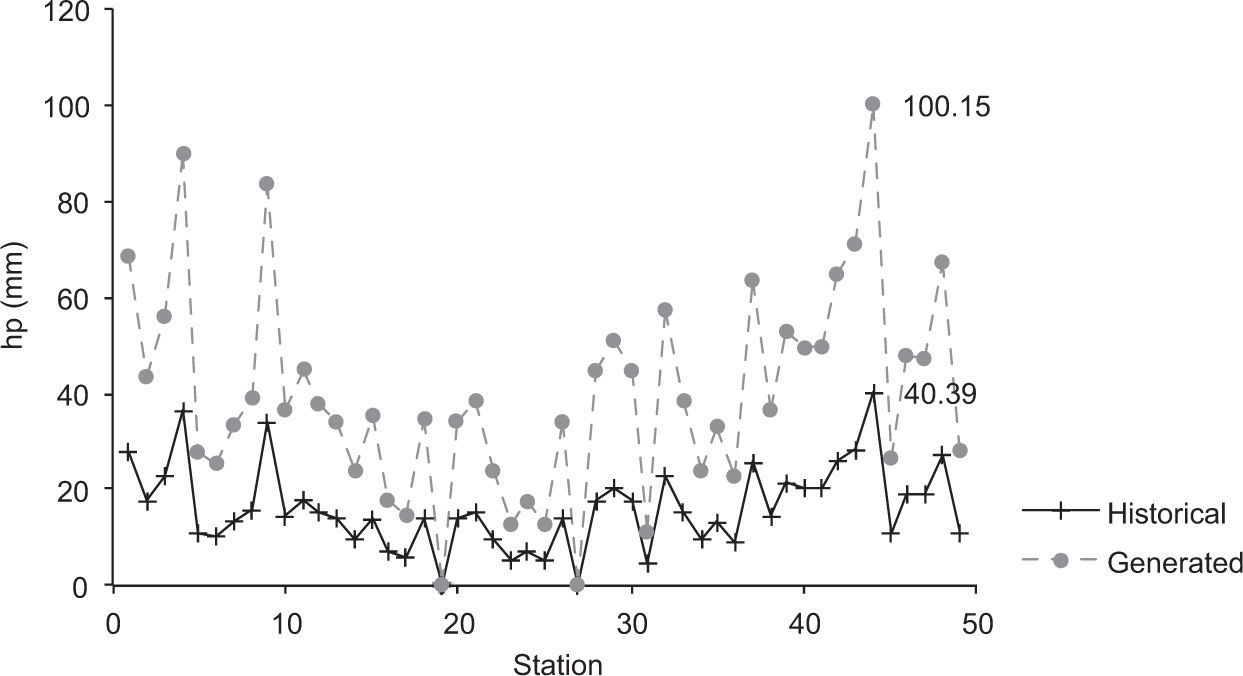
Figure 4 illustrates an example of the first generated storm, in which the obtained maximum synthetic precipitation value (step 3) was 100.15 mm. On the other hand, the randomly selected historical storm, identified with number 102 (step 4), recorded a maximum precipitation value of 40.39 mm (observed at station 44). In order to generate precipitation values for this storm in all 49 sites, we defined a relationship between the maximum values of precipitation in the synthetic data and the historical record (100.15/40.39). Recorded values in all stations were then multiplied by this factor, producing a synthetic event with the same statistical properties as those observed in the historical record. By repeating the procedure, 1000 synthetic storms were generated.

Fig. 4.

Example of scaling procedure for the first storm generated.

4.1.1

Validation of the first procedure

According to the proposed validation procedure, the comparison between the empirical cumulative distribution function values obtained for historical and synthetic storms is shown in Figures 5, 6.

Fig. 5.

Empirical probability distributions of the maximum precipitations. First procedure.

Fig. 6.

Empirical probability distributions for the spatial average rainfalls. First procedure.

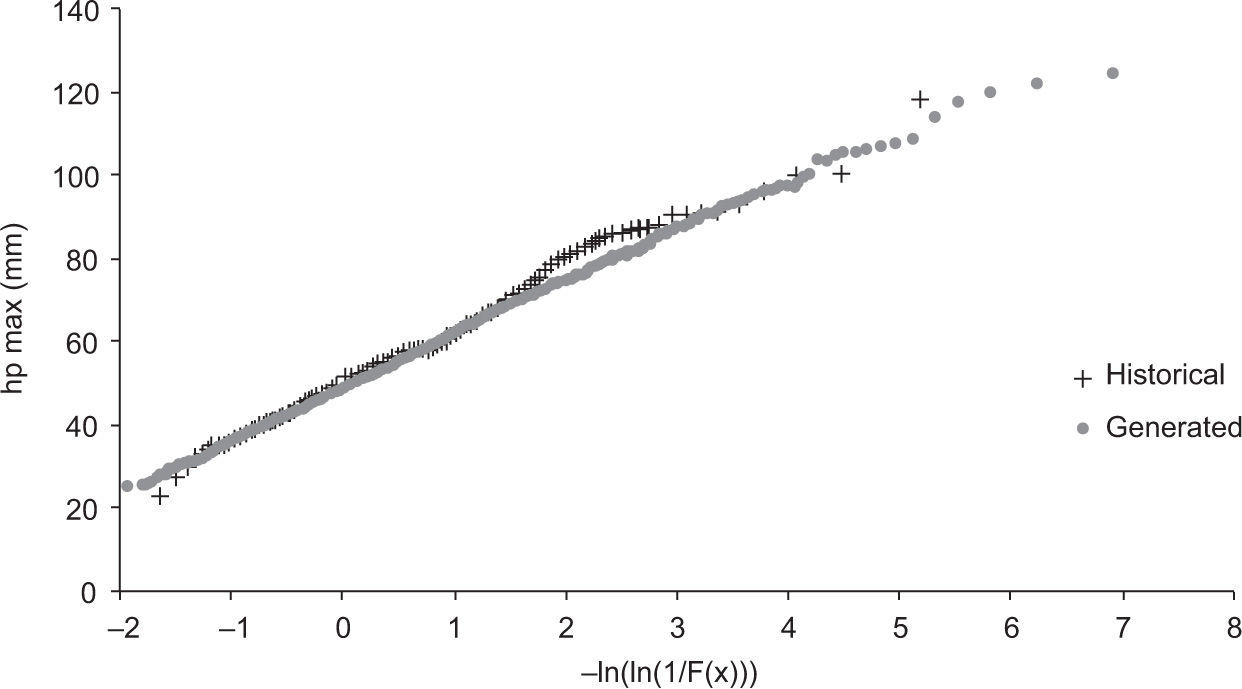
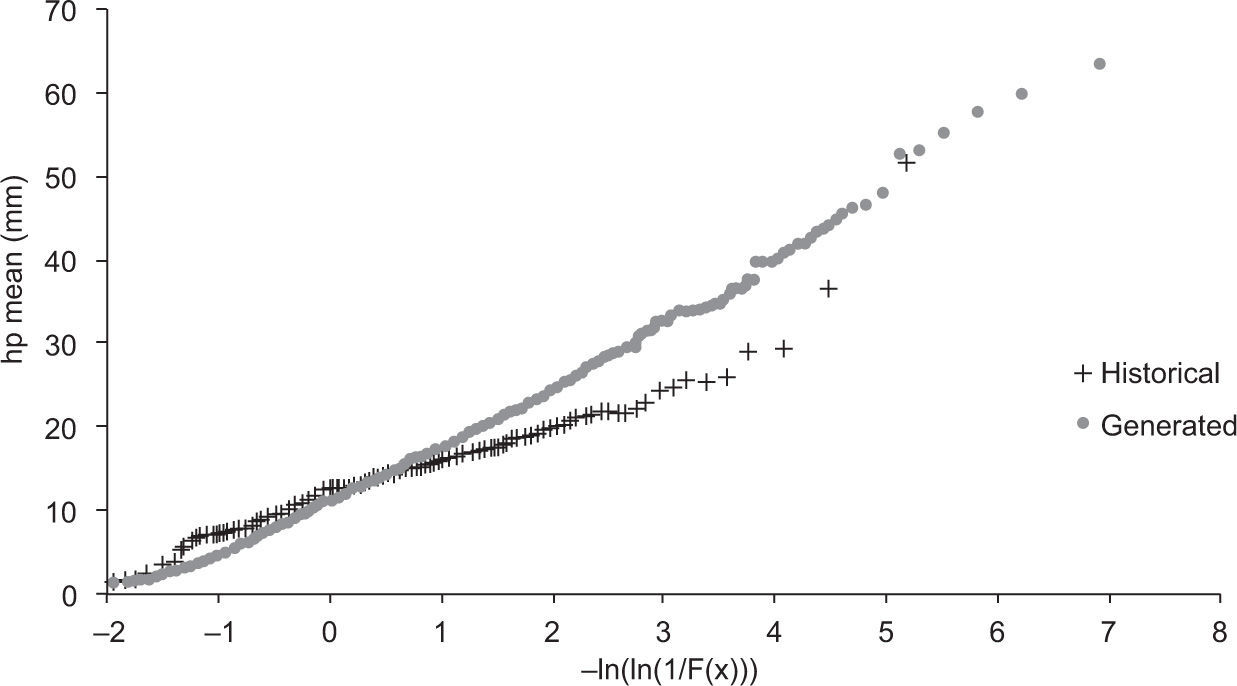
Figure 5 shows that the distribution function of the maximum rainfalls was reproduced satisfactorily whereas, in the case of average precipitation (Fig. 6), the corresponding values for generated storms are greater than the historical ones on a region of the figure.

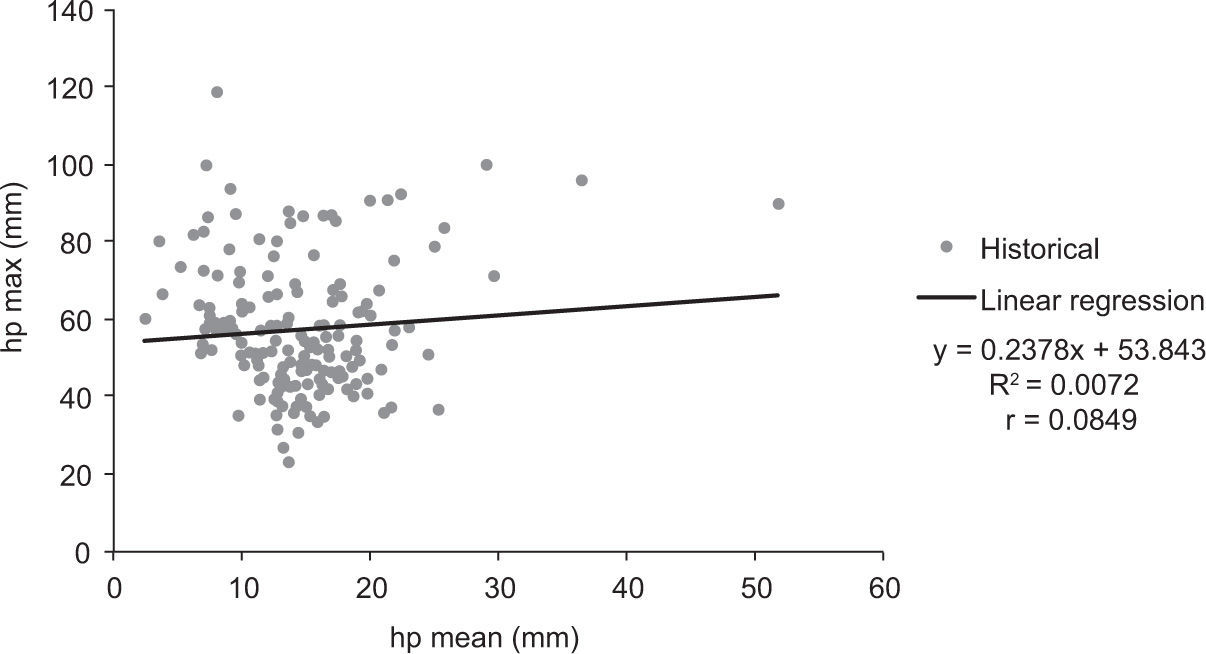
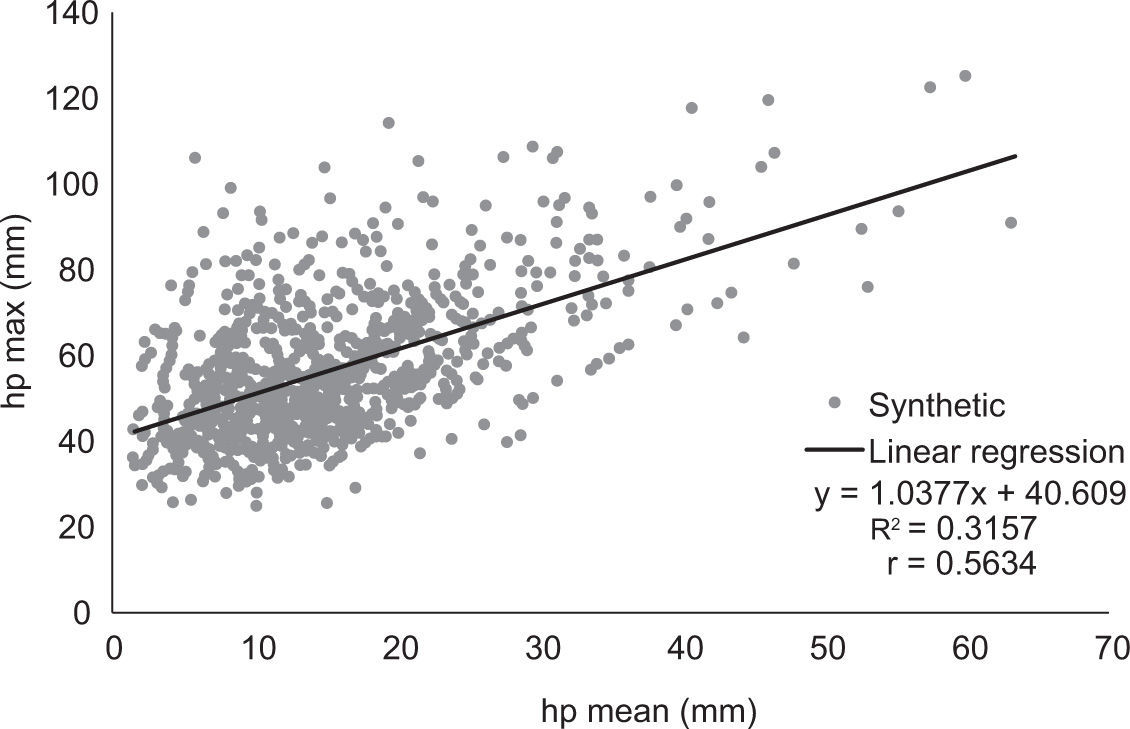
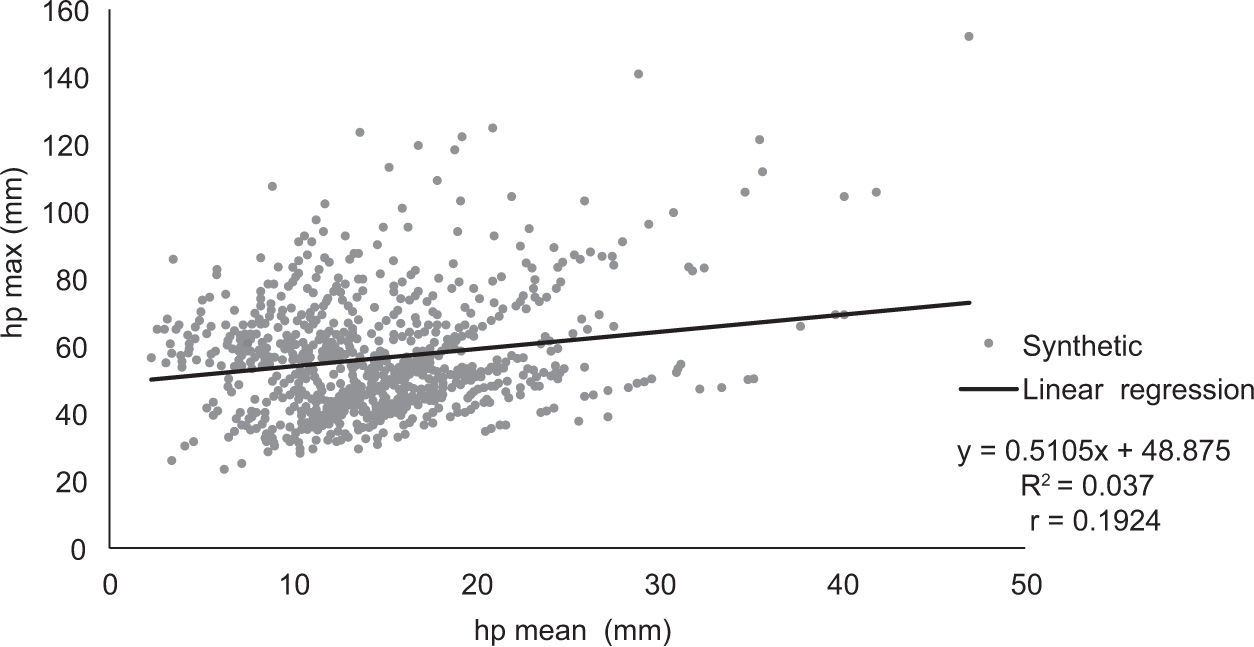
In order to identify the causes of the differences between the synthetic and historical average precipitations, we compared, in Figures 7, 8 the relationships between the maximums and the average rainfalls for historical and synthetic storms, respectively. On these graphs, it is shown that the synthetic sample produced a higher correlation between average and maximum rainfalls compared with the historical storms.

Fig. 7.

Relationship between spatial average rainfall and maximum rainfall of 177 historical storms.

Fig. 8.

Relationship between average and maximum values. First procedure.

Figure 7 shows a low correlation between maximum precipitation and spatial average rainfall, which leads to think that there is not interdependence between the maximums and the spatial shape of the historical storms. Nevertheless, calculated mean values from observed rainfall are partially determined by its registered maximum value, and as such, the relationship can be considered spurious (Echávez-Aldape and Arrioja, 2006).

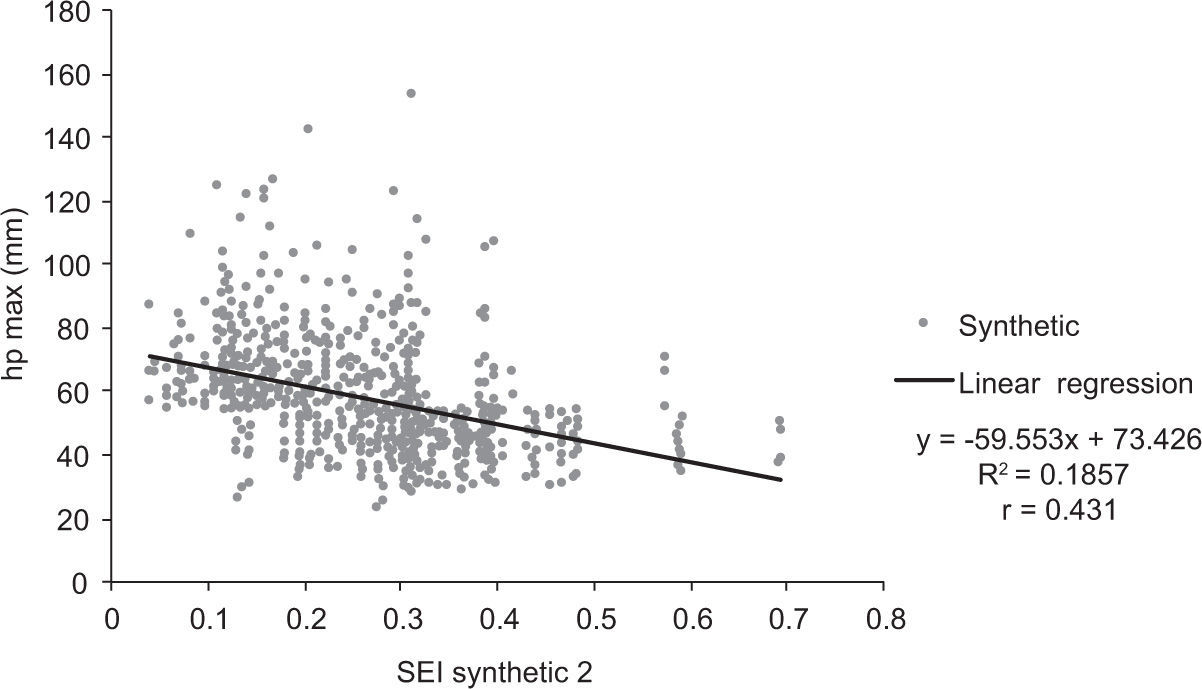
In order to avoid this problem a spatial extension index (SEI_i) obtained as the ratio between the average rainfall in the storm i and the maximum value in that storm was defined. This is equivalent to calculate the means of the standardized storms in which the maximum value is always equal to 1. According to its definition, the SEI_i is obtained as:

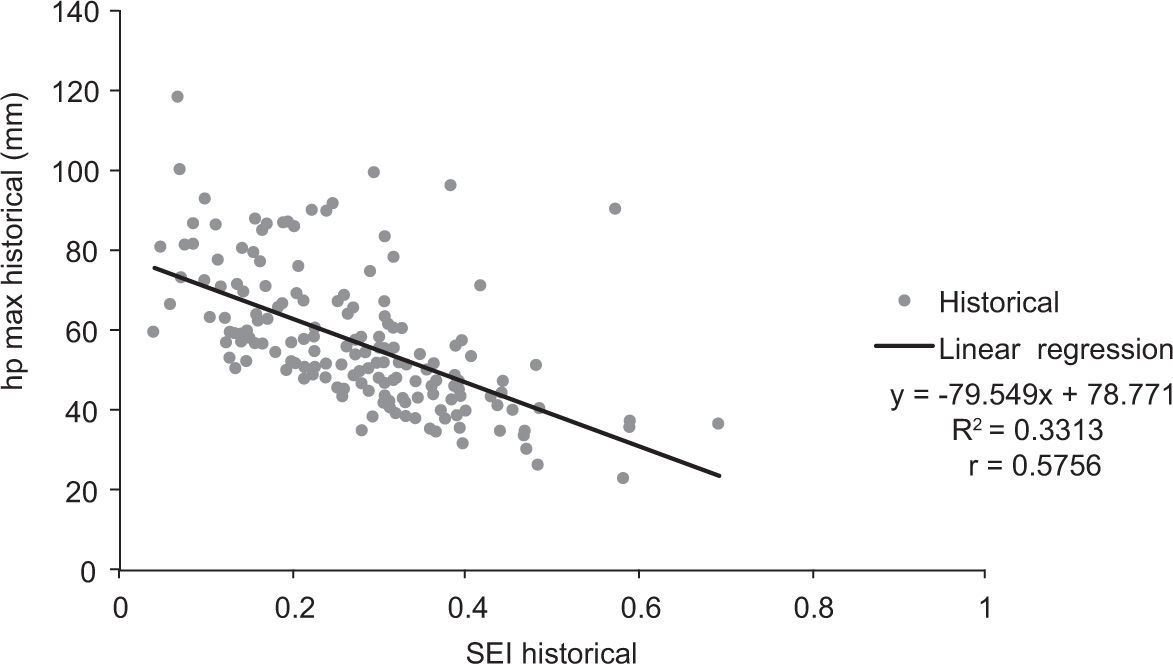
For the historical storms, the relationship between the maximum precipitations and the index (SEI_i) shows that the spatial extent of the storms decreases as the magnitude of the maximum value increases (Fig. 9). This indicates that the most intense precipitation events tend to be less extended.

Fig. 9.

Relationship between the spatial extension index (SEI_i) and the maximum precipitation for historical storms.

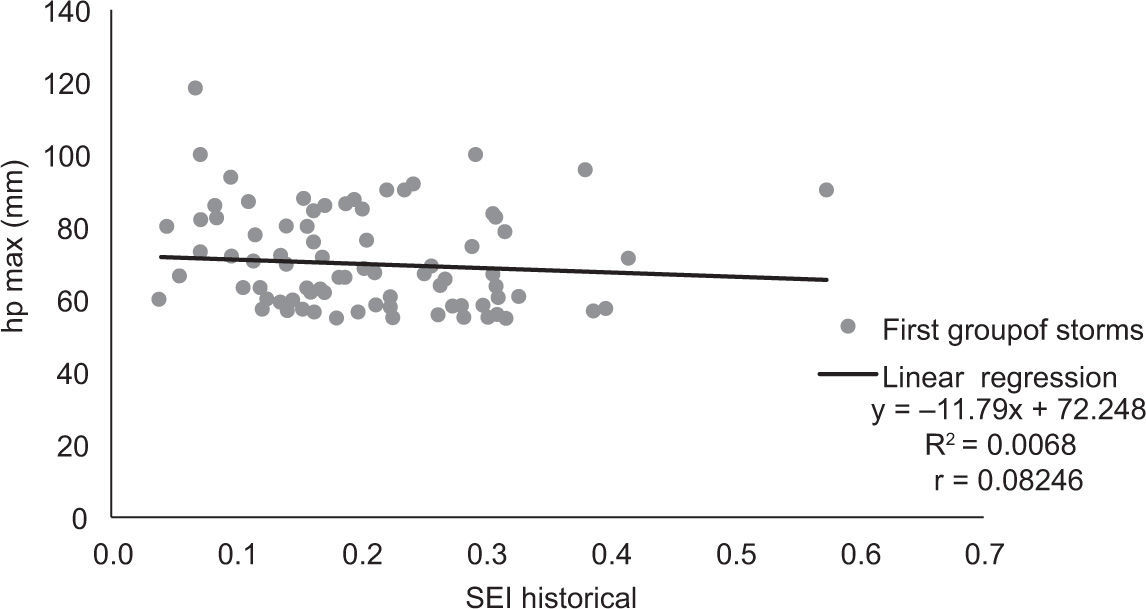
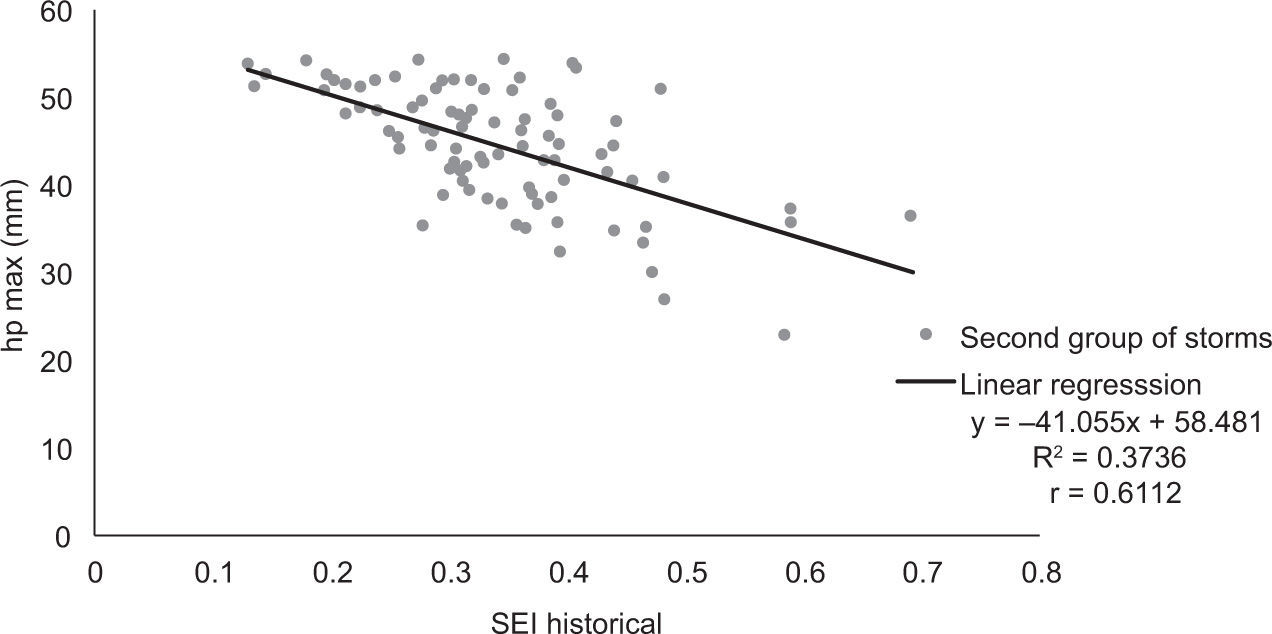
4.2

Second-generation procedure (two-groups analysis)

According to the results summarized in Figure 9, a second generation procedure was proposed, in which historical storms were classified into two groups: the first one was selected by a visual inspection of Figure 9, which shows that the points corresponding to values of h_pmax above 55 mm (that is the median of the h_pmax values) do not show interdependence with the spatial extension index, and the second one considers the rest of the values. By relating the maximum precipitation of each one of these two groups with the corresponding values of (SEI_i), Figures 10, 11 were obtained.

Fig.10.

Relationship between the maximum precipitation and the spatial extension index (SEI_i). First set of historical storms.

Fig.11.

Relationship between the precipitation and the spatial extension index (SEIi). Second set of historical storms.

It is interesting to notice that, as shown in Figure 10, the first group of storms contains not only the largest maximum precipitation values, but also covers all the range of SEI_i values; also, that the correlation between SEI_i and maximum values is practically negligible, and that in Figure 11, which corresponds to the lower maximum precipitation values, there is still a significant correlation.

Therefore, the first procedure to generate synthetic storms was modified: when the maximum value of PSMAX_k obtained in step 3 is greater than or equal to the threshold for the corresponding median of the maximum historical, one of the storms from the first group (storms with large maximum value) is randomly selected. Otherwise a storm from the second group is selected.

4.2.1

Application of the second-generation process

It was determined that the median of the maximum point rainfall is 55 mm.

Historical storms were ranked from the highest to the lowest, according to their maximum precipitation. They were divided into two groups, the first one formed with the first 89 storms and the second with the remaining 88.

With the distribution function given by Eq. (2), 1000 random numbers were generated in order to obtain 1000 maximum precipitation synthetic values PSMAX_k: k = 1,2,...,1000.

For the selection of the storms that should be scaled, it was considered that when synthetic maximum precipitation PSMAX_k is greater or equal to the median, a randomly selected storm from the group of large storms should be selected; otherwise, the selection is made randomly from the second group of historical storms.

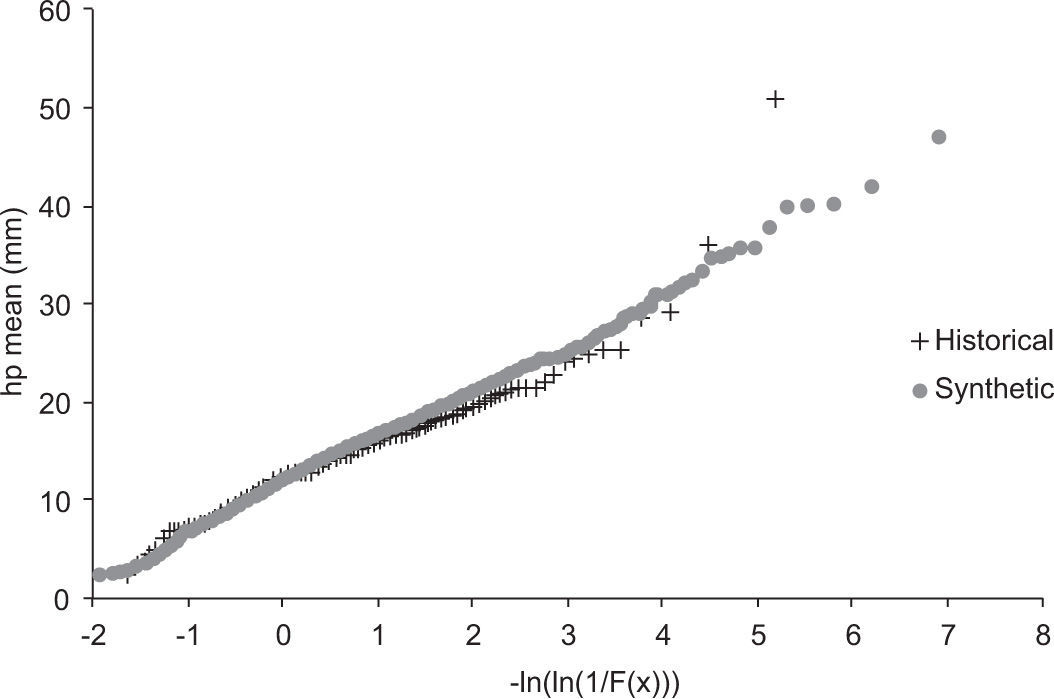
In Figure 12, the empirical distribution functions corresponding to the maximum historical and synthetic values are compared. It is shown that the distribution function for the maximum historical storms is adequately reproduced.

Fig.12.

Empirical probability distributions of the maximum precipitations. Second procedure.

In addition, the empirical distribution of mean synthetic precipitation obtained with the second-generation procedure was determined. Figure 13 shows that the distribution function of the means of historical storms is accomplished with the new procedure.

Fig. 13.

Empirical probability distributions for the spatial average precipitations. Second procedure.

When drawing the relationship between the average and maximum precipitation for the generated storms (Fig. 14), a very low correlation was found, as obtained for the historical record shown in Figure 7.

Fig. 14.

Relationship between average and maximum values. Second procedure.

Figure 15 shows a similar correlation to that obtained for historical storms (Fig. 9). Furthermore, a comparable trend is also identified with regards to events associated to lager peaks, which tend to be less spatially extended.

Fig. 15.

Value of SEIi and maximum precipitation (synthetic storms). Second procedure.

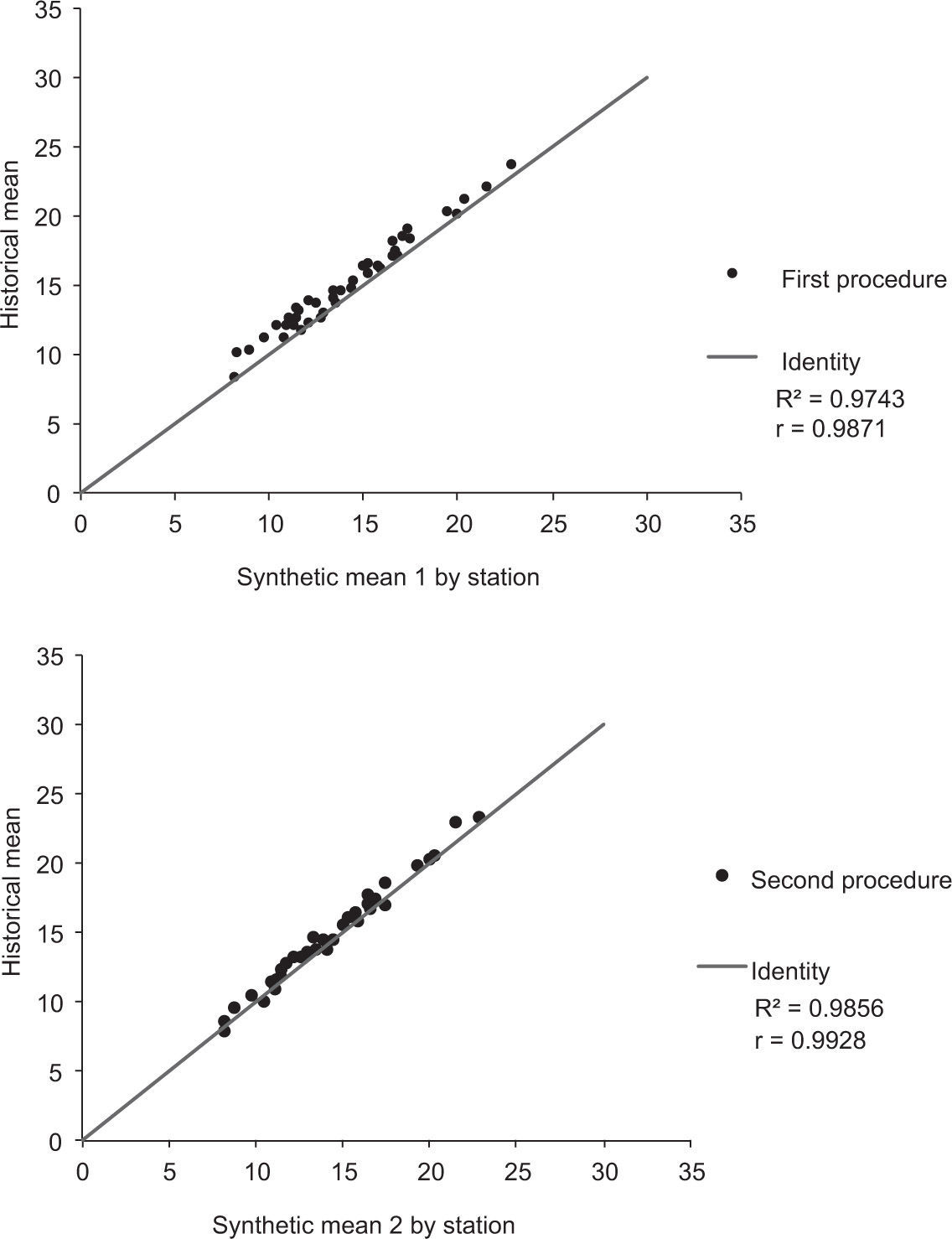
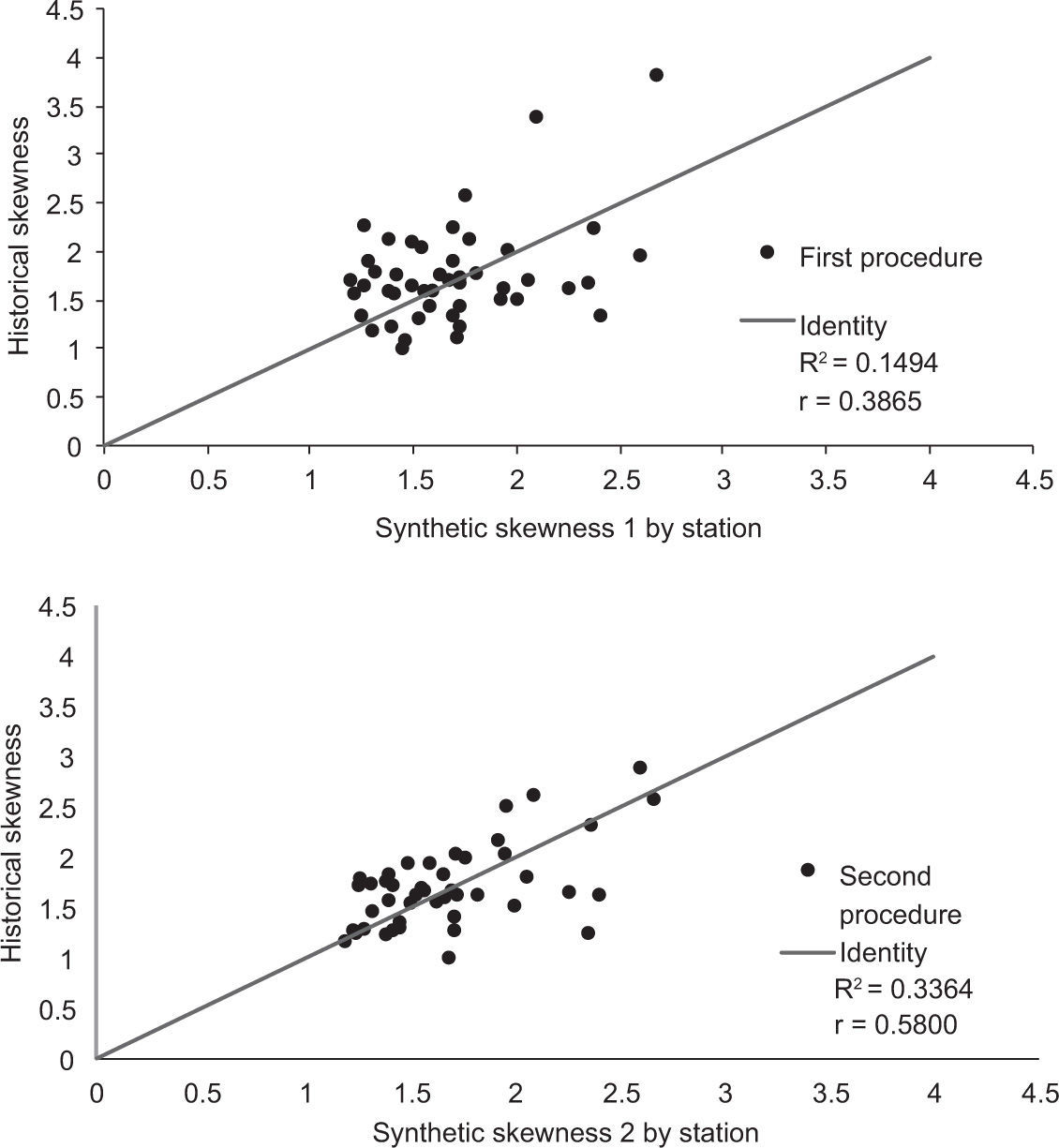
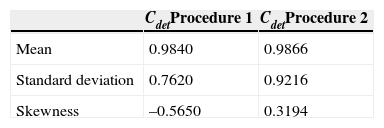
Since the general statistical characteristics (maximum, average and SEI_i) for historical storms were adequately reproduced, results were analyzed considering the values obtained for each station. Figures 16-18 contain information to compare the statistical parameters (mean, standard deviation and skewness) calculated at the 49 stations for the synthetic storms, as obtained with the first and the second procedure, vs. their corresponding historical values. In order to simplify the analysis, the comparison for each procedure is made by using the identity function as a benchmark.

Fig. 16.

Behavior of the mean for each station.

Fig. 17.

Behavior of the standard deviation for each station.

Fig. 18.

Behavior of the skewness coefficient for each station.

The correlation coefficients shown on Figures 16-18 measure how the points clustered to the line that best fits the data pairs, but not necessarily to the 45 degree line that represents the identity. In order to estimate the correlation between the values of the parameters corresponding to the historical storms and the parameters obtained from the synthetic storms, a new coefficient was calculated by means of the following procedure:

For each statistical parameter (mean, standard deviation and skewness coefficient) a determination coefficient C_det is obtained, which takes into account the variance of the differences between the values obtained for the historic and the synthetic storms:

where Var_y represents the variance of the statistical parameter y on the 49 recording stations, for the historical sample; Var_ε the variance of the differences between the statistical parameters y of the historical sample and of the synthetic sample; and y the parameters mean, standard deviation and skewness, successively.

The comparison between the coefficients of determination thus obtained for each generation procedure is presented in Table I.

Table I.

Comparison of coefficients of determination.

	CdetProcedure 1	CdetProcedure 2
Mean	0.9840	0.9866
Standard deviation	0.7620	0.9216
Skewness	–0.5650	0.3194

It is pointed out, again, that the second proposed procedure significantly improves the preservation of the statistics of each station, particularly in the case of the standard deviations and skewness.

5

Conclusions and recommendations

A procedure based on the fragments method of Svanidze was applied to generate 1000 synthetic storms, from 177 storms recorded at 49 pluviometers in the basin of Mexico City. An analysis of the results shows that the distribution function of the spatial average for the historical storms was not adequately reflected, as it is clearly shown in Figure 6. For this reason, the correlation of the maximum vs. the mean values was neither reproduced adequately. This correlation was low (0.0849) for historical storms, while it was high for synthetic records (0.5618), as shown in Figures 7, 8.

A detailed analysis of the variables included in Figure 7 shows a spurious correlation between maximum and mean precipitation. This is ascribed to the fact that maximum precipitations are used in the evaluation of both the independent and dependent variables. In order to avoid this spurious correlation, a spatial extension index (SEI_i) was defined. This parameter enabled to demonstrate that the magnitude of the maximum precipitations is correlated with the spatial extent of the storms. So, as the maximum precipitation is more intense, precipitation events tend to be less extensive, as shown in Figure 9.

According to these results, two groups of historical storms were defined, each one about the same size: the first group contained storms with maximum precipitations greater than the median and with a low significance correlation between the maximum precipitation and the spatial extension index, and the second group contained the remaining storms. The procedure to generate synthetic storms was then modified so that the selection of the storm that would be scaled depended on the maximum value randomly generated.

By using the second method of generation it was possible to preserve the basic statistical characteristics of historical storms on the generated ones: the distribution functions of the maximum and the mean precipitations, as well as the correlation between the maximum and average precipitations (in this case equal to 0.082, similar to the corresponding for historical storms).

In addition, the synthetic precipitations obtained in the 49 stations were also analyzed. The results showed that the second procedure allowed reproducing adequately the statistical mean and standard deviation of each one, as is shown in Figures 16, 17.

In the case of the skewness, Figure 18 shows that a general agreement between synthetic and historical values was achieved, but the correlation between them was smaller, which seems logical considering that skewness is a statistic that depends on the third moment of the probability distribution function, usually difficult to reproduce.

Acknowledgments

We would like to thank Rafael Ibarra Contreras for reviewing the structure of the document and Humberto Guzmán García for his support in the preparation of graphs.