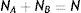New perspectives on the computational characterization of the kinetics of binding-unbinding in drug design: implications for novel therapies

Abstract

The efficiency and the propensity of a drug to be bound to its target protein have been inseparable concepts for decades now. The correlation between the pharmacological activity and the binding affinity has been the first rule to design and optimize a new drug rationally. However, this argument does not prove to be infallible when the results of in vivo assays have to be confronted. Only recently, we understand that other magnitudes as the kinetic rates of binding and unbinding, or the mean residence time of the complex drug-protein, are equally relevant to draw a more accurate model of the mechanism of action of a drug. It is in this scenario where new computational techniques to simulate the all-atom dynamics of the biomolecular system find its valuable place on the challenge of designing new molecules for more effective and less toxic therapies.

Resumen

La eficiencia de un fármaco se ha relacionado habitualmente con su constante de afinidad, magnitud que puede ser medida experimentalmente in vitro y que cuantifica la propensión mostrada por la molécula ligando para interaccionar con su proteína diana. Este modo de entender el mecanismo de acción ha guiado durante años el desarrollo de nuevas moléculas con potencial farmacológico. Sin embargo, dicho modelo o criterio no es infalible cuando se confronta con los resultados de ensayos in vivo. Otras magnitudes, como las constantes cinéticas de asociación o disociación o el tiempo de residencia del ligando acoplado a su proteína diana, demuestran ser igualmente necesarias para comprender y predecir la capacidad farmacológica del compuesto químico. En este nuevo escenario, con ayuda de las técnicas computacionales de simulación molecular, la correcta caracterización del proceso dinámico de unión y desunión del ligando y receptor resulta imprescindible para poder diseñar racionalmente nuevas moléculas que permitan terapias más eficaces y menos tóxicas.

1

Introduction

The simplest paradigm of drug-protein binding has been described as a two-state kinetic model between the unbound state, where the ligand molecule (drug) and the receptor (target protein) are two independent uncoupled (non-interacting) bodies, and the bound state, where the receptor hosts the ligand interacting each other and behaving as a unique body: a molecular complex. This description has proven successful modeling in silico (using computer simulations) the biochemical processes observed in vitro (in a ‘test tube’ under controlled conditions), where the concentration of ligands and targets are kept constant, and the system is closed and thereby in equilibrium. Due to the complexity of the titanic challenge of designing a new drug, the main criterion to predict a priori if a new compound shows a high pharmacological activity has been the characterization of the interatomic interactions between ligands and receptors at the binding site, with the aim of discerning whether it is more likely for the system to stay associated (bound) or dissociated (unbound). However, this paradigm fails most of the time when the result of in vivo assays has to be rationalized. The following example illustrates the limit of these prior assumptions. Maschera et al.¹ investigated the different resistance effects conferred by some HIV-protease mutations to the AIDs drug saquinavir. They found that when measuring the IC50 (half maximal inhibitory concentration) in vitro experiments, the resistance of the mutant virus could not be explained attending to the binding affinity of the drug (more affinity, more target proteins affected by the ligand) but to the kinetic rate of dissociation. This apparent contradiction with the classical binding kinetic model in equilibrium was the only evidence used by Copeland et al. (2006)² to propose the need to give more credit to concepts such as the binding and unbinding rates or the drug-protein residence time in our way of understanding the inhibitory effect of a drug. At present, ten years later, we can already find on the market the first drug rationally designed with the residence time (dissociation half-life > 300 min) in its prescribing information label:³ Tykerb® (lapatinib), a new anticancer drug approved in 2007 for patients with metastatic HER2 positive breast cancer. Other examples of new molecules designed or optimized taking into account the kinetic rates are now frequently reported in the literature. Some of them already are in clinical trials.⁴ However, far from making an exhaustive and systematic collection of cases in which there are no correlations between the binding affinity and the pharmacological efficiency observed in vivo assays, this review was written in an effort to introduce a non-specialized community to some of the novel concepts in the forefront of the field of rational drug design and optimization and, at the same time, describing the state of the art. In the following sections, the reader with no specific background in this field will find keys to understanding the relevance of these concepts to be able to anticipate some of the characteristics of the future new drugs.

2

Limit of the classical paradigm of binding thermodynamics

There is a consensus among scientists devoted to the rational design, discovery, and optimization of new drugs on asserting that the most relevant feature of a molecule explaining its pharmacological activity is the binding affinity for the target protein. This binding affinity can be defined as the propensity of ligand and target to be found associated in comparison with the tendency to be unbound behaving as two non-interacting elements. This way, a ligand with low affinity will be rarely found coupled to the target, while those chemical compounds with high affinity will find the bound state energetically more favorable than being ‘unbound’. The binding affinity is a macroscopic magnitude accounting for the interactions (electrostatic, polar, steric, hydrogen bonds) between atoms from two molecules. These interactions can be measured in a laboratory with experiments such as the Isothermal Titration Calorimetry (ITC)—the ‘golden standard’ for the quantitative characterization of the interaction between ligand and receptor^5–7—pull-down experiments, ELISA, equilibrium dialysis or spectroscopic assays.^8–10 This concept has not been the only guiding principle to describe the effect of a drug. Any biological function occurred in any living being is described at its lowest level of detail by atomic interactions between molecules. These molecules can be proteins, peptides, nucleic acids, lipids, ions or waters, among other organic molecules. The ability to interact specifically with them, under certain conditions, triggers and regulates every physiological process. It is then reasonable to think for every researcher with basic knowledge of chemistry and biology that the higher is the binding affinity of a ligand molecule interacting with an enzyme, ion channel, receptor or any other macromolecular target,¹¹ the stronger is the effect of its mechanism of action. Thus, optimizing the interactions between ligand and receptor at atomic scale with a more favorable electrostatic interaction, adding a new hydrogen bond, or reducing the steric effects should entail a higher pharmacological efficiency. Unfortunately, although this can be a good starting point in the process of rationally designing a chemical compound with pharmacological properties, when the molecule is tested in an in vivo assay, many times the binding affinity fails as a good pre-indicator of the activity observed.

To understand why ligands showing a similar binding affinity in silico or in vitro assays can have a different pharmacological activity, we have to begin with what is known in statistical physics as the first-order kinetic model of a two-state closed dynamical system. This simple model, used to characterize and predict the behavior of many physical processes and chemical reactions since a century now can be described as follows. A system is composed of N particles, where each particle can be either in the state A or B. The system is dynamical, meaning that any particle can change its state from A to B at any moment with a fixed probability represented here as P_AB, and from B to A with a probability P_BA. Additionally, the system is closed, meaning that the number of particles in A (n_A(t)) plus the number of particles in B (n_B(t)) is constantly equal to N (the total number of particles never changes). It is known, mathematically derived, that given any initial population of A and B after a transient period, the system relaxes to its stationary equilibrium, where the number of particles in each state will not longer vary in the time remaining constant to their values N_A and N_B. This final amount of particles in each state can be previously deduced satisfying the following two equations:

This final stationary situation does not mean that any particles are changing their state. There are transitions indeed, but the average number of particles per unit time moving from A to B is equally balanced by the same average number of (other) particles moving from B to A. This is the meaning of Eq. 2, known as the equation of detailed balance condition (valid in equilibrium).

Now, once the generic model has been introduced to the reader in a rigorous manner, the analogy with the drug-protein association process emerges immediately. In an imaginary a vessel in a laboratory, molecular ligands, and target proteins freely move in an aqueous medium. After a certain initial period, a constant concentration of dissociated molecules, C_d, and a constant concentration of associated complexes (ligand + receptor), C_a, stabilizes the equilibrium state of the system. At last, the binding affinity can be formally defined and measured as the rate C_a/C_d. Then, the higher is the affinity, the higher is the propensity of a ligand and receptor to be bound. Consistently with the standard notation used to describe a chemical reaction, the general Eq. 2 can be re-written as

where K_on and K_off play the role of transition probabilities between the states, usually named as binding and unbinding kinetic rates (or association and dissociation rates).

Nevertheless, why this description fails, and molecular ligands with similar binding affinity have a different effect in vivo? Why is not the binding affinity the only parameter to work with when the efficiency of a drug has to be predicted? The answer is simple. Unfortunately for the chemical medicine but luckily for us, biological processes do not fit in the model. We are not closed systems, and life is constantly out of equilibrium. That is the reason why a drug should not rationally be optimized attending only to the propensity to be bound to the target protein.

3

Relevance of the binding kinetics and residence time of the drug-protein complex

Assuming we could accurately calculate the physical atomic properties of a molecular ligand to check its complementarity with the physical atomic properties of the binding site in the target protein, and also assuming we could repeat this operation at a reasonable short period to be able to screen millions of possible molecules finding the candidate with the highest binding affinity, these actions do not guarantee a successful pharmacological effect prediction. This condition would be enough to reproduce the result of in vitro experiments in the laboratory where the system is closed and in equilibrium. However, the mere consideration of the binding affinity is not enough to foresee the effect of the ligand in an open system. To illustrate this fact and its implications, we have the following less academic and more mundane example: the sleeping time of a cat. Since it was adopted months ago, the cat spends 2/3 of the time sleeping. This fact is extremely unpleasant for the owner since it only allows the owner to enjoy its company during 8 h per day, i.e. the cat spends twice as much time sleeping than awake. Therefore, if the reader was to visit, the probability to get to meet the cat asleep is higher (twice) than awake. However, does it mean the reader will not have the opportunity to play with the cat during the visiting time? We do not have enough information to answer this question. The reader does not know if the cat sleeps 16 uninterrupted hours, or quite the opposite, he sleeps 20 minutes to be active during 10 minutes between nap and nap. His total sleeping time per day is the same, but the chances for the visitor to play with the cat are different in both scenarios. This happens because the system (house with cat and visitor) is an open system. The number of elements is variable given that the presence of the visitor is not constant and the period of interaction is limited. A different situation would be locking the door once the reader is in the house, making a closed system. After a transient period, enough to observe the cat several times awake and asleep, the visitor would enjoy his company 1/3 of the time no matter how long his naps are. At that moment, we could say that the system is closed and the equilibrium was reached. This fictional example addresses the implications of having an open system, giving an important hint of understanding why drugs with a similar binding affinity (cats with similar probability to be awake) do not elicit the same pharmacological effects: the frequency or probability of changing between states.

Back to the behavior of the ligand and receptor system, the binding affinity previously described as the rate C_a/C_d does not offer any information about the time length of uninterrupted association of both molecules (lifetime or residence time), quantitatively defined as the inverse of the dissociation rate constant (1/K_off). However, the detailed balance equation of a closed system (Eq. 2) allows us to find another definition of binding affinity depending only on the kinetic rate constants: Ca/Cd is the same rate as K_on/K_off. Thus, different ligands can bind a receptor with the same propensity but with different binding and unbinding characteristic times. For example, three inhibitors can have the same association-dissociation propensity interacting with an enzyme, e.g. 1:1, but different kinetic constants. The first inhibitor makes 60 times the transition bound↔unbound per hour, which implies 1 min lifetime of the enzyme inhibited on average. The second inhibitor transits between the two states not so easily, four times per hour (inhibition lifetime of 15 min); and for the third inhibitor-enzyme system, the association-dissociation process is a rare event observed two times per week (inhibition lifetime 3.5 days). This different dynamical behavior might not be relevant when the inhibition is studied in vitro (in a closed system), but the implications for living beings treated with these drugs can be crucial.

4

Pharmacological implications

The absorption, distribution, metabolism, and excretion of a drug is a process complex enough to presume that the pharmacological activity of a chemical compound will be entirely determined by the binding affinity measured in equilibrium at the bench of a laboratory. All those steps require specific attributes for a molecule to perform as a drug with the appropriate bioavailability, the adequate activity and efficiency, and without toxic side effects.

The drug, since the very moment of its administration until it is introduced into the bloodstream for its distribution, has to move through several membranes and physiological barriers. To facilitate the motion through these barriers, the physicochemical properties, such as the size of the molecule, permeability, solubility, lipophilicity or the ionization constant, have to be properly combined in addition to those chemical motifs providing with the atomic interactions relevant for the selectivity and affinity of the ligand with the target protein.^12,13 A drug with low solubility will result in a low artificial activity measured both in vitro and in vivo. The compound precipitates in the aqueous solvent decreasing the concentration of molecules with the ability to interact with the target protein. In order to counteract this effect, the dose can be increased overlooking the corresponding potential toxic drug-drug interaction. A drug with low permeability will have a similar effect. This time the activity measured in vitro will be higher than in vivo because of its problems to cross the cellular membranes. It is clear now that if any of these attributes do not behave optimally, the number of survival molecules reaching its target will be too low. For that reason, optimizing the effect of every molecule interacting with its target it is of great importance. Moreover, as it is described below, the K_on and K_off kinetic rates can be a power tool for this mission.⁴

However, these four steps of the pharmacokinetic process have not been mentioned only to illustrate the numerous and different conundrums a scientist has to face to rationally design and optimize a drug. They justify something more relevant: drugs enter into the organism to be ultimately excreted. As a result, the concentration of drug molecules into the tissues is not homogeneously distributed and do vary in time. The possibility of a target protein to find a ligand molecule to host is not always the same. In a hypothetical case, the enzyme mentioned in the previous section could belong to a tissue or region of the cellular space visited at this moment by the arrival of drug molecules, which will bind to the protein inhibiting its activity. During this period and only in this region, the amount of enzymes associated with the inhibitors is well defined by the binding affinity. However, as soon as the drugs start to be excreted decreasing the concentration of available ligands, or the enzyme abandons the encounter zone, the pharmacological activity will depend on the K_off rate. At this moment, the third inhibitor described in the previous section, the one with the longest residence time, proves to be the most efficient. In this case, a low dissociation rate, K_off, can keep a sustained pharmacological activity during a longer period. If the drug has been optimized to reach a low K_off, it might be the case that the lifetime of the drug-target complex could be larger than the time the body takes clearing the drug.^14,15 In this situation, the time between doses could be increased significantly, reducing the possibility of intoxication by overdose in long treatments, and reducing the side effects of the treatment due to unwanted interactions between the drug and other off-target proteins.

It is worth mentioning that, although it is not a closed system and will never reach equilibrium, the binding affinity still plays an essential role. The dissociation constant K_off has brought much attention recently given the promising results for the quality of future treatments.^4,16–19 However, this rate is only one of the ingredients of the model. Drugs with the same residence time could have different in vivo activities due to different K_on rates. No general rules apply for all cases; it is the interplay between all transition rates in the binding-unbinding kinetic model what describes the effect of the drug on the receptor. Furthermore, this model, characterized by only two states (associated or dissociated complex), is an over-simplistic image of a real process where the argument of two bodies interacting in two-state processes as if they were two rigid bodies with the same shape, geometry and accessible area to the solvent, is no longer valid. Thanks to in silico molecular simulations, we have learned that local physical changes as amino acid side-chain rotations, geometrical changes and motions involving larger regions, the participation of few water molecules or ions, or even a second different drug also interacting with the receptor, enrich the binding-unbinding model with numerous intermediate states and kinetic rates between the fully dissociated complex and the most stable bound pose. Moreover, this complex landscape, far from being a disadvantage, can be the source of new treatments involving a lot of different mechanisms and effects. The possibility to modulate the effect of a drug with a second different chemical compound interacting with the target protein through a different binding site is being explored with the discovery of the allosteric modulators.^20–23 The possibility to design different chemical compounds acting over the same region of the target protein in a different way, and thereby triggering different responses as if they were toggling a switch, is already explored and described in the literature as signaling biased drug design.^24,25 Finally, the impact of protein-protein interactions and the oligomerization of receptors in the cell membrane remain unclear but could open new horizons to be explored in the challenge of rational design and optimize a drug.^26,27

5

New computational approaches, new scenarios

The recent advances in the pharmacological sciences are the result of a new multi-disciplinary way of working where physics, chemistry, mathematics and computer science meet biology. The scientific background and technical experience of experimentalists testing and validating hypothesis in vitro and in vivo are combined today in hospitals, research institutes, and universities with a third vertex completing a virtuous triangle: the availability of in silico methods. These three different approaches are mutually reinforced when the value and limitations of each of them are recognized: in silico methods depend on theoretical models, but help to generate a new scientific hypothesis, new scenarios at a low cost to predict and explain the performance of in vivo and in vitro experiments. In vitro assays validate the theoretical models, and characterize the behavior of the system under controlled conditions to predict in vivo results. On the other hand, in vivo assays are the last experimental battlefield, where the success of the scientific hypothesis has to be proven given at the same time invaluable feedback to correct the prediction machinery generating new theories and computational tools.

Since 1950s, theoretical models of interatomic interactions have being developed based on classical and quantum physics to describe the thermodynamics and kinetics of molecular systems. Those molecular models based on classical mechanics represent each atom as the smallest indivisible entity, coarse-graining electrons, neutrons and protons, and the effect they can cause in their interaction with other atoms at the temperature and time scales of interest. Covalent bonds, electrostatic and Van der Waals interactions, pi-stacking, and hydrogen-bonds or disulfide bridges are described as ad hoc parametrized harmonic, torsion and dihedral potentials, and short- and long-range Coulomb and Lennard-Jones potentials. These interactions, together with the precise knowledge of the topology and chemical composition of a molecule (atom types, relative position in space and covalent bonds) are already enough information to predict some simple physicochemical attributes of the molecule. This set of parameters to quantitatively model the interatomic interactions is known as ‘classical force-field.’ At the present day, there are various force fields of public domain, constantly tested and improved, to mimic the intra- and intermolecular interactions of all kind of organic molecules such as peptides, proteins, nucleic acids, lipids, ions or water molecules.²⁸ The right selection of parameters, sometimes tuned or adapted, depends on the physics of the particular system to be simulated. At this point, we have a toolbox to build static virtual molecules whose interactions have to be necessarily evaluated computationally. A small portion of membrane—made of lipids of different nature and molecules of cholesterol, with an embedded protein as an opioid receptor or an ionic channel, solvated with water molecules and ions—add up to ∼50,000 atoms. Assuming that every atom interacts with any other atom of the system using long-range forces, the number of equations to be solved is out of the human capability making use of a piece of paper and a pen. Already this rigid and static description provides with useful information about the system, but there are statistical physics methods to stochastically integrate the equations of motion of every atom, including in the model the conditions of temperature and pressure. These theoretical frameworks from physics science translated into code lines in a computer allow us to reproduce the time evolution of the biomolecular system. At this point, we have what is known as the all-atom Molecular Dynamics Simulation,^29–31 and the result is the three-dimensional position, velocity vector, and energy potential of every atom at every time step, usually in the range of 2 to 5 femtoseconds (10⁻¹⁵ s). Depending on the molecular system, the time simulated and the data required for the analysis, the size of this information can extend from megabytes to terabytes in the hard-drive. Hence, using this technology we can observe the behavior of the molecular models in time as if we were using a microscope^32,33 with a precise resolution able to distinguish significant variations of interatomic distances in the order of ∼0.1 Angstroms (10⁻¹¹ m). However, how useful is an all-atom molecular dynamics simulation to describe a biological process? The answer depends on two factors: the time scale and size of the biomolecular system we want to study, and the power of our computational facilities. The mean lifetime of a hydrogen bond between water molecules in bulk is around ∼3 ps (10³ integration steps).³⁴ The rotation of the side-chain of an amino acid takes in the order of ∼10 ns (10⁶ steps). Furthermore, the conformational changes involving a large number of atoms or secondary structures are observed in the order of ∼100-1000 ns (10⁸ steps), and a small protein folding or an ion channel gating is around ∼10-100 μs (10¹⁰ steps).³³ This former number of steps required to integrate few microseconds looks astronomical. Nevertheless, today it is affordable with the big and powerful supercomputers, like ANTON, the fastest supercomputer dedicated to the simulation of biological systems with 512 nodes working in parallel to achieve ∼17 μs of simulation per day for a system with 23 × 10³ atoms.³⁵ However, with the computational resources found in a well-equipped standard laboratory as it could be a 36 cores CPU or the last consumer GPU (GTX 1080), the times achieved are 78 ns/day and 418 ns/day, respectively.³⁶ These numbers may seem disappointing for the non-specialist general reader, particularly when the need of simulating the rates of association and dissociation of a drug-protein complex has been discussed here, and these time scales required to observe these events range from seconds to hours (5 hours in the case of the anticancer drug lapatinib).³ However, working with these computational tools does not only consist of performing brute-force molecular dynamics simulations. The scientific community in this field works hard combining creativity with a deep knowledge of thermodynamics, statistical physics, computational biophysics, and big data analysis to overcome these limitations with new theories and computational techniques predicting the seemingly unreachable observations. Finally, to illustrate this fact, some of the novel computational approaches that are currently being developed and tested to compute the binding affinity and the kinetic rates are briefly described here for the sake of offering a complete view of the current state of this matter.

6

Binding affinity: free energy perturbation methods

Once the target protein has been identified, and some structural or physicochemical information of the binding site is available (the 3D structure of the receptor or a pharmacophore), one of the first steps of a computational drug design campaign is the screening of a large set of different chemical compounds, looking for candidates with a suitable binding affinity. This task can be computationally very expensive given that the first set of candidates is usually set up with ∼10⁵-10⁶ chemical compounds. An exhaustive analysis with all-atom force fields and flexible ligand and receptor seem a very demanding task for a first pre-selection. Instead, a coarse-grained screening is performed searching for the set of compounds best matching the physical attributes required to optimize the interatomic interactions. Notice that, at this point, no quantitative prediction was made based the binding affinity of the complex, there is no propensity for the ligand to be unbound calculated. Sometimes a rough estimation based on simple solvation models is included as one of the attributes to be fulfilled, but usually considering the molecules ligand and receptor as a two rigid bodies in a vacuum. The process briefly described is called High Throughput Virtual Screening, and it has been extensively used with successful results in designing new drugs.^37,38 At present, a new computational approach is being tested by computational laboratories and pharmaceutical companies to screen chemical compounds, calculating the relative free energy of binding (magnitude proportional to the binding affinity), including the flexibility of the molecules in addition to every possible effect present in the all-atoms simulation box (ions and water interactions, and conformational changes among others). The computational framework called Free Energy Perturbation methods,^39–43 is based on theoretical concepts developed and applied by physicists to different dynamical systems since years. Only recently, the different relative propensities have been adopted to computationally evaluate a set of ligands to be bound to the target protein. Taking advantage of the virtual character of the computational molecular model, given two different chemical compounds, X and Y, the all-atom dynamics of X is simulated transforming little by little their set of parameters in those defining the compound Y, whereas the difference in relatively free energy is integrated along this path. The strategy of a virtual transformation of the ligands along the all-atoms dynamics, named alchemical transformation,⁴¹ allows both ligands and target protein to move freely and adjust their atoms to the most favorable configuration at any moment. Thus, prominent pharmaceutical companies as Bayer Pharma AG or GlaxoSmithKline Pharmaceuticals Ltd. are already exploring this approach. Bayer started the first round of tests to validate the usability of this technique on 2015,⁴⁴ and Glaxo followed simultaneously the same steps.⁴⁵ The approach, although at this moment is used only experimentally, it is providing accurate quantitative results to predict the relative binding affinity. To evaluate absolute binding affinities, new computational techniques as YANK,⁴⁶ an approach to perform alchemical transformations between the drug-protein associated and dissociated, are under current in development.

7

Binding-unbinding kinetics route map

Regarding the characterization of the binding-unbinding process of a ligand, several techniques have to predict the thermodynamics of the process, and sometimes the kinetics: accelerated dynamics, metadynamics, umbrella sampling, replica exchange methods, and an extensive list of enhanced molecular dynamics approaches.^47–50 However, those methodologies based on Markov State Models,^51,52 Multi Ensemble Markov State Models,⁵³ and Adaptive Sampling^54–56 deserve special attention. The strategy, well grounded, relies on measuring local transition probabilities sampling the conformational space with multiple short trajectories. Three recent works must be highlighted to understand the power of this promising approach. The first one, by Pande et al., reported the use of this strategy using the Google's cloud computing platform to simulate during 2.15 min the interaction between the protein β2-adrenergic receptor in the presence of two different ligands.⁵⁷ The second work is the binding-unbinding complex route map, involving different intermediate metastable states of the serine protease trypsin and its inhibitor benzamidine, reconstructed by De Fabritiis et al.⁵⁸ Finally, the third work by Noé et al. is the computational prediction of the kinetic unbinding rate K_off of the same system, by means of combining multiple short unbiased trajectories with umbrella sampling simulations.⁵³ All these computational works describe the binding-unbinding process as a map of multiple metastable intermediate states driving the system along different transitions with different kinetic rates from the dissociate complex state to the most stable bound state.

To conclude, the binding and unbinding process of a drug interacting with its target protein cannot be accurately described with a traditional two states kinetic model. The assumptions made for a closed system in equilibrium are no longer valid in a context where the concentration of ligands available to be captured and host by a receptor is not constant in time and space. Thus, the binding affinity does not always correlate well with the pharmacological activity observed in vivo. Other ingredients, as the kinetic rates or the associated residence time, have to be considered by the drug design community if new compounds have to be developed and optimized with a more precise mechanism of action and less toxic effects. It is in this scenario where the last computational advances assist us, working side by side with experimentalists, to understand and characterize a more complex and rich interaction mechanism between both molecules drug and protein.

Funding

The authors have no support or funding to report.

Conflict of interest

The authors declare no conflicts of interest of any nature.