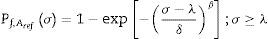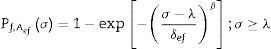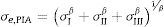El vidrio y la cerámica presentan un comportamiento frágil, lo que implica una gran dispersión en los resultados de ensayos. Esta dispersión se debe principalmente a la inevitable presencia de microfisuras superficiales, defectos de borde o defectos internos, que deben tenerse en cuenta mediante criterios de fallo apropiados no deterministas, sino probabilistas. Entre las distribuciones de probabilidad existentes, generalmente se utiliza la distribución de Weibull bi o triparamétrica en el ajuste de resultados de resistencia de materiales.
En primer lugar se realiza un amplio programa experimental utilizando probetas planas de vidrio recocido de distintas dimensiones bajo flexión a 4 puntos y flexión con anillos concéntricos dobles. Seguidamente se presentan los modelos de elementos finitos realizados para cada tipo de ensayo, así como el ajuste de los parámetros de la función de distribución (fdd) triparamétrica de Weibull (λ: localización; β: forma; δ: escala) para un criterio de fallo determinado y el cálculo de las áreas efectivas a partir de la fdd determinada.
Con todo ello, el trabajo pretende generalizar la utilización de la fdd triparamétrica de Weibull en elementos de vidrio estructural con distribuciones de carga no descritas analíticamente, permitiendo aplicar el modelo probabilista propuesto a distribuciones generales de solicitación.
Glass and ceramics present a brittle behaviour so a large scatter in the test results is obtained. This dispersion is mainly due to the inevitable presence of micro-cracks on its surface, edge defects or internal defects, which must be taken into account using an appropriate failure criteria non-deterministic but probabilistic. Among the existing probability distributions, the two or three parameter Weibull distribution is generally used in adjusting material resistance results, although the method of use thereof is not always correct.
Firstly, in this work, the results of a large experimental programme using annealed glass specimens of different dimensions based on four-point bending and coaxial double ring tests was performed. Then, the finite element models made for each type of test, the adjustment of the parameters of the three-parameter Weibull distribution function (cdf) (λ: location, β: shape, δ: scale) for a certain failure criterion and the calculation of the effective areas from the cumulative distribution function are presented.
Summarizing, this work aims to generalize the use of the three-parameter Weibull function in structural glass elements with stress distributions not analytically described, allowing to apply the probabilistic model proposed in general loading distributions.
El uso de elementos estructurales de vidrio se ha incrementado y diversificado en la industria de la construcción, combinando los conceptos de sostenibilidad, funcionalidad y estética con su empleo en cubiertas, fachadas e interiores.
En la actualidad, prácticamente todos los edificios altos o singulares cuentan con la presencia de vidrio en sus estructuras. Sin embargo, hasta el momento no se cuenta con una norma de cálculo de vidrio estructural basada en criterios probabilísticos o semiprobabilísticos, y la demanda arquitectónica va muy por delante del dimensionamiento que, en muchos casos, se fundamenta únicamente en la experiencia y en la aplicación de reglas básicas empíricas.
A pesar de los estudios realizados y de los avances alcanzados, persisten algunos puntos críticos que impiden un conocimiento real del estado límite del vidrio bajo diferentes tipos de solicitación. Por ello resulta necesario el desarrollo de una norma global de vidrio que, considerando sus características específicas como material frágil con presencia de defectos, permita su aplicación en condiciones de seguridad y fiabilidad similares a las de otros materiales estructurales convencionales, como el acero, el hormigón y la madera [1–4].
Hasta ahora muchos autores y algunas normas tienden a utilizar un ajuste estadístico de los resultados experimentales poco riguroso y en ocasiones incorrecto. El fallo más comúnmente cometido es la realización del ajuste estadístico en base a un valor máximo y local del criterio de fallo, obviando la distribución de dicho criterio de fallo en otras zonas del espécimen ensayado. Esto, a efectos estadísticos, supone atribuir ese valor máximo a toda la extensión estudiada, sin tener en cuenta que pueden existir zonas con una probabilidad de fallo mucho menor.
En este trabajo se aplica una metodología probabilística general [5] que permite evaluar y comparar la caracterización mecánica de diferentes tipos de vidrio monolítico bajo solicitación de flexión a 4 puntos (4P) y de anillos concéntricos de pequeña superficie de solicitación, ajustando los resultados experimentales a funciones de distribución (fdd) triparamétricas de Weibull e incluyendo el efecto de escala a través de la consideración del área efectiva de cada ensayo.
Metodología experimentalMaterialesEn el programa experimental se utilizaron 30 probetas de vidrio monolítico recocido por cada tipo de ensayo. Todas las probetas se obtuvieron a partir de una misma placa matriz fabricada por flotado, evitando así posibles diferencias en la composición del vidrio que podrían implicar diferencias en su comportamiento mecánico y dudas o errores en la interpretación de resultados.
EnsayosPara la caracterización de la resistencia de los vidrios estudiados se realizaron ensayos de flexión a 4P y ensayos de anillos concéntricos con pequeña superficie de solicitación (CS). En ambos casos los ensayos se realizaron en control de desplazamiento equivalente a una velocidad incremento de tensión de 2MPa/s hasta la rotura, tal como indican las normas UNE-EN_1288-3:2000 y UNE-EN_1288-5:2000 [6,7].
Los ensayos de flexión a 4P se llevaron a cabo en un marco de ensayos con un servoactuador Series AH100/250 de Walter+Bai AG de 100kN de carga máxima y probetas de 1.100mm de largo, 360mm de ancho y 5mm de espesor, mientras que para los ensayos de anillos concéntricos se utilizó una máquina MTS Bionix Uniaxial con una célula de carga de 15kN y probetas cuadradas de 250mm de lado y 5mm de espesor.
La tabla 1 recoge las dimensiones características de los 2 tipos de ensayos realizados, siendo L0 y L1 las distancias entre apoyo y carga y entre cargas, respectivamente, en el ensayo de flexión a 4P, y r1 y r2 los radios de los anillos de carga y soporte, respectivamente, en el ensayo de anillos concéntricos, tal como se indica en las figuras 1 y 2.
En este trabajo se ha implementado para cada tipo de ensayo, en el código comercial de elementos finitos ABAQUS/Explicit v6.12, un modelo numérico completo.
El vidrio ha sido mallado con elementos tipo SC8R (elementos hexaédricos con integración reducida tipo Continuum Shell). Imitando el proceder experimental, la carga se aplica imponiendo un desplazamiento vertical a los rodillos o anillo de carga. Este desplazamiento es el medido por la máquina de ensayos desde el momento inicial hasta la rotura de la probeta en cada uno de los ensayos realizados. De este modo, se tiene una simulación para cada probeta ensayada con su consiguiente distribución de tensiones, indispensable para el análisis probabilístico posterior.
Para la validación del modelo numérico se hace una triple comprobación:
- •
Comparativa de la reacción obtenida en el modelo de elementos finitos con la obtenida mediante la célula de carga en cada ensayo.
- •
Comparativa del registro de deformaciones obtenido por galgas extensiométricas en diferentes zonas de la probeta: punto central, bordes libres y bajo los rodillos de carga para flexión a 4P, y punto central y bajo el anillo de carga en el caso de anillos concéntricos.
- •
Comparación de la distribución de desplazamientos obtenida en el modelo numérico con la obtenida mediante videocorrelación de imágenes digitales con el equipo ARAMIS5M de la firma GOM.
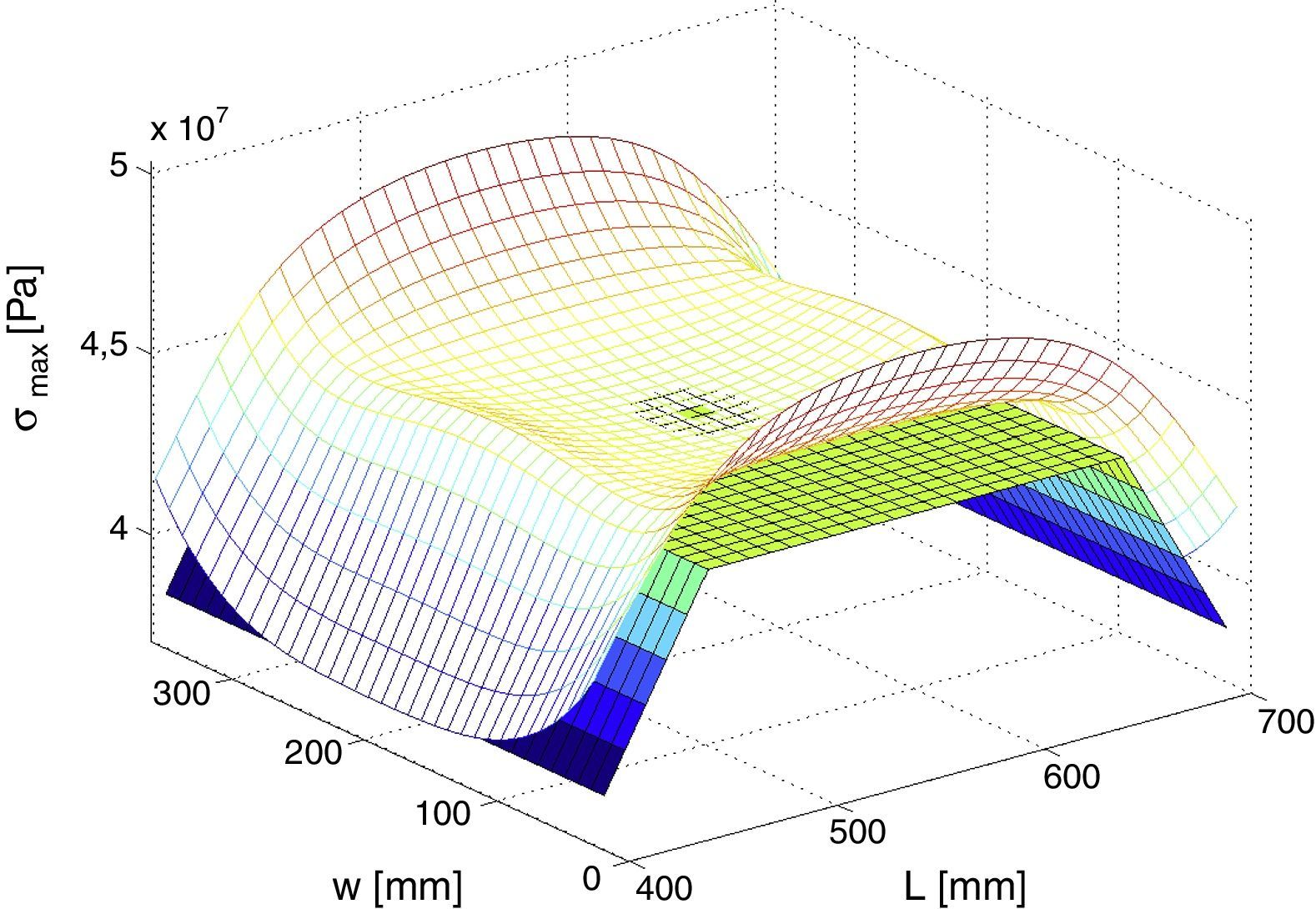
En la figura 3 se muestra la parte central de la placa en flexión a 4P y la diferencia entre considerar un perfil de tensiones uniforme, con la tensión máxima calculada según la norma, y la distribución real de tensiones, que ha sido obtenida mediante el método de elementos finitos y corroborada de varias maneras. Como se puede observar, debido a las dimensiones de la placa, se tienen mayores tensiones en los bordes y bajo los rodillos de carga que en la zona central, donde la tensión cae por debajo incluso del valor analítico.
Modelo probabilísticoEn la caracterización mecánica del vidrio la presencia de defectos superficiales distribuidos aleatoriamente, tanto en tamaño como en orientación, y la dispersión de resultados característica de los materiales cerámicos obligan a recurrir a métodos basados en criterios probabilísticos.
En 1939 Weibull [8] desarrolló una formulación para describir estadísticamente la rotura frágil en componentes sometidos a tensiones uniaxiales de tracción. A partir de entonces surgieron modelos para solicitación multiaxial basados en la teoría del eslabón más débil [9]. Entre ellos, los más utilizados internacionalmente son los de la tensión normal promediada [10], el principio de acciones independientes, conocido como PIA, que fue propuesto por Barnett [11] en 1967 y Freudenthal [12] en 1968, el modelo de Batdorf de densidad de defectos [13] y el modelo de resistencia multiaxial desarrollado por Evans en 1978 [14].
El modelo biparamétrico de Weibull ha sido aceptado tradicionalmente en la literatura para componentes frágiles [15,16] debido a que aporta resultados conservadores al suponer λ=0. Esto supone que para cualquier estado tensional, por muy pequeño que sea, existe una probabilidad de fallo, mientras que la inclusión de un factor de localización λ≠0 implica la definición de un umbral por debajo del cual nunca se produciría el fallo. La caracterización estadística de la resistencia del vidrio supone el ajuste indirecto del tamaño de defectos existentes en la muestra. El valor del factor de localización está asignado al tamaño máximo de defecto existente en toda la población, con lo que la utilización de la función biparamétrica supone la aceptación de un tamaño infinito de defecto, bajo el cual una solicitación prácticamente nula ocasiona el fallo, lo que no es conceptualmente aceptable. Por otra parte, el modelo triparamétrico converge al modelo biparamétrico automáticamente en el caso de que los resultados experimentales comiencen para cargas muy pequeñas. Estos hechos han motivado especialmente la utilización del modelo triparamétrico de Weibull, en lugar del biparamétrico.
La probabilidad de fallo de un área Aref tensionada uniaxial y uniformemente se expresa como función de distribución (fdd) triparamétrica de Weibull de valores mínimos, según la ecuación:
donde λ y β son los parámetros de localización y forma, respectivamente, y dependen únicamente de las propiedades del material y no de su geometría, mientras que el parámetro de escala δ depende del área de referencia considerado.El problema subyacente en estas y muchas otras campañas experimentales de vidrio es que no puede conseguirse que sobre la totalidad del modelo exista una distribución tensional uniforme [17], por lo que la aplicación del modelo de Weibull directamente conduce a errores. Por este motivo, en el presente trabajo se ha utilizado una metodología que permite calcular para cada experimento un área efectiva que, sometida uniformemente a la máxima tensión principal alcanzada, posee la misma probabilidad de fallo que la distribución real de tensiones.
El factor de escala nos permite hallar la probabilidad de fallo para cualquier tamaño de área, y por tanto la probabilidad de fallo de cada celda (elemento finito) a una tensión determinada mediante la ecuación2.
Bajo el supuesto de validez del principio del eslabón más débil y la independencia entre las distribuciones estadísticas de las celdas, la probabilidad de fallo de toda la placa se determina por:
donde Ps,ΔAi=1−Pf,ΔAi.Teniendo en cuenta la distribución de las tensiones resistentes obtenidas numéricamente para cada probeta, esta se puede referir a un área efectiva, Aef, tal que, sometida a una tensión máxima constante (σmax), presente la misma probabilidad de rotura que la placa completa.
El área efectiva puede ser calculada para modelos biparamétricos de Weibull según Sung et al. [18]. Sin embargo, este artículo propone la corrección para el mismo método y para un modelo triparamétrico de Weibull, deduciendo así la expresión [4] para calcular el Aef característica de cada uno de los ensayos.
donde σeq(x, y, z) es la tensión equivalente obtenida del modelo numérico en la simulación del ensayo para cada uno de los elementos de la placa, σ* es una tensión de referencia, que es la máxima obtenida durante el ensayo, y A es el área total de la probeta.Por tanto, la probabilidad de fallo para un Aef determinada es:Esto implica la introducción de un nuevo concepto, el área de referencia (Aref), que es el área elegida para hacer la representación de la curva fdd ajustada de los datos experimentales. Cabe destacar que este valor puede ser escogido libremente, no siendo obligatorio, pero sí aconsejable, tomar un valor similar al tamaño real de los especímenes ensayados.
Con este modelo probabilístico se comprueba la diferencia entre un estudio analítico y un estudio por elementos finitos. En el estudio analítico se considera un perfil de tensiones en el que la tensión máxima es constante entre rodillos de carga o en el área que se encuentra bajo el anillo de carga, para la flexión a 4P y anillos concéntricos, respectivamente, mientras que en el estudio por elementos finitos se obtiene una tensión más realista y, por lo tanto, no uniforme (ver fig. 3).
Por otra parte, con el fin de reducir el estado biaxial de tensiones del ensayo de anillos concéntricos a un estado uniaxial, en este trabajo se optó por calcular la tensión equivalente propuesta en el criterio PIA, σe,PIA, en función de los valores no negativos de las tensiones principales σI, σII, y σIII, obtenidas de los cálculos de elementos finitos realizados en las probetas tipo placa ensayadas, y el parámetro de forma β de la fdd de Weibull, como se indica a continuación:
Análisis de resultadosAplicando el modelo probabilístico propuesto a los 2 tipos de ensayos realizados, la tabla 2 recoge los parámetros de las fdd de Weibull estimadas a partir del modelo de elementos finitos y el modelo probabilístico desarrollado, considerando un Aref de 50.000mm2 y la tabla 3 considerando un Aref de 100.000mm2. Se muestran los parámetros obtenidos a partir de los 30 ensayos de flexión a 4P, los 30 ensayos de anillos concéntricos dobles con pequeña superficie de solicitación (CS) y los ensayos de anillos concéntricos tras aplicar el principio de acciones independientes, o PIA (CSPIA).
Observando la tabla 2 comprobamos que los parámetros de forma (β) y de localización (λ) coinciden prácticamente para los casos de flexión a 4P y CSPIA, mientras que en el caso de anillos concéntricos (CS), con el criterio de fallo de tensión máxima, λ difiere ligeramente. Así mismo, el parámetro de escala (δ) es prácticamente igual para CS y CSPIA y algo mayor para 4P; esto indica que el criterio PIA da buenos resultados pero que es mejorable.
Si comparamos ambas tablas, vemos que al variar el área de referencia la única diferencia reside en el parámetro de escala (δ), demostrando así el buen funcionamiento del modelo probabilístico y la no influencia del Aref escogido a la hora de calcular β y λ. La función de distribución de Weibull (fdd) es propiedad del material; por tanto, es independiente del tipo de ensayo realizado, pero es importante utilizar un criterio de fallo apropiado.
En la figura 4 se representan los resultados experimentales obtenidos, a los cuales se les ha atribuido una probabilidad de fallo en función del valor máximo de la tensión obtenido en cada uno de ellos, mediante el estimador de Bernard, Pf=(i–0,3)/(N+0,4), siendo i el orden secuencial de fallo y N el tamaño de la muestra. Por otra parte, se muestran las curvas de probabilidad de fallo estimadas para cada tipo de ensayo en función de los parámetros de Weibull expuestos en las tablas 2 y 3, existiendo una buena correlación entre las curvas de predicción y los resultados experimentales obtenidos. La metodología presentada permite comparar criterios de fallo diferentes, para evaluar de este modo cuál es el más preciso. Además, en la figura 4a) se muestran las predicciones de fallo de los ensayos de flexión a 4P utilizando los ajustes (parámetros de la función triparamétrica de Weibull) obtenidos para anillos concéntricos (CS) considerando el criterio de tensión máxima y el criterio de PIA. Si se utiliza como criterio la tensión máxima, se obtienen funciones muy diferentes entre flexión a 4P y anillos concéntricos, por lo que se demuestra que el criterio no es el adecuado. Por otro lado, el criterio PIA ofrece una solución más ajustada.
Si se aplica el criterio PIA para flexión a 4P se obtendría la misma curva fdd, lo que es debido a las características propias del ensayo y a que las tensiones σII y σIII son casi despreciables frente a σI.
En la figura 5 se observan las áreas efectivas calculadas, tanto por la ecuación 4 como por el método iterativo del modelo probabilístico, para cada tipo de ensayo y criterio de fallo.
ConclusionesDel trabajo desarrollado se desprenden las siguientes conclusiones:
- 1.
La metodología desarrollada pretende una caracterización probabilística de vidrio monolítico estructural con independencia del tipo de ensayo considerado.
- 2.
La llamada función de distribución primaria triparamétrica de Weibull, referida a un área de referencia, Aref, tensionada uniaxialmente, junto con la aplicación de un criterio de fallo adecuado, permite determinar la probabilidad de rotura de un elemento de vidrio sometido a una distribución general de tensiones.
- 3.
Las funciones de distribución de Weibull obtenidas mediante el modelo probabilístico a partir de la distribución de tensiones calculadas por elementos finitos muestran una buena coincidencia.
- 4.
No es correcto realizar un ajuste estadístico en base a un valor máximo y local del criterio de fallo, obviando la distribución de dicho criterio de fallo en otras zonas del espécimen ensayado. Esto, a efectos estadísticos, supone atribuir ese valor máximo a toda el área estudiada, sin tener en cuenta que pueden existir zonas con una probabilidad de fallo mucho menor.
- 5.
El principio de acciones independientes (PIA) aporta soluciones sensiblemente mejores que el criterio de la tensión máxima; sin embargo, se considera necesario continuar la búsqueda de un criterio óptimo de rotura frágil bajo solicitación biaxial que aporte mejores resultados.
Los autores agradecen la financiación recibida de los Planes Nacional y Regional de Investigación, a través de los proyectos IB09-136, BIA2011-28959 y SV-PA-11-012, así como la beca FPI BES-2012-053159 concedida por el Ministerio de Economía y Competitividad y la beca BP12042 concedida por el Gobierno Regional del Principado de Asturias bajo el programa Predoctoral Severo Ochoa.