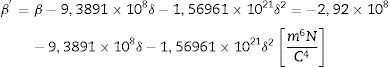Un modelo teórico fundamentado en la teoría de Ginzburg-Landau-Devonshire se ha desarrollado para estudiar y predecir los efectos que produce la disminución del tamaño de partícula en una nanoesfera de PbTiO3, sometida a la acción simultánea de campos de despolarización y esfuerzos mecánicos. Se consideró una nanoesfera con una capa de cargas espaciales en su superficie, y con dominios de 180° generados por la minimización de la energía libre de despolarización. Las densidades de energía de despolarización, de pared de dominio y la densidad de energía electro-elástica fueron incorporadas en la energía libre del sistema. Para la determinación de la polarización espontánea y de la temperatura de transición de la nanopartícula se minimizó la energía libre. Se observa que la estabilidad de la fase ferroeléctrica de la nanoesfera se ve favorecida con la reducción del grosor de la capa de cargas espaciales en la superficie, con la aplicación de esfuerzos de tensión y para configuraciones con un número de dominios de 180° elevado. Además, el modelo predice que no es posible un cambio de orden de la transición ferroeléctrica en la nanoesfera con dominios de 180° bajo la acción de esfuerzos mecánicos.
A theorical model has been developed based on the theory of Ginzburg-Landau-Devonshire to study and predict the effects the decreasing of size particle in a nanosphere of PbTiO3 subjected to the action of depolarization fields and mechanical stress. It was considered that the nanosphere is surrounded by a layer of space charges on its surface, and containing 180° domains generated by minimizing free energy of depolarization. Energy density of depolarization, wall domain and electro-elastic energy have been incorporated into the free energy of the theory Ginzburg-Landau-Devonshire. Free energy minimization was performed to determine the spontaneous polarization and transition temperature system. These results show that the transition temperature for nanosphere is substantially smaller than the corresponding bulk material. Also, it has been obtained that the stability of the ferroelectric phase of nanosphere is favored for configurations with a large number of 180° domains, with the decreasing of thickness space charge layer, and the application of tensile stress and decreases with compressive stress.
La evolución hacia la miniaturización de los sistemas en electrónica y en comunicación se dirige hoy a la escala nanométrica, lo cual demanda conocer las propiedades físicas de los materiales nanoestructurados que compondrían dichos sistemas [1]. Se conoce que las propiedades físicas de los materiales masivos cambian cuando se transita a dimensiones del orden de los nanómetros, lo cual se conoce como «el efecto de tamaño».
En relación con el efecto de tamaño en materiales ferroeléctricos se han realizado investigaciones teóricas y experimentales [2]. Dentro de las primeras existen modelos fenomenológicos, cálculos computacionales con primeros principios o con el modelo de Ising, y dentro de las segundas, existen mediciones de temperatura de Curie y/o polarización espontánea en micro y nanopartículas, así como en películas ultradelgadas [3–5].
Particularmente, Shih et al. [6] estudiaron el efecto de tamaño en la transición ferroeléctrica de un cristal cúbico micrométrico de titanato de bario (BT), considerando que las causas de dicho efecto son el campo de despolarización y las cargas espaciales. Sus resultados dan cuenta de la reducción paulatina de la temperatura de Curie y de la polarización espontánea con la reducción del tamaño de partícula. Dicho estudio no considera la posible influencia de esfuerzos mecánicos provenientes, por ejemplo, de la transición ferroeléctrica.
En el presente trabajo se estudia teóricamente el efecto que sobre las propiedades ferroeléctricas produce la disminución del tamaño de partícula de una nanoesfera de titanato de plomo, PbTiO3 (PT), con una configuración de dominios de 180°, rodeada por una capa de cargas espaciales en su superficie y sometida a la acción simultánea del campo de despolarización y de esfuerzos mecánicos. Se eligió el titanato de plomo por cuanto es uno de los mejores materiales ferroeléctricos con alta permitividad y aplicable en junturas túnel [6,7]. Se considera la forma esférica por cuanto esta geometría admite únicamente la acción de esfuerzos hidrostáticos y así se facilita el cálculo de la densidad de energía electro-elástica. La geometría esférica para nanopartículas de PT se sustenta en las evidencias experimentales de Roy et al. [8], Sittiketkorn et al. [9] y Sancho [10], quienes reportan granos y partículas con geometría casi esférica. En cuanto a la estructura de dominios, Sancho [10] y Meyer et al. [11] reportan la existencia de paredes de dominio de 180° paralelas a los planos (100) en el PT.
Por otra parte, se sabe que el PT posee una transición de fase ferroeléctrica de primer orden a 760K y a presión atmosférica. Desde hace varios años existen estudios teóricos y experimentales que dan cuenta de un cambio del orden de la transición del PT por causa de la aplicación de un esfuerzo [12–16]. Evidencias experimentales de tal cambio se han obtenido en cristales de PT con tamaño micrométrico a temperatura ambiente por espectroscopia Raman [13], por absorción óptica [15], por difracción de rayos X [16], o por XANES [17]. Un aspecto común en tales estudios experimentales es el tamaño micrométrico de las muestras, tamaño que permitiría la presencia y el movimiento de dominios de 90°, y quizá la presencia de este tipo de dominios influye en el cambio del orden de la transición al aplicar presión. Por ello, en este trabajo también se estudia la posibilidad de cambio del orden de la transición ferroeléctrica por aplicación de esfuerzo mecánico a una partícula de PT pero de tamaño nanométrico, y con dominios de 180° únicamente.
Modelo teóricoLa metodología sigue el trabajo de Shih et al. [6], y consiste en incluir términos de la densidad de energía de despolarización, la densidad de energía de paredes de dominio y densidad de energía electro-elástica en la densidad de energía libre de Ginzburg-Landau-Devonshire de la nanoesfera de PT [18,19]. Posteriormente, se minimiza dicha energía para calcular la polarización espontánea y, del análisis de la expresión de dicha polarización, se obtiene la temperatura de Curie de la transición ferroeléctrica-paraeléctrica.
La densidad volumétrica de energía libre de un cristal ferroeléctrico en ausencia de campos eléctricos externos, FP, se expresa como serie de potencias pares de la polarización P, ecuación (1) [19]:
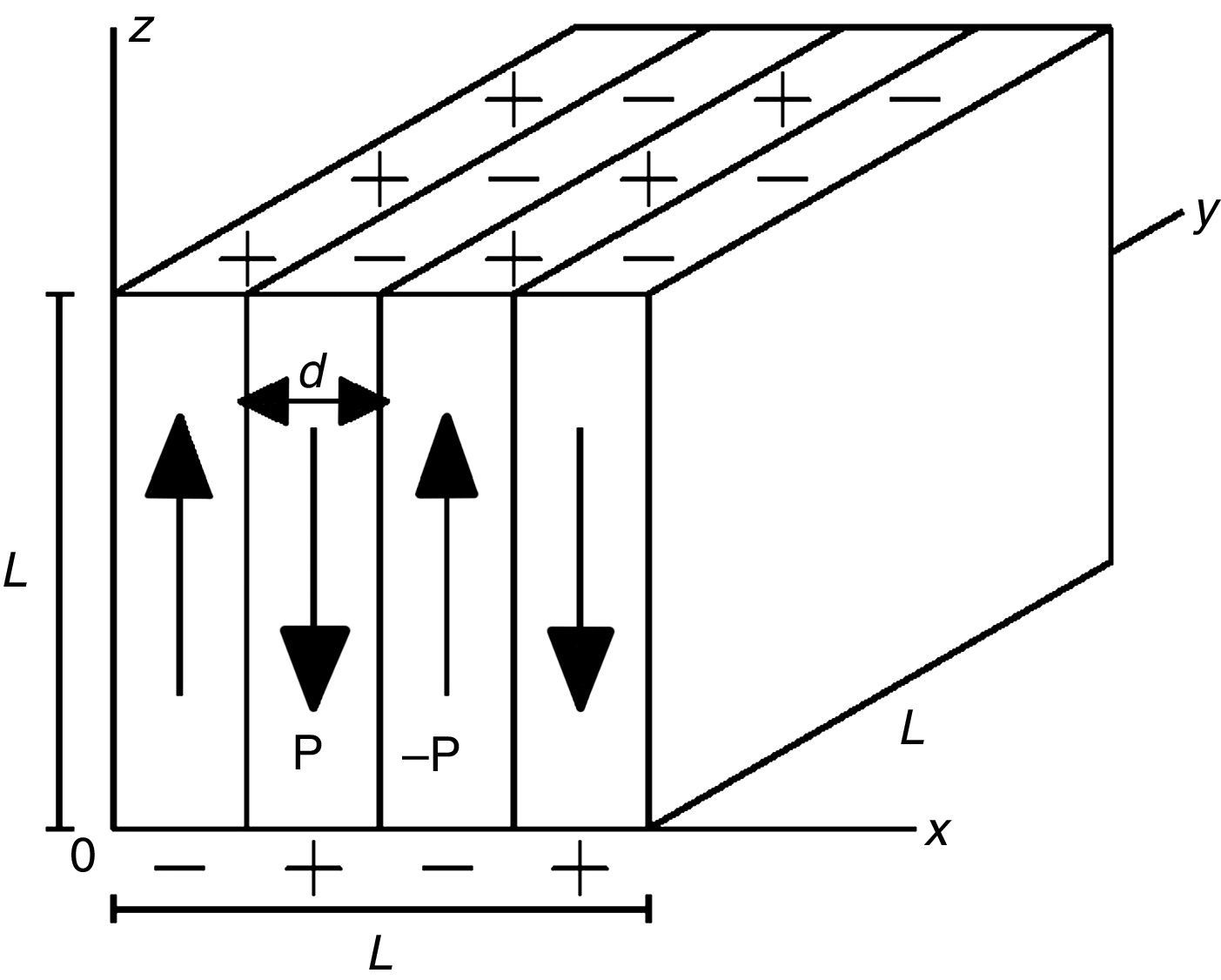
donde α, β y ζ son coeficientes cuyos valores pueden obtenerse desde experimentos, o pueden calcularse por métodos de primeros principios [20].Energía debida al campo de despolarizaciónUn campo de despolarización se origina por la polarización del material y se opone a ella. Por facilidad de cálculo se obtiene primero la energía de despolarización del cristal ferroeléctrico cúbico de lado L de la figura 1, con dominios de 180° y espesor d. Este cálculo se basa en un desarrollo similar realizado por Chikazumi [21] para cristales ferromagnéticos.
Cristal ferroeléctrico cúbico con dominios de 180° [6].
Si el cristal es neutro, la densidad volumétrica de carga es nula y el potencial eléctrico ψ debe cumplir la ecuación de Laplace (2):
El potencial ψ es función de las variables x y z, mas no de la variable y (fig. 1), pues se supone una distribución de carga uniforme en las superficies superior e inferior de cada dominio; con lo cual la componente Ey del campo de despolarización es nula: Ey=−∂ψ∂y=0.
La ecuación (2) se resolvió por el método de separación de variables, con condiciones de frontera periódicas, tanto en la pared de dominio como en las caras del cristal dadas por los planos x=0 y x=L. Se asume que el campo de despolarización creado al interior de cada dominio es similar en naturaleza. Además, se supone que en la pared de dominio existe un plano donde la polarización es nula, tal que la componente Ez del campo de despolarización allí también es nula, lo cual se puede atribuir a un potencial constante o cero; se considera el potencial cero. Con todo lo cual se obtiene la solución (3):
donde Aj son constantes. Esta relación describe también el hecho de que el potencial eléctrico tiende a cero a una distancia muy lejana de la dirección z. El campo eléctrico de despolarización en el interior del cristal se obtiene de la expresión (3) con la relación E=−∇ψ, así:para j impar. Para valores de j par los coeficientes Aj del potencial eléctrico resultan ser nulos para configuración de dominios de 180°.Además, la componente z del campo de despolarización en un dominio cualquiera puede escribirse de igual manera como:
La energía depende del cuadrado del campo eléctrico E2=Ex2+Ez2, pero los aportes de los términos con j>1 de las ecuaciones (4) y (5) pueden despreciarse frente a los términos con j=1, por lo que la densidad de energía eléctrica debida al campo eléctrico de despolarización, y almacenada dentro del cristal de volumen V, está dada por:
donde ε*=4ε0π3.Capa de cargas espacialesEn un dieléctrico real, es muy probable la presencia de cargas espaciales en las fronteras de grano, en dislocaciones, en defectos puntuales en cristales iónicos o en la interfase dieléctrico-electrodo. Las cargas espaciales, a diferencia de la carga ligada de polarización, tienen origen físico en vacantes de oxígeno, centros de captura de iones y por la aplicación de campos eléctricos sobre el ferroeléctrico [6,22–27]. Las propiedades físicas de los materiales ferroeléctricos pueden afectarse debido a la carga espacial [24–27]. En el presente trabajo se analiza cómo influye, sobre las propiedades ferroeléctricas, la presencia de una capa de carga espacial en la superficie de la partícula de PT. Por simplicidad, se ha considerado una capa homogénea de carga espacial de espesor constante. Se puede pensar como modelo físico en una cerámica de PT, con granos esféricos, en cuyos bordes existen cargas espaciales.
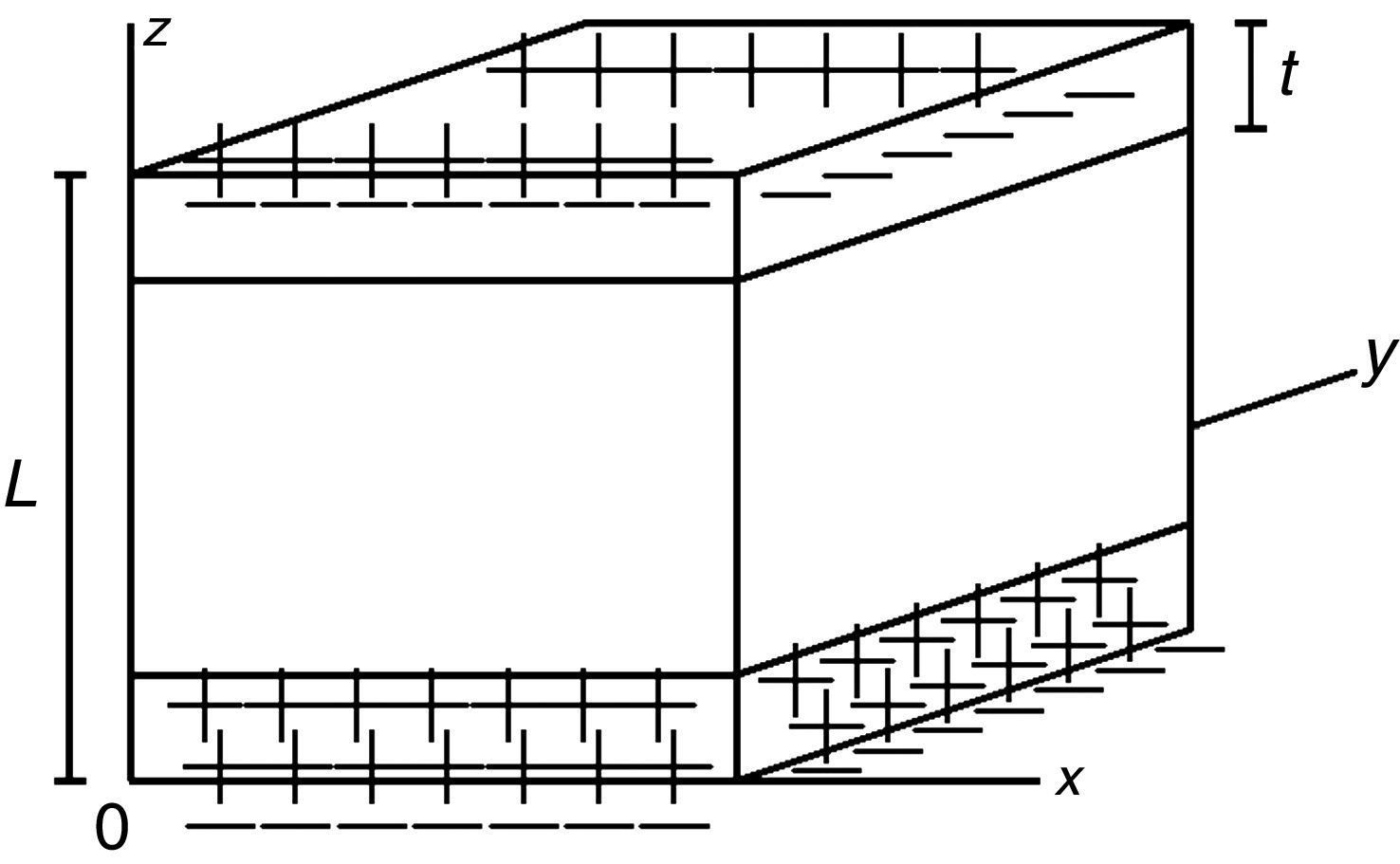
De acuerdo con Shih et al. [6], se considera una capa de cargas espaciales de grosor t, de distribución uniforme ubicada en los planos z=0 y z=L del cristal (fig. 2). Las cargas espaciales se suponen totalmente balanceadas por las cargas de polarización de signo opuesto; por lo cual la densidad volumétrica de carga en la capa es dada por (8):
Capas de carga espacial uniforme de grosor t. [6].
Utilizando la relación: div E→=−ρε0=−Pε0t, y siguiendo el mismo análisis de Shih et al.[6], se asume que el campo eléctrico generado por las cargas espaciales posee solamente una componente en la dirección z, es decir que dEdz=−Pε0t. Además, considerando que el campo fuera de la capa es despreciable dada la formación de los dominios de 180°, y que en el interior de la capa se opone al campo de despolarización de cada dominio del cristal, se obtiene la ecuación (9): [6]
Para la estimación del efecto de la capa de cargas espaciales en la densidad de energía de despolarización, primeramente se calculó esta densidad para un monodominio sin capa de cargas libres, y luego para un monodominio con dicha capa. Después, se calculó para un cristal multidominio de 180°. La densidad volumétrica de energía de despolarización con una capa de cargas espaciales de grosor t en el cristal de multidominio de la figura 1 se expresa por (10):
Este resultado es diferente del obtenido por Shih et al. [6] por la presencia del factor 1−e−2πLd, y se debe a que al obtener la energía de despolarización del cristal de la figura 1 se integra el campo eléctrico solamente en el cristal y no sobre todo el espacio, ya que la energía de interés es la almacenada en su interior y no en sus alrededores.
Densidad de energía para una esfera ferroeléctrica con dominios de 180°Hasta aquí se ha calculado la densidad volumétrica de energía de despolarización para el cristal cúbico de la figura 1, pero el propósito del presente trabajo es estudiar una nanoesfera de PT, con diámetro D, dividida en varios dominios de 180°, cada uno de grosor d.
Para obtener la densidad de energía de despolarización para esta geometría esférica, se usó una aproximación grotesca, ya usada en desarrollos realizados Chikazumi [21] para nanoesferas magnéticas de dominios de 180°. Esta aproximación consiste en usar el resultado dado por la ecuación (10) y en reemplazar a la arista L del cristal de la figura 1 por el diámetro D de la esfera (es decir, se considera la esfera inscrita en el cristal de la figura 1, con el mismo tipo de dominios del cubo). Entonces, la densidad volumétrica de energía de despolarización para la nanoesfera ferroeléctrica está dada por la ecuación (11):
Densidad de energía de pared de dominioSea γ la energía de pared de dominio de 180° por unidad de superficie en la nanoesfera de PT. La densidad volumétrica de energía dada por las paredes de dominio puede ser calculada como:
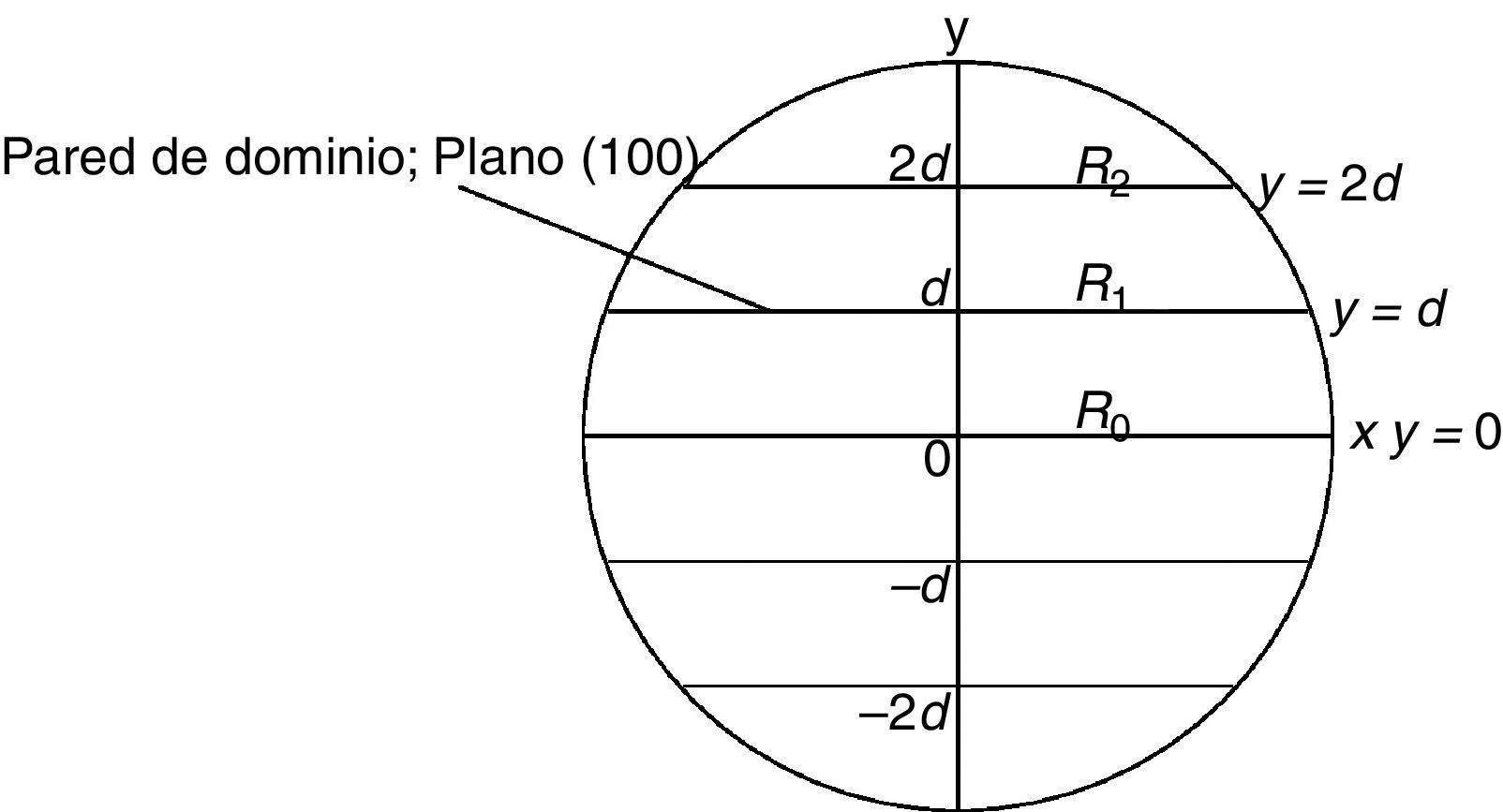
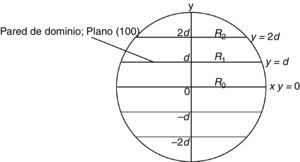
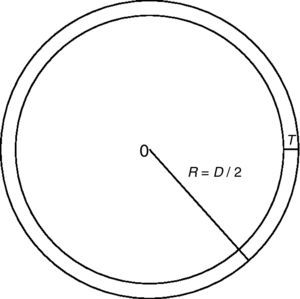
El área total de la superficie de las paredes de dominio en la esfera es la suma de las áreas de los círculos, cuyos radios R0=R,R1,R2,…,Rn2−1 se ilustran en la figura 3 para n par, donde R es el radio de la esfera. Se calculan los radios Ri, y luego el área de las paredes de dominio, y reemplazándola en la ecuación (12) se obtiene (con V=43πD23) la densidad de energía de pared de dominio (13):
donde n = D/d es el número de dominios de 180°.Entonces, la densidad de energía libre, incluyendo la energía de despolarización y la energía de las paredes de dominio de una esfera ferroeléctrica con capa de carga espacial, es:
donde Fd y Fw son la densidad de energía de despolarización y la densidad de energía de pared de dominio de las ecuaciones (11) y (13), respectivamente.Polarización espontánea y temperatura de CurieMinimizando la densidad de energía libre dada por la ecuación (14) respecto a la polarización se obtiene:
La temperatura de transición Tc de la esfera se determina analizando el dominio de la función de la polarización dada por la ecuación (15), a fin de que la polarización presente valores reales. Se obtiene que:
donde T0∞ es la temperatura de Curie del cuerpo masivo.Además, el análisis de la ecuación (15) muestra que el rango de valores reales de la polarización espontánea es:
con β < 0. La polarización espontánea del sistema experimenta un descenso desde el valor a T = 0K hasta el valor de PT=TC=−β2ζ. Para temperaturas mayores que TC, la ecuación (15) tiene soluciones no reales para la polarización, y entonces aquí se asume que para estas temperaturas se ha alcanzado la fase paraeléctrica.Efecto de los esfuerzos mecánicosA continuación se considera una partícula esférica ferroeléctrica sometida al campo de despolarización, y a la acción de esfuerzos mecánicos generados en la transición desde una fase ferroeléctrica tetragonal a una fase paraeléctrica cúbica.
Bajo un esfuerzo externo σ=(σ1, σ2, σ3, σ4, σ5, σ6), la parte de la energía libre correspondiente a la energía mecánica, y en las inmediaciones de la transición de fase para un cristal ferroeléctrico tipo perovskita, se escribe como [28]:
donde Pi son las componentes de la polarización, sij son las componentes de la complianza elástica y Qij son los coeficientes electroestrictivos. Los valores de estas cantidades y de otras cantidades termodinámicas se presentan en la tabla 1 para el PT.Debido a que la fase ferroeléctrica del PT es tetragonal, la polarización se determina únicamente por su componente P3[29]: P = (0, 0, P3), es decir, P = P3.
La condición de presión hidrostática para la transición de fase, es decir, que σ1=σ2=σ3=σ y σ4=σ5=σ6=0 [28], se aplica a la geometría esférica de la partícula, ya que los esfuerzos de cizalladura resultan ser efectivamente nulos. Entonces, la densidad de energía libre debida a esfuerzos mecánicos hidrostáticos para la fase tetragonal en las inmediaciones de la transición es:
La densidad de energía libre, incluyendo los efectos del campo de despolarización, de las paredes de dominio y de los esfuerzos, es la siguiente:
Minimizando la densidad de energía libre dada por la ecuación (21) respecto a la polarización se obtiene:
Analizando el subradical de la expresión (22), se llega a que la temperatura de transición es:
Así mismo, un análisis de la ecuación (22) muestra que el rango de valores reales que toma la polarización espontánea está dado por la relación (18).
Análisis del carácter de la transición de faseSani et al. [16] afirman que en presencia de esfuerzos la temperatura de transición de las perovskitas ferroeléctricas decrece y que, en el caso específico del PT masivo, la transición de fase pierde su carácter de transición de primer orden y gradualmente se transforma a una transición de segundo orden. No se conoce si tal cambio de orden ocurre también a escala nanométrica. Para analizar dicha posibilidad en el presente caso, se analiza el coeficiente β que aparece en la densidad de energía libre de Gibbs, dada por la ecuación (21).
Shih et al.[6] proponen que los esfuerzos σ sobre un grano esférico que aparecen en la transición ferroeléctrica se pueden estimar de la siguiente manera:
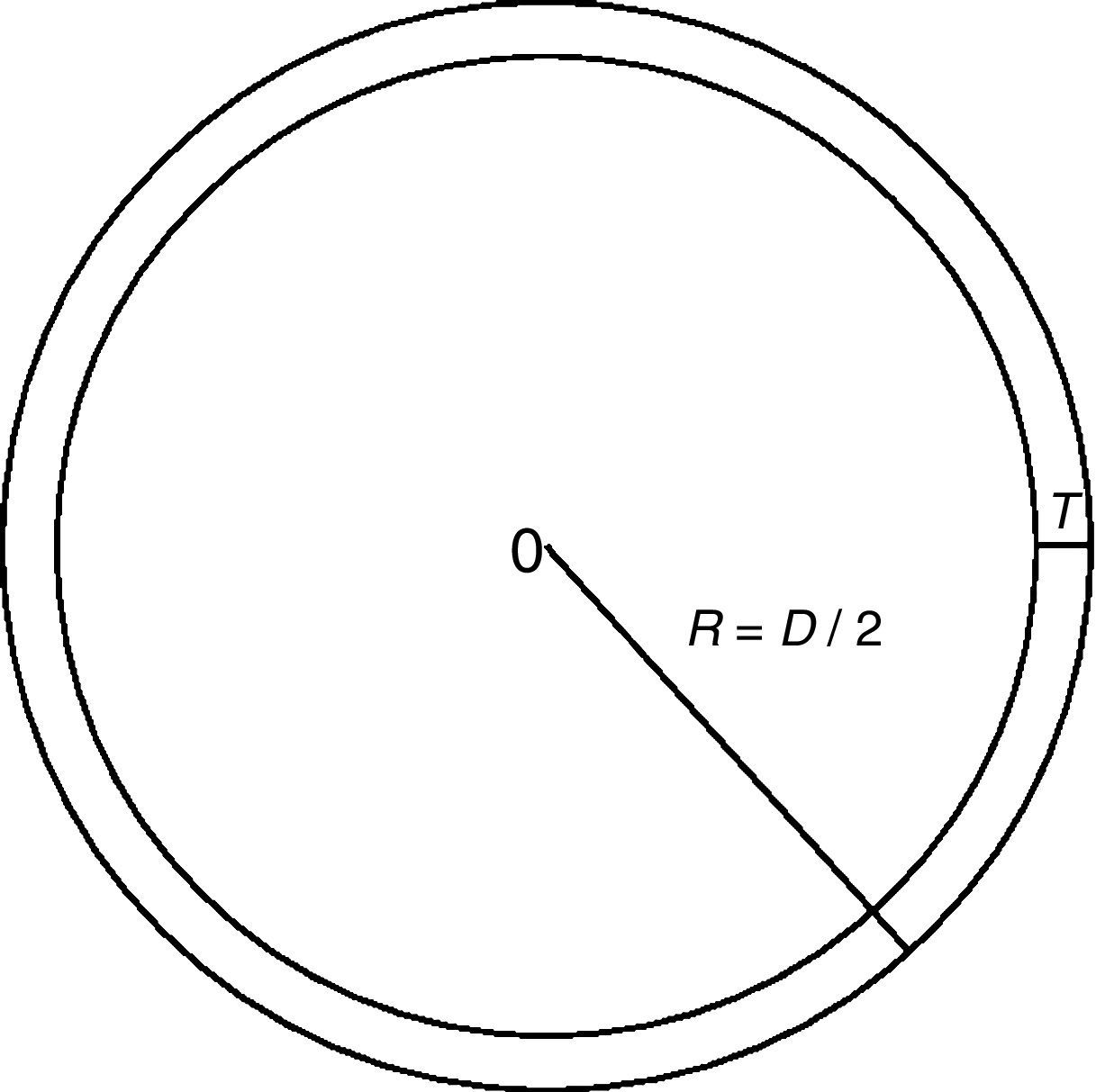
donde los subíndices c y s se refieren a los esfuerzos de compresión y cizalladura, respectivamente, N es el número de celdas unitarias a lo largo de todo el radio del grano, n es el número de celdas unitarias en la capa contraída originada por la deformación en el radio (fig. 4). El grano se deforma bajo la acción de los esfuerzos mecánicos; E es el módulo de Young del material, a es la constante de red y δa es la cambio de la constante de red bajo la compresión.A los números N y n, se los puede estimar en términos del radio de la esfera R y del grosor τ de la capa contraída, así:
con lo cual:Además, aquí se asume que la nanoesfera de PT sigue siendo esférica bajo la influencia de esfuerzos mecánicos de tipo hidrostático.
Se sabe que cuando ocurre la transición ferroeléctrica del PT el ion Ti se desplaza y la red se deforma. Cuando las aristas de la celda están a lo largo de la dirección seudocúbica, las deformaciones e en la fase tetragonal pueden expresarse por [28,30]:
donde el superíndice 0 indica que se tratan de deformaciones espontáneas. Las deformaciones de la celda unitaria del PT en la transición pueden evaluarse mediante las constantes de red en la fase ferroeléctrica tetragonal, tomando en cuenta una deformación lineal, así [28]:donde a0 es la constante de red seudocúbica. Luego, la variación δa es:Reemplazando las relaciones (29) y (30) en la ecuación (27), y el resultado en la ecuación (21), se llega a que los términos con la potencia cuarta de la polarización son:
Entonces, la energía libre de este sistema ferroeléctrico tiene un coeficiente β’ que se calcula de la ecuación (31):
El signo de β’ y la naturaleza del mismo se analiza en la siguiente sección.
Hasta aquí se han obtenido expresiones para la polarización espontánea y la temperatura de Curie de una partícula esférica ferroeléctrica con dominios de 180°, con una capa superficial de cargas libres, sometida al campo de despolarización y a esfuerzos mecánicos. A continuación, se analizan los resultados para el caso del PT a escala nanométrica.
Resultados y discusiónLos resultados que se presentan a continuación se han obtenido utilizando los valores de magnitudes físicas del PT anotados en la tabla 1. El grosor de dominio d se calcula a partir del diámetro D de la nanoesfera, con la relación d = D/n, donde n es el número de dominios de 180°.
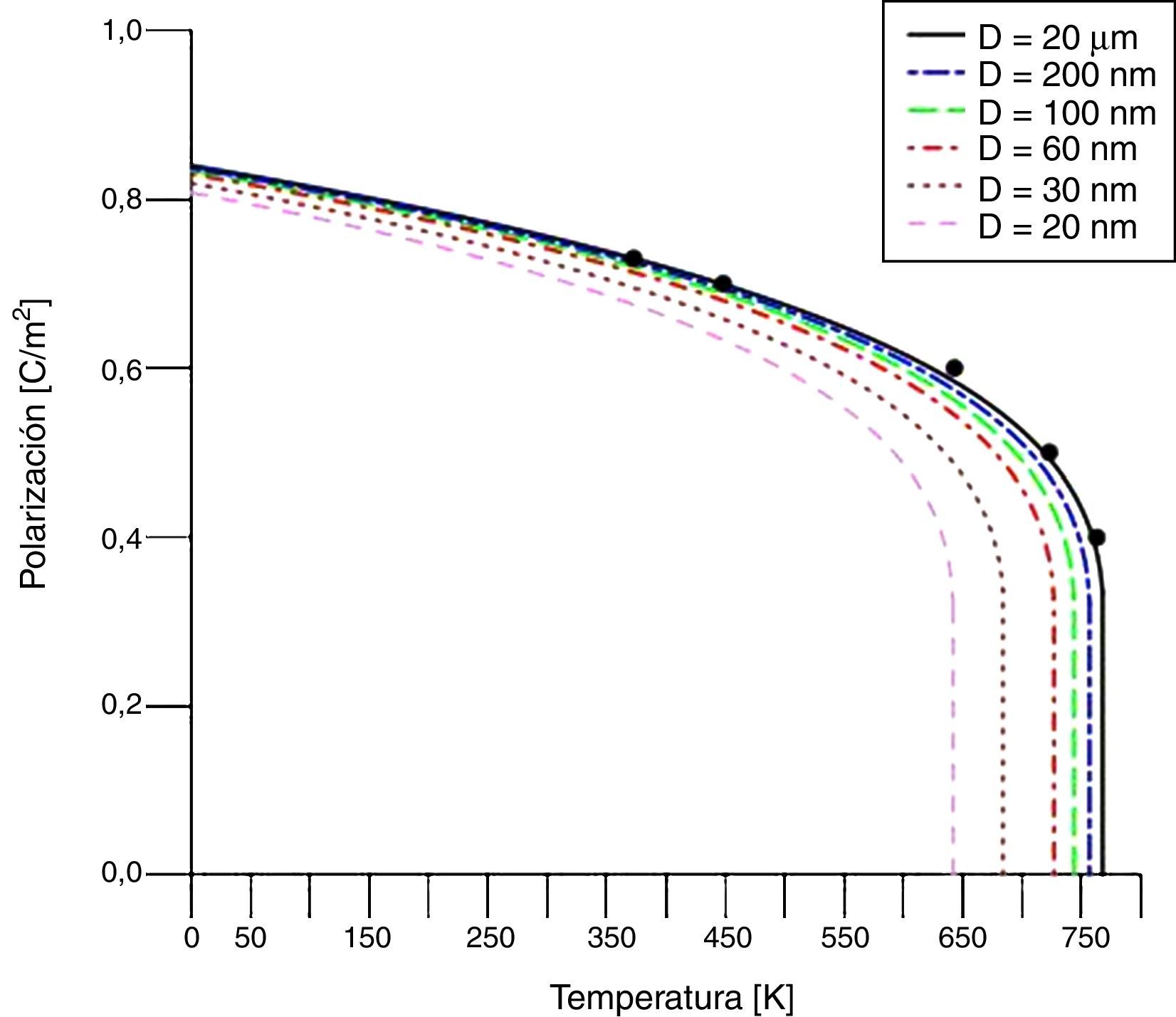
Efecto del campo de despolarización, con capa de cargas espacialesLa figura 5 presenta la polarización espontánea de la nanoesfera de PT en función de la temperatura, ecuación (15), para diferentes valores de D, con capa de cargas libres de espesor t=0,2nm y con n=3. Roelofs et al. [31] han encontrado 2 dominios para granos de PT de tamaño entre 40 y 50nm; para tamaños menores, se han encontrado monodominios; es entonces posible suponer la presencia de 3 dominios para tamaños en torno a 50nm.
Polarización en función de la temperatura para varios tamaños de nanopartícula esférica de PT, con n=3 y t=0,2nm. Los puntos son extraídos de resultados obtenidos de Huan et al. [7].
Para todos los diámetros y, como es de esperar, la polarización decrece con el aumento de la temperatura. Los resultados predichos para diámetros de partícula D=20μm y 200nm, y para t=0,2nm, muestran concordancia con datos obtenidos por Huan et al. [7], correspondientes al PT masivo y en ausencia de esfuerzos. No se han encontrado datos experimentales para nanopartículas.
Para todos los valores de D la polarización es discontinua cuando se alcanza la temperatura de transición dada por la ecuación (24), y toma el valor PT=TC=−β2ς=0,3059C/m2. Para temperaturas mayores que Tc la polarización no es real, por lo que se supone que ya se ha alcanzado la temperatura de transición, y que la polarización es nula. Para D=20μm y 200nm, la temperatura de transición es mayor que 750K, y se reduce al disminuir el tamaño de partícula.
Shih et al. [6] muestran que la polarización y el cociente c/a de los parámetros de red en Tc son independientes del tamaño de cristales cúbicos de BT. El valor de PT=TC=−β2ς con datos de β y ζ de Rabe et al. [19] para el BT, es de 0,1745C/m2[19]; este valor es cercano a 0,1835 C/m2 reportado por Shih et al. [6]. Se puede decir entonces que el valor de polarización de 0,3059C/m2 en la temperatura de transición para el PT, independiente del tamaño de la partícula, se debe a que en la transición el PT experimenta una deformación espontánea c/a−11/2 constante.
Para espesores mayores de capa de cargas espaciales, por ejemplo para t=1nm (no mostrado), la temperatura de Curie decrece marcadamente al reducir D, la fase ferroeléctrica se hace más inestable. Es decir, el efecto de la reducción del tamaño de partícula es más pronunciado con el aumento del grosor de la capa de cargas libres.
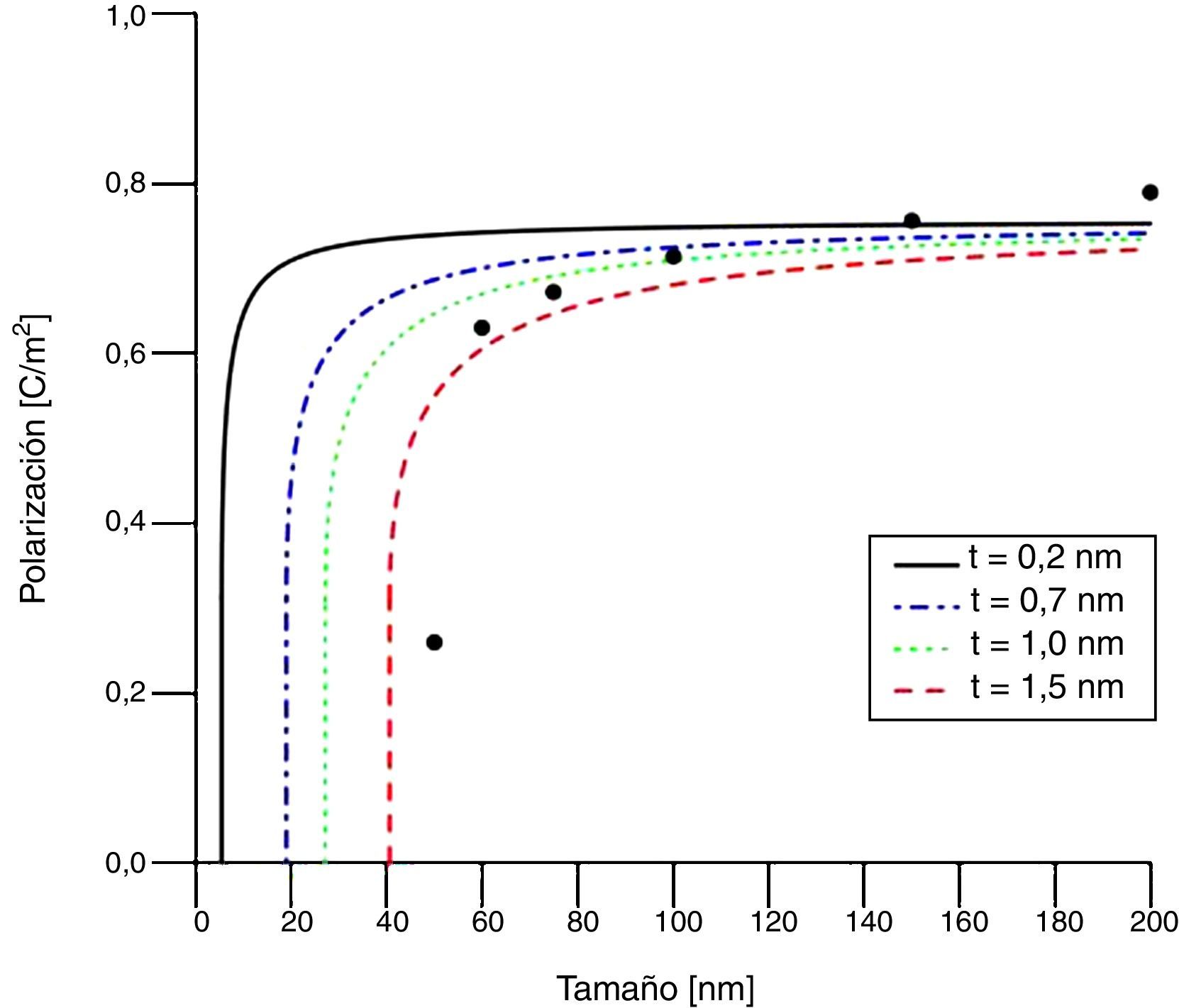
La figura 6 presenta la polarización frente al diámetro de la nanoesfera de PT obtenida de la ecuación (15), para varios valores de t, y a temperatura ambiente, T=298,15K. La polarización decrece con la reducción del tamaño de la nanopartícula. Este decrecimiento no es tan pronunciado en cierto rango de diámetros, hasta que a partir de cierto valor la polarización se reduce abruptamente hasta alcanzar un valor próximo a 0,3059C/m2. Posteriormente, la ecuación (15) proporciona soluciones no reales de la polarización, por lo cual aquí se asume que la polarización es nula; esto significaría que se ha alcanzado un tamaño crítico en el cual la fase ferroeléctrica de la nanoesfera desaparece. Además, el efecto de la capa de cargas espaciales es más pronunciado cuando su espesor aumenta.
Polarización en función del diámetro de la nanopartícula de PT para T=298,15K y n=3. Las líneas son las predicciones de este trabajo. Los puntos han sido extraídos de un modelo para películas delgadas de Junquera et al. [32]. En las películas D se refiere a su grosor.
El comportamiento de las curvas de la figura 6 tiene cierto grado de concordancia con datos experimentales extraídos de un modelo de despolarización para películas delgadas [32], considerando que D es el espesor de las películas.
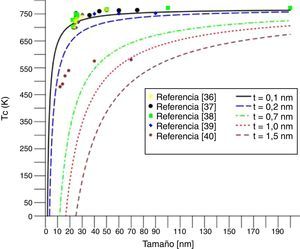
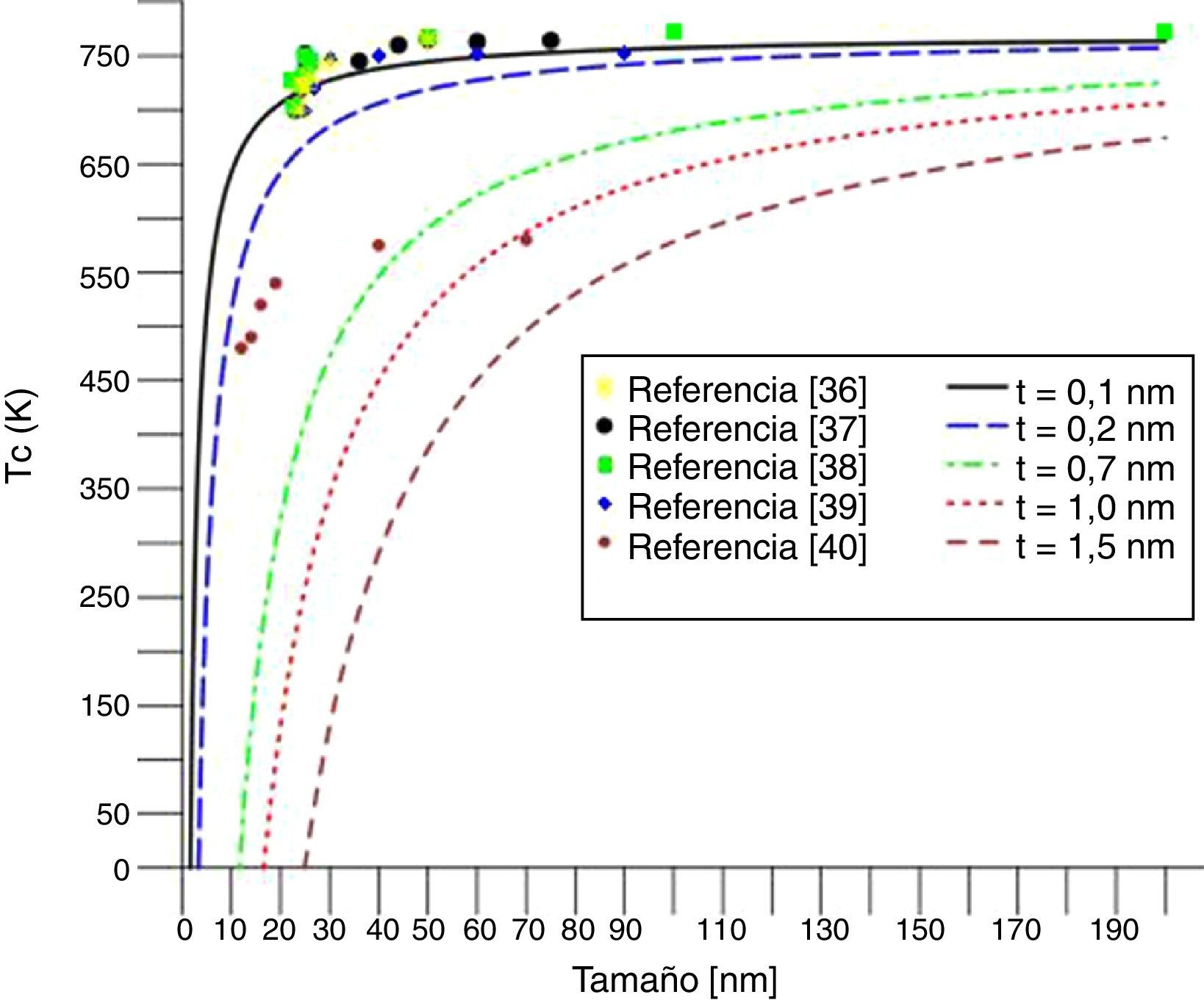
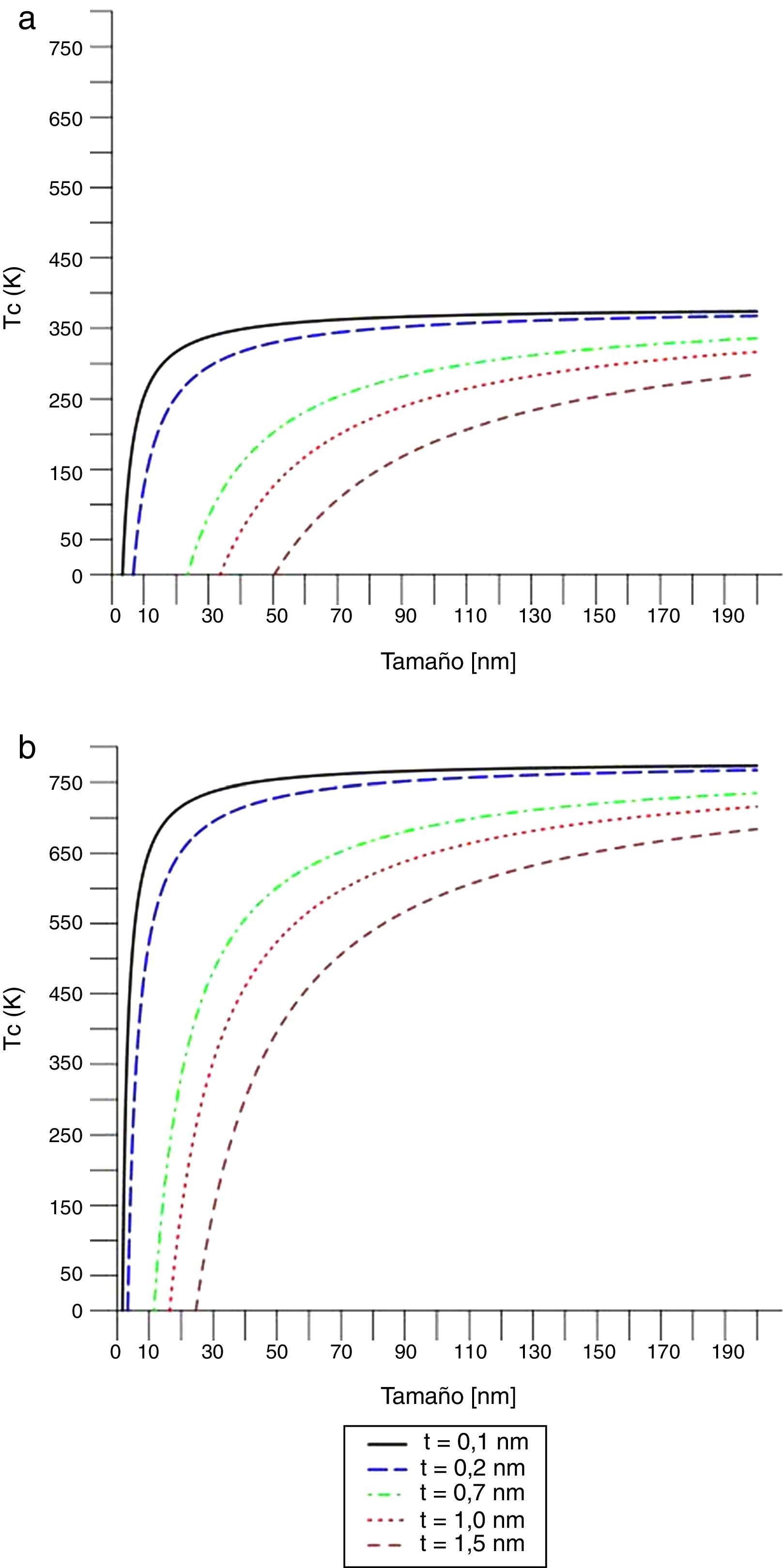
La figura 7 muestra la temperatura de transición Tc, frente al diámetro de la nanoesfera de PT, ecuación (17), para diferentes valores de t. Se observa que la temperatura de transición decrece con la reducción del diámetro D de la nanopartícula; tal reducción es leve para cierto rango de D, hasta un valor desde el cual el decrecimiento es muy pronunciado y Tc llega a adquirir valores muy cercanos a 0K para cierto valor crítico de tamaño de partícula. Los valores de Tc no superan el valor correspondiente al del cuerpo masivo, que es de 765,4 K. Los resultados obtenidos para t=0,1nm y n=3 tienen buena concordancia con datos experimentales de Ishikawa et al. [36], Jiang et al. [37], Yuguo et al. [38], Yu et al. [39] y Glinchuk et al. [40].
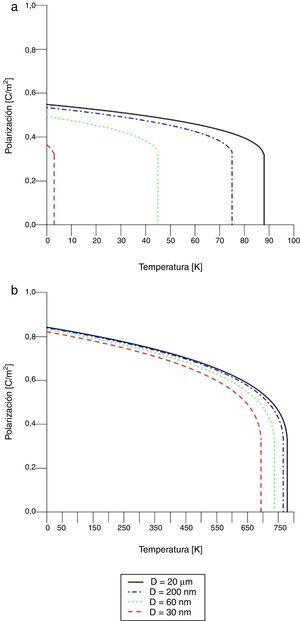
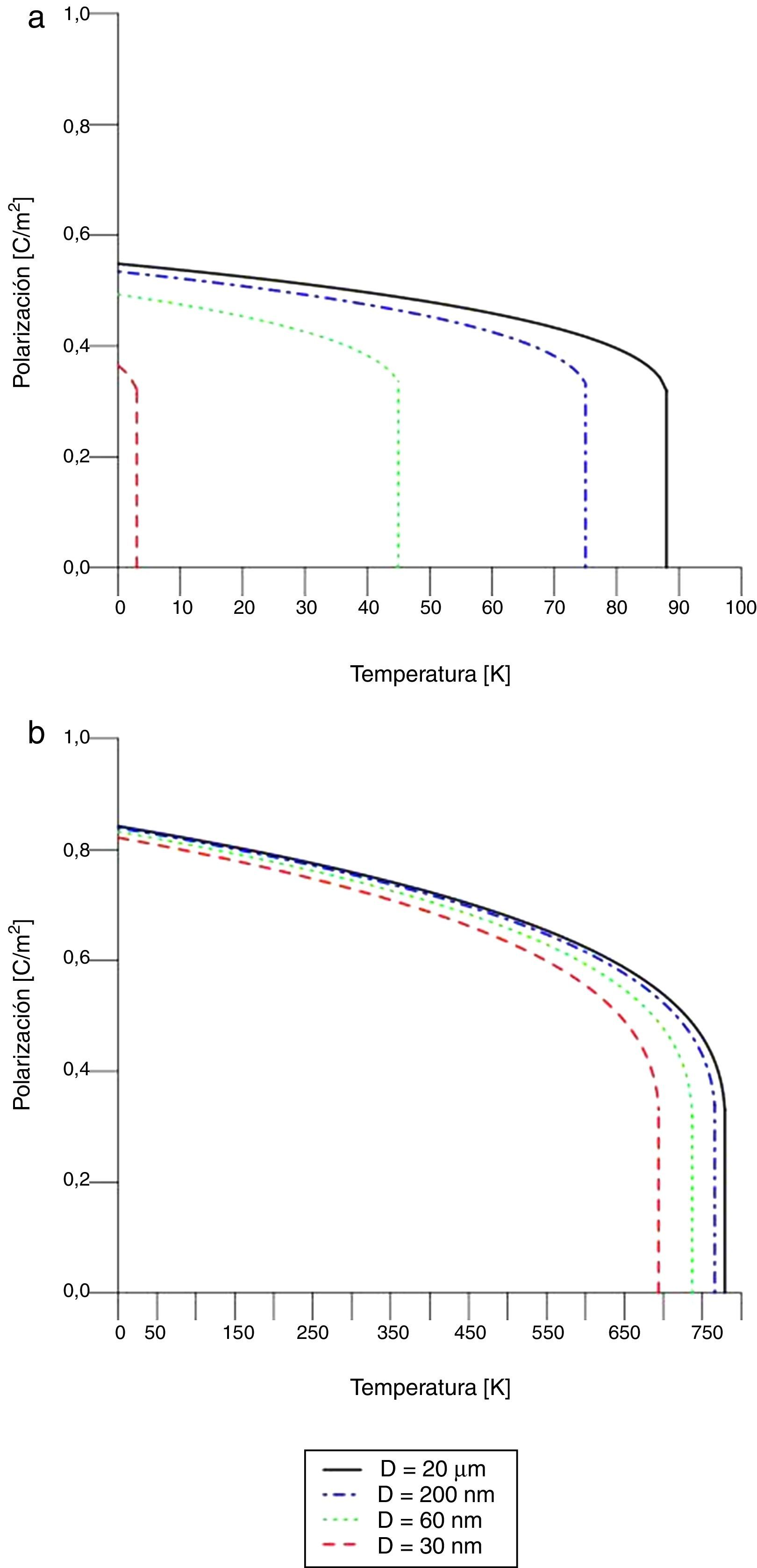
Efecto de los esfuerzos mecánicosLa figura 8 presenta la polarización frente a la temperatura, ecuación (22), con t=0,2nm, y bajo la acción de un esfuerzo mecánico σ. Los valores de esfuerzos σ=−7GPa (compresión) y σ=+0,1GPa (tensión) fueron escogidos de modo que otorguen resultados claros del comportamiento de la polarización espontánea. La polarización espontánea decrece con el aumento de la temperatura, hasta llegar al valor de PT=TC=−β2ς, donde se supone que se ha alcanzado la temperatura de transición; a temperaturas superiores la polarización no es una cantidad real.
Si D es de 30nm, para el esfuerzo σ=−7GPa la temperatura de transición está alrededor de 4K, mientras que para el esfuerzo σ=+0,1GPa tal temperatura está alrededor de 700K. Entonces, la acción de los esfuerzos mecánicos modifica la estabilidad de la fase ferroeléctrica de la nanoesfera de PT: un esfuerzo de compresión reduce la temperatura de Curie y un esfuerzo de tensión la incrementa, es decir, aumenta la estabilidad de la fase ferroeléctrica.
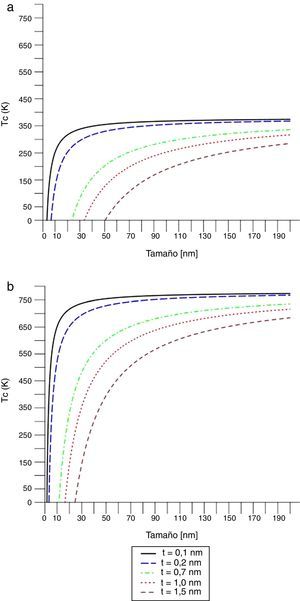
La figura 9 muestra la temperatura de transición frente al diámetro de la nanoesfera bajo la acción de esfuerzos mecánicos, ecuación (24), y con n=3 dominios. Se observa que la temperatura de transición decrece con la reducción del diámetro D de la partícula y el comportamiento es similar a aquel observado en la figura 7. Un esfuerzo de compresión (σ < 0) reduce la temperatura de transición y aumenta los valores de diámetro crítico de partícula. Mientras que la acción de un esfuerzo de tensión (σ>0) aumenta la temperatura de transición y disminuye los valores de diámetros críticos de la partícula.
Acerca del cambio de orden de la transición en la nanoesfera de titanato de plomoPara analizar el coeficiente β’ de la ecuación (32) es necesario el uso de las cantidades s11=−2,5m2/C12N,s11=9m2C12N,Q11=0,089m4C2,Q12=−0,026m4C2 para el PT [10], y el valor del módulo de Young para la fase tetragonal del PT de E=61GPa [3].
Definiendo δ=τ2D2>0 se tiene que:
La partícula tendría una transición de fase ferroeléctrica-paraeléctrica continua si β’>0. Como el parámetro δ es positivo, se observa que β’ < 0 para todo valor de δ, luego la transición de fase será discontinua. Entonces, el presente modelo no predice un cambio en el orden de la transición ferroeléctrica en una nanoesfera de PT con una estructura de dominios de 180° únicamente. En Sani et al. [16] se dice que el cambio en el orden de transición para el PT es posible bajo la acción de esfuerzos mecánicos a escala de los micrómetros, el cual es un sistema diferente debido a que en la escala microscópica existen también dominios de 90° [33,34]. La diferencia de escala incide en la posibilidad de cambiar el orden de la transición de fase ferroeléctrica bajo la acción de esfuerzos mecánicos, debido a la diferente estructura de dominios ferroeléctricos.
Además, con las ecuaciones obtenidas es posible mostrar que el aumento del número n de dominios de 180° hace que el efecto de tamaño de partícula sea menos pronunciado.
ConclusionesLa fase ferroeléctrica de una partícula esférica de PT, con tamaño nanométrico y con dominios de 180°, se hace inestable a medida que su diámetro decrece, por cuanto la polarización espontánea tiende a desaparecer. Tal inestabilidad es más pronunciada si existe una capa de cargas espaciales en la superficie de la partícula; el aumento del grosor de esta capa hace que el efecto del tamaño de partícula sobre las propiedades ferroeléctricas sea cada vez más evidente. Un comportamiento similar ocurre si la partícula soporta esfuerzos de compresión, al contrario de lo que sucede con la presencia de esfuerzos de tensión; bajo esfuerzos de tensión el carácter ferroeléctrico se ve favorecido. Finalmente, un resultado importante del presente trabajo es que, a escala nanométrica y con la presencia de esfuerzos mecánicos, el modelo desarrollado no predice el cambio de orden de la transición ferroeléctrica-paraeléctrica en el PT con dominios de 180°. Un estudio posterior deberá incluir la presencia de dominios de 90°.






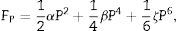
![Cristal ferroeléctrico cúbico con dominios de 180° [6]. Cristal ferroeléctrico cúbico con dominios de 180° [6].](https://static.elsevier.es/multimedia/03663175/0000005600000001/v1_201702110054/S0366317516300553/v1_201702110054/es/main.assets/thumbnail/gr1.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
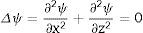
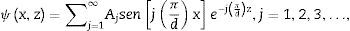
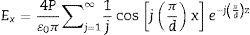
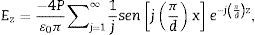
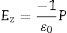
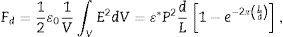

![Capas de carga espacial uniforme de grosor t. [6]. Capas de carga espacial uniforme de grosor t. [6].](https://static.elsevier.es/multimedia/03663175/0000005600000001/v1_201702110054/S0366317516300553/v1_201702110054/es/main.assets/thumbnail/gr2.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
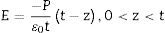
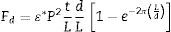
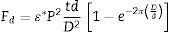
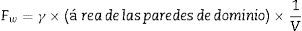
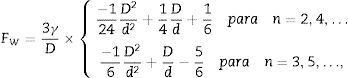
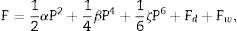
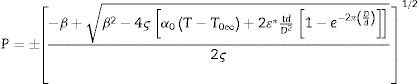
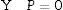
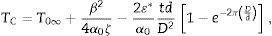
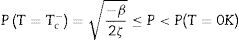
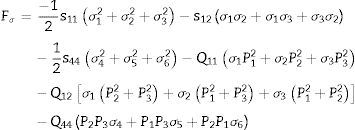
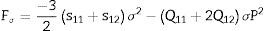
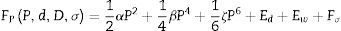
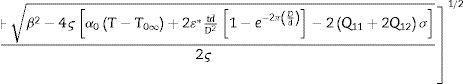
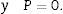
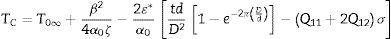
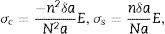
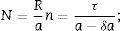
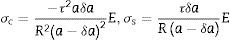
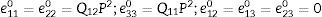
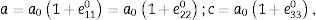
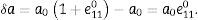
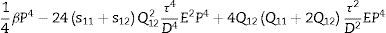
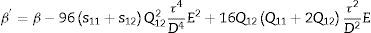
![Polarización en función de la temperatura para varios tamaños de nanopartícula esférica de PT, con n=3 y t=0,2nm. Los puntos son extraídos de resultados obtenidos de Huan et al. [7]. Polarización en función de la temperatura para varios tamaños de nanopartícula esférica de PT, con n=3 y t=0,2nm. Los puntos son extraídos de resultados obtenidos de Huan et al. [7].](https://static.elsevier.es/multimedia/03663175/0000005600000001/v1_201702110054/S0366317516300553/v1_201702110054/es/main.assets/thumbnail/gr5.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Polarización en función del diámetro de la nanopartícula de PT para T=298,15K y n=3. Las líneas son las predicciones de este trabajo. Los puntos han sido extraídos de un modelo para películas delgadas de Junquera et al. [32]. En las películas D se refiere a su grosor. Polarización en función del diámetro de la nanopartícula de PT para T=298,15K y n=3. Las líneas son las predicciones de este trabajo. Los puntos han sido extraídos de un modelo para películas delgadas de Junquera et al. [32]. En las películas D se refiere a su grosor.](https://static.elsevier.es/multimedia/03663175/0000005600000001/v1_201702110054/S0366317516300553/v1_201702110054/es/main.assets/thumbnail/gr6.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)