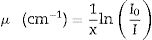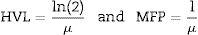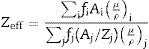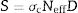This study aims to investigate the utility of using 15PbF2–(60x)TeO2–25WO3–xNd2O3 (0.1≥x≥1.5) glasses in the nuclear shielding applications for mixed radiation fields at energies ranging from 15keV to 15MeV. The effect of Nd3+ ions on gamma attenuation properties of the present glass system was discussed in detail. The radiation attenuation features were investigated for the present glass system by using Monte Carlo radiation transport simulation via Geant4 toolkit. The simulation results were theoretically approved by using Phy-X approach over the entire considered energy range. The obtained results indicate that the values of Zeff and Neff were both highest in the in the τ/ρ dominated energies due to the atomic number dependence of the cross sections of the τ/ρ absorption processes. Moreover, FNRCS values were 0.1152, 0.1152, 0.1153, and 0.1153cm−1 for PWTN1, PWTN2, PWTN3, and PWTN4 respectively. Finally, an extensive comparative study is also presented between the studied glass system and standard traditional shielding materials. The study suggests PWTN4 is the best photon shield amongst the studied PWTN-glasses.
Este estudio tiene como objetivo investigar la utilidad del uso de vidrios 15PbF2–(60x)TeO2–25WO3–xNd2O3 (0,1≥x≥1,5) en las aplicaciones de blindaje nuclear para campos de radiación mixtos a energías que van desde 15keV hasta 15MeV. Se discute en detalle el efecto de los iones Nd3+ sobre las propiedades de atenuación gamma de este sistema de vidrio. Se investigan las características de atenuación de radiación para este sistema de vidrio utilizando la simulación de transporte de radiación de Monte Carlo con el conjunto de herramientas Geant4. Los resultados de la simulación se han corroborado teóricamente utilizando la aproximación Phy-X en todo el rango de energías considerado. Los resultados obtenidos indican que los valores de Zeff y Neff fueron los más altos en las energías dominantes en τ/ρ debido a la dependencia con el número atómico de las secciones transversales de los procesos de absorción τ/ρ. Además, los valores de FNRCS fueron 0,1152; 0,1152; 0,1153 y 0,1153cm−1 para PWTN1, PWTN2, PWTN3 y PWTN4, respectivamente. Por último, también se presenta un extenso estudio comparativo entre el sistema de vidrio analizado y los materiales de blindaje estándar y tradicionales. El estudio muestra que PWTN4 es el mejor escudo de fotones de entre los vidrios PWTN estudiados.
Advances in nuclear technology has brought about evolution in the way we perceive and use ionizing radiation (IR). Today, IR such as photons (X- and gamma-rays), protons, electrons and neutrons are used in medicine, for sterilization of medical tools, diagnosis and treatment of health challenges such as cancer. Radiation is also used in nuclear power plants, for the generation of cheap and enduring electricity; for food processing and preservation in food and agricultural industries, environmental conservation, material processing and characterization [1–4]. In all these applications, and other areas where nuclear technology has become useful, the interaction mechanism of the different radiations with a target medium is an important process. Ionizing radiation from processes within and outside the nucleus of an atom interacts with matter in diverse ways. One common denominator among the modes of interactions, is the energy exchange between the IR and the atoms of the interacting medium. In many cases, the energy deposited by the IR within the medium causes excitation and ionization of the atoms within the interacting medium. The cross section of either process depends on the nature and energy of the radiation, angle of interaction/incidence, geometry and chemical description of the medium among other parameters [5,6]. Macroscopically, the ionization and excitation processes subsequently lead to changes in the chemical, structural, phase, electrical, and optical definition of a material [5,6]. In biological systems, the ionization and excitation processes produce meta-stable radicals which combine with one another to form new chemical species that are alien and whose functionality perturbs the natural working condition of the biological system [7]. These changes of properties (of biological or non-biological units) are sometimes undesirable as they could lead to system failure and subsequently economic losses and in some cases threat to lives. However, some of these changes in non-biological materials and related phenomena (such as scintillation and luminescence) have been adopted in many applications to detect and measure IR. The biological changes are also advantageous when tumors are treated with radiation. Furthermore, the understanding of the different ways in which radiation interacts with matter and consequent effects has advanced the application of IR in different human spheres and improved radiation protection techniques.
Improvement in radiation protection technology has sustained and continued to advance the use of IR. The International Commission of Radiological Protection [8] has laid down a generally accepted guideline for IR protection. This guideline is based on the principle of justification and optimization of technologies and procedures involving IR and dose limitation in those practices. Optimization and dose limitation to man and his environment can be achieved efficiently with little or no administrative control via the use of radiation shields. Radiation shields refer to barriers used to confine radiations and their sources within a volume of space. Such barriers ensure that radiation dose beyond the confinement is controlled to an acceptable/safe level. However, the performance of a shield depends on several parameters. Nearly any material can be used as a radiation shield, but the nature of radiation, its energy, acceptable dose outside the shield, cost of design, geometry of the intended shield, maintenance, available space, radiation source and size are some of the factors that narrows the choice of shielding material, its size (thickness) and structural design. Concrete and lead are two classical shielding materials that have been adopted since the early days of radiation applications. their fortune for this purpose has however plummeted in recent times. Although concrete is cheap and easy to prepare, its thermal and chemical (water content) instability are some of the challenges associated with its choice as a radiation shielding material. On the other hand, lead is a good gamma radiation attenuator, its weight and environmental toxicity concerns have limited its use in many areas of radiation technology. Radiation shielding engineers and scientists have over the years suggested arrays of other materials which can function well as radiation barriers. These materials include alloys [9,10], steels [11], heavy metal based glasses [12] and many more. Still the search for a highly efficient radiation shield with novel properties continues to grow. This is due to emerging nuclear technology which has required radiation shields to possess other features (apart from the ability to absorb radiation) in order to function effectively as shields in certain applications. For example, a structural shield may be required to be transparent, strong and durable in order to monitor the patient during radiation intervention procedure and for long term cost effectiveness. In other applications, shields may be required to be mechanically flexible, light and thermally stable. All these requirements have ensured that research into shielding efficacy of different materials continues to grow.
Research into the IR shielding efficacy of glass materials of different chemical compositions have risen in recent times [13–20] for a lot of reasons. Two major factors that contributed to this increasing trend is firstly, the ease at which glasses can be produced, and secondly, the fact that the chemical composition of glasses can be altered to obtain glasses with desired features. Thus, glass shields that are cost effective, free from toxic chemicals, and possessing attractive secondary properties such as high mechanical strength and durability can be produced and deployed for radiation shielding purposes. Many glass systems (borate, silicate, phosphate, tellurite etc.) have been investigated for radiation shielding purposes with stupendous results [13–20]. One major conclusion from these investigations is that the composition of a glass plays the major role in its shielding and other properties. A careful choice of a glass chemical composition is hence very crucial. Furthermore, the composition also determines the type of radiation the shield can effectively absorb. Glass containing oxides of heavy metals such as Pb, W, Bi, Ba etc. have proven to be relatively better for absorbing photons while those rich in Li, B, and Cd have good absorption capacity for fast neutrons [12,13,17,18,21,22]. Designing glass shields that can absorb these two types of radiation effectively would thus require that careful choice and combination between light and heavy components be effectively made. To achieve this optimization, the radiation shielding parameters of the different possible glass matrices should be investigated. For photons these parameters include, mass/linear attenuation coefficient, half value layer, effective atomic number etc. while for neutrons, the microscopic/macroscopic removal cross section can be used. A comparison between these parameters would definitely reveal the best glass matrix for mixed radiation field shielding application. Detailed determination of shielding parameters via experiments, Monte-Carlo simulations or direct calculation is thus very essential before the classification of any glass composition as a good radiation shield.
The present study aims to investigate the 15PbF2–(60x)TeO2–25WO3–xNd2O3 glasses by means of their nuclear radiation shielding properties for mixed radiation fields at the energies ranging from 15keV to 15MeV. Geant4 toolkit was successfully used to simulate the radiation attenuation features of the present glass system. Moreover, Phy-X approach was applied to prove the results obtained from Geant4 simulations. Furthermore, buildup factors and neutron attenuation cross sections were studied for the present glass system. Finally, an extensive comparative study is also presented between the studied glass system and standard traditional shielding materials.
Materials and methodsTeO2-based glass system is one of the most important systems that have aroused significant research interest due to their attractive and unique properties. Such glass systems use in several fields including medicine, civil, military, and etc. In the current work, we reported the radiation attenuation properties of the PWTNx glass system in the chemical form of 15PbF2–(60x)TeO2–25WO3–xNd2O3 (x varies between 0.1 and 1.5mol% with a step of 0.5). This glass system was selected from Ref.[23]. The studied sample codes, chemical concentration for each oxide in mol%, and sample density are illustrated in Table 1.
Due to the high cost of raw materials of glasses and the unavailability of radiation sources at our desired energies to perform experimental measurements, Monte Carlo (MC) method is used via Geant4 toolkit to simulate the radiation attenuation features of the present PWTNx glass system. MC technique is a promising tool in radiation studies to mimic experiments for radiation propagation in materials by using a software environment with low cost and short time. In this research article, Geant4 toolkit was carried out to simulate the attenuation features of the present PWTNx glass system for energies up to 15MeV [24]. As a first step, Geant4 input file was written by using C++ language with respect of all the definitions of the present glass system, radiation source, and detector information. Actually there are three mandatory input files (well-known as mandatory classes) as follows:
- 1.
Detector Construction class that is used to define the simulation geometry including the dimensions of the samples, detector, gamma source, and the distances between all of the equipment's.
- 2.
Primary Generator Action class that is utilized to set the dimensions of gamma source with its initial position as well as all of the angular distributions. Furthermore, the gamma energy range can be controlled and selected in this class.
- 3.
Physics List class that is the most important class to model and describe the physical concepts of the problem under study. For example, one needs to active all the photon, neutron, charged particles (such as electron) interactions to carry out simulation for radiation shielding studies. Such interaction can be written as G4eplusAnnihilation, G4eMultipleScattering, G4eBremsstrahlung, and etc.
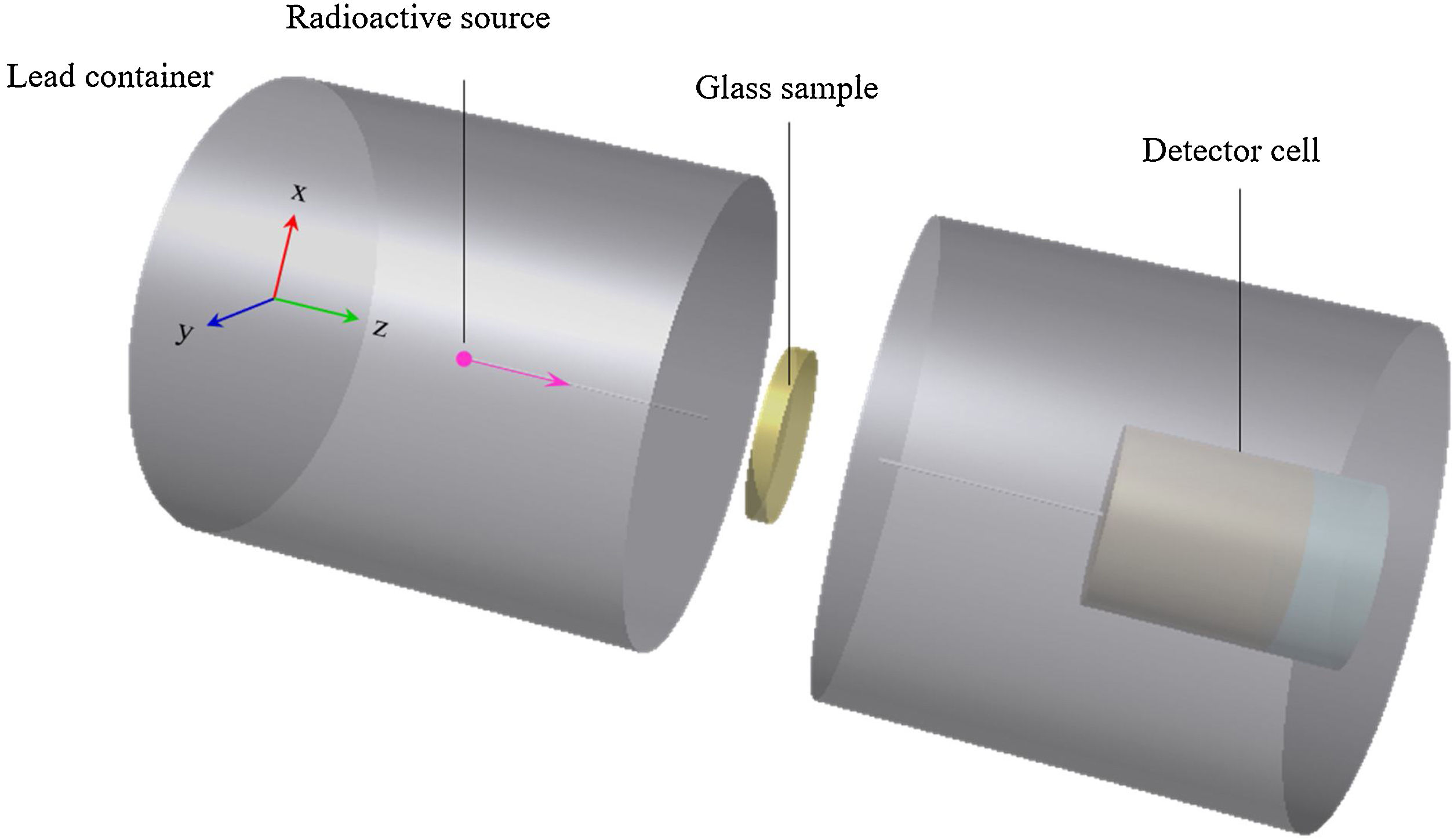
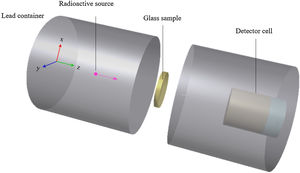
A point source of radiation and a NaI detector were located in a Lead (Pb) shield block. Such shielding is very important to remove the secondary particles. Furthermore, the present PWTNx glass system was defined with respect of its chemical properties described in Table 1. Finally, it should mention that the simulation was repeated for each glass sample two times at each photon energy with the range cut value of 0.01cm. Fig. 1 shows a 3D view for the simulation geometry and more details can be found in our previous publications [25,26].
The Geant4 simulation was used to obtain the main attenuation factor namely linear attenuation coefficient (μ) that is given by the equation below [27]:
Here, x is the glass thickness that is given according to 2≤y≤4, where y=ln(I0/I) [28]. I0 is the original number of photons that is adjusted to be 106 in our present simulation. I is the transmitted photons. The mass attenuation coefficient is obtain directly as a ratio between μ and glass density (ρ). Thereafter, the other attenuation factors such as HVL, MFP, and effective atomic number (Zeff) can be derived from μ according to the equations below [29–32]:Moreover, the technical Phy-X program is a strong toolkit to study the attenuation features of materials over different energies and by using more than 15 factors [33]. The Phy-X program was used to compare our simulation results in one hand and to calculate buildup factors for the present glass system on the other hand.
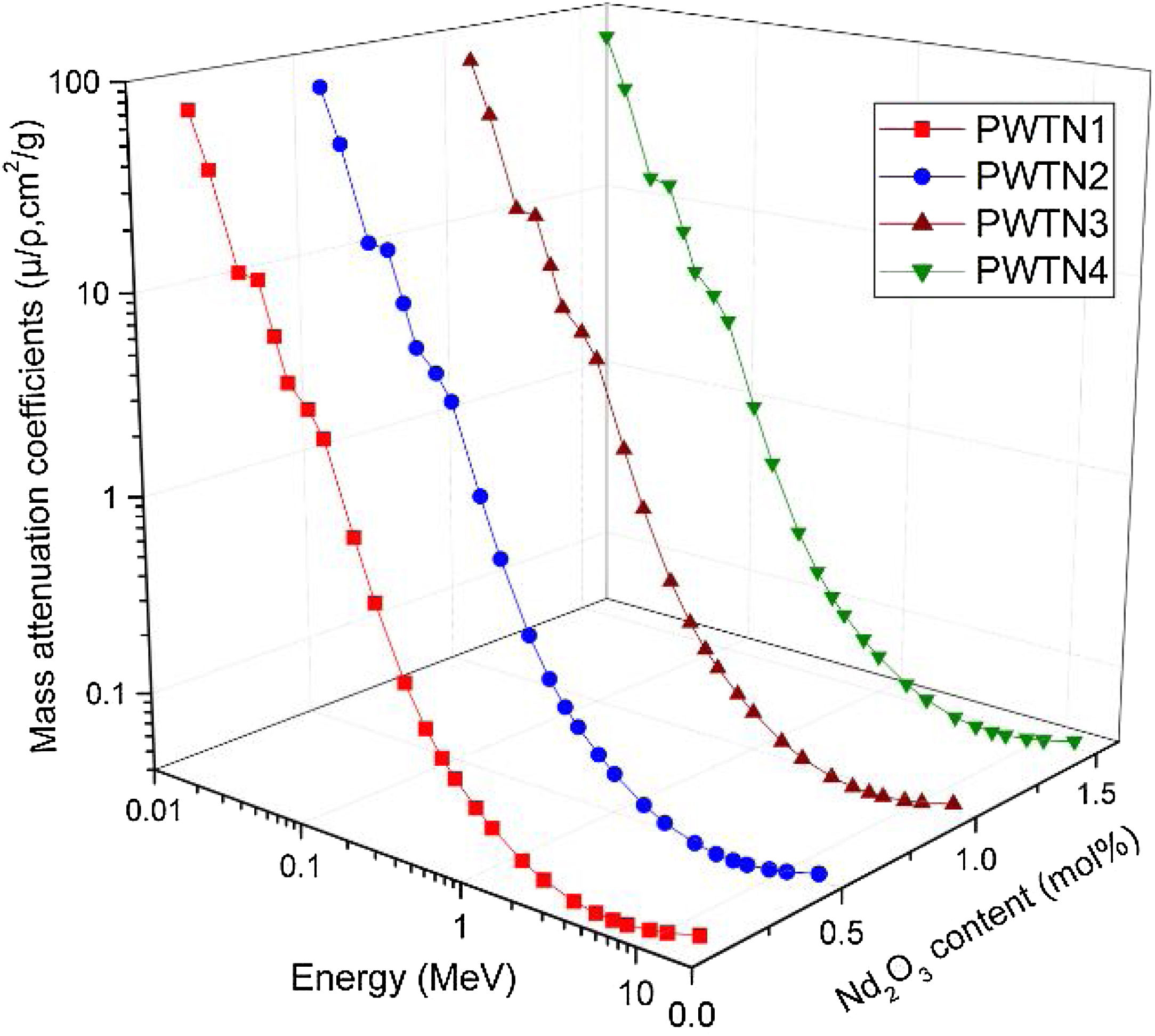
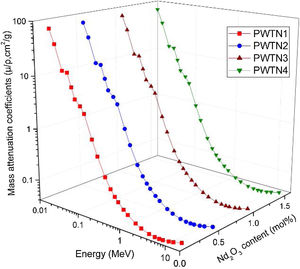
Results and discussionAs a photon interaction parameter, the mass attenuation coefficient (μ/ρ) of a material may also be used as a parameter for evaluating the relative shielding competence of an interacting or attenuation medium with respect to others. Calculated μ/ρ for the PWTN-glasses for standard photon energies (E) between 15keV and 15MeV are presented in Fig. 2. According to the result, μ/ρ varies from 72.511–0.0362, 72.586–0.0363, 72.679–0.0363, and 72.771–0.0363cm2g−1 as energy progresses from 15keV–15MeV for PWTN1–4 respectively. The value of the obtained μ/ρ is mainly the sum of partial mass attenuation due to photoelectric (τ/ρ), Compton scattering (σ/ρ), and the pair production (κ/ρ) absorption processes. Hence, the general behavior of μ/ρ with respect to photon energy and chemical composition of the glasses can be explained based on the variation of each of the three absorption processes with these parameters (energy and chemical composition). Fig. 2 shows that μ/ρ generally decreases steadily with E up to 5MeV before subsequently increasing for the remaining part of the energy spectrum. The rate of the decrease was very high for E≤60keV while for, 0.06<E≤5MeV the reduction rate was less vigorous. However, between 30 and 40keV, the rapid decrease seems to flatten-out, this could be due to the high value of μ/ρ recorded at 40keV as a result of absorption edge of Te atom (a major chemical component of the PWTN-glasses system). Ordinarily, a spike in μ/ρ value is expected at this absorption edge, however, the high μ/ρ of the glass system compared to that of Te atom dwarfed the expected spike.
The behavior of μ/ρ for E≤60keV is attributed to the energy dependence of τ/ρ. Within this energy range, τ/ρ influences μ/ρ more compared to the other two absorption processes. Since τ/ρ∝E−3.5[34] for the said energy range, the rapid reduction in the value of μ/ρ is hence justified. The photoelectric process absorbs photons completely by converting them to photoelectrons, this explains why τ/ρ and hence μ/ρ was highest at the least photon energy. On the other hand, photon absorption via the Compton scattering process mostly influences the values of μ/ρ at energies within the range 0.06<E≤5MeV. The cross section for σ/ρ∝E−1 hence, the observed decrease in the decline rate of μ/ρ compared to the photoelectric effect dominated energies. The Compton scattering process decrease the energy of photons via incoherent scattering, and thus increasing their chances (after multiple Compton scattering) of absorption via other processes that occur at lower energies. Contrary to τ/ρ and σ/ρ, κ/ρ increases with photon energy beyond a threshold energy of 1.012MeV. This explains the observed slight increase in the values of μ/ρ of the glasses as energy increases beyond 5MeV. It should however be noted that the lower/upper bound of the range of energies within which each of the three partial photon absorption processes dominate shifts to higher/lower energies depending on the chemical composition of the absorbing medium. The similar chemical composition of the PWTN-glasses explains why the energy range in which the partial photon absorption processes is dominant is the same. A comparison of the values of μ/ρ of the four glasses at similar energies within the 0.015–15MeV spectrum reveal close proximity between them. However, a slight increase in μ/ρ values of the glasses follow the sequence: (μ/ρ)PWTN1<(μ/ρ)PWTN2<(μ/ρ)PWTN3<(μ/ρ)PWTN4. This increase is more (less) conspicuous in the energy region where τ/ρ (σ/ρ) dominates the absorption processes respectively. The greater difference in the photoelectric absorption dominated region is rooted in the chemical composition differences of the glasses. Since τ/ρ∝Z3, the increase in the Nd (Z=60) content of the glasses compared to Te (Z=52) is believed to increase the Z value of the glasses and hence the observed greater differences in the mass attenuation coefficient. On the other hand, mass attenuation coefficient values of the glasses were closer at each energy in the σ/ρ and κ/ρ dominated energies due to σ/ρ∝Z0 and κ/ρ∝Z dependence.
The μ/ρ of a composite material sometimes increase with their mass density, for the increase in the Nd2O3 content was observed to also increase the mass density and photon absorption capacity of the glasses. Based on the aforementioned results, one can safely conclude that PWTN4 is the best photon shield amongst the studied PWTN-glasses. The accuracy of μ/ρ results was theoretically proved by using Phy-X program for each glass sample at the entire considered energy range. Table 2 shows a comparison between Geant4 and Phy-X predications for the present glasses of PWTN1, PWTN2, and PWTN3. While the results of μ/ρ for PWTN4 and PWTN5 are shown in Table 3. Clearly, the differences between Geant4 and Phy-X are very small and this confirms the accuracy of the values in the present article.
Mass attenuation coefficient (μ/ρ) of the PWTN1 and PWTN2 glasses obtained by Geant4 simulations and Phy-X program with different photons energies.
| Photon energy (MeV) | PWTN1 | PWTN2 | ||||
|---|---|---|---|---|---|---|
| Phy-X | Geant4 | Dev.% | Phy-X | Geant4 | Dev.% | |
| 0.015 | 72.511 | 71.608 | 1.25 | 72.586 | 71.466 | 1.54 |
| 0.02 | 39.535 | 39.053 | 1.22 | 39.549 | 39.049 | 1.26 |
| 0.03 | 13.673 | 13.532 | 1.03 | 13.676 | 13.493 | 1.34 |
| 0.04 | 13.248 | 13.074 | 1.31 | 13.179 | 12.943 | 1.79 |
| 0.05 | 7.401 | 7.334 | 0.91 | 7.443 | 7.384 | 0.79 |
| 0.06 | 4.588 | 4.541 | 1.03 | 4.614 | 4.554 | 1.31 |
| 0.08 | 3.621 | 3.576 | 1.25 | 3.628 | 3.589 | 1.09 |
| 0.1 | 2.730 | 2.689 | 1.50 | 2.731 | 2.699 | 1.19 |
| 0.15 | 0.997 | 0.990 | 0.74 | 0.998 | 0.988 | 1.00 |
| 0.2 | 0.514 | 0.510 | 0.68 | 0.514 | 0.507 | 1.39 |
| 0.3 | 0.232 | 0.229 | 1.08 | 0.232 | 0.229 | 1.34 |
| 0.4 | 0.149 | 0.148 | 0.94 | 0.149 | 0.148 | 1.30 |
| 0.5 | 0.114 | 0.113 | 0.54 | 0.114 | 0.113 | 1.10 |
| 0.6 | 0.094 | 0.093 | 1.46 | 0.094 | 0.093 | 1.25 |
| 0.8 | 0.074 | 0.073 | 1.00 | 0.074 | 0.073 | 1.23 |
| 1 | 0.063 | 0.062 | 1.04 | 0.063 | 0.062 | 1.46 |
| 1.5 | 0.049 | 0.048 | 1.23 | 0.049 | 0.048 | 1.15 |
| 2 | 0.043 | 0.043 | 0.67 | 0.043 | 0.042 | 1.47 |
| 3 | 0.038 | 0.038 | 0.96 | 0.038 | 0.038 | 1.39 |
| 4 | 0.037 | 0.036 | 0.81 | 0.037 | 0.036 | 1.12 |
| 5 | 0.036 | 0.036 | 0.82 | 0.036 | 0.036 | 1.13 |
| 6 | 0.036 | 0.036 | 1.33 | 0.036 | 0.036 | 0.63 |
| 8 | 0.038 | 0.037 | 1.37 | 0.038 | 0.037 | 1.25 |
| 10 | 0.039 | 0.039 | 1.26 | 0.039 | 0.039 | 1.41 |
| 15 | 0.043 | 0.043 | 0.88 | 0.043 | 0.043 | 1.38 |
Mass attenuation coefficient (μ/ρ) of the PWTN3 and PWTN4 glasses obtained by Geant4 simulations and Phy-X program with different photons energies.
| Photon energy (MeV) | PWTN3 | PWTN4 | ||||
|---|---|---|---|---|---|---|
| Phy-X | Geant4 | Dev.% | Phy-X | Geant4 | Dev.% | |
| 0.015 | 72.679 | 71.614 | 1.47 | 72.771 | 71.927 | 1.16 |
| 0.02 | 39.566 | 38.874 | 1.75 | 39.583 | 39.094 | 1.24 |
| 0.03 | 13.681 | 13.525 | 1.14 | 13.685 | 13.514 | 1.26 |
| 0.04 | 13.093 | 12.875 | 1.66 | 13.009 | 12.838 | 1.31 |
| 0.05 | 7.494 | 7.427 | 0.90 | 7.545 | 7.463 | 1.09 |
| 0.06 | 4.647 | 4.588 | 1.28 | 4.680 | 4.622 | 1.24 |
| 0.08 | 3.637 | 3.587 | 1.38 | 3.646 | 3.591 | 1.50 |
| 0.1 | 2.733 | 2.707 | 0.95 | 2.735 | 2.715 | 0.70 |
| 0.15 | 0.998 | 0.988 | 1.02 | 0.999 | 0.992 | 0.62 |
| 0.2 | 0.514 | 0.511 | 0.52 | 0.514 | 0.512 | 0.52 |
| 0.3 | 0.232 | 0.229 | 1.15 | 0.232 | 0.229 | 1.39 |
| 0.4 | 0.150 | 0.148 | 1.14 | 0.150 | 0.148 | 0.72 |
| 0.5 | 0.114 | 0.113 | 0.54 | 0.114 | 0.113 | 0.99 |
| 0.6 | 0.094 | 0.093 | 1.14 | 0.095 | 0.093 | 1.10 |
| 0.8 | 0.074 | 0.073 | 0.92 | 0.074 | 0.073 | 1.16 |
| 1 | 0.063 | 0.062 | 1.20 | 0.063 | 0.062 | 0.92 |
| 1.5 | 0.049 | 0.048 | 1.43 | 0.049 | 0.048 | 1.43 |
| 2 | 0.043 | 0.042 | 1.46 | 0.043 | 0.043 | 0.56 |
| 3 | 0.038 | 0.038 | 1.17 | 0.038 | 0.038 | 0.88 |
| 4 | 0.037 | 0.036 | 1.13 | 0.037 | 0.036 | 1.45 |
| 5 | 0.036 | 0.036 | 1.36 | 0.036 | 0.036 | 0.67 |
| 6 | 0.036 | 0.036 | 0.85 | 0.036 | 0.036 | 0.59 |
| 8 | 0.038 | 0.037 | 1.36 | 0.038 | 0.037 | 0.66 |
| 10 | 0.039 | 0.039 | 1.07 | 0.039 | 0.039 | 0.52 |
| 15 | 0.043 | 0.043 | 1.44 | 0.043 | 0.043 | 0.92 |
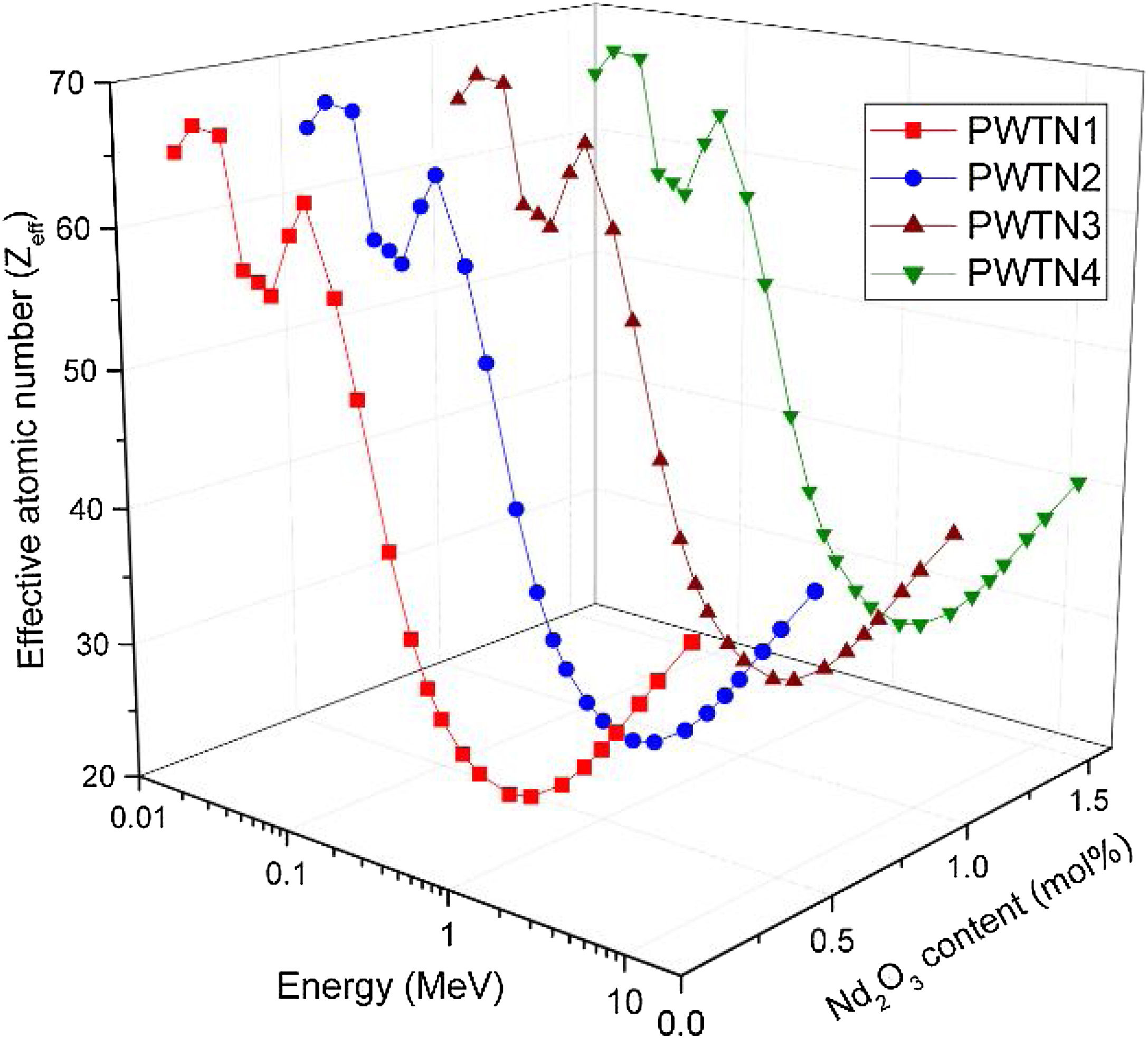
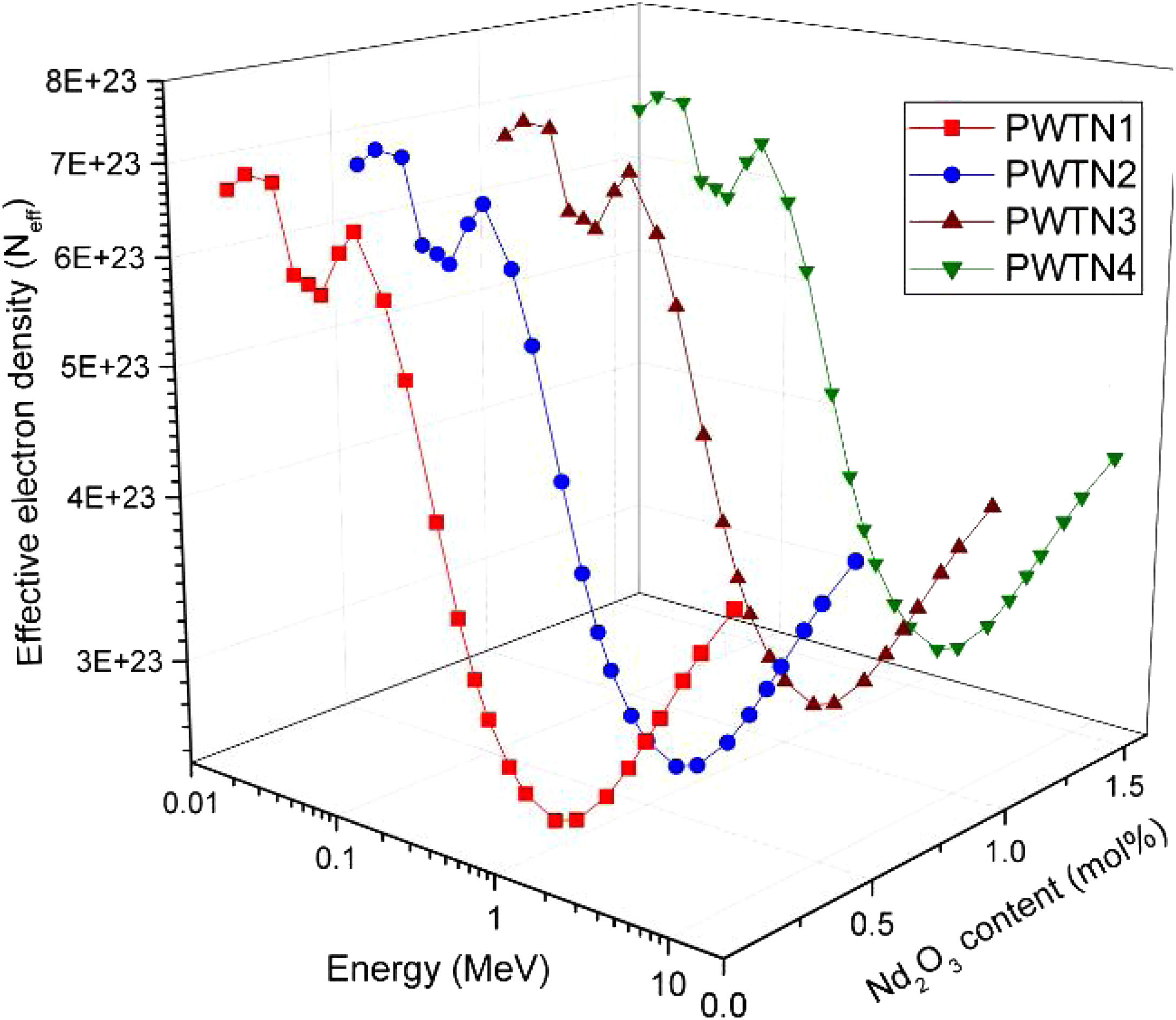
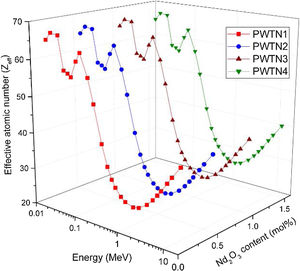
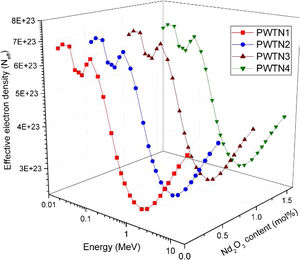
The influence of chemical composition on the photon interaction processes that lead to photon absorption is sometimes expressed in the form of effective atomic number (Zeff) and electron density (Neff). These parameters give an idea of the electrons available (per unit mass) for photon interaction. Figs. 3 and 4 depict the variations of calculated Zeff and Neff of the glasses with respect to photon energy. Clearly, these parameters vary similarly with photon energy, showing that they with photon interaction as well. Zeff varies from 26.46–67.17, 26.50–67.15, 26.54–67.13, and 26.58–67.10 while Neff varies from 2.72–6.90, 2.72–6.89, 2.72–6.88, and 2.72–6.86×1023electrons/g for PWTN1–4 respectively. Values of Zeff and Neff were both highest (lowest) in the in the τ/ρ (σ/ρ) dominated energies due to the atomic number dependence of the cross sections of these absorption processes. Except at energies <30keV, the trend of Zeff and Neff is similar to that of mass attenuation coefficient. Thus, the relative values of Zeff and Neff of the glasses translates to their relative photon absorption capacity. The spectra of the two parameters show a peak at 100keV due to the K-absorption edge of Pb (a major constituent of the glasses). Beyond 1MeV, the spectra of Zeff and Neff show similar variation with E as of μ/ρ; an indication of the strong relationship between the parameters.
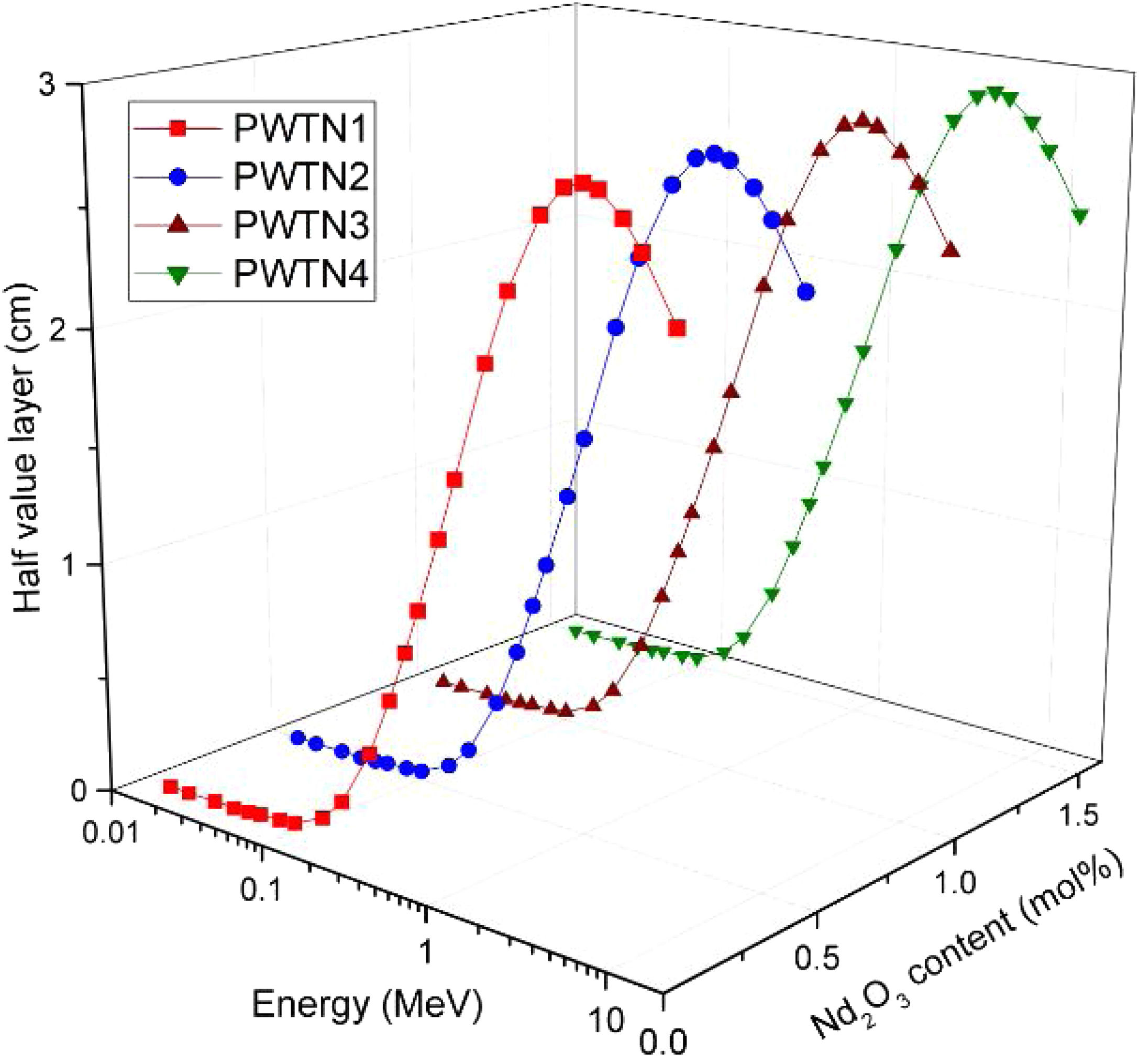
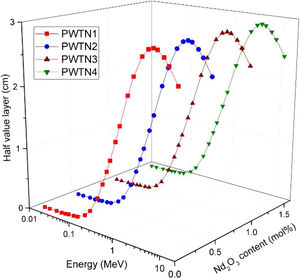
Fig. 5 presents the HVL (in cm) of PWTN1–4 as a function of energy and molar concentration (in mol%) of Nd2O3. The HVL is a more practical and convenient parameter (compared to μ/ρ) for comparing photon shielding competence of different absorbers. Fig. 4 reveals a growth in the value of HVL with E up to 5MeV, beyond which it descends as energy increases. The initial increase implies that higher energy photons penetrate further, hence, a thicker absorber is required to absorb as energy increases. Furthermore, the cross sections of photon interaction processes dominating absorption process decrease with E for E≤5MeV thus accounting for the high penetration ability of higher energy photons. At E>5MeV, the decrease of HVL with E is due to par production absorption whose cross section increase with E. the HVL of the glasses varies from 0.001–2.435, 0.001–2.432, 0.001–2.428, and 0.001–2.424cm respectively for PWTN1–4 for energy increase from 15keV–15MeV. Obviously, the HVL reduces at specific photon energies as Nd2O3 of the glasses increases signifying improvement in photon attenuation competence.
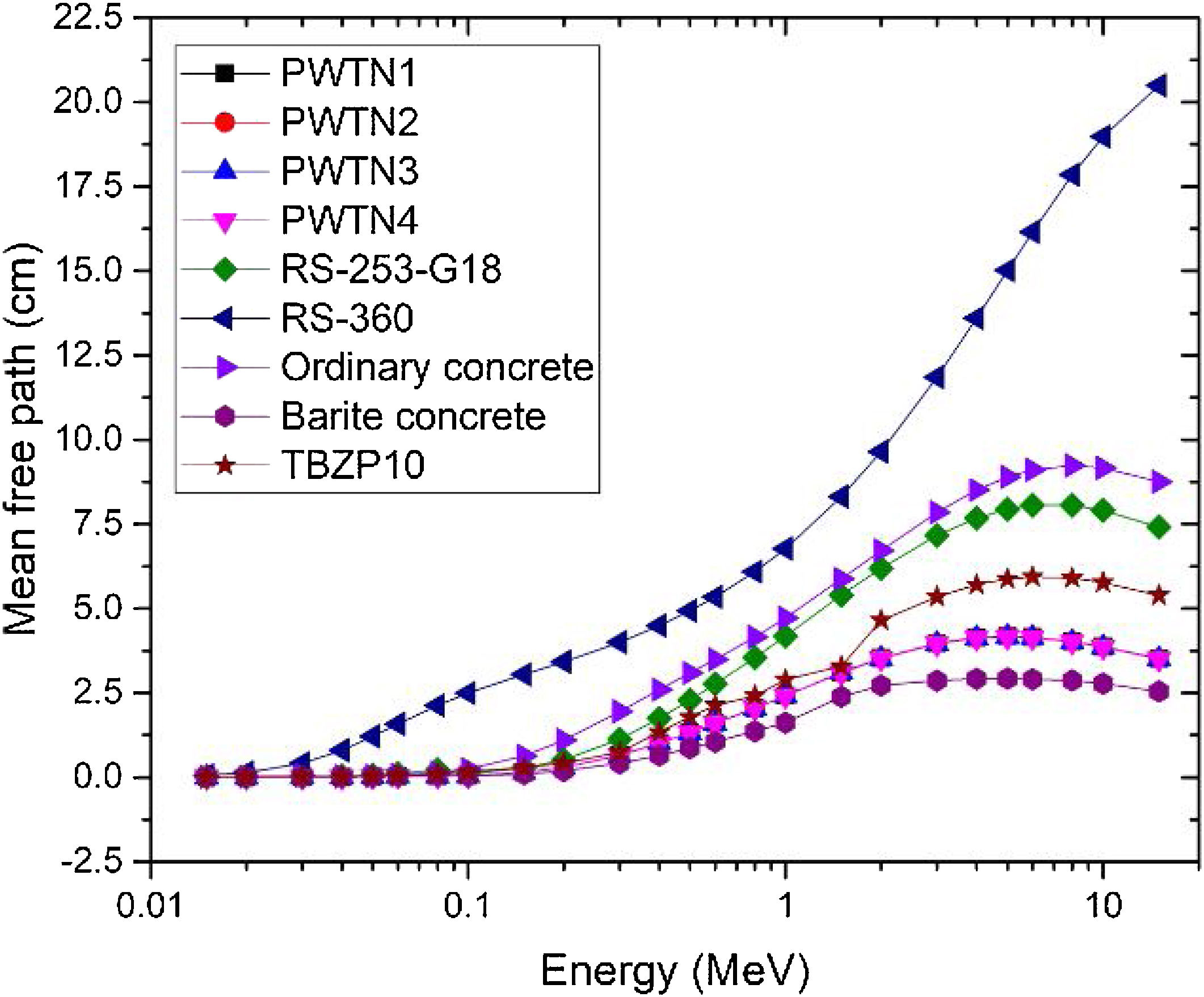
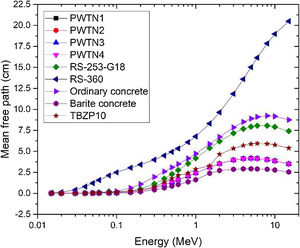
In order to compare the photon attenuation and protection status of the present PWTN-glasses with existing conventional shields, the variations in the value MFP of the glasses together with those of two commercial glass shields with trade names RS-253-G18 and RS-360 [35], two concrete species concretes (ordinary and barite) [36] and recently developed TBZP10 glass [37] with energy is illustrated in Fig. 6. Generally, the MFP value increases with energy with a strong overlapping in the spectra of the PWTN-glasses. This shows that the mean distance between photon interactions in the glass is comparable. The minimum (maximum) value of MFP of the PWTN-glasses were 0.002 (4.175), 0.002 (4.171), 0.002 (4.165), and 0.002 (4. 159) cm respectively at photon energy of 15keV (5MeV). Compared with other materials, Fig. 5 shows that with the exception of barite concrete with lower MFP value across the energy spectrum, the shielding competence of the PWTN1–4 glasses were superior compared to the commercial glass shields, ordinary concrete and TBZP10. The PWTN-glasses may hence be considered ahead of these materials as choices of glass shields in nuclear technology.
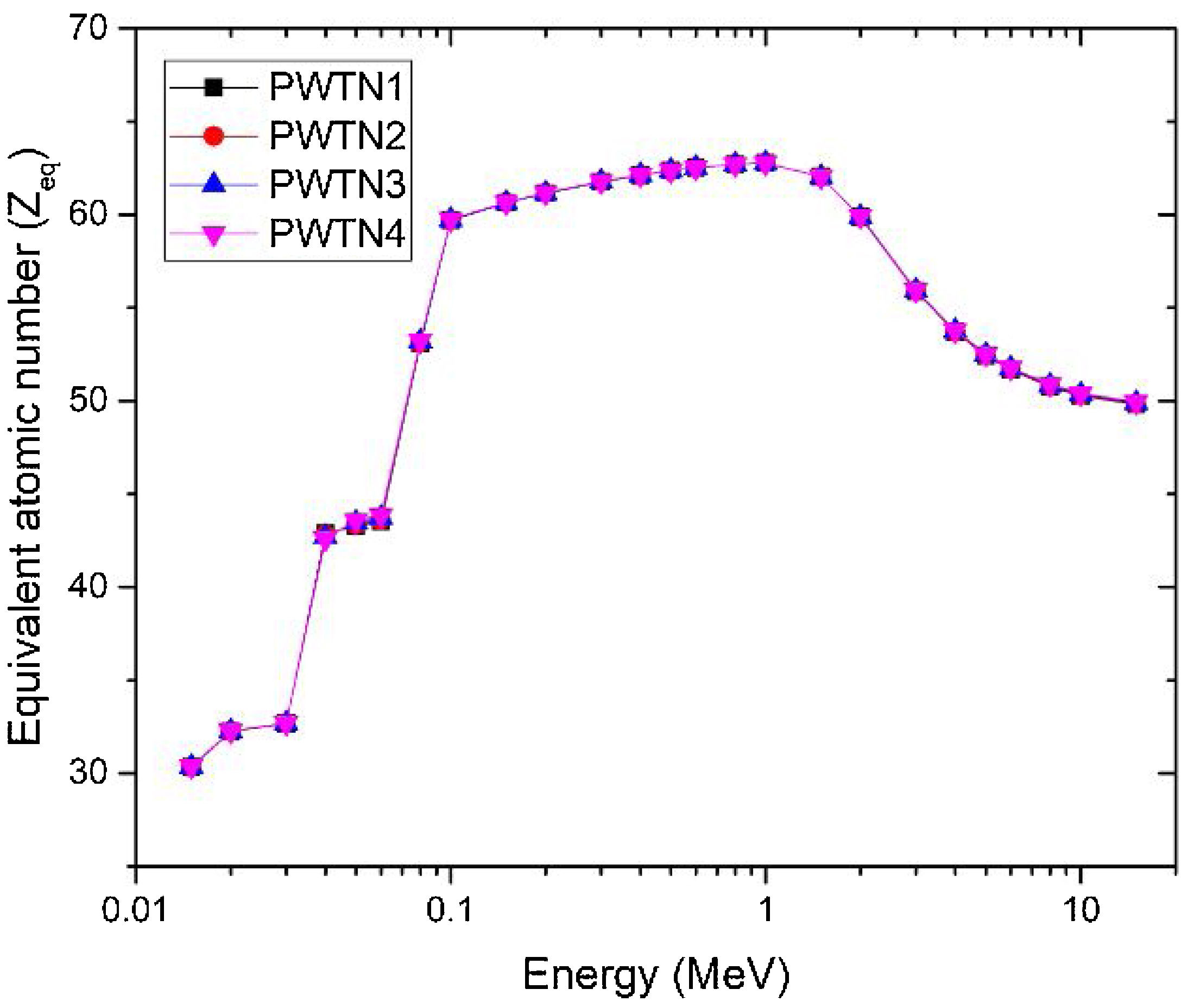
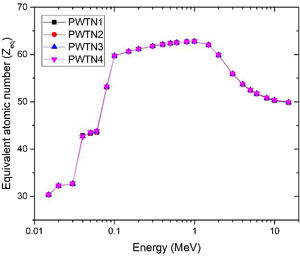
The production of secondary photons within an absorbing medium impairs its shielding competence as such secondary photons (buildup) are transmitted through the shield barrier. The exposure buildup factor (EBF) is one in which the detector response is exposure. The EBF is a parameter which is also used to characterize the relative photon absorption and protection ability of a material and may also be used to estimate the fraction of photon transmitted through it. High EBF signifies high transmission and low shielding efficiency. In the evaluation of EBF via the GP fitting method, the equivalent atomic number Zeq of the glasses were first calculated. Zeq of a composite material is the atomic number of an element which produces and transmits the same magnitude of secondary photons (buildup). The Zeq of the under studied glasses across the studied energy spectrum is presented in Fig. 7. Tables 4 and 5 present the values of Zeq and all of the fitting parameters that are necessary for buildup factors calculations. The value of the equivalent atomic number varies between 30.33–62.78 for the glasses. The observed strong overlapping of the Zeq shows that the magnitude and spectra secondary photons produced in the glasses are close.
Equivalent atomic number (Zeq) and G-P exposure buildup factors (EBF) for PWTN1 and PWTN2 glasses.
| Photon energy (MeV) | Zeq | PWTN1 | Zeq | PWTN2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | Xk | a | b | c | d | Xk | |||
| 0.015 | 30.33 | −0.245 | 1.002 | 1.840 | 0.208 | 11.328 | 30.35 | −0.245 | 1.002 | 1.838 | 0.208 | 11.330 |
| 0.02 | 32.25 | 0.552 | 1.452 | 0.654 | −0.761 | 11.502 | 32.25 | 0.551 | 1.453 | 0.655 | −0.760 | 11.503 |
| 0.03 | 32.68 | 0.174 | 1.865 | 0.595 | −0.105 | 18.494 | 32.68 | 0.174 | 1.866 | 0.596 | −0.105 | 18.500 |
| 0.04 | 42.88 | 0.089 | 3.897 | 0.429 | −0.043 | 23.721 | 42.80 | 0.089 | 3.901 | 0.419 | −0.042 | 23.689 |
| 0.05 | 43.26 | −0.216 | 3.173 | 0.115 | 0.006 | 12.781 | 43.35 | −0.209 | 3.178 | 0.120 | 0.003 | 12.840 |
| 0.06 | 43.53 | 0.871 | 2.518 | 0.051 | −0.129 | 14.955 | 43.62 | 0.858 | 2.525 | 0.054 | −0.128 | 14.803 |
| 0.08 | 53.10 | 0.381 | 1.918 | 0.107 | −0.052 | 15.877 | 53.14 | 0.376 | 1.920 | 0.108 | −0.051 | 15.883 |
| 0.1 | 59.70 | 0.394 | 1.529 | 0.120 | −0.076 | 16.404 | 59.71 | 0.393 | 1.529 | 0.120 | −0.075 | 16.411 |
| 0.15 | 60.63 | 0.421 | 1.196 | 0.190 | −0.235 | 13.788 | 60.64 | 0.421 | 1.196 | 0.190 | −0.235 | 13.788 |
| 0.2 | 61.14 | 0.216 | 1.173 | 0.413 | −0.115 | 14.188 | 61.14 | 0.216 | 1.173 | 0.413 | −0.115 | 14.188 |
| 0.3 | 61.77 | 0.139 | 1.256 | 0.555 | −0.065 | 13.819 | 61.77 | 0.139 | 1.256 | 0.555 | −0.065 | 13.819 |
| 0.4 | 62.12 | 0.096 | 1.345 | 0.680 | −0.053 | 14.202 | 62.12 | 0.096 | 1.345 | 0.680 | −0.053 | 14.202 |
| 0.5 | 62.36 | 0.072 | 1.415 | 0.757 | −0.044 | 14.139 | 62.36 | 0.072 | 1.415 | 0.757 | −0.044 | 14.139 |
| 0.6 | 62.52 | 0.055 | 1.461 | 0.813 | −0.035 | 13.762 | 62.52 | 0.055 | 1.461 | 0.813 | −0.035 | 13.762 |
| 0.8 | 62.71 | 0.035 | 1.520 | 0.883 | −0.027 | 13.685 | 62.71 | 0.035 | 1.520 | 0.883 | −0.027 | 13.685 |
| 1 | 62.78 | 0.022 | 1.539 | 0.936 | −0.022 | 13.474 | 62.78 | 0.022 | 1.539 | 0.936 | −0.022 | 13.474 |
| 1.5 | 62.03 | 0.000 | 1.507 | 1.036 | −0.016 | 13.910 | 62.03 | 0.000 | 1.507 | 1.036 | −0.016 | 13.910 |
| 2 | 59.88 | 0.002 | 1.529 | 1.043 | −0.021 | 13.110 | 59.89 | 0.002 | 1.529 | 1.043 | −0.021 | 13.110 |
| 3 | 55.88 | 0.017 | 1.540 | 1.016 | −0.043 | 13.329 | 55.90 | 0.017 | 1.540 | 1.016 | −0.043 | 13.331 |
| 4 | 53.70 | 0.027 | 1.499 | 1.000 | −0.054 | 13.599 | 53.72 | 0.028 | 1.499 | 0.999 | −0.054 | 13.600 |
| 5 | 52.42 | 0.055 | 1.534 | 0.932 | −0.079 | 13.787 | 52.45 | 0.055 | 1.534 | 0.932 | −0.079 | 13.788 |
| 6 | 51.67 | 0.063 | 1.522 | 0.921 | −0.086 | 13.988 | 51.70 | 0.063 | 1.523 | 0.921 | −0.086 | 13.989 |
| 8 | 50.76 | 0.076 | 1.562 | 0.915 | −0.097 | 14.162 | 50.80 | 0.076 | 1.564 | 0.915 | −0.097 | 14.162 |
| 10 | 50.26 | 0.047 | 1.521 | 1.036 | −0.070 | 14.175 | 50.30 | 0.047 | 1.523 | 1.036 | −0.070 | 14.175 |
| 15 | 49.82 | 0.026 | 1.592 | 1.205 | −0.057 | 13.915 | 49.85 | 0.026 | 1.592 | 1.205 | −0.057 | 13.914 |
Equivalent atomic number (Zeq) and G-P exposure buildup factors (EBF) for PWTN3 and PWTN4 glasses.
| Photon energy (MeV) | Zeq | PWTN3 | Zeq | PWTN4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | Xk | a | b | c | d | Xk | |||
| 0.015 | 30.36 | −0.244 | 1.002 | 1.836 | 0.207 | 11.332 | 30.38 | −0.243 | 1.002 | 1.834 | 0.207 | 11.334 |
| 0.02 | 32.26 | 0.551 | 1.454 | 0.656 | −0.760 | 11.504 | 32.26 | 0.551 | 1.455 | 0.657 | −0.759 | 11.506 |
| 0.03 | 32.69 | 0.174 | 1.867 | 0.596 | −0.105 | 18.508 | 32.69 | 0.174 | 1.868 | 0.596 | −0.105 | 18.515 |
| 0.04 | 42.70 | 0.089 | 3.906 | 0.407 | −0.041 | 23.649 | 42.60 | 0.089 | 3.911 | 0.395 | −0.040 | 23.608 |
| 0.05 | 43.46 | −0.200 | 3.183 | 0.127 | −0.002 | 12.912 | 43.58 | −0.191 | 3.189 | 0.134 | −0.006 | 12.982 |
| 0.06 | 43.73 | 0.841 | 2.533 | 0.057 | −0.127 | 14.615 | 43.85 | 0.824 | 2.540 | 0.061 | −0.125 | 14.431 |
| 0.08 | 53.19 | 0.369 | 1.921 | 0.109 | −0.049 | 15.889 | 53.24 | 0.363 | 1.923 | 0.110 | −0.048 | 15.896 |
| 0.1 | 59.72 | 0.392 | 1.529 | 0.120 | −0.075 | 16.420 | 59.73 | 0.391 | 1.529 | 0.121 | −0.075 | 16.429 |
| 0.15 | 60.64 | 0.421 | 1.196 | 0.189 | −0.235 | 13.788 | 60.65 | 0.421 | 1.196 | 0.189 | −0.235 | 13.788 |
| 0.2 | 61.15 | 0.216 | 1.173 | 0.413 | −0.115 | 14.188 | 61.16 | 0.216 | 1.173 | 0.413 | −0.115 | 14.188 |
| 0.3 | 61.77 | 0.139 | 1.256 | 0.555 | −0.065 | 13.819 | 61.78 | 0.139 | 1.256 | 0.555 | −0.065 | 13.819 |
| 0.4 | 62.12 | 0.096 | 1.345 | 0.680 | −0.053 | 14.202 | 62.13 | 0.096 | 1.345 | 0.680 | −0.053 | 14.202 |
| 0.5 | 62.37 | 0.072 | 1.415 | 0.757 | −0.044 | 14.139 | 62.37 | 0.072 | 1.415 | 0.757 | −0.044 | 14.139 |
| 0.6 | 62.52 | 0.055 | 1.461 | 0.813 | −0.035 | 13.762 | 62.52 | 0.055 | 1.461 | 0.813 | −0.035 | 13.762 |
| 0.8 | 62.71 | 0.035 | 1.520 | 0.883 | −0.027 | 13.685 | 62.71 | 0.035 | 1.520 | 0.883 | −0.027 | 13.685 |
| 1 | 62.78 | 0.022 | 1.539 | 0.936 | −0.022 | 13.474 | 62.78 | 0.022 | 1.539 | 0.936 | −0.022 | 13.473 |
| 1.5 | 62.04 | 0.000 | 1.507 | 1.036 | −0.016 | 13.910 | 62.04 | 0.000 | 1.507 | 1.036 | −0.016 | 13.911 |
| 2 | 59.90 | 0.002 | 1.529 | 1.043 | −0.021 | 13.110 | 59.91 | 0.002 | 1.528 | 1.043 | −0.021 | 13.110 |
| 3 | 55.93 | 0.017 | 1.540 | 1.016 | −0.043 | 13.332 | 55.95 | 0.017 | 1.540 | 1.016 | −0.043 | 13.333 |
| 4 | 53.76 | 0.028 | 1.499 | 0.999 | −0.054 | 13.601 | 53.79 | 0.028 | 1.500 | 0.999 | −0.054 | 13.603 |
| 5 | 52.48 | 0.055 | 1.535 | 0.931 | −0.079 | 13.790 | 52.52 | 0.055 | 1.535 | 0.931 | −0.079 | 13.791 |
| 6 | 51.74 | 0.063 | 1.524 | 0.920 | −0.086 | 13.990 | 51.78 | 0.064 | 1.525 | 0.920 | −0.086 | 13.992 |
| 8 | 50.84 | 0.076 | 1.566 | 0.915 | −0.097 | 14.163 | 50.88 | 0.076 | 1.568 | 0.915 | −0.097 | 14.163 |
| 10 | 50.34 | 0.047 | 1.526 | 1.036 | −0.070 | 14.174 | 50.38 | 0.047 | 1.528 | 1.037 | −0.070 | 14.173 |
| 15 | 49.89 | 0.026 | 1.592 | 1.206 | −0.057 | 13.913 | 49.94 | 0.026 | 1.592 | 1.206 | −0.057 | 13.912 |
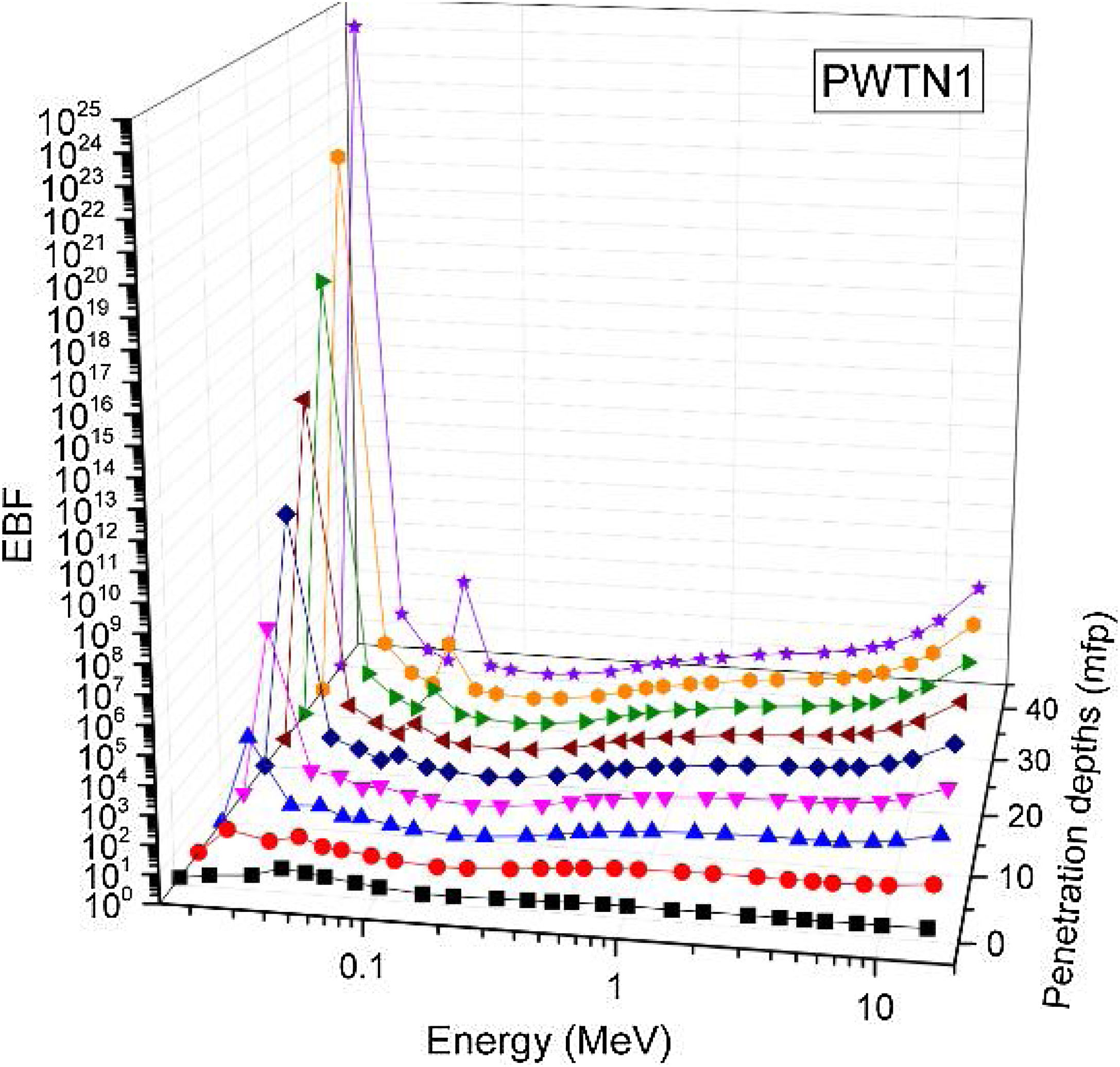
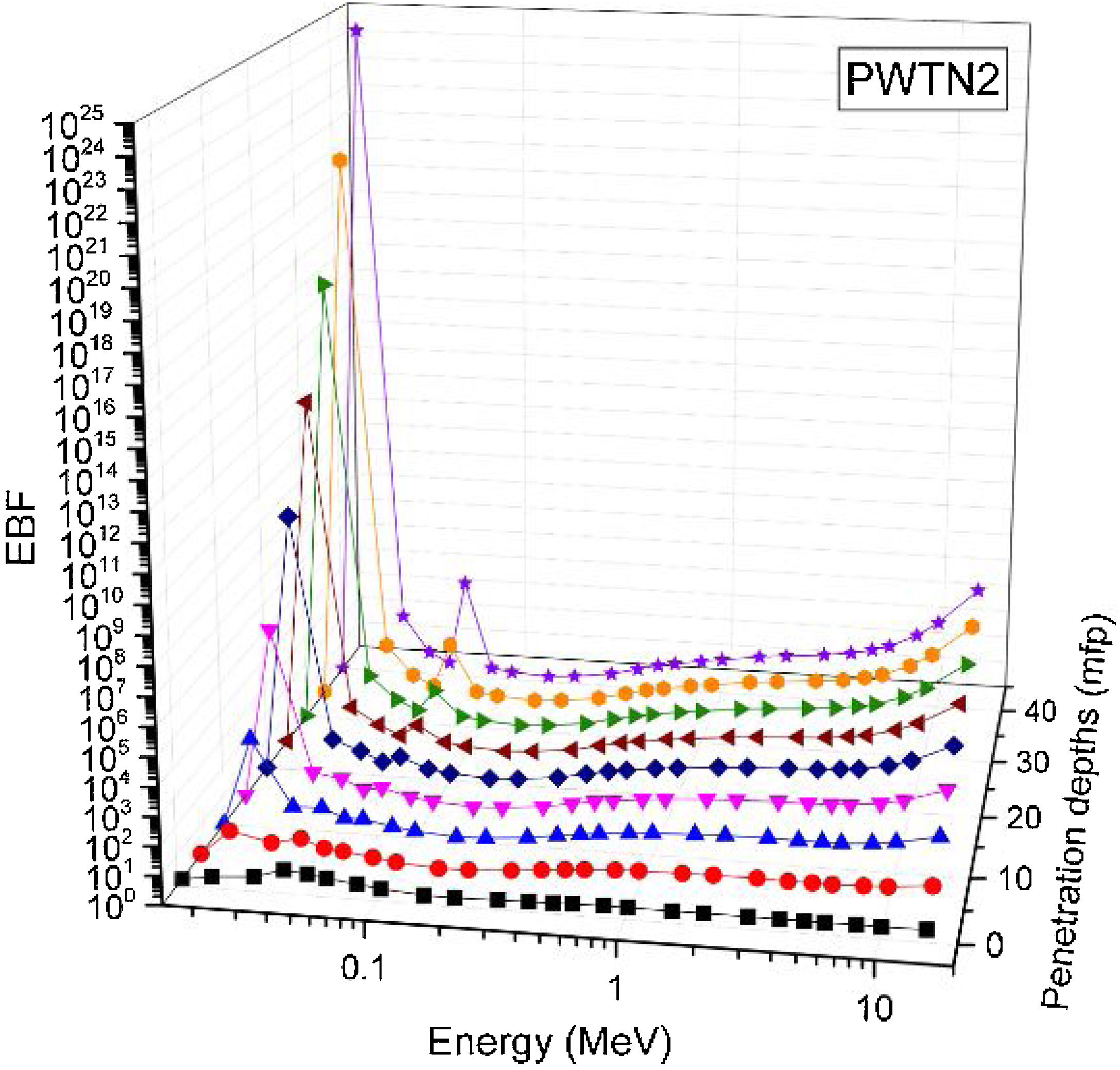
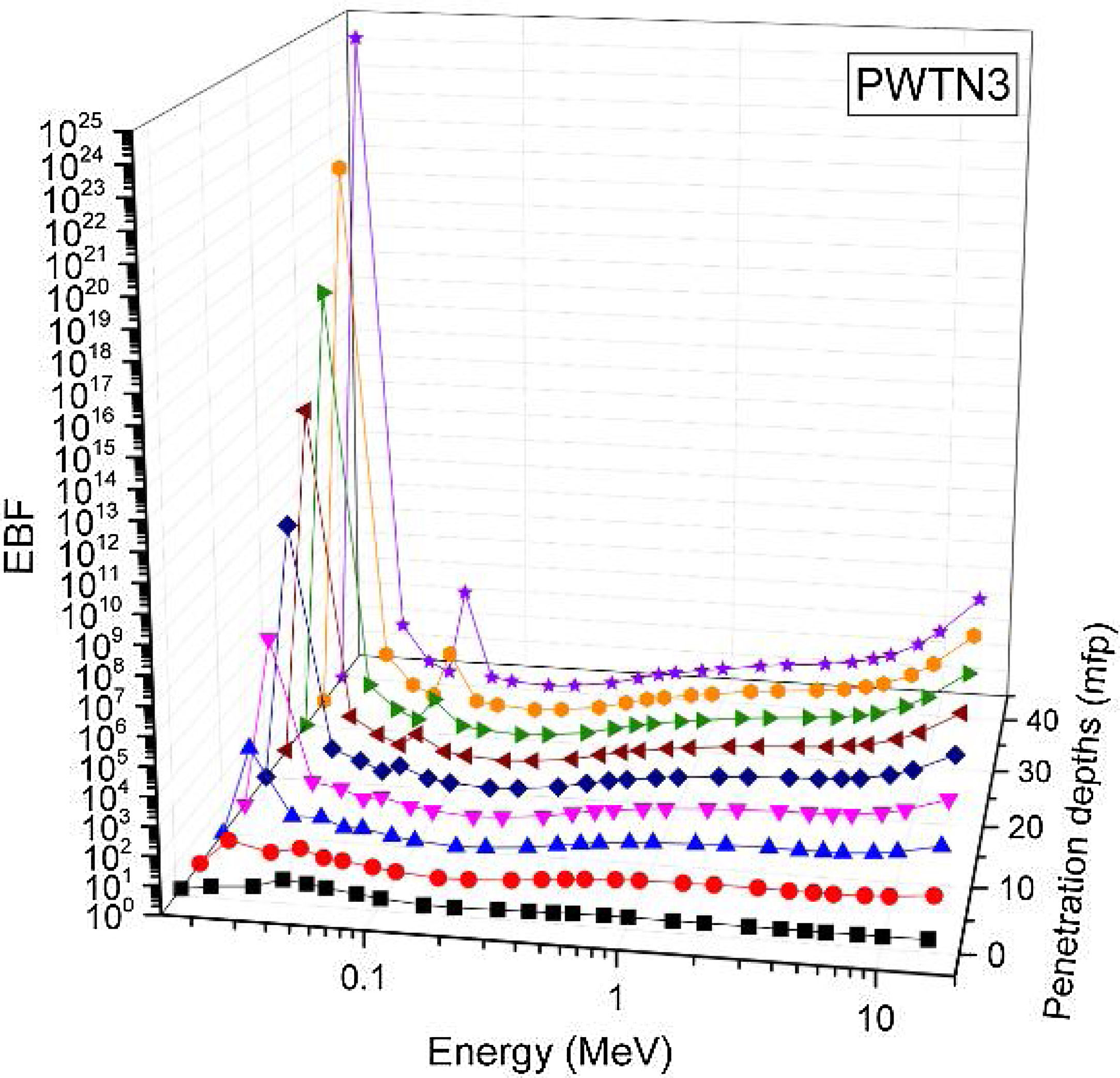
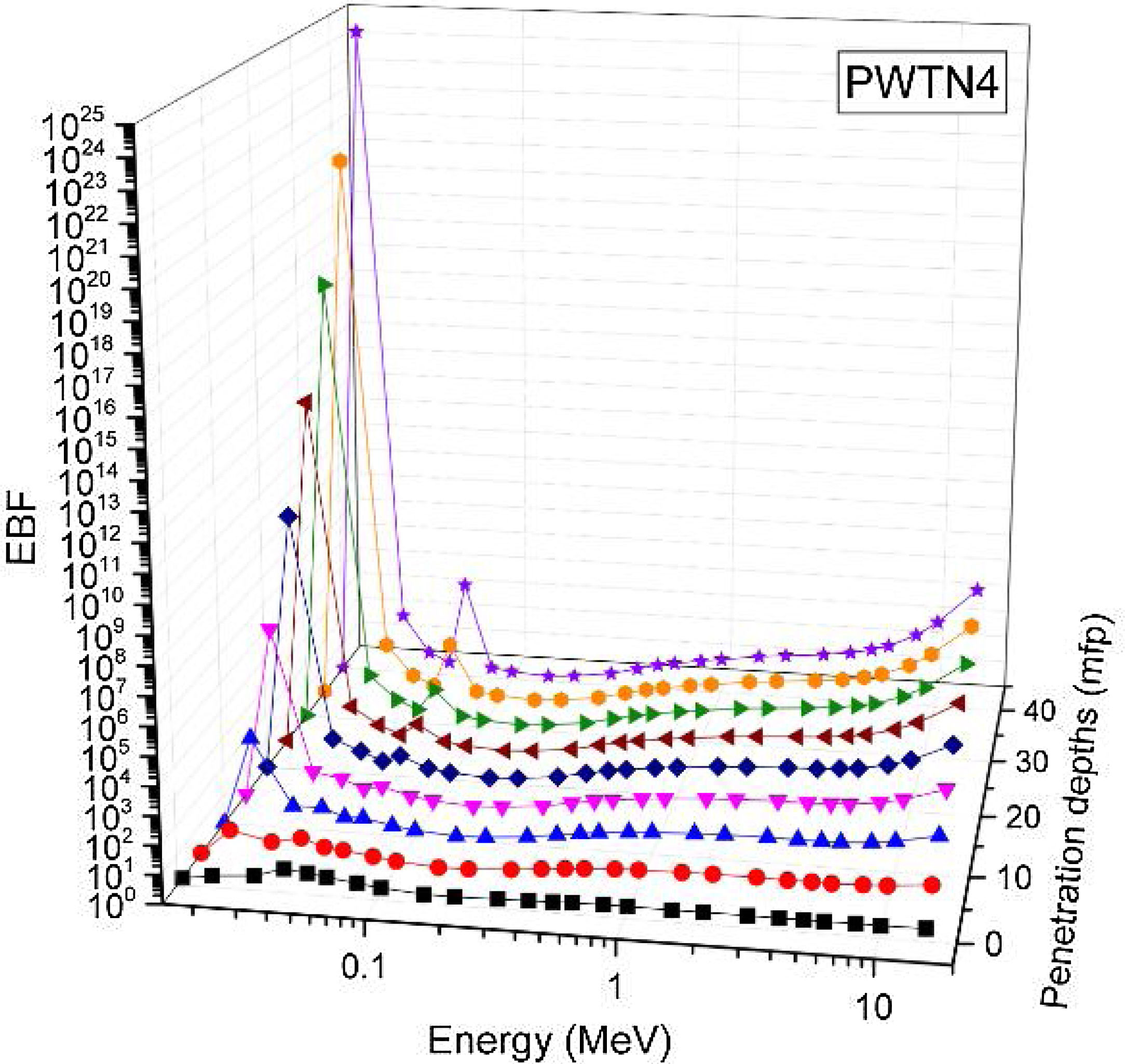
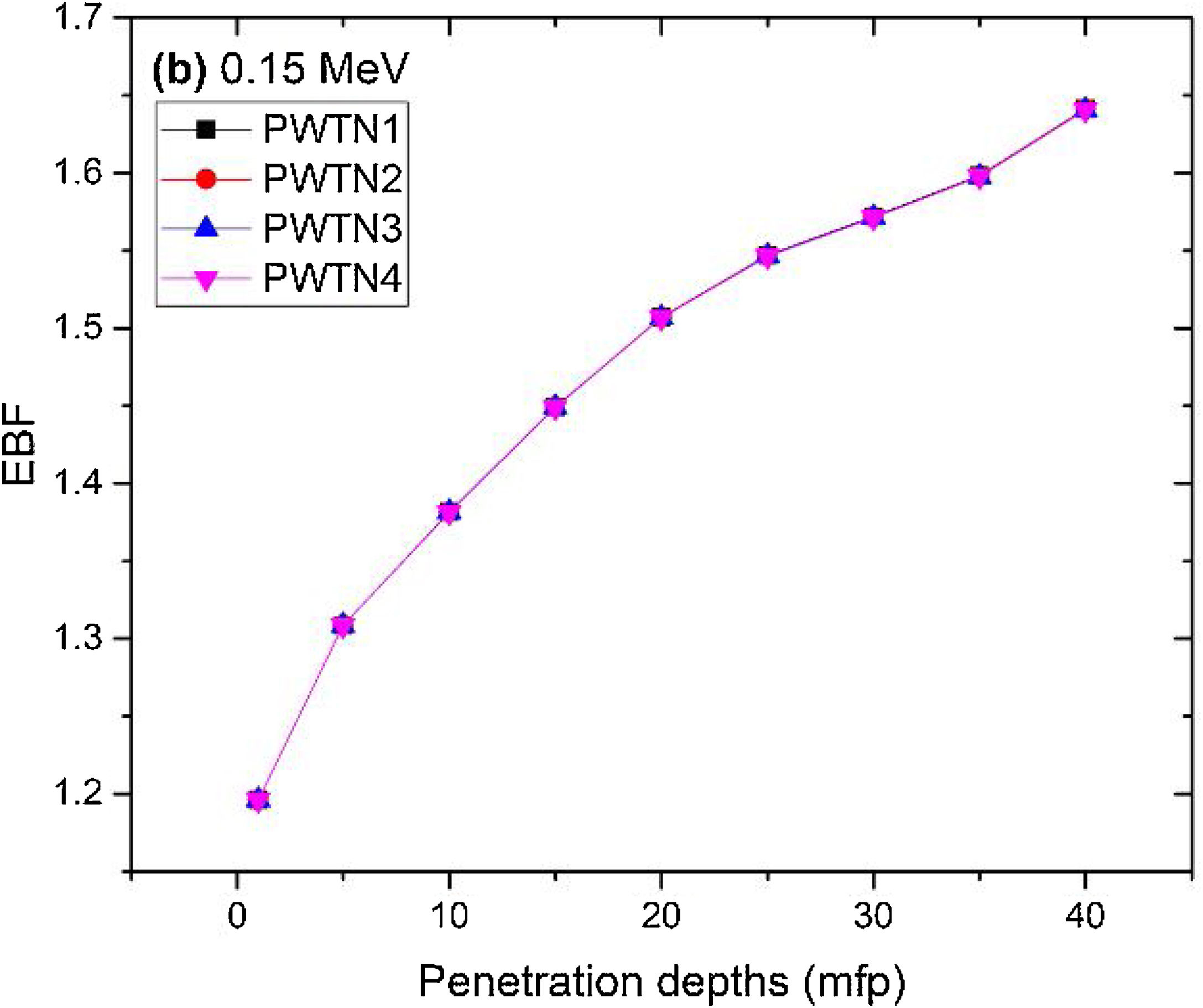
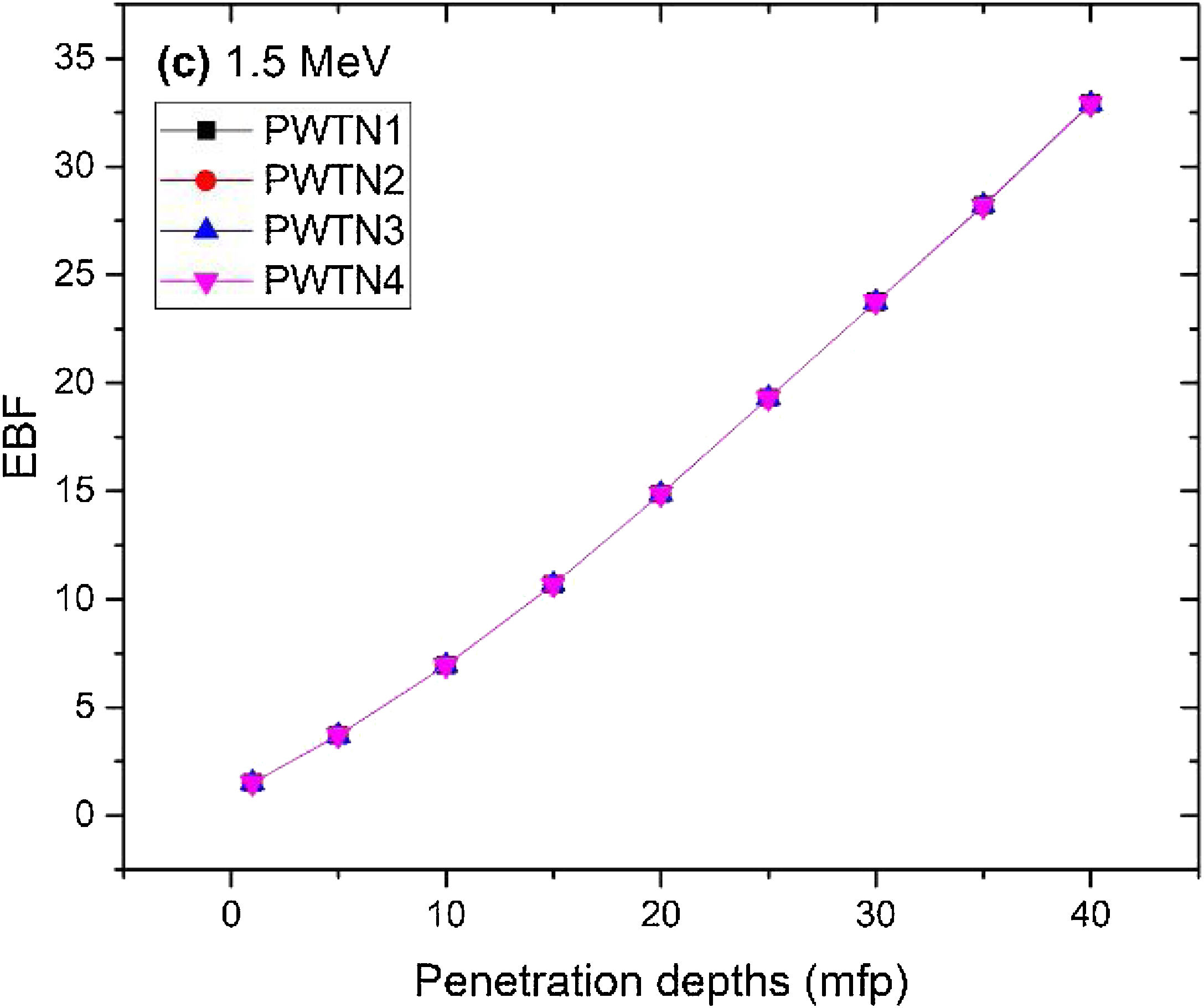
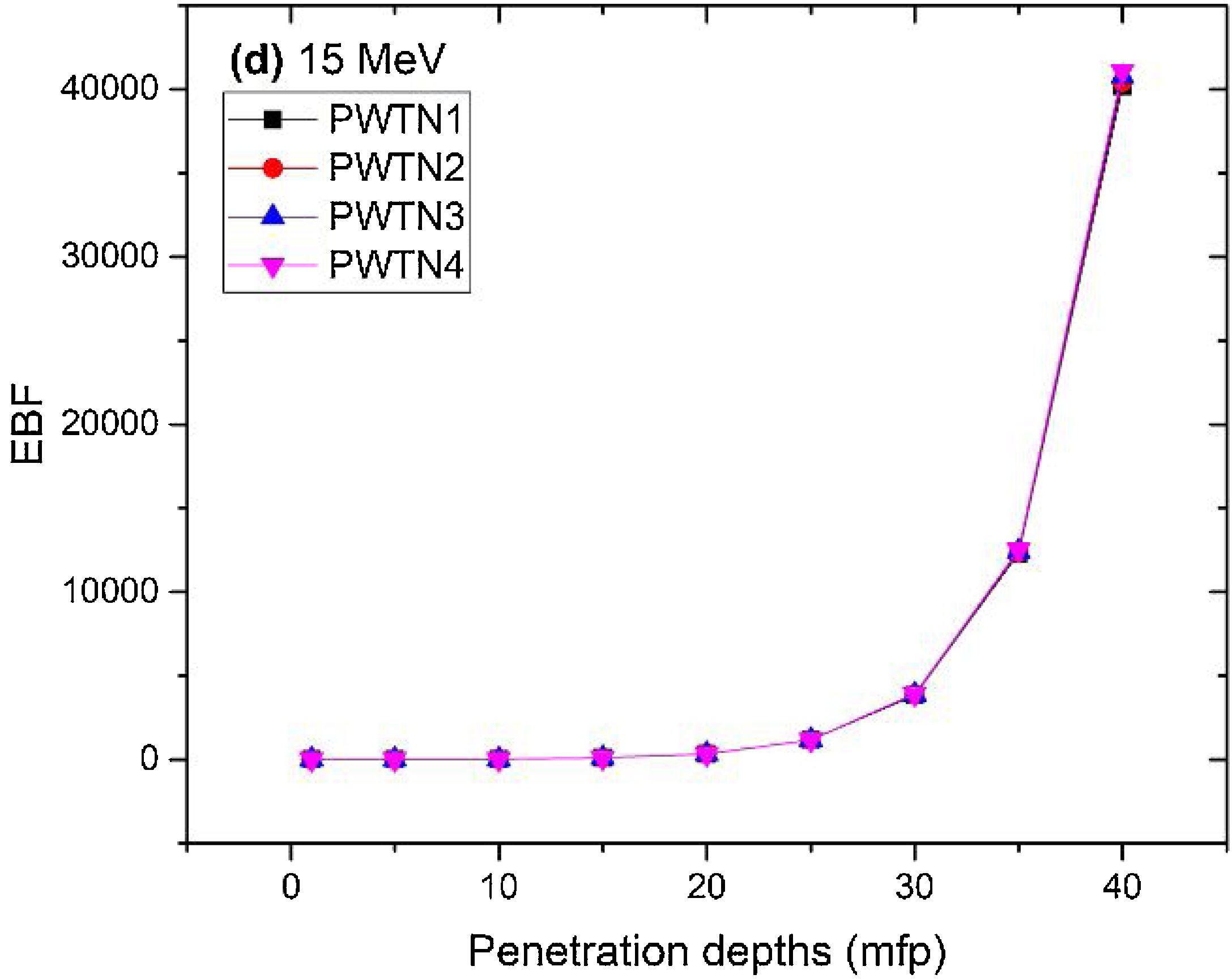
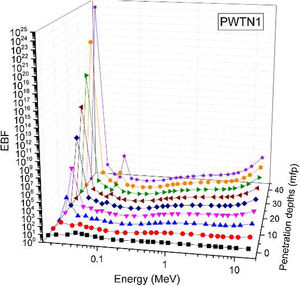
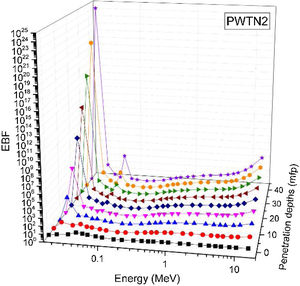
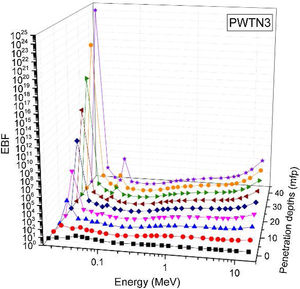
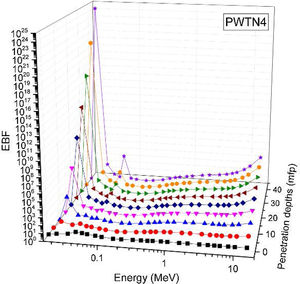
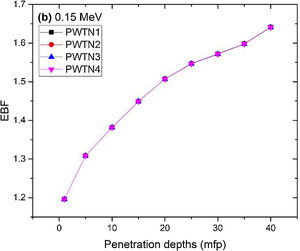
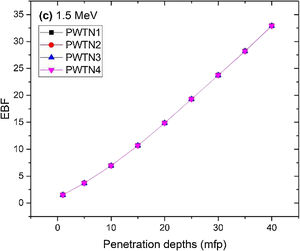
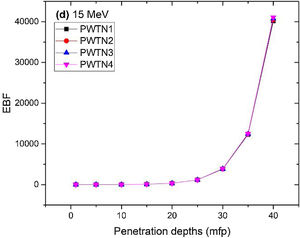
Figs. 8–11 show the variation of EBF with energy for the glasses at selected depths D (1≤D≤40 MFP) for each studied glass namely PWTN1 (Fig. 8), PWTN2 (Fig. 9), PWTN3 (Fig. 10), and PWTN4 (Fig. 11). The variations have similar features for all the glasses at corresponding D. Firstly, the EBF increases in intensity as D increases; the cross section for photon scattering increases with absorbers thickness as described by the equation [38]:
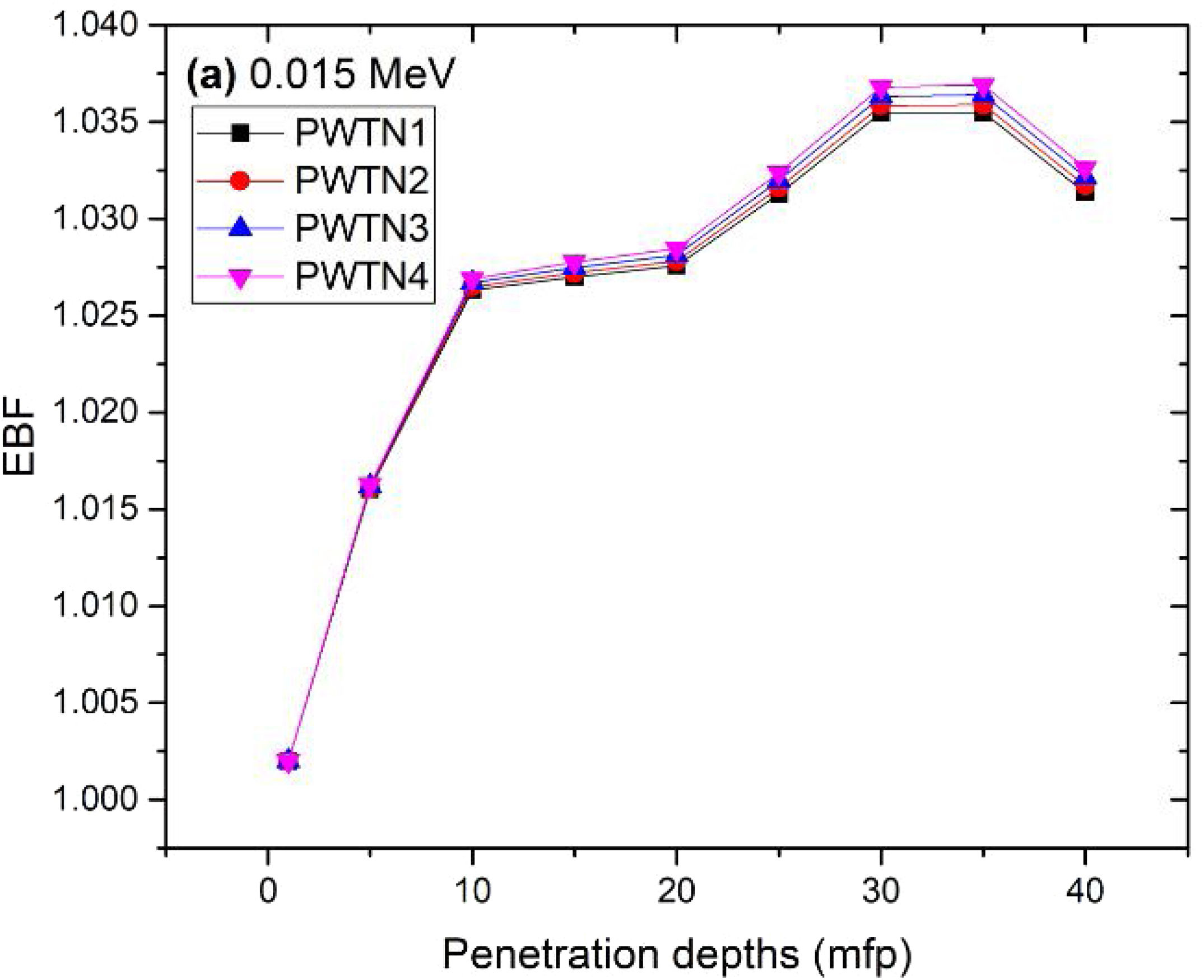
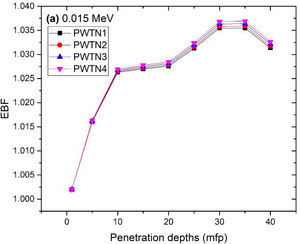
where, S and σc represent the ratio of scattered to transmitted photons and Compton scattering cross section for the absorber. Secondly, a spike appears on the EBF spectra for depths above 1mfp at 20keV and another at 60keV at depth greater than 20 MFP. These spikes could be due to de-excitation of L1- (Pb) and K-electrons (W) atoms. The absorption and de-excitation of atoms produce secondary photons and hence high EBF. Aside from the spikes on the spectra, EBF mostly increases with energy at depths greater than 1mfp; the partial photon processes (τ/ρ, σ/ρ and κ/ρ) are responsible for these observations.Figs 12–15 depict the EBF of the glasses at selected energies 0.015 (Fig. 12), 0.15 (Fig. 13), 1.5 (Fig. 14), and 15 MeV (Fig. 15). The growth in EBF with respect to glass thickness is clearly revealed in the figures. The figures also reveal that EBF of the glasses were almost equal, however at 15keV and at depth beyond 5 MFP, a slight increase in the value of EBF with increase in Nd2O3 concentration was noticed. The dependence of the photoelectric effect on effective atomic number is believed to be responsible for this observation as the increment trend is in consonance with that of Zeff relatively lower κ/ρ will ultimately produce higher EBF. Similar findings were observed in different glass systems elsewhere [39–44].
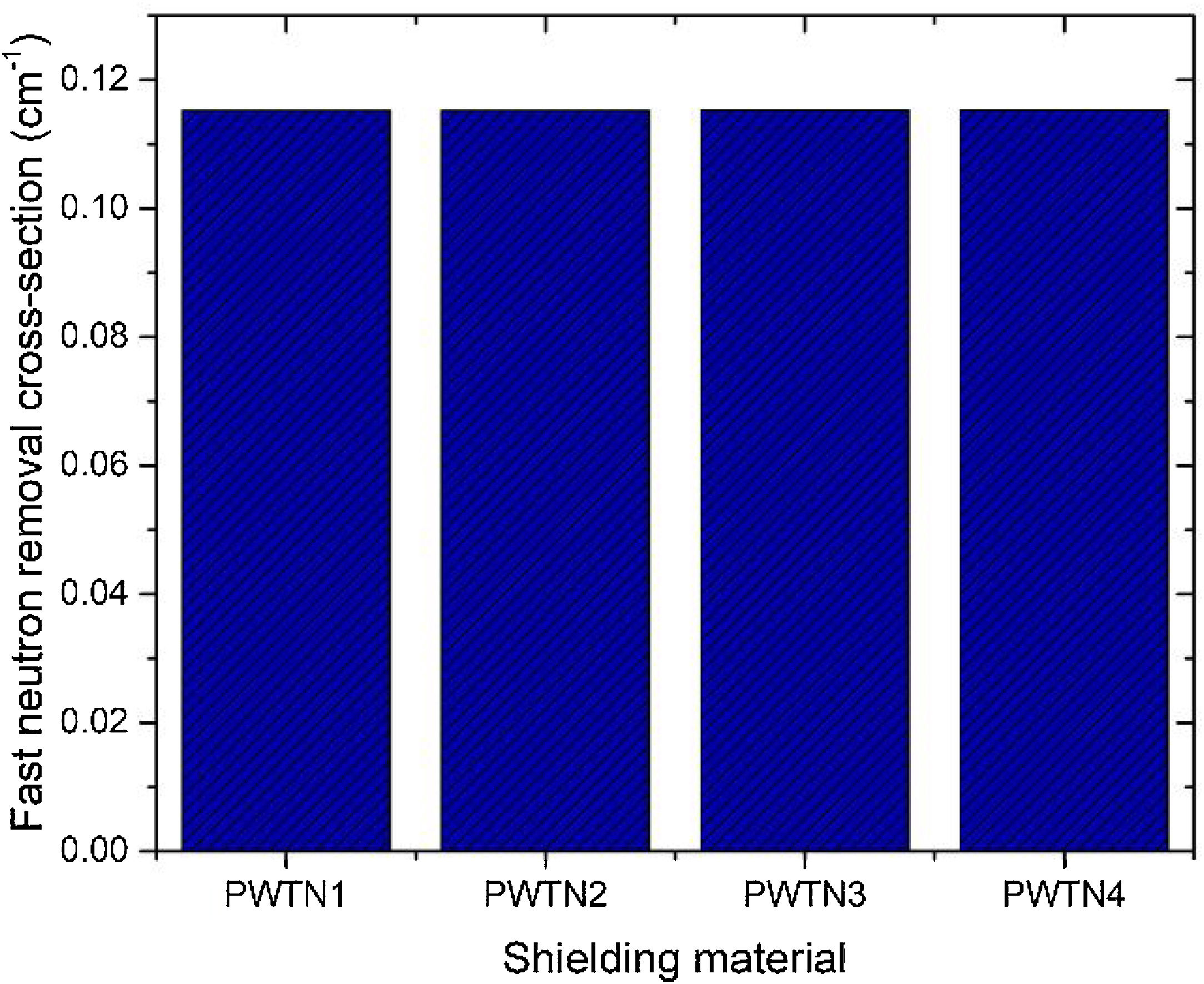
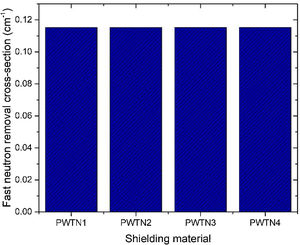
Fig. 16 depicts the fast neutron removal cross section (FNRCS) of the PWTN-glasses. Calculated values of FNRCS were 0.1152, 0.1152, 0.1153, and 0.1153cm−1 for PWTN1, PWTN2, PWTN3, and PWTN4 respectively. The slight increase in the FNRCS of the glasses as Nd2O3 content of the glasses increases can be attributed to the gradual increase in partial density of the Nd content relative to Te in the glasses. PWTN4 had the best fast neutron absorbing capacity compared to the other three PWTN glasses. The FNRCS of the present glasses are better than that of ordinary concrete (0.0937cm−1) [35].
ConclusionIn the current work, we reported on the radiation attenuation properties of 15PbF2–(60x)TeO2–25WO3–xNd2O3 (0.1≥x≥1.5) glasses for the nuclear shielding applications for mixed radiation fields at energies ranging from 15keV to 15MeV. A positive and significant effect of Nd3+ ions on gamma attenuation properties of the present glass system. The radiation attenuation features were investigated by using Geant4 MC simulation and the obtained results were theoretically approved by using Phy-X approach for each glass involved over the entire considered energy range. The results of the present work indicate that the μ/ρ varies from 72.511–0.0362, 72.586–0.0363, 72.679–0.0363, and 72.771–0.0363cm2g−1 as energy progresses from 15keV–15MeV for PWTN1–PWTN4 respectively. Moreover, the values of Zeff and Neff were both highest in the in the τ/ρ dominated energies due to the atomic number dependence of the cross sections of the τ/ρ absorption processes. Moreover, FNRCS values were 0.1152, 0.1152, 0.1153, and 0.1153cm−1 for PWTN1, PWTN2, PWTN3, and PWTN4 respectively. Finally, an extensive comparative study is also presented between the studied glass system and standard traditional shielding materials. The study suggests PWTN4 is the best photon shield amongst the studied PWTN-glasses.
The authors extend their appreciation to the Deanship of Scientific
Research at King Khalid University, Saudi Arabia for funding this work
through Research Groups Program under grant number R.G.P.1/237/42.