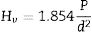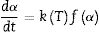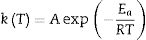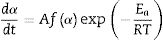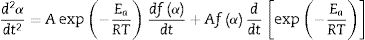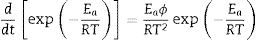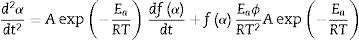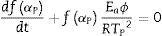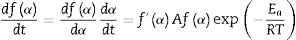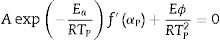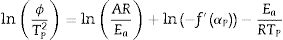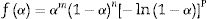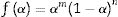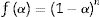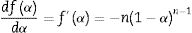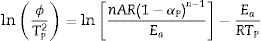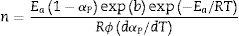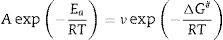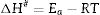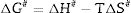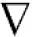Microstructure, thermal expansion, hardness and thermodynamic parameters of cordierite materials synthesized from Algerian natural clay minerals and magnesia

Abstract

Low-cost, dimensionally stable, and hard cordierite ceramic materials were prepared by reaction sintering two Algerian natural clay minerals and synthetic magnesia. The microstructure and hardness of the developed materials were characterized by a scanning electron microscope and a hardness tester, respectively. Differential thermal analysis, dilatometry, and Raman spectroscopy were used to analyze the transformation of phases and sintering behavior. The coefficient of thermal expansion (α) was determined from dilatometry experiments. The microstructure of DT00M sample synthesized from stoichiometric powder mixture (clay minerals and synthetic magnesia) consisted of cordierite only. Whereas cordierite, magnesium silicate, and sapphirine phases were present in DT04M and DT08M samples prepared from non-stoichiometric powder mixtures containing excess magnesia of 16 and 20 wt.%, respectively. The values of the activation energy (E_a) and frequency factor (A), for cordierite crystals, varied from 577 to 951 kJ/mol, and 1.54 × 10¹⁸ to 1.98 × 10³⁰ S⁻¹, respectively. The kinetic parameter n for the formation of cordierite had values between 2 and 3. While the Gibbs free energy (ΔG^#), enthalpy (ΔH^#), and entropy (ΔS^#) values were found to be in the range 431–483 kJ/mol, 564–938 kJ/mol, and 70–313 J/mol, respectively. Samples sintered at 1300 °C for 2 h showed higher values of hardness compared with those sintered at 1250 °C. The DT04M sample had the highest hardness value of 9.45 GPa, demonstrating an increase of 12.5% with respect to monolithic cordierite (DT00M). In the temperature range 100–1300 °C, DT04M and DT08M samples showed better dimensional stability compared to monolithic cordierite. The DT08M sample showed the lowest thermal expansion (α = 2.32 × 10⁻⁶/°C), demonstrating a decrease of 31.3% with respect to monolithic cordierite.

Resumen

Se prepararon materiales cerámicos de cordierita duras, de bajo costo y dimensionalmente estables mediante reacción sinterizando dos minerales arcillosos naturales de arcilla y magnesia sintética. La microestructura y la dureza de los materiales desarrollados se caracterizaron por un microscopio electrónico de barrido y un probador de dureza, respectivamente. Se utilizaron análisis térmicos diferenciales, dilatometría y espectroscopía Raman para analizar la transformación de fases y el comportamiento de sinterización. El coeficiente de expansión térmica (α) se determinó a partir de experimentos de dilatometría. La microestructura de la muestra DT00M sintetizada a partir de una mezcla de polvo estequiométrico (minerales arcillosos y magnesia sintética) consistió únicamente en cordierita. Mientras que las fases cordierita silicato de magnesio y safirina estaban presentes en las muestras DT04M y DT08M preparadas a partir de mezclas de polvo no estequiométricas que contenían un exceso de magnesia del 16 y 20% en peso, respectivamente. Los valores de la energía de activación (E_a) y el factor de frecuencia (A), para cristales de cordierita, variaron de 577 a 951 kJ/mol, y 1,54 × 10¹⁸ a 1,98 × 10³⁰ S^-1, respectivamente. El parámetro cinético n para la formación de cordierita tenía valores entre 2 y 3. Mientras que los valores de energía libre de Gibbs (ΔG^#), entalpía (ΔH^#) y entropía (ΔS^#) se encontraron en el rango 431-483 kJ/mol, 564-938 kJ/mol y 70-313 J/mol, respectivamente. Las muestras sinterizadas a 1.300 °C durante 2 h mostraron mayores valores de dureza en comparación con las sinterizadas a 1.250 °C. La muestra DT04M tuvo el mayor valor de dureza de 9,45 GPa, lo que demuestra un aumento del 12,5% con respecto a la cordierita monolítica (DT00M). En el rango de temperatura de 100-1.300 °C, las muestras DT04M y DT08M mostraron una mejor estabilidad dimensional en comparación con la cordierita monolítica. La muestra DT08M mostró la expansión térmica más baja (α = 2,32 × 10^-6 °C^-1), lo que demuestra una disminución del 31,3% con respecto a la cordierita monolítica.

Introduction

Cordierite ceramics [1], whether in the form of monolithic cordierite [2] or materials based on cordierite [3], have achieved outstanding technological importance. As one of the main phases of the magnesia-alumina-silica system, cordierite has values of 2.53 g/cm³, 1470 °C, and >10¹² Ω cm for its density, melting temperature, and electrical resistivity, respectively. Additionally it has very low thermal expansion and conductivity [4–7]. Furthermore, it possesses satisfactory mechanical characteristics and is very stable in harsh environments [4,5]. Because of these attributes, cordierite materials are widely used in several industries [4–7]. They are candidate materials for packaging and thermal insulation applications [7]. Moreover, they are very suitable for making turbine heat exchanger components or supports for catalysts in the automotive industry [4–6]. Due to the unavailability of cordierite as natural material [8], it is usually prepared from diverse raw and/or waste materials using many methods [8–17]. However, reaction sintering abundant natural clay minerals or waste [4,7,18–24] remained the preferred way to produce unexpansive cordierite materials. Intentionally, additives such as nickel dioxide [25], zinc [26], phosphorous and boron oxides [27], phosphorous oxide [28], ceria [29], nickel dioxide and titania [30], barium oxide [31], magnesia [32,33], and calcium oxide [8,34–37] are added to facilitate sintering and ease cordierite production.

The formation of cordierite and phase transformation kinetics in cordierite materials [8,25–31,38–41] were characterized by differential thermal analysis [28–31,38,39], differential scanning calorimetry [8,39,40], and X-ray diffraction [8,25–27]. Non-isothermal [8,25,28–31,38–41] and isothermal [25–27,35] experiments were carried out and activation energy values from 170 to 964 kJ/mol were obtained [2,3,8,25–31,38–43]. The large variation in the obtained activation energies was attributed to the: “(i) nature and composition of precursors used to obtain cordierite, (ii) type of processes used to synthesize cordierite, (iii) conditions under which cordierite forms i.e. isothermal or non-isothermal, and (iv) presence of sintering aids to facilitate the formation of cordierite” [3]. Phase transformations [44], microstructural changes [1,45,46], and properties [44,47–51] of cordierite ceramic materials were found to largely dependent on the above factors. Therefore, extensive research work has been devoted to the enhancement of the mechanical and functional properties of cordierite ceramics through appropriate processing and microstructure design. Recently, the authors synthesized low-cost stoichiometric [2] and non-stoichiometric [3] cordierite ceramic materials, by reaction sintering Algerian natural clay minerals and synthetic magnesia, and studied the effect of temperature and MgO on cordierite formation. In this study, the influence of MgO on the microstructure, coefficient of thermal expansion, and hardness of the developed materials will be investigated. DTA, dilatometry, and Raman spectroscopy will be used for further analysis of the transformation of phases and sintering behavior. The frequency factor (A), the kinetic parameter n, and thermodynamic parameters (ΔG^#, ΔH^#, and ΔS^#) for the formation of cordierite will be determined.

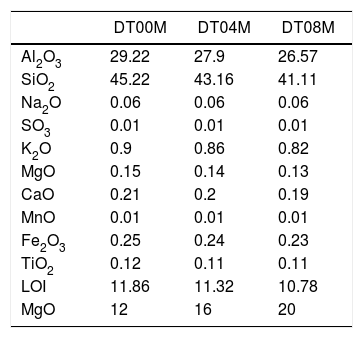
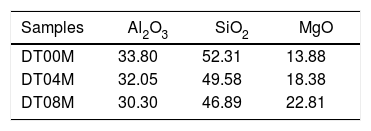
Materials and methods

Materials and experimental methods

Three powder mixtures of DD1 kaolin, TK kaolin, and magnesia were used to synthesize stoichiometric and non-stoichiometric cordierite ceramics. The chemical composition of the three prepared powders (in weight percent) is given in Table 1. The approach used to develop cordierite materials was presented in previous works, where the chemical composition of the two kaolinite materials was reported [2,3]. The first mixture contains 12 wt.% of MgO (to obtain monolithic cordierite) will be named DT00M sample. The second mixture contains 16 wt.% of MgO (i.e. stoichiometric cordierite containing extra 4 wt.% of MgO) will be named DT04M sample. The third mixture contains 20 wt.% of MgO (i.e. stoichiometric cordierite containing extra 8 wt.% of MgO) will be named DT08M sample. Table 2 shows the chemical composition of the three powder mixtures. The water and impurities present in the raw materials were neglected in order to know the percentage of Al₂O₃, SiO₂, and MgO basic oxides, in the ternary phase diagram, that make up the three powders. From the table it is clear that the DT00M sample (33.8 wt.% Al₂O₃, 52.31 wt.% SiO₂, 13.88 wt.% MgO) has the closest chemical composition to the stoichiometric composition of typical cordierite (34.8 wt.% Al₂O₃, 51.4 wt.% SiO₂, 13.8 wt.% MgO). Milling time of 5 h, sintering time of 2 h, and sintering temperature ranging from 900 to 1350 °C were selected as detailed elsewhere [2,3].

Table 1.

The chemical composition (wt.%) of the prepared powders.

	DT00M	DT04M	DT08M
Al2O3	29.22	27.9	26.57
SiO2	45.22	43.16	41.11
Na2O	0.06	0.06	0.06
SO3	0.01	0.01	0.01
K2O	0.9	0.86	0.82
MgO	0.15	0.14	0.13
CaO	0.21	0.2	0.19
MnO	0.01	0.01	0.01
Fe2O3	0.25	0.24	0.23
TiO2	0.12	0.11	0.11
LOI	11.86	11.32	10.78
MgO	12	16	20

Table 2.

The chemical composition (wt.%) of the three powders without water and impurities.

Samples	Al2O3	SiO2	MgO
DT00M	33.80	52.31	13.88
DT04M	32.05	49.58	18.38
DT08M	30.30	46.89	22.81

Characterization methods

TG and DTA non-isothermal measurements were carried out on, the prepared samples, from room temperature to 1400 °C (at 10, 20, 30, 40, and 50 °C/min) using SETARAM equipment (LABSYS EVO DTA/DSC-TG). Activation energies were determined from DTA results using Kissinger method as reported elsewhere [2,3]. The coefficient of thermal expansion (α) of samples (sintered for 2 h at 1350 °C) was determined from dilatometry experiments carried out at 5 °C/min using a NETZSCH dilatometer model Dil 402C. Raman spectroscopy analysis was performed using BRUKER SENTERRA apparatus. JEOL scanning electron microscope (model JSM-7001F) and MRD PANalytical diffractometer (ISM) were used to characterize the formed phases and analyze the microstructure. The prepared samples were indented by a Zwick-Roell hardness tester and the microhardness was calculated using the following equation.

where “P is the applied load (in N) and d is the diagonal length (in mm). Values for the reported hardness were the average of 10 readings. A load of 500 g and a dwell time of 10 s were used” [24].

Calculation methods

Kinetics of the processes in condensed phase is often described by the so-called general rate equation signifying the reaction rate dα/dt as a product of two mutually independent functions [52–54]:

where α is the fractional conversion, f(α) is the function of α which represents the reaction mechanism known as the “kinetic model”, k(T) is the rate constant at temperature T, which mostly takes the Arrhenius equation form [54]:

where A represents the pre-exponential factor or frequency factor, E_a is the activation energy, R is the gas constant and T is the absolute temperature.

If Eq. (2) is combined with Eq. (1) and rearranged, then we will get the following Eq. (3)[54]:

The second differential of Eq. (3) is as follow [54,55]:

Given the identity [55]:

where φ is known as the constant heating rate dT/dt[53,55], if Eq. (5) is combined with Eq. (4) and rearranged, then we get the following equation [55]:

At the peak maximum position (T = T_P and α = α_p), Eq. (6) is combined [55]:

where α_p is the fractional conversion (or so-called the degree of transformation [55]) reached for the temperature T_p, and Eq. (7) becomes [55]:

Given the identity:

If Eq. (9) is combined with Eq. (8) and rearranged we get [55]:

where f′(α) is the derivative form of f(α) [54], Solving for φ/T_p² and taking the natural logarithm, yields to:

From this equation, which represents the familiar Kissinger equation, the activation energy E_a and the frequency factor A may be determined from the known equation f(α). There are many forms of the conversion function, with their analytical expressions relying both on the shape of solid-state grains and on the intergranulary surface or bulk phenomena which have to be described. One of these forms is that of Sestak and Berggren [56], in most cases, unknown for solid state processes, generally being of the form [56–59]:

where m, n and P are constants [58] that depending on the combination of m, n, and p can represent a number of different reaction models [57]. However, only two kinetic parameters (m and n) are enough to describe any experimental curve (in our case to describe the thermal analysis). Thus, after eliminating the third exponential term in Eq. (12) (p = 0 in Eq. (12)), the final form will be [56,60]:

This form is so-called in literature as Sestak–Berggren SB (m,n) kinetic model, which is used specially in thermal analysis. This kinetic model with other models were used to determine: (i) the pre-exponential factor, (ii) the invariant activation energy, (iii) the true values of Sestak–Berggren exponents, m and n and to eliminate false compensation effects [56]. The kinetic exponents m and n are the constants related to the reaction mechanism. The function is often simplified so that m is set to zero and the remaining kinetic exponent n can be then considered as the reaction order. This leads to the following [61]:

Derivation of Eq. (14) leads to the following:

If Eq. (15) is combined with Eq. (11) and rearranged, then we get [61]:

Eq. (16) is a linear equation written in the form y = f(x) = ax + b. Where x = 1/T_p, a = E_a/R represents the slope and b = ln (nAR(1 − α_p)ⁿ⁻¹)/E_a) represents the y-intercept of the graph y = f(x). From Eq. (16), n is calculated using the following expression [61]:

After the kinetic parameters E and A are determined, the thermodynamic parameters of activation can be expressed by the following equations [55,62]:

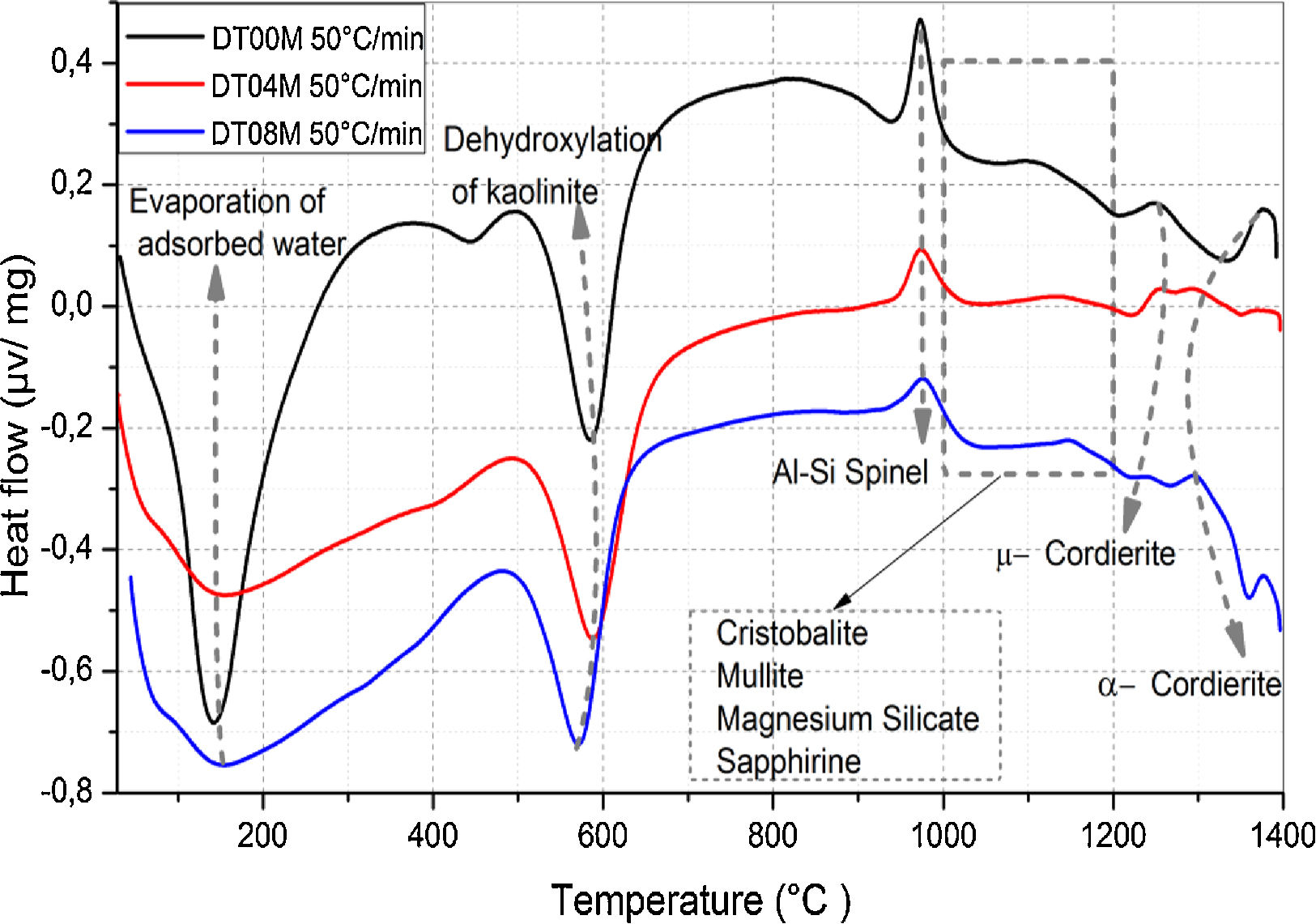
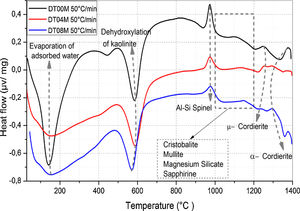
where ΔG^#, ΔH^# and ΔS^# are the Gibbs free energy, enthalpy, and entropy, respectively. υ = K_BT/h. where K_B is the Boltzmann constant and h is Plank constant.

Results and discussion

DTA and dilatometry

Typical DTA curves for DT00M, DT04M, and DT08M powders, heated from room temperature to 1400 °C at 50 °C/min, are presented in Fig. 1. The endothermic peaks in the 50–320 and 500–700 °C temperature ranges are associated with the evaporation of adsorbed water and transformation of kaolinite to metakaolinite (dehydroxylation), respectively. The exothermic peaks in the 950–1050 and 1050–1200 °C temperature ranges are characteristic of spinel and various phases (cristobalite, mullite, and magnesium silicate). While the exothermic peaks occurring at 1200–1270 °C and 1270–1400 °C are due the μ and α allotropes of cordierite, respectively.

Fig. 1.

DTA curves of DT00M, DT04M, and DT08M powders at heating rate of 50 °C/min.

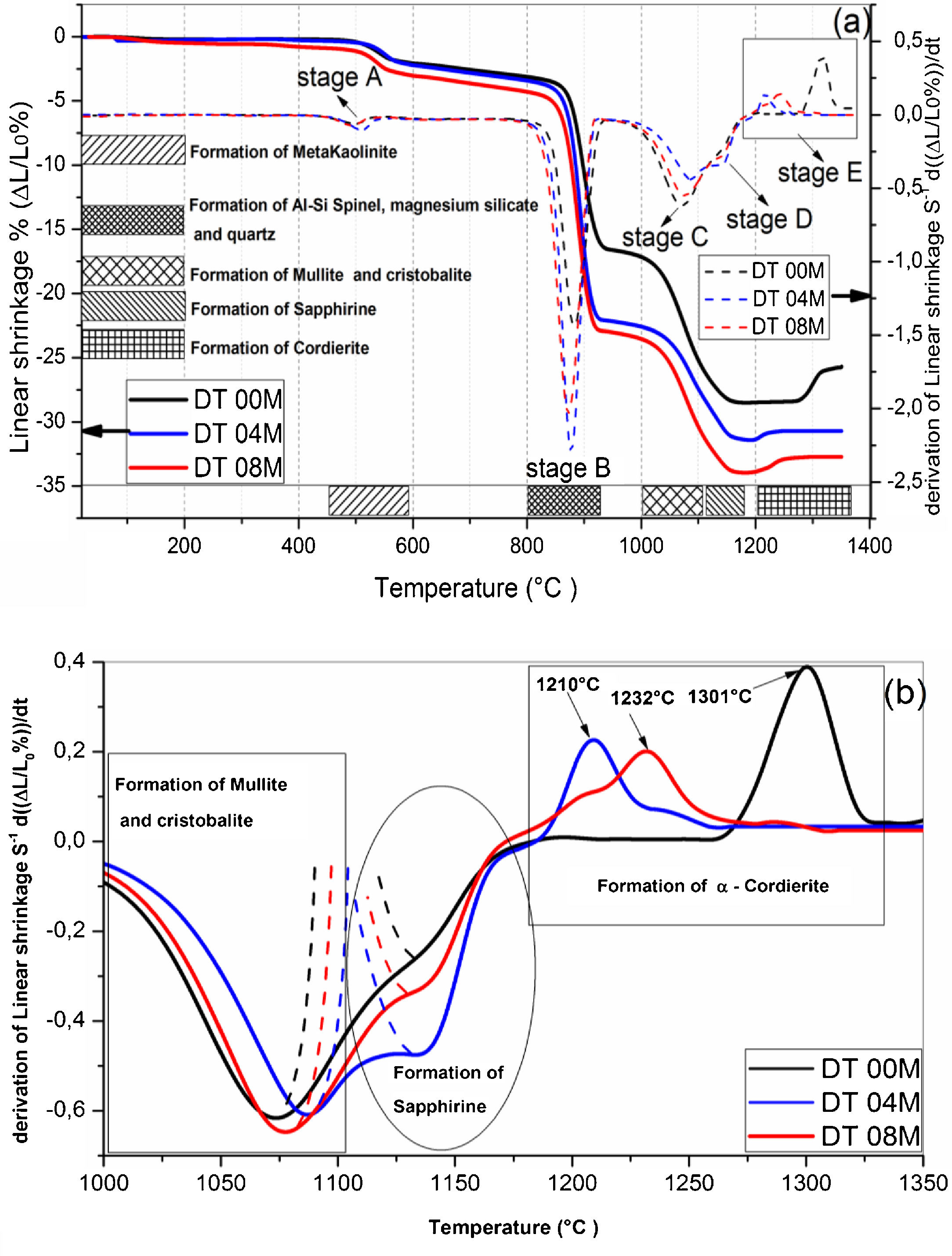
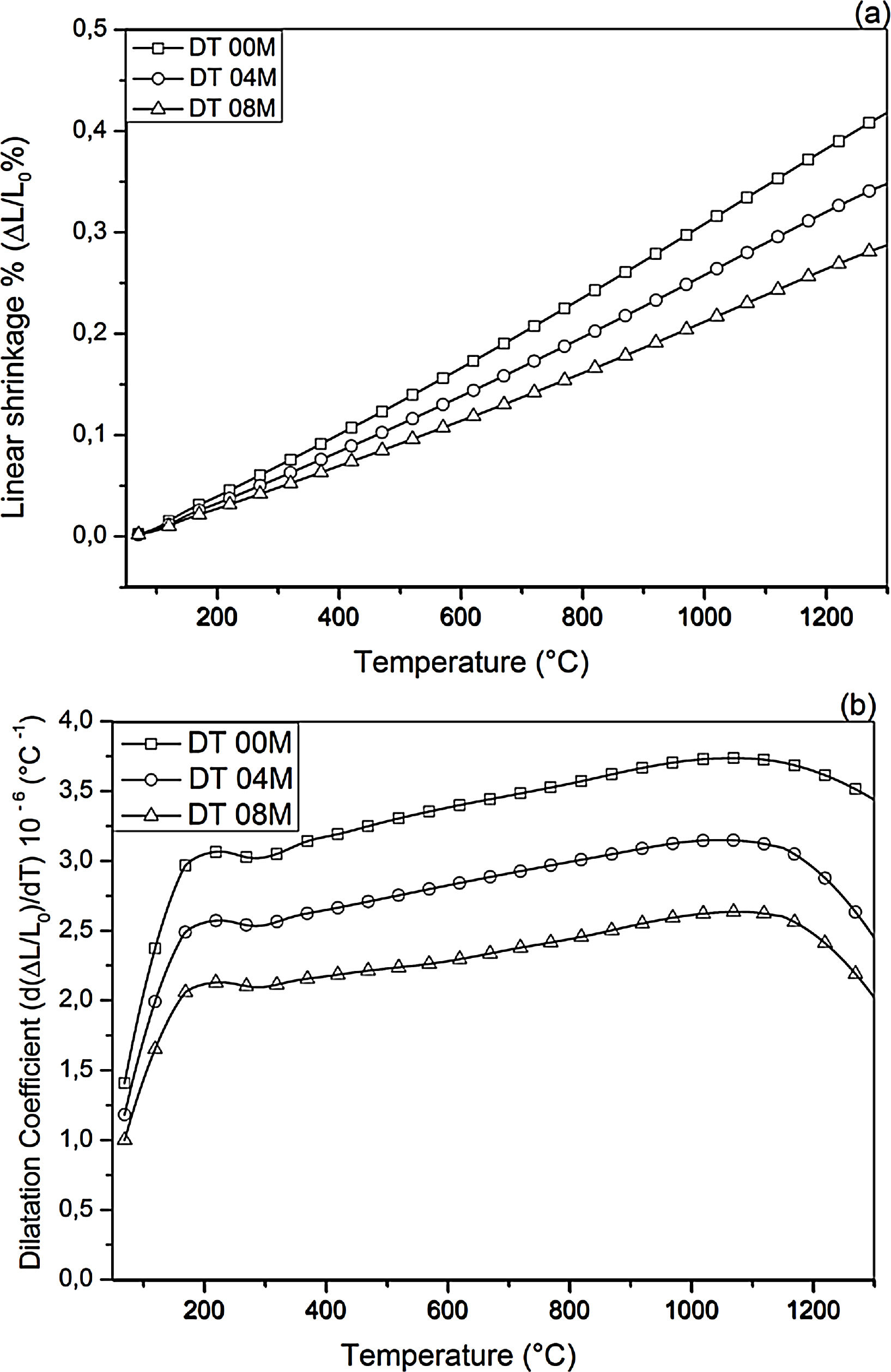
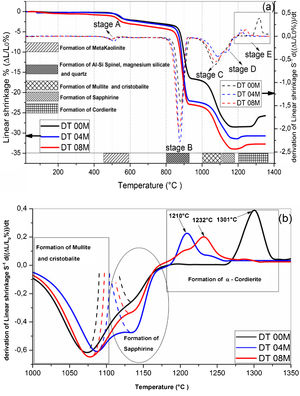
Fig. 2 shows linear shrinkage curves (a) and their first derivatives (b) for DT00M, DT04M, and DT08M samples heated at 5 °C/min to 1400 °C. Five stages labeled A, B, C, D, and E can be easily distinguished. The shrinkage in stage A, occurring at a temperature lower that 600 °C, is related to the transformation of kaolinite to metakaolinite (dehydroxylation). The shrinkage in stage B started at 800 °C and ended at 950 °C, with a maximum rate at 890 °C. This shrinkage is relatively large and is due to the formation of Al–Si spinel phase, magnesium silicate and quartz. As can be clearly seen in Fig. 2, the shrinkage in stage C started at 970 °C and ended at 1090 °C and is related to the formation of mullite and cristobalite. The rates of this shrinkage were maximum at 1072, 1086, 1076 °C for DT00M, DT04M, DT08M samples, respectively. Stage D is characterized with a small shrinkage associated with the formation of sapphirine between 1110 °C and 1171 °C. The expansion observed in stage E, between 1177 and 1362 °C, corresponds to the formation of cordierite in all samples. One can conclude that the extra MgO added to the samples resulted in the decrease of the temperature at which the rate of cordierite formation was maximum. This decrease was from 1301 °C (DT00M sample) to 1210 °C (DT04M) sample.

Fig. 2.

Dilatometry curves of DT00M, DT04M, and DT08M samples, (a) linear shrinkages and their derivatives, (b) enlarged view in the temperature range 1000–1350 °C.

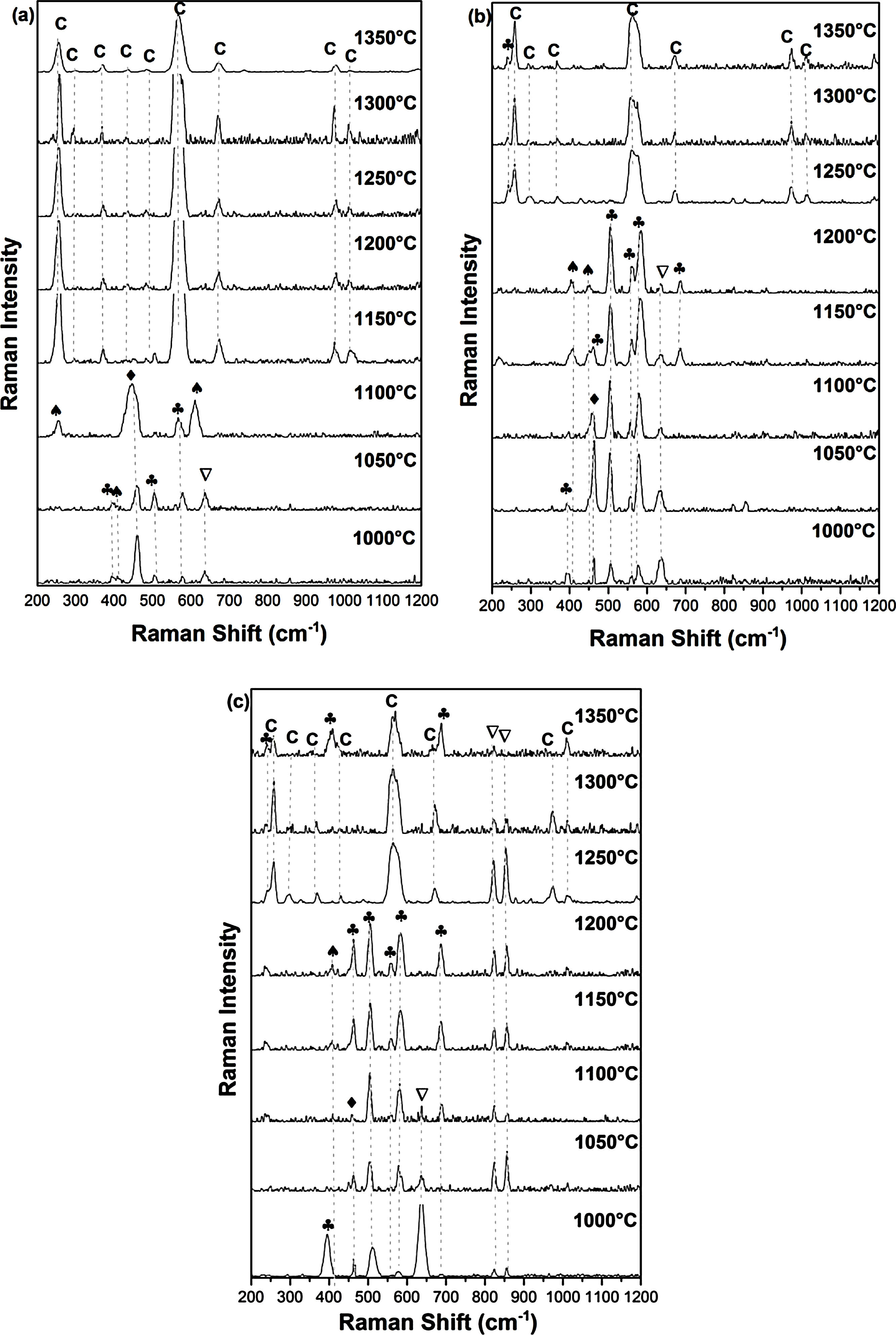
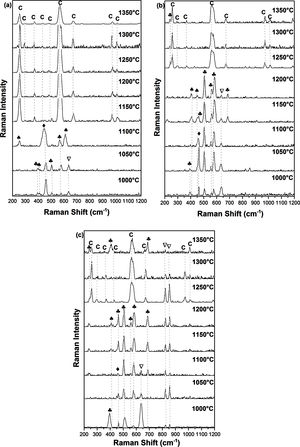
Raman spectroscopy and XRD

Fig. 3 shows Raman spectra of specimens sintered for 2 h at 1000, 1050, 1100, 1150, 1200, 1250, 1300, 1350 °C. For the DT00M sample sintered at 1000 and 1050 °C, peaks at 393, 507, and 580 cm⁻¹ are characteristic of sapphirine phase; and the peak at 643 cm⁻¹ is associated with magnesium silicate phase. While, peaks at 406 and 465 cm⁻¹ belongs to mullite and quartz, respectively. At 1100 °C, quartz (strong band at 465 cm⁻¹), mullite (strong bands also at 254 and 611 cm⁻¹) and sapphirine (medium intensity band at 580 cm⁻¹) are present. In the temperature range 1150–1350 °C, Raman bands of cordierite located at around 253, 292, 370, 435, 487, 565, 670, 975 and 1014 cm⁻¹ can be clearly seen in all the spectra.

Fig. 3.

Raman spectra of (a) DT00M, (b) DT04M, and (c) DT08M powders treated at different temperatures for 2 h. (

: Magnesium silicate,

: Quartz;

: Mullite,

: Sapphirine, C: Cordierite).

For the sample of DT04M sintered at 1000 and 1050 °C, the strong peaks at 461 cm⁻¹ and at 393, 507, 560, and 580 cm⁻¹, and the weak peaks at 406 and 445 cm⁻¹ and at 634 cm⁻¹ are due to the quartz, sapphirine, mullite and magnesium silicate, respectively. The peak at 393 cm⁻¹ characteristic of sapphirine disappeared from the spectrum of the specimen sintered at 1100 °C, however, the peak at 685 cm⁻¹ appeared in the spectrum of the specimen sintered at 1150 °C. The same Raman spectra were present in the spectrum of the specimen sintered at 1200 °C except one peak of sapphirine (band at 461 cm⁻¹) disappeared. Peaks of mullite disappeared from the spectra of the specimens sintered at 1250, 1300 and 1350 °C, and only cordierite peaks (bands at 253,292, 370, 565, 670, 975 and 1014 cm⁻¹) and sapphirine peak (medium intensity band at 237 cm⁻¹) were present. Although, XRD analysis showed the presence of magnesium silicate phase at high temperatures as discussed below, Raman spectra did not reveal this phase may be because of its volume fraction.

Raman peaks at 393, 507, 560, 580 and 685 cm⁻¹ present in the spectrum of DT08M sample sintered at 1000 °C are due to sapphirine. While peaks at 406 cm⁻¹, at 461 cm⁻¹ and at 634, 822 and 858 cm⁻¹ are associated with mullite, quartz and magnesium silicate, respectively. The peak at 393 cm⁻¹, characteristic of sapphirine, disappeared from the spectra of the specimens sintered at 1050 and 1100 °C. Another peak at 634 cm⁻¹, characteristic of mullite, disappeared from the spectra of the specimens sintered at 1150 and 1200 °C. The new bands at 237 cm⁻¹ and at 256, 292, 370,435, 565, 670, 975 and 1014 cm⁻¹ seen in the spectra of specimens sintered at 1250 and 1300 °C are associated with sapphirine and cordierite, respectively. The magnesium silicate peaks at 822 and 858 cm⁻¹ are still present. The new peaks seen at 410 and 685 cm⁻¹ in the spectrum of the specimen sintered at 1350 °C were attributed to sapphirine.

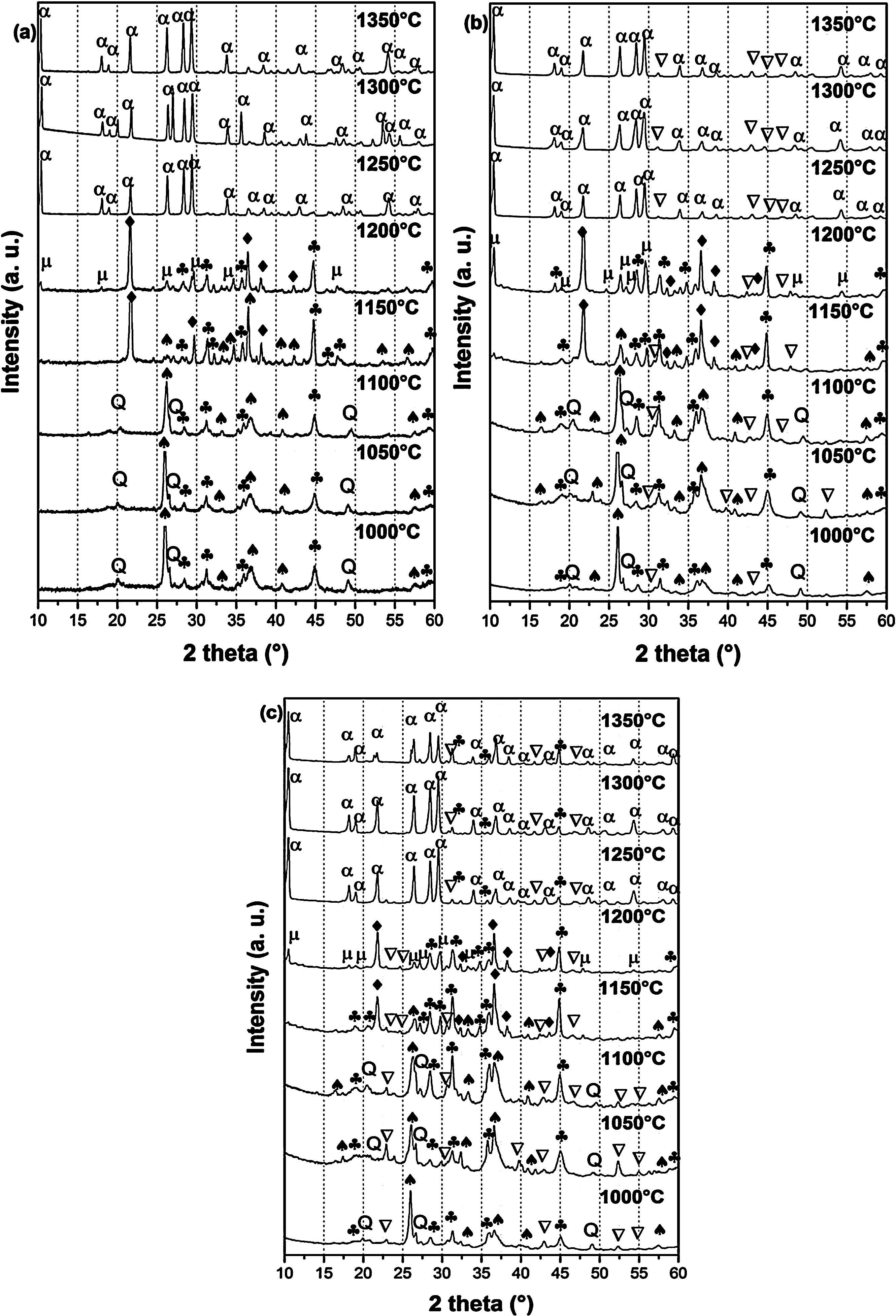
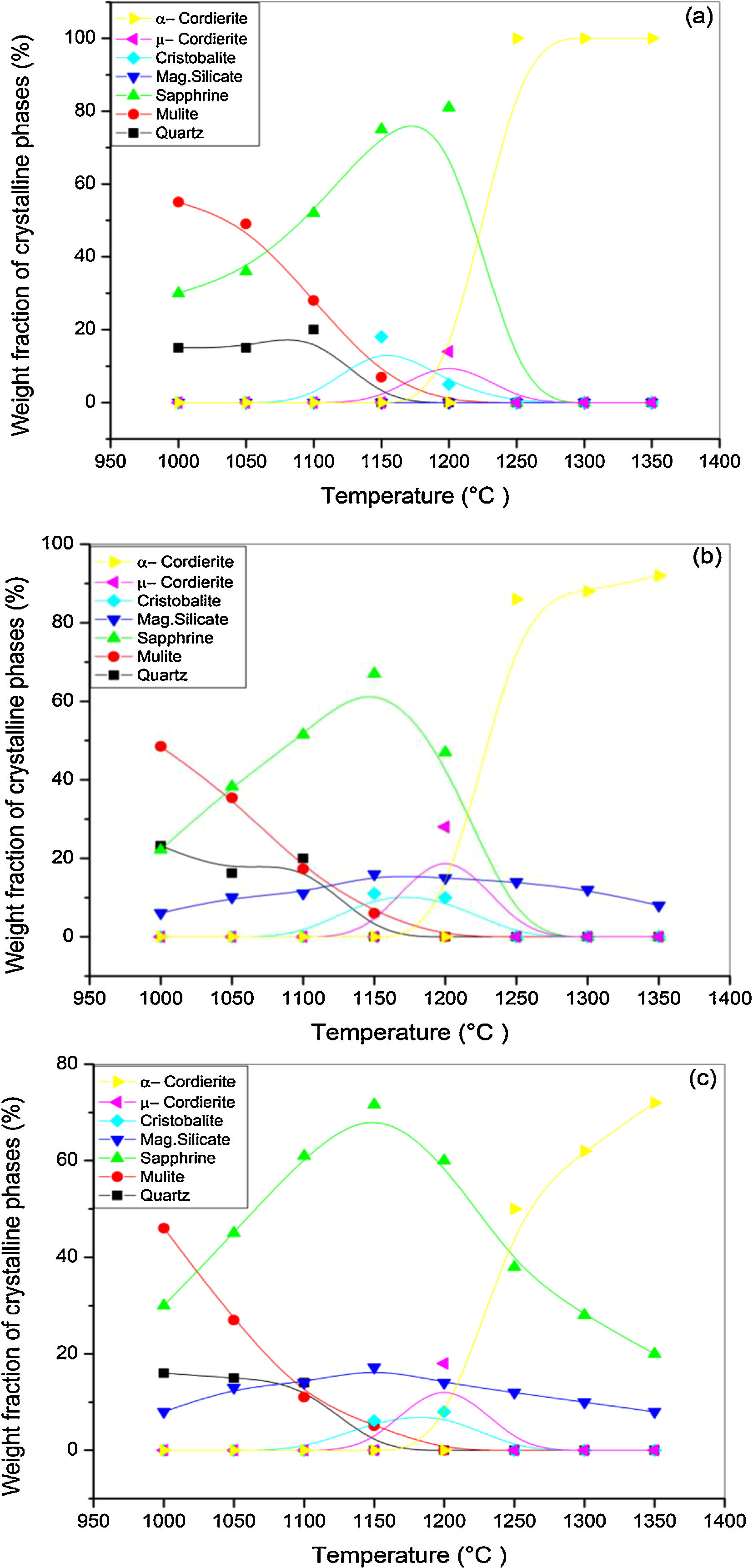
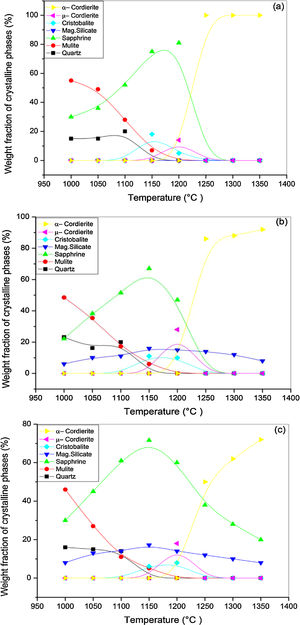
X-ray diffraction spectra of DT00M, DT04M, and DT08M samples treated at 1000, 1050, 1100, 1150, 1200, 1250, 1300 and 1350 °C for 2 h are presented in Fig. 4, and the corresponding fraction of phases is shown in Fig. 5.

Fig. 4.

XRD spectra of (a) DT00M, (b) DT04M, and (c) DT08M powders treated at different temperature for 2 h. (

: Magnesium silicate, Q: Quartz,

: Mullite,

: Sapphirine,

: Cristobalite, μ: μ-Cordierite and α: α-Cordierite).

Fig. 5.

Weight fraction of crystalline phases present in (a) DT00M, (b) DT04M, and (c) DT08M samples sintered at different temperature for 2 h.

For DT04M sample, Fig. 4(a) and 5(a) indicate that quartz, mullite and sapphirine phases were present at 1000 °C; and their mass fractions were 15, 55, and 30 mass %, respectively. Raising the temperature to 1050 °C decreased the mass fraction of mullite to 35.4 and increased the mass fractions of sapphirine to 36%, and quartz diffraction peak was detected. At 1100 °C, mullite, quartz, and sapphirine were present at fractions of 28, 20, and 52%, respectively. This indicates a decrease in mullite and an increase in quartz, and sapphirine. Phases present at 1150 °C were sapphirine (75 mass %), mullite (7 mass %) and cristobalite (18 mass %). At 1200 °C, mullite phase disappeared, μ-cordierite appeared (14 mass %), the mass fraction of cristobalite decreased to 5%, while the mass fraction of sapphirine increased to 81%. At 1250 °C and above, only α-cordierite was present.

Quartz, mullite, sapphirine and magnesium silicate at mass fractions of 23.2, 48.5, 22.2 and 6.1%, respectively, were present in DT04M sample treated at 1000 °C as can be seen in 4(b) and 5(b). The mass fractions of quartz and mullite decreased to 20 and 17.3%, respectively, while those of sapphirine and magnesium silicate increased to 51.5 and 11.1 mass %, respectively, when the temperature was raised to 1100 °C. At 1150 °C, the sample was mainly made of mullite (6 mass %), sapphirine (67 mass %), magnesium silicate (16 mass %), and cristobalite (11 mass %). At 1200 °C, the mass fractions of sapphirine, magnesium silicate, and cristobalite decreased to 47, 15, and 10%, respectively, and μ-cordierite (26.3 mass %) was present. Magnesium silicate and α-cordierite were present at 1250 °C with mass fractions 14 and 86%, respectively. With the increase in temperature to 1350 °C, the amount of magnesium silicate decreased to 8 mass % and the amount of α-cordierite increased to 92 mass%.

Figs. 4(c) and 5(c) show that at 1000 °C, DT08M sample is composed of 16 mass % quartz, 46 mass % mullite, 30 mass % sapphirine, and 8 mass% magnesium silicate. At 1100 °C, the mass fractions of quartz and mullite decreased to 14 and 11 mass%, respectively, while the fraction of sapphirine and magnesium silicate phase increased to 61 and 14 mass%, respectively. At 1150 °C, mullite (5.1 mass %), sapphirine (71.6 mass %), magnesium silicate (17.2 mass %) and cristobalite (6.1 mass %), were present. At 1200 °C, mullite phase disappeared, μ-cordierite phase (18 mass %) appeared, the amount of cristobalite increased (8 mass %), and the amount of sapphirine and magnesium silicate phases decreased to 60 and 14 mass %, respectively. At 1250 °C, cristobalite and μ-cordierite phases disappeared, α-cordierite phase (50 mass %) appeared, and the amount of sapphirine and magnesium silicate phases decreased to 38 and 12 mass%, respectively. At 1350 °C, the sample is made of α-cordierite (72 mass %), sapphirine (20 mass %) and magnesium silicate (8 mass %) phases. It is worth mentioning here that the amount of impurities is very small and their influence on sintering is negligible [63].

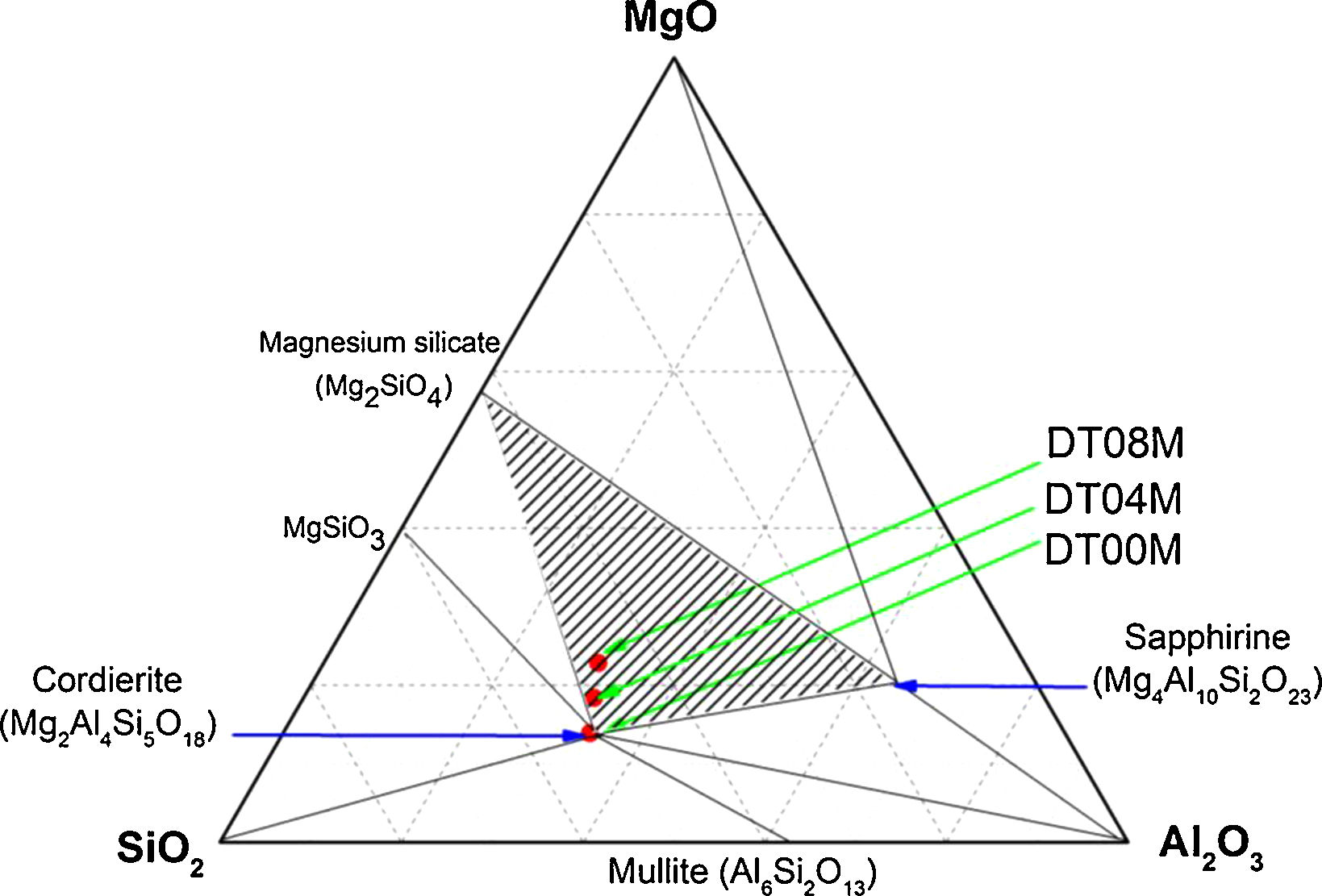
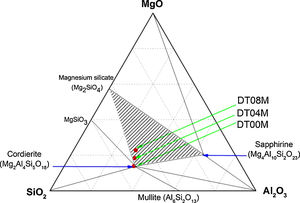
In order to shed more light on phases present in the prepared samples, the ternary phase diagram of Al₂O₃–Si₂O–MgO system at 1300 °C is presented in Fig. 6. The diagram can be divided to eight different areas. The ratio points where the chemical compositions are close to the stoichiometric and non-stoichiometric composition of cordierite ceramics are marked in red dots. It can be seen that: (i) cordierite is the only phase present in DT00M sample, (ii) cordierite and magnesium silicate are the two phases formed in DT04M sample, and (iii) cordierite, sapphirine and magnesium silicate are the three phases in DT08M sample. The phases present in the three samples are located in the cordierite region [63]. These results support those of DTA, dilatometry, Raman spectroscopy, and XRD.

Fig. 6.

Phase diagram of Al₂O₃–SiO₂–MgO ternary system at 1300 °C.

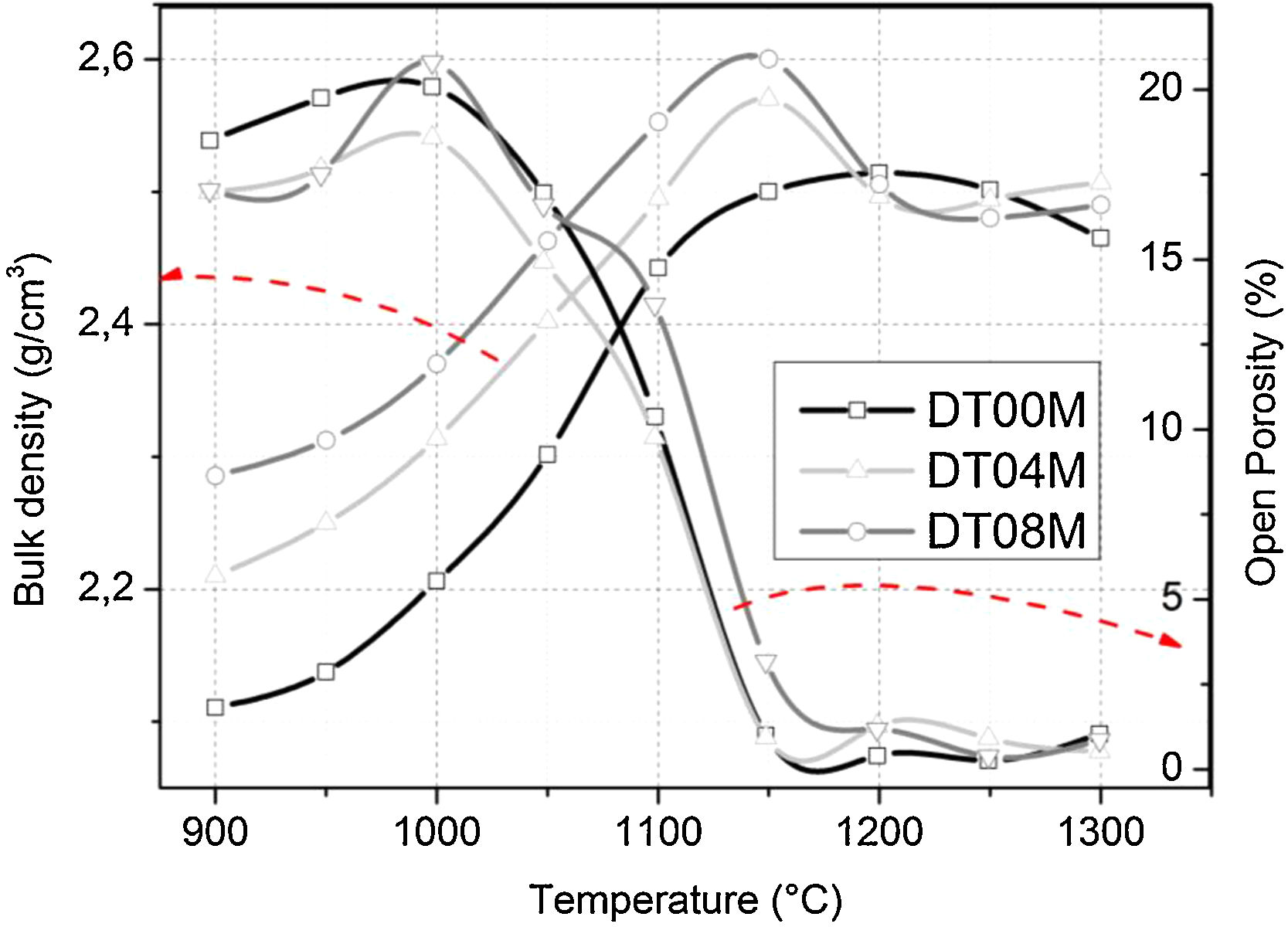
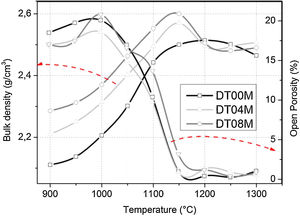
Density and microstructure

The changes in the open porosity and bulk density of sintered specimens are shown in Fig. 7. The density of samples gradually increased when the temperature was raised from 900 to 1150 °C, at an interval of 50 °C, then slightly decreased and almost remained constant at 1200, 1250, and 1300 °C. The opposite trend was observed for the change in the open porosity. This is due to the fact the sintering promotes densification and reduces porosity. Cordierite is known to have a bulk density of 2.53 g/cm³[4]. The density values obtained in this work and presented in Fig. 7, for specimens sintered at 1250 and 1300 °C for 2 h, ranged from 2.46 to 2.5 g/cm³. These values are close to values reported by researchers [46,64–66] who synthesized cordierite materials from diverse raw and/or waste materials using different methods and obtained density values such as 2.33 g/cm³[64], 2.4 g/cm³[46], 2.52 and 2.58 g/cm³[64], and 2.58 g/cm³[66].

Fig. 7.

Bulk density and open porosity of samples sintered at different sintering temperatures for 2 h.

Fig. 8(a) and (b) shows SEM micrographs at different magnifications of DT00M powder mixture wet milled for 5 h. It can be seen that milling yielded a homogenous powder. Typical SEM micrographs, at different magnifications, of a fractured DT00M sample, sintered for 2 h at 1300 °C, are shown in Fig. 8(c) and (d). The microstructure of sample DT00M synthesized from stoichiometric powder mixtures (clay minerals and synthetic magnesia) consists of cordierite only. It is well accepted that precursor materials used to produce cordierite influence the morphology of its crystals [4]. In this regard, cordierite was obtained by sintering Moroccan stevensite and andalusite [46] or mixtures of kaolin waste, talc, and magnesium oxide C [4] at 1350°. SEM micrographs of DT04M and DT08M samples, prepared from non-stoichiometric mixtures (containing 4 and 8 wt% excess magnesia) and sintered at 1300 °C for 2 h, are shown in Fig. 9(a) and (b), respectively. The microstructures of both samples consist of cordierite and sapphirine phases. From the micrographs presented in Figs. 8 and 9, it can be noticed that all samples are almost fully dense and have homogenous microstructures. Furthermore, sapphirine is uniformly distributed in cordierite. Additionally, small pores are present in sample DT08M that contains relatively large amount of the sapphirine phase. The microstructures of sintered samples is in agreement with the dilatometry, XRD, and TDA results, which showed that sample DT00M was made of cordierite only, while samples DT04M and DT08M contained both cordierite and sapphirine phases.

Fig. 8.

SEM micrographs of DT00M powder mixture. (a) and (b) wet milled for 5 h, and (c) and (d) sintered at 1300 °C for 2 h.

Fig. 9.

SEM micrographs of samples sintered at 1300 °C for 2 h (a) DM04 and (b) DM08.

Hardness

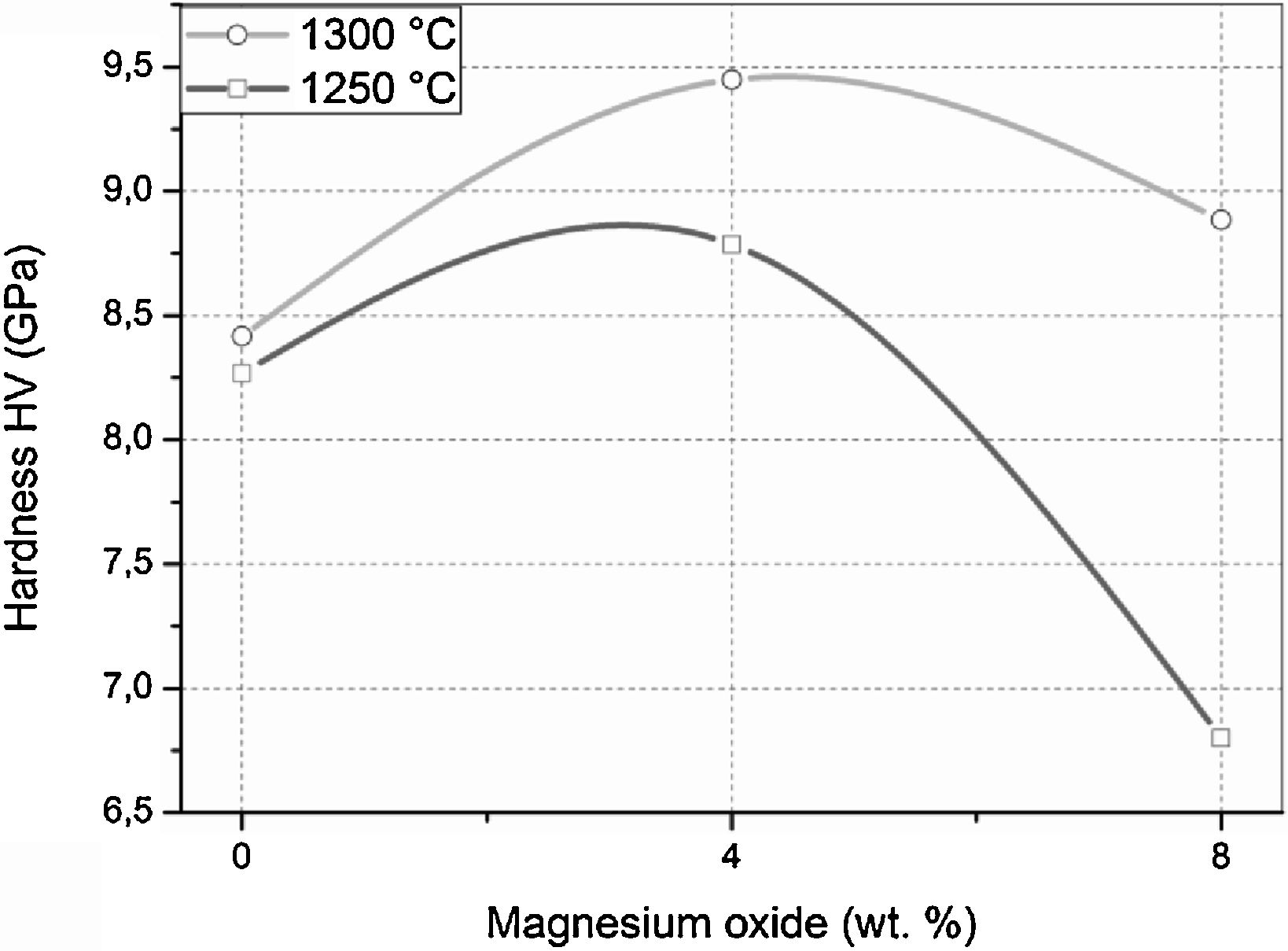
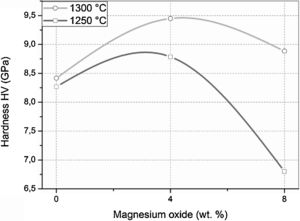
The Vickers hardness values of samples sintered at 1250 and 1300 °C for 2 h are presented in Fig. 10. The DT00M sample sintered at 1250 and 1300 °C had hardness values of 8.25 and 8.40 GPa, respectively. It is worth mentioning here that only α-cordierite was present in this sample, at these temperatures, as revealed by XRD results presented in Figs. 4 and 5; and the density slightly changed as can be clearly seen in Fig. 7. Therefore, the minor increase in hardness with the increase in temperature may be due to better densification and reduced porosity as depicted by the microstructure shown in Fig. 8(c) and (d). Hardness values of 8.77 and 9.45 GPa were obtained for DT04M sample sintered at 1250 and 1300 °C, respectively. This constitutes an increase of 6.3 and 12.5% compared with DT00M sample. As pointed out in XRD results discussed above, in the temperature range 1250–1350 °C, only α-cordierite and magnesium silicate phases were present in this sample. It was reported in the literature that magnesium silicate (forsterite: Mg₂O₄Si) may have hardness values as low as 7.11 GPa (sintered at 1400 °C, relative density of 88%) [67] and as high as 9.7 GPa (sintered at 1200 °C) [68]. Therefore, the improvement in the hardness of DT04M sample is believed to be due to the existence of a hard magnesium silicate phase. The DT08M sample sintered at 1250 and 1300 °C had hardness values of 8 and 8.88 GPa, respectively. The low hardness at 1250 °C may be due to incomplete sintering and densification. In fact, with the increase in temperature to 1300 °C, the hardness increased to 8.88 GPa, an improvement of 5.71% compared with DT00M sample. The low hardness of DT08M sample compared with DT04M is believed to be due the large size of the secondary phases, dispersed in the cordierite matrix, as can be seen in Fig. 9(a) and (b) for samples sintered at 1300 °C. From the XRD results, in the temperature range 1250–1350 °C, it was concluded that the DT08M sample is made of a mixture of α-cordierite, magnesium silicate, and sapphirine phases. The enhancement in the hardness of DT08M sample compared with DT00M is believed to be due the existence of the relatively hard magnesium silicate and sapphirine phases. The later is known to have a hardness of 7.5 on Mohs scale [69].

Fig. 10.

Vickers hardness of samples sintered at 1250 and 1300 °C for 2 h.

The same trend in hardness change was noticed in mullite-zirconia composite materials [24] synthesized by reaction sintering halloysite with boehmite and ZrO₂[24]. Where the hardness increased by 19.47% (from 11.3 to 13.5 GPa) because of the addition of 10 wt.% ZrO₂, and then decreased to 12 GPa because of further increase in ZrO₂ content to 30%. The hardness values between 8 and 9.45 GPa obtained in this work for cordierite and cordierite-sapphirine materials are higher than: (i) the maximum value of 6 GPa reported for glass ceramics, composed of anorthite and cordierite as the major phases, synthesized by mixing kaolin and doloma [8], (ii) values between 6.6 and 7.5 GPa obtained for glass-ceramics prepared from wastes generated from silica sand and kaolin clay [47], and (ii) values between 7.4 and 7.6 GPa achoived for diopside-anorthite and anorthite-diopside samples obtained from CaO–MgO–Al₂O₃–SiO₂ glass-ceramics using waste materials and dolomite (CaMg(CO₃)₂) [48]. The values are comparable with the average hardness values of 8.6 and 9.6 GPa reported for cordierite and cordierite-30 wt.% mullite prepared from cordierite and mullite powders [49]. However, the developed cordierite materials remain less hard than mullite-zirconia composite materials synthesized from halloysite, boehmite and ZrO₂, which had hardness between 12 and 13.5 GPa [24].

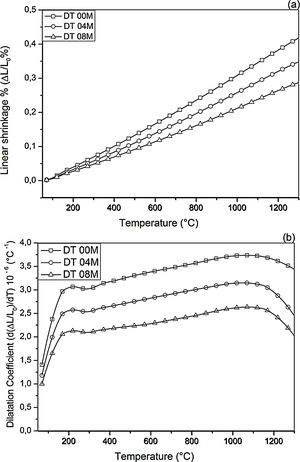
Thermal expansion

Linear shrinkage and dilatation coefficient curves are illustrated in Fig. 11. The CTE values, measured between 100 and 1300 °C, for DT00M, DT04M, and DT08M samples were 3.38 × 10⁻⁶/°C, 2.82 × 10⁻⁶/°C and 2.32 × 10⁻⁶/°C, respectively. The cordierite ceramics (samples DT04M and DT08M) showed lower values of CTE compared with monolithic cordierite (sample DT00M). Sample DT008 possessed the lowest value of CTE demonstrating a decrease of 31.3% with respect to monolithic cordierite. The low CTE values of cordierite ceramics may be due to the sapphirine phase. The obtained CTE values are comparable with CTE value of cordierite of 2.5 × 10⁻⁶/°C reported in the literature [50]. Cordierite is well known for its very low thermal expansion [51], however, CTE of cordierite ceramics may depend on the nature and amount of phases that coexist with cordierite in the final product. The CTE values obtained in this work for cordierite ceramics are lower than values between 7.57 and 9.05 × 10⁻⁶ K⁻¹, reported “for mullite-zirconia composite materials synthesized by reaction sintering Algerian halloysite with boehmite and zirconia at 1600 °C for 2 h” [24]. They are also less than the value of 5.2 × 10⁻⁶/°C obtained between 30 and 380 °C for [47] and values of 6.7 × 10⁻⁶/°C (30–380 °C) and 4.7 × 10⁻⁶/°C reported for [48].

Fig. 11.

Linear shrinkage (a) and dilatation coefficient (b) curves of DT00M, DT04M and DT08M samples sintered at 1350 °C for 2 h.

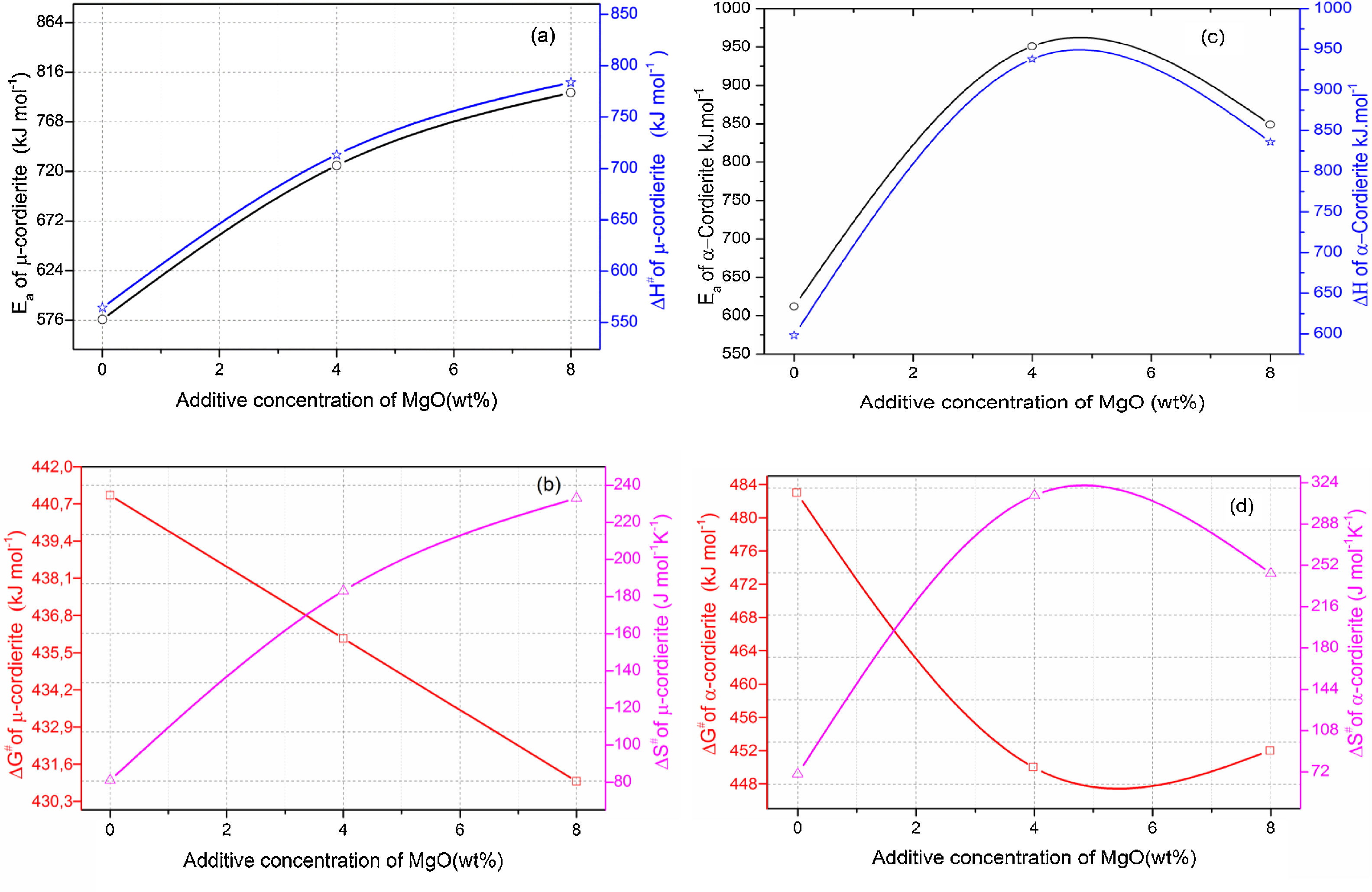
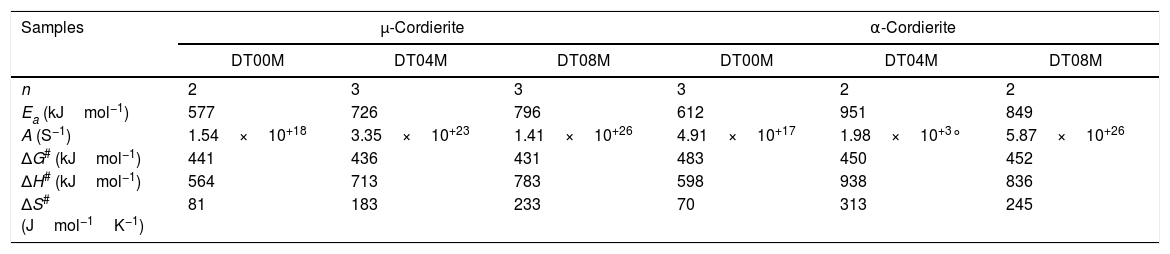
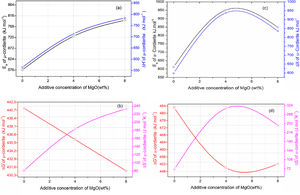
Activation energy and thermodynamic parameters

Eqs. (16) and (17) were used to calculate the frequency factor (A), activation energy (E_a), and the mode of crystallization parameter (n). On the other hand, the free enthalpy (ΔG^#), enthalpy (ΔH^#), and entropy (ΔS^#), for the formation of μ-cordierite and α-cordierite were calculated using equation 18, 19, and 20, respectively. The values of n, E_a, A, ΔG^#, ΔH^#, and ΔS^# are presented in Table 3. Fig. 12 shows the activation energy for the formation of μ-cordierite and α-cordierite in the prepared samples, and the influence of MgO concentration on thermodynamic parameters (ΔG^#, ΔH^#, and ΔS^#).

Table 3.

The values of n, E_a, A, ΔG^#, ΔH^# and ΔS^# for the formation of cordierite.

Samples	μ-Cordierite			α-Cordierite
	DT00M	DT04M	DT08M	DT00M	DT04M	DT08M
n	2	3	3	3	2	2
Ea (kJ mol^−1)	577	726	796	612	951	849
A (S^−1)	1.54 × 10^+18	3.35 × 10^+23	1.41 × 10^+26	4.91 × 10^+17	1.98 × 10^+3°	5.87 × 10^+26
ΔG^# (kJ mol^−1)	441	436	431	483	450	452
ΔH^# (kJ mol^−1)	564	713	783	598	938	836
ΔS^# (J mol^−1 K^−1)	81	183	233	70	313	245

Fig. 12.

The influence of MgO concentration on thermodynamic parameters of μ-cordierite (a) and (b) and α-cordierite (c) and (d).

The activation energy values for the formation of μ-cordierite were 577, 726 and 796 kJ/mol for the DT00M, DT04M and DT08M samples, respectively. Whereas the values were 612, 951, 849 kJ/mol for α-cordierite. The obtained activation energy values are comparable with those reported by researchers who synthesized cordierite from different materials and evaluated the activation energy from non-isothermal DTA or DSC measurements [8,29–31,38–41]. For instance, Boudchicha et al. [8] obtained anorthite and cordierite rich materials through sintering of a glass powder, of the calcium oxide–magnesia–alumina–silica system, prepared by melting followed by quenching and crushing. The authors reported a value of 450 kJ/mol for the activation energy of crystallization. While, Donald [39] obtained cordierite from mixtures of alumina, silica, and magnesia; and reported activation energies between 532 and 574 for μ-cordierite and between 399 and 426 kJ/mol for α-cordierite. Also, cordierite formation from titania doped magnesia-alumina-silica glass was investigated by Goel and co-workers [41]. The authors obtained formation energy values of 340 and 498 kJ/mol for μ-cordierite and α-cordierite, respectively. Furthermore, activation energy for the crystallization of cordierite from diphasic gels was found to be equal to 467 kJ/mol [38]. Moreover, activation energy values for the formation of μ-cordierite and α-cordierite in NiO-added glass samples [30] were equal to 300 and 500 kJ/mol, respectively. In this work, the addition of MgO was found to increase the activaion enrgy for cordierite formation, as seen Fig. 12(a) and (c). This is in agreement with the findings of song and co-researchers [40] who obtained cordierite through the crystallization of potassium and feldspar and reported values from 230.77 to 279.81 kJ/mol for the activation energy of formation of α-cordierite. However, in the presence of leucite these values increased to 348.85–374.33 kJ/mol. However, Kim and Lee [29] indicated that the addition of ceria decreased cordierite energy formation. They obtained average energy values of 653 and 418 kJ/mol for cordierite developed from the crystallization of ceria free and ceria containing glasses, respectively. Also, Başaran and co-workers showed that co-doping with TiO₂ and Bi₂O₃ decreased the activation energy for cordierite formation in the magnesia–alumina–silica glass. They used industrial waste to prepare cordierite materials and obtained energy values of 410 kJ/mol [42] for cordierite formed in the titania doped magnesia–alumina–silica glass; and values of 336, 218, and 170 kJ/mol [43] for cordierite formed in the same system when Bi₂O₃ was added at 2.5, 5, and 10 wt.%, respectively. In their work, Hu and Tsai [31] found that the energy for cordierite formation first increased and then decreased gradually with the increase in BaO content. They reported energy value of 366 kJ/mol and values between 290 and 487 kJ/mol for the formation of cordierite in barium dioxide free and barium dioxide containing samples, respectively. Analysis of the literature shows that the variation in the reported activation energy values was significant and the influence of additives was not ordinary. The discrepancy in the obtained activation energy values was attributed to: (i) the diverse precursor materials and methods used to synthesize cordierite, (ii) the role of sintering aids added to facilitate sintering and ease cordierite production, and (iii) the various thermal analysis and calculation methods employed to determine the activation energy. In DT00M sample, the kinetic parameter n, which depicts the crystallization mode, had values of 2 and 3 for μ- and α-cordierite, respectively. This implies that the formation of intermediate μ-cordierite is controlled by surface nucleation followed with one-dimensional growth, while the formation of α-cordierite is controlled by volume nucleation followed by two-dimensional growth [3]. The opposite trend was observed for the formation of μ- and α-cordierite in DT04M and DT08M samples.

It can be clearly seen from Table 3 and Fig. 12(a) and (b) that, for μ-cordierite, the increase in MgO content from 0 to 8 wt.% did not change the difference between the activation energy and enthalpy (E_a – ΔH^#), which remained equal to 13 kJ/mol for all samples. Therefore, it does not influence the μ-cordierite formation temperature [3]. However, it decreased the free enthalpy from 441 to 431 kJ/mol and increased the entropy from 81 to 233 J/mol. As for α-cordierite, Table 3 as well as Fig. 12(c) and (d) show that the increase in MgO content from 0 to 8 wt.% did not change significantly the difference between the activation energy and enthalpy (E_a – ΔH^#), which remained equal to 14 kJ/mol for DT00M sample and 13 kJ/mol for DT04M and DT08M samples. The free enthalpy decreased from 483 kJ/mol (DT00M sample) to 452 and 450 kJ/mol for DT04M and DT08M samples, respectively. The entropy increased from 70 to 313 J/mol with the increase in MgO content from 0 to 4 wt.%, then decreased to 245 J/mol with further increase in MgO content to 8 wt.%.

Conclusion

The microstructure, dimensional stability, hardness, and thermodynamic parameters of cordierite ceramics prepared by reaction sintering Algerian natural clay minerals and synthetic magnesia were characterized using SEM, XRD, DTA, dilatometry, and Raman spectroscopy. The microstructure of DT00M sample synthesized from stoichiometric powder mixture (clay minerals and synthetic magnesia) consisted of cordierite only. Whereas cordierite, magnesium silicate, and sapphirine phases were present in DT04M and DT08M samples prepared from non-stoichiometric powder mixtures containing excess magnesia of 16 and 20 wt.%, respectively. The values of the activation energy (E_a) and frequency factor (A), for cordierite crystals, varied from 577 to 951 kJ/mol, and 1.54 × 10¹⁸ to 1.98 × 10³ S⁻¹, respectively. The kinetic parameter n for the formation of cordierite had values between 2 and 3. While the Gibbs free energy (ΔG^#), enthalpy (ΔH^#), and entropy (ΔS^#) values were found to be in the range 431–483 kJ/mol, 564–938 kJ/mol, and 70–313 J/mol, respectively. Samples sintered at 1300 °C for 2 h showed higher values of hardness compared with those sintered at 1250 °C. The DT04M sample had the highest hardness value of 9.45 GPa, demonstrating an increase of 12.5% with respect to monolithic cordierite (DT00M). In the temperature range 100–1300 °C, DT04M and DT08M samples showed better dimensional stability compared to monolithic cordierite. The DT08M sample showed the lowest thermal expansion (α = 2.32 × 10⁻⁶/°C), demonstrating a decrease of 31.3% with respect to monolithic cordierite.

Acknowledgements

The authors would like to thank the General Directorate for Scientific Research and Technological Development, ministry of higher education and scientific research, Algeria, for its patronage and support for this research.