Son bien conocidas las aplicaciones de los ultrasonidos en tratamientos médicos y estéticos de piel y de movilización subcutánea de tejidos grasos. El transductor tipo utilizado consta de un disco piezoeléctrico adherido a una línea de retardo metálica en forma de cápsula. El diseño de la cápsula es un punto crítico, ya que el elemento piezoeléctrico por sí solo, la cápsula independientemente y los 2 elementos adheridos presentan modos de vibración que, si no son estudiados y aprovechados convenientemente, pueden provocar diseños muy ineficientes y con distribuciones de vibración muy irregulares. Esto último debe ser o conocido o evitado para no insonificar en forma incorrecta con distribuciones de presión acústica y calor que podrían ser ineficientes o dañinas.
En este trabajo, usando herramientas de elementos finitos y de análisis vibracional por interferometría láser, se ha llegado a una solución de vibración tipo pistón que permite aplicar correctamente las dosis de presión acústica.
Applications of ultrasound are well known in medical and aesthetic skin and subcutaneous fatty tissue mobilization treatments. The basic transducer used consists of a piezoelectric disk adhered to a metal delay line in capsule shape. The capsule design is critical since the two bonded elements have vibration modes which can cause very inefficient designs and vibration distributions very irregular if they are not properly studied and utilized. This must be known to avoid distributions of heat and sound pressure that could be ineffective or harmful.
In this paper, using Finite Element Method and laser interferometric vibrational analysis, it has reached a piston-type solution that allows properly implement sound pressure vibration dose.
Hoy en día la fisioterapia es una disciplina muy importante dentro del marco de la salud. Dentro de ella, los tratamientos por ultrasonidos son muy habituales. Desde hace más de 5 décadas este tipo de tratamiento es uno de los más empleados por los profesionales del mundo de la fisioterapia y, sin embargo, es uno de los que más dudas suscita ([1], [2]).
Este tratamiento consiste en aplicar una señal ultrasónica, o lo que es lo mismo, una señal cuya frecuencia está por encima de 20 kHz, límite superior del rango de audición humano. En el caso de los ultrasonidos, en fisioterapia la frecuencia más habitual es 1 MHz, pudiendo llegar en algunos equipos comerciales hasta 3 MHz. Los transductores están constituidos principalmente por una cerámica piezoeléctrica de PZ26 pegada a una membrana metálica que es la parte del mismo en contacto con el paciente.
Durante los últimos años se han realizado numerosos estudios sobre el funcionamiento de esta técnica, y parece que no puede demostrarse su utilidad terapéutica a pesar de los datos científicos in vitro que muestran una correlación dosis/beneficio ([3], [4], [5], [6], [7]). Uno de los principales problemas es la dificultad para comparar las condiciones de medida y criterios usados en cada estudio ([3]), ya que en este tipo de tratamiento influyen numerosas variables; unas son controlables porque son las referentes al equipo, como pueden ser la frecuencia de la señal o la intensidad que proporciona el transductor, pero otras no son controlables, ya que son las que tienen que ver con el tejido donde se aplica o con la anatomía del cuerpo.
Teoría y modelo comercialPor lo tanto, no se tiene una idea clara de por qué este tratamiento funciona unas veces y otras no. La idea motriz de este trabajo es sostener que uno de los factores que falla en este tratamiento es el del patrón de vibración y, por lo tanto, la distribución de presión acústica de los transductores comerciales. A pesar de que las normas internacionales tienen en cuenta que el patrón de vibración puede producir niveles de presión anormales que tienen que ser localizados en la caracterización de los mismos, los equipos comerciales no dan información de ello normalmente y, en todo caso, dan un valor genérico de la no uniformidad de la presión emitida (beam non-uniformity ratio).
Cuando se adquiere uno de estos transductores se supone que el patrón de vibración es similar al de un pistón ([8]) en el que todos sus puntos vibran en fase y con la misma amplitud. Si esto fuera así, existen modelos teóricos para predecir tanto el comportamiento electromecánico de los mismos como el patrón de insonificación (difracción). Se puede predecir a qué frecuencia vibrará el transductor y la impedancia eléctrica con el conocimiento de la geometría del mismo y de los datos de los materiales (Tabla 1).
Tabla 1. Datos de los materiales de los transductores
| Espesor (mm) | Velocidad del sonido (m/s) | Densidad (kg/m3) | |
| Aluminio | 0,8 | 6.400 | 2.700 |
| PZ26 | 2 | 4.080 | 7.700 |
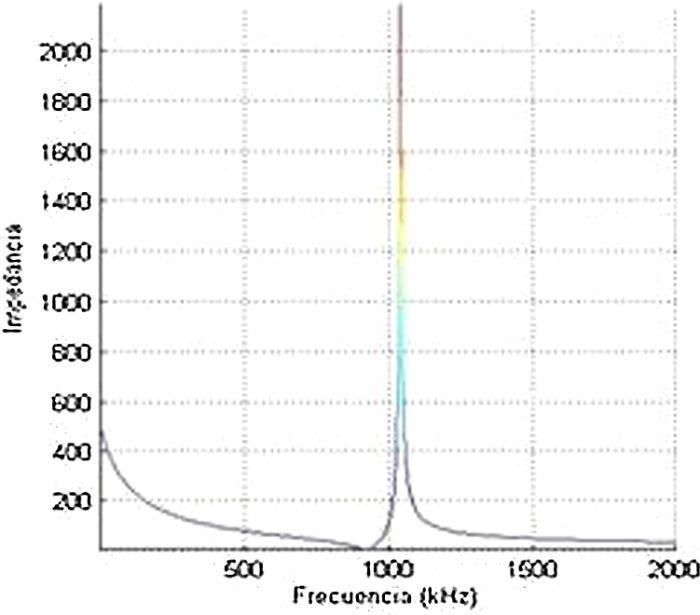
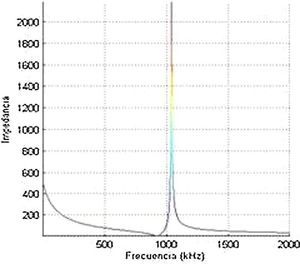
El estudio de estos transductores con modelos monodimensionales clásicos ayuda a entender su funcionamiento y sus propiedades, pero es solo un paso inicial. Así, se puede usar un modelo circuital clásico como es el KLM ([9]), que permite simular la impedancia eléctrica de entrada de un resonador piezoeléctrico en un modo puro monodimensional conociendo las propiedades del material y la dimensión relacionada con dicho modo, En la Figura 1 se muestra el módulo de la impedancia de la cerámica piezoeléctrica simulado con el modelo teórico, KLM, donde se ve que el mínimo de la impedancia eléctrica de esta cerámica de 2 mm de espesor y 30 mm de diámetro está casi en 1 MHz.
Figura 1. Modelo monodimensional del módulo de la impedancia eléctrica de una cerámica piezoeléctrica con los datos de la tabla 1 .
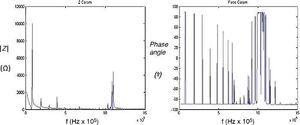
Pero este modelo monodimensional solo tiene en cuenta el modo a espesor de la cerámica. Cuando se mide la impedancia eléctrica de forma experimental de uno de estos resonadores piezoeléctricos aparecen en las gráficas de módulo y fase una gran cantidad de modos de vibración que se corresponden con los modos radiales. Estos modos están originados por la dimensión finita asociada al diámetro. El efecto del contorno de la cerámica y su simetría se pueden apreciar claramente en la Figura 2.
Figura 2. Módulo y fase de la impedancia en función de la frecuencia de la cerámica piezoeléctrica con los datos de la tabla 1 medida con el analizador de impedancias Agilent 4294A Precision Impedance Analyzer 40 Hz to 110 MHz.
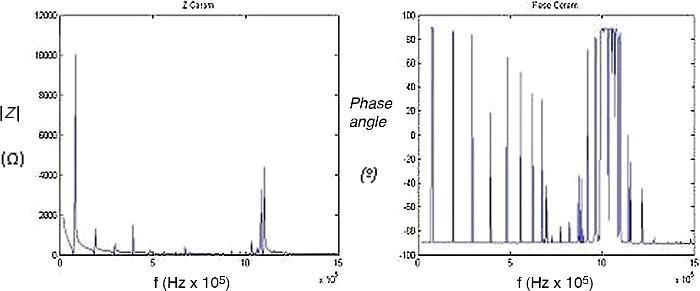
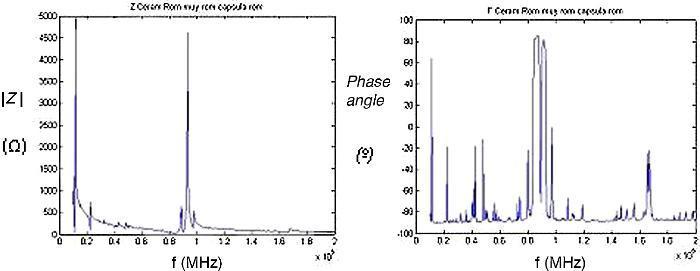
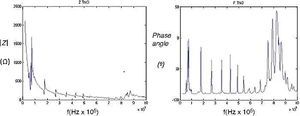
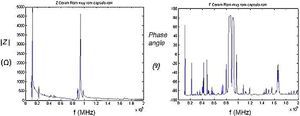
Si además se considera el caso del conjunto formado por la cerámica piezoeléctrica y la cápsula metálica, el comportamiento en resonancia es aún más complicado. En la Figura 3 se muestran las gráficas del módulo y la fase de la impedancia eléctrica de un transductor comercial tomado como referencia (cerámica de diámetro 35 mm y espesor 2 mm, diámetro de la membrana 50 mm y espesor de membrana 1 mm). En dicha figura se aprecia que existen modos radiales ahora asociados a toda la estructura cápsula & piezocerámica, así como la resonancia asociada a la vibración «a espesor» que disminuye debido a la cápsula de aluminio que actúa como una línea resonante unida a la cerámica.
Figura 3. Módulo y fase de la impedancia eléctrica del transductor comercial.
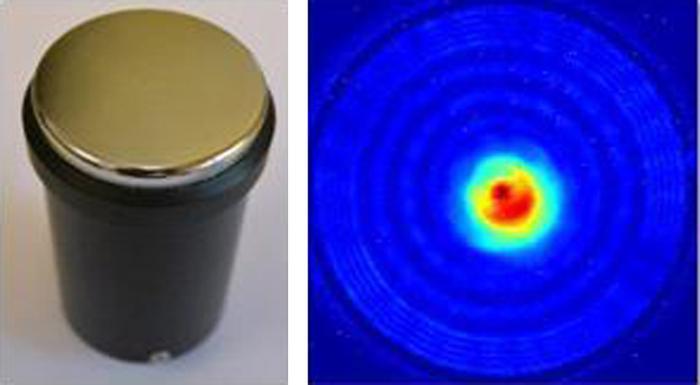
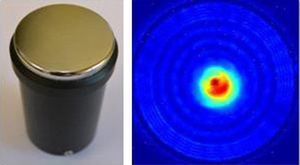
En la Figura 4 la imagen de la izquierda muestra la foto del transductor comercial, en el que se diferencia su membrana de aluminio, que contiene pegada en su cara interior la cerámica piezoeléctrica, y a la derecha se ve la superficie de vibración del transductor medida con un vibrómetro láser (POLITEC OFV-505 Sensor Head) al excitarlo a su frecuencia de resonancia de 750 kHz. En dicha superficie se ve que la proporción que vibra con mayor amplitud es muy pequeña en comparación con la superficie total, y se aprecia la presencia de los nodos circulares con fases opuestas. Esto muestra claramente que este transductor no vibra como un pistón.
Figura 4. Imagen del transductor comercial y de su superficie de vibración.
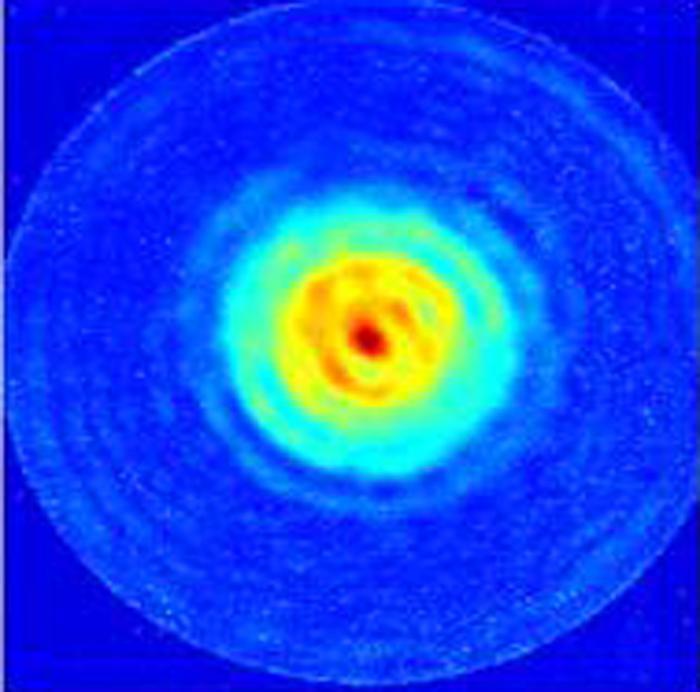
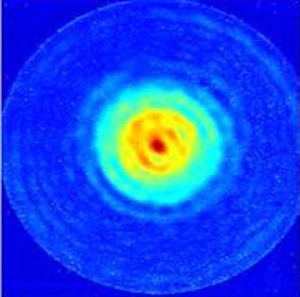
En la Figura 5 se ve la comparación entre el campo acústico que generaría un pistón ideal de diámetro y frecuencia iguales que las del transductor comercial, y el campo acústico que genera realmente el mismo. En el campo que genera un pistón ideal se conoce perfectamente la difracción acústica y, por tanto, la distribución de sus máximos, incluyendo el que será el de mayor amplitud. Como era de esperar, tras comprobar el perfil de vibración del mismo, la medida del campo que genera el transductor tiene una distribución de sus máximos que nada tiene que ver con la de un pistón de su diámetro y frecuencia. De hecho, el máximo de mayor amplitud se encuentra a menos profundidad, efecto que se debe a la apodización en amplitud que presenta.
Figura 5. Campo acústico simulado generado por un pistón ideal, y campo medido generado por el transductor comercial. Profundidad de campo: 50 × 50 mm.
Como resultado de estas medidas se puede afirmar que el transductor comercial no cumple la condición de vibrar como un pistón, y por tanto esto dificulta la capacidad de predecir su efecto —calentamiento de los tejidos— al aplicar un tratamiento con él. Por lo tanto, se necesita llevar a cabo el diseño de transductores que se comporten como pistones.
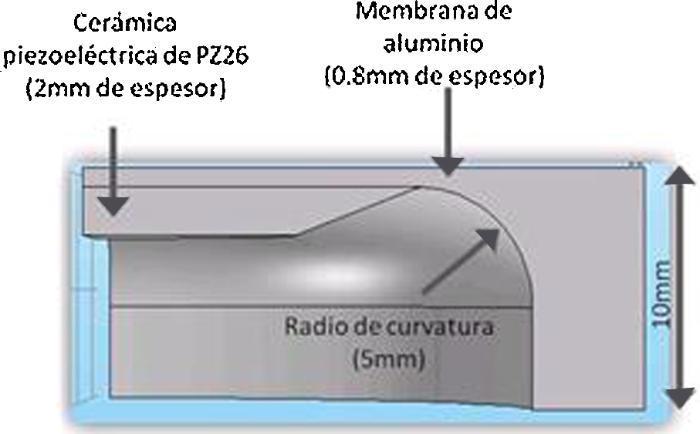
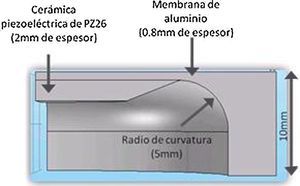
Modificaciones propuestas y resultadosEn la Figura 6 se muestra un diseño con las modificaciones introducidas en la cápsula y la cerámica piezoeléctrica con el fin de lograr una superficie de vibración tipo pistón. La imagen muestra el perfil de una sección de la cápsula. La cerámica piezoeléctrica, que antes tenía forma de disco, ahora tiene un chaflán en el borde que reduce la superficie que no está en contacto con el aluminio de 30 mm de diámetro a 20 mm. La parte interior de la membrana tiene un radio de curvatura de 5 mm de radio. Estas modificaciones se introducen con la idea de reducir la influencia de los modos radiales al hacer que no haya bordes tan abruptos. Para estudiar el comportamiento de esta estructura tanto en su comportamiento electromecánico como vibracional se ha usado un software de FEM (COSOL V4.4). Este modelo ha sido calculado.
Figura 6. Perfil de la sección de la cápsula modificada El espesor de la membrana de aluminio es de 0,8 mm y el de la cerámica, de 2 mm. La parte activa de la cerámica es de 20 mm y el diámetro total de la cápsula es de 50 mm.
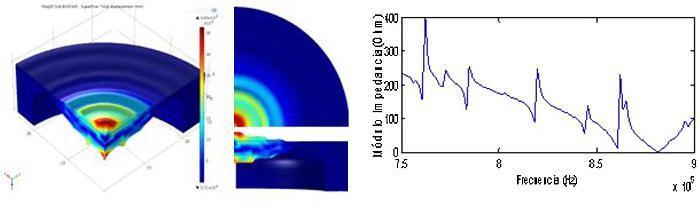
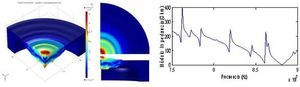
La modificación realizada muestra resultados favorables en las imágenes obtenidas de la simulación. La Figura 7 muestra los resultados de la vibración a la frecuencia de resonancia, así como el módulo de la impedancia eléctrica en el entorno de la resonancia donde se ve cómo vibra la cápsula a su frecuencia de resonancia, 880 kHz. Se observa que con esta geometría la proporción de la superficie vibrando con mayor amplitud coincide con la de la parte activa de la cerámica piezoeléctrica, y además la presencia de modos radiales es mucho menor. La gráfica del módulo de la impedancia está menos influenciada por la presencia de los modos radiales si se compara con la Figura 3 en el rango de frecuencia entre 7,5 y 9 MHz.
Figura 7. Cápsula modificada simulada vibrando a su frecuencia de resonancia desde 3 vistas y módulo de la impedancia eléctrica en el intervalo de frecuencias simulado.
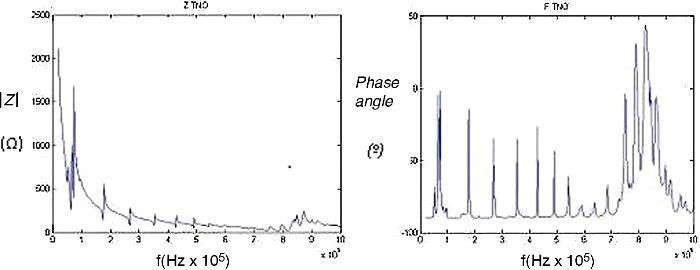
Tras fabricar un prototipo basado en este modelo, en la Figura 8 se muestra el módulo y la fase de la impedancia del prototipo medido experimentalmente. Se aprecia la esperada importante reducción de la amplitud de los modos radiales. Esto apoya la primera idea obtenida de las simulaciones.
Figura 8. Módulo y fase de la impedancia eléctrica del nuevo prototipo de transductor.
En la Figura 9 se muestra la superficie de vibración del prototipo a su frecuencia de resonancia (830 kHz). Como se aprecia, la superficie de vibración coincide con la parte activa de la piezocerámica, al contrario de lo mostrado con el transductor comercial de referencia, sin que presente variaciones de fase. Esto asegura un comportamiento tipo pistón al medir su patrón de difracción acústica.
Figura 9. Superficie de vibración del nuevo transductor.
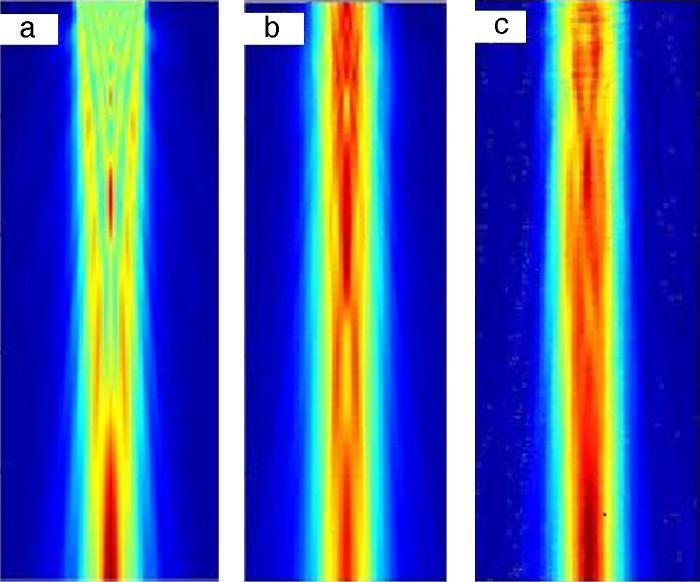
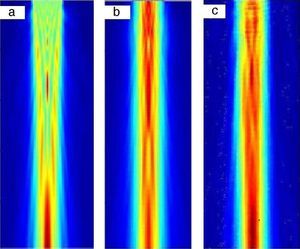
La Figura 10 consta de 3 imágenes: la primera de ellas (a) es la simulación del campo generado por un pistón ideal que tiene el diámetro de la superficie activa de la cerámica; la segunda imagen (b) es la simulación de un pistón del mismo diámetro pero apodizado en amplitud con los valores aproximados de apodización que presenta el transductor real en el barrido de vibración a la frecuencia de resonancia (Figura 9). Por último, la tercera imagen (c) de la figura muestra la medida experimental del campo generado por el nuevo diseño de transductor, observando una gran similitud con la difracción calculada. La imagen de la medida difiere de la simulación de un pistón ideal (a), ya que la amplitud de vibración no es constante y depende del radio pero presenta sus máximos de amplitud a la misma profundidad que el pistón equivalente, lo que hace predecible el conocimiento de la distribución de presión y, por tanto, del aumento de calor en la zona insonificada con solo conocer el dato del diámetro, la frecuencia y la amplitud de vibración para cada nivel de potencia usada.
Figura 10. Imágenes de simulaciones (a,b) y medida de campo acústico (c).
ConclusionesDe las medidas anteriores se pueden concluir 2 principales puntos.
1. El trabajo realizado pone en evidencia que los transductores comerciales no vibran con el patrón de un pistón ideal y presentan un comportamiento impredecible en cuanto a su difracción acústica, lo que puede ser uno de los principales causantes de la falta de fiabilidad de estos tratamientos fisioterapéuticos.
2. En este trabajo se ha propuesto, modelado y realizado un nuevo transductor con el fin de estandarizar la fabricación de transductores de fisioterapia de tal forma que, independientemente de la frecuencia y del tamaño, presenten un patrón de vibración semejante al de un pistón.
El trabajo se ha realizado con financiación de los proyectos CICYT DPI2013-46915-C2-1-R y MAT2013-48009-C4-3-P.
Recibido 22 Julio 2015
Aceptado 22 Octubre 2015
Autor para correspondencia. eiglesia.jml@gmail.com