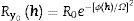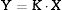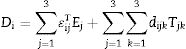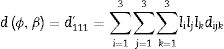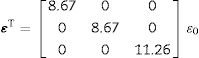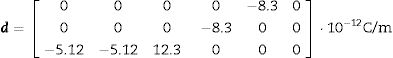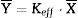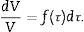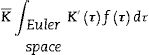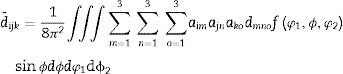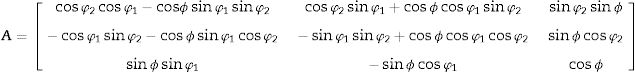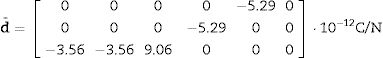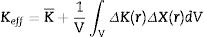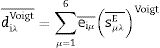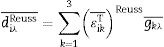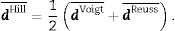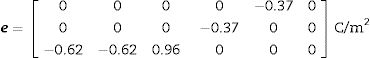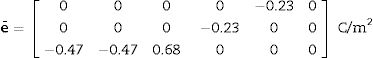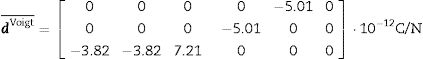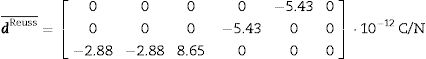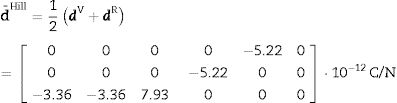A computer-aided methodology for the approximate prediction of axially textured polycrystals’ properties is presented. The input data for the developed application consist of: (a) the two-dimensional diffraction pattern of the material under investigation and (b) the tensors of the elasto-piezo-dielectric properties of the single crystal case. Program ANAELU 2.0 allows the determination of the fiber axis inverse pole figure by means of a Rietveld-type procedure. The Material Properties Open Database (MPOD, http://mpod.cimav.edu.mx) provides free access to the experimentally determined values of the tensor properties for several crystal species. Practical estimates of polycrystals’ properties may be obtained by averaging single crystals’ properties tensors, with the orientation distribution function (the symmetry-axis inverse pole figure, in fiber textures) as a weight factor. This treatment, with the application of the Voigt, Reuss and Hill approaches, requires special precautions when it comes to the coupling properties (e.g. piezoelectricity, magnetostriction, magnetoelectricity). Some key physical, mathematical and computational aspects related to the considered topic are discussed. Program GISELLE systematizes the calculation of polycrystal properties under the considered treatments. The application of the proposed methodology to real-world events is illustrated by means of a case study.
Se presenta una metodología asistida por computadora para la predicción aproximada de las propiedades de policristales con textura axial. Los datos de entrada para la aplicación desarrollada consisten en: a) el patrón de difracción bidimensional del material bajo investigación y b) los tensores de las propiedades elasto-piezo-dieléctricas para el caso del monocristal. El programa ANAELU 2.0 permite determinar la figura inversa de polos del eje de la fibra mediante un procedimiento de tipo Rietveld. La base de datos de propiedades de los materiales Material Properties Open Database (MPOD, http://mpod.cimav.edu.mx) proporciona acceso gratuito a los valores experimentales de las propiedades tensoriales de numerosas especies monocristalinas. Una metodología de valor práctico para el pronóstico aproximado de las propiedades de policristales texturados consiste en promediar los tensores de las propiedades de los cristales individuales, con la función de distribución de orientaciones (la figura inversa de polos del eje de simetría, en texturas de fibra) como factor de peso. Este tratamiento, con la aplicación de los enfoques de Voigt, Reuss y Hill, requiere de precauciones especiales cuando se trata de las llamadas propiedades de acoplamiento (por ejemplo, piezoelectricidad, magnetostricción, magnetoelectricidad). Se discuten algunos aspectos clave (físicos, matemáticos y computacionales) relacionados con el tema considerado. El programa GISELLE sistematiza el cálculo de las propiedades del policristal bajo los tratamientos considerados. Se muestra la aplicación de la metodología propuesta a un caso ilustrativo.
The structuralcharacterization→properties prediction route for polycrystals must include the evaluation of the texture effect. This article focuses on two aspects of the aforementioned topic: the diffractometric measurement of texture and the prediction of the texture's contribution to physical properties, particularly piezoelectricity.
The most widespread methods of measuring crystallographic texture are based on diffraction techniques. Electrons [1,2], neutrons [3–5] and X-rays [6–8] are mainly used.
In recent years, advances in two-dimensional detectors [9–11] have led to the development of new measurement methods leading to the determination of the orientation distribution function (ODF) [12], the misorientation distribution function [13] and the orientation distribution map [14]. In the field of functional ceramics (bulk and thin films) the uniaxial compression and sputtering processes give rise to textures with axial symmetry (“fiber” textures). Some methods and programs, representative of the state of the art in diffractometric texture analysis, are described in the references [15–19]. Texture analysis via two-dimensional (2D) Rietveld refinement is a novel trend in which our group has contributed the ANAELU program [20]. This program has been used successfully in the characterization of diverse materials [21–23]. Section 2 in this paper describes the characteristics of the current ANAELU version and presents its use in a representative case of functional ceramics.
The polycrystal properties, in first approximation, are those of the single crystal, moderated by the texture. Section 3 of this article presents a brief recap on single crystal properties. The MPOD database [24,25] is introduced.
The influence of texture on physical properties may be significant. Reference [26] describes the use of texture as a property optimization tool. Mechanical properties have been linked with texture for a long time and these studies are still of interest [27–29]. In piezoelectricity, texture can lead to the improvement or disappearance of this response [30–32]. Fiber texture is common in several processes and affects, among others; the optical and elastic properties [33], electric conductivity [30], magnetic properties [34,35] and piezoelectricity [36,37].
Being able to predict approximately different properties, supported by prior knowledge of texture (axial case), can be of great help to save time and efforts in the laboratory. The contribution of this article consists in the implementation of a computer-aided methodology to predict polycrystal tensor properties, particularly piezoelectricity, starting from the 2D diffractogram and the single crystal tensors. The application of the well-known Voigt [38], Reuss [39] and Hill [40] approximations to piezoelectricity is reviewed. The ideas and methods presented here integrate preceding partial contributions [41,42] into a self-contained cycle. Sections 4 and 5 analyze polycrystals properties. Program GISELLE is introduced. Section 6 illustrates the application of the suggested methodology to a study case.
Throughout this article, scalar quantities are represented in italics, vectors and tensors in bold.
2D diffraction. The ANAELU programThe ANAELU program (ANAlytical Emulator Laue Utility) [20,41] allows the diffractometric determination of the inverse pole figure (IPF) Ry0h[43] associated to the symmetry axis y0 of a polycrystalline sample with axial texture. In the mentioned case, the IPF of the symmetry axis is equivalent to the ODF. Taking as reference the experimental two-dimensional diffractogram of interest, the user proposes the crystalline structure, the fiber texture component and the estimated width of the orientation distribution.
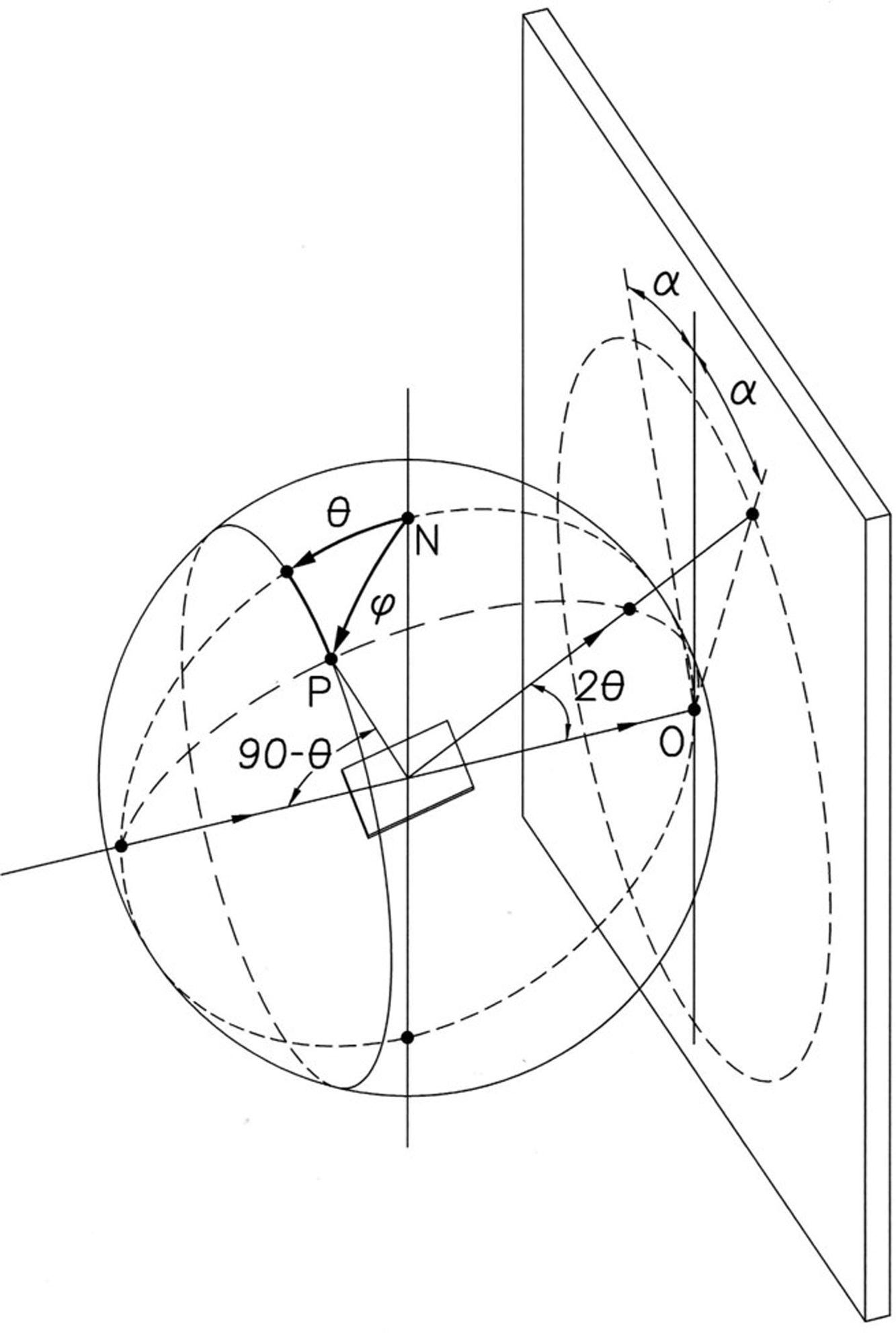
Fig. 1 schematically shows how the pole figure Ph(ϕ), associated with the reciprocal vector h=[h, k, l], modulates the intensities distribution along the Debye ring associated with the reflection h in the 2D diffractogram. Mathematically:
Scheme of the intensities modulation, in a Debye ring, by the pole figure of the family of planes associated with the ring.
The relationship that links the angles of the figure is:
The pole figures Ph(ϕ) corresponding to the IPF considered are calculated by applying the fiber textures fundamental equation [18]:
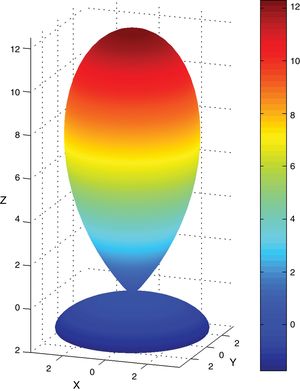
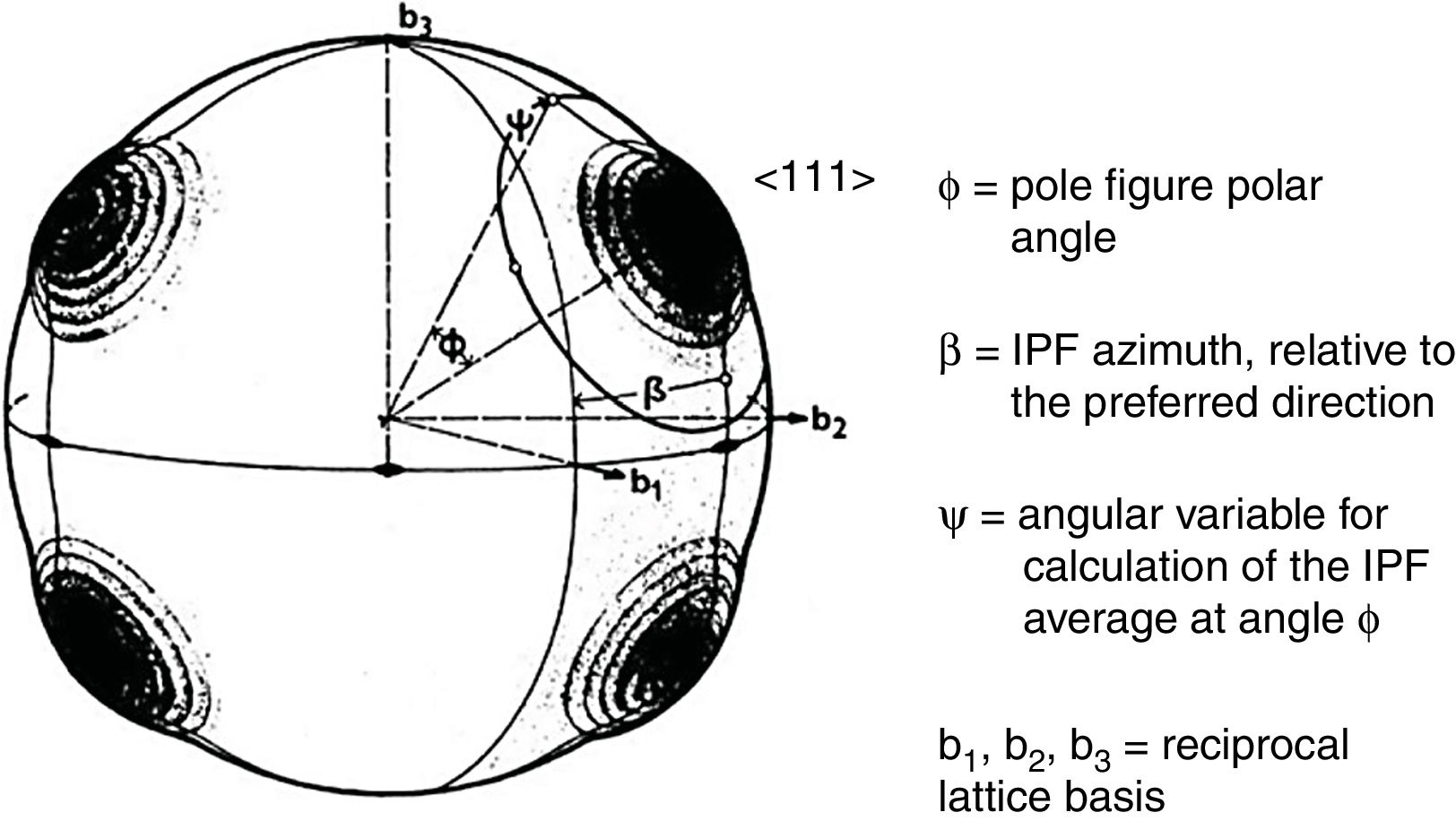
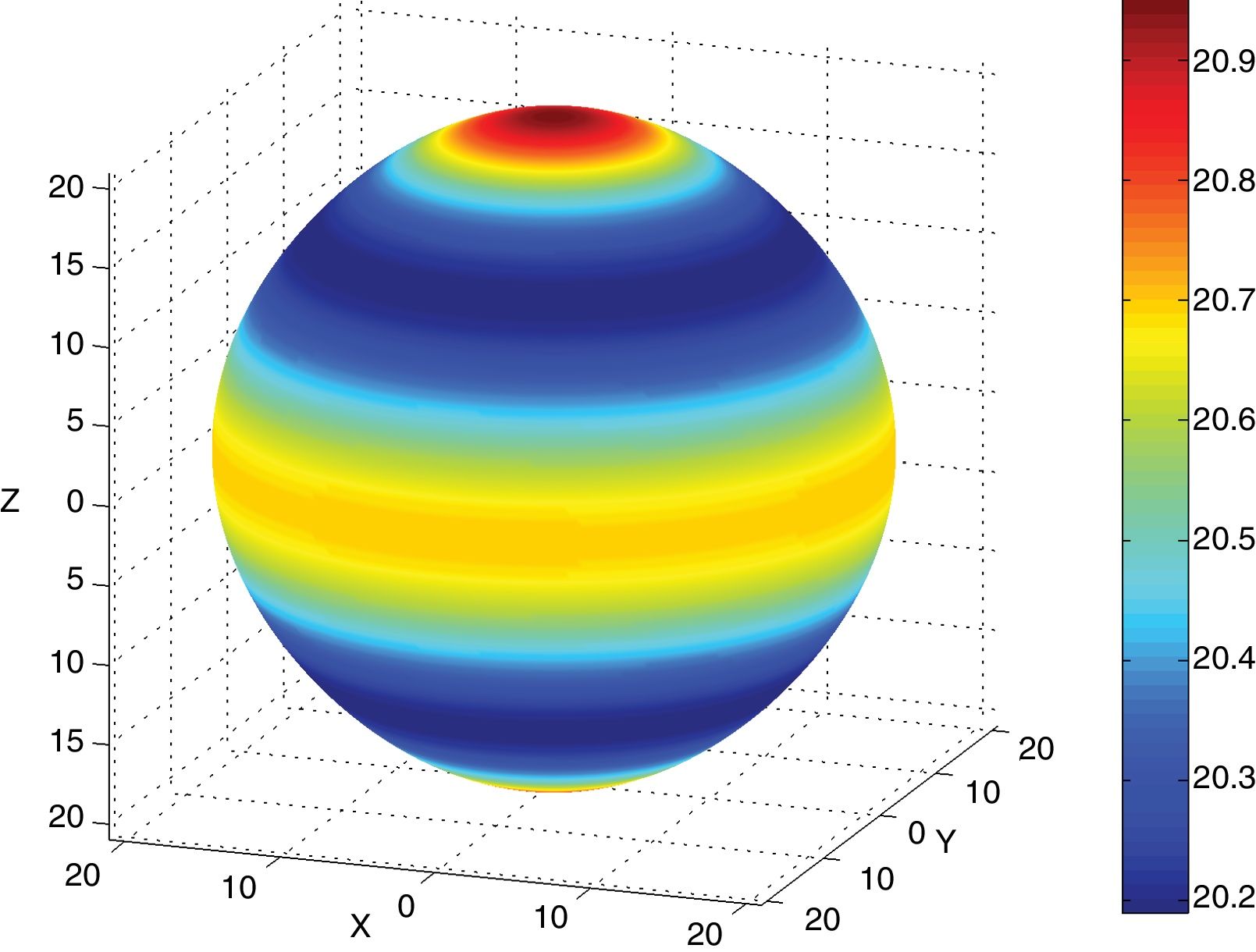
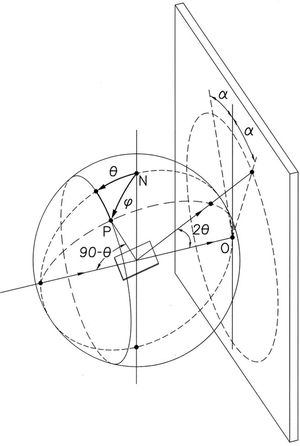
Fig. 2 shows an example of a pole figure calculation by application of Eq. (3). Calculation details can be found in [44].
Application of the fiber textures fundamental equation (Eq. (3)). The scheme represents the fiber axis inverse pole figure of a hypothetical sample with texture components at vectors 〈1, 1, 1〉 in reciprocal space. Crystal point group is 32. Averaging the inverse pole figure lengthwise angle ψ, along the circumference at angle ϕ with respect to reciprocal direction [1,1,1] leads to the direct pole figure P111(ϕ).
In ANAELU, IPFs are represented by Gaussian distributions, Eq. (4). R0 is a scale factor, which is adjusted by normalization conditions. Ω characterizes the orientation distribution width.
The current version of ANAELU approximates a 2D-Rietveld refinement program. The program models the intensities distribution along the Debye rings, it represents the diffractogram background by using a smooth surface, compares the calculated and experimental patterns quantitatively, calculates descriptors of goodness of fit and allows variations of textural parameters in the search of an optimal fit. Crystallographic calculations are performed by using the CrysFML Fortran library [45]. The computer-user interface is programmed using the wrapper wxPython [46] and the Fortran-Python mixed programming is achieved through the F2PY binding module [47]. The automatic fitting of additional microstructural parameters in under development.
Figs. 3 and 4 illustrate a real-world application of ANAELU to functional materials. The investigated sample is a film of ZnO nanorods that have grown with a tendency for their crystallographic axes c to be oriented perpendicular to the glass substrate. Fig. 3 displays a cross sectional SEM micrograph of the considered sample [48]. Figure S1 of the Appendix/Supplementary Information describes the grazing incidence 2D-XRD experimental setup at the Stanford synchrotron beamline 11-3. Field (a) of Fig. 4 shows a representative sector of the two-dimensional measured diffractogram. Fig. 4, field (b) displays the diffractogram modeled by ANAELU under the hypothesis of one fiber texture component, with h0=[001] directions aligned with the sample plane normal and a distribution width Ω=20° (Eq. (4)). The model achieves a semi-quantitative adjustment with the 2D-diffraction experiment and a satisfactory coincidence with the electron microscopy observations.
Scanning electron micrograph of a thin sheet formed by ZnO textured nanorods on a glass substrate.
The concept of linear physical property considered in this paper is that of the magnitude K that relates in first approximation the tensor descriptors of action (X) and response (Y), measurable in a given material. Mathematically:
If the ranks of X and Y are respectively, m and n, then K is a tensor of rank r=m+n. The direct dielectric and piezoelectric effects, in tensor components notation, are described by the constitutive relationship (6):
In Eq. (6), the actions (independent variables) are the electric field strength E and the stress T. The response (dependent variable) is the electric displacement D. The considered properties are the constant stress permittivity εT=εijT (r=2) and the piezoelectric charge constant d=dijk (r=3). Additional tensor properties applied in the present work are the impermittivity β=ε−1, the compliance s, the stiffness c=s−1 and the piezoelectric constants e (T=−e·E) and g (E=−g·T).
An alternative representation of the properties is given by the longitudinal surfaces, scalar descriptors dependent on orientation [49]. The longitudinal piezoelectric surface dϕ,β, a function of the polar angle ϕ and the azimuth β, is given by Eq. (7):
The coefficients li are the direction cosines of the ϕ,β direction.
Both the tensor representations and the longitudinal surfaces of the properties satisfy the symmetry requirements summarized in the Neumann principle: The symmetry group of any macroscopic property contains as a subgroup the considered structure point group.
The usual way to present the elasto-piezo-dielectric tensors is by using the compact matrix notation [50,51]. In this one, piezoelectricity is represented by a 3×6 matrix and elasticity with 6×6 matrices. The methodology for measuring the mentioned properties is described in [52–54]. The primary reference for material properties databases is the Landolt–Bornstein's classic work [55,56]. The Materials project[57,58], from California's University at Berkeley, offers numerous theoretically calculated properties. The database Material Properties Open Database (MPOD) [24] facilitates free access to a relatively wide collection of single crystal's tensor properties, experimentally determined.
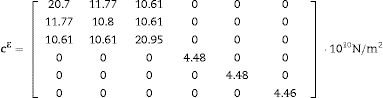
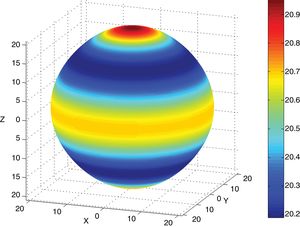
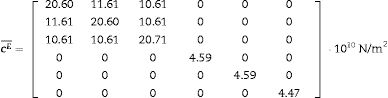
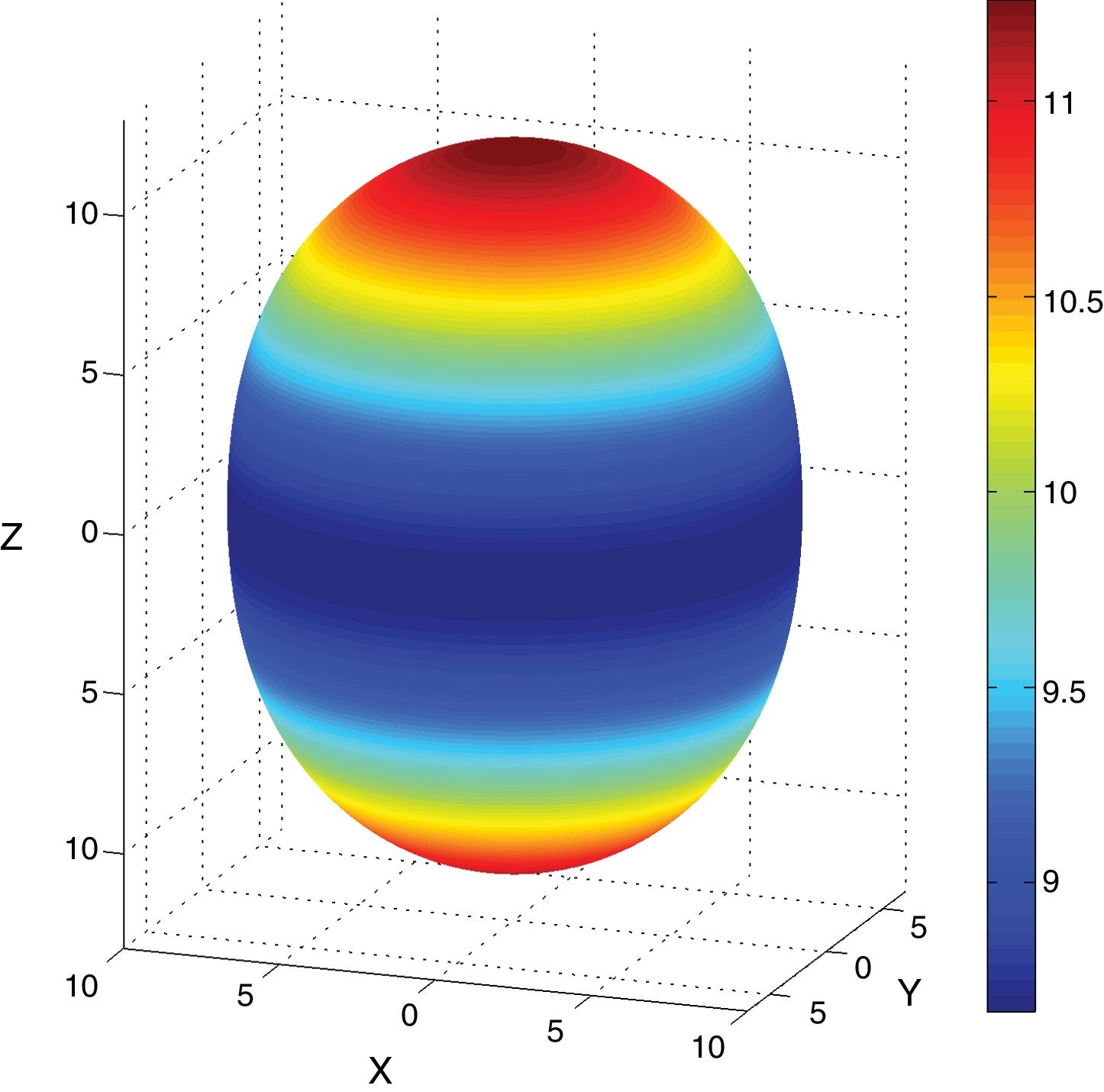
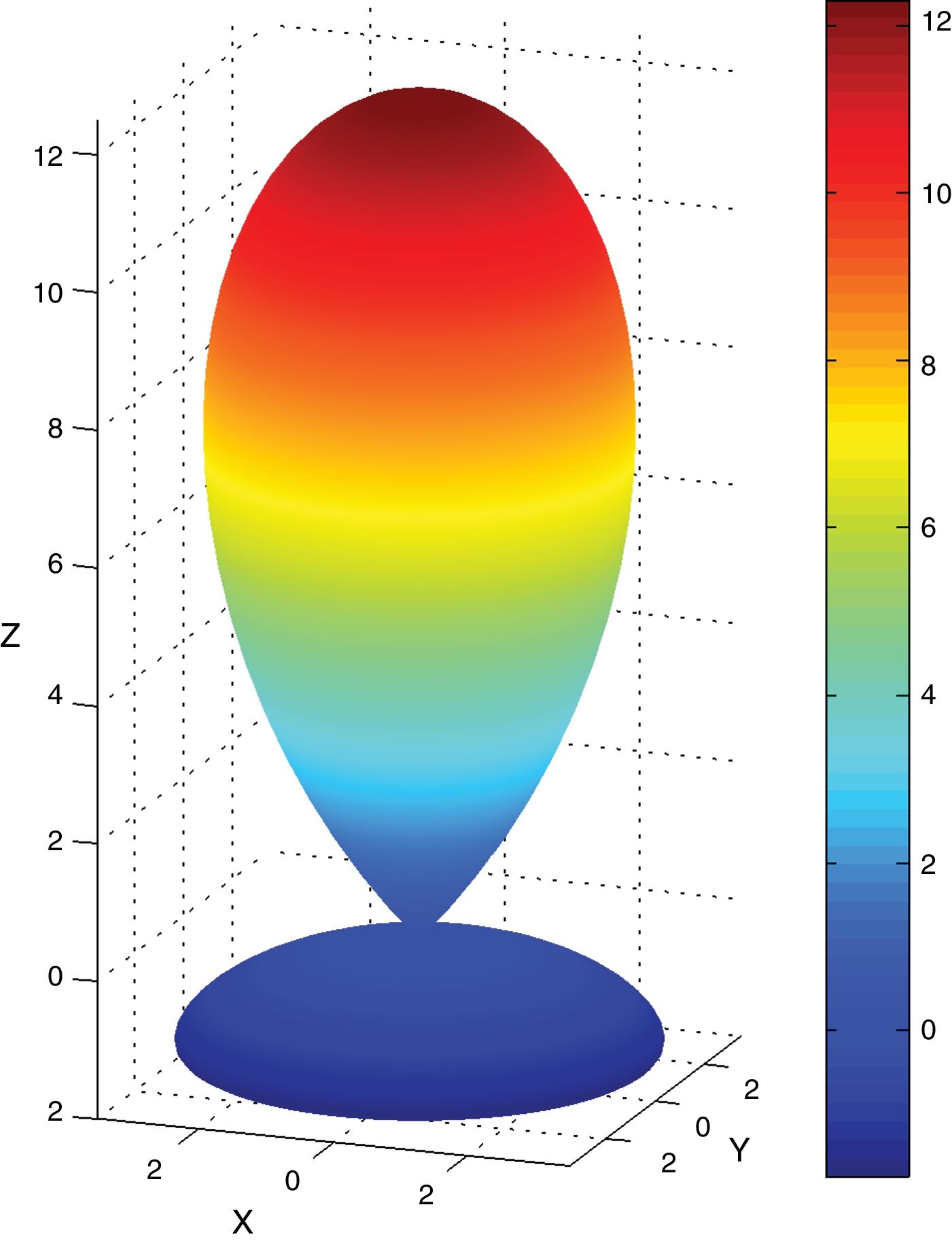
Eqs. (8)–(10) and Figs. 5–7 show a selection of ZnO single crystal elasto-piezo-dielectric matrices and their surface representations. Numerical data were taken from Kobiakov [59]. The symmetry groups of all the properties’ surfaces include the structural symmetry point group (6mm) as a subgroup.
The effective magnitude Keff that characterizes a tensor property of a polycrystalline macroscopic body is the tensor that links the macroscopic action X¯ with the macroscopic response Y¯:
A first approximation to Keff can be obtained by calculating the average tensor K¯ from the individual crystals’ properties that form the polycrystal. Following Bunge [39] the crystal orientation dependence of the properties is taken into account through the use of the ODF, f(τ), as a statistical weight factor:
The ODF represents the volumetric fraction dV/V of crystals with orientation around the point τ=φ1,ϕ,φ2 in the orientation space, known as Euler's space.
The average of K is calculated by application of Eq. (13):
K′τ is the expression of the K tensor transformed to the orientation of the crystal coordinate system in the τ orientation.
To illustrate the indicated procedure, the calculation of the average piezoelectric charge constant d for the ZnO textured thin film analyzed in Section 2 is described next.
The starting data are the single crystal tensor d and the axial texture characterization. Eq. (9) represents the single crystal piezoelectric tensor. Texture characteristics (h0=[001], Ω=20°) are those derived from the considered 2D-diffraction experiment.
The particular expression of (13) for this case, in terms of the components d¯ijk of the average piezoelectric tensor d¯ is Eq. (14).
The coefficients aim are the elements of matrix A that transforms the coordinate system of the sample into the rotated crystal system according to the angles φ1,ϕ,φ2:
Eq. (16) shows the result of performed calculations
It is worth comparing the obtained d¯33=9.06 pC/N with the measured d33=7.4pC/N, reported by Muralt [60] for a similar ZnO textured thin film. The coincidence is semi-quantitative.
Voigt, Reuss and Hill approximations. GISELLE programNext, we consider in more detail the role of the average K¯ as an approach to the effective property Keff: According to Bunge [43], Eq. (17) represents a valid representation of the role of averaging on polycrystal physical properties:
The average K¯ is a good approximation to the effective property Keff in case the independent variable X remains constant in the entire volume of the sample (ΔX(r)=0). The analysis of various configurations, paying close attention to the Eq. (17), leads to the approximations of Voigt (“parallel” configuration), Reuss (“series” configuration) and Hill (average of the averages according to Voigt and Reuss). The Voigt, Reuss and Hill approximations require particular precautions when it comes to the coupling properties (for example: piezoelectricity, magnetostriction, magnetoelectricity).
The piezoelectric charge constant d, defined by the relations D=d·T; S=d·E satisfies the invariance of T in a Reuss configuration (series geometry), but the invariance of E only applies to the Voigt approximation (parallel structure).
The present path to estimate the effective properties, particularly the piezoelectric charge constant d, begins by discriminating (say, by microscopy) if the Voigt, Reuss, or Hill approach is preferable. The pertinent independent elastic and electrical variables are selected, the tensors of the related properties are averaged and, if necessary, the relevant averages are combined by means of known relationships.
Below are presented, in a compact manner, the calculation schemes for the estimation of deff according to the Voigt, Reuss and Hill approximations (VRH).
Voigt approximation: Taking the inverse pole figure (IPF) and the single crystal's properties as data, e¯ and cE¯ are calculated (Eq. (13)). The inverse of cE¯ is sE¯Voigt. We determine dVoigt¯:
Reuss approximation: The g and βT averages are calculated. From βT¯, we determine εT¯Reuss. dReuss¯ is calculated:
Finally:
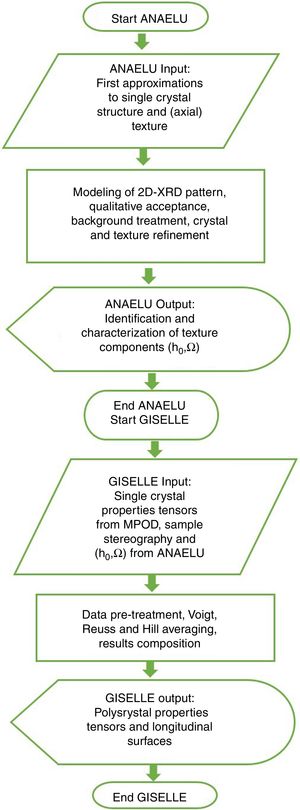
In order to perform the required tensor calculations, the programs’ system GISELLE (Global Integration System for Estimating Longitudinal and Lateral Effects) has been developed.
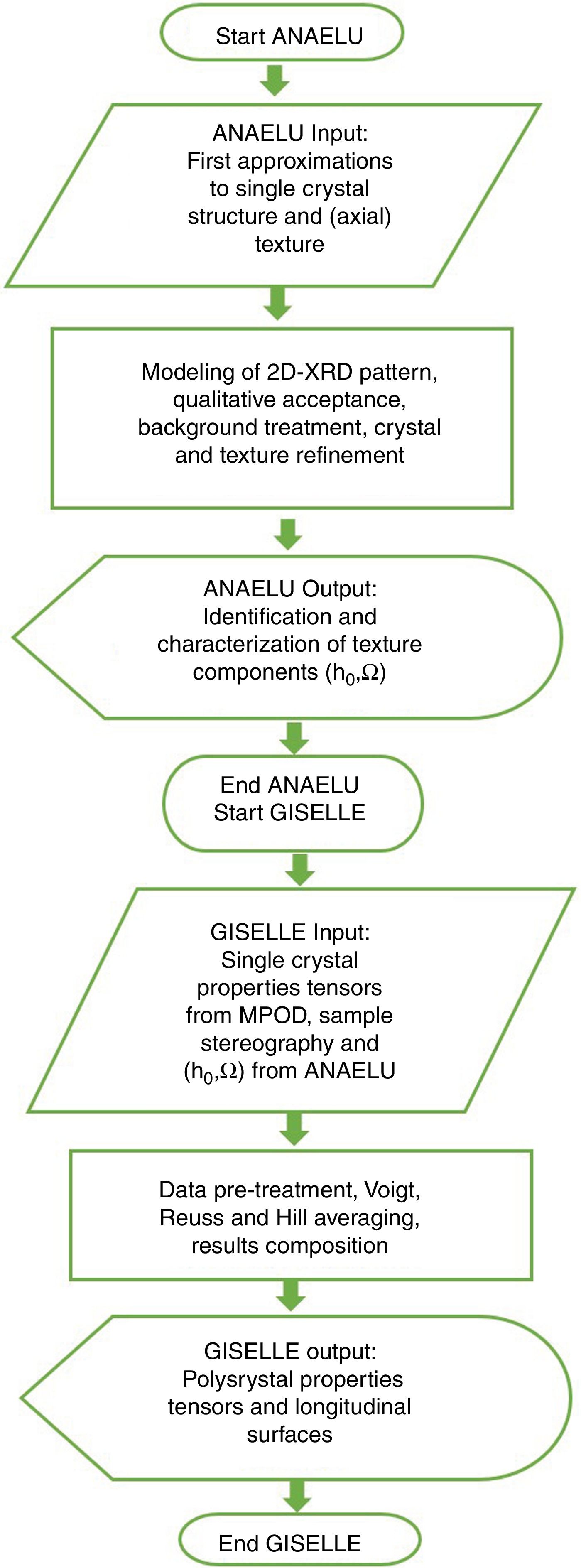
Fig. 8 shows the block diagram of the complete ANAELU→MPOD→GISELLE procedure. The working sequence is as follows: The IPF parameters (preferred orientation h0 and width distribution Ω) are determined by means of the ANAELU program. Several matrices of the elasto-piezo-dielectric tensors can be found in MPOD. Mentioned data are given to GISELLE and the effective properties are estimated following the Voigt, Reuss and/or Hill schemes.
The developed codes are open source and are provided at the request of the interested party.
A VRH case studyAs an application example of the proposed methodology, we reconsider the ZnO textured thin film of Sections 2 and 4. The sample microstructure, its similarity with a collection of parallel rods, suggests the Voigt (constant strain, constant electric field) condition. To apply the Voigt approximation, the single crystal tensor cE is given in Eq. (10) and e is presented in Eq. (21). Both tensors were taken from [59].
Average e¯ and cE¯ are calculated as explained earlier. The obtained results are the following:
From these, dVoigt¯ (Eq. (18)) is determined as:
For the application the Reuss procedure, required single crystal tensors are g and βT. Performing the corresponding calculations, the Reuss matrix for dReuss¯ is found to be:
Finally, the Hill approximation tensor d¯Hill is the following:
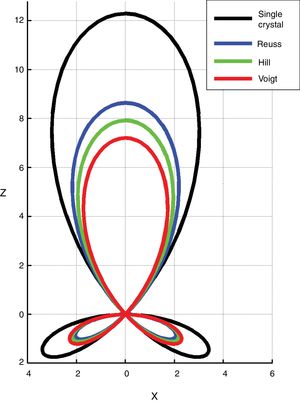
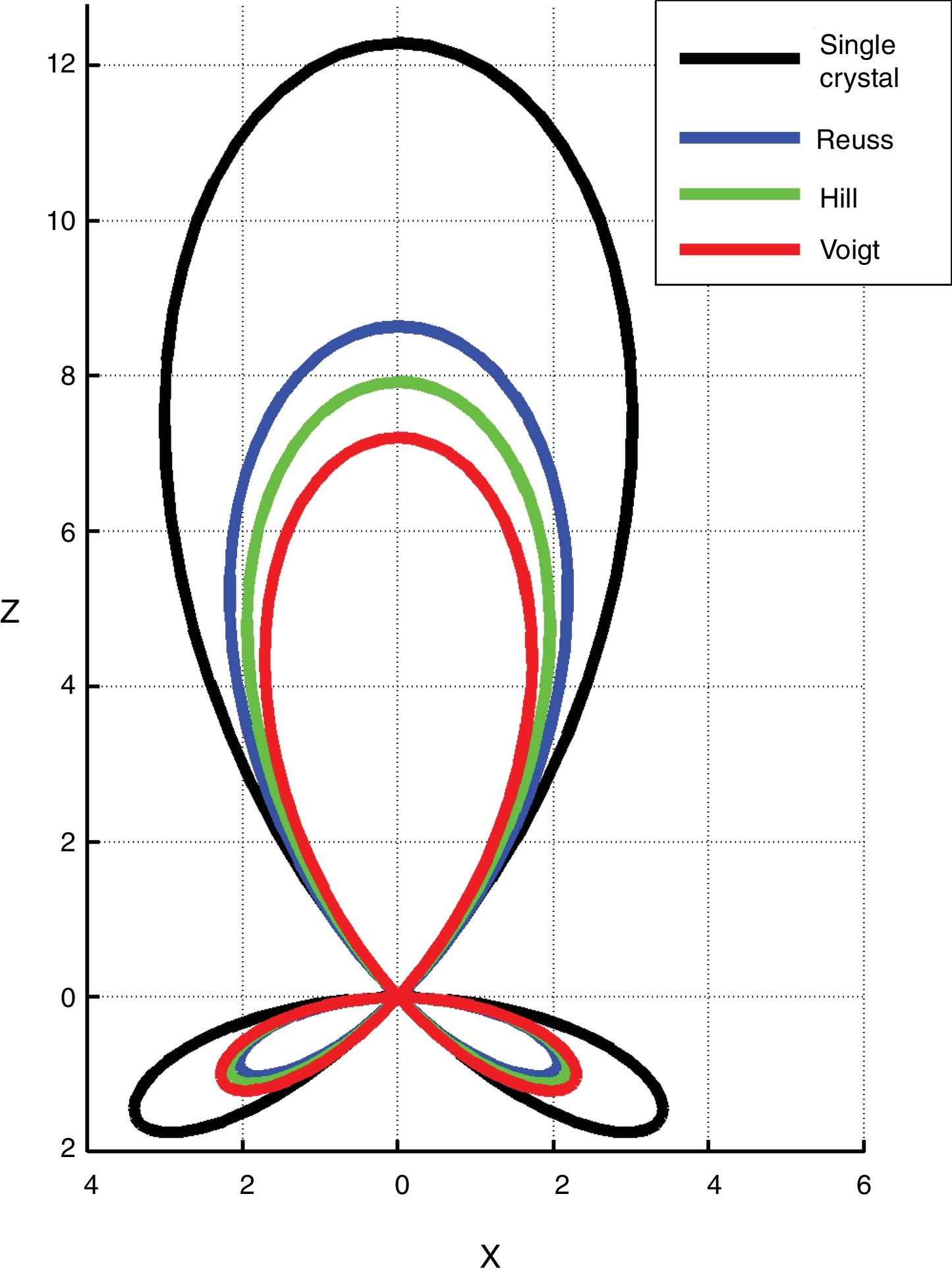
Fig. 9 shows vertical cuts of the longitudinal surfaces d(ϕ, β) of the piezoelectric charge constant of ZnO single crystal (black) and textured polycrystal with Ω=20°, under the Voigt, Reuss and Hill approximations (colored).
Vertical cut of the piezoelectric surfaces d(ϕ, β) for ZnO. The black contour corresponds to the single crystal. The colored ones represent the textured polycrystal, with Ω=20°, in the Voigt, Reuss and Hill approximations. Units in the graph are pC/N. The values to be observed in an experiment, in terms of texture influence, can be expected to be between the Voigt and Reuss bounding curves.
As general procedure, a valid criterion is to apply the Hill averaging. In this particular case, the sample parallel rods microstructure suggests the use of the Voigt approximation. In fact the d33Voigt¯ value (7.21 pC/N) practically coincides with one reported by Muralt [60]. This level of coincidence is to be considered fortuitous. Macroscopic properties depend not only on texture. As discussed by Hauke et al. [61], real samples contain additional microstructural complexity (local chemical and physical inhomogeneities, structural defects pinning domains mobility in case of ferroelectric materials, grain boundary chemistry and grain size effect) that play a role in tensors determination.
ConclusionThe occurrence of axial symmetry textures is common in piezoelectric ceramics and is one of the determining factors in the effective properties of these materials. In the present work a computer-aided methodology is proposed to estimate the contribution of texture to the physical properties of piezoceramics, given the elasto-piezo-dielectric matrices of the single crystal and the two-dimensional X-ray diffraction pattern of the considered sample.
The ANAELU program, using a Rietveld-type methodology, is capable of characterizing the inverse pole figure of the symmetry axis. MPOD database provides the user with experimentally obtained physical properties data from single crystals. The GISELLE software package approximately predicts the polycrystalline properties under the Voigt, Reuss and Hill averages, adapted to the elasto-piezo-dielectric case. The proposed system has been applied in real cases, with coincidences within the margins of the experimental tolerance.
The programs system ANAELU-MPOD-GISELLE is open source and is available at the request of the user.
The sponsorship given by Consejo Nacional de Ciencia y Tecnología (CONACYT, México), Projects 257912 and 270738, is appreciated. Support from the Project MAT2017-86168-R “Piezocerámicas ecológicas para la generación de ultrasonidos” (CSIC, Spain), is acknowledged. This research has received funding from the European Union's Horizon 2020 research and innovation program under grant agreement No. 689868, SOLSA project.







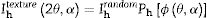
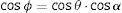
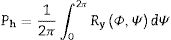
![Application of the fiber textures fundamental equation (Eq. (3)). The scheme represents the fiber axis inverse pole figure of a hypothetical sample with texture components at vectors 〈1, 1, 1〉 in reciprocal space. Crystal point group is 32. Averaging the inverse pole figure lengthwise angle ψ, along the circumference at angle ϕ with respect to reciprocal direction [1,1,1] leads to the direct pole figure P111(ϕ). Application of the fiber textures fundamental equation (Eq. (3)). The scheme represents the fiber axis inverse pole figure of a hypothetical sample with texture components at vectors 〈1, 1, 1〉 in reciprocal space. Crystal point group is 32. Averaging the inverse pole figure lengthwise angle ψ, along the circumference at angle ϕ with respect to reciprocal direction [1,1,1] leads to the direct pole figure P111(ϕ).](https://static.elsevier.es/multimedia/03663175/0000005900000005/v1_202010080725/S0366317519301001/v1_202010080725/en/main.assets/thumbnail/gr2.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)