En la aplicación de modelos estadísticos en investigación clínica, la multicolinealidad en modelos de regresión aplicados a estudios observacionales es un problema frecuente. En este documento se revisa el concepto, origen e implicaciones de la multicolinealidad. Se presentan algunos procedimientos para detectarla y los métodos que con frecuencia se emplean para corregirla. Se propone el uso de análisis de conglomerados como una estrategia alternativa en problemas que involucran covariables altamente correlacionadas.
In observational studies, multicollinearity is a common issue. In this paper, a review is presented on the concept, origin and consequences of multicollinearity. Some methods for detecting problems with this issue are presented and reviewed. Using cluster analysis is proposed as an alternative strategy for analyzing data with highly correlated covariates.
Los modelos de regresión múltiple han sido ampliamente aplicados en las ciencias de la salud. Se utilizan para modelar y explicar la relación entre varias variables independientes y una dependiente. En estudios observacionales, es común encontrar variables independientes que están fuertemente correlacionadas entre sí de tal manera que si se incluyen simultáneamente en un modelo, impiden explicar de manera correcta el efecto que cada una de las regresoras tiene sobre la variable respuesta. El análisis de componentes principales, la eliminación de variables y la regresión por cordillera son estrategias que se usan con frecuencia para resolver el problema numérico de estimación de los efectos; sin embargo, persiste el conflicto de su interpretación.
En este artículo se discute el problema de multicolinealidad en términos de sus implicaciones en la explicación de los efectos más que en la capacidad predictiva del modelo. Se presentan diferentes formas de detectar el problema y también se propone como alternativa de análisis el uso de conglomerados. La idea básica de esta propuesta es resumir la variación conjunta de las variables independientes para formar los conglomerados y después comparar los cambios en la variable respuesta al pasar de un grupo a otro.
La metodología propuesta se ejemplifica usando un problema documentado en la literatura, y se discuten las ventajas y desventajas con respecto a otras estrategias.
Modelo de regresión lineal múltipleEl modelo1 considera que existe una población de elementos Ui, a los que se les mide una variable numérica Yi que funciona conceptualmente como la dependiente o respuesta y un conjunto de variables numéricas que funcionan como independientes o regresoras, X1i,X2i,X3i,…,Xpi. Bajo el supuesto de que existe una relación lineal entre las variables respuesta y regresoras, se plantea el modelo:
son parámetros desconocidos, llamados coeficientes de regresión, y ¿i es un error aleatorio que ocurre en la unidad Ui. Los errores son independientes entre sí y tienen una distribución normal con media cero y varianza σ2 en la población de unidades, con valores fijos para las X's. La parte sistemática del modelo es el promedio poblacional de los valores de Yi en la población con valores fijos de X1, a Xp y está dado por la siguiente expresión:
La interpretación de un coeficiente de regresión, por ejemplo b3, se hace en términos del cambio en las medias poblacionales de las Y's, específicamente al pasar de una población con un valor dado de X3= x3 a otra con un valor de X3= x3 + 1 considerando que las demás X's permanecen constantes. Si algunas de las demás X's son función de X3, por ejemplo X5=X32 o X4= X3X2, entonces la interpretación previa de b3 ya no es válida, debido a la imposibilidad de mantener constantes al resto de las regresoras. En tales casos, habría que estimar las medias de Y al cambiar X3 y X5 o X3, X4 y X2 simultáneamente.
¿Qué es la multicolinealidad?El término multicolinealidad2 se refiere a que existen correlaciones fuertes entre las variables independientes, es decir, entre los coeficientes de correlación que miden el grado de asociación lineal entre 2 variables. En general, se dice que una correlación mayor, en valor absoluto a 0.9 implica multicolinealidad3. Esto es que, en algunas situaciones, diversas variables reflejan una misma propiedad general de las unidades. Por citar algunos ejemplos prácticos, se tiene que la condición económica de una familia hace que indicadores del estado de nutrición como índice de masa corporal, niveles de lípidos y pliegues tricipitales tiendan a variar juntos. Si un organismo es “grande”, tendrá sus partes y órganos grandes. Si una empresa es “exitosa”, tendrá altas ganancias, ventas altas y eficiencia en los procesos. Es importante considerar que la dependencia funcional entre algunas variables puede ser no lineal; por ejemplo, si X5=X32, se tiene que un cambio en X3 implica un cambio simultáneo en X5 que no es linealmente proporcional y que no necesariamente se detecta a través del coeficiente de correlación. En la siguiente sección presentamos, además de la correlación, algunas otras estrategias para su detección.
Detección de la multicolinealidadExisten varias formas de detectar la multicolinealidad. Es importante aclarar que en este proceso solo participan las variables independientes. Aquí se presentan 4 estrategias: la primera está basada en los coeficientes de correlación entre las variables independientes. Si uno o más coeficientes de correlación son grandes, se tiene un problema de multicolinealidad que tiende a ser más grave conforme las correlaciones se acercan al valor absoluto de 1. Sin embargo, la presencia de correlaciones grandes es una condición suficiente pero no necesaria para que exista la multicolinealidad.
Una segunda forma de identificar la multicolinealidad es usar el error estándar (EE) de los coeficientes de regresión estimados, cuya expresión es:
Donde σ2 es la varianza de los errores ¿i en cada población; SXj2 es la varianza de los valores en la muestra de la variable Xj y Rj2 es el coeficiente de determinación entre Xj y el resto de las X's; es decir, es la R2 en un modelo con Xj como dependiente, y las demás X's como independientes. Si Rj2 = 0, entonces Xj es ortogonal o independiente de las otras X's Al sustituir Rj2 = 0 en la expresión anterior, se obtiene el error estándar del coeficiente de regresión, que se tendría si solo se tiene a Xj como independiente en el modelo. Esto indica, entonces, que no existe el problema de multicolinealidad con esa variable.
En el caso opuesto, conforme Rj2 crece, también la magnitud del segundo término, llamado factor de inflación de varianza (FIV), mejor conocido por sus siglas en inglés VIF
crece y en consecuencia “infla” la varianza del coeficiente estimado. En otras palabras, debido a la multicolinealidad, la varianza de se incrementa o se infla por la relación lineal de Xj con las otras variables independientes3. La gran mayoría de los “paquetes” estadísticos tienen una opción para obtener los FIV. Uno o más FIV > 5 indican multicolinealidad4; además, los FIV pueden ayudar a identificar qué variables independientes están implicadas.
El tercer método usa los valores propios de la matriz de correlaciones entre las X's. Si el número de condición, definido como la raíz cuadrada del cociente del valor propio máximo entre el mínimo es 30 o más, entonces se dice que existe multicolinealidad de moderada a severa3. Este criterio puede variar dependiendo de los autores.
Finalmente, como cuarta alternativa se tiene la observación de la prueba de significancia F para la nulidad de todos los coeficientes y las pruebas t individuales. Si el valor de F resulta estadísticamente significativo, pero la mayoría de las t individuales para cada coeficiente no lo son, usualmente se tiene un problema de multicolinealidad.
El problema de la explicaciónCuando las variables independientes están fuertemente correlacionadas entre sí, se presentan 2 problemas de interpretación. El primer problema se tiene cuando se intenta variar una de las X's dejando fijas las otras; dada la dependencia entre las regresoras, esto no es posible en la práctica. Es decir, un cambio en una variable Xj necesariamente va asociado a cambios en las otras variables, y el efecto sobre la Y se “reparte”, por lo que la interpretación usual de las b's, como coeficientes de regresión parciales, es una idealización que no se cumple. En consecuencia, no es posible explicar la dimensión y dirección en la que cambios en los valores de una Xj por sí solos tienen sobre las medias de Y. ¿Acaso es posible imaginar un cambio en la temperatura corporal de una persona manteniendo constante la frecuencia cardíaca?, o ¿puede cambiar la concentración de lípidos de alta densidad mientras otro tipo de lípidos permanecen constantes?
El segundo problema es el derivado del uso frecuente de selección de variables independientes según su significancia. Es práctica común eliminar variables del modelo que no contribuyen significativamente a cambios en la dependiente. Sin embargo, al eliminar una variable independiente Xj que está correlacionada con Xk, se supone, incorrectamente, que cambios en Xj no afectan a las medias de Y; pero en realidad, cambios en la variable Xj ocurren simultáneamente cuando cambia la variable Xk que sí está incluida en el modelo. En este sentido, bk representa el cambio en la media de Y al cambiar Xk, pero también al cambiar todas las otras X's correlacionadas con Xk y que no están en el modelo (llamado error de especificación del modelo).
Así, entonces, la explicación del efecto de Xk sobre Y debe basarse en términos de los cambios conjuntos de Xk y las variables independientes con las que está correlacionada.
Consecuencias computacionales de la multicolinealidadLa multicolinealidad trae serias consecuencias en la estimación de los parámetros. En el modelo de regresión, los estimadores de los coeficientes por mínimos cuadrados ordinarios siguen siendo lineales, insesgados y óptimos5, pero los intervalos de confianza para los estimadores tienden a ser mucho más amplios comparados con los obtenidos en ausencia de multicolinealidad. Además, con frecuencia se obtienen coeficientes de regresión con signos contrarios a los esperados. Es común que la mayoría de las hipótesis de nulidad sobre cada coeficiente de regresión (Ho: βj= 0 para j = 1,… p) no se rechacen; sin embargo, la prueba de nulidad simultánea de los coeficientes Ho: β1= β2= … = βp= 0 sí se rechaza, sugiriendo que cambios en una o más de las variables independientes se asocian con cambios grandes en la media de la Y. Por otro lado, aun cuando uno o más coeficientes no sean estadísticamente significativos, el coeficiente de determinación del modelo completo (R2 en regresión lineal) tiende a ser grande; es decir, en conjunto las variables independientes explican un elevado porcentaje de la variación de la Y, pero no se logra identificar el efecto que individualmente tiene cada una de ellas. En las investigaciones de tipo “explicativo” o “analíticas”, es particularmente importante detectar cualquier evidencia de multicolinealidad entre regresoras antes de establecer conclusiones.
Soluciones al problema de la multicolinealidadPara solucionar el problema numérico de la multicolinealidad, tradicionalmente se recurre a eliminar variables, emplear regresión por cordillera o efectuar un análisis de componentes principales con las X's y usar los componentes como variables independientes en un modelo final.
La eliminación de una o más de las variables explicativas que están altamente correlacionadas con alguna variable que permanece en el modelo reducirá o, en el mejor de los casos, eliminará la multicolinealidad en las variables X's que quedan en el modelo, minimizando el problema de estimación de los parámetros. Sin embargo, el problema de la explicación del fenómeno quedará reducido a unas cuantas variables y se perderá la oportunidad de explicar de manera integral la influencia que todas las variables regresoras tienen sobre la respuesta. Además, la decisión sobre qué variables dejar o eliminar del modelo es un tanto arbitraria.
En el método de regresión por cordillera propuesto por Hoerl y Kennard6, se busca obtener estimadores de los coeficientes de regresión con varianzas pequeñas aunque sean sesgados (error cuadrático medio menor que el de estimadores por mínimos cuadrados). No es objetivo de este documento explicar el tratamiento matemático con detalle; sin embargo, es importante decir que la solución involucra un valor k tal que la correlación efectiva entre xi y xj ahora es, donde rij es la correlación muestral entre xi y xj. En otras palabras, todas las correlaciones son artificialmente reducidas por el factor 1/(1+ k), de tal forma que se reduce la multicolinealidad. Valores grandes de k reducen la multicolinealidad, pero incrementan el sesgo en la estimación de los coeficientes de regresión, mientras que un k = 0 no introduce sesgos, pero no corrige la multicolinealidad. Y ahora la pregunta es: ¿qué valor de k debe ser utilizado? Para valores de k (entre 0 y 1), se calculan los coeficientes de los estimadores de regresión por cordillera, se dibuja el gráfico de estos valores contra k, y con base en este gráfico se escoge el menor valor de k en el que se observe que los estimadores se estabilizan. El uso de regresión por cordillera evita los problemas numéricos en la estimación de parámetros, pero no soluciona el problema de la interpretación de los coeficientes de regresión, por lo que no es recomendable.
El análisis de componentes principales7 es un procedimiento que crea un conjunto de nuevas variables, Zi para i = 1, 2,… q con q ≤ p, no correlacionadas entre sí pero linealmente relacionadas con el conjunto original de variables estandarizadas, Xi i = 1, 2,…, p. Las ecuaciones que relacionan las Zi con las Xj son de la forma: Zi = ai1X1 + ai2X2+ … +aipXpi = 1, 2,…, q. Los valores de las αij se obtienen de manera tal que la varianza de Z1 sea la máxima posible, después se plantea una nueva Z2 que tenga máxima varianza y sea no correlacionada con Z1. Se sigue cada nueva Zi con máxima varianza y no correlacionada con las primeras Z's. A estas Z's se les llama “componentes principales”. A medida que la estructura de correlación entre las variables independientes es más fuerte, se requiere de un menor número de Z's para explicar la variabilidad de las X's. Dado que estos componentes resultan ser una mezcla de las variables originales, su interpretación en el contexto del problema generalmente no es clara y cuando participan como variables independientes en un modelo de regresión subsisten dificultades en la explicación de la influencia que cada una de las independientes originales (X's) tiene sobre la dependiente, aunque el problema numérico de estimación esté resuelto. En casos excepcionales, cuando las Z's tienen una clara interpretación en términos de las X's, la evaluación de la influencia de las X's se sustituye por la de las Z's sobre Y. Ahora las Z's en conjunto representan a las X's, y en estos casos se tiene una solución aceptable al problema de multicolinelidad.
Está claro que estas 3 estrategias tradicionales resuelven el problema numérico de la estimación de los coeficientes, pero en general, no los problemas en la interpretación de los resultados desde un punto de vista explicativo. En este artículo se propone un método alternativo para lidiar con el problema de multicolinealidad basado en el análisis de conglomerados. A partir de una tipificación de los conglomerados, la explicación de los efectos de las X's deja de ser cuantitativa e individual para ser una evaluación integral.
ConglomeradosCuando existe una fuerte estructura de correlación entre las variables X's, no es difícil identificar patrones de variación entre ellas, en el sentido de que al cambiar los valores de una variable, las otras cambian en forma concomitante, algunas aumentando y otras disminuyendo pero en forma conjunta. Es muy común observar este tipo de situaciones en la naturaleza y, en el resto de este documento serán referidas como “tipologías”.
El análisis de conglomerados es una técnica estadística que forma grupos de elementos semejantes en el interior pero diferentes entre ellos; la semejanza entre los elementos de los grupos, se valora en función de varias variables. Una vez formados los grupos, se deberán caracterizar de acuerdo con el patrón que presentan las variables; de esta manera, el conjunto de variables independientes originales se reduce a una sola variable categórica. Después, a través de un análisis de varianza de un criterio, se evalúa la asociación de la variable dependiente con esos conglomerados o tipologías. El problema de estimación de parámetros (los coeficientes de regresión) ya no se presenta; a su vez, el problema de la explicación queda resuelto, ya que se puede valorar cómo el cambio conjunto de las X's, representado por los conglomerados, produce cambios en las medias de Y.
Formación de conglomeradosCon frecuencia, el primer paso es estandarizar las variables Xi, sobre todo si se trata de variables que se miden con diferentes escalas, se busca que todas ellas tengan roles equitativos en el análisis.
Para generar los conglomerados, se tienen básicamente 2 métodos de agrupamiento: jerárquico y no jerárquico8. Independientemente del método seleccionado, una vez formados los conglomerados, es necesario caracterizarlos o tipificarlos. Es decir, averiguar qué tipo de patrones de las variables independientes se formaron en cada grupo. La estandarización previa de las variables y la elaboración de gráficas que representen sus promedios en cada conglomerado facilita esta tarea porque rápidamente se puede determinar qué variables describen mejor cada conglomerado, al identificar si se encuentran por arriba o por debajo de la media y la magnitud de su desviación.
Número de conglomeradosUn problema en todas las técnicas de aglomeración es la determinación del número de grupos, y con frecuencia la elección se hace de manera subjetiva, porque no existe un método consensuado. A continuación se describe una manera más objetiva de decidirlo: como primer paso, se forman 2 conglomerados y se identifica la pertenencia de cada elemento a esos 2 grupos, luego se repite el proceso formando 3, 4, 5, y así se continúa hasta 9 (κ = 1, 2,…, 9) (el número máximo de conglomerados que se han de explorar depende del tamaño de muestra).
Como segundo paso, se modifica la base de datos para obtener nuevas variables, las que se refieren a la identificación de los conglomerados (son categóricas) y una más donde se apilan los valores de todas las variables estandarizadas (aunque se refieran a diferentes dimensiones, son comparables por estar estandarizadas). La nueva base tendrá tantos renglones como el producto del número de variables por el tamaño de muestra, y tantas columnas como agrupamientos se hicieron más uno.
El tercer paso consiste en realizar un análisis de varianza con un criterio para cada valor de κ (la columna que contiene la identificación de los κ grupos), donde la variable dependiente es el apilado de todas las independientes originales estandarizadas; de cada análisis se obtiene el cuadrado medio del error (CME).
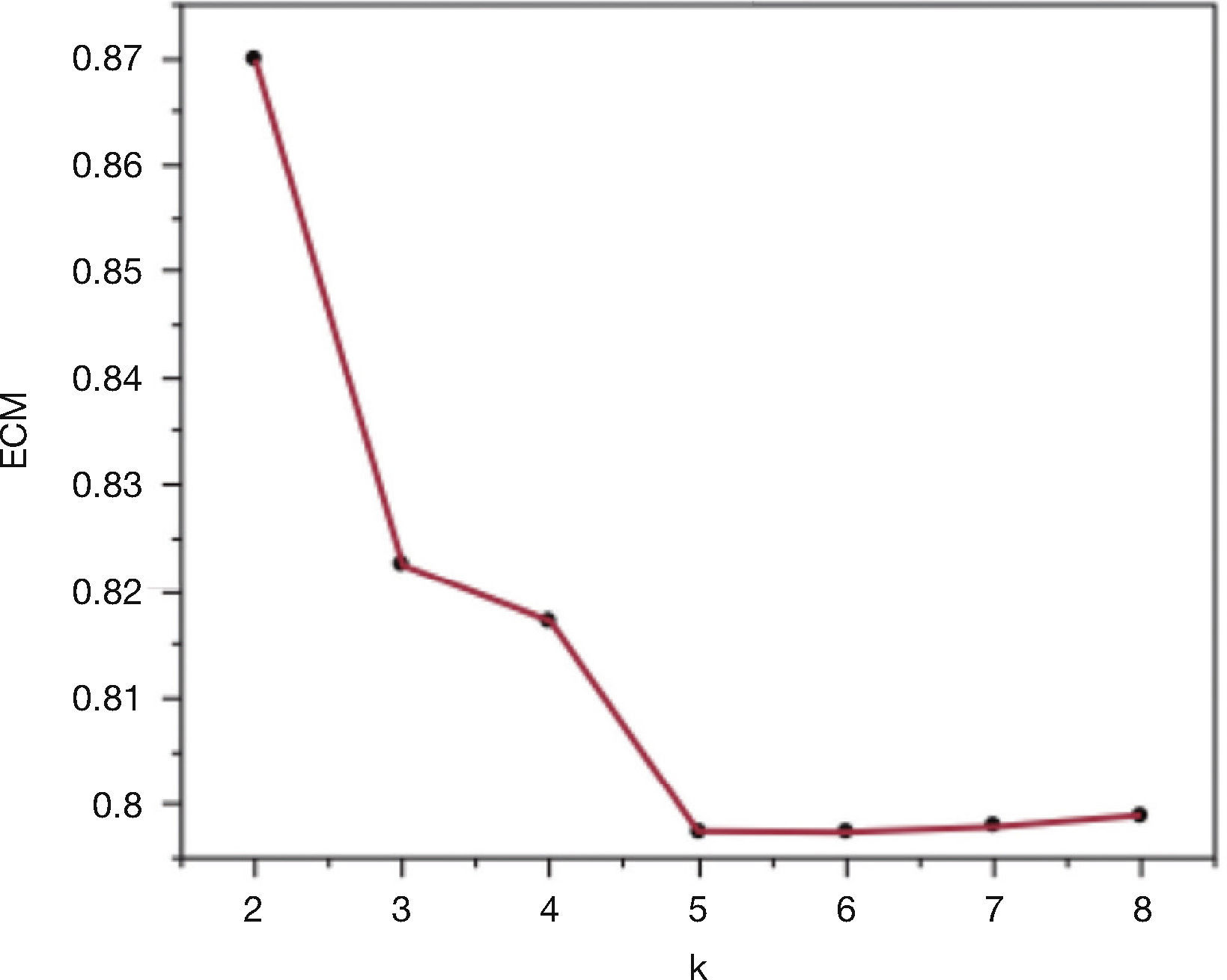
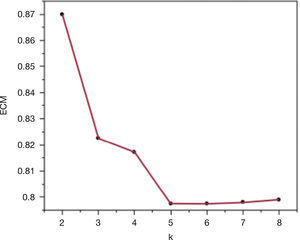
En el cuarto paso se construye la gráfica bivariada de los CME contra el número de conglomerados (κ). Se espera una gráfica de “sedimentos” (scree plot), donde disminuye el CME al tener más conglomerados. El punto donde se dé una reducción mayor y después una estabilización será el número de conglomerados recomendado.
Es importante mencionar que si se tienen elementos muy alejados del resto (valores atípicos), estos tienden a formar un solo conglomerado y se tendrá que tomar una decisión respecto a la pertinencia de estos elementos en el análisis.
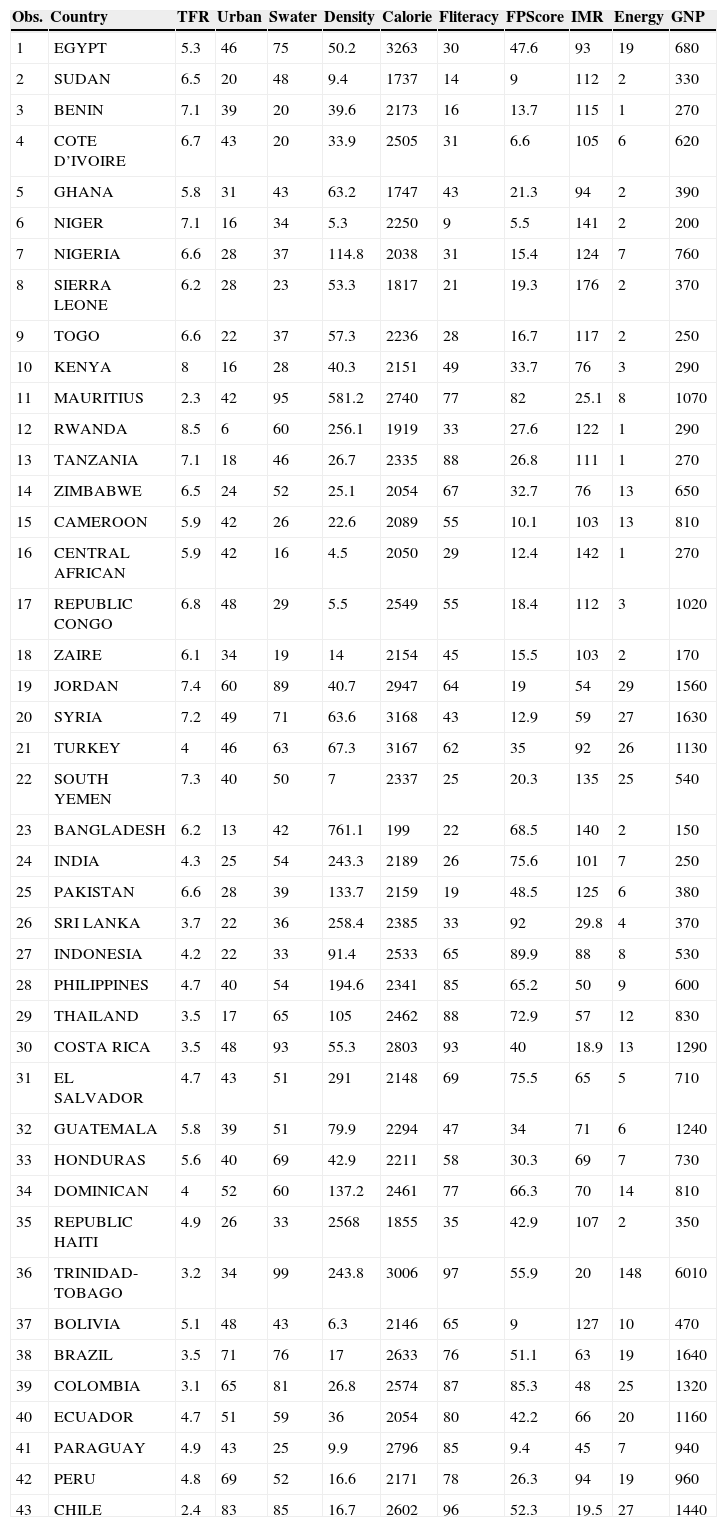
Ejemplo: en 2005, Sufian9 analizó la asociación que tienen algunas variables socioeconómicas, en conjunto con los indicadores de un programa de planificación familiar con la tasa de fertilidad. El estudio consideró a 43 países en desarrollo de Asia, América y África en 1987. Dada la fuerte estructura de correlación entre las covariables, el autor abordó el problema usando el análisis de componentes principales. Con el mismo conjunto de datos, en este artículo se ejemplifica el uso del análisis de conglomerados como solución a la multicolinealidad usando el paquete estadístico JMP10. La unidad de estudio es cada uno de los 43 países participantes, la variable dependiente es la tasa de fertilidad total (TFR: Y) y las independientes son: porcentaje de la población total que vive en áreas urbanas (URBAN: X1), porcentaje de población con acceso seguro al abastecimiento del agua (SWATER: X2), población por kilómetro cuadrado (DENSITY: X3), calorías per cápita diarias (CALORIE: X4), porcentaje de la población femenina de 15 años que puede leer y escribir (FLITERACY: X5), calificación del esfuerzo del programa de la planificación familiar basada en 4 componentes: ajuste de la política y de la etapa, servicios, mantenimiento de registros y evaluación, disponibilidad y accesibilidad (FPSCORE: X6), número de muertes infantiles por mil nacimientos vivos (IMR: X7), uso de la energía per cápita (ENERGY: X8), y producto nacional bruto per cápita (GNP: X9). Los datos se presentan en la tabla 1.
- •
Detección de la multicolinealidad. Primero se calcularon los coeficientes de correlación de Pearson. Las correlaciones más altas se identificaron entre ENERGY y GNP (r = 0.95); FLITERACY e IMR (r = –0.75) y SWATER e IMR (r = –0.67). Estos valores proporcionaron los primeros indicios sobre el problema de multicolinealidad, mismo que se confirmó al observar que el ajuste de un modelo de regresión múltiple indicaba un coeficiente de determinación R2= 0.72 con un valor P global de 0.0001, pero solo 2 coeficientes fueron significativamente diferentes de 0 y 2 factores de inflación de varianza fueron > 5 (tabla 2).
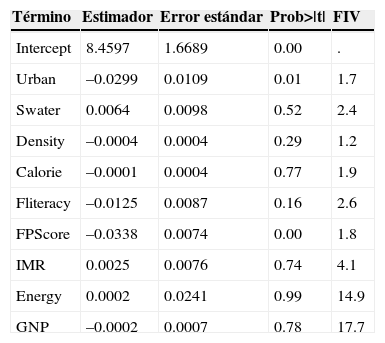
Tabla 2.Resultados del modelo de regresión múltiple donde la tasa de fertilidad total fue la variable de respuesta
Término Estimador Error estándar Prob>|t| FIV Intercept 8.4597 1.6689 0.00 . Urban –0.0299 0.0109 0.01 1.7 Swater 0.0064 0.0098 0.52 2.4 Density –0.0004 0.0004 0.29 1.2 Calorie –0.0001 0.0004 0.77 1.9 Fliteracy –0.0125 0.0087 0.16 2.6 FPScore –0.0338 0.0074 0.00 1.8 IMR 0.0025 0.0076 0.74 4.1 Energy 0.0002 0.0241 0.99 14.9 GNP –0.0002 0.0007 0.78 17.7 FIV: factor de inflación de varianza; TFR: tasa de fertilidad total.
El contraste entre el valor de R2 y los niveles de significancia de los estimadores, aunado a los valores de FIV altos, indican un problema de multicolinealidad.
- •
Formación de conglomerados. Para el ejemplo, se utilizó el método jerárquico aglomerativo de Ward con las variables independientes estandarizadas. En la figura 1, se muestra la gráfica de sedimentos (scree plot), donde se observa que con 5 conglomerados el CME tiende a estabilizarse.
Datos usados en el ejemplo. Variables socioeconómicas, indicadores de un programa de planificación familiar y tasa de fertilidad en 43 países en desarrollo de Asia, América y África
| Obs. | Country | TFR | Urban | Swater | Density | Calorie | Fliteracy | FPScore | IMR | Energy | GNP |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | EGYPT | 5.3 | 46 | 75 | 50.2 | 3263 | 30 | 47.6 | 93 | 19 | 680 |
| 2 | SUDAN | 6.5 | 20 | 48 | 9.4 | 1737 | 14 | 9 | 112 | 2 | 330 |
| 3 | BENIN | 7.1 | 39 | 20 | 39.6 | 2173 | 16 | 13.7 | 115 | 1 | 270 |
| 4 | COTE D’IVOIRE | 6.7 | 43 | 20 | 33.9 | 2505 | 31 | 6.6 | 105 | 6 | 620 |
| 5 | GHANA | 5.8 | 31 | 43 | 63.2 | 1747 | 43 | 21.3 | 94 | 2 | 390 |
| 6 | NIGER | 7.1 | 16 | 34 | 5.3 | 2250 | 9 | 5.5 | 141 | 2 | 200 |
| 7 | NIGERIA | 6.6 | 28 | 37 | 114.8 | 2038 | 31 | 15.4 | 124 | 7 | 760 |
| 8 | SIERRA LEONE | 6.2 | 28 | 23 | 53.3 | 1817 | 21 | 19.3 | 176 | 2 | 370 |
| 9 | TOGO | 6.6 | 22 | 37 | 57.3 | 2236 | 28 | 16.7 | 117 | 2 | 250 |
| 10 | KENYA | 8 | 16 | 28 | 40.3 | 2151 | 49 | 33.7 | 76 | 3 | 290 |
| 11 | MAURITIUS | 2.3 | 42 | 95 | 581.2 | 2740 | 77 | 82 | 25.1 | 8 | 1070 |
| 12 | RWANDA | 8.5 | 6 | 60 | 256.1 | 1919 | 33 | 27.6 | 122 | 1 | 290 |
| 13 | TANZANIA | 7.1 | 18 | 46 | 26.7 | 2335 | 88 | 26.8 | 111 | 1 | 270 |
| 14 | ZIMBABWE | 6.5 | 24 | 52 | 25.1 | 2054 | 67 | 32.7 | 76 | 13 | 650 |
| 15 | CAMEROON | 5.9 | 42 | 26 | 22.6 | 2089 | 55 | 10.1 | 103 | 13 | 810 |
| 16 | CENTRAL AFRICAN | 5.9 | 42 | 16 | 4.5 | 2050 | 29 | 12.4 | 142 | 1 | 270 |
| 17 | REPUBLIC CONGO | 6.8 | 48 | 29 | 5.5 | 2549 | 55 | 18.4 | 112 | 3 | 1020 |
| 18 | ZAIRE | 6.1 | 34 | 19 | 14 | 2154 | 45 | 15.5 | 103 | 2 | 170 |
| 19 | JORDAN | 7.4 | 60 | 89 | 40.7 | 2947 | 64 | 19 | 54 | 29 | 1560 |
| 20 | SYRIA | 7.2 | 49 | 71 | 63.6 | 3168 | 43 | 12.9 | 59 | 27 | 1630 |
| 21 | TURKEY | 4 | 46 | 63 | 67.3 | 3167 | 62 | 35 | 92 | 26 | 1130 |
| 22 | SOUTH YEMEN | 7.3 | 40 | 50 | 7 | 2337 | 25 | 20.3 | 135 | 25 | 540 |
| 23 | BANGLADESH | 6.2 | 13 | 42 | 761.1 | 199 | 22 | 68.5 | 140 | 2 | 150 |
| 24 | INDIA | 4.3 | 25 | 54 | 243.3 | 2189 | 26 | 75.6 | 101 | 7 | 250 |
| 25 | PAKISTAN | 6.6 | 28 | 39 | 133.7 | 2159 | 19 | 48.5 | 125 | 6 | 380 |
| 26 | SRI LANKA | 3.7 | 22 | 36 | 258.4 | 2385 | 33 | 92 | 29.8 | 4 | 370 |
| 27 | INDONESIA | 4.2 | 22 | 33 | 91.4 | 2533 | 65 | 89.9 | 88 | 8 | 530 |
| 28 | PHILIPPINES | 4.7 | 40 | 54 | 194.6 | 2341 | 85 | 65.2 | 50 | 9 | 600 |
| 29 | THAILAND | 3.5 | 17 | 65 | 105 | 2462 | 88 | 72.9 | 57 | 12 | 830 |
| 30 | COSTA RICA | 3.5 | 48 | 93 | 55.3 | 2803 | 93 | 40 | 18.9 | 13 | 1290 |
| 31 | EL SALVADOR | 4.7 | 43 | 51 | 291 | 2148 | 69 | 75.5 | 65 | 5 | 710 |
| 32 | GUATEMALA | 5.8 | 39 | 51 | 79.9 | 2294 | 47 | 34 | 71 | 6 | 1240 |
| 33 | HONDURAS | 5.6 | 40 | 69 | 42.9 | 2211 | 58 | 30.3 | 69 | 7 | 730 |
| 34 | DOMINICAN | 4 | 52 | 60 | 137.2 | 2461 | 77 | 66.3 | 70 | 14 | 810 |
| 35 | REPUBLIC HAITI | 4.9 | 26 | 33 | 2568 | 1855 | 35 | 42.9 | 107 | 2 | 350 |
| 36 | TRINIDAD-TOBAGO | 3.2 | 34 | 99 | 243.8 | 3006 | 97 | 55.9 | 20 | 148 | 6010 |
| 37 | BOLIVIA | 5.1 | 48 | 43 | 6.3 | 2146 | 65 | 9 | 127 | 10 | 470 |
| 38 | BRAZIL | 3.5 | 71 | 76 | 17 | 2633 | 76 | 51.1 | 63 | 19 | 1640 |
| 39 | COLOMBIA | 3.1 | 65 | 81 | 26.8 | 2574 | 87 | 85.3 | 48 | 25 | 1320 |
| 40 | ECUADOR | 4.7 | 51 | 59 | 36 | 2054 | 80 | 42.2 | 66 | 20 | 1160 |
| 41 | PARAGUAY | 4.9 | 43 | 25 | 9.9 | 2796 | 85 | 9.4 | 45 | 7 | 940 |
| 42 | PERU | 4.8 | 69 | 52 | 16.6 | 2171 | 78 | 26.3 | 94 | 19 | 960 |
| 43 | CHILE | 2.4 | 83 | 85 | 16.7 | 2602 | 96 | 52.3 | 19.5 | 27 | 1440 |
GNP: producto nacional bruto; IMR: tasa de mortalidad infantil; TFR: tasa de fertilidad total.
Fuente: Sufian9.
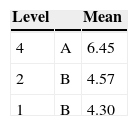
Los tamaños de muestra por grupo en ese orden, son 9, 10, 1, 22, 1. Los 2 “conglomerados” formados por un solo elemento son: Trinidad y Tobago y Haití, por lo que en el resto del documento esos 2 países se consideran como observaciones atípicas y el análisis se concentra en los 3 conglomerados restantes, mismos que serán referidos como los conglomerados 1, 2 y 4.
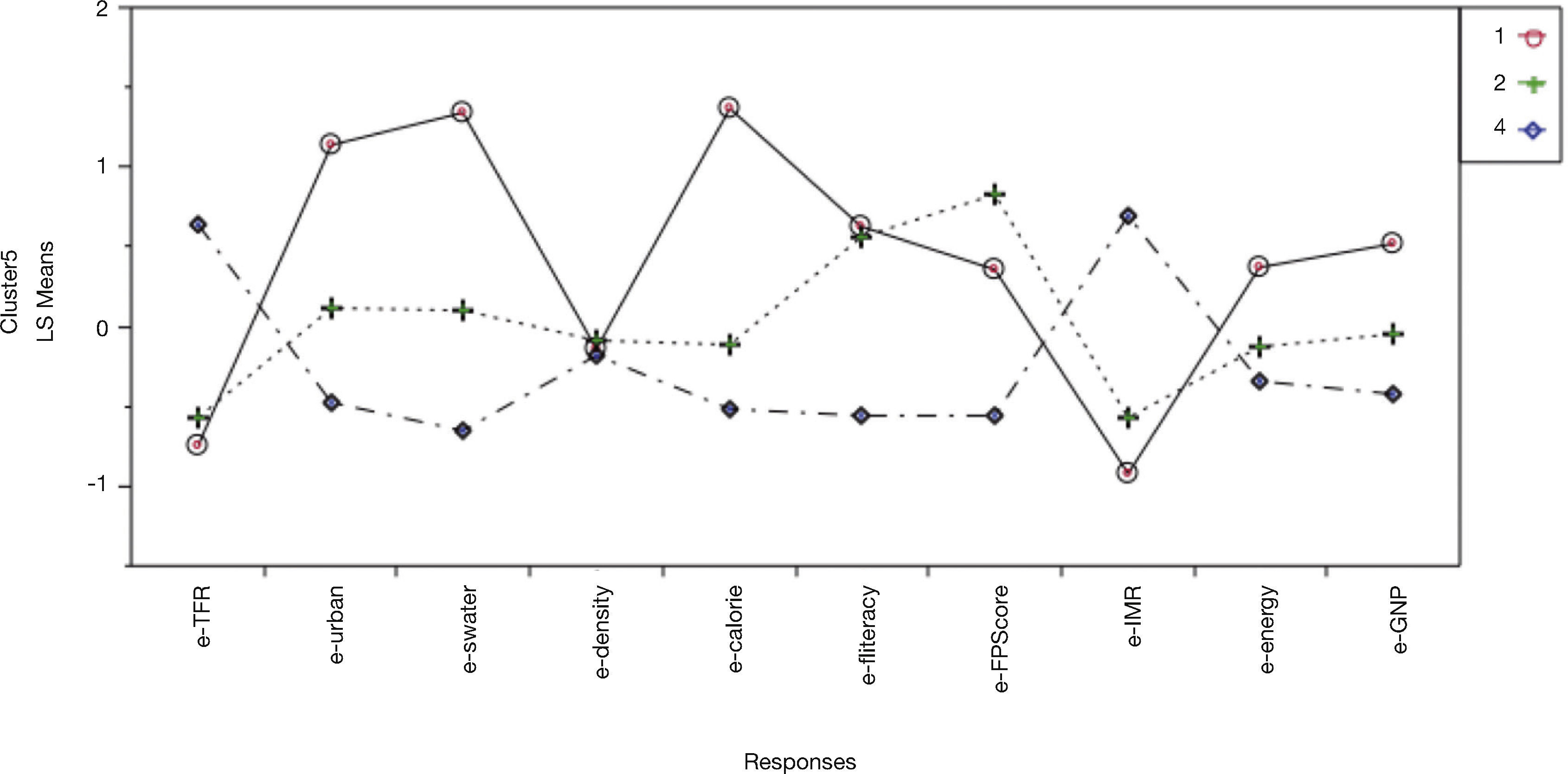
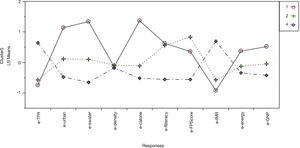
Caracterización de los conglomeradosLa figura 2 muestra las medias de cada variable independiente estandarizada, donde cada línea representa un conglomerado. Los países que se agruparon en el conglomerado 1 se caracterizan por tener una tasa de mortalidad infantil baja, son principalmente urbanos, con un producto nacional bruto per cápita (GNP) que en promedio supera al de los otros conglomerados, cuentan con buenos servicios y una calificación regular para el esfuerzo del programa de planificación familiar. El conglomerado 2 está formado por países con menor porcentaje de población urbana que tienen un GNP intermedio y mortalidad infantil baja pero con un esfuerzo muy alto del programa de planificación familiar. Es notable que en este grupo, aunque más pobre y con menos servicios, la tasa de mujeres alfabetas es igual a la observada en grupo 1. En el conglomerado 4 se encuentran agrupados los países con población principalmente rural que cuentan con pocos servicios, tienen altas tasas de mortalidad infantil, y valores bajos en GNP, así como en el porcentaje de mujeres que sabe leer y escribir; además, la calificación del esfuerzo del programa de planificación familiar es inferior al obtenido en los otros grupos. En general, a partir de esta caracterización los conglomerados podrían describirse como los países en vías de desarrollo “ricos”, “intermedios” y “pobres”, respectivamente. La densidad poblacional no parece asociarse con ninguno de los conglomerados.
Asociación de la dependiente con conglomeradosEn el análisis de varianza se obtiene un valor de P de 0.0006. Al efectuar la prueba de Tukey, se obtienen los resultados que se muestran en la tabla 3. De aquí se interpreta que los grupos 1 y 2 son muy semejantes en TFR pero ambos con tasas menores que la del grupo 4 (los pobres). Es posible sugerir la hipótesis de que los países del conglomerado 2 alcanzan TFR e IMR bajas, semejantes a las del grupo 1, porque el alfabetismo de las mujeres y el esfuerzo de los programas de planificación familiar compensan las deficiencias de servicios.
DiscusiónEn este documento se revisó el problema de multicolinealidad entre variables independientes y sus principales consecuencias en el uso “explicativo” de los modelos lineales. Se plantearon algunos procedimientos que se llevan a cabo para detectarla, así como diferentes estrategias tradicionales para corregirla. Por otro lado, se presentó un método alternativo basado en el análisis de conglomerados, que a través de una interpretación integral de las variables permite dar respuesta al problema explicativo de la regresión.
La presencia de multicolinealidad impide valorar adecuadamente la influencia individual de las variables independientes sobre la dependiente. La solución que aquí se propone, cuando se trata de ver la relación de la dependiente con las independientes, es hacer un análisis de conglomerados. La idea es pasar de p variables independientes a una sola variable categórica formada por los conglomerados, que representan la variación conjunta de las variables independientes. El problema se reduce a la evaluación de la relación de la variable dependiente con los conglomerados.
Sufian, en su artículo9, no interpreta la asociación de TFR con los componentes principales; a cambio, asevera que “los coeficientes no estandarizados muestran que por una unidad de incremento en el puntaje de esfuerzo del programa de planificación familiar el número de hijos por mujer disminuye en 0.033; un incremento de 1% en la población urbana se asocia con una reducción de 0.031 niños por mujer; también que un incremento de 1% en la tasa de alfabetismo femenil está asociado con una reducción de 0.012 niños por mujer; y que un incremento de la mortalidad infantil de 1 por 1000 nacimientos vivos esta asociado con un incremento de 0.004 niños por mujer”. Desde el punto de vista de los autores de este documento, este es precisamente el punto crítico de la interpretación, ya que al efectuar los componentes principales y después la regresión de TRF sobre ellos, para obtener combinaciones de los coeficientes, se resuelve el problema numérico de la multicolinealidad, pero subsiste el problema de la explicación. Al interpretar el efecto individual de cada variable independiente sobre la dependiente como el cambio en cada variable manteniendo constantes a las demás, se idealiza una situación que en la realidad no puede sostenerse, ya que las variables cambian de manera simultánea. En contraste, el método aquí propuesto permite hacer una interpretación integral de las variables recreando diferentes escenarios generados a través de los conglomerados, considerando así el cambio simultáneo de variables independientes.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Se agradece la colaboración de la licenciada Deisy Lozano Salado, de la Universidad Autónoma de Guerrero, durante el “verano de la investigación” de 2007.