Introducción
Si entre los diversos tipos de artículos de la bibliografía médica tuviésemos que elegir a un paria, uno de los candidatos aventajados sería, sin duda, el que se refiere a la investigación sobre pruebas diagnósticas (PD), especialmente si lo comparamos con el protagonismo de los artículos dirigidos a investigar la efectividad de las actuaciones terapéuticas1. Ello no deja de ser paradójico si tenemos en cuenta que, para que la efectividad de un tratamiento se investigue correctamente, se necesita antes de un diagnóstico correcto2,3, apoyado en el buen rendimiento y la acertada indicación de, generalmente, más de una PD.
La intención de este artículo no es examinar los diversos enfoques posibles de una investigación en PD, ni los grados de evidencia, cuando tal investigación se plantea como un ensayo clínico, con sus diversas fases4, o como otro tipo de diseño, que existen al igual que en los estudios sobre actividades terapéuticas. Tampoco se trata de relatar los posibles sesgos o debilidades en su diseño o desarrollo, que los hay y muchos5, o las normas que se aconseja seguir para que sean estudios de calidad y se publiquen correctamente, que aquí se denominan STARD6, al igual que para los ensayos terapéuticos están las normas CONSORT7. El objetivo es mucho más sencillo: mostrar cómo deben interpretarse y para qué sirven ciertos índices diagnósticos básicos que aparecen en este tipo de trabajos8.
Las matemáticas fundamentales
La estadística bayesiana gira alrededor del teorema de Bayes, o de las probabilidades condicionales, o sea, la probabilidad de que algo ocurra si ha ocurrido antes otra cosa, y esto es en realidad la base de todo proceso diagnóstico. Lo característico del bayesianismo es que el resultado que ofrece una investigación en concreto hay que mezclarlo con el conocimiento previo que existe sobre la cuestión, para acabar obteniendo un nuevo conocimiento, que no es otra cosa que el conocimiento previo actualizado tras el resultado de la investigación puntual. Precisamente esto lo diferencia del proceder estadístico clásico, valores p incluidos, que sólo se dirige a la investigación puntual, en todo caso enfrentada a una teoría general, pero cuya probabilidad de ser cierta en ningún momento se tiene en cuenta para los cálculos. Existe una forma muy comprensible de formular el teorema de Bayes:
Probabilidad previa #009;de algo x Resultado de un estudio = Probabilidad posterior.
Visto así, muestra su clara relación con el proceso diagnóstico:
Probabilidad de partida de una enfermedadx Resultado de una PD = Probabilidad posterior (probabilidad previa #009;actualizada) tras la PD.
Estas probabilidades posteriores son los llamados valores predictivos y es realmente lo que hace que se asiente o no un diagnóstico. Es más, si se indicara otra PD a continuación, la probabilidad de partida sería esta vez la antigua probabilidad posterior, y así sucesivamente, hasta aclarar debidamente el diagnóstico final, cuando la postrera probabilidad posterior nos pareciera suficientemente alta, en sentido positivo o negativo. Para manejar estas fórmulas hay que introducir las probabilidades en forma de odds ratio. Después, el resultado hay que transformarlo de nuevo a probabilidad.
Las matemáticas aplicadas
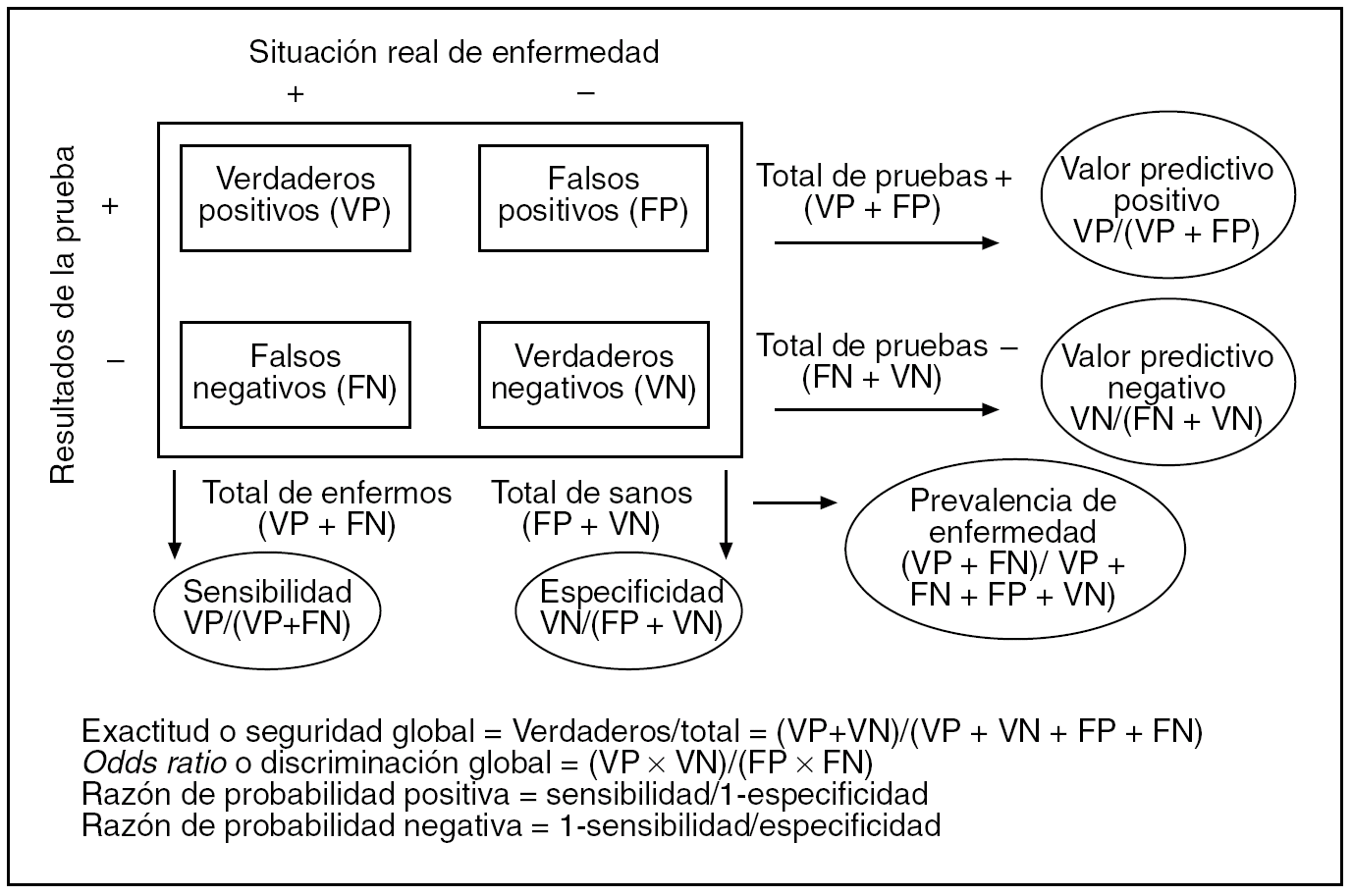
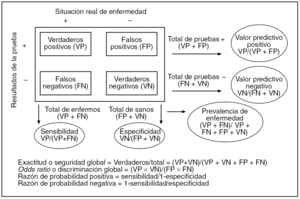
Toda investigación sobre PD parte del conocimiento de que una enfermedad existe o no en un grupo de individuos de una muestra. Se necesita, pues, algo que defina este punto. Concretamente, se precisa una PD suficientemente acreditada en ese momento que puntualice la existencia real de enfermedad. Es lo que se llama prueba patrón de referencia, o gold standard, que a veces será una sola prueba, otras una serie de pruebas, el resultado del seguimiento de los casos, etc. No siempre este patrón será todo lo fiable que nos gustaría, pero para el desarrollo del artículo supondremos que lo es. A él se enfrenta la PD en evaluación que llamaremos test. Para definir el resultado de un test es preciso aplicar un criterio diagnóstico, cuya menor o mayor claridad y facilidad de interpretación serán también cruciales para el resultado de la evaluación. Muchas veces, tanto el patrón como el test presentarán un resultado dicotómico, positivo o negativo, con lo cual su enfrentamiento se podrá resumir en una tabla de contingencia 2 x 2 (2 filas y 2 columnas), como la de la figura 1. La prueba patrón suele colocarse en columnas y el test en filas, para mayor claridad.
Fig. 1. Tabla de contingencia para la evaluación de una prueba diagnóstica de resultado dicotómico.
La combinación de positivos y negativos del patrón y del test configura los verdaderos y los falsos resultados del propio test. Los totales (o marginales, en lenguaje más técnico) de filas y columnas tienen interés sólo para el cálculo de los índices diagnósticos que definen al test, aunque de ellos surge uno con interés propio y trascendental, que es el total de la columna de los auténticos enfermos, ya que determina la prevalencia de enfermedad, lo que denominábamos probabilidad previa. La combinación por columnas de verdaderos y falsos da lugar a los índices diagnósticos fundamentales que definen a un test: la sensibilidad y la especificidad. Estos 2, junto con la prevalencia, y de acuerdo con la fórmula de Bayes que mostrábamos antes, originan los valores predictivos positivo y negativo (VPP y VPN, respectivamente), que son probabilidades posteriores y determinan el auténtico rendimiento diagnóstico del test. En la misma figura 1 se ofrecen otros índices diagnósticos que sintetizan, de una forma más global, la capacidad diagnóstica del test. Hay que destacar a las razones de probabilidad (likelihood ratios en inglés), tanto positivas como negativas, pues son un resumen unificado de la sensibilidad y la especificidad.
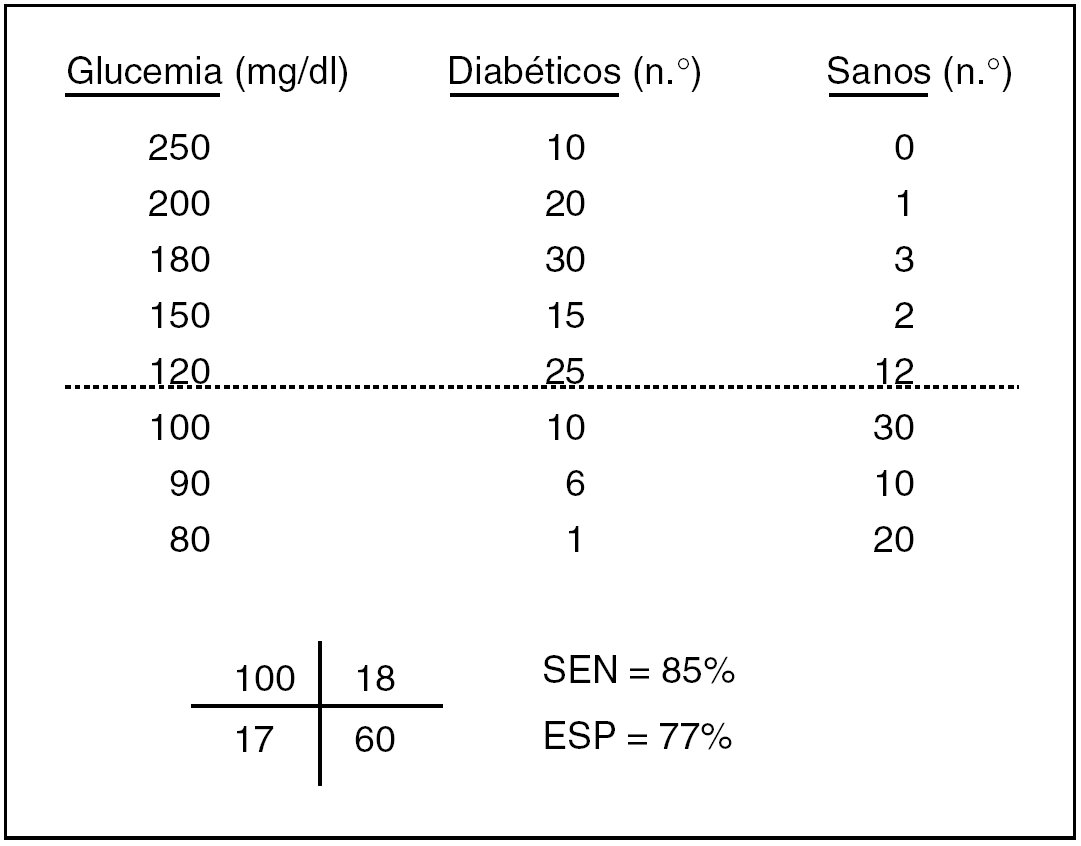
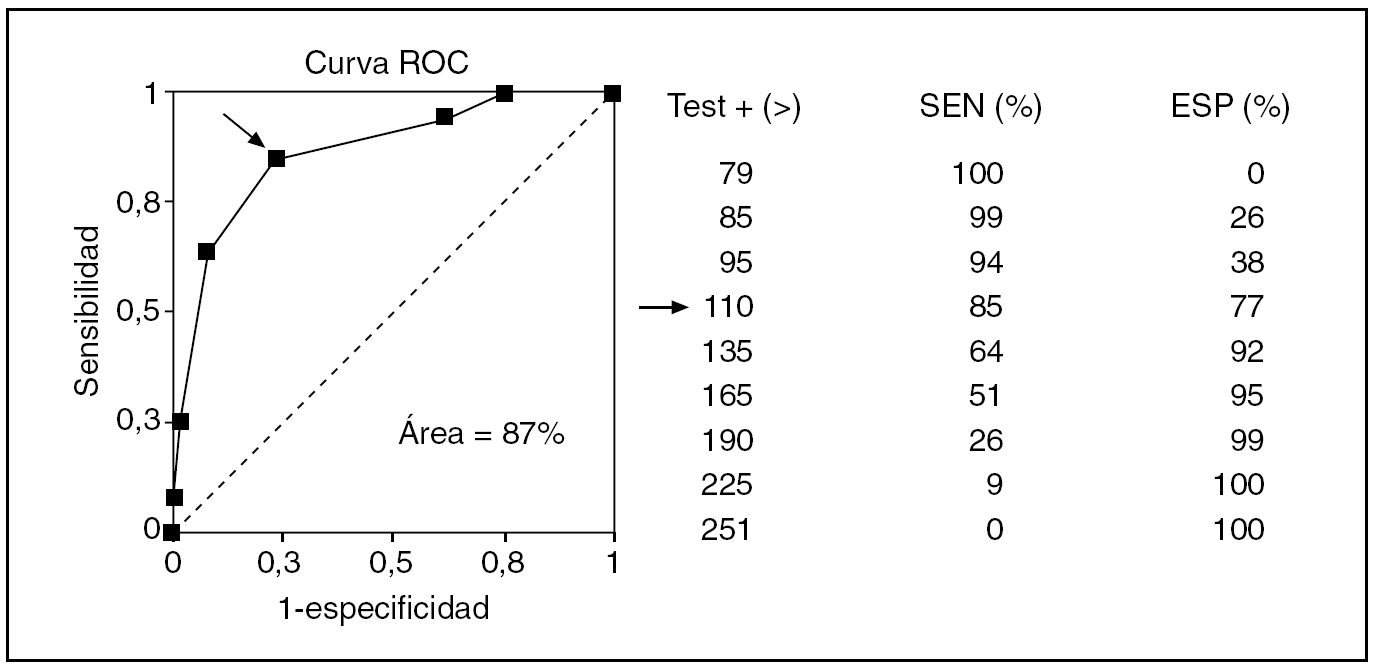
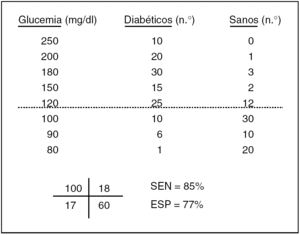
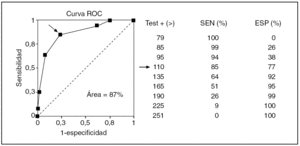
Cuando el resultado de un test no es una cualidad positiva o negativa sino una magnitud, como es el caso de un resultado de bioquímica hemática, la cosa cambia algo, aunque al final todo acaba en una tabla 2 x 2. En la figura 2 se exponen las determinaciones de glucemia que, por ejemplo, podrían darse en una muestra de diabéticos y de sanos. No es una tabla 2 x 2, pero al colocar la línea horizontal discontinua que indica el límite de lo normal, se transforma en una tabla 2 x 2, con la suma de los casos que caen en cada casilla, lo que da lugar, a su vez, a unos índices diagnósticos propios y peculiares de ese límite de normalidad. Si ese nivel o corte de normalidad lo elevamos o descendemos, estos índices cambian: si ascendemos ganamos especificidad y perdemos sensibilidad, y viceversa. Con estos datos, se puede confeccionar la llamada curva ROC (fig. 3), con la sensibilidad, y la especificidad (su complementario en este caso), que se obtienen sucesivamente moviendo arriba y abajo la línea discontinua de la figura 2 que indica el límite de normalidad. Esta curva ROC, en concreto la proporción de la superficie total o área que determina por debajo (area under curve [AUC]), define la eficacia discriminadora del test, igual que la exactitud o la seguridad en el caso de un test de resultado dicotómico.
Fig. 2. Esquema básico para la evaluación de una prueba diagnóstica de resultado cuantitativo. SEN: sensibilidad; ESP: especificidad. La línea discontinua indica uno de los posibles cortes de normalidad.
Fig. 3. Curva de ROC (características operativas del receptor) confeccionada a partir de diferentes cortes posibles de normalidad. La flecha señala el corte de máximo rendimiento conjunto en sensibilidad (SEN) y especificidad (ESP).
Generalmente, cualquier índice diagnóstico se expresa o se reporta en forma de porcentaje, a excepción de los odds ratio, y de las razones de probabilidad, que son odds, es decir, cocientes de opuestos. Todos ellos, incluso el porcentaje de superficie bajo la curva ROC, se deben acompañar de su intervalo de confianza, habitualmente con el 95% de seguridad. En el caso de los porcentajes, y en este terreno de las PD, nunca se debe olvidar que el valor nulo o cero de la escala es el 50%. En efecto, un índice cuya estimación puntual sea el 50%, o cuyo intervalo de confianza contenga ese 50%, equivale a una utilidad diagnóstica 0, pues sería igual que si diagnosticáramos echando una moneda al aire; es más, un valor en porcentaje menor del 50% nos estaría indicando que el test es más engañoso que certero. En el caso de los índices expresados en odds, el valor nulo sería el 1. Pero, por otra parte, también hemos de ser conscientes de que cuando en los resultados de la evaluación de un test veamos unos índices óptimos, es decir, porcentajes que igualan o superan el 80%, y el límite inferior de su intervalo de confianza se acerque mucho, iguale, o descienda de ese 50%, generalmente no será a causa de que el test sea deficiente, sino de que el estudio está mal diseñado en cuanto al tamaño de la muestra, ya que la amplitud de un intervalo de confianza depende mucho del número de observaciones. Aquí no tiene mucho sentido el uso de los valores de p y de las pruebas de significación.
Las matemáticas interpretadas
Los índices más característicos de un test son, pues, su sensibilidad y su especificidad. Si vemos la figura 1 comprenderemos que la sensibilidad es la proporción de verdaderos positivos o la probabilidad de verdadero positivo, o ya de forma más completa, probabilidad condicionada de que habiendo enfermedad el test sea positivo. La especificidad es la proporción de verdaderos negativos, la probabilidad de verdadero negativo o la probabilidad de que, no habiendo enfermedad, el test sea negativo. Estas definiciones son ciertas desde el punto de vista matemático, pero en muchas ocasiones llevan a desorientarnos sobre lo que significa, en la práctica, cada cosa.
En efecto, las matemáticas muchas veces nos hacen ver la realidad como reflejada en un espejo (fig. 4), por tanto, nos la hace interpretar al revés. En el caso de la sensibilidad, en su columna de la tabla 2 x 2 también constan los falsos negativos, y son éstos precisamente los que debemos observar para interpretarla, para darle la vuelta al espejo. De este modo, si una prueba tiene una alta sensibilidad es porque tendrá a priori pocos falsos negativos y, si esto es así, su mejor utilidad se dará cuando resulte negativa, puesto que nos podremos fiar mucho de esta negatividad. Las pruebas muy sensibles son, pues, más útiles cuando son negativas, y se deben elegir cuando lo que más nos interesa dentro del proceso diagnóstico es que la prueba fuese negativa. A esto se llama capacidad de descartar enfermedad. Si además queremos considerar a los verdaderos positivos, ya que, a fin de cuentas, entran en su fórmula, bastará que recordemos a la sensibilidad como la capacidad a priori de descartar-detectar enfermedad, pero sobre todo descartar, aunque descartar y detectar sean conceptos complementarios.
Fig. 4. Reflejo en espejo de la realidad inducida por una fórmula matemática.
Con la especificidad de una PD ocurre algo similar. En su columna aparecen los falsos positivos, que serán también muy escasos si el test es muy específico. Su mejor utilidad se dará, pues, cuando el test sea positivo, porque al haber pocos falsos de este tipo, estaremos ante una confirmación muy fiable de la enfermedad. Debemos, así, recordar la especificidad como la capacidad a priori de confirmar la existencia de enfermedad, de modo que una prueba muy específica es más útil cuando sea positiva, y se debe elegir primero cuando lo que andamos buscando es una confirmación de algo de lo que tenemos firmes sospechas. La prueba más específica que existe es la biopsia.
La sensibilidad y la especificidad, en principio y por definición, deberían ser constantes y uniformes para cada test, pero en la práctica no lo son. Varían según el ámbito donde se apliquen, por ejemplo, entre la medicina primaria y la hospitalaria; varían por desgracia según quién interprete el test, pues no todos somos igual de competentes para ello9; también lo hacen según el aparato de medida, y sobre todo, según el grado de enfermedad10,11. No obstante, todo test tiene una capacidad promedio mínima que el clínico estaría obligado a conocer, aunque no recuerde cifras exactas, por lo menos, debería saber si es más sensible que específico, o al contrario.
Pero esta aparente separación conceptual entre sensibilidad y especificidad no es más que otro artificio matemático. En la práctica, una influye sobre la otra, de modo que actúan como una unidad, que es el propio test, cara a su aplicación a priori en un paciente. La mejor expresión de esta unidad son las razones de probabilidad8,12, en cuya fórmula intervienen ambas (fig. 1). Razón de probabilidad positiva y razón de probabilidad negativa son odds, como ya se ha dicho, y también tienen en cuenta a la vez la salud y la enfermedad. La razón de probabilidad positiva define cuántas veces es más probable hallar un resultado positivo del test en un enfermo que en un sano. El hecho de hablar de resultado positivo la sitúa en la estela conceptual de la especificidad, pero balanceada por la sensibilidad. La razón de probabilidad negativa define cuántas veces es más probable hallar un resultado negativo en un enfermo que en un sano. Como se trata de resultados negativos se sitúa ahora en la estela conceptual de la sensibilidad, pero balanceada por la especificidad. Si el 1 es el valor nulo de la escala para un odds, esta razón de probabilidad negativa conviene, pues, que sea menor de 1, y cuanto más baja mejor, mientras que la otra conviene que supere en mucho el 1.
La interpretación práctica de estas razones de probabilidad es oscura como toda medida expresada en odds, a pesar de su gran refinamiento conceptual que hace que algunos epidemiólogos las consideren por encima de la sensibilidad y la especificidad a las que representan. Pero, en lo inmediato, sirven realmente para introducirlas en la fórmula de Bayes, o en algún nomograma que la sustituya12, y calcular, junto con la prevalencia, los valores predictivos como objetivo final.
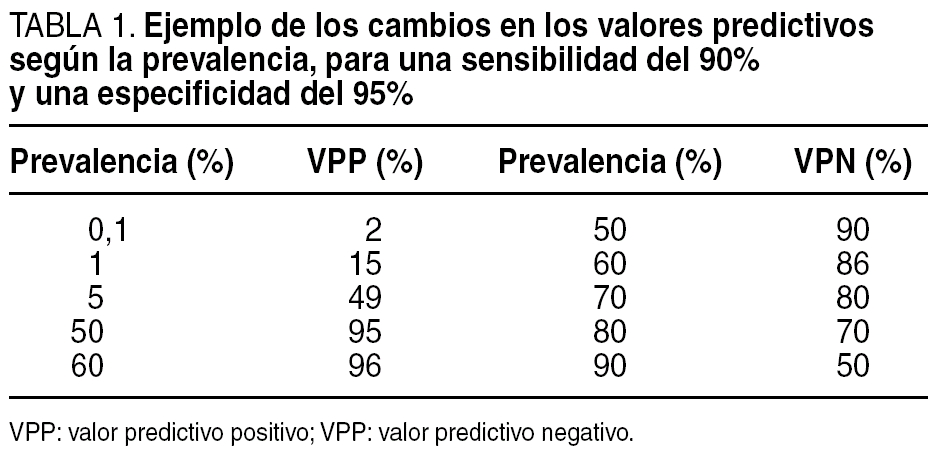
Matemáticamente, el VPP es la probabilidad condicionada de que si el test es positivo el paciente tenga la enfermedad. El VPN se refiere a que si el test es negativo el paciente está sano. Como se ve, son probabilidades a posteriori, después de haber aplicado la prueba, no a priori como la sensibilidad y la especificidad; por tanto, son los que sientan o descartan finalmente el diagnóstico. No obstante, aquí hemos de tener siempre una enorme precaución: los valores predictivos no son exportables de un contexto a otro, sólo valen donde se calculan. Leer en la bibliografía un valor predictivo no tiene ninguna aplicación para nadie más que para el autor del trabajo. Esto ocurre porque dependen mucho de la prevalencia de enfermedad que haya en cada ambiente concreto, aún considerando constante la sensibilidad y la especificidad del test.
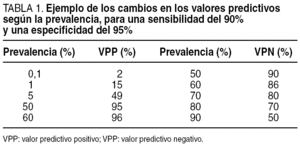
Efectivamente, el VPP en la tabla 2 x 2 se calcula en sentido horizontal y en él intervienen los falsos positivos, igual que en la especificidad. Dependerá, pues, y ante todo, o en mayor parte, de la especificidad, pero en segundo término, de la prevalencia. Así, pruebas muy específicas tenderán a dar valores predictivos positivos más altos, sobre todo en presencia de una prevalencia alta de enfermedad. Por el contrario, pruebas muy sensibles tenderán a dar VPN mayores, sobre todo en presencia de una prevalencia baja. Para un mismo ámbito, en el cual la sensibilidad y la especificidad puedan ser constantes para la misma prueba, a mayor prevalencia, mayor VPP y menor VPN, y viceversa. Esto puede verse en la tabla 1.
Por ejemplo, una mamografía, prueba muy sensible en principio, si resulta negativa en un ámbito como el screening, donde la prevalencia de cáncer de mama es muy baja, lleva a un VPN prácticamente del 100%, lo que descarta finalmente la enfermedad9. Por el contrario, aunque la mamografía es también bastante específica, su positividad combinada con la baja prevalencia lleva a un VPP mediocre, que no acaba de confirmar la enfermedad. Se precisa otra prueba mucho más específica como la biopsia. Una prevalencia baja hace, pues, que un resultado negativo tenga más visos de verdad, mientras que a un positivo le resta posibilidades de ser cierto, y viceversa.
La exactitud diagnóstica, la seguridad (accuracy en inglés), la eficiencia diagnóstica, etc. (pues se denomina de muy diversas maneras), es la proporción global de los verdaderos del tests, tanto verdaderos positivos como negativos. No tiene interés práctico, puesto que una buena exactitud puede esconder una sensibilidad o una especificidad mediocres, a costa de la excelencia de la otra. Además, también está influida por la prevalencia, y es imposible de interpretar para un paciente concreto, al contrario que los valores predictivos. Su utilidad es más bien académica, en el sentido de que sirve, como la curva ROC, para comparar, en general, 2 pruebas diagnósticas. Algo similar ocurre con los odds ratio del test, propiamente dichos. Se trata de una medida discriminante que define cuántas veces más se obtendrá un verdadero que un falso resultado con el test en cuestión. Conviene, pues, que sea mayor que 1, cuanto más, mejor. Si vale 100, son 100 verdaderos por cada falso. Igualmente, la superficie bajo la curva ROC define la probabilidad de que si tuviésemos delante a 2 sujetos de rasgos promedio y elegidos al azar, uno enfermo y otro sano, y aplicásemos el test, éste discriminará correctamente el uno del otro.
Las matemáticas y los protocolos diagnósticos
Rara vez un protocolo diagnóstico se confecciona de modo totalmente científico, utilizando alguna versión de las matemáticas que se han explicado aquí, y con conocimiento de causa tras una amplia revisión bibliográfica y una comprobación, aunque sea somera, de la realidad de nuestro entorno, llámese prevalencia, o sensibilidad y especificidad de las pruebas que se incluirán. Pero, aunque sea de modo "medio intuitivo", hay detalles que se deben considerar a la hora de confeccionar un protocolo diagnóstico.
Por un lado, hay que conocer qué ocurre con la sensibilidad y la especificidad cuando se aplican pruebas sucesivas, bien en serie, bien en paralelo8. Por otro lado, hay que atender a lo que es ganancia diagnóstica, lo que es la capacidad de cambio de estrategia terapéutica que pueda tener un test, y la toma de decisión entre diagnosticar y tratar, tratar directamente sin más pruebas o abstenerse de ambas cosas.
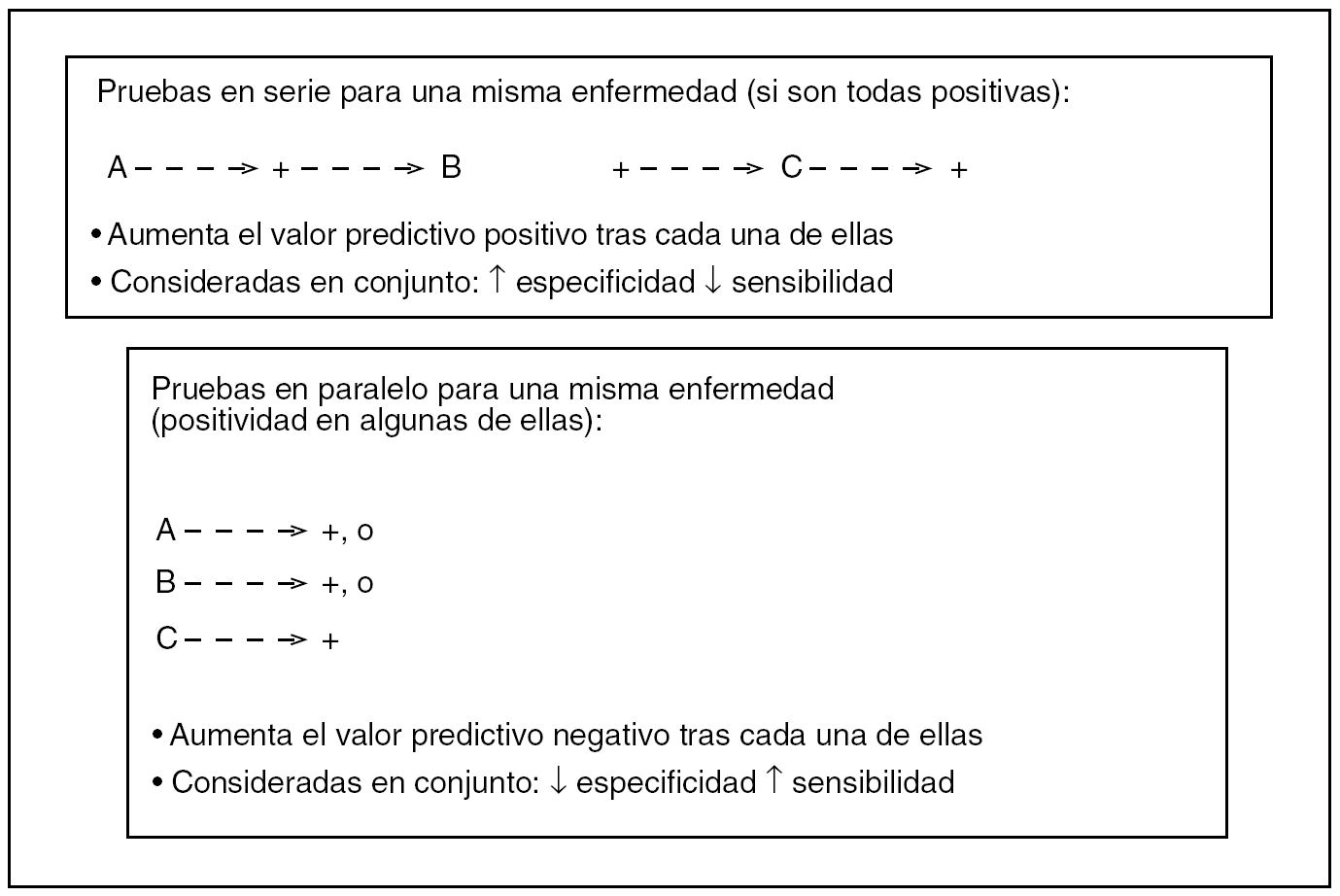
En general, todo protocolo diagnóstico tiene 2 fases más o menos superpuestas: una inicial, en la que el objetivo es la detección o el descarte de la enfermedad, y otra subsiguiente, en la que se tratará de confirmarla. Al principio, interesa la sensibilidad, y después habrá que buscar la especificidad. Como no hay PD perfectas, muchas veces habrá que recurrir a múltiples pruebas. En la figura 5 se resume qué ocurre cuando en una batería de PD éstas se aplican a la vez (en paralelo), o una tras conocer el resultado de la otra (en serie).
Fig. 5. Repercusión sobre algunos índices diagnósticos de una batería de pruebas.
La situación "en paralelo", por su mayor sensibilidad global, debe producirse al comienzo, porque cualquier positivo en alguna de ellas lleva a detectar el problema en principio, y si todas las pruebas son negativas lleva a un enorme VPN necesario para descartar una enfermedad. Esta situación es la típica de urgencias hospitalarias, donde interesa un diagnóstico rápido, ya sea positivo o negativo, y sólo existe una inmediata disponibilidad de pruebas relativamente insensibles pero, por su menor especificidad, este esquema necesitará alguna otra prueba más adelante para confirmar el diagnóstico. También cuando esta situación produzca más de un diagnóstico, por esta escasa especificidad conjunta, llevará a unos VPP muy bajos que representan el sobrediagnóstico originario, muchas veces falso, de los grandes centros hospitalarios.
La situación "en serie" se produce cuando el clínico ya no tiene prisa en conocer un diagnóstico que ya vislumbra, sino que lo que pretende es la confirmación definitiva de una enfermedad. Esto es posible aquí por el aumento de especificidad conjunta que esta estrategia conlleva. Generalmente, aquí se incluirán las pruebas más caras y quizá peligrosas; por ello, si tenemos en mente aplicar varias pruebas en serie, se debe elegir primero la más específica de todas, pues así puede que sean innecesarias las demás, si con una de ellas ya se alcanza un VPP cercano al 100%.
El concepto de ganancia nunca hay que olvidarlo si queremos ser eficientes en costes y proporcionar la máxima seguridad al paciente. La ganancia se define como la diferencia entre el VPP y la prevalencia de partida. Es el beneficio neto que nos proporciona el test. Para el VPN es la diferencia entre éste y la no prevalencia, es decir, 1prevalencia. Generalmente, en un protocolo nos referiremos siempre a la ganancia en positivo, en confirmación. Hemos de ser conscientes que un diagnóstico habitualmente queda sentado a partir de un VPP del 90%, mucho más si éste iguala o supera el 95%. Por tanto, una ganancia del 5% o menor suele ser demasiado exigua como para resultar rentable en costes o riesgos. Si en un carcinoma de páncreas una tomografía computarizada (TC) ya revela invasión vascular, para lo cual es muy específica, mucho más que sensible, es muy probable que no haya que añadir una resonancia magnética, y menos aún una prueba invasiva, como es la angiografía visceral.
Que un test pueda cambiar la estrategia terapéutica que se produciría sin su concurso es un valor añadido que debe tenerse en cuenta en un protocolo. Un test capaz de ello se situará habitualmente al final del proceso diagnóstico, puesto que lo que aporta no es ya el propio diagnóstico, que debe estar claro a esas alturas, sino algún matiz más o diagnóstico relacionado, como la presencia de metástasis insospechadas, o cualquier otro detalle que induzca un cambio de planteamiento. Es la vía por la que una prueba como la tomografía por emisión de positrones (PET) se está introduciendo poco a poco en el protocolo de evaluación de cánceres como los esofágicos o pancreáticos, especialmente en los casos avanzados13-15. La laparoscopia diagnóstica en tumores avanzados gástricos o pancreáticos también sería otro buen ejemplo16. Para que esta capacidad de cambio sea provechosa de forma incontestable desde luego tendría que ser mayor del 10%, no digamos ya si se sitúa por encima del 15 o el 20%. Entonces la realización de tal prueba sería inexcusable.
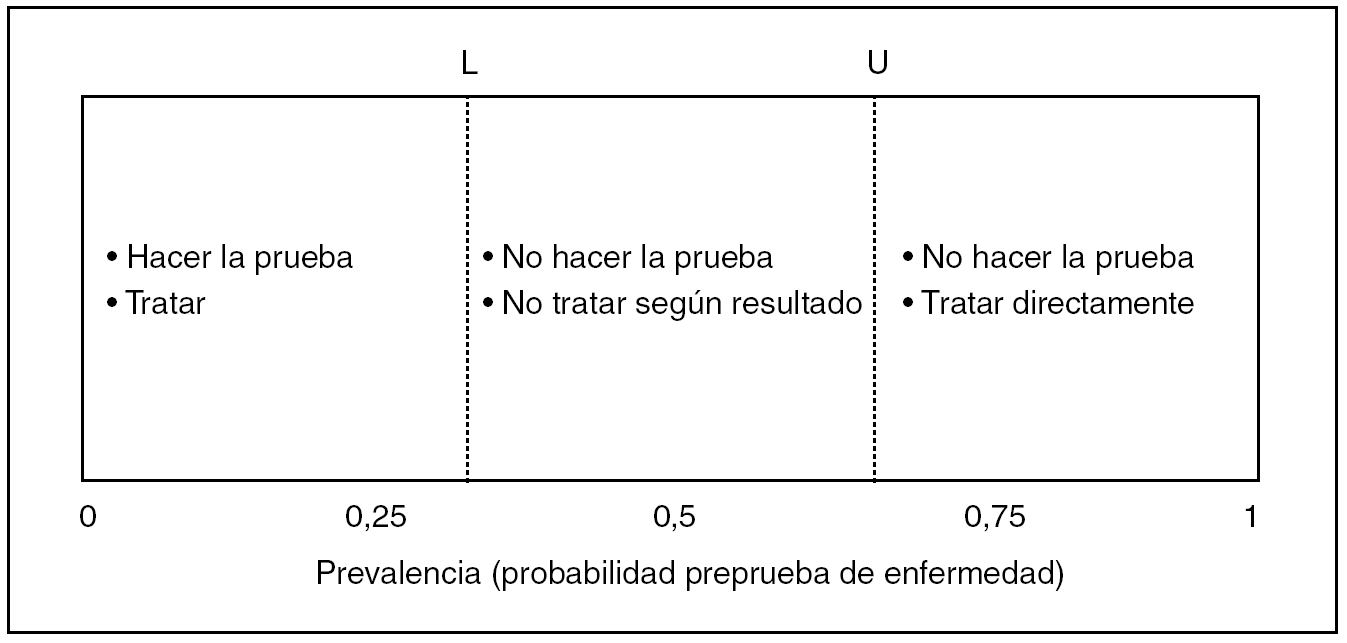
El proceso clínico lleva a la toma de decisión de diagnosticar y tratar después en consecuencia, tratar directamente, o abstenerse de ambas cosas. Los momentos en que acaba lo uno y empieza lo otro pueden entrar en conflicto y afectar a la seguridad del paciente. Hay toda una teoría acerca de ello basada en las características fundamentales de una PD, su sensibilidad y su especificidad, y en la prevalencia de enfermedad existente en un escenario determinado (fig. 6). Pauker y Kassirer17 fueron sus introductores; posteriormente, Glasziou18 y Bernstein19 simplificaron el planteamiento considerando solamente la sensibilidad y la especificidad de la prueba, y la prevalencia. No por ser bastante desconocida esta teoría de los umbrales de decisión relacionados con el diagnóstico deja de ser útil e informativa en cuanto a la seguridad del paciente en un protocolo de aplicación de un test. La explicaremos atendiendo a un ejemplo real20 sobre la indicación de linfadenectomía axilar (tratamiento) con respecto a la biopsia del ganglio centinela de la mama (test).
Fig. 6. Umbrales prueba-tratamiento. L: umbral inferior de decisión; U: umbral superior de decisión.
Imaginemos que tal test tuviese, en nuestras manos, una sensibilidad del 87,5% y una especificidad del 86,4%. La clave del problema está en marcar un nivel de seguridad para el paciente que lo ponga a salvo de cualquier imperfección diagnóstica, es decir, un máximo de riesgo general de fallo diagnóstico, en este caso de axila positiva, a partir del cual habría que tratar y no hacer caso del resultado del test. Para la biopsia del ganglio centinela mamario actualmente se suele exigir un mínimo de VPN del 95% para la presencia de ganglios axilares infiltrados. Esto es así porque el máximo riesgo tolerable es ese 5% restante, y está muy influido por la prevalencia de la enfermedad axilar a la que nos enfrentemos, de modo que es ella la que marca los límites de las 3 posturas posibles. Si aplicamos para el ejemplo las fórmulas adecuadas17-19, los umbrales de decisión serían estos:
Umbral inferior (L): 0,8%. Si en una determinada neoplasia de mama la prevalencia inicial de axila afectada es igual o menor que esta cifra, no vale la pena llevar a cabo el test del ganglio centinela, ni mucho menos una linfadenectomía. Esto es compatible, por ejemplo, con la realidad de un carcinoma in situ.
Umbral superior (U): 27%. Si se iguala o supera este riesgo de partida de axila positiva, esta prevalencia de enfermedad en la axila es tan alta que sitúa al test fuera del límite de seguridad de su valor predictivo que habíamos marcado; por tanto, tampoco hay que llevar a cabo la prueba del ganglio centinela, y hay que pasar directamente a la linfadenectomía. Esto es compatible, por ejemplo, con lo que ocurre en tumores de más de 2,5-3 cm de diámetro, donde la prevalencia de ganglios positivos axilares puede superar el 30% de los casos20.
En las pacientes que puedan situarse entre ambos umbrales de prevalencia de positividad axilar, es donde la prueba dadas su sensibilidad y su especificidad, ayuda realmente a tomar una decisión terapéutica que será mayoritariamente correcta.
El mensaje es claro: cualquier PD tiene su espacio vital donde es útil. Por debajo, su aplicación es innecesaria, y por encima, puede estar desbordada en cuanto a su competencia, y llevarnos a la confusión, cara a una decisión terapéutica acertada. Este espacio vital lo marca la prevalencia de enfermedad de acuerdo con el margen de error máximo que estemos dispuestos a permitirle a la prueba y, naturalmente, con el potencial en sensibilidad y especificidad de la propia prueba, que debe ser absolutamente conocido si la decisión terapéutica es trascendental.
Agradecimientos
Queremos expresar nuestro agradecimiento a la Dra. María Teresa Torres Sánchez por permitirnos transcribir alguno de los resultados de su magnífica tesis doctoral.
Correspondencia: Dr. J. Escrig-Sos.
Hospital General de Castellón. Servicio de Cirugía.
Avda. Benicassim, s/n. 12004. Castellón de la Plana. España.
Correo electrónico: escrig_vicsos@gva.es
Manuscrito recibido el 11-11-2005 y aceptado el 23-1-2006.