Introducción
La respuesta a la pregunta que hace el título es contundente: porque no sólo permiten conocer la significación estadística de un resultado, sino que además permiten valorar la significación clínica, es decir, su importancia práctica. Posiblemente por ello, desde hace ya muchos años, el uso de los intervalos de confianza (IC) ha sido recomendado insistentemente por los directores y editores de importantes revistas médicas1 como modo de complementar el resultado principal de un estudio, bien acompañando al valor p o incluso como su sustituto2,3. Actualmente, es posible que muchas revistas de alto factor de impacto no permitieran publicar un resultado fundamental únicamente complementado con su valor p.
Si la referida al principio es la razón cardinal para su uso, hay otras ventajas que tampoco son nimias, entre las que destacan que permite valorar también la equivalencia entre dos variables4 y como base para calcular la probabilidad de que un resultado supere o alcance una determinada magnitud, probabilidad conocida como nivel de confianza5 (NC) y que también es muy útil para valorar la significación clínica, puesto que permite una interpretación explícita.
Las pruebas estadísticas de significación e hipótesis, con su valor p, causaron una auténtica revolución en el modo de analizar los resultados de cualquier investigación biomédica, sobre todo a partir de la década de los cuarenta del pasado siglo xx. Sin embargo, casi tan frecuentes como su uso fueron las críticas que recibieron, que se siguen prolongando incluso en la actualidad, siempre a causa del mal uso y de las interpretaciones erróneas a que lleva este valor p con demasiada reincidencia6. Los IC, en realidad, expresan genéricamente lo mismo, y su cálculo se basa en la misma mecánica matemática, tienen las mismas limitaciones, pero su interpretación es mucho menos críptica que la del valor p y mucho más completa7. A pesar de todo, el valor p sigue representando un buen método para dar objetividad al resultado de un estudio, desde luego es mejor que nada, o que la dictadura científica que en su ausencia pudiera imponer cualquier sapientísimo gurú de la medicina, que siempre los ha habido. Por ello, aunque sea de forma intuitiva, y antes de conocer cómo utilizar los IC, es bueno que se entienda definitivamente el mensaje del valor p.
La vía hipotético-deductiva y el valor p
A finales del siglo xix y primeros del xx el razonamiento hipotético-deductivo se impuso en el método científico y perdura todavía. Hasta entonces predominó la vía inductiva, que partía fundamentalmente de la observación para formular una teoría sobre un determinado fenómeno, y la iba modificando con sucesivas observaciones. No cabe duda de que esta vía rindió buenos beneficios a la ciencia, ahí está el señor Darwin y sus teorías, incluso es de uso habitual en el razonamiento clínico diario. Su expresión estadística es el bayesianismo. Pero para cierto tipo de ciencias, como la física, que por aquellos tiempos empezaba a tomar gran auge, en las que se manejaban fenómenos menos tangibles que en biomedicina, esta vía inductiva no acababa de rendir lo suficiente. Era necesario plantear teorías que no se basaran exclusivamente en la observación y en principio tuvieran carta de certeza, y montar después los experimentos de laboratorio sobre la base de dichas teorías hasta apuntalarlas como definitivamente ciertas o rechazarlas. Cuando este razonamiento llegó a la estadística, no tardó en aparecer el concepto del valor p8.
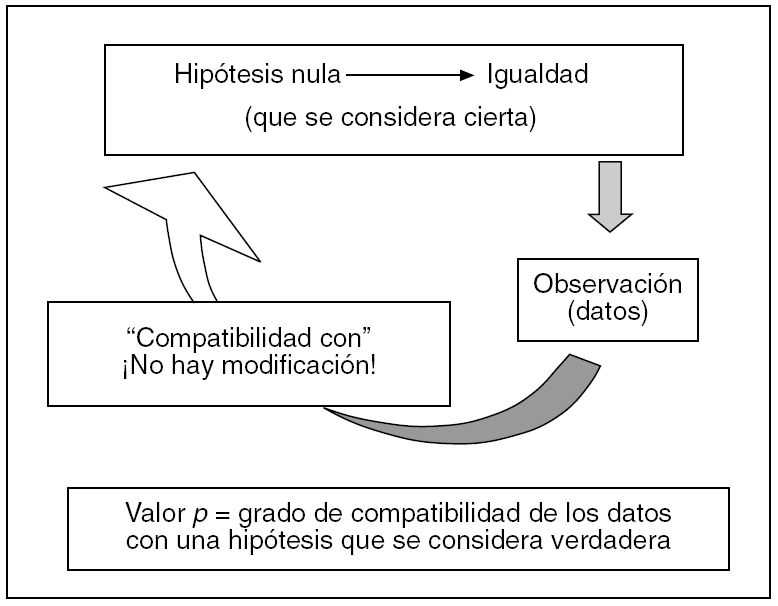
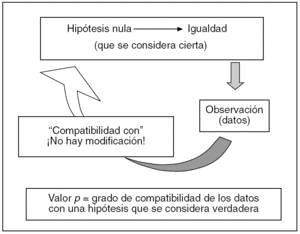
Esta teoría de partida, más bien ideal, que se plantea en la vía hipotético-deductiva, en la llamada estadística clásica está representada por la hipótesis nula, que siguiendo la filosofía de este planteamiento, de entrada se considera cierta, mientras no se demuestre lo contrario. Esto nunca se debe olvidar si se quiere entender el valor p. Aplicada a una diferencia concreta entre dos variables A y B, viene a decir generalmente que tal diferencia es cero, algo que desde luego es muy difícil que se dé en la realidad al medir dos variables. El valor p es una probabilidad, pero un poco rara de explicar y de entender para los no matemáticos. Para nosotros, es mejor definirlo como el grado de compatibilidad de esa diferencia hallada puntualmente con la hipótesis nula, que, insistimos, de entrada se considera cierta (fig. 1). Este grado va de 0 a 1, o del 0 al 100%. Por ejemplo, si la p vale 0,05, la diferencia A B es muy poco compatible con la igualdad que representa la hipótesis nula, también si vale 0,08; si vale 0,80 o más, nadie negará que es bastante compatible. Lo peor es que p valga 0,50, porque entonces no sabremos a qué atenernos. Así es como en sus orígenes se debía interpretar el valor p, y seguramente así lo deberíamos seguir interpretando.
Fig. 1. Vía hipotético-deductiva y valor p.
Como consecuencia, si la hipótesis nula se considera cierta de entrada y tenemos presente que prácticamente siempre entre dos variables alguna diferencia hallaremos, aunque sea mínima, entonces, si el grado de compatibilidad de tal diferencia, con la en principio innegable igualdad absoluta, es alto, bien podremos considerar que la diferencia hallada puede ser casual, debida al azar. Si el grado de compatibilidad es bajo, bien podremos pensar que el resultado no es casual, y puede también llevar a pensar que aquella hipótesis nula quizá no fuera cierta (dado que en ambos supuestos consideramos que el experimento está bien confeccionado). Ni en una situación ni en la otra demostramos fehacientemente que la hipótesis nula sea cierta o falsa9, ni se calcula su probabilidad de ser real, simplemente podremos aceptarla o rechazarla provisionalmente hasta nuevos ensayos, porque nos fiamos de nuestro experimento y de nuestras mediciones de A y B. Pues bien, el valor p no da más de sí. A partir de este punto, surgen dos problemas añadidos.
El primero, eso sí, con toda la buena intención, lo introdujeron Neyman et al10 al considerar que había que establecer un límite claro en el valor p para aplicar los razonamientos anteriores de forma absoluta. Este valor crítico de p generalmente es el famoso 0,05 y marca el mítico límite de la significación estadística y, verdaderamente, el inicio de los problemas en su interpretación. En realidad esto no debería dar tal conflicto, pues sus introductores lanzaron este lema exclusivamente bajo el punto de vista de la toma de decisión ante un problema que fuera trascendente y en el que, digamos, urgiera tal toma de decisión: rechazar o no la hipótesis nula con sus consecuencias derivadas. Lo que ocurre es que se ha universalizado demasiado y se lo ha sacado de su contexto, y si no, fíjese el lector en que se suele aplicar en cualquier inferencia estadística, aunque el fin de la investigación no suponga obligación alguna de tomar una decisión tan drástica, basada en la ley del todo o nada. Por eso la mala interpretación está servida: si p es mayor que el 5%, el resultado del estudio no vale para nada; si es menor, hemos hecho un gran descubrimiento, totalmente cierto. Algunos, de forma irónica, a esta postura tan drástica y que pocas veces está realmente justificada la consideran una auténtica enfermedad llamada significantitis11 o es como un problema de conciencia: "to p or not to p"12.
El segundo problema deriva de la propia mecánica de cálculo del valor p, que no es que sea falaz, pero lleva también a la falacia en su interpretación cualitativa, a poco que nos descuidemos. En efecto, ante una idéntica diferencia entre A y B, cuanta más muestra se haya analizado, más pequeño es tal valor, y viceversa. Sin embargo, el fenómeno que se escruta es el mismo. Aunque pueda parecer una falacia, en realidad no lo es. Nuestra propia intuición o sensatez lo puede imitar perfectamente. Imaginemos una gran diferencia entre los efectos de dos técnicas quirúrgicas, por ejemplo, del 40% en mortalidad. Si hemos operado a 10 pacientes, 5 con cada técnica, lo primero que piensa alguien sensato es que esto puede ser fruto del azar. Si hemos operado a 1.000 pacientes, 500 con cada técnica, difícilmente pensaremos que tal diferencia fuera obra del azar. Aquí pues, ninguna falta hace el valor p. El problema para nuestra intuición viene cuando la muestra ni es tan grande ni es tan pequeña. Ahí sí que viene bien disponer del valor p, pero sabiendo que cambia con el tamaño de la muestra analizada y teniendo en cuenta, además, que si este valor puede variar con el tamaño de la muestra ante una misma diferencia entre las mismas variables, no es pues, de ninguna manera, un indicador de la importancia real de tal diferencia, sea o no compatible con la hipótesis de nulidad9. Esto enlaza con los IC que, precisamente, vienen a dar luz sobre estos puntos más oscuros del valor p.
Los intervalos de confianza y su interpretación
El IC puede calcularse para infinidad de estadísticos7, sean medias, porcentajes, razones, coeficientes de correlación, etc., pero sólo deben acompañar a la estimación puntual de un resultado que traduzca una diferencia, y que sea el principal (o los principales) en cuanto al objeto de investigación en un estudio. No es correcto, pues, aplicarlos para cualquier cálculo secundario o marginal de los muchos que aparecen en una publicación. Si ante una estimación puntual de una diferencia que valga un 10% su IC oscila entre el 8 y el 12% con un cierto grado de seguridad (habitualmente será calculado con una seguridad del 95%, cifra complementaria del mítico 5% de la significación estadística), en términos prácticos que no matemáticos2,13 debe interpretarse como que el verdadero valor de esa diferencia, que en nuestro estudio vale un 10%, puede situarse realmente entre el 8 y el 12%, a causa de que cualquier determinación puntual está sujeta a cierto grado de error aleatorio. En este caso, el margen de error es del 5%, pues trabajamos con una seguridad del 95%; por lo tanto, si dentro del IC de una diferencia estuviera el valor nulo, que aquí es 0, estaríamos ante un resultado estadísticamente no significativo, perfectamente compatible con la hipótesis nula, y si hubiésemos calculado el valor p de tal diferencia, es seguro que sería mayor de 0,05. Si no contiene el 0, p será menor del 5%. No es necesario para el clínico aprenderse las fórmulas de los IC. Actualmente están los ordenadores y los paquetes estadísticos, que se las conocen perfectamente y no se equivocan al multiplicar o dividir.
En sustancia, pues, un IC es un sucedáneo del valor p, y como él variará de amplitud alrededor de la estimación puntual según la dispersión de las observaciones individuales y según el tamaño de la muestra analizada: a más tamaño muestral y menor dispersión, obtendremos intervalos más estrechos, y viceversa. Y cuanto más estrecho es un intervalo, más preciso es, y más improbable es que pueda contener el valor nulo. Del mismo modo, si trabajamos con menor seguridad, el intervalo también será más estrecho, y viceversa de nuevo. Pero utilizar un IC como mero sustituto del valor p es una gran estupidez. Así no le sacamos ningún partido: para eso ya está el valor p. Esto simplemente es una información preliminar a la hora de valorar el resultado de un estudio, aunque determine su significación estadística.
Lo que viene a continuación es más importante2,14,15. Basta que nos hagamos una sencilla pregunta: entre los límites de un IC, ¿hay valores relevantes desde el punto de vista práctico o clínico? La mayoría de las veces, si el IC contiene valores de relevancia práctica, se situarán más bien cerca de alguno de sus límites, y ahí es donde debemos mirar para matizar más la importancia de un estudio y de su resultado. Dos son las situaciones que nos podemos encontrar:
Que el IC contenga el valor nulo (0 para una diferencia, 1 para una razón como el riesgo relativo) y, por lo tanto, que el resultado no sea estadísticamente significativo. En este caso, debemos dirigir la mirada hacia el límite superior del IC y preguntarnos si ese límite superior tiene relevancia. Si la tiene, el estudio, pese a no ser concluyente (algunos los llaman negativos) al no presentar significación estadística, debe ser considerado como no definitivo, pues quizá de haber manejado mayores tamaños de muestra hubiésemos llegado a conclusiones de importancia. Valdría la pena, pues, volver sobre la cuestión con un mejor diseño. Si ese límite superior no tiene relevancia práctica, el estudio, aparte de ser negativo en cuanto a significación estadística, puede ser considerado como definitivo en cuanto a que el asunto investigado seguramente carece de importancia real.
Que el IC no contenga el valor nulo y, por lo tanto, que estemos ante un resultado que posiblemente no se deba al azar. En este caso, debemos dirigir la mirada hacia el límite inferior del IC y preguntarnos de nuevo si ese límite tiene relevancia. Si la tiene, el estudio, además de ser concluyente o positivo en cuanto a significación estadística, será también definitivo en cuanto a su importancia práctica pues, aún en el peor de los casos que representa ese límite inferior, hay significación práctica además de significación estadística. Si ese límite inferior no presenta relevancia clínica a pesar de la significación estadística, no podremos considerar como definitivo su resultado. Otra vez valdría la pena volver sobre la cuestión con otro enfoque que pudiera aclarar la duda.
De estos cuatro escenarios, con el que debemos ser más perspicaces es cuando el valor nulo, el 0 para una diferencia, está dentro del IC y cercano al límite inferior. Esto se corresponde con valores p que algunos llaman casi significativos, que pueden llegar incluso hasta cifras de 0,15. Ahí es donde por culpa de una interpretación maximalista de p podríamos desechar por intrascendente un resultado que presentara importantes repercusiones prácticas, incluso gravedad. Así pues, podemos afirmar que hay una zona peligrosa de valores p que van de 0,05 a 0,15 y se prestan más que otros a interpretaciones incorrectas. Posiblemente sea éste el escenario concreto donde más rendirá intelectualmente observar con detenimiento un IC.
Los intervalos de confianza y la bioequivalencia
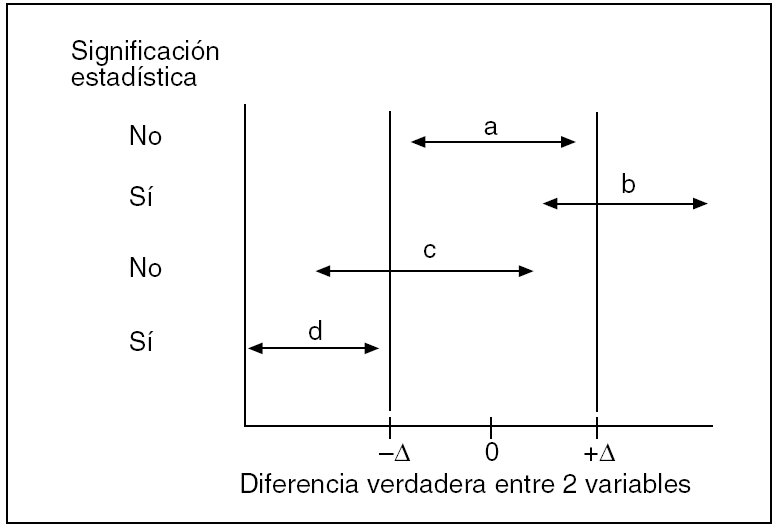
El otro gran error conceptual al interpretar un valor p no significativo es creer que entre A y B existe igualdad o que los efectos de A son equivalentes a los de B. Aunque la hipótesis nula se dé como cierta de entrada, y aunque el resultado sea altamente compatible con ella, ya apuntamos que esto no supone demostración fehaciente sobre su certeza o su validez. Aprovechemos aquí un famoso aserto de Douglas Altman16 aplicable al valor p de la diferencia entre dos variables, y recordémoslo siempre: "La ausencia de evidencia no es evidencia de la ausencia". La equivalencia no es por sí misma un concepto estadístico, es un concepto puramente práctico que se basa en la instauración, por pura convención, de unos límites entre las diferencias de efecto de dos variables, de acuerdo con nuestros conocimientos sobre la materia. Lógicamente, estos límites pivotarán alrededor de la diferencia nula entre A y B (fig. 2) y los podemos denominar Δ. Por fuera de ellos no hay equivalencia de efectos. Cualquier IC que los contenga producirá, pues, incertidumbre en cuanto a ella, al igual que producía incertidumbre en cuanto a la existencia real de una diferencia si comprendía el valor nulo.
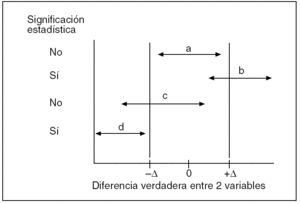
Fig. 2. Equivalencia y significación estadística (modificado de Jones et al4).
Esta idea es muy interesante para los cirujanos17, sobre todo porque tras el advenimiento de la cirugía laparoscópica se diseñan muchos estudios en los que se pretende demostrar diferencias para ciertas variables, como estancia, uso de analgesia, etc., mientras que para lo que es el efecto fundamental de la intervención, lo que se pretende demostrar es equivalencia entre la cirugía laparoscópica y la convencional. Veamos la figura 2 y entenderemos que el uso exclusivo de valores p no es apropiado para despejar ambos objetivos, más bien nos lleva a un error muy extendido en la literatura, que es pensar que p > 0,05 demuestra tal equivalencia. En esta figura se representan cuatro IC que se podría obtener con respecto a una diferencia entre dos variables. Se han establecido los límites Δ alrededor de la diferencia cero que marcan lo que clínicamente sería equivalente, es decir, una diferencia sin repercusión real alguna. La diferencia "a" no es estadísticamente significativa, pues su IC engloba el valor nulo, pero denota equivalencia puesto que su IC cae dentro de los límites Δ establecidos previamente. La diferencia "b" es estadísticamente significativa, pues su IC no contiene el valor nulo, pero incierta en cuanto a equivalencia puesto que su IC engloba uno de los límites Δ. La diferencia "c" no es ni significativa ni muestra certeza para equivalencia, pues su IC engloba tanto el valor nulo como uno de los límites Δ. Por último, la diferencia "d" es a su vez significativa estadísticamente y claramente no equivalente, pues su IC no engloba el valor cero y está fuera de los límites de equivalencia establecidos.
Puede haber otras combinaciones posibles de un resultado en cuanto a significación estadística y equivalencia, por ejemplo, que un IC no contenga el valor nulo y se sitúe entre éste y uno de los límites Δ. Entonces se combinaría significación estadística y equivalencia. Pero con estos ejemplos ya podemos estar convencidos que significación estadística nada tiene que ver con equivalencia, ni cuando hay tal significación ni cuando deja de haberla, mientras que con los IC es posible aproximarse a ambos conceptos. Los enfoques de equivalencia generalmente tienen unos límites Δ muy ceñidos alrededor de la diferencia nula y, por lo tanto, van a precisar de tamaños muestrales elevados para que el IC sea estrecho y pueda caer entre ellos, mucho más elevados que si el objetivo fuera demostrar superioridad; de lo contrario, lo más fácil es que el resultado sea incierto. Éste es el principal escollo de esta clase de estudios.
Los intervalos de confianza y el nivel de confianza
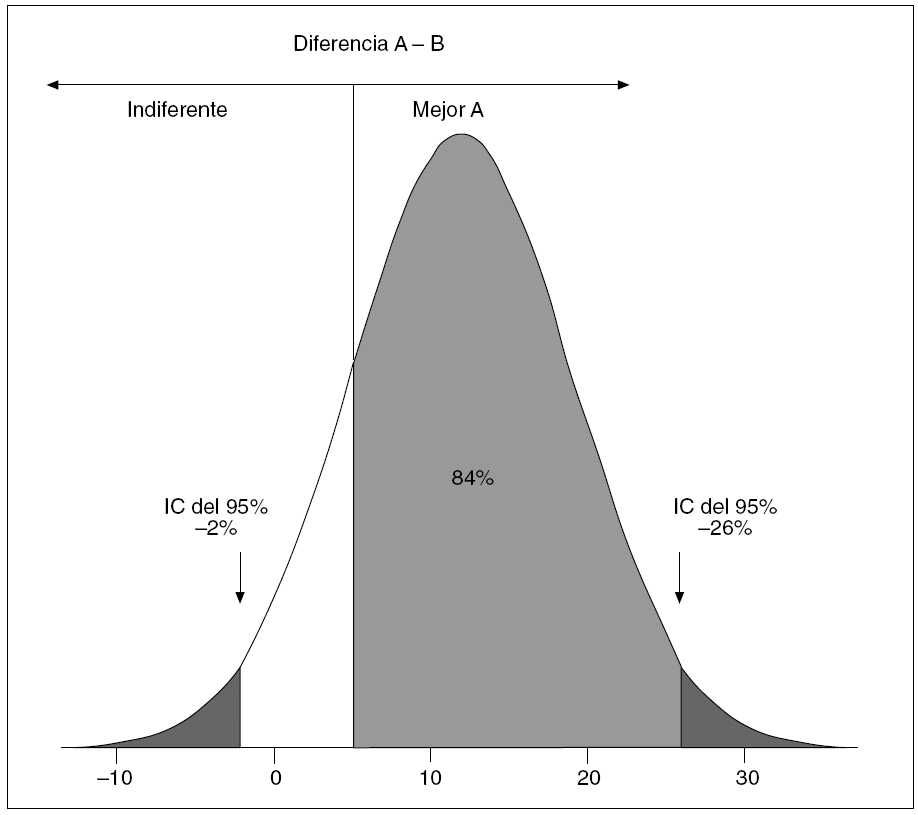
Ya se ha comentado que cuando se calcula una diferencia en una muestra sólo estamos haciendo una estimación puntual, la mejor de las posibles si la muestra es representativa, de la verdadera diferencia que hay en la población, pero que hay otros valores posibles que, precisamente, son los que engloba el IC. Sin embargo, no todos estos valores posibles, mejor dicho, los diversos tramos entre ellos, tienen la misma probabilidad de existir. Esto se debe a que estos valores contenidos en un IC siguen una determinada distribución de probabilidad, generalmente de tipo normal cuando se trata de diferencias entre proporciones (fig. 3), aunque pueda ser de otro perfil. Puede ocurrir también que pretendamos acotar el límite de la importancia clínica de una diferencia, por ejemplo y en la figura 3, que la diferencia A-B sea trascendente a partir de un 5%, de modo que así se considere al tratamiento A claramente superior al B y, por lo tanto, con una utilidad clínica que pueda merecer la pena. La pregunta a plantear sería entonces la siguiente: de acuerdo con el resultado, ¿qué probabilidad hay de que A sea ≥ 5% superior a B en cuanto al efecto deseado? Esta probabilidad es la que define el llamado NC.
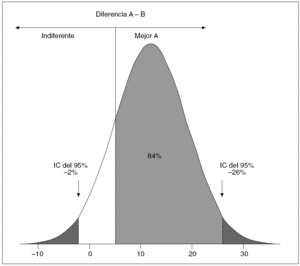
Fig. 3. Nivel de confianza y significación clínica. IC: intervalo de confianza.
De nuevo, esta información es imposible de lograr atendiendo sólo al valor p, tanto si muestra como si no muestra significación estadística. Hay que partir del IC de la diferencia hallada, y de ahí calcular la superficie que hay bajo la curva de distribución de probabilidad del IC, desde del límite de importancia clínica que hayamos establecido como conocedores de la materia que tratamos. Ese porcentaje de superficie bajo la curva es la probabilidad (NC) que buscamos. En la figura 3 vemos el ejemplo de una diferencia del 12% estadísticamente no significativa (IC del 95% de seguridad, 2% a 26%), pero con una alta probabilidad (84%) de que el tratamiento A sea superior, clínicamente hablando, al tratamiento B, a partir de un valor del 5% de diferencia en cuanto a sus efectos. Esta forma de proceder en la apreciación de la significación clínica puede ser de gran ayuda en la toma de decisiones; desde luego, muy superior a la aportación del lema de Neyman et al.
Naturalmente, el cálculo de esta probabilidad necesita bien de ciertos conocimientos en el manejo de curvas de distribución de probabilidad, bien de estar pertrechados con el apoyo informático necesario. Shakespeare et al5 explicaron muy bien su uso, y además, en la página web18 de ese autor se ofrece gratuitamente una hoja de cálculo para obtener el NC sin necesidad de conocer las fórmulas de las distribuciones de probabilidad y calcular integrales. En dicha hoja de cálculo también es posible balancear beneficios y riesgos de dos tratamientos para una toma de decisión clínica más fundada.
Conclusiones
Los IC no suponen la solución a cualquier incertidumbre que nos planteemos, tienen limitaciones inherentes a su propio origen matemático, que es idéntico al del valor p, pero sobre éste presentan importantes ventajas para interpretar un resultado de investigación y no son tan proclives como el valor p a llevarnos a errores conceptuales. La ventaja fundamental está en que posibilitan la aproximación desde diversos enfoques a la importancia clínica del resultado obtenido, también a la equivalencia entre dos intervenciones. Por otra parte, es posible utilizarlos como base para valorar la credibilidad de un ensayo clínico, como recientemente se publicó en esta misma Revista19, motivo por el cual no se ha hecho mención de ello en este artículo.
Correspondencia: Dr. J. Escrig Sos.
Servicio de Cirugía General y Digestiva. Hospital General de Castellón.
Avda. Benicasim, s/n, Planta 5.a B, Secretaría. 12004 Castellón de la Plana. España.
Correo electrónico: escrig_vicsos@gva.es
Manuscrito recibido el 20-6-2006 y aceptado el 23-10-2006.