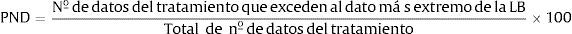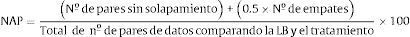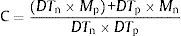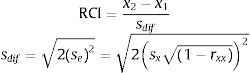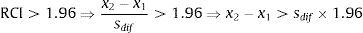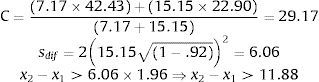En este trabajo se presentan dos técnicas para el análisis de datos de los diseños de caso único en la investigación de los tratamientos psicológicos: los índices de no solapamiento de datos para estimar el tamaño del efecto del tratamiento (o magnitud del cambio terapéutico) y la aproximación estadística de Jacobson y Truax (1991) para estimar la significación clínica del efecto. A partir del caso de una víctima del terrorismo que sufría de trastorno por estrés postraumático, trastorno depresivo mayor y trastorno de angustia con agorafobia y que recibió terapia cognitivo conductual centrada en el trauma, se ejemplifica el cálculo y aplicación del porcentaje de datos no solapados (PND), el porcentaje de datos que exceden la mediana (PEM), el no solapamiento de todos los pares (NAP) y la aproximación estadística a la significación clínica y se discuten sus ventajas y limitaciones como complemento al análisis visual de los datos.
This paper presents two techniques for the data analysis of single case designs in psychological treatment research: indices of data overlap between phases to estimate the size of treatment effect (or the magnitude of therapeutic change) and Jacobson and Truax's (1991) statistical approach to estimate the clinical significance of treatment effect. Based on a case of a victim of terrorism who suffered from posttraumatic stress disorder, major depressive disorder and panic disorder with agoraphobia and received trauma-focused cognitive-behavioral therapy, this paper illustrates the computation and application of percentage of non-overlapping data (PND), percentage of data points exceeding the median (PEM), non-overlap of all pairs (NAP), and statistical approach to clinical significance, and discusses their advantages and limitations as a complement of visual analysis of data.
Uno de los rasgos que ha caracterizado el campo de la psicología clínica y de salud en los últimos 20-25 años ha sido el desarrollo del movimiento de los tratamientos basados en la evidencia o, para evitar el anglicismo, de los tratamientos basados en pruebas científicas, que inicialmente se denominaron tratamientos apoyados empíricamente (Labrador Encinas y Crespo López, 2012). Este movimiento ha acentuado, por un lado, la necesidad de fundamentar empíricamente la eficacia y utilidad clínica de los tratamientos psicológicos y, por otro, el reconocimiento de la brecha entre investigación y práctica clínica. La realización y diseminación de estudios con diseños de caso único, especialmente de los denominados cuasi-experimentales (Kazdin, 1992), podría ayudar de manera singular a cerrar esa brecha a la vez que a profundizar en la investigación sobre tratamientos. Los datos obtenidos en esos estudios podrían contribuir de forma directa a la base de conocimientos científicos, podrían generar hipótesis para ser investigadas con diseños más rigurosos y, en el camino, podrían conseguir que la investigación sobre tratamientos se ajustara más y fuera más relevante para la práctica clínica (Kazdin, 2008).
Uno de los obstáculos con los que se encuentran los psicólogos clínicos y de la salud que quieren realizar ese tipo de investigaciones es cómo analizar adecuadamente los datos que obtienen. Tradicionalmente, el análisis de datos en los estudios con diseños de caso único se ha venido realizando mediante un análisis visual de la presentación gráfica de los datos tomados durante la fase (o fases) de línea base (LB) y durante la fase (o fases) de tratamiento (Barlow y Hersen, 1988; Bono Cabré y Arnau Gras, 2014; Kazdin, 1992; Kratochwill y Levin, 1992; Kratochwill et al., 2013). Este análisis visual trata de identificar que tras el tratamiento se ha producido un cambio en los datos que es consistente, fiable y poco probable que sea debido a fluctuaciones azarosas de los datos entre las fases, de manera que se pueda determinar si el tratamiento ha tenido efecto sobre los problemas o trastornos psicológicos y cuál ha sido la magnitud de ese efecto. Para ello, en esos análisis se examina visualmente, por ejemplo, la estabilidad, variabilidad y tendencia de los datos en la LB, los cambios que se producen en el tratamiento respecto a la tendencia de los datos y su nivel y la latencia de dichos cambios, es decir, el tiempo que transcurre entre el inicio del tratamiento y los cambios en la tendencia y nivel de los datos. El argumento de los defensores de este tipo de análisis es sencillo y directo: si un investigador no puede ver con sus ojos un efecto o un cambio terapéutico cuando lo representa gráficamente, es que no existe o es clínicamente irrelevante.
A pesar de lo convincente que puede parecer este argumento, la literatura científica ha demostrado que en el análisis visual hay una tendencia importante a cometer errores de tipo I. En concreto, se ha encontrado que en el 25% de las ocasiones se considera efectivo un tratamiento que no lo es (Campbell y Herzinger, 2010). Así mismo, varios estudios han encontrado una baja fiabilidad interjueces a la hora de interpretar los resultados de los diseños de caso único sobre la base del análisis visual, de manera que dos observadores distintos pueden mostrar poca coincidencia sobre si un tratamiento es efectivo y sobre la magnitud o relevancia de su efecto (Campbell y Herzinger, 2010). Ambos problemas subrayan las limitaciones que supone una evaluación basada en los juicios subjetivos de un observador, a pesar de que estos juicios no son completamente subjetivos ya que deben seguir una serie de criterios específicos que determinan la toma de decisiones y los datos en que se basen deben cumplir unos requisitos determinados (Kratochwill y Levin, 1992; Kratochwill et al., 2013).
Por otro lado, algunos de los requisitos mínimos necesarios para realizar un análisis visual adecuado de los datos no se cumplen en muchos estudios con diseños de caso único. Por ejemplo, se ha propuesto que es necesario contar con al menos tres datos en cada una de las fases de LB y tratamiento para poder identificar e interpretar un patrón de datos en una fase dada (Kratochwill et al., 2013). Sin embargo, en muchos estudios con diseños de caso único es difícil cumplir ese estándar, especialmente en la LB, ya que por cuestiones éticas y clínicas no se puede alargar la LB e incluso, en algunos casos, tan solo se cuenta con un único dato en la LB: la medida pretratamiento.
Finalmente, dada la alta heterogeneidad de los estudios con diseños de caso único respecto a sus características básicas (p. ej., duración de las fases de LB y de tratamiento, número y tipos de medidas, número de fases, tipo de diseño, etc.), es difícil con un simple análisis visual de los datos comparar los resultados de un estudio con los de otro (p. ej., comparar si un tratamiento ha sido más eficaz en un paciente que en otro o comparar la efectividad de un tratamiento con la que se ha encontrado en estudios previos) o incluso comparar distintos resultados en un mismo estudio (p. ej., comparar si un tratamiento ha sido más eficaz para reducir la sintomatología de estrés postraumático que la sintomatología depresiva).
El análisis estadístico de los datos en los diseños de caso único, aunque mucho menos utilizado, ha pretendido resolver algunos de los problemas que aquejan al análisis visual, especialmente los vinculados a su “subjetividad”, al proporcionar un método cuantitativo y un conjunto de reglas para determinar si un cambio terapéutico es significativo. Por lo tanto, muchos especialistas recomiendan complementar el análisis visual con algún tipo de análisis estadístico (Bono Cabré y Arnau Gras, 2014; Campbell y Herzinger, 2010), postura que también es compartida por muchos defensores del análisis visual de los datos (p. ej., Kazdin, 1988, 1992). Sin embargo, las técnicas estadísticas más conocidas por los psicólogos clínicos y de la salud como, por ejemplo, las pruebas t y F, no son apropiadas para los diseños de caso único ya que tales estadísticos paramétricos presuponen la independencia entre los errores de cualquier par de datos, mientras que los datos en los diseños de caso único suelen correlacionar entre sí ya que proceden de la misma persona y, además, son observaciones sucesivas en una serie temporal en la que podrían influirse unas a otras, es decir, pueden mostrar dependencia serial o autocorrelación (Bono Cabré y Arnau Gras, 2014). Como alternativa se han propuesto fundamentalmente tres tipos de análisis estadísticos: el análisis de series temporales, las pruebas no paramétricas basadas en la aleatorización y los índices para la estimación del tamaño del efecto basados en el no solapamiento de los datos entre las fases, aunque la lista de métodos estadísticos es mucho más amplia e incluye algunos que muy raramente han sido utilizados (Bono Cabré y Arnau Gras, 2014; Kazdin, 1988; Parker y Brossart, 2003).
De esos tres tipos principales de análisis, los dos primeros presentan problemas muy graves para su utilización en la práctica clínica. Los análisis de series temporales requieren un número muy grande de datos en cada fase de LB y de tratamiento para que sus resultados sean precisos (p. ej., un mínimo de 50 datos en cada fase; Glass et al., 1975, citado por Bono Cabré y Arnau Gras, 2014). Además, su utilización es compleja en términos de los conocimientos estadísticos y del trabajo computacional necesarios (Bono Cabré y Arnau Gras, 2014; Kazdin, 1988). Las pruebas no paramétricas de aleatorización, por su parte, requieren la aleatorización de algún aspecto del diseño. Por ejemplo, en el diseño de caso único más básico y más empleado en la práctica clínica, el diseño con una sola fase de LB y una sola fase de tratamiento (diseño A-B), las pruebas no paramétricas de aleatorización requieren decidir al azar el momento en que se aplica el tratamiento (Bono Cabré y Arnau Gras, 2014). Sin embargo, por razones clínicas, prácticas y éticas esto no suele ser posible en la práctica clínica, ya que dicha selección podría resultar en una aplicación muy tardía que fuera imposible o contraproducente.
En contraposición con estos dos tipos de análisis, los índices para estimar el tamaño del efecto basados en el no solapamiento de los datos entre las fases parecen especialmente relevantes para analizar los estudios con diseño de caso único en la práctica clínica, ya que pueden utilizarse con todo tipo de diseños, se pueden calcular incluso con un número muy pequeño de datos en la LB o en el tratamiento, son más robustos que los índices basados en los cambios de medias o medianas entre fases, especialmente en esos casos tan frecuentes en la práctica clínica en los que hay pocos datos en la LB o en el tratamiento, y su cálculo es extremadamente simple y fácil, pudiéndose realizar a mano a partir de los gráficos de datos (Parker, Vannest y Davis, 2011). Estos índices no tratan de comprobar la significación estadística del efecto o cambio terapéutico, sino de cuantificar ese cambio y valorar su magnitud, lo que permitiría superar algunos de los problemas que afectan al análisis visual de los datos y precisar de forma válida las inferencias basadas en este (Bono Cabré y Arnau Gras, 2014). Así, estos índices son capaces de ofrecer una medida de la magnitud del cambio terapéutico que es más objetiva que la que se puede obtener mediante un análisis visual y que se puede comparar entre distintos estudios, pacientes o medidas. Por otro lado, es importante señalar que los índices de no solapamiento de datos desarrollados en los últimos 10 años están basados en distribuciones de muestreo establecidas que permiten la construcción de sus intervalos de confianza y permiten poner a prueba el tamaño del efecto frente a una hipótesis de nulidad, lo cual es especialmente útil con diseños de caso único con pocos datos (Parker et al., 2011). Finalmente, estos índices responden muy bien a las exigencias del movimiento de los tratamientos basados en la evidencia y a su necesidad de sustentar empíricamente los tratamientos con un índice que refleje la magnitud de la mejoría del paciente (Parker et al., 2011).
Por todas estas ventajas, el primer objetivo del presente trabajo fue presentar algunos de los índices de tamaño del efecto más conocidos y más útiles para el análisis de datos de los diseños de caso único en la práctica clínica, así como ilustrar su utilización mediante su aplicación en un caso clínico.
Una limitación que presentan todos los índices de tamaño del efecto es que un cambio terapéutico de magnitud grande no implica necesariamente que dicho cambio sea clínicamente significativo o tenga un valor práctico, es decir, que sea, por ejemplo, el cambio requerido para que un paciente pueda funcionar en la sociedad o que produzca alguna diferencia real para ese paciente o para las personas de su entorno en su funcionamiento y vida diaria. Es cierto que hay una mayor relación entre el tamaño del efecto y la significación clínica que entre esta última y la significación estadística y que habitualmente los efectos terapéuticos de magnitud grande suelen ser también clínicamente significativos, pero aun así es posible obtener en una investigación de caso único índices de tamaño del efecto iguales a 100% sin que necesariamente los cambios terapéuticos tengan una repercusión clara en el funcionamiento cotidiano del paciente. Tales índices de tamaño del efecto pueden hacer creer al clínico o investigador que el tratamiento ha sido efectivo, pero en este contexto, efectivo querría decir que ha producido un cambio beneficioso de una magnitud grande, pero no que ese cambio sea lo suficiente grande para suponer que el paciente se ha recuperado de su trastorno psicológico y ha vuelto a su funcionamiento normal o simplemente que se ha producido en dicho trastorno una mejoría de una magnitud clínicamente relevante y con efectos prácticos en la vida del paciente.
En consecuencia, el segundo objetivo del presente artículo fue presentar un procedimiento para evaluar la significación clínica de los cambios terapéuticos en un diseño de caso único que, por su simplicidad y relevancia, puede ser especialmente útil en la práctica clínica, así como ilustrar su utilización mediante su aplicación en un caso clínico.
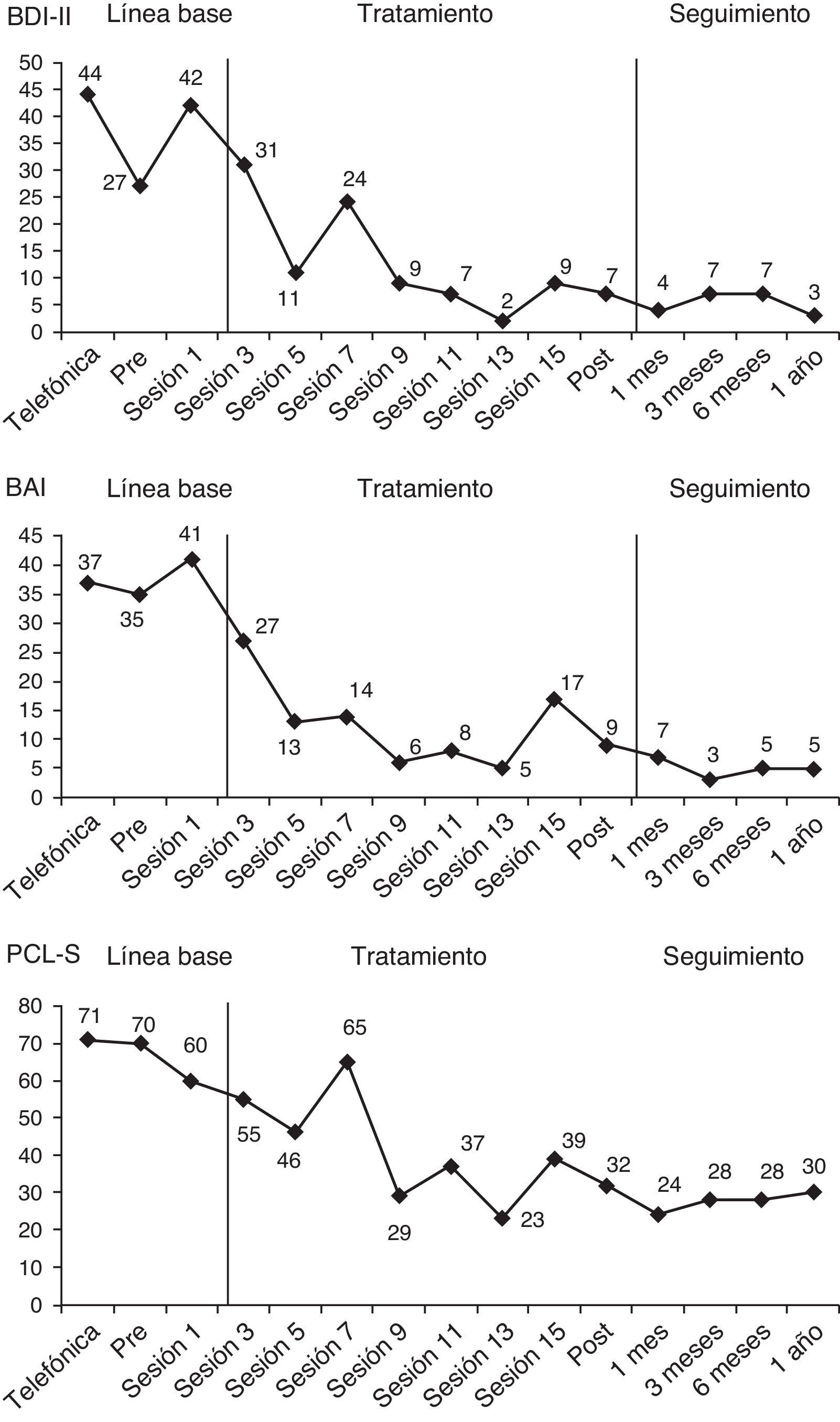
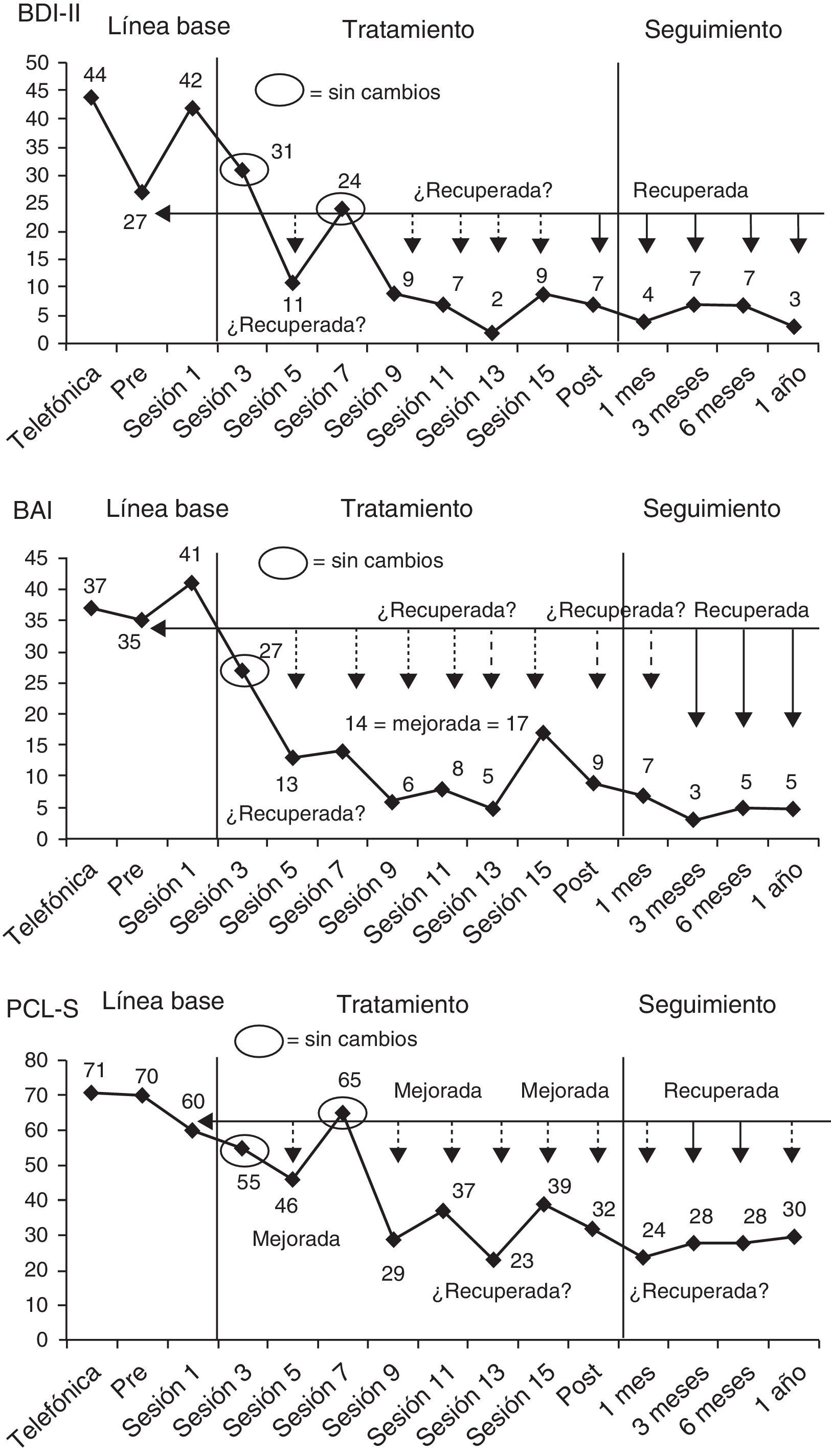
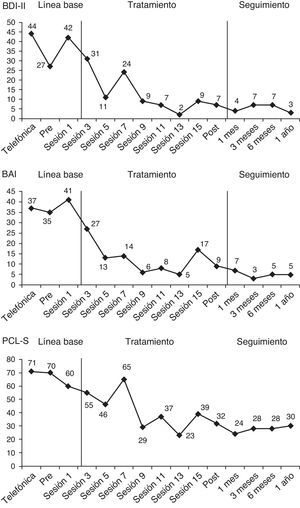
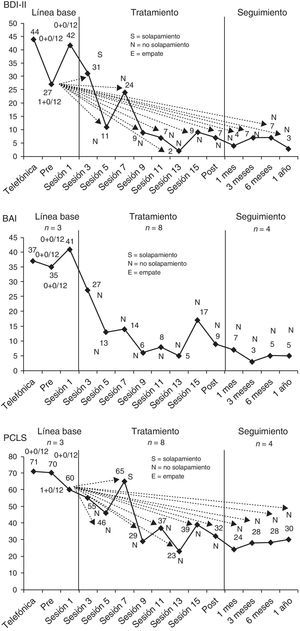
Un ejemplo de diseño de caso único: el tratamiento de una víctima del terrorismoPara ilustrar el cálculo y la interpretación de las técnicas de análisis de datos que se describirán en este trabajo, en la figura 1 se presentan los gráficos de evolución terapéutica de una de las víctimas del terrorismo que fue tratada en el marco de un proyecto de investigación sobre las consecuencias psicopatológicas de los atentados terroristas a muy largo plazo (más de 20-30 años) y sobre la eficacia y utilidad de los tratamientos psicológicos de dichas consecuencias (Moreno et al., manuscrito en edición editorial). El proyecto de investigación implicaba: (a) contactar telefónicamente con todos los socios de varias asociaciones de víctimas del terrorismo, en especial de la Asociación Víctimas del Terrorismo (AVT), (b) aplicar, mediante una entrevista telefónica, diversos instrumentos de cribado psicopatológico a todas las víctimas adultas que accedían a participar voluntariamente en el proyecto, (c) detectar a las víctimas que pudieran presentar un trastorno psicológico relacionado con el atentado terrorista sufrido, (d) citar a estas víctimas para la realización de una entrevista diagnóstica estructurada presencial que corroborara la presencia de un trastorno por estrés postraumático, de un trastorno depresivo o de un trastorno de ansiedad y (e) ofrecer a todas las víctimas que sufrían alguno de esos trastornos la posibilidad de recibir gratuitamente un tratamiento psicológico para los mismos.
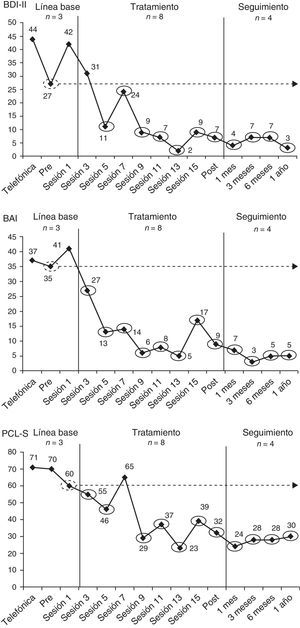
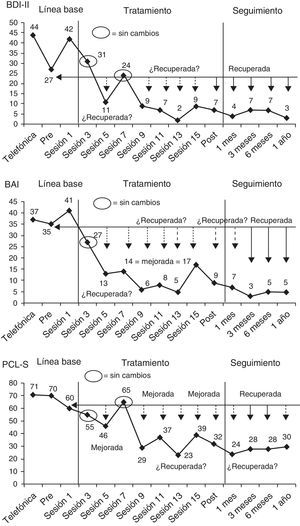
La víctima, Nuria (nombre ficticio), era una mujer soltera de 65 años, jubilada y con estudios de formación profesional superior, que resultó herida en el atentado ocurrido el 13 de septiembre de 1974 en la cafetería Rolando de Madrid. La banda terrorista ETA colocó una bomba en los aseos de la cafetería y causó la muerte de 13 personas y heridas a otras 60. Nuria presentaba un trastorno por estrés postraumático acompañado de un trastorno depresivo mayor recidivante y de un trastorno de angustia con agorafobia. Por tanto, se le ofreció participar en un programa de tratamiento individual de 16 sesiones semanales de terapia cognitivo conductual centrada en el trauma que incluía, además, algunas técnicas terapéuticas específicas para el trastorno depresivo mayor y el trastorno de angustia (p. ej., planificación de actividades agradables, exposición interoceptiva) (García-Vera et al., en prensa; Moreno et al., manuscrito en edición editorial). Durante la evaluación diagnóstica pretratamiento, Nuria completó las adaptaciones españolas del Inventario de Depresión de Beck-II (BDI-II; Beck, Steer y Brown, 2011), del Inventario de Ansiedad de Beck (BAI; Beck y Steer, 2011) y de la Lista de Verificación del Trastorno por Estrés Postraumático, versión específica (PCL-S; Vázquez, Pérez-Sales y Matt, 2006; Weathers, Litz, Herman, Huska y Keane, 1993), instrumentos que fueron posteriormente aplicados cada dos semanas de tratamiento empezando por la sesión 1, tal y como se muestra en la figura 1. Para entender mejor esta figura y las figuras y ejemplos que se presentarán más adelante sobre este caso, cabe recordar que el rango de puntuaciones del BDI-II y del BAI es de 0 a 63 y el de la PCL-S es de 17 a 85 y en los tres instrumentos una mayor puntuación indica una mayor frecuencia y gravedad de síntomas de depresión, ansiedad o estrés postraumático, respectivamente.
Durante la entrevista de cribado telefónico Nuria también había completado la PCL-S, una versión breve del BDI-II (BDI-II-SF; Sanz, García-Vera, Fortún y Espinosa, 2005) y una versión breve del BAI (BAI-PC; Beck, Steer, Ball, Ciervo y Kabat, 1997; Sanz y García-Vera, 2012). Tras convertir, mediante las oportunas ecuaciones de regresión (Sanz et al., 2005; Sanz y García-Vera, 2012), las puntuaciones del BDI-II-SF y del BAI-PC a puntuaciones del BDI-II y del BAI, respectivamente, esas medidas psicopatológicas de la evaluación telefónica pasaron a formar parte de la LB junto con las medidas tomadas durante la evaluación diagnóstica pretratamiento y las tomadas durante la primera sesión de tratamiento (véase la fig. 1). Después de la última sesión de terapia se llevó a cabo una evaluación psicológica postratamiento así como seguimientos psicológicos al mes, a los tres meses, a los seis meses y al año y durante todos ellos Nuria volvió a completar el BDI-II, el BAI y la PCL-S. Estas medidas tomadas en el postratamiento y en los seguimientos pasaron a formar parte de las medidas de la fase de tratamiento-seguimiento junto con las tomadas durante las sesiones de terapia 3, 5, 7, 9, 11, 13 y 15 (véase la fig. 1).
Evaluación de la magnitud del cambio terapéutico o tamaño del efecto del tratamientoEn los últimos años se han desarrollado multitud de índices basados en el no solapamiento de los datos entre fases para evaluar el tamaño del efecto del tratamiento en los diseños de caso único. Parker et al. (2011) revisaron nueve de ellos, notando muchas semejanzas entre los mismos, pero también diferencias que implican un perfil diferencial de ventajas y limitaciones en términos de su potencia estadística, de la posibilidad de corregir una tendencia positiva en la LB, de su sensibilidad para discriminar los tratamientos más efectivos, etc. Por esta razón, se suele recomendar la utilización de varios de ellos para determinar si se obtienen resultados consistentes (Maggin, Briesch y Chafouleas, 2013).
En cualquier caso, la mayoría de los índices basados en el no solapamiento de los datos no deberían utilizarse o hacerlo con mucha precaución cuando exista: (a) una tendencia positiva en la fase de LB y (b) una tendencia fuerte también positiva en la fase de intervención. Cuando se cumplen ambas condiciones podría ocurrir que el tratamiento no tiene efecto alguno, sino que meramente permite continuar la tendencia positiva que ya existía en la LB, lo cual se vería reflejado en el gráfico por una diagonal que cruza ambas fases bien de forma ascendente o descendente (según la dirección de la funcionalidad); a pesar de ello, la mayoría de los índices indicarían erróneamente que el tratamiento muestra el máximo efecto posible (100%). Por otro lado, cuando se cumple las anteriores dos condiciones también podría ocurrir que el tratamiento sí tuviera efecto aumentando la pendiente de la tendencia mostrada en la LB, pero esto no quedaría adecuadamente reflejado por los índices que, de nuevo, siempre indicarían la máxima efectividad independientemente de cuál fuera la pendiente.
Por razones de espacio, a continuación se describirán solo tres índices basados en el no solapamiento de los datos que han sido elegidos, los dos primeros en función principalmente de su popularidad y facilidad de cálculo y el tercero por sus buenas propiedades estadísticas (p. ej., alta potencia estadística, buena sensibilidad, etc.).
Porcentaje de datos no solapados (PND)El porcentaje de datos no solapados [percentage of nonoverlapping data o PND] es uno de los índices más antiguos para evaluar la magnitud del cambio terapéutico en un diseño de caso único y, a pesar de sus limitaciones, ha sido el más utilizado en la literatura científica (Scruggs y Mastropieri, 2013; Scruggs, Mastropieri y Casto, 1987). Así, por ejemplo, se ha utilizado en más de 40 meta-análisis de estudios de diseño de caso único (Maggin et al., 2013; Scruggs y Mastropieri, 2013), por lo que la posibilidad de comparar los resultados obtenidos con los de la literatura científica es mayor que con otros índices. El PND se define como el porcentaje de datos de la fase de tratamiento que excede al dato más extremo de la LB, y se calcula contando el número de datos de la fase de tratamiento que superan (por encima en las medidas funcionales o por debajo en las medidas disfuncionales) al dato más extremo de la LB (el más alto en las medidas funcionales o el más bajo en las medidas disfuncionales) y dividiendo este número por el número total de datos en la fase de tratamiento:
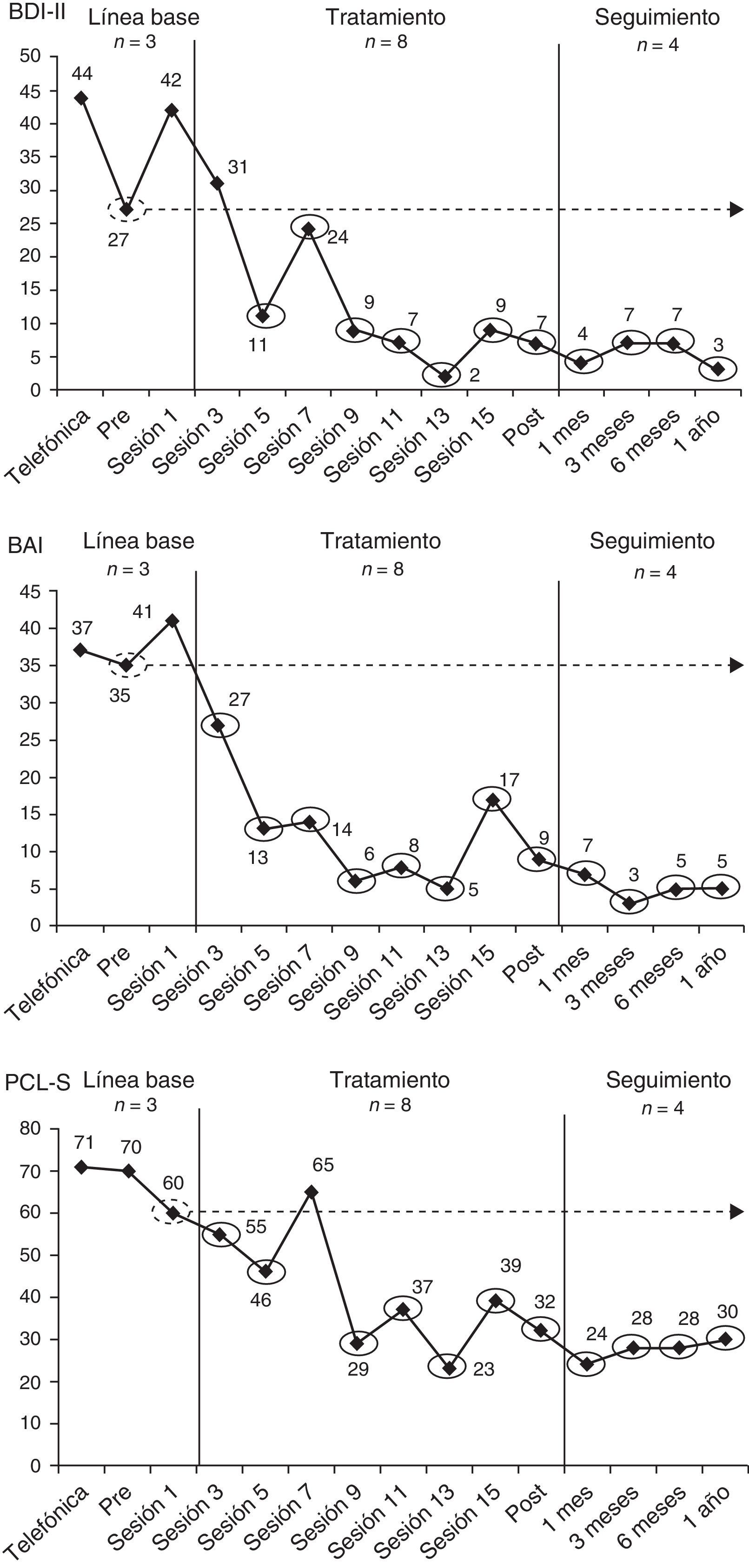
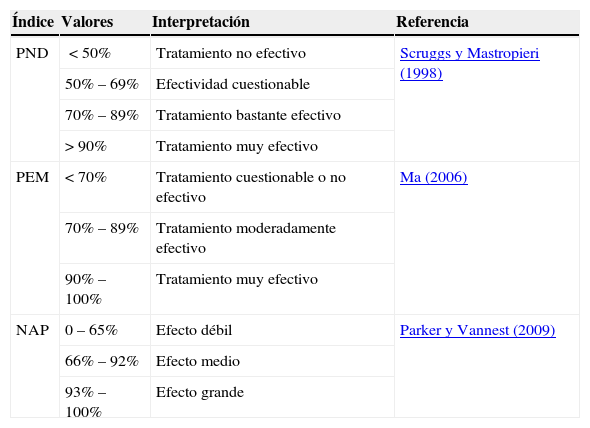
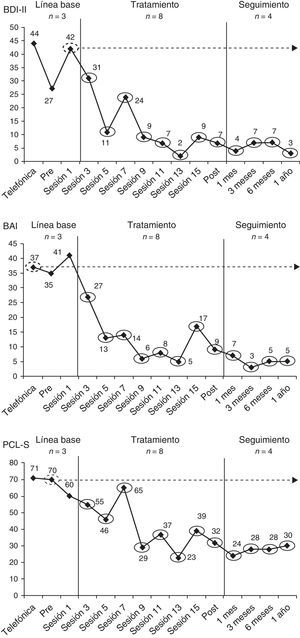
El rango de valores del PND varía de 0 a 100% y sus creadores han propuesto una guía para su interpretación en términos de la efectividad de un tratamiento (Scruggs y Mastropieri, 1998). Esta guía se recoge en la tabla 1. En la figura 2 se ilustra el cálculo del PND en cada una de las medidas psicopatológicas tomadas en el caso de la víctima del terrorismo. Por ejemplo, respecto al BDI-II, la puntuación más extrema (en este caso, más baja) durante la LB fue 27 y once de los doce puntuaciones del BDI-II durante la fase de tratamiento-seguimiento estaban por debajo de 27, por lo que PND = (11 / 12) x 100=91.6%, mientras que, respecto al BAI, la puntuación más baja en la LB fue 35 y las doce puntuaciones del BAI en la fase de tratamiento-seguimiento estaban por debajo de 35, por lo que PND=(12 / 12) x 100=100%.
Valores convencionales para interpretar los índices de tamaño del efecto PND, PEM y NAP en diseños de caso único
| Índice | Valores | Interpretación | Referencia |
|---|---|---|---|
| PND | <50% | Tratamiento no efectivo | Scruggs y Mastropieri (1998) |
| 50% – 69% | Efectividad cuestionable | ||
| 70% – 89% | Tratamiento bastante efectivo | ||
| > 90% | Tratamiento muy efectivo | ||
| PEM | < 70% | Tratamiento cuestionable o no efectivo | Ma (2006) |
| 70% – 89% | Tratamiento moderadamente efectivo | ||
| 90% – 100% | Tratamiento muy efectivo | ||
| NAP | 0 – 65% | Efecto débil | Parker y Vannest (2009) |
| 66% – 92% | Efecto medio | ||
| 93% – 100% | Efecto grande |
Nota. PND = porcentaje de datos no solapados; PEM = porcentaje de datos que exceden la mediana; NAP = no solapamiento de todos los pares.
Cálculo del porcentaje de datos no solapados (PND) para el Inventario de Depresión de Beck-II (BDI-II), el Inventario de Ansiedad de Beck (BAI) y la Lista de Verificación del Trastorno por Estrés Postraumático, versión específica (PCL-S), en el tratamiento de una víctima del terrorismo.
Uno de los problemas del PND es que, puesto que está basado en un único dato de la LB, la presencia de valores muy atípicos en la LB podría distorsionar la estimación de la magnitud del efecto. Por ejemplo, si en el gráfico de la figura 2 correspondiente al BAI en lugar de encontrarse en la evaluación de pretratamiento una puntuación de 35 que, aunque la más extrema, es relativamente consistente con los otros dos valores de la LB, se hubiera encontrado un valor atípico de 5, el PND sería de tan solo 8.3% [(1 / 12) x 100], a pesar de que, según refleja la figura 2, el tratamiento parece mucho más efectivo en función del descenso tan inmediato y marcado en las puntuaciones del BAI y la estabilidad del descenso a lo largo del tratamiento y de los seguimientos.
Porcentaje de datos que exceden la mediana (PEM)El porcentaje de datos que exceden la mediana [percentage of data points exceeding the median o PEM] se define como el porcentaje de datos de la fase de tratamiento que supera (por encima en las medidas funcionales o por debajo en las medidas disfuncionales) a la mediana de los datos de la LB (Ma, 2006). El PEM asume que la mediana es un buen resumen de las puntuaciones de la LB y que cuando el tratamiento no tiene efecto alguno, los datos de la fase de tratamiento deberían fluctuar en torno a la línea de la mediana. El PEM ha sido utilizado en varios metaanálisis de diseños de caso único como índice de tamaño del efecto (Ma, 2009; Preston y Carter, 2009).
Para calcular la mediana, se ordenan de forma creciente todos los datos de la LB y si el número de datos de la LB es impar la mediana es el dato que los divide en dos partes iguales, superiores e inferiores a él y si el número de datos de la LB es par se identifican los dos datos que dividen en dos partes iguales la serie ordenada de datos y esos dos datos se promedian. A continuación, para calcular el PEM se dibuja desde la mediana una línea que atraviese la fase de tratamiento y se calcula el porcentaje de datos de la fase de tratamiento que están por encima de la línea de la mediana (en las medidas funcionales) o por debajo (en las medidas disfuncionales), de manera que:
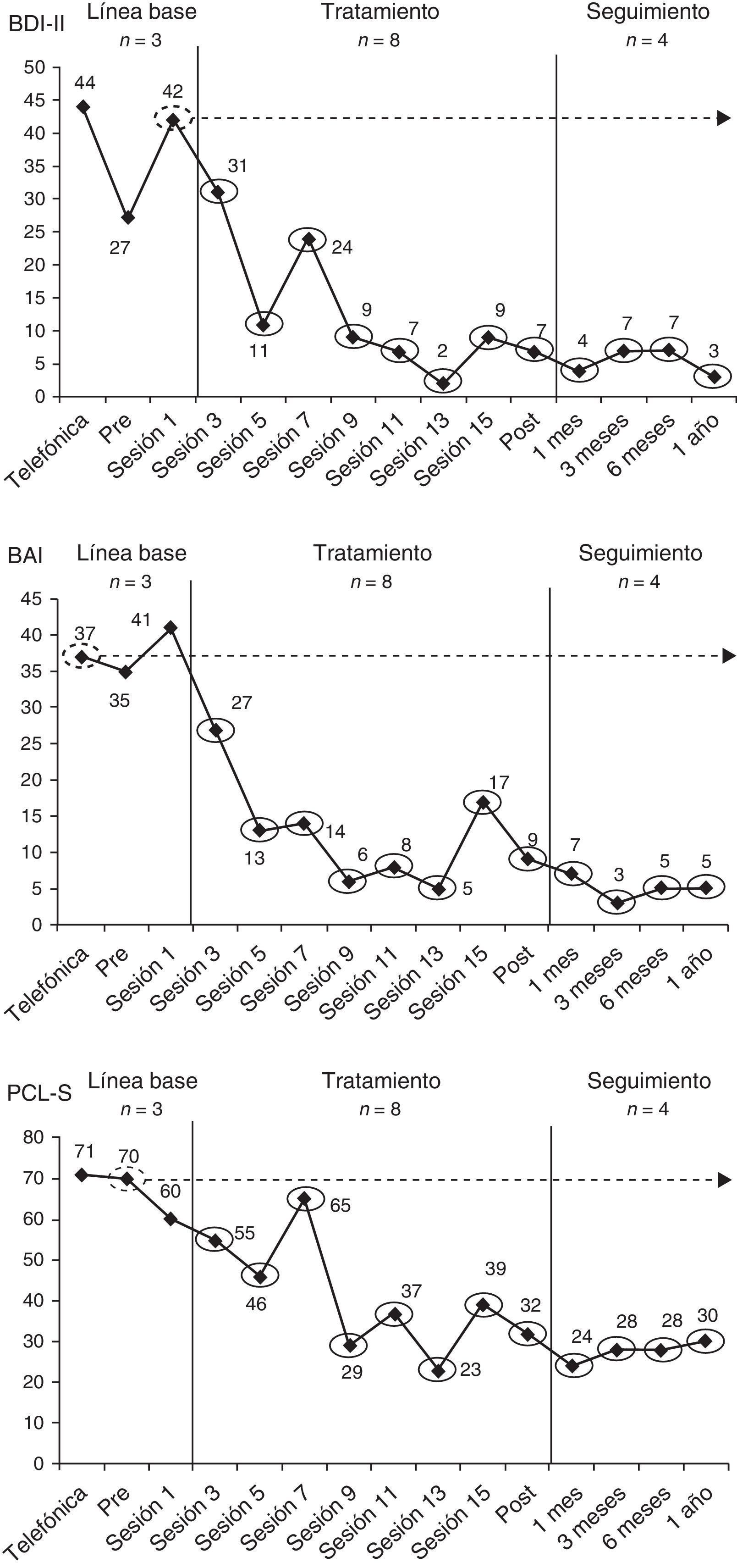
En la figura 3 se ilustra el cálculo del PEM en el caso del tratamiento de la víctima del terrorismo (véase también la tabla 2). Por ejemplo, en relación con el BAI, tras ordenar crecientemente los datos de la LB (35, 37 y 41) la mediana fue 37. A partir de este dato se dibujó una línea que atravesaba la fase de tratamiento-seguimiento y se contabilizaron 12 datos de esa fase que estaban por debajo de la línea de la mediana, por lo que PEM=(12 / 12) x 100=100%.
Cálculo del porcentaje de datos que exceden la mediana (PEM) para el Inventario de Depresión de Beck-II (BDI-II), el Inventario de Ansiedad de Beck (BAI) y la Lista de Verificación del Trastorno por Estrés Postraumático, versión específica (PCL-S), en el tratamiento de una víctima del terrorismo.
Efectividad de la terapia cognitivo conductual centrada en el trauma para una víctima del terrorismo en función del índice de tamaño del efecto
| Variable de resultado | Índice de tamaño de efecto | ||
|---|---|---|---|
| PND | PEM | NAP | |
| Depresión (BDI-II) | 91.6%[tratamiento muy efectivo] | 100%(73.5% - 100%)[tratamiento muy efectivo] | 97.2%(89.2% - 100%)[efecto grande] |
| Ansiedad (BAI) | 100%[tratamiento muy efectivo] | 100%(73.5% - 100%)[tratamiento muy efectivo] | 100%(100% - 100%)[efecto grande] |
| Estrés postraumático (PCL-S) | 91.6%[tratamiento muy efectivo] | 100%(73.5% - 100%)[tratamiento muy efectivo] | 97.2%(89.2% - 100%)[efecto grande] |
Nota. Los datos son los valores de los correspondientes índices de tamaño del efecto, con sus intervalos de confianza al 95% entre paréntesis (excepto para PND, ya que no es posible su cálculo; Parker y Vannest, 2009) y su interpretación convencional entre corchetes. PND = porcentaje de datos no solapados; PEM = porcentaje de datos que exceden la mediana; NAP = no solapamiento de todos los pares; BDI-II = Inventario de Depresión de Beck-II; BAI = Inventario de Ansiedad de Beck; PCL-S = Lista de Verificación del Trastorno por Estrés Postraumático, versión específica.
El rango de valores del PEM oscila entre 0 y 100% y su creadora, Ma (2006), ha sugerido que para su interpretación los criterios más adecuados serían los propuestos por Scruggs, Mastropieri, Cook y Escobar (1986) para el PND y que se recogen en la tabla 1.
El PEM solventa el problema del PND respecto a la existencia de datos muy atípicos en la LB, pero también tiene algunas limitaciones, entre las cuales destaca que no es un índice sensible a la magnitud de los datos que están por debajo (o por encima) de la mediana, de forma que dos tratamientos pueden obtener el mismo PEM (p. ej., 100%) independientemente de que uno consiga reducir todas las puntuaciones de un instrumento a 0 y otro consiga reducir todas las puntuaciones en tan solo un punto por debajo de la mediana de la LB.
No solapamiento de todos los pares (NAP)El índice de no solapamiento de todos los pares [nonoverlap of all pairs o NAP] fue desarrollado por Parker y Vannest (2009) para superar las limitaciones de otros índices de solapamiento de datos entre fases como el PND o el PEM. Como estos últimos, el NAP resume el no solapamiento de datos entre las fases de LB y tratamiento, pero se diferencia de ellos por el hecho de que tiene en cuenta todos los solapamientos posibles entre la LB y el tratamiento, ya que compara por pares todos los datos de la fase de la LB con todos los datos de la fase de tratamiento, por lo que podría interpretarse como el porcentaje de datos sin solapamiento entre las fases de LB y tratamiento o el porcentaje de datos que muestran una mejoría respecto a la LB.
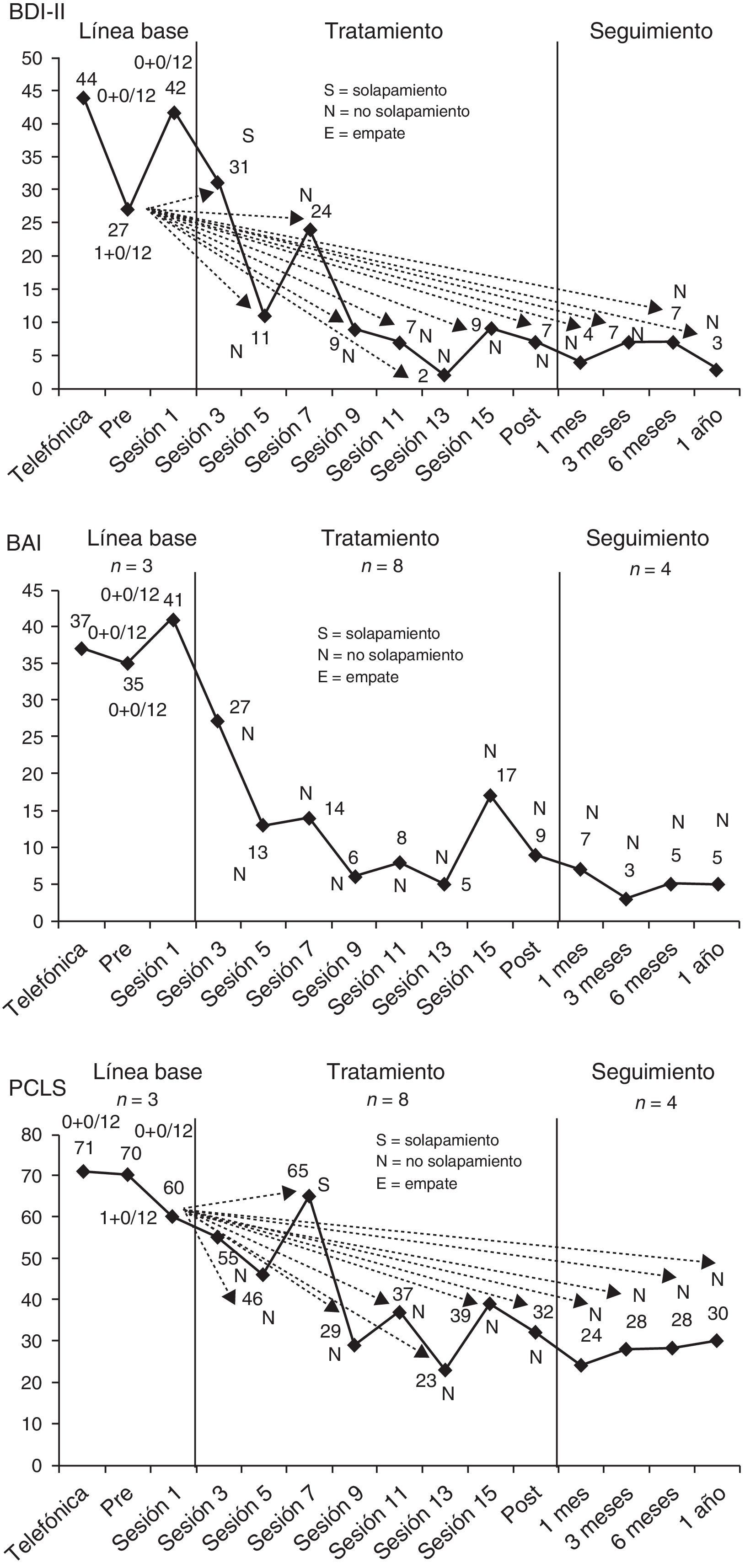
En la figura 4 se ilustra el cálculo del NAP en el caso del tratamiento de la víctima del terrorismo (véase también la tabla 2). Para calcular el NAP se compara cada dato de la LB con cada dato del tratamiento-seguimiento. En la figura 4 las flechas del gráfico sobre la evolución terapéutica en el BDI-II y en la PCL-S muestran, para una mayor claridad, esas comparaciones por pares y sus resultados para un único dato de la LB, el dato de la evaluación pretratamiento en el caso del BDI-II (27) y el dato de la sesión 1 en el caso de la PCL-S. Un par de datos se considera no solapamiento (N) si el dato de la fase de tratamiento-seguimiento supera (en la dirección de la funcionalidad) al de la fase de LB, en este caso si el dato del tratamiento-seguimiento es menor que el dato de la LB, mientras que se considera un solapamiento (S) si el dato del tratamiento-seguimiento no supera (en la dirección de la funcionalidad) al de la LB, en este caso si dicho dato es mayor que el de la LB, y se considera un empate (E) si ambos datos son iguales. Cuando se comparó el dato del pretratamiento en el BDI-II (27) con todos los datos del tratamiento-seguimiento, se encontró 1 solapamiento (S), 11 no solapamientos (N) y 0 empates (E). Puesto que habitualmente es más fácil contar el número de solapamientos y empates y restarlos al número total de pares para obtener así el número de no solapamientos (n° de N=n° de pares – n° de S – n° de E), en la figura 4 se muestra el resultado de las comparaciones en términos del número de solapamientos y empates del total de pares: (n° de S + n° de E) / n° de pares. Así, para la puntuación pretratamiento en el BDI-II (27) ese resultado es (1 + 0) / 12, es decir, 1 par con solapamiento y 0 pares con empate, de 12 pares que lo comparan con los datos del tratamiento-seguimiento. En el caso de los otros dos datos del BDI-II de la LB (44 y 42), no existe ningún dato del tratamiento-seguimiento que sea igual o mayor que ellos, por lo que en ambos casos el número de solapamientos y empates sobre el total de pares es (0 + 0) / 12. Por tanto, el número posible de pares de datos comparando la LB con el tratamiento-seguimiento sería 36 (12 + 12 + 12), número que se calcula de forma general simplemente multiplicando el número de datos de la LB por el número de datos del tratamiento-seguimiento (n° de datos de LB x n° de datos del tratamiento-seguimiento=3 x 12=36), mientras que el número de pares sin solapamiento sería 35 (n° de pares – n° de solapamientos – n° de empates=36 – 1 – 0=35). Finalmente, en el cálculo del NAP, la mitad de los empates se consideran no solapamientos y la otra mitad solapamientos, por lo que, la fórmula general para el cálculo del NAP es:
Cálculo del índice de no solapamiento de todos los pares (NAP) para el Inventario de Depresión de Beck-II (BDI-II), el Inventario de Ansiedad de Beck (BAI) y la Lista de Verificación del Trastorno por Estrés Postraumático, versión específica (PCL-S), en el tratamiento de una víctima del terrorismo.
Utilizando esta fórmula para el BDI-II, NAP=((35 + (0.5 x 0)) / 36) x 100=97.2% (véase la tabla 2).
Como ocurre con el caso de la víctima del terrorismo, en muchos diseños de caso único el NAP es muy sencillo de calcular porque visualmente es fácil apreciar que ninguno de los datos de la LB (véase la fig. 4 respecto al BAI) o muy pocos de ellos (véase la fig. 4 respecto al BDI-II y la PCL-S) se solapan o empatan con los datos del tratamiento, pero su cálculo puede ser más tedioso cuando los cambios terapéuticos que se analizan son de menor magnitud, y por tanto hay un mayor número de solapamientos y empates, y cuando se ha tomado un número mayor de datos en la LB o en el tratamiento. Para facilitar el cálculo del NAP, sus autores han creado una aplicación muy sencilla en Internet que, además, permite comparar distintas fases de LB y de tratamiento en diseños de caso único más complejos (p. ej., diseños A-B-A-B o A-B-C-B): http://www.singlecaseresearch.org/calculators/nap. Lamentablemente, la aplicación asume que la funcionalidad implica un dato en la fase de tratamiento mayor que en la LB y, por tanto, no puede utilizarse con medidas en las que una puntuación menor implica una mayor funcionalidad o mejoría, tal y como es el caso del BDI-II, el BAI o la PCL-S. Sin embargo, puesto que el NAP es igual al área bajo la curva [area under the curve o AUC], multiplicado por 100, de un análisis de la curva ROC [receiver operating characteristic] o curva de la característica operativa del receptor (curva COR), el NAP se puede calcular con cualquier programa estadístico estándar que realice un análisis de la curva ROC como, por ejemplo, entre los comerciales el SPSS o entre los gratuitos el EPIDAT (Xunta de Galicia, Organización Panamericana de la Salud y Universidad CES de Colombia, Santiago de Compostela, España; http://dxsp.sergas.es).
El análisis de la curva ROC es una herramienta desarrollada a partir de la Segunda Guerra Mundial para mejorar la detección de las señales de radar y se utiliza en la actualidad en un amplio abanico de contextos, en particular en el análisis de la precisión o eficacia diagnóstica de pruebas y tests para detectar casos positivos y negativos respecto a una determinada enfermedad o característica patológica (Swets, 1988). El área bajo la curva ROC puede oscilar entre 0 a 1 y en ese contexto un valor de .5 indica que la capacidad de la prueba o test para diagnosticar correctamente un caso positivo o negativo es igual a la de un diagnóstico realizado al azar, mientras que un área con un valor de 1 indica que la prueba o test logra un diagnóstico perfecto del conjunto de casos analizados (Swets, 1988).
En términos de su equivalencia con el área bajo la curva ROC, el NAP refleja la probabilidad de que un dato elegido al azar de la fase de tratamiento exceda (en la dirección de la funcionalidad) a un dato elegido al azar de la fase de LB. Por tanto, para su cálculo a partir del análisis de la curva ROC, por ejemplo con el SPSS, la “variable de prueba” serían los datos tomados durante la LB y el tratamiento y la “variable de estado” (positivo o negativo) sería la fase en que se tomó el dato (LB o tratamiento). Además, habría que indicar el valor de la variable estado que indica un caso positivo, en este caso el valor que indica que el dato pertenece a la fase de tratamiento, y la dirección de la variable de prueba, es decir, si un valor más grande o más pequeño indica un caso positivo o en este caso si un dato más grande o más pequeño indica funcionalidad o mejoría respecto a la LB. Una de las ventajas de calcular el NAP con al análisis de la curva ROC es que permite obtener el intervalo de confianza del área bajo la curva ROC, es decir, el intervalo en el que con un nivel de confianza de, por ejemplo, un 95% se encuentra el NAP verdadero. Este intervalo de confianza permite evaluar el NAP obtenido con mayor cautela, siendo consciente de sus limitaciones en función del número de datos con el que ha sido obtenido, a la vez que permite estimar si dicho NAP difiere de forma estadísticamente significativa de .50 o 50%, lo cual ocurriría cuando el límite inferior de su intervalo de confianza al 95% fuera mayor que .50 e inferir, en consecuencia, si se ha producido en la fase de tratamiento un cambio de nivel respecto a la LB. El cálculo del intervalo de confianza también es posible para el PEM mediante la prueba binomial de comparación de una proporción con la proporción teórica de .50 que representaría la mediana (Parker y Vannest, 2009).
Para interpretar los valores del NAP, Parker y Vannest (2009) han propuesto unos valores de referencia que pueden consultarse en la tabla 1. Por otro lado, puesto que el NAP se calcula en una escala de 50% a 100%, donde 50% es el resultado que se esperaría por azar y que indicaría que los datos de las dos fases no pueden diferenciarse (hay un 50% de probabilidades de que un dato de una fase exceda al de la otra), se puede convertir a una escala de 0 a 100% usando la siguiente fórmula: NAP0-100=(NAP / 0.5) – 1, de manera que así se pueden comparar mejor los resultados del NAP con los obtenidos con otros índices como el PND o el PEM y sus respectivos criterios de interpretación (véanse las tablas 1 y 2).
Finalmente, es importante señalar que, como cabría esperar, los estudios indican que el NAP supera en su rendimiento estadístico al PND o el PEM (Parker et al., 2011) y de hecho es una de las técnicas para estimar el tamaño del efecto en diseños de caso único que mejor se comportan en presencia de dependencia serial o de un cambio en la variabilidad de los datos (Manolov, Solanas, Sierra y Evans, 2011).
Evaluación de la significación clínica de los cambios terapéuticosEn la literatura científica se han propuesto tres grandes estrategias para evaluar la significación clínica de los cambios terapéuticos: métodos que comparan al paciente con muestras normativas de personas, bien sean muestras normales o bien muestras disfuncionales, métodos basados en la evaluación subjetiva por parte del entorno social del paciente o por parte de expertos y métodos basados en medidas del impacto social (Kazdin, 1992; Ogles, Lunnen y Bonesteel, 2001). Sin embargo, el método que se ha utilizado con mayor frecuencia para evaluar si desde el punto de vista de la significación clínica un paciente está igual, ha empeorado o ha mejorado de sus problemas psicológicos, o incluso si ya se ha recuperado, es el método comparativo propuesto por Jacobson y Truax (1991), que implica una aproximación estadística a la significación clínica (Ogles et al., 2001).
Aproximación estadística a la significación clínicaEl método de Jacobson y Truax (1991) asume que un cambio clínicamente significativo supondría la vuelta a una población funcional de un paciente que antes del tratamiento pertenecía a una población disfuncional, es decir, que dicho cambio supondría que la puntuación de un paciente en un instrumento psicopatológico (p. ej., en el BDI-II, el BAI o la PCL-S) o en un instrumento que mide salud mental, calidad de vida, inadaptación o cualquier otro constructo relacionado relevante ya no pertenece a la distribución de puntuaciones en dicho instrumento de una población disfucional (p. ej., los pacientes españoles con trastornos psicológicos) sino a la distribución de una población funcional (p. ej., la población general española).
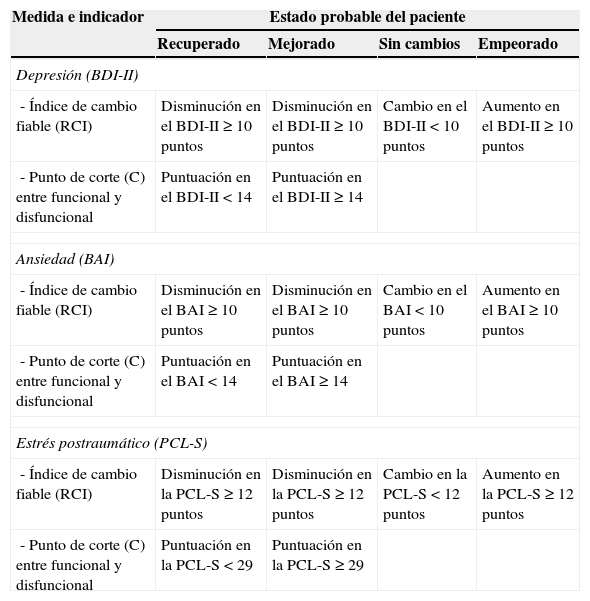
Para determinar la existencia de un cambio clínicamente significativo en un paciente, el método de Jacobson y Truax (1991) (ver también McGlinchey, Atkins y Jacobson, 2002) implica, en primer lugar, establecer una puntuación de corte (C) en el instrumento de referencia que el paciente debe alcanzar para pasar de una distribución disfuncional a una funcional. Para establecer esa puntuación de corte, los autores proponen tres definiciones operativas alternativas de C:
- 1.
La puntuación que se corresponde con dos desviaciones típicas por debajo o por encima (en la dirección de la funcionalidad) de la media de la distribución disfuncional, de manera que el nivel de funcionamiento del paciente tras la terapia estaría fuera del rango de la población disfuncional.
- 2.
La puntuación que se corresponde con dos desviaciones típicas por debajo o por encima (en la dirección de la funcionalidad) de la media de la distribución funcional, de manera que el nivel de funcionamiento del paciente tras la terapia estaría en el rango de la población funcional.
- 3.
La puntuación que se corresponde con el punto medio ponderado entre la media de la distribución funcional y la media de la distribución disfuncional, de manera que el nivel de funcionamiento del paciente tras la terapia le situaría más cerca de la población funcional que de la disfuncional.
La tercera definición parece la menos arbitraria y, además, cuando las dos distribuciones se solapan, como ocurre por ejemplo en el BDI-II, el BAI o la PCL-S (Sanz, 2013, 2014; Reguera et al., 2014) y en muchos otros instrumentos psicopatológicos, es la más adecuada. Para su cálculo se utiliza la siguiente fórmula:
en la que DTn y DTp representan las desviaciones típicas del instrumento en la población normal (o general) y en la de pacientes, respectivamente, y Mn y Mp las medias del instrumento en la población normal y en la de pacientes, respectivamente.
Obviamente, para el cálculo de C según esa tercera definición se requiere contar con información sobre la media y desviación típica de las puntuaciones del instrumento en muestras normativas de la población normal y de la población de pacientes; cuando sólo se tiene esa información de una de las poblaciones, la de pacientes o la normal, habría que utilizar la primera o la segunda definición, respectivamente. Sin embargo, hay que advertir que para muchos instrumentos psicopatológicos (p. ej., BDI-II, BAI o PCL-S) el criterio de dos desviaciones típicas por debajo (o por encima, según la dirección de la funcionalidad) de la media de la población de pacientes puede dar lugar a una puntuación extremadamente baja (p. ej., 0 en el BDI-II y el BAI y 17 en la PCL-S) que se encuentra muy por debajo de la media de la población normal (Sanz, 2013, 2014; Reguera et al., 2014) y, por tanto, sería un criterio de mejoría o recuperación excesivamente exigente. De forma parecida, el criterio de dos desviaciones típicas por encima (o por debajo, según la dirección de la funcionalidad) de la media de la población normal puede dar lugar a una puntuación extremadamente alta (p. ej., 25 en el BDI-II y 39 en el BAI) que indica todavía niveles moderados de sintomatología (Sanz, 2013, 2014) y, por tanto, no puede considerarse un criterio de mejoría o recuperación. En estos casos, sería mejor utilizar una desviación típica por encima o por debajo de la media o bien la propia media o la mediana como valores de C (véase Sanz, Perdigón y Vázquez, 2003; para una discusión y ejemplificación de estas opciones para la segunda definición de C en relación con el BDI-II y el BAI, respectivamente véase Magán, Sanz y García-Vera, 2008).
En segundo lugar, el método de Jacobson y Truax (1991) implica estimar si el cambio que indican las puntuaciones de un instrumento no se debe a su error de medida sino que refleja un cambio fiable, real en el nivel de sintomatología, salud mental, calidad de vida, inadaptación, etc. del paciente. Para ello, estos autores proponen un índice de cambio fiable [reliable change index; RCI] que tiene en cuenta el error típico de la diferencia entre dos puntuaciones del instrumento (sdif), el cual depende de su error típico de medida (se) que, a su vez, depende de su fiabilidad (rxx):
en las que x2 sería la puntuación en el instrumento de un paciente en un momento dado (p. ej., postratamiento), x1 la puntuación en el instrumento en un momento anterior (p. ej., pretratamiento), sx la desviación típica de las puntuaciones del instrumento en la población de pacientes y rxx la fiabilidad de consistencia interna del instrumento en dicha población. El error típico de la diferencia entre las dos puntuaciones (sdif) describiría la amplitud de la distribución de las puntuaciones de cambio que se esperaría si no ocurriera ningún cambio real, de manera que un RCI mayor que 1.96 sería muy poco probable (p<.05) que sucediera sin que ocurriera un cambio real. En consecuencia, el cambio en las puntuaciones en el instrumento de un paciente determinado debería superar ese valor del RCI para asegurar que dicho cambio no se debe a los errores de medida del instrumento:
Basándose en estos dos criterios, el método de Jacobson y Truax (1991; McGlinchey et al., 2002) clasifica a un paciente como recuperado si su puntuación en un instrumento supone un cambio que excede ese valor de 1.96 del RCI y si dicha puntuación ha superado la puntuación C, mejorado si la puntuación supone un cambio que excede el valor de 1.96 del RCI, pero no supera la puntuación C, sin cambios si la puntuación no supera el valor de 1.96 del RCI, y empeorado si la puntuación supone un cambio que supera el valor de 1.96 del RCI, pero en la dirección de un empeoramiento.
Por ejemplo, Reguera et al. (2014) encontraron en una muestra de 589 víctimas de atentados terroristas que la media y la desviación típica de la adaptación española de la PCL-S en las víctimas sin ningún trastorno psicológico (n=314) eran 22.90 y 7.17, respectivamente, mientras que en las víctimas con trastornos psicológicos (n=275) eran 42.43 y 15.15, respectivamente; además, en estas últimas víctimas la PCL-S mostraba una fiabilidad de consistencia interna (alfa de Cronbach) de .92. Teniendo en cuenta estos datos, la puntuación C y el cambio en las puntuaciones de la PCL-S que se corresponde con un valor de 1.96 del RCI serían:
En consecuencia, con dicha adaptación, un paciente cuya puntuación en la PCL-S ha descendido 12 puntos o más y dicha puntuación es menor de 29 se podría considerar recuperado de su trastorno por estrés postraumático; si su puntuación ha descendido 12 puntos o más, pero la misma no es más baja de 29, se podría considerar mejorado; si su puntuación no ha descendido 12 puntos, se podría considerar sin cambios y si la puntuación refleja un aumento de 12 puntos o más se podría considerar que ha empeorado (véase la tabla 3).
Aproximación estadística a la significación clínica de los cambios terapéuticos para las adaptaciones españolas de tres medidas de síntomas psicológicos
| Medida e indicador | Estado probable del paciente | |||
|---|---|---|---|---|
| Recuperado | Mejorado | Sin cambios | Empeorado | |
| Depresión (BDI-II) | ||||
| - Índice de cambio fiable (RCI) | Disminución en el BDI-II ≥ 10 puntos | Disminución en el BDI-II ≥ 10 puntos | Cambio en el BDI-II < 10 puntos | Aumento en el BDI-II ≥ 10 puntos |
| - Punto de corte (C) entre funcional y disfuncional | Puntuación en el BDI-II < 14 | Puntuación en el BDI-II ≥ 14 | ||
| Ansiedad (BAI) | ||||
| - Índice de cambio fiable (RCI) | Disminución en el BAI ≥ 10 puntos | Disminución en el BAI ≥ 10 puntos | Cambio en el BAI < 10 puntos | Aumento en el BAI ≥ 10 puntos |
| - Punto de corte (C) entre funcional y disfuncional | Puntuación en el BAI < 14 | Puntuación en el BAI ≥ 14 | ||
| Estrés postraumático (PCL-S) | ||||
| - Índice de cambio fiable (RCI) | Disminución en la PCL-S ≥ 12 puntos | Disminución en la PCL-S ≥ 12 puntos | Cambio en la PCL-S < 12 puntos | Aumento en la PCL-S ≥ 12 puntos |
| - Punto de corte (C) entre funcional y disfuncional | Puntuación en la PCL-S < 29 | Puntuación en la PCL-S ≥ 29 | ||
Nota. BDI-II = Inventario de Depresión de Beck-II; BAI = Inventario de Ansiedad de Beck; PCL-S = Lista de Verificación del Trastorno por Estrés Postraumático, versión específica.
Los cálculos de C y del RCI para las adaptaciones españolas del BDI-II y del BAI se pueden encontrar en Sanz (2013, 2014) y los valores resultantes se recogen en la tabla 3. Morley y Dowzer (2014) han desarrollado una aplicación para Excel de Windows que permite realizar fácilmente los cálculos de C y del RCI con los datos psicométricos de otros instrumentos y test clínicos adaptados en España. Esta aplicación se puede encontrar en: http://medhealth.leeds.ac.uk/info/618/clinical_psychology_dclinpsychol/797/leeds_reliable_change_index.
Combinando los dos criterios basados en la puntuación C y en el índice RCI, se puede evaluar la significación clínica de los cambios terapéuticos en una investigación de caso único cuando incluso solo se tienen en cuenta dos datos, la puntuación pretratamiento y la puntuación postratamiento. Sin embargo, la evaluación será más completa y llegará a conclusiones más sólidas cuando se tienen en cuenta más datos de la fase de LB y de la fase de tratamiento. Por ejemplo, para analizar la significación clínica de los cambios terapéuticos encontrados en el caso de la víctima del terrorismo se ha elegido, siguiendo la lógica del índice PND, el dato más extremo de la LB, esto es, la puntuación más baja en el BDI-II, en el BAI o en la PCL-S, y se han comparado con él todos los datos de la fase de tratamiento-seguimiento, categorizando cada dato en función de los criterios de la tabla 3 como un indicador de que la víctima o no había experimentado cambios en el momento de la evaluación en que se tomó ese dato o había empeorado o había mejorado o se podría considerar recuperada. En la figura 5 se ha recogido gráficamente ese análisis de la significación clínica de los cambios terapéuticos y, como puede observarse en dicha figura, los resultados indican, en general y para todas las medidas de sintomatología psicológica, que los cambios observados tras la terapia cognitivo conductual centrada en el trauma fueron clínicamente significativos, de manera que a partir de la sesión 9 de la terapia se encontraron mejorías consistentes que incluso podrían considerarse recuperaciones en el postratamiento y en los seguimientos, todo los cual parecía indicar que la paciente se había recuperado de sus trastornos psicológicos al finalizar el tratamiento y que dicha recuperación se mantenía en el seguimiento.
Aproximación estadística a la significación clínica aplicada al análisis de la evolución terapéutica de una víctima del terrorismo en el Inventario de Depresión de Beck-II (BDI-II), el Inventario de Ansiedad de Beck (BAI) y la Lista de Verificación del Trastorno por Estrés Postraumático, versión específica (PCL-S).
Es más, si se considera, siguiendo al DSM-IV (APA, 1994/1995), que una persona se ha recuperado de un episodio depresivo mayor cuando durante 2 meses seguidos hay una remisión completa de los síntomas depresivos, y este criterio temporal se extiende al trastorno por estrés postraumático y al trastorno de angustia con agorafobia, los datos de la figura 5 sugieren que en la víctima del terrorismo se podría hablar de recuperación del trastorno depresivo mayor, en función de la evolución terapéutica en el BDI-II, a partir del postratamiento y durante todo el seguimiento, y de recuperación del trastorno de angustia con agorafobia y del trastorno por estrés postraumático, en función de la evolución en el BAI y de la PCL-S, respectivamente, a partir del seguimiento a los 3 meses y durante todo el seguimiento (excepto en el seguimiento al año para la PCL-S, en el que estrictamente sólo se observó un mejoría).
No obstante, es importante recordar que la valoración del estado de un paciente en relación con su recuperación y la posibilidad de darlo de alta debería tener en cuenta la información relevante sobre otros problemas del paciente, sobre su nivel de funcionamiento en sus actividades laborales o sociales habituales o en sus relaciones con los demás, etc.
Magnitud del cambio terapéutico clínicamente significativoA partir de la aproximación estadística de Jacobson y Truax (1991), se podría combinar la evaluación de la significación clínica del cambio terapéutico con alguno de los índices de tamaño del efecto mencionados antes para así crear un índice de la magnitud del cambio terapéutico clínicamente significativo o un índice de la efectividad clínicamente significativa del tratamiento. Por ejemplo, se podría utilizar una variante del PND, definida como el porcentaje de datos de la fase de tratamiento que son mejorías o recuperaciones clínicamente significativas respecto al dato más extremo de la LB. Como puede observarse en la figura 5, esta variante del PND resultaría, en el caso del tratamiento aplicado a la víctima del terrorismo, en índices de efectividad clínicamente significativa de 83.3%, 91.6% y 83.3% para el BDI-II, el BAI y la PCL-S, respectivamente, índices que complementan y matizan la información proporcionada por el PND habitual, el cual parece que sobrestima la efectividad clínica del tratamiento (91.6%, 100% y 91.6%, respectivamente; véase la tabla 2). De forma parecida, se podría utilizar una variante del PEM o del NAP que sustituyera el cálculo de los no solapamientos por el cálculo de los datos que indican una mejoría o recuperación según los criterios de la aproximación estadística de Jacobson y Truax (1991).
Evaluación del efecto del tratamiento y validez interna en los diseños de caso únicoLas técnicas e indicadores que se han presentado para analizar los datos de los diseños de caso único y evaluar la magnitud y significación clínica de los cambios terapéuticos no proporcionan la clave necesaria para entender cuál es el factor responsable de esos cambios terapéuticos. De hecho, tampoco el análisis visual o el análisis estadístico de los datos de los diseños de caso único proporcionan dicha clave. El análisis estadístico sólo indica si un cambio es estadísticamente significativo, es decir, si existen prueba estadísticas de que hay un cambio, pero no indica qué ha causado ese cambio. Las conclusiones sobre qué factor o factores son los responsables del cambio y, en concreto, las conclusiones sobre si el tratamiento es el responsable se basan más en las características del diseño que en la simple demostración de la significación estadística del cambio o en la obtención de un cambio grande o clínicamente significativo.
La extracción de conclusiones sobre la relación causa-efecto entre el tratamiento y los cambios terapéuticos observados implica la utilización de un diseño adecuado de caso único que descarte el mayor número de amenazas a su validez interna y no depende en cambio de las técnicas que se utilicen para analizar los datos. Por tanto, el análisis de la magnitud y significación clínica del cambio en un diseño A-B no eleva su capacidad para descartar las amenazas a la validez interna y sacar conclusiones causales sobre los efectos del tratamiento, ni tampoco lo hacen el análisis visual o el análisis estadístico. En contraposición, los diseños experimentales de caso único tales como los diseños de retirada A-B-A-B, los diseños de LB múltiple o los diseños de tratamientos alternos comparten una serie de características (p. ej., retirada y presentación alterna del tratamiento, de la LB o de ambas, evaluación de la conducta de forma continua en el tiempo y bajo diferentes condiciones) que combaten directamente las amenazas a la validez interna (p. ej., historia, maduración, regresión a la media, administración repetida de pruebas) y permiten eliminar explicaciones alternativas a la hipótesis de que ha sido el tratamiento, y únicamente el tratamiento, el responsable del cambio observado en la conducta (Kazdin, 1992).
No obstante, se pueden planificar las investigaciones con diseño A-B para que reúnan algunas de esas características y así aumentar el grado en el cual se pueden descartar las amenazas a la validez interna o hacerlas poco plausibles. Para ello, se puede planear:
- 1)
La obtención de múltiples medidas del problema o conducta clave tanto durante la LB como durante el tratamiento y después de que este haya finalizado (seguimientos), cuantas más mejor, de manera que se pueda establecer una LB relativamente estable y se puedan apreciar también cambios estables durante el tratamiento y después del mismo.
- 2)
La replicación o comparación de los cambios terapéuticos en el mismo paciente mediante la obtención de múltiples indicadores del problema o de la conducta clave (p. ej., diversas medidas de disfuncionalidad o de funcionalidad o de ambas).
- 3)
La replicación o comparación de los cambios terapéuticos en varios pacientes, a ser posible heterogéneos en cuanto a sus características sociodemográficas y clínicas.
Por otro lado, otras circunstancias que no están bajo control del clínico o investigador pueden ayudar a que una investigación con un diseño A-B pueda descartar ciertas amenazas a la validez interna y hacer inferencias más firmes sobre el papel causal del tratamiento en los cambios que se observan. Por ejemplo, si los cambios terapéuticos que finalmente se encuentran en la investigación aparecen de forma inmediata tras la aplicación del tratamiento y son de gran magnitud es mucho más plausible que el responsable del cambio sea el tratamiento en lugar de otros factores (p. ej., historia, maduración).
En este sentido, en el caso de la víctima del terrorismo tratada con terapia cognitivo conductual centrada en el trauma se cumplió esta última circunstancia (cambios inmediatos y grandes) así como dos de las características anteriormente mencionadas (1 y 2) que permiten eliminar explicaciones alternativas a la hipótesis de que ha sido la terapia la responsable del cambio observado en la sintomatología de depresión, ansiedad y estrés postraumático.
ConclusionesLa utilización de diseños de caso único en la práctica habitual de la psicología clínica y de la salud puede aumentar la base de conocimientos científicos sobre la eficacia y utilidad clínica de los tratamientos psicológicos además de reducir la brecha que existe entre investigación y práctica clínica. Uno de los obstáculos para realizar ese tipo de investigaciones tiene que ver con la manera de analizar sus datos, puesto que el análisis visual tradicional presenta problemas como, por ejemplo, la escasa fiabilidad entre jueces o el aumento en errores de tipo I. Para paliar estos problemas se ha propuesto la utilización complementaria de un buen número de análisis estadísticos, pero no existe acuerdo sobre cuál sería el más adecuado y, además, muchos de ellos son impracticables con el tipo de diseños de caso único que se suelen llevar a cabo en la práctica clínica, ya que tales análisis exigen un número demasiado grande de datos en las fases de LB y de tratamiento, requieren unos conocimientos estadísticos y un trabajo computacional excesivos o necesitan retrasar la puesta en marcha del tratamiento hasta el momento que se decida por un procedimiento aleatorio, sin tener en cuenta las razones éticas, prácticas y clínicas que dictan iniciar el tratamiento tan pronto como sea posible.
En el presente trabajo se han presentado dos técnicas para el análisis de los datos de un estudio con diseño de caso único que permiten obtener dos tipos de información muy relevantes en la investigación de los tratamientos basados en la evidencia: el tamaño del efecto del tratamiento (o magnitud del cambio terapéutico) y la significación clínica de dicho efecto o cambio. Además, dichas técnicas son especialmente relevantes en los casos en que esos diseños se realizan en la práctica clínica, aunque obviamente también son útiles en otros contextos de investigación.
La primera técnica consiste en estimar la magnitud del cambio terapéutico o tamaño del efecto del tratamiento utilizando índices basados en el no solapamiento de los datos entre fases como, por ejemplo, el PND, el PEM y el NAP. Estos índices cuantifican el cambio terapéutico y valoran su magnitud de forma más objetiva que el análisis visual y, por tanto, son un perfecto complemento para este análisis. Además, estos índices pueden utilizarse con todo tipo de diseños de caso único, se pueden calcular incluso con un número muy pequeño de datos en la LB o en el tratamiento y su cálculo es sumamente simple y fácil, permitiendo considerar si el cambio terapéutico tras un tratamiento ha sido débil, moderado o grande y, por tanto, el tratamiento es cuestionable o no efectivo, bastante efectivo o muy efectivo.
La segunda técnica, complementaria con la anterior, consiste en valorar la significación clínica de los cambios terapéuticos a través de la aproximación estadística a dicha significación que proponen Jacobson y Truax (1991). Esta aproximación permite estimar en qué medida los cambios terapéuticos, más allá de su significación estadística o su magnitud, han podido conseguir de manera fiable que un paciente que antes del tratamiento pertenecía a una población disfuncional vuelva a la población funcional. La aproximación estadística de Jacobson y Truax (1991) se puede calcular también con un número muy pequeño de datos en la LB o en el tratamiento, incluso con tan solo dos datos, pretratamiento y postratamiento (o seguimiento), y su cálculo es también sumamente simple y fácil, permitiendo considerar a un paciente como sin cambios, empeorado, mejorado o recuperado.
La aplicación de ambas estrategias al análisis de los datos obtenidos tras aplicar terapia cognitivo conductual centrada en el trauma a una víctima del terrorismo, que presentaba un trastorno por estrés postraumático simultáneamente con un trastorno depresivo mayor y un trastorno de angustia con agorafobia, ha permitido constatar que dicho tratamiento produce cambios terapéuticos grandes y clínicamente significativos en la sintomatología depresiva, ansiosa y de estrés postraumático. Estos cambios corroboran en un caso con una elevada comorbilidad la eficacia y utilidad clínica que la terapia cognitivo conductual centrada en el trauma ha demostrado previamente para el trastorno por estrés postraumático (García-Vera et al., en prensa), además de ejemplificar la utilidad de ambas técnicas de análisis.
Extended SummaryThe use of single case designs in the practice of clinical psychology and health may increase the scientific knowledge base on the efficacy and clinical utility of psychological treatments and reduce the gap between research and clinical practice. One obstacle for such a research concerns how to analyze single case data, since the traditional visual analysis of graphed data presents problems such as poor inter-rater reliability or an increased risk of type I errors. To solve these problems, a variety of statistical analyses has been proposed as a supplement to visual analysis, but there is no consensus regarding the most appropriate statistical technique. In addition, many of them are impracticable with the kind of single case designs that are often carried out in clinical practice, since such statistical techniques require large numbers of data during the baseline and treatment phases, demand excessive statistical knowledge and computational work, or need to delay the start of treatment to a time determined by a random procedure, regardless of ethical, practical, and clinical reasons that dictate to start treatment as soon as possible.
This paper presents two techniques for the data analysis of single case designs in psychological treatment research: indices of data overlap between phases to assess the size of treatment effect (or the magnitude of therapeutic change) and a statistical approach to assess the clinical significance of treatment effect.
An Example of a Single Case Design: The Treatment of a Victim of TerrorismTo illustrate the computation and application of the techniques for assessing the size and clinical significance of treatment effect, baseline and treatment/follow-up data were obtained from the treatment of a 69-year-old female victim of terrorism who suffered from posttraumatic stress disorder, major depressive disorder, and panic disorder with agoraphobia. She received a 16-session treatment program of trauma-focused cognitive-behavioral therapy in combination with specific therapeutic techniques for depression and panic (e. g., pleasant activity scheduling, interoceptive exposure) (García-Vera et al., in press; Moreno et al., manuscrito en edición editorial). She completed the Spanish adaptations of the Beck Depression Inventory-II (BDI-II; Beck, Steer, & Brown, 2011) or a short version of the BDI-II (BDI-II-SF; Sanz, García-Vera, Fortún, & Espinosa, 2005), the Beck Anxiety Inventory (BAI; Beck & Steer, 2011) or a short version of the BAI (BAI-PC; Beck, Steer, Ball, Ciervo, & Kabat, 1997; Sanz & García-Vera, 2012), and the PTSD Checklist, specific version (PCL-S; Weathers, Litz, Herman, Huska, & Keane, 1993; Vázquez, Pérez-Sales, & Matt, 2006), at a telephone screening assessment, a pretreatment assessment, each two therapy sessions, a post-treatment assessment, and 1-month, 3-month, 6-month, and 1-year follow-up assessments. BDI-II, BAI, and PCL-S data for the baseline phase were taken from the screening, pretreatment, and 1st-session assessments, and BDI-II, BAI and PCL-S data for the treatment/follow-up phase were taken from the remaining assessments (see Fig. 1).
Assessment of the Magnitude of Therapeutic Change or the Size of Treatment EffectThere are many indices of data overlap between phases to assess the size of treatment effect in single case designs (Parker, Vanest, & Davis, 2011). This article describes the definition, calculation, application, advantages, and limitations of three indices: percentage of non-overlapping data (PND), percentage of data points exceeding the median (PEM), and non-overlap of all pairs (NAP), since the first two are widely used and ease of calculation and the third one shows good statistical properties (e.g., good statistical power, adequate sensitivity). The reporting of multiple indices is highly recommended to determine whether consistent results are observed (Maggin, Briesch, & Chafouleas, 2013). Although non-overlap indices are more robust than indices of mean or median level changes across phases, most of them are insensitive to positive baseline trend, and they should not be used, or at least they should be used with caution, when there is a positive trend in the baseline phase and a strong positive trend in the treatment phase.
PND is defined as the percentage of treatment phase data exceeding the single most extreme baseline data point (the lowest or the highest data point according to the direction of the functionality) (Scruggs, Mastroiperi, & Casto, 1987). PND is the most widely published and the basis of more than 40 meta-analyses (Maggin et al., 2013; Scruggs & Mastropieri, 2013). When an outlier is present in the baseline phase, PND can distort the size of treatment effect. PEM was developed by Ma (2006) to solve this problem.
PEM is defined as the percentage of treatment phase data exceeding the median of the baseline phase. It has also been used as the effect size index in meta-analysis of single case designs. PEM assumes that the median is a good summary for baseline data, but it is not the case for the data often seen in single case design. NAP was developed mainly to improve upon PEM (and PND) by individually comparing all baseline and treatment phase data points (Parker & Vannest, 2009).
NAP is defined as the percentage of all pairwise comparison across baseline and treatment phases, which show non-overlap (or improvement) across phases. NAP equals the area under the curve (AUC) from a receiver operator characteristic curve (ROC) analysis and, in this framework, is interpreted as the probability that a data point drawn at random from the treatment phase will exceed (overlap) that of a data point drawn at random from the baseline phase. AUC, its confidence interval, and its inference testing are calculated by most software package used for full statistical analysis (e. g., SPSS, EPIDAT).
PND and PEM can range from 0% to 100%, whereas NAP range from 50% to 100%, although it can be rescaled to 0% to 100% scale. Interpretation guidelines for all indices are available in Table 1. The calculation of PND, PEM, and NAP with the data of the victim of terrorism is depicted graphically in figures 2, 3 and 4, respectively, and the resulting values and interpretations are displayed in Table 2. These values indicate that the therapeutic change observed in the victim of terrorism after a treatment program of trauma-focused cognitive-behavioral therapy was large and suggest that this treatment was effective.
Assessment of the Clinical Significance of Therapeutic ChangesThe magnitude of therapeutic change (or the size of treatment effect) is not the same as its clinical significance. Although large effect sizes are usually clinically significant, they do not necessarily indicate that improvements are meaningful or important in the experience of the patient.
Jacobson and Truax's (1991) statistical approach to clinical significance can be used to assess the clinical significance of therapeutic changes. This approach assumes that a clinically significant change occurs when the score of a patient in an instrument measuring a relevant construct (symptomatology, mental health, maladjustment, quality of life, etc.) no longer belong to the score distribution of a dysfunctional population, but it returns to the score distribution of a functional population.
Jacobson and Truax's (1991) method involves, firstly, establishing a cut-off point (C) for each client that must be crossed in moving from the dysfunctional to the functional distribution. Secondly, that method involves determining whether a patient's change in instrument scores (e.g., from pre- to post-test) is reliable, rather than simply an artifact of measurement error. To assess this, Jacobson and Truax (1991) proposed a reliable change index (RCI) that each patient has to pass in order to demonstrate that his or her change in symptomatology, mental health, quality of life, or any relevant construct is not simply due to measurement error. This RCI takes into account the standard error of the difference between two scores that depends on the standard error of measurement that, in turn, depends on reliability and standard deviation of test scores.
Applying Jacobson and Truax's (1991) method to the data of the Spanish adaptation of the PCL-S in victims with and without mental disorders (see Table 3 and Reguera et al., 2014), a patient could be classified as “recovered” if his or her PCL-S score shows a decrease of 12 points or greater and is lower than 29 (i.e., passes both RCI and cut-off criteria), “improved” if his or her PCL-S score shows a decrease of 12 points or greater but is not lower than 29 (i.e., passes RCI criterion, but not the cut-off criterion), “unchanged” if his or her PCL-S score does not show a decrease or an increase of 10 points 14 (i.e., does not pass RCI criterion in any direction), or “deteriorated” if his or her BAI score shows an increase of 10 points of greater (i.e., passes RCI criteria in a worsening direction). Similar guidelines have also been developed for the Spanish adaptations of the BDI-II and BAI (Sanz, 2013, 2014). These three guidelines are displayed in Table 3 and their application to the treatment of the victim of terrorism is depicted graphically in Figure 5. The results of this application that the therapeutic change observed in the victim of terrorism after a treatment program of trauma-focused cognitive-behavioral therapy was clinical significant. They also suggest that the patient had recovered from their psychological disorders at the end of treatment and remained recovered throughout the follow-up.
Finally, the statistical approach to clinical significance and the non-overlap indices could be combined to assess the size of clinically significant effects of a treatment. So, it may be very informative to calculate PND, PEM, or NAP as the percentage of treatment phase data showing clinically significant improvement or recovery in comparison, respectively, with the single most extreme baseline data point, the median of baseline data points or all baseline data points.
Assessment of Treatment Effect and Internal Validity in Single Case DesignsTechniques and indicators that have been presented to analyze data in single case designs and assess the magnitude and clinical significance of therapeutic changes do not provide the necessary key to understanding the factor responsible for these therapeutic changes. Causal conclusions about whether treatment is responsible for changes are based more on the design features of a single case study than on obtaining a large or clinically significant change or even a statistically significant change. In this sense, single-case experimental designs such as the A-B-A-B, multiple-baseline, and alternating-treatment designs provide arrangements that rule out threats to internal validity and allow to draw causal conclusions about the effects of a treatment. However, the single case design typically carried out in the clinical practice (the A-B design, that is, the design with only one baseline phase and only one treatment phase) can be arranged to greatly increase the extent to which threats to internal validity are ruled out or made implausible. Some of these arrangements involve increasing the number and timing of the assessment occasions during both the baseline and treatment/follow-up phases, replicating therapeutic changes in the same patient across multiple indicators of his or her psychological problems or disorders, and replicating therapeutic changes across multiple patients, especially with a heterogeneous set of patients.
ConclusionsThis paper has presented two techniques for the data analysis of single case designs in psychological treatment research: indices of data overlap between phases to assess the size of treatment effect (or the magnitude of therapeutic change) and a statistical approach to assess the clinical significance of treatment effect. These techniques are very informative and ease to use and, therefore, can improve the visual analysis traditionally used in single case studies. Furthermore, they can foster the use and analysis of single case designs in clinical practice and at doing so they can reduce the gap between research and clinical practice. The usefulness of these two techniques has been illustrated in the case of the treatment of a victim of terrorism with posttraumatic stress disorder, major depressive disorder, and panic disorder with agoraphobia. Their results allow us to state that trauma-focused cognitive-behavioral therapy is followed by large and clinically significant therapeutic changes in depressive, anxious, and posttraumatic stress symptomatology. The efficacy and clinical usefulness of trauma-focused cognitive-behavioral therapy have been previously shown for posttraumatic stress disorder (García-Vera et al., in press). Results found with the two statistical techniques presented in this paper suggest that their clinical usefulness can be extended to cases with a high psychopathological comorbidity.
FinanciaciónEste artículo ha sido en parte posible gracias a la ayuda de investigación del Ministerio de Ciencia e Innovación (PSI2011-26450).
Conflicto de interesesLos autores de este artículo declaran que no tienen ningún conflicto de intereses.