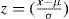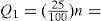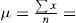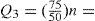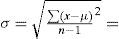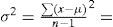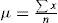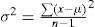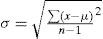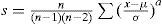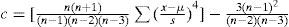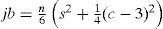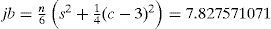Este trabajo analiza la recaudación del impuesto sobre nóminas y asimilados en el estado de Quintana Roo de 2000 a 2010. La aportación principal es identificar el comportamiento estadístico recaudatorio mediante la aproximación fractal, estableciendo patrones iterativos en el nivel estatal, municipal, por la totalidad de la serie analizada de 132 meses y en periodos menores, sirviendo como detonante para aplicarse en otras localidades y gravámenes con el fin de profundizar en algunas características de la fiscalidad. Dos criterios estadísticos fueron empleados para determinar la normalidad, o no, de las series de recaudación fiscal municipal en el periodo de estudio; dichos criterios son el de la regla empírica y el que utiliza parámetros del teorema de Chebyshev; como contraste, se aplicó la prueba Jarque-Bera a los residuos, concluyendo que la recaudación por ejercicio fiscal en Quintana Roo (con datos municipales) no sigue una distribución normal, razón por la cual se utilizó la aproximación fractal. Los resultados con datos de recaudación fiscal por municipios para ese estado muestran la presencia de un comportamiento fractal (repetitivo y cíclico) en la recaudación, lo que puede interpretarse como la presencia de una base fiscal consolidada, justificando así la conclusión de que hay fuerza (el nivel de recaudación observado) en las finanzas públicas locales. La misma conclusión se tiene, con diferentes cortes temporales, al analizar y detectar presencia de comportamiento fractal específica para la recaudación observada en los municipios de Benito Juárez (Cozumel) y Othón P. Blanco, de 2000 a 2010.
This paper analyzes the tax collection from payroll tax on staff and non-staff in the state of Quintana Roo from 2000 to 2010. Its main contribution is to identify the statistical revenue behavior using a fractal approach, establishing iterative patterns at both state and municipal level, for the entire analyzed series of 132 months as well as shorter time periods. It serves as a trigger for application in other locations and charges in order to explore some features of taxation. Two statistical criteria were used to determine normal or abnormal series of municipal tax collection during the study period, namely, the Empirical Rule criteria and parameters using Chebyshev’s theorem. As a contrast, the Jarque-Bera test was applied on residuals, concluding that the fiscal revenue from the state of Quintana Roo (municipal data) does not follow a normal distribution, which is why the fractal approach has been used. The results with data for tax collection by municipalities throughout Quintana Roo show the presence of a fractal behavior (repetitive and cyclic) in revenue, which can be interpreted as the presence of a consolidated tax base, thus justifying the conclusion that there is strength (the observed level of collection) in local public finances. The same conclusion is obtained, with different temporal cuts, when analyzing and detecting the presence of specific fractal revenue behavior observed in municipalities of Benito Juarez (Cozumel) and Othon P. Blanco from 2000 to 2010.
La recaudación fiscal ha significado a lo largo de la historia un tema de relevante interés debido a la materialización de recursos públicos necesarios para pagar bienes y financiar programas de redistribución de la renta, situación que se aplica en los niveles de gobierno federal, estatal y municipal (Samuelson y Nordhaus, 2005).
Han existido interesantes propuestas en materia fiscal de nivel macroeconómico, destacando la propuesta de Arthur Betz Laffer (2004), la cual plantea que el incremento en las tasas de impuestos aumenta la recaudación sólo hasta cierto punto, ya que a partir del máximo óptimo un mayor incremento provoca una menor recaudación fiscal. Resulta interesante el análisis en la pérdida en peso muerto que puede ser generada por un sistema tributario, argumentando que a una menor tasa de impuesto los ingresos se incrementan con una tasa de impuesto adecuada o media, mientras que los ingresos tributarios se incrementan en una mayor medida; sin embargo, con una tasa impositiva demasiado alta, los ingresos tributarios sólo se incrementan en una pequeña parte, del resto se dice que es un espacio o pérdida en peso muerto (Mankiw, 2009).
En un esfuerzo por comprender el comportamiento en la recaudación fiscal local existen diversos estudios contemporáneos, destacando un análisis realizado en diez países latinoamericanos en donde se reconoce la importancia de la fiscalidad y su incidencia en el desarrollo económico territorial; no obstante, el grado de análisis no ha ido más allá que el de establecer comparativas en la normatividad, cobertura y tasas impositivas (Cuervo y Williner, 2009); por lo anterior, se identifica la necesidad de realizar análisis más profundos en las recaudaciones locales que permitan conocer el comportamiento de la recaudación fiscal. Resultó interesante iniciar con una orientación a la propuesta de la geometría fractal impulsada por Benoit Mandelbrot (2003), referente a la presencia constante de objetos y circunstancias con patrón iterativo y análisis enfocados a la economía a través del comportamiento de los mercados de valores (Peters, 1994; Mandelbrot y Hudson, 2006; Braun, 1994); se incluye a detalle el comportamiento de la recaudación fiscal en el estado de Quintana Roo, específicamente en lo que se refiere al Impuesto sobre Nóminas y Asimilados, concepto que representa el 47.46% del total de impuestos que figuran en la Ley de Ingresos para el estado de Quintana Roo para el ejercicio fiscal 2012 (Congreso del Estado, 2011). Asimismo, se desarrolla un análisis gráfico, donde se hacen presentes periodos con picos altos, repetitivos, en escalas distintas en el nivel estatal, municipal, inclusive con diferentes rangos y periodos.
Composición de la recaudación fiscal estatalConforme a la Ley de Ingresos del estado de Quintana Roo para el Ejercicio Fiscal de 2012 por concepto de impuestos se contempló recaudar 1 257 886 393, de los cuales el 597 041 831 corresponden al impuesto sobre nóminas y asimilables, lo que significa el 47.46% del total de ingresos por conceptos de impuestos.
El elemento fundamental para la investigación lo constituye la recaudación informada oficialmente y de la cual se desprenden los análisis numéricos y gráficos.
11 La información original no fue expresada en miles, el haberla incluido de esta forma corresponde a razones de espacio y formato.
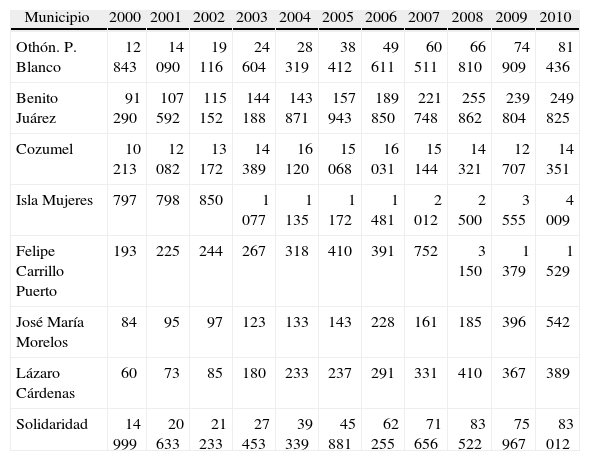
| Municipio | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| Othón. P. Blanco | 12 843 | 14 090 | 19 116 | 24 604 | 28 319 | 38 412 | 49 611 | 60 511 | 66 810 | 74 909 | 81 436 |
| Benito Juárez | 91 290 | 107 592 | 115 152 | 144 188 | 143 871 | 157 943 | 189 850 | 221 748 | 255 862 | 239 804 | 249 825 |
| Cozumel | 10 213 | 12 082 | 13 172 | 14 389 | 16 120 | 15 068 | 16 031 | 15 144 | 14 321 | 12 707 | 14 351 |
| Isla Mujeres | 797 | 798 | 850 | 1 077 | 1 135 | 1 172 | 1 481 | 2 012 | 2 500 | 3 555 | 4 009 |
| Felipe Carrillo Puerto | 193 | 225 | 244 | 267 | 318 | 410 | 391 | 752 | 3 150 | 1 379 | 1 529 |
| José María Morelos | 84 | 95 | 97 | 123 | 133 | 143 | 228 | 161 | 185 | 396 | 542 |
| Lázaro Cárdenas | 60 | 73 | 85 | 180 | 233 | 237 | 291 | 331 | 410 | 367 | 389 |
| Solidaridad | 14 999 | 20 633 | 21 233 | 27 453 | 39 339 | 45 881 | 62 255 | 71 656 | 83 522 | 75 967 | 83 012 |
Fuente: Elaboración propia con datos de la Secretaría de Hacienda de Quintana Roo
Es importante mencionar que la información corresponde a los municipios que existían en los años referidos, haciendo la aclaración de que al año 2012 se agregarán los municipios de Tulum2 y Bacalar en los informes de recaudación.
Comportamiento del impuesto sobre nómina y asimiladosEn distintos análisis latinoamericanos enfocados a variables económicas (Gálvez, 2005), inspirados en las propuestas relativamente recientes de la geometría fractal de Mandelbrot (2003), establecen como eje fundamental determinar los estadísticos descriptivos de las series de tiempo de interés para obtener factores iterativos como uno de los elementos de inferencia al comportamiento fractal.
La metodología para obtener las estadísticas consistió en tabular los datos por ejercicio fiscal, totalizando por meses. Para determinar la normalidad, o no, en la distribución se emplearon los siguientes criterios: mediante localizadores z para determinar si los datos cumplían con los criterios de la regla empírica y del teorema de Chebyshev (Anderson, Sweeny y Williams, 2008). También se determinaron los cuartiles Q1, Q3 para establecer el rango intercuartílico (Triola, 2011) y medir la normalidad mediante los límites superior e inferior; asimismo, se analizaron los residuos mediante la prueba Jarque-Bera (Ciuiu, 2005) que determinará finalmente la existencia de colas gruesas y el impacto asimétrico y de curtosis; de igual forma, se realizó un análisis gráfico por periodos de diciembre a febrero del siguiente ejercicio a efectos de identificar patrones que evidenciaran interactividad en un primer paso con la información de nueve años en el nivel estatal; posteriormente, con el comportamiento de un municipio y, finalmente, gráficas de periodos de 14 meses de distintos años y municipios.
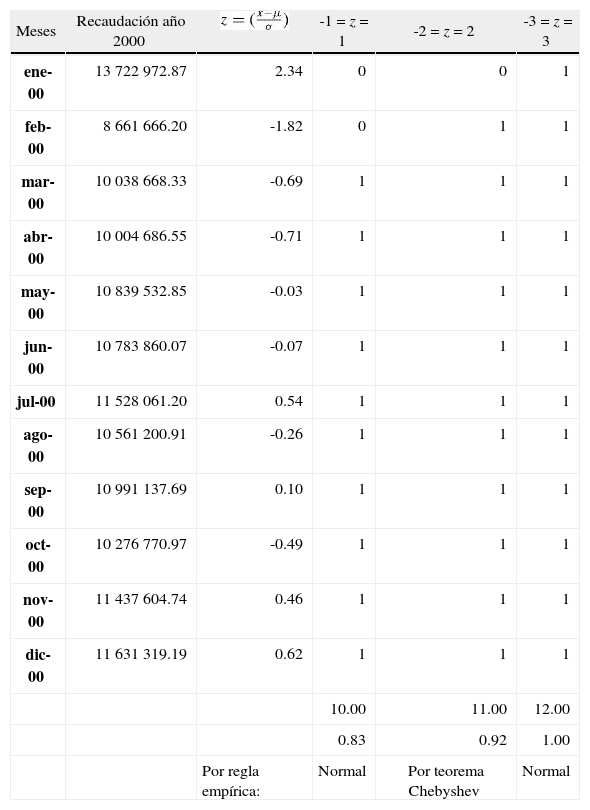
A continuación, a manera de ejemplo, se presenta el análisis correspondiente al ejercicio 2000, haciendo la aclaración de que para todos los años se replicó la misma forma tabular, determinando los datos de interés.
| Meses | Recaudación año 2000 | -1 = z = 1 | -2 = z = 2 | -3 = z = 3 | |
| ene-00 | 13 722 972.87 | 2.34 | 0 | 0 | 1 |
| feb-00 | 8 661 666.20 | -1.82 | 0 | 1 | 1 |
| mar-00 | 10 038 668.33 | -0.69 | 1 | 1 | 1 |
| abr-00 | 10 004 686.55 | -0.71 | 1 | 1 | 1 |
| may-00 | 10 839 532.85 | -0.03 | 1 | 1 | 1 |
| jun-00 | 10 783 860.07 | -0.07 | 1 | 1 | 1 |
| jul-00 | 11 528 061.20 | 0.54 | 1 | 1 | 1 |
| ago-00 | 10 561 200.91 | -0.26 | 1 | 1 | 1 |
| sep-00 | 10 991 137.69 | 0.10 | 1 | 1 | 1 |
| oct-00 | 10 276 770.97 | -0.49 | 1 | 1 | 1 |
| nov-00 | 11 437 604.74 | 0.46 | 1 | 1 | 1 |
| dic-00 | 11 631 319.19 | 0.62 | 1 | 1 | 1 |
| 10.00 | 11.00 | 12.00 | |||
| 0.83 | 0.92 | 1.00 | |||
| Por regla empírica: | Normal | Por teorema Chebyshev | Normal |
Mediante los análisis por ejercicio se integra una síntesis de varianzas, desviaciones estándar, medias y puntos o localizadores z, también se indica el cumplimiento o no de la distribución normal y la presencia de datos atípicos.
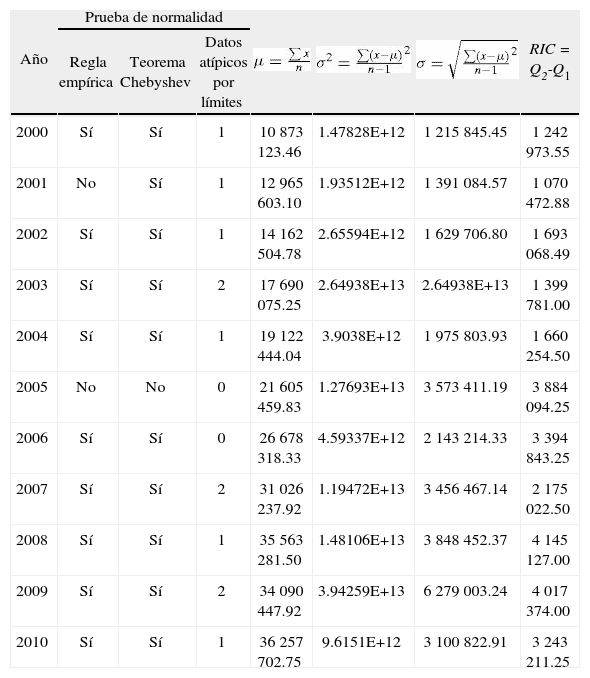
Síntesis de la normalidad y estadística descriptiva
| Año | Prueba de normalidad | RIC = Q2-Q1 | |||||
| Regla empírica | Teorema Chebyshev | Datos atípicos por límites | |||||
| 2000 | Sí | Sí | 1 | 10 873 123.46 | 1.47828E+12 | 1 215 845.45 | 1 242 973.55 |
| 2001 | No | Sí | 1 | 12 965 603.10 | 1.93512E+12 | 1 391 084.57 | 1 070 472.88 |
| 2002 | Sí | Sí | 1 | 14 162 504.78 | 2.65594E+12 | 1 629 706.80 | 1 693 068.49 |
| 2003 | Sí | Sí | 2 | 17 690 075.25 | 2.64938E+13 | 2.64938E+13 | 1 399 781.00 |
| 2004 | Sí | Sí | 1 | 19 122 444.04 | 3.9038E+12 | 1 975 803.93 | 1 660 254.50 |
| 2005 | No | No | 0 | 21 605 459.83 | 1.27693E+13 | 3 573 411.19 | 3 884 094.25 |
| 2006 | Sí | Sí | 0 | 26 678 318.33 | 4.59337E+12 | 2 143 214.33 | 3 394 843.25 |
| 2007 | Sí | Sí | 2 | 31 026 237.92 | 1.19472E+13 | 3 456 467.14 | 2 175 022.50 |
| 2008 | Sí | Sí | 1 | 35 563 281.50 | 1.48106E+13 | 3 848 452.37 | 4 145 127.00 |
| 2009 | Sí | Sí | 2 | 34 090 447.92 | 3.94259E+13 | 6 279 003.24 | 4 017 374.00 |
| 2010 | Sí | Sí | 1 | 36 257 702.75 | 9.6151E+12 | 3 100 822.91 | 3 243 211.25 |
Como se observa, conforme a los criterios de la regla empírica, la cual implica que al menos el 68% de los datos estandarizados se encuentren a no más de una desviación estándar, 95% a no más de dos y el 99% dentro de tres desviaciones estándar, nueve de los once ejercicios analizados tendrían una distribución normal y dos no.
Con respecto a evaluar la normalidad mediante el criterio establecido en el teorema de Chebyshev, en donde el 75% de los datos estandarizados deben estar dentro de dos desviaciones estándar y al menos el 89% se encuentren a no más de tres desviaciones estándar, diez de los once ejercicios tendrían una distribución normal.
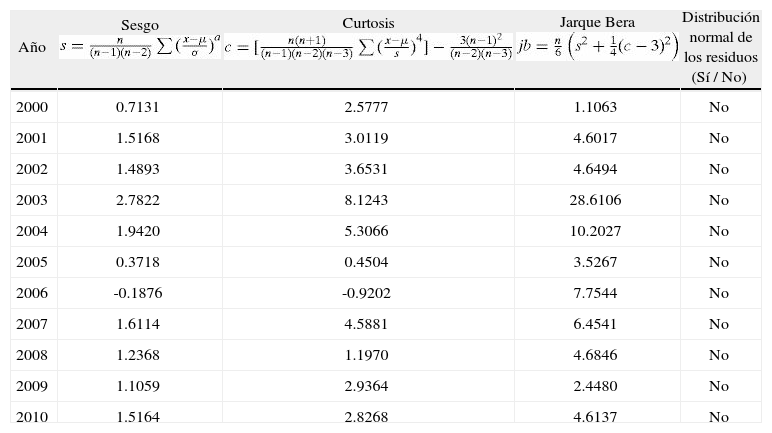
Se decidió aplicar la prueba Jarque-Bera con el fin de analizar los residuos, teniendo como eje principal los valores para una distribución normal en donde la curtosis debe ser 3 y el sesgo adquirir un valor de 0. En los casos en que la curtosis resultó mayor a 3 se establece la existencia de residuos con un comportamiento de cola pesada y en los resultados en donde se obtuvo un valor menor a 3 se determina un comportamiento liviano de los residuos.
El criterio utilizado en la prueba Jarque-Bera3 se estableció con base en lo que ha sido considerado en investigaciones precedentes (Ciuiu, 2005; Saporta, 1998; Gál- vez, 2005)4, utilizando como elementos fundamentales los coeficientes de sesgo (s) y curtosis (c), por ejercicio individual y por el total de la series de tiempo. Se adoptan dos grados de libertad y con un nivel de confianza del 95%, estableciendo como hipótesis nula el valor de 5.99 que correspondería a una curva normal. El cuadro 4 muestra la síntesis de los resultados por ejercicio.
Evaluación de los residuos y aplicación de la prueba Jarque-Bera
| Año | Sesgo | Curtosis | Jarque Bera | Distribución normal de los residuos (Sí / No) |
| 2000 | 0.7131 | 2.5777 | 1.1063 | No |
| 2001 | 1.5168 | 3.0119 | 4.6017 | No |
| 2002 | 1.4893 | 3.6531 | 4.6494 | No |
| 2003 | 2.7822 | 8.1243 | 28.6106 | No |
| 2004 | 1.9420 | 5.3066 | 10.2027 | No |
| 2005 | 0.3718 | 0.4504 | 3.5267 | No |
| 2006 | -0.1876 | -0.9202 | 7.7544 | No |
| 2007 | 1.6114 | 4.5881 | 6.4541 | No |
| 2008 | 1.2368 | 1.1970 | 4.6846 | No |
| 2009 | 1.1059 | 2.9364 | 2.4480 | No |
| 2010 | 1.5164 | 2.8268 | 4.6137 | No |
Considerando los resultados en residuos, se rechaza la hipótesis nula estableciendo que en todos los ejercicios analizados, no se trataría de una distribución normal inclusive por los valores del sesgo y la curtosis, fortaleciendo la aproximación fractal debido a que la presencia de colas pesadas o irregularidad de su forma como la apreciación de Mandelbrot y otros autores (Domínguez Monterroza y Garzón, 2011), evidenciando la persistencia de residuos alejados de la centralidad y, además, contrastando con los estadísticos descriptivos y los criterios de regla empírica y teorema de Chebyshev.
El comportamiento estadístico evidencia también el mismo patrón obtenido en la mayoría de los ejercicios analizados individualmente, notando la presencia de un coeficiente Jarque-Bera de significancia para un comportamiento que no es normal.
Análisis gráfico e inferencia fractalLa directriz principal fue localizar la presencia de evidencia repetitiva en la recaudación, en principio aceptando réplicas constantes aunque no correspondieran exactamente a una misma escala, tal como lo han argumentado distinguidos investigadores como Mandelbrot (2009) y Bouchaud y Potters (2000).
Se consideraron estudios previos aplicados a la economía, específicamente los enfocados al mercado de valores e índice de precios y cotizaciones como los realizados por Peters (1994) y Mandelbrot y Houdson (2006); en éstos la iteración e identificación de patrones definidos fueron básicos; además de que en general para el análisis gráfico fue directriz encontrar, en sentido intuitivo, una forma y la continuación de la misma en cualquier escala que arrojase el análisis.
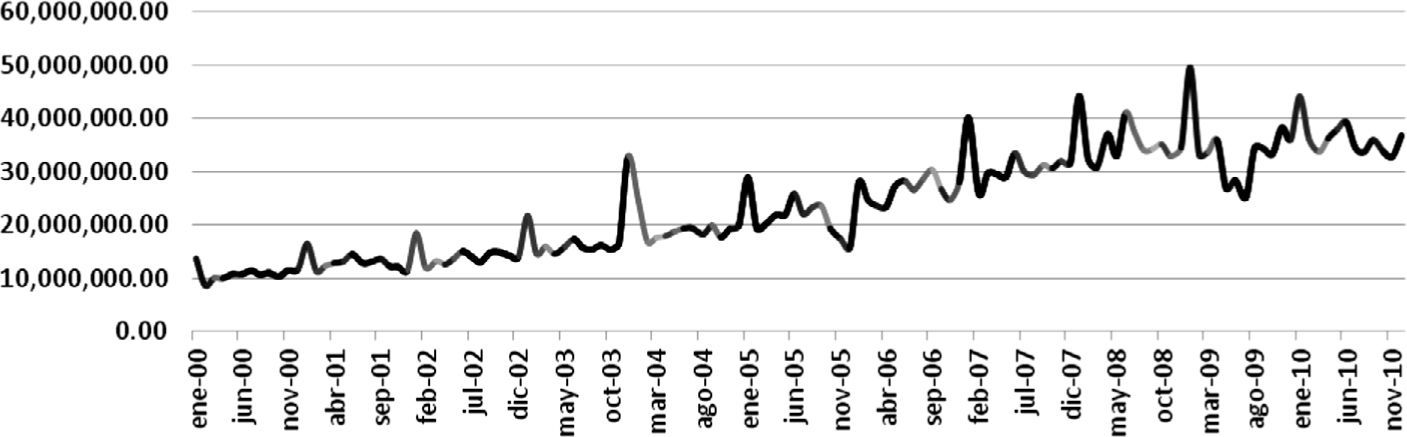
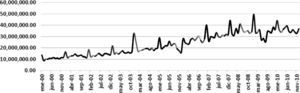
En un primer momento se tuvo interés en visualizar el comportamiento del total de la serie de datos correspondiente a nueve años, de 2000 a 2010. El resultado fue un comportamiento repetitivo, cíclico, a manera de picos altos durante todos los periodos con la excepción del ejercicio 2005 en que sucedió el impacto del Huracán Wilma y del ejercicio 2009 por causas de la contingencia sanitaria por influenza H1N1. En la gráfica 1 se aprecia las réplicas encontradas.
Al analizar visualmente la gráfica 1 es clara la presencia de réplicas en ciertos periodos, por lo que considerando la amplitud de la serie que incluye 132 meses con los datos oficiales de la recaudación existe sin lugar a dudas el criterio considerado por Mandelbrot como esencial de una situación fractal y los incrementos estacionarios que se presentan han sido considerados anteriormente (Embrechts y Maejima, 2002; Ramírez, Torres y Romero, 2012; Beran, 1994).
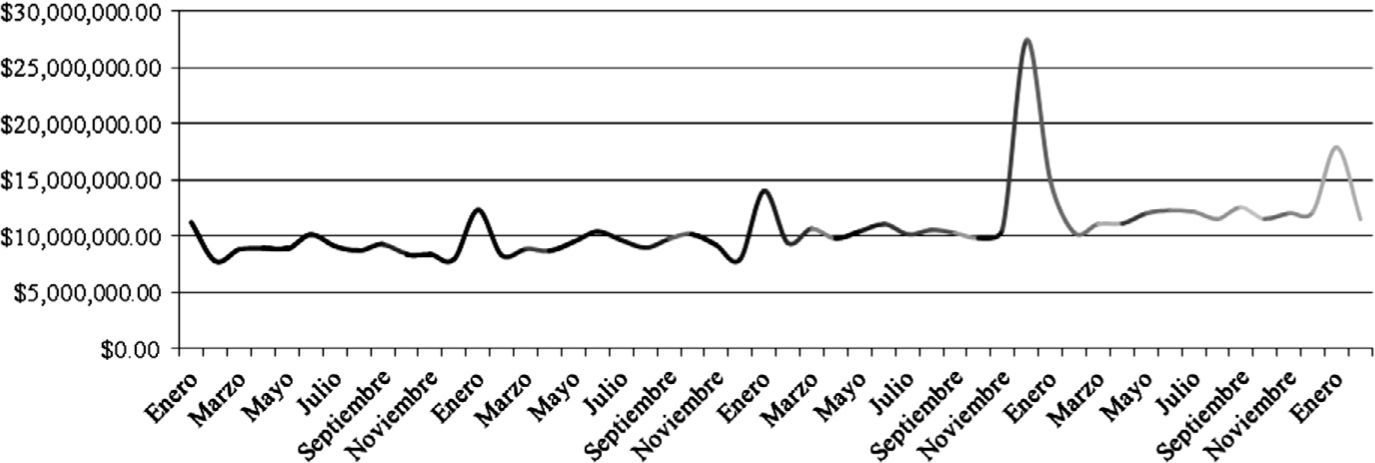
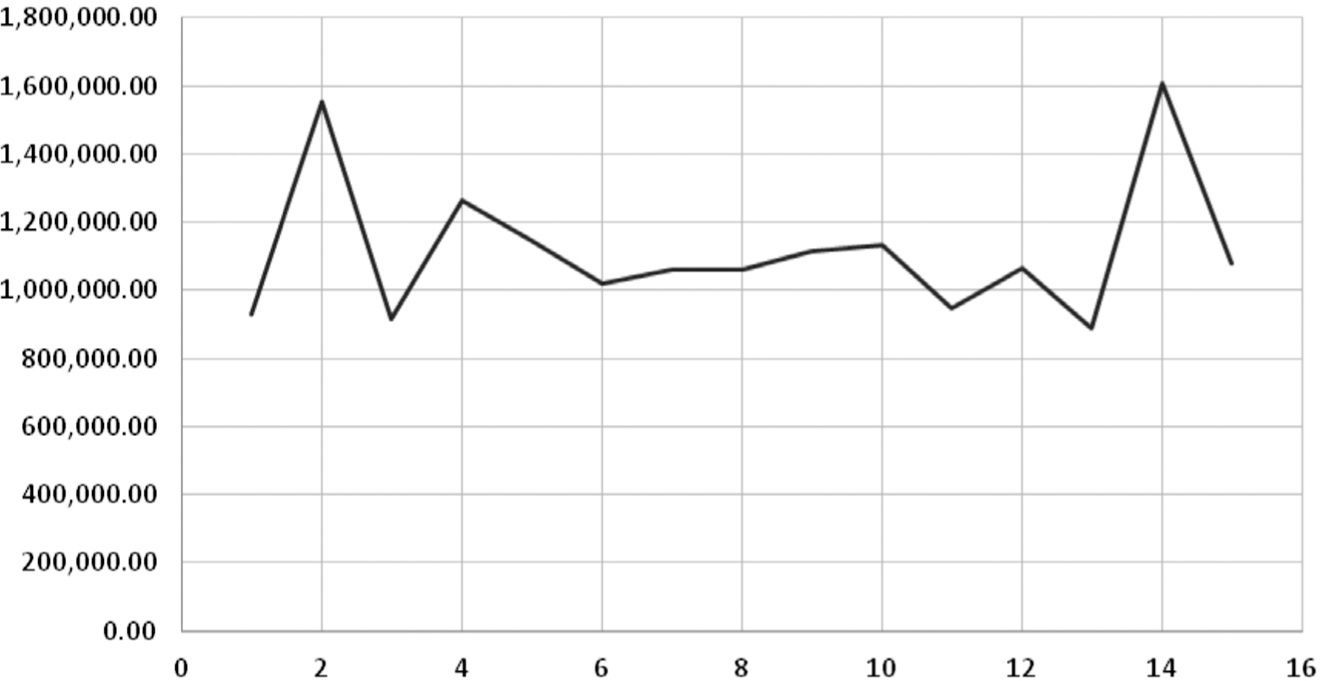
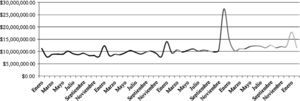
El siguiente punto de interés fue establecer si el comportamiento fractal además de estar presente en el nivel de la recaudación estatal también se encontraba en niveles inferiores, concretamente municipales, fueron tabulados los datos en los municipios de Benito Juárez, Cozumel y Othón P. Blanco, encontrando nuevamente la presencia fractal.
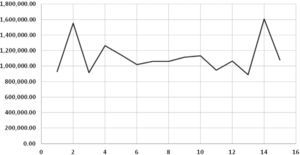
Para verificar lo anterior, se desarrollaron gráficas en periodos más cortos, de enero a febrero del siguiente año, en meses de años distintos y también diferentes periodos y municipios: Cozumel y Othón P. Blanco. En esta ocasión los datos fueron analizados mediante el programa Scientific Notebook que brinda una mejor reproducción en las líneas, los resultados nuevamente fueron imágenes replicadas en picos altos como se aprecia en las gráficas 3 y gráfica 45.
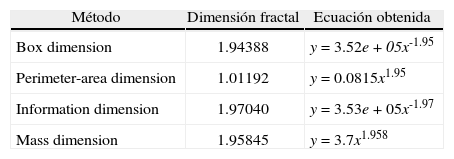
Finalmente, pretendiendo cumplir con la característica del grado de irregularidad e interrupción de la fractalidad y su reconocimiento a modelos cada vez más realistas (Mandelbrot, 2009) se determina la dimensión fractal mediante el software Benoit, versión 1.31, realizando cálculos correspondientes a los parámetros de autosimilitud con cuatro diferentes métodos6: box dimension, perimeter-area dimension, information dimension y mass dimension. Para llevar a cabo lo anterior fue necesario realizar representaciones gráficas que incluyeron 132 observaciones correspondientes a la recaudación por cada mes; posteriormente, las gráficas se transformaron al formato de imagen con la extensión bmp, lo que hizo posible aplicar los distintos métodos para dimensión fractal y obtener las ecuaciones correspondientes. Los resultados se presentan en el siguiente cuadro:
ConclusionesLas pruebas de normalidad tradicionales con enfoque al teorema del límite central, como el criterio de regla empírica y los parámetros del teorema de Chebyshev, aplicadas a la recaudación fiscal analizada, son insuficientes para establecer enfáticamente la normalidad, ya que mediante los análisis a los residuos por coeficiente de asimetría y curtosis, calculados en lo individual y como insumos en la prueba de Jarque-Bera, sugieren que no necesariamente existe un comportamiento normal en la distribución del impuesto sobre nóminas y asimilado a salarios. La anterior situación evidenciaría la necesidad de incluir preguntas de investigación en los estudios fiscales similares realizados en otras entidades federativas; es decir, evitando asumir un comportamiento normal para el impuesto sobre nóminas.
Considerando los resultados en las estadísticas para los residuos, se estaría frente a la característica planteada por Mandelbrot con respecto a la irregularidad, cumpliendo también con la otra característica de autosimilitud obtenida en la gráfica, con que se concluye que el comportamiento fractal se encuentra presente.
El análisis también gráfico, aplicado a la totalidad de la serie de tiempo, que incluyó 132 observaciones mensuales, arrojó un patrón de evidente iteración, a excepción del año 2005 en que aconteció el embate del huracán Wilma y del año 2009 en que tuvo lugar la contingencia sanitaria para el virus H1N1; esta situación reforzaría algunos planteamientos de la teoría del caos (Prigogine, 2009) en donde un elemento de entrada puede causar múltiples situaciones distintas al patrón del orden común.
Posteriormente a la distorsión gráfica que se observa en los ejercicios 2005 y 2009, la gráfica de forma paulatina, pero también determinante, retoma el comportamiento observado de los denominados picos altos en periodos muy específicos en cada año, normalmente en los meses de enero.
Al tratar de localizar evidencia repetitiva en la recaudación fiscal, además del nivel estatal constatado, se indagó en el comportamiento gráfico para los cuatro municipios más importantes del estado de Quintana Roo, encontrando iteración constante pese a la distorsión de incidencias negativas en 2005 y 2009.
Los incrementos en la recaudación observados en la totalidad de la serie, que correspondió a los once ejercicios fiscales, no son motivo para descartar la iteración y el proceso de autosimilitud, conclusión apoyada por lo dicho en otros planteamientos que reconocen la existencia de incrementos estacionales en un proceso de autosimilitud (Embrechts y Maejima, 2002; Ramírez, Torres y Toral, 2012).
Si bien se han realizado diversos estudios de tipo fractal con aplicación a las finanzas, la mayoría se ha orientado al índice de precios y cotizaciones (Chorofas, 1999; Ludlow, 1997; Peters, 1994); sin embargo, es importante hacer extensivas las aplicaciones al campo de la contaduría y en especial a la recaudación fiscal ya que —debido al comportamiento mostrado en el presente artículo, con énfasis en la iteración y los periodos que en gráficas representaron picos altos— debería ser parte de los criterios para formular la política fiscal en cada entidad, previendo excesos de asignación de recursos y posteriores limitantes presupuestales a las dependencias y entidades, procurando la estabilidad en el logro de programas específicos.
La información original no fue expresada en miles, el haberla incluido de esta forma corresponde a razones de espacio y formato.
El municipio de Tulum inició recientemente en el año 2009, cuya administración estuvo a cargo de un consejo municipal hasta mediados del 2011, mismo año en que inicia el municipio de Bacalar.
En los estudios previos analizados fueron identificadas dos fórmulas que hacen referencia a la prueba Jarque – Bera, comprobando la obtención de los mismos resultados en ambos casos. La otra opción distinta a la adoptada en el trabajo fue
En el caso del trabajo de investigación de Gálvez (2005) se observó un planteamiento distinto.