En este trabajo se utiliza la metodología de bicorrelación cruzada, la cual permite capturar periodos de trascendencia no lineal por medio de funciones ventana y momentos de tercer orden. Esto se aplicó al retorno de cuatro series de commodities del café (arábica colombiano, suave, brasileño y otras) que cotiza en el mercado de Nueva York durante el periodo del 20 de junio de 1997 al 27 de octubre de 2010. Los resultados muestran que existe una bicorrelación entre las cuatro series, donde el líder es el café tipo brasileño y hay una menor bicorrelación en los otros, lo que complica las decisiones de los inversionistas en este tipo de series.
This paper uses the cross bicorrelation methodology, which can capture nonlinear trascendence periods through window functions and third-order moments. It applies to the return of four sets of commodities of coffee traded on the New York market (Arabica Colombian, mild Arabica, Arabica Brazilian and Other Arabicas), during the 20/06/1997 - 27/10/2010 period. The results conclude that there is a cross bicorrelation among the four series, with Brazilian type coffee being the leader and a lower bicorrelation with other Arabicas. This complicates decisions for investors in such series.
Los mercados financieros se han estudiado desde distintas perspectivas: económicas, financieras, estadísticas y físicas; estas últimas utilizan conceptos, aplicaciones y métodos a lo que se le conoce como Econofísica (Mantegna y Stanley, 2000). Este tipo estudio se ha empleado para pronosticar el rendimiento, analizar el valor en riesgo, la volatilidad, la teoría de mercados eficientes, las correlaciones, entre otros.
En cuanto a la correlación, ésta se ha realizado desde el simple coeficiente de Pearson hasta con la teoría de matrices aleatorias, la cual a su vez tiene que ver con la correlación cruzada1. Existe una variedad de aplicaciones multivariadas utilizando la correlación cruzada a series financieras (Conlon et al., 2009; Utsugi et al., 2003; Podobnick et al., 2009; Tóth y Kertész, 2005; Laloux et al., 1999, 2000; Plerou et al., 1999; Potters et al., 2005, Wilcox y Gebbie, 2007; Sharifi et al., 2004; Nakayama y Iyetomi, 2008; Altay, 2003). Estas aplicaciones han tratado de explicar la correlación entre dos series; se estudia sus eigenvalores para compararlos con la correlación estática; se extrae información del grado de correlación que hay entre un par de series, lo cual es útil para emplearla en el pronóstico, excluir oportunidades de arbitraje y determinar si no existen correlaciones espurias entre el par de series.
Por otra parte, es importante recordar que entre las distintas series financieras que se manejan en el mercado internacional están las commodities2 como son: oro, plata, cobre, petróleo, gas natural, vacuno, cerdo, azúcar, soya, algodón, cacao, maíz, café y trigo. En el nivel mundial uno de los commodities más importantes es el café, cuyo principal productor es Brasil, después le siguen Vietnam, Indonesia, Colombia y México (FAO, 2005); los principales mercados internacionales donde se cotiza este producto son Nueva York y Londres (Gómez, 2003). Para la Organización Internacional del Café (OIC, 2002) existen cuatro tipos de cafés3: 1) arábica suave colombiana, que se representa por el Colombian Excelso European Preparation Screen Size 15; 2) otras arábicas suaves, representados por Costa Rica: Hard Bean, El Salvador: Strictly High Grown, Guatemala: Hard Bean, Nicaragua: Strictly High Grown; 3) arábicas naturales brasileñas y otras arábicas naturales, que se representa por Brazilian Santos 4; y 4) la arábica robusta, representada por Cote d’Ivoire Grade 2, Indonesia EK Grade 4, Uganda Standard y Vietnam Grade 2.
Existen diversos estudios que analizan la relación del precio spot de estos distintos tipos de café, para lo cual utilizan distintas metodologías (Vogelvag, 1992; Milas y Otero, 2002, Milas et al., 2004, Otero y Milas, 2001). Estos trabajos señalan que hay una relación entre los pares de series de los distintos tipos de café, lo cual hay que considerar al momento de realizar el pronóstico. De igual forma, existe una nueva metodología que se ha aplicado a series financieras y no financieras para probar la no linealidad entre la relación de dos series de tiempo lead/lag a través de la bicorrelación cruzada (Brooks y Hinich, 1999; Czamanski et al., 2007) Está prueba es una extensión del estadístico hinich portmanteau, la cual permite capturar periodos de trascendencia no lineal por medio de funciones ventana y momentos de tercer orden (Hinich, 1996).
Por lo anterior, el objetivo de nuestro trabajo es aplicar la bicorrelación cruzada,4 lo cual dará la dirección de la bicorrelación a los rendimientos diarios internacionales de los distintitos tipos de café que se cotizan en el mercado de Nueva York, utilizando como principal serie el café tipo brasileño. Los resultados encontrados son congruentes con el trabajo de Milas y Otero (2002), quienes concluyen que las series están cointegradas; sin embargo, una diferencia de esta metodología es que el estadístico de bicorrelación cruzada determina los periodos donde ocurre la bicorrelación cruzada.
El trabajo está estructurado de la siguiente manera. En el siguiente apartado se describe el estadístico que detecta la bicorrelación cruzada de dos series; después se indican los datos de la muestra; posteriormente, se presentan los resultados obtenidos y finalmente se ofrecen las conclusiones.
Bicorrelación cruzadaSe tiene la muestra de dos series estacionarias5X(tk) y y(tk) de tamaño N en la que cada serie se separa en pequeños marcos (ventanas) de igual longitud no traslapadas. Donde t es un entero y k es la k-ésima ventana y ambas series tienen covarianzas estacionarias conjuntas, las cuales han sido estandarizadas.
Las hipótesis son: H0: las series X(tk) y y(tk) tienen bicovarianzas cruzadas Cxxy(r, s)=E[x(tk)x(tk+r)y(tk+s)]=0∀ r, sexcepto cuando r=s=0 y H1: la series X(tk)y y(tk) tienen bicovarianzas cruzadas Cxxy(r, s)=E [x(tk)x(tk+r)y(tk+s)]≠0. La invarianza del E [x(tk)x(tk+r)y(tk+s)] para las permutaciones (t1, t2) implica estacionalidad, lo que lleva al E [x(tk)x(tk+r)y(tk+s)] que sea una función de dos rezagos y entonces Cxxy(– r, s)=Cxxy(r, s). Si el máximo rezago usado es L<N, entonces el dominio principal para las bicovarianzas es el rectángulo {1≤ r ≤ L, – L ≤ s ≤ L } (Brooks y Hinich, 1996).
Si se rechaza la hipótesis nula se sabe que el par de series son dependientes, entonces existe un segundo o tercer rezago entre las dos series que lleva a Cxxy(r, s) ≠ 0 para al menos un valor de r o un par de valores (r,s), respectivamente. Así que la bicorrelación cruzada se denota por
Por lo tanto, el estadístico que detecta bicorrelaciones cruzadas a través de momentos de tercer orden es:
Donde el número de rezagos L=Nc, 0<c<0.5 y cuando N → ∞, Hxxy(N) sigue una distribución χ2 con L(2 L – 1) grados de libertad.
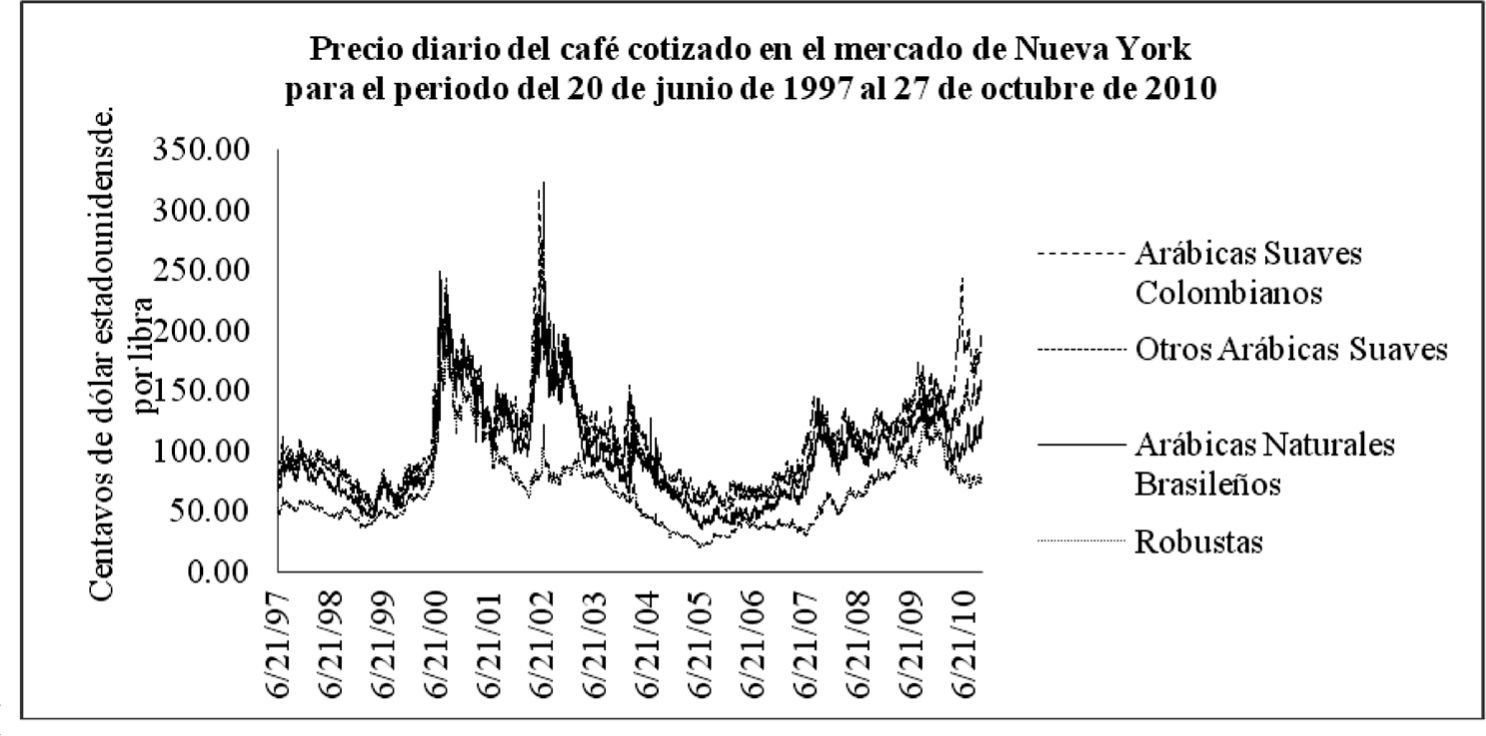
DatosLa muestra consiste en el precio diario para los cuatro tipos de café que cotizan en el mercado de Nueva York en centavos de dólar estadounidense por libra para el periodo del 20 de junio de 1997 al 27 de octubre de 20106 (ver gráfica 1). Los tipos de café son los siguientes: arábica suave colombiana (proveniente de Colombia), otras arábicas suaves (proveniente de Costa Rica, El Salvador, Guatemala y México), arábicas naturales brasileñas (proveniente de Brasil) y las robustas (provenientes de Costa de Marfil, Uganda, Vietnam e Indonesia). El total de datos para cada una de las series es de 4 860.
En la gráfica 1 se muestra cómo las cuatro series de los distintos tipos de café siguen el mismo comportamiento. Los tres primeros están casi encimados uno de otro a excepción de las robustas que se aleja, lo cual indica que hay algún tipo de correlación entre ellos.
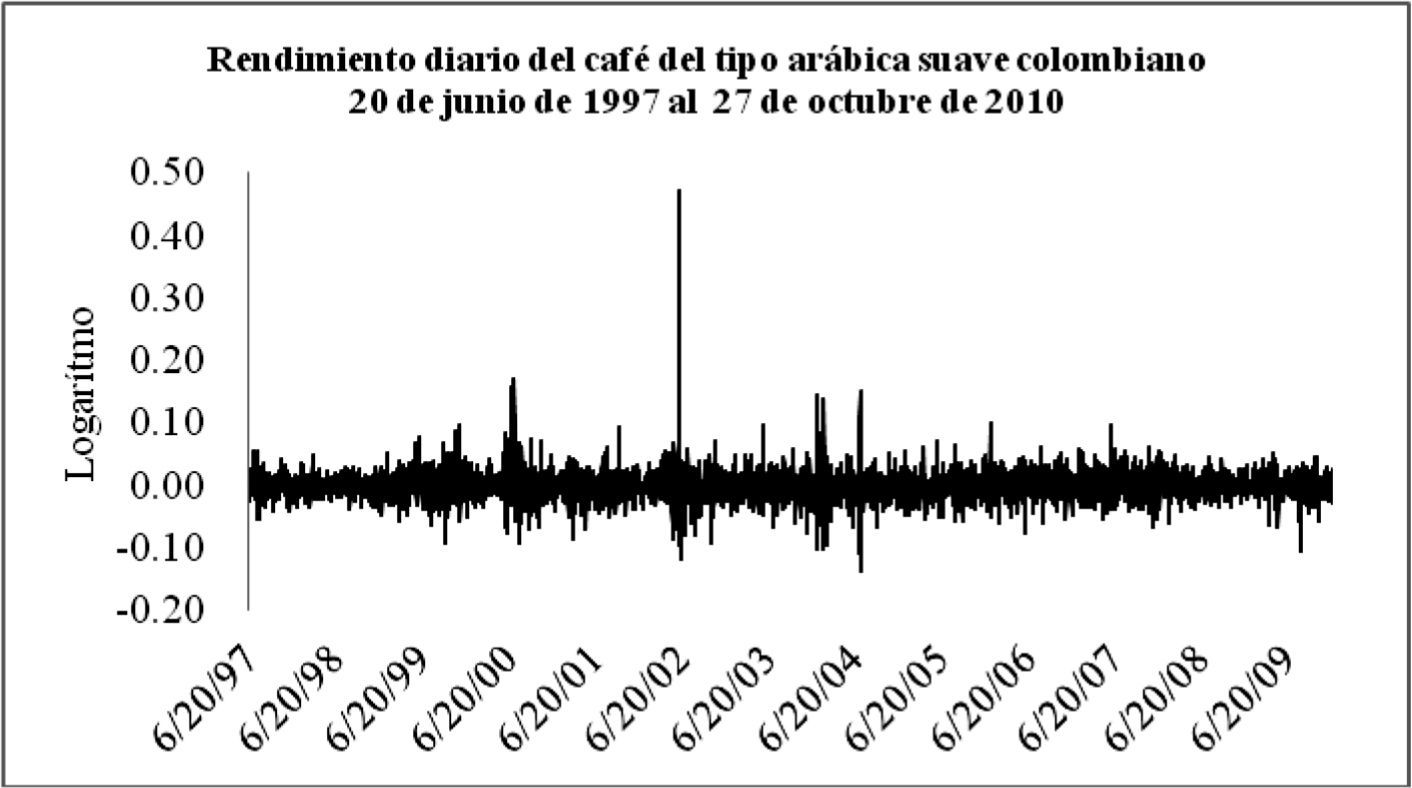
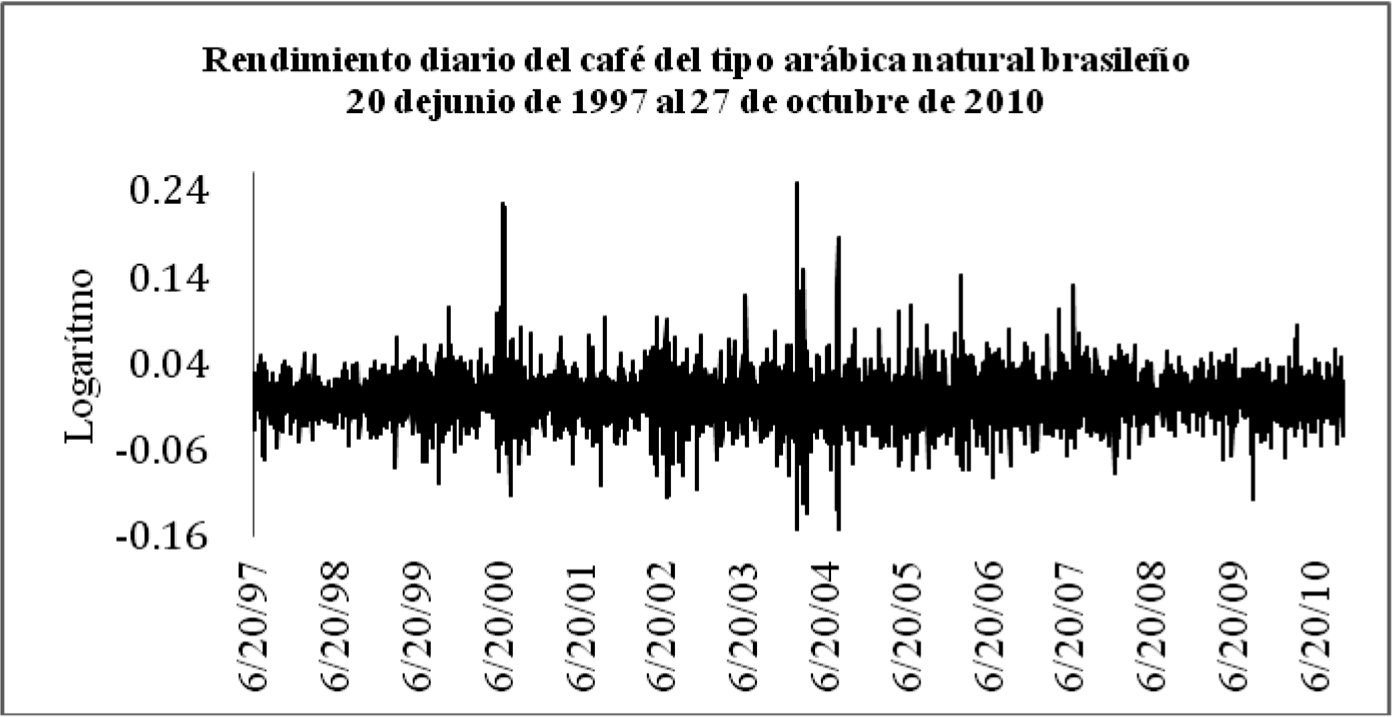
Para el cálculo del rendimiento se transformó cada una de las series a su escala logarítmica RCt=ln(pt/ pt –1) para evitar cualquier existencia de dependencia lineal en las innovaciones; es decir, se rechazó que las series son un proceso ruido blanco puro; se ajustaron los residuales de cada una de las series a un proceso autorregresivo AR(p); se prefirió el mejor p de acuerdo con el criterio de Schwarz. Este criterio de Schwarz (conocido como SC en inglés), a diferencia de otros estadísticos como el criterio de información de Akaike (AIC siglas en inglés), fue consistente para un determinado AR(p) con respecto a la hipótesis nula de que se genera un mecanismo lineal (Panagiotidis y Pelloni, 2003); esto es, es un criterio que optimiza la selección de rezagos para evitar que resulte un sobre ajuste, ya que resuelve el problema de un sobre ajuste penalizando el número de rezagos, lo que hace que sea más robusto que el AIC, por lo cual se elige entre distintos modelajes el que tenga el menor SC. Se encontró que se ajusta cada una de las series a un AR(2) (ver cuadro 1 y los gráficos 2,3,4 y 5).
| Rezago | Coeficientes | |||
|---|---|---|---|---|
| A | B | C | D | |
| 1 | 0.0044880 | -0.0055870 | 0.0068000 | 0.0590700 |
| Estadístico t | 3.5600000 | -4.1600000 | 2.7800000 | 5.3700000 |
| 2 | -0.0204000 | -0.0361200 | -0.0311200 | -0.0417600 |
| Estadístico t | -2.9800000 | -4.2500000 | -3.5000000 | -4.2300000 |
| Criterio de Schwarz | -23191.13 | -22756.74 | -21868.47 | -25024.92 |
A=Café colombiano, B=Café brasileño, C=Otros, D=Robustas. La suma de los coeficientes es menor o igual que 1
Para poder rechazar la hipótesis nula de (1) de acuerdo con el estadístico de (2) primero se dividió cada una de las series en 162 ventanas no traslapadas con un c=0.4, L=48600.4≈30 con un umbral de 0.05 para cada serie. Como son cuatro series, se realiza la combinación de pares de series, lo que dio como resultado seis combinaciones de ello. Los resultados se muestran en el cuadro 27.
Resultados de ventanas significativas con bicorrelaciones cruzadas para los distintos tipo de café que cotiza en Nueva York. 20 de junio de 1997 al 27 de octubre 2010
| Serie | Umbral | AR(p) Ajustado | # Windows | Tamaño de la ventana | Número total de ventanas con bicorrelaciones cruzadas significativas H | Ventanas con bicorrelación cruzada | Correlaciones | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cxxy | Cyyx | Cxxx | Cyyy | (xxy,yyx) | (xxy,xxx) | (xxy,yyy) | (yyx,xxx) | (yyx,yyy) | (xxx,yyy) | ||||||
| A/B | 0.05 | p=2 | 162 | 30 | 30(18.5%) | 1(0.6%) | 1(0.6%) | 6(3.7%) | 22(13.6) | 0.15 | 0.09 | 0.06 | 0.01 | 0.06 | 0.21 |
| A/C | 14(8.6%) | 1(0.6%) | 1(0.6%) | 6(3.7%) | 6(3.7%) | 0.17 | 0.17 | 0.03 | -0.14 | 0.19 | -0.03 | ||||
| A/D | 17(10.5%) | 3(1.9%) | 2(1.2%) | 6(3.7%) | 6(3.7%) | 0.09 | 0.13 | 0.01 | -0.05 | 0.3 | 0.01 | ||||
| B/C | 28(17.3%) | 1(0.6%) | 0 | 21(13.0%) | 6(3.7%) | 0.03 | 0.25 | -0.01 | 0 | 0.04 | 0.13 | ||||
| B/D | 28(17.3%) | 1(0.6%) | 0 | 21(13.0%) | 6(3.7%) | 0.06 | 0.28 | -0.03 | 0.02 | 0.09 | 0 | ||||
| C/D | 1(0.6%) | 0 | 0 | 1(0.6%) | 0 | 0.13 | 0.21 | 0.06 | 0.10 | 0.23 | 0.09 | ||||
A=Café Colombiano, B=Café Brasileño, C=Otros, D=Robustas.
Los resultados del cuadro 2 muestran el número de ventas que existieron con bicorrelaciones cruzadas. Se observa que existieron 30 ventanas entre los tipos de café colombiano y brasileño; en segundo lugar la bicorrelación entre Brasil y otros, y Brasil con robustas. La menor correlación es entre otros y robustas, los primeros provienen de Centroamérica y los segundos en su mayoría de África; por lo tanto, existe una fuerte correlación entre el primero, segundo y tercer par de series. Así, también se muestra la correlación entre ellas, la cual es muy pequeña, aunque la correlación más grande se presenta entre el par A/B con un 0.21. En consecuencia, existe una bicorrelación cruzada entre las distintas series, utilizando momentos de tercer orden. Los resultados concuerdan con Milas y Otero (2002), sólo que con una metodología diferente.
ConclusionesLos resultados obtenidos concluyen, en primer lugar, que las series están bicorrelacionadas utilizando momentos de tercer orden. La correlación más fuerte ocurre entre los tipos de café colombiano y los tipos de café brasileño. Encontrar estos episodios donde ocurren estas bicorrelaciones permitirá en futuras investigaciones indagar qué es lo que pasa en dichos episodios, así como tomar en cuenta las decisiones de pronóstico cuando se quiera invertir en commodities. Además, este tipo de productos no solamente son muy vulnerables a la oferta y demanda, sino también a aspectos climatológicos como sequías, inundaciones, heladas, entre otros. De igual forma, pueden ser vistos como un instrumento de la política económica en los países de origen, ya que son países en desarrollo, los cuales pueden tomar decisiones sobre el movimiento del precio.
Interprétese correlación cruzada como la covarianza de dos vectores aleatorios.
Producto heterogéneo que se vende a granel y que puede constituir una alternativa de inversión para distintos tipos de inversores en mercados financieros.
Estos cuatro tipos de café son lo que cotizan en el mercado de Nueva York.
La bicorrelación cruzada se entiende como la correlación entre los valores presentes de una serie y los valores previos de la bicorrelación cruzada entre dos series.
Dado que se trabaja con pequeñas muestras en todas las series, la estacionalidad no es un supuesto estricto.