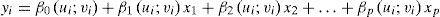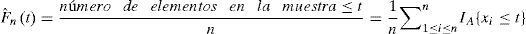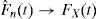El sistema de tren ligero referido en el presente trabajo es un sistema eficiente y popular de transporte público que sirve en extensas áreas de la zona metropolitana del Valle de México. Encuestas a los pasajeros muestran que la demora en los trenes es el reto más importante a satisfacer. La demanda de pasajeros es el dato más relevante para la programación del servicio. Ha habido pocos intentos por abordar esta problemática: la carencia de información confiable ha sido una fuerte limitante. El propósito de esta investigación fue modelar la demanda diaria de pasajeros utilizando los datos obtenidos por los dispositivos de entrada (torniquetes) a las estaciones, prescindiendo de técnicas tradicionales para describir la afluencia de pasajeros. De manera que la investigación se orientó a obtener funciones de distribución continuas que se ajustaran a la demanda de pasajeros en una línea particular y sus estaciones. Se obtuvieron y analizaron datos correspondientes al flujo del año 2010 y se introdujeron en una base de datos compatible con software estadístico. Los modelos propuestos fueron obtenidos por estimación de máxima verosimilitud y corresponden a funciones de distribución de probabilidad continuas, con soporte en los reales positivos.
Light rail train system of this work is a popular and efficient public transportation system serving over large areas of the Metropolitan Area of the Valley of Mexico. Passenger surveys show that the delay in the trains is the most important challenge to be met. Passenger demand is the most relevant information to schedule the train service. Few attempts have been made to address this problem; the lack of reliable information has been a serious constraint. The purpose of this research was to model the daily passenger demand using data from turnstiles located in the stations. Typical techniques were not used to model passenger demand. Therefore, research was focused on obtaining continuous distribution functions, which will adjust to the passenger demand for a particular train line and its stations. Transportation flow data for the whole of 2010 were collected and analyzed, and then they were entered into a statistical software supportable database. The proposed models were obtained by maximum likelihood estimation; they correspond to continuous probability distribution functions with support on the positive real numbers.
El tren ligero objeto de esta investigación presta servicio en extensas áreas de la zona metropolitana del Valle de México (ZMVM). Su operación y explotación está a cargo del organismo público descentralizado denominado Sistema de Transporte Colectivo (STC o el Sistema) y su administración está a cargo del Proyecto Metro del D.F., organismo desconcentrado perteneciente a la Secretaría de Obras y Servicios del D.F. La construcción del Sistema comenzó el 19 de junio de 1967, en la Línea 1 con un tramo planeado de 12.660km y 16 estaciones. Actualmente cuenta con 12 líneas y 195 estaciones.
Inaugurado el 4 de septiembre de 1969, el Sistema ha ocupado, a nivel mundial, hasta el cuarto lugar en transporte de pasajeros con más de 1,600 millones de usuarios en 2012, solo superado por los de Moscú, Tokio y Nueva York. La línea de pasajeros bajo estudio es conducida por vía férrea externa y se denomina Línea A; fue la novena línea del Sistema en ser inaugurada. La Línea A está integrada por 10 estaciones y su trazo se localiza al sur-oriente de la ZMVM con dirección predominante oriente-poniente; tiene una longitud de vía de 17.192 kilómetros (Sistema de Transporte Colectivo, 2007). El Sistema tiene aceptación y demanda creciente de usuarios por ser económico, seguro y eficiente como transporte de pasajeros. Debido a que existe una lenta expansión del Sistema que impide atender la creciente demanda con la misma calidad del servicio, se manifiestan de manera frecuente múltiples dificultades o incidencias, principalmente: aglomeraciones en su infraestructura, tiempos de traslado crecientes e inseguridad. Estas y otras singularidades del servicio no siempre han podido ser anticipadas o prevenidas adecuadamente para reaccionar ante situaciones contingentes, tal vez por falta de presupuesto, falta de estudios en la materia, etc.
De las encuestas para mejorar el servicio, se infiere que la mayor preocupación de los usuarios son las demoras de los trenes (32%, la seguridad (26%), el mantenimiento (6%), el ambulantaje (11%), la limpieza (6%), y siguen en menor proporción, taquillas, horario de servicio, escaleras mecánicas y torniquetes, tal como se indica en la segunda sección del Decálogo de Proyectos y Acciones 2010 que se encuentra en la siguiente dirección electrónica: http://www.metro.df.gob.mx/organismo/decalogo 10.html (Sistema de Transporte Colectivo, 2014).
Una forma efectiva de abordar la problemática anterior es obtener un modelo cuantitativo-predictivo de la demanda diaria de pasajeros. Analizar la demanda de pasajeros es importante en las sociedades desarrolladas debido a la necesidad de movilidad personal para acceder a actividades económicas y servicios. Planeadores e investigadores necesitan saber cuándo y por qué ocurre la demanda de pasajeros en estaciones y corredores de transporte público interurbano (Parsons Brinckerhoff, 1996). En el contexto de los viajes interurbanos hay componentes estacionales en el comportamiento de la demanda de pasajeros. Los modelos de demanda desagregados sirven para analizar esta demanda, planteada en el marco de procesos de toma de decisión de los individuos, microeconomía, elecciones discretas y teoría de la utilidad aleatoria (Ortúzar y Román, 2003). Su aplicación se extiende a la economía del transporte y a contextos relacionados con la economía de las elecciones.
Otros ejemplos son los modelos «probit», descriptivos de elección binaria y discreta: el conjunto de elección se reduce a 2 alternativas mutuamente excluyentes, registradas por cuestionarios sujetos a análisis estadístico, que permite realizar un análisis desagregado de las elasticidades de la demanda y del valor subjetivo del tiempo de los viajeros (Tamin y Sulistyorini, 2009). Las fuentes de información en modelos desagregados son las preferencias reveladas y las preferencias declaradas. Las primeras se basan en las elecciones realizadas por los individuos e indagan sobre la importancia relativa de las variables que influyen en la decisión. Las preferencias declaradas captan esta idea y, en cambio, se basan en la construcción de escenarios hipotéticos presentados al consumidor para que indique su elección. El inconveniente de estas técnicas es que los individuos no siempre hacen lo que declaran que van a hacer y los estudios son onerosos porque implican realizar encuestas microeconómicas regulares.
Otros países han realizado estudios que emplean tarjetas inteligentes para analizar y modelar la demanda de pasajeros. Estos estudios utilizan datos almacenados en la tarjeta que muestran la ruta, el horario y los transportes utilizados. Así se conoce el comportamiento del viajero y se examina la demanda de pasajeros para proponer soluciones a diversas problemáticas (Choi, Lee, Park y Jung, 2010). Desafortunadamente, el uso de la tarjeta inteligente se ha retrasado en el transporte público mexicano, sobre todo, por falta de recursos.
Los estudios sobre demanda de transporte público adquieren relevancia por la escasez de presupuesto en los gobiernos. En las estaciones de transporte público, la demanda o flujo de pasajeros tiene un sustento geográfico, la demanda en las estaciones puede incrementarse ante la proximidad de altas densidades de población, concentración del empleo y factores econométricos (Cervero, 2006). En el estudio de la demanda se ha utilizado con éxito el modelo de 4 etapas: generación, distribución, asignación y reparto modal (McNally, 2007) que tiene por inconveniente su alto costo –encuestas– y sofisticación. Aunque utiliza regresión múltiple y análisis de categorías en las etapas de generación y atracción de viajes, en la etapa de generación utiliza modelos de entropía (Marshall y Grady, 2006) y datos de elección discreta en la etapa de reparto. Este modelo analiza las características econométricas en la vecindad de las estaciones para explicar la relación entre inversión y uso del servicio de transporte.
Los modelos de predicción directa de la demanda a nivel de estación cuestan menos que el modelo de 4 etapas y utilizan regresión múltiple por mínimos cuadrados ordinarios (MCO). Se utiliza la regresión múltiple suponiendo la estabilidad paramétrica de los resultados; tal estabilidad de los predictores (betas) implica que la magnitud de los coeficientes de regresión permanece constante en el tiempo (Walters y Cervero, 2003). El coeficiente de determinación mide cuánto se explica la variable dependiente y, bajo el supuesto anterior, pensar en un coeficiente de determinación igual para todo el conjunto de observaciones resulta inadecuado porque induce a un problema conocido en la literatura como inestabilidad paramétrica (Arbia y Baltagi, 2006).
La inestabilidad paramétrica denota trabajar con valores extremos de una muestra multivariada; es decir, puntos en los cuales algunos componentes tienen valores excepcionalmente altos. La inestabilidad provoca que cambios ligeros en los datos puedan inducir altas desviaciones y resultados disímiles en las variables que conformen el modelo final. Por otra parte, los datos espaciales no cumplen la hipótesis de independencia, debido a que normalmente están autocorrelacionados, por lo que la fuerza de la relación entre las variables del modelo no será la misma en toda el área de estudio. Los modelos de predicción directa usan variables que miden las características de las estaciones y sus entornos, utilizando sistemas de información geográfica para estimar directamente la demanda mediante variables correspondientes al entorno de la estación y su área de influencia (Kuby, Barranda y Upchurch, 2004). Tal es el caso de las estaciones de tren ligero en el metro de Madrid (Gutiérrez et al., 2011).
Dichos modelos aumentan su capacidad explicativa utilizando técnicas de regresión geográficamente ponderada (geographically weighted regression, GWR) Esta mide la inestabilidad paramétrica a partir de la magnitud que presentan los coeficientes a través del territorio. En los modelos que utilizan los sistemas de información geográfica y las técnicas de GWR, el estudio se enfoca en la vecindad a la estación de trenes: sus unidades de análisis son los entornos de las estaciones y no las zonas de transporte. Los datos de movilidad necesarios para los modelos de predicción directa son proporcionados por estudios sobre el aforo de las estaciones, como sería el resultado de la encuesta Origen-Destino 2007, llevada a cabo en la ZMVM.
El concepto GWR alude a una familia de modelos de regresión «ajustados al espacio» donde el efecto de una variable explicativa sobre la variable dependiente es «pesado» por el efecto geográfico y econométrico de los regresores, dando mayor peso a las observaciones más cercanas a la estación, y viceversa. Se trata de ajustar tantas regresiones como observaciones (unidades espaciales) se consideren en el análisis; se pueden realizar estimaciones ajustadas a cada observación, aplicando su correspondiente ecuación. Las variables utilizadas para la GWR en Madrid fueron identificadas a partir de varios trabajos que estudiaron los factores que afectan al número de usuarios que entran en las estaciones.
La principal característica de la GWR es distinguir explícitamente la componente espacial en los datos, incorporando en su ecuación el valor de las coordenadas geográficas de las observaciones, ya sea un punto, un centroide de polígono o una celda, logrando que los coeficientes βj(j=0, 1,…, p) de los j predictores xj(j=1,…, p) varíen en cada localización. Es decir, cada localización está definida por sus coordenadas: (ui; vi). El valor de la variable dependiente yi será:
En Madrid, el modelo final incorpora 4 variables independientes: 3 relativas al área de influencia de la estación (cantidad de ocupados, cantidad de empleos, número de líneas de autobuses interurbanos) y una relativa a las características de las estaciones (número de líneas que pasan por la estación). El ajuste del modelo global (MCO) ofreció unos R2 y R2 ajustado de 0,56 y 0,57, respectivamente.
Los modelos de funciones de distribución aquí propuestos exponen el comportamiento estocástico de las personas que ingresan a las estaciones sin atender a datos correlacionados como número de autobuses o combis, cantidad de desempleados, etc.; y no hay punto de comparación con otras metodologías, excepto su objetivo. Los modelos de funciones de densidad sirven para realizar simulaciones muy precisas con las densidades obtenidas y su utilidad reside en su sólida sencillez, el ajuste por máxima verosimilitud y las pruebas de bondad de ajuste para rechazar o aceptar la hipótesis nula: el flujo de pasajeros se ajusta a un modelo teórico conocido con parámetros obtenidos mediante máxima verosimilitud.
Los dispositivos que registran el acceso con importe pagado a las estaciones del Sistema se denominan «torniquetes», giran conforme el usuario ingresa a la estación y registran el número de usuarios. Este trabajo se concentró en obtener un modelo estocástico de la demanda diaria de pasajeros a partir de los registros obtenidos en los torniquetes y en él no se incluyen modelos regresivos geográficamente ponderados porque propone un análisis in situ de la demanda diaria por cada estación de la Línea A. Dado que se tuvo acceso a los archivos de conteo en los torniquetes, y debido a limitaciones presupuestales, se escogió este planteamiento: se obtuvieron modelos basados en funciones de distribución continuas para describir el comportamiento aleatorio del flujo de pasajeros en demanda por transporte. Por su parte, el Sistema elabora pronósticos mediante series de tiempo que modelan una demanda anualizada. Estos datos son considerados confidenciales por el Sistema.
En el Sistema, los períodos de máxima demanda en las terminales y estaciones de mayor afluencia presentan gran número de anomalías, y son causantes de retrasos en los servicios. Por ser un circuito, una incidencia afecta a toda la línea en la que esta se presenta e, indirectamente, a las líneas con las que tiene transferencia, lo que es percibido por el usuario como demora. Las anomalías se propician por un factor de temporalidad, que obedece a las fluctuaciones de personas que ingresan por las estaciones, y ocurren de manera discontinua y aleatoria. Estos flujos difieren por horario y locación en la ZMVM. El Sistema tiene un decálogo de proyectos para abatir la problemática reconocida en sus encuestas y planea disminuir la demora de trenes, incrementar su frecuencia, dosificar usuarios en las estaciones, etc., tal como lo propone el Decálogo de Proyectos y Acciones 2010.
Los ejes del Programa Institucional del Sistema de Transporte Colectivo 2007-2012 buscan mejorar la calidad del servicio y atención al usuario. Para agilizar el servicio del Sistema, investigadores del Instituto de Investigaciones en Matemáticas Aplicadas y Sistemas (IIMAS) de la UNAM desarrollan un modelo para establecer el tiempo máximo de espera en las estaciones, controlar el flujo de usuarios a los andenes y el espaciamiento de los trenes (Pineda y Gershenson, 2011). En la presente investigación se utilizaron los datos obtenidos por los dispositivos de entrada a las estaciones. Se ha prescindido de técnicas de muestreo econométricas para modelar la demanda de pasajeros, suponiendo que estos datos poseen un comportamiento estocástico que debe revisarse.
Se eligió analizar la Línea A porque las mediciones de afluencia se obtienen directamente de los datos almacenados en los torniquetes de cada estación y la única conexión con otra línea ocurre en una de las terminales, lo que propicia la independencia de los datos. Sin un modelo de la demanda diaria, el Sistema puede caer en anomalías de servicio al usuario. La carencia de un modelo incide en diversas tareas: los servicios se desfasan y se genera la aglomeración. Tal situación incrementa el deterioro de las instalaciones y la inseguridad, poniendo en riesgo al usuario.
Un modelo de la demanda diaria de pasajeros deja anticipar el flujo de personas en tránsito y puede mejorar la planeación de los servicios. El modelo para cuantificar la demanda diaria permitirá analizar diversos problemas en favor del usuario. Conociendo esta demanda, pueden prevenirse las aglomeraciones y evitar extender los tiempos de traslado. Particularmente, el flujo de pasajeros tiene un comportamiento que puede describirse con modelos de carácter estocástico.
Obtención de los datos y su adecuación para el análisisLos torniquetes contabilizan el acceso con porte pagado a las estaciones de la Línea A; los registros se capturan y envían a un departamento especializado del Sistema para darles un tratamiento informático. Se obtuvo un registro del flujo de pasajeros con pago solventado transportados por el Sistema (en archivos electrónicos tipo data-base-file.dbf), con datos contenidos en archivos «planos», sin estructura, para llevar a cabo búsqueda relacional. Los archivos obtenidos fueron cedidos con base en su disponibilidad: el Sistema lleva un desfase de 3 meses o más entre la obtención de los registros y su acopio para análisis. Estos se consideran estratégicos y no son accesibles al público.
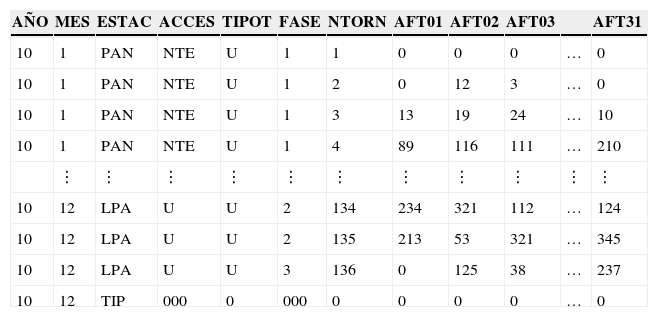
Los registros suministraron observaciones de los 365 días del año 2010 en cada una de las estaciones de la Línea A del Sistema. Se utilizaron los datos del 2010, pero la naturaleza estocástica del fenómeno permite analizar con validez una fracción de los datos totales para inferir un comportamiento general. Debido a la independencia estocástica de los eventos, la metodología del estudio puede aplicarse a cualquier otro conjunto de datos. Los resultados del 2010 pudieran no ser efectivos posteriormente, pero con datos actualizados el análisis mostrará resultados similares en función de la solidez de los supuestos y de los algoritmos de ajuste (máxima verosimilitud). Los datos de la demanda en el archivo original (aflto110.dbf) fueron capturados como lo muestra la tabla 1.
Aspecto inicial de los datos
| AÑO | MES | ESTAC | ACCES | TIPOT | FASE | NTORN | AFT01 | AFT02 | AFT03 | AFT31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 1 | PAN | NTE | U | 1 | 1 | 0 | 0 | 0 | … | 0 |
| 10 | 1 | PAN | NTE | U | 1 | 2 | 0 | 12 | 3 | … | 0 |
| 10 | 1 | PAN | NTE | U | 1 | 3 | 13 | 19 | 24 | … | 10 |
| 10 | 1 | PAN | NTE | U | 1 | 4 | 89 | 116 | 111 | … | 210 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| 10 | 12 | LPA | U | U | 2 | 134 | 234 | 321 | 112 | … | 124 |
| 10 | 12 | LPA | U | U | 2 | 135 | 213 | 53 | 321 | … | 345 |
| 10 | 12 | LPA | U | U | 3 | 136 | 0 | 125 | 38 | … | 237 |
| 10 | 12 | TIP | 000 | 0 | 000 | 0 | 0 | 0 | 0 | … | 0 |
Fuente: Gómez-Eguiarte (2013).
La simbología de la tabla en las columnas indica el año de acopio de datos (2010); el mes y la estación de Línea A, la columna ACCES indica la posición donde se encuentra la batería de torniquetes, el acceso indica el tipo de torniquete (U=único), la FASE es un control temporal interno, NTORN indica en qué torniquete se está efectuando la «lectura» y a continuación las columnas AFTO1…AFTO31 indican los totales obtenidos desde el día 1 al día 31 del mes.
Un examen a la tabla revela que tal concentración no es apta para su análisis, los campos registrados en las columnas no son las variables de interés. Las variables de interés «estaciones» (ESTAC) están en los renglones (PAN=Pantitlán; Agrícola Oriental=AGO,…, LPA=La Paz); en ellas se registra la demanda de pasajeros que circula por día en cada estación. Se modificaron los registros de lecturas para obtener archivos con una estructura compatible con una base de datos y una matriz de información.
El proceso consistió en realizar transformaciones del archivo plano inicial (aflto110.dbf) para obtener archivos compatibles con diversas herramientas de software estadístico. Afortunadamente las mediciones se realizaron en escala de orden, o racional, correspondiente al máximo nivel de medición. Pueden compararse las diferencias en puntuaciones en lo relativo a magnitud de la demanda: el cero representa la ausencia de la característica o propiedad. Así, los datos correspondientes al flujo de pasajeros que ingresan diariamente por las estaciones de la Línea A forman una muestra aleatoria de mediciones de tipo finito contable en escala racional.
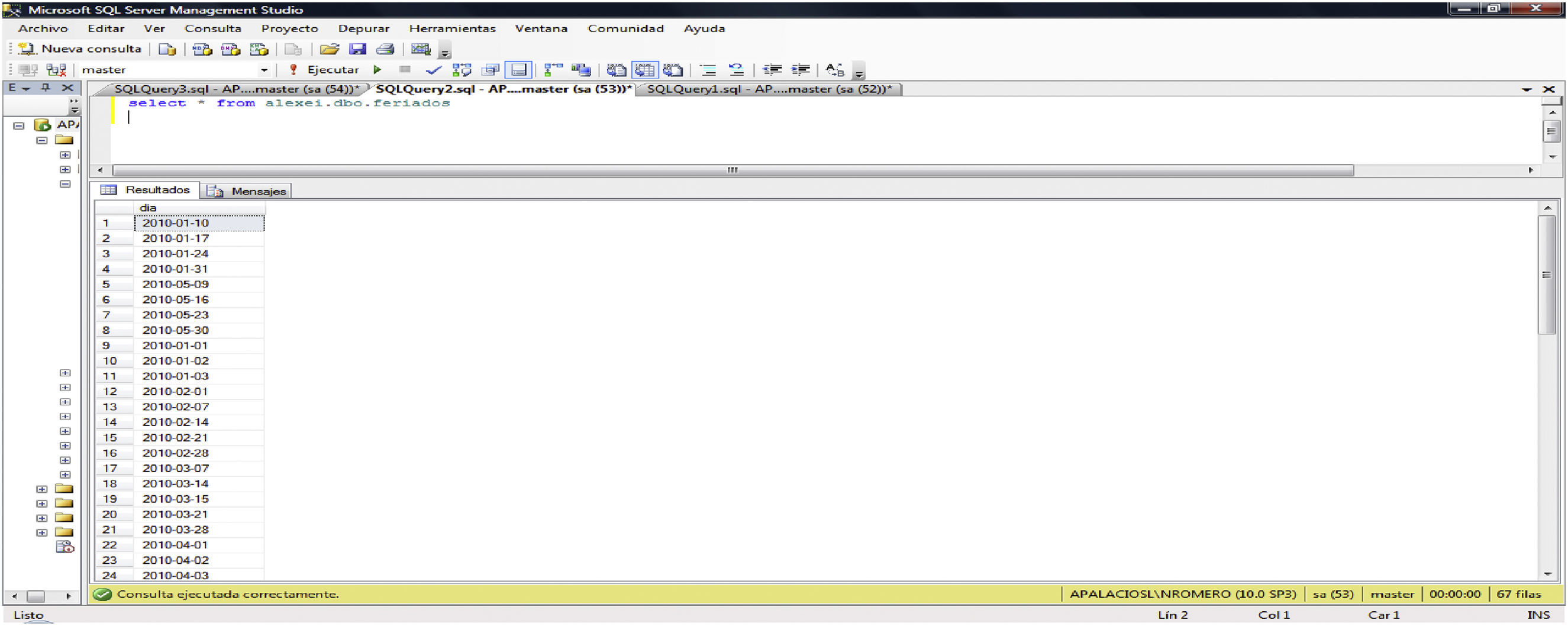
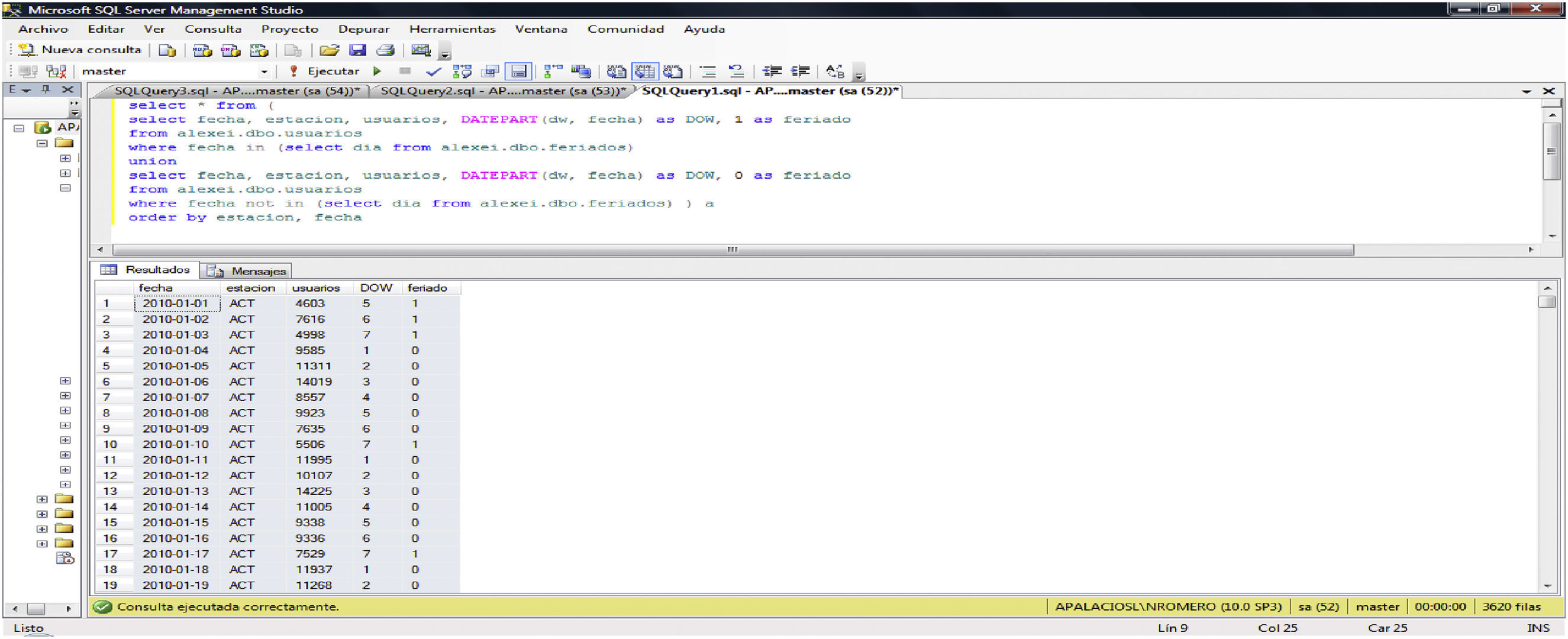
El archivo obtenido (db_llena) posee propiedades de una base de datos, con relaciones entre sus variables y permite la búsqueda de caracterizaciones a partir de elementos comunes. Su construcción se llevó a cabo mediante operaciones en un manejador de bases de datos, SQL. Para transformar el archivo inicial, la construcción de la tabla alexei.dbo.usuarios tuvo que realizarse ejecutando varias líneas de código de programación, como las siguientes:
| select * from (select fecha, estacion, usuarios, DATEPART(dw, fecha) as DOW, 1 asferiadofromalexei.dbo.usuarioswhere fecha in (selectdiafromalexei.dbo.feriados)unionselect fecha, estacion, usuarios, DATEPART(dw, fecha) as DOW, 0 as feriadofromalexei.dbo.usuarioswherefecha not in (select dia from alexei.dbo.feriados)) aorderbyestacion, fecha |
El código de búsqueda o query anterior hace uso de otra tabla que contiene los días feriados (tabla 2). En la tabla 3 se muestra la modificación de registros, pasando de números asignados a una lista por fechas hasta obtener una relación entre fechas, estaciones y número de usuarios por día. Se obtienen los resultados que se copian y pegan en el archivo Acumulados.xls y se muestran en la tabla 2 (Gómez-Eguiarte, 2013).
La tabla 3 muestra la forma de construcción de la tabla alexei.dbo.usuarios.
De esta manera se obtiene un archivo con la forma de una base de datos compatible con software estadístico, hojas de cálculo, SPSS, el lenguaje R y otros.
La conjunción de datos de tipo diverso da como resultado el archivo Acumulados.xls, que representa el total de la información requerida para obtener los datos relevantes a la investigación.
El análisis de datos exploratorioInicialmente se obtuvieron medidas y gráficos, auxiliándose del Exploratory Data Analysis (EDA) (Beat, Chambers, Cleveland y Tukey, 1983), obteniéndose conclusiones preliminares de la demanda de usuarios. En adelante se designa como variable del tipo aleatorio (VA) a cada estación: con la letra X, subíndice i=1, 2, …, 10 y la variable Y (T) representa el comportamiento de la Línea A en total, (ver tabla 4).
Codificación de las estaciones de Línea A
| Pantitlán | AgrícolaOriental | Canal deSan Juan | Tepalcates | Guelatao | Peñón Viejo | Acatitla | Sta. Marta | Los Reyes | La Paz |
|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 |
Fuente: Gómez-Eguiarte (2013).
Se analizaron las 10 estaciones de la Línea A mediante técnicas gráficas y estadísticos simples, revelando en las variables diversas características de la demanda de pasajeros. A continuación se muestran las distintas gráficas y tablas estadísticas utilizadas en el análisis de las VA en cuestión. En este artículo solamente se dan los resultados de X1 y X8: Pantitlán y Santa Marta.
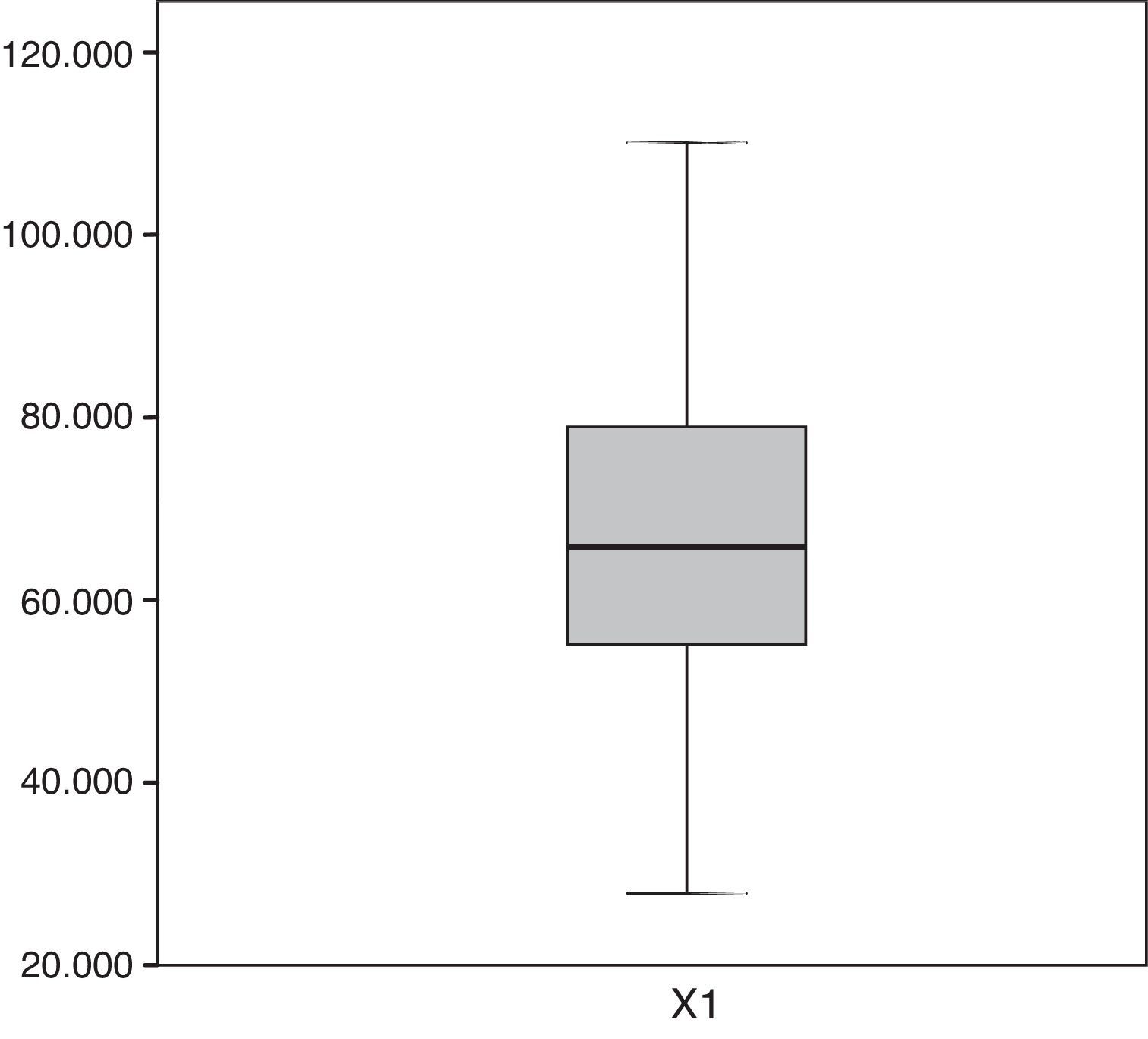
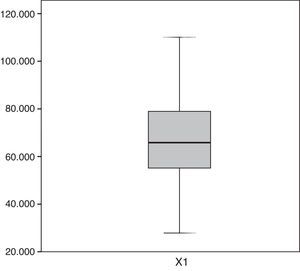
Para X1 (ver fig. 1) la distribución de los datos se encuentra sesgada a la derecha y sin datos fuera de rango, lo que implica una regularidad en la cantidad de pasajeros que ingresan a la estación X1, Pantitlán (tabla 5).
Diagrama de «caja» de la VA X1.
Fuente: Gómez-Eguiarte (2013).
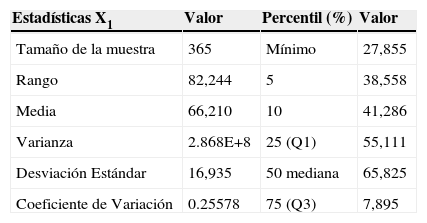
Datos estadísticos de la VA X1
| Estadísticas X1 | Valor | Percentil (%) | Valor |
|---|---|---|---|
| Tamaño de la muestra | 365 | Mínimo | 27,855 |
| Rango | 82,244 | 5 | 38,558 |
| Media | 66,210 | 10 | 41,286 |
| Varianza | 2.868E+8 | 25 (Q1) | 55,111 |
| Desviación Estándar | 16,935 | 50 mediana | 65,825 |
| Coeficiente de Variación | 0.25578 | 75 (Q3) | 7,895 |
Fuente: Gómez-Eguiarte (2013).
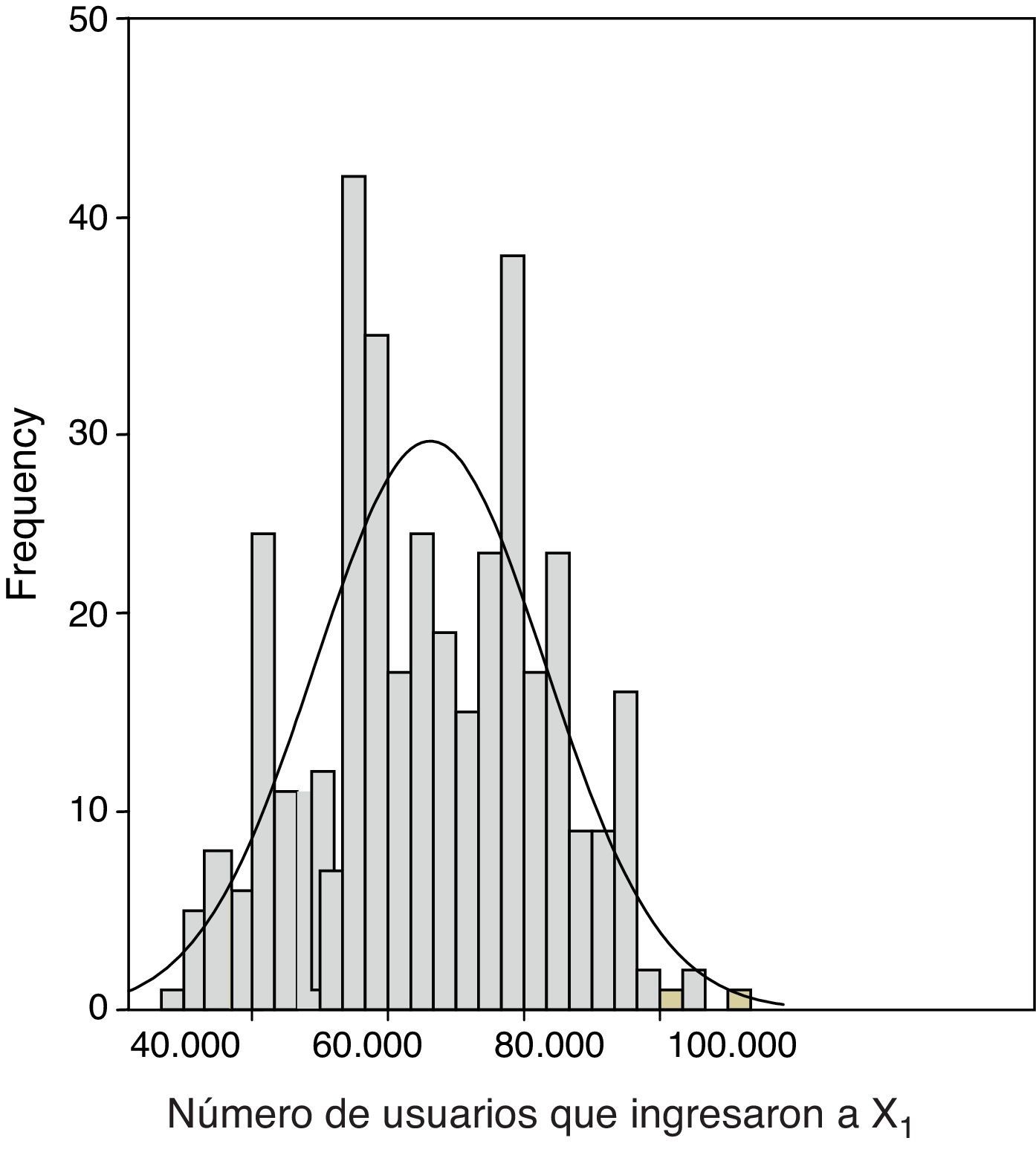
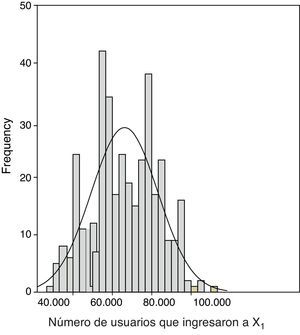
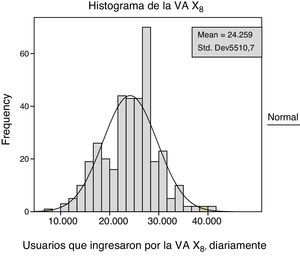
Se observó un flujo máximo de 110,000 usuarios aproximadamente y un mínimo de 30,000. Los datos estadísticos de la VA X1 muestran la diferencia entre el valor de la media y la mediana, revelando un sesgo negativo en el flujo de X1 e implicando una distribución asimétrica. En la figura 2, el histograma muestra la distribución comparándola con una distribución normal. Puede observarse que existen valores multimodales y la gráfica del histograma confirma la asimetría en los datos. Utilizando el paquete SPSS se ajusta una distribución normal que no concuerda con el flujo de pasajeros en esa estación.
Histograma de la VA X1
Fuente: Gómez-Eguiarte (2013).
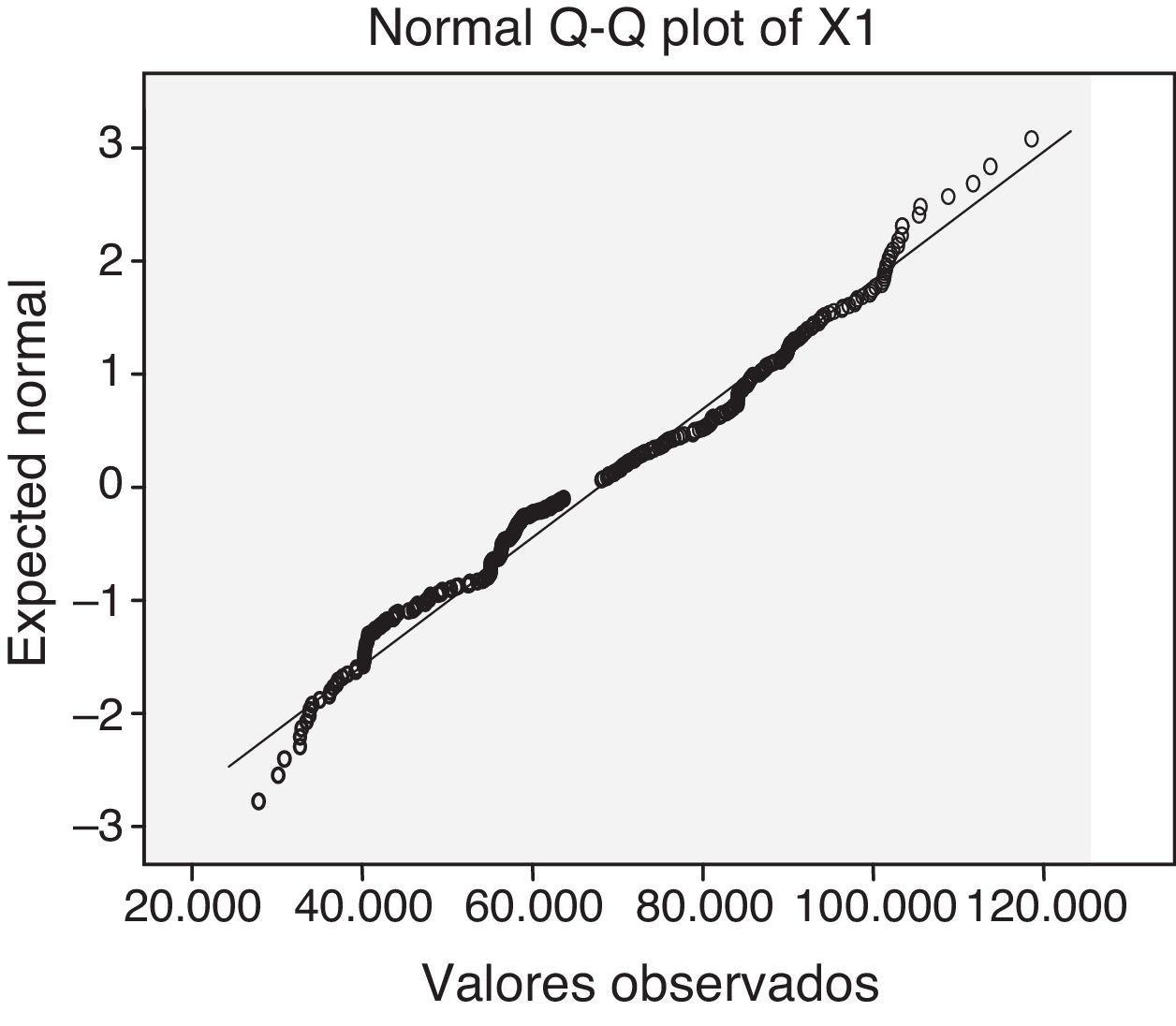
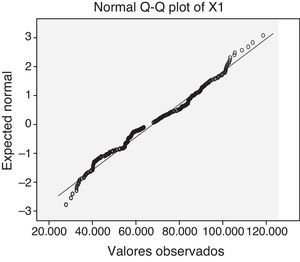
La figura 3, diagrama cuantil-cuantil, compara el comportamiento de pasajeros en la variable X1 con una distribución normal, confirmando un comportamiento poco asintótico con esa distribución y para valores esperados teóricos y flujo empírico de pasajeros entre 95,000 y 120,000 individuos.
Diagrama cuantil-cuantil de la VA X1
Fuente: Gómez-Eguiarte (2013).
La distribución empírica del flujo de pasajeros en la VA X1 Pantitlán no se ajusta al modelo normal propuesto (μ=66,209.3; σ2=2.868 E8) asignado por el paquete estadístico, lo cual implica buscar distribuciones alternativas.
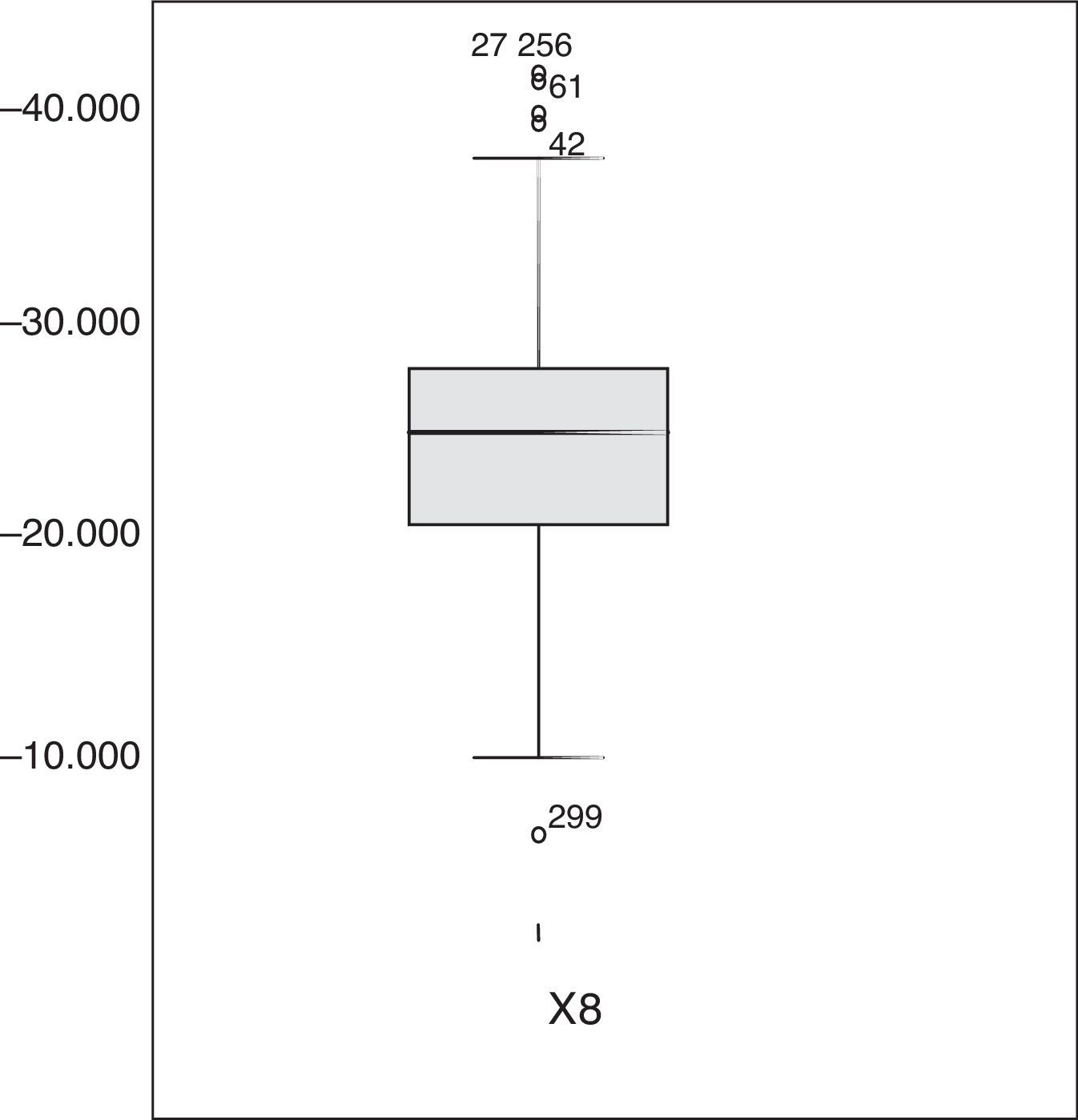
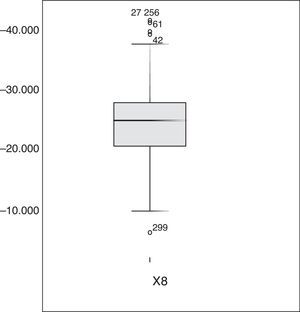
En la figura 4, en X8 se observaron valores atípicos, por encima del máximo (40,000), ocurridos en las observaciones 27, 42, 61 y 256. Una indagación posterior mostró que estos valores corresponden a días de gran flujo laboral, lunes o miércoles. Similarmente ocurre en la observación del día 299, por debajo del flujo mínimo, jueves (tabla 6).
Diagrama de «caja» de la VA X8
Fuente: Gómez-Eguiarte (2013).
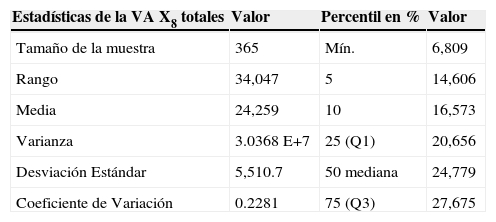
Datos estadísticos de la VA X8
| Estadísticas de la VA X8 totales | Valor | Percentil en % | Valor |
|---|---|---|---|
| Tamaño de la muestra | 365 | Mín. | 6,809 |
| Rango | 34,047 | 5 | 14,606 |
| Media | 24,259 | 10 | 16,573 |
| Varianza | 3.0368 E+7 | 25 (Q1) | 20,656 |
| Desviación Estándar | 5,510.7 | 50 mediana | 24,779 |
| Coeficiente de Variación | 0.2281 | 75 (Q3) | 27,675 |
Fuente: Gómez-Eguiarte (2013).
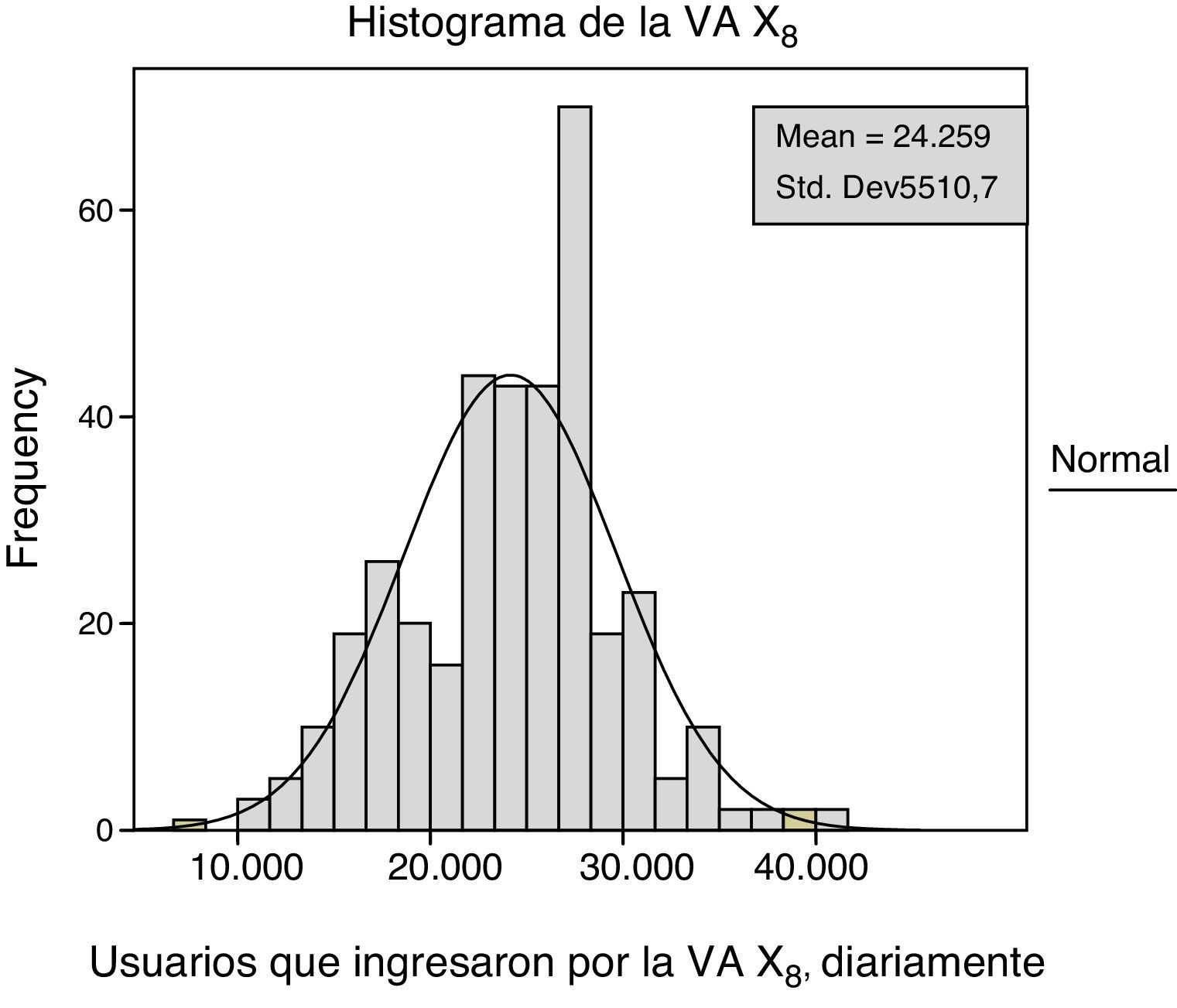
La tabla 6 muestra las estadísticas de la VA X8. La tabla revela poca diferencia entre la media y la mediana; el coeficiente de variación es pequeño comparado con las otras variables aleatorias lo que habla de una regularidad estadística en la VA X8. La distribución está ligeramente sesgada negativamente y aplanada. En el histograma de la VA X8, se notan elementos atípicos que sugieren días donde la afluencia es mayor con respecto a la demanda de pasajeros común. Por tal motivo, sería conveniente separar los registros en días específicos, que permitan diferenciar días de gran afluencia con aquellos de baja afluencia (ver fig. 5).
Histograma de la VA X8
Fuente: Gómez-Eguiarte (2013).
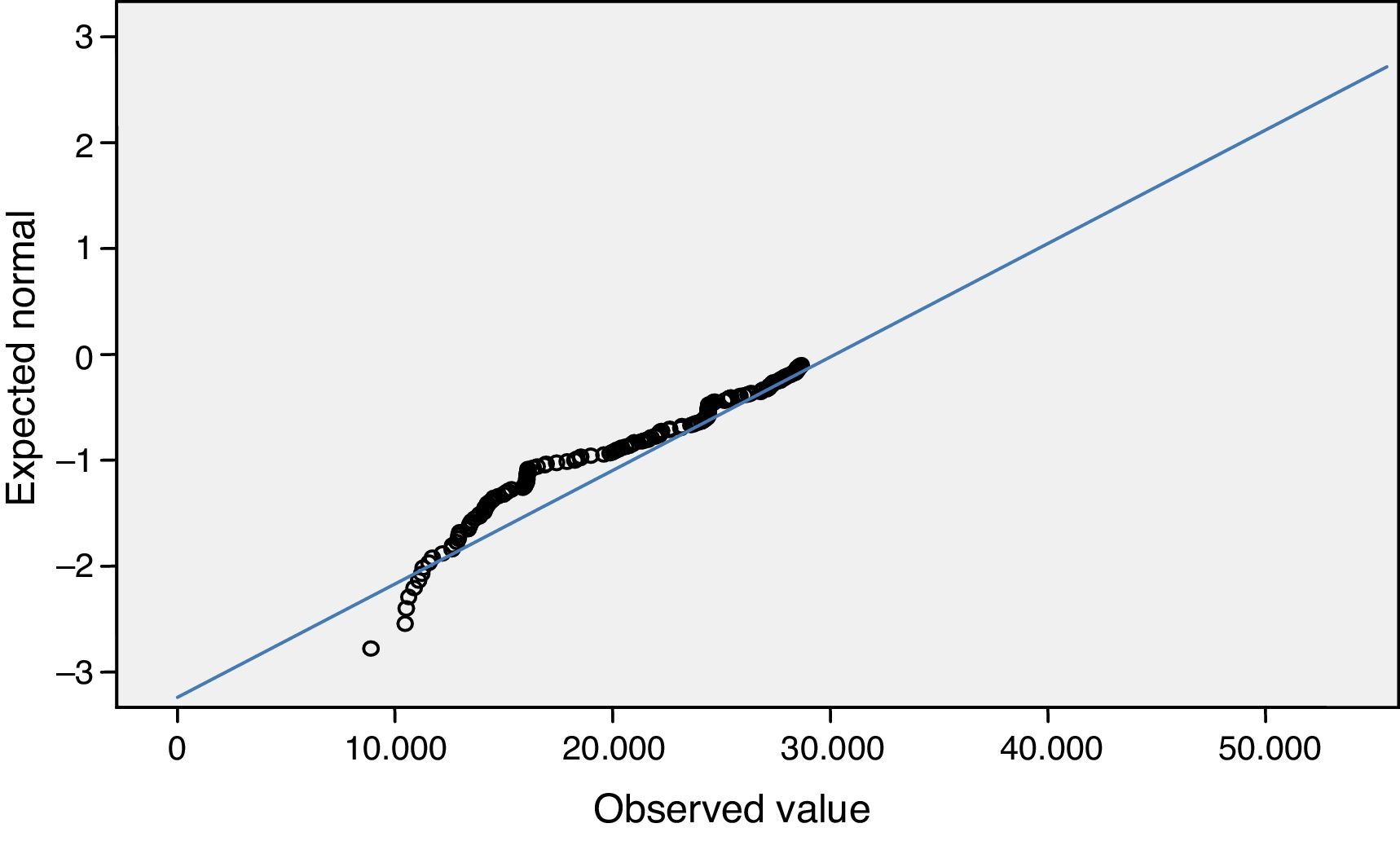
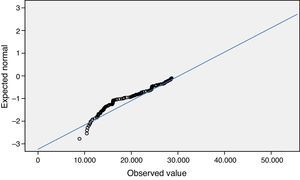
En el diagrama cuantil-cuantil de la figura 6, se observa que la distribución normal está lejos de ajustar adecuadamente al flujo de pasajeros en la estación X8 Santa Marta. La gráfica cuantil-cuantil de X8 muestra una dispersión de datos empíricos que se aleja del modelo normal en valores extremos al flujo de personas, los valores (10,000; 40,000). Los análisis gráficos han mostrado que es necesario buscar modelos alternativos al normal.
Gráfica cuantil-cuantil de la VA X8
Fuente: Gómez-Eguiarte (2013).
El análisis EDA (Hoaglin y Velleman, 1981) mostró que los pasajeros fluyen a las estaciones de la Línea A en distribuciones multimodales, con valores extremos que muestran «oleadas» de personas. Los diagramas de caja y bigotes señalaron la diferencia entre la afluencia media en las estaciones Xi y su mediana, e indican un flujo de personas sesgado, indicativo de «colas pesadas» que inclinan la distribución. Del examen en los gráficos cuantil-cuantil se deduce que el flujo de pasajeros se explica mediante distribuciones continuas a pesar de que los datos provienen de un conteo, el cual se realiza en una escala de tiempo (continua). Así: la probabilidad de un evento discreto será cero (ejemplo: probabilidad de que accedan exactamente 20,000 personas cierto día, en la estación X1).
Estos hallazgos descartan utilizar una distribución simétrica, continua y con soporte en los reales, como la normal, en la modelación del flujo de pasajeros. Por tanto, el estudio se limitó a funciones de distribución continuas con soporte en los reales positivos, discretizando los resultados mediante truncamiento. La forma de los histogramas y los valores extremos mostrados en los diagramas de «caja» —en días específicos— sugiere hacer una «reclasificación» del tipo de datos. Se decidió clasificar en 3 tipos los días para su análisis: días laborales, lunes a viernes, excluyendo días «feriados o puentes» dados como festividades del calendario laboral. Los «puentes» incluyen un día laboral adyacente al fin de semana; se decidió clasificar en un mismo tipo los días domingo-festivos.
Faltando por definir una categoría excluyente de las otras dos, se optó por los días sábado, y se conformó la tercera categoría de clasificación: laborales, sábados y domingos-festivos (Lsd). La agregación del comportamiento general sin discriminar el tipo de día se designó como totales.
La tabla 7 (afluencia 2010) muestra el flujo de pasajeros que circuló en cada una de las variables aleatorias en cuestión durante ese año. El orden concuerda con el volumen de usuarios registrado por las cifras de operación del mismo año (Sistema de Transporte Colectivo, Cifras de Operación 2010) ratificando cuáles son las estaciones más concurridas y de mayor importancia para el estudio, marcadas por letras negritas.
Afluencia 2010
| Rango | Estación | Usuarios del año (2010) |
|---|---|---|
| 1 | X1(T) | 24,166,626 |
| 2 | X10(T) | 9,833,887 |
| 3 | X8(T) | 8,817,978 |
| 4 | X9(T) | 6,965,835 |
| 5 | X5(T) | 5,834,860 |
| 6 | X4(T) | 5,099,594 |
| 7 | X7(T) | 4,995,321 |
| 8 | X3(T) | 3,868,356 |
| 9 | X6(T) | 3,510,557 |
| 10 | X2(T) | 3,276,542 |
| Y(T) | Total | 76,369,556 |
Fuente: Gómez-Eguiarte (2013).
Estaciones más concurridas, en negrita las más importantes para el estudio.
Un análisis posterior requirió ajustar una función de distribución teórica a la distribución empírica de cada una de las VA. La distribución empírica se obtuvo en cada una de las VA y está asociada inequívocamente a cada conjunto de datos. La función de distribución empírica se define como:
Donde IA es la función indicador del evento A, es igual a uno cuando el evento A ocurre y cero en cualquier otro caso.La función de distribución es una función no decreciente y continua por la derecha con valores en el intervalo [0,1], donde n es el número de elementos en la muestra. Se tiene que para cualquier t∈ℝ puede aplicarse la ley de los grandes números a la secuencia I{Xi≤t}; para t=1, 2,…, n y se puede afirmar que:
La ecuación anterior es una versión del teorema de Glivenko-Cantelli. El teorema indica que la función de distribución de probabilidad común a las variables de una sucesión muestral converge de manera casi segura a una función de distribución teórica (Khale, 2006). Con esto, se establece que FX(t) es una función teórica, que puede estimarse en términos de los datos utilizando la función de distribución empírica. De manera que mientras la función de distribución suministra como función de t la probabilidad de que cada una de las VA Xisea menor o igual a un número t, la función de distribución empírica —calculada mediante los datos— proporciona la frecuencia relativa con la que los valores observados son menores o iguales a cierta cantidad t. Debe notarse que Fˆnt es un estimador insesgado para FX(t).
El proceso de ajuste de la función de distribución empírica hasta la obtención de la distribución teórica y sus parámetros se llevó a cabo por el método de máxima verosimilitud y requirió de software especializado. Los modelos obtenidos por máxima verosimilitud fueron validados mediante pruebas de bondad de ajuste: la de Kolmogorov-Smirnov, la de Anderson-Darling y la Ji-cuadrada. Tras realizar el análisis de la demanda de pasajeros en las estaciones de la Línea A, el resultado es un conjunto de modelos teóricos de densidad probabilística.
Los resultados en la Línea A son modelos que pertenecen a la familia de la distribución general de valor extremo (DGVE) y Weibull, modelos gamma, log-normal y log-logísticos con diversos parámetros, entre otros. Particularmente, los resultados correspondientes a las estaciones (VA) Pantitlán flujo diario sin particionar por día (X1-Total) y estación Santa Marta en flujo diario sin tomar en cuenta día laboral, festivo o sábado (X8-Total) son:
Un modelo DGVE con parámetros k=−0.29706; σ=17236.0; μ=60287.0 para X1. Y un modelo de la distribución Weibull —perteneciente a la familia de distribuciones de valor extremo— con parámetros: α=4.9905; β=26270.0 correspondiente a la VA X8.
La DGVE es una familia de distribuciones de probabilidad continua desarrollada dentro de la teoría de valor extremo para combinar las familias de distribuciones de Gumbel, Fréchet y Weibull, también conocidas como distribuciones de valor extremo tipo i, ii y iii. Por el teorema del valor extremo, la DGVE es la única distribución límite posible al máximo de una secuencia de variables aleatorias independientes e idénticamente distribuidas normalizadas de forma apropiada. Teniendo en cuenta que no necesariamente existe una distribución límite, se requieren condiciones de regularidad en el extremo (cola) de la distribución. A pesar de ello, la DGVE se usa con frecuencia como una aproximación para modelar el máximo de una larga secuencia (finita) de variables aleatorias.
Las funciones resultantes señalan estrechamente el comportamiento de la demanda de pasajeros. Esta corresponde al comportamiento de la VA propuesta (estación de la Línea A). Resultó útil particionar los datos de la demanda de pasajeros en 4 clases mutuamente excluyentes: demanda total, por días laborales, demanda en sábados y demanda en domingos y días festivos. Se analizaron las 11 variables aleatorias que corresponden a cada una de las 3 categorías de la partición. Debido a la extensa cantidad de objetos analizados, en este artículo se incluyeron 2 VA de afluencia demostrativa y significación estadística.
ResultadosLos modelos encontrados concuerdan con el tipo de patrones propuestos por el análisis EDA inicial, modelos continuos con soporte en los reales positivos y cuya cota inferior es el cero. La tabla 8 muestra los modelos asignados a las estaciones Pantitlán y Santa Marta Total, es decir sin particionar los días en la muestra.
Modelos asignados a Pantitlán y Santa Marta-Total
| Variable Aleatoria | Función de distribución | Parámetros |
|---|---|---|
| X1 total | General valor extremo | k=−0.29706 σ=17,236.0 μ=60,287.0 |
| X8 total | Weibull | α=4.9905 β=26,270.0 |
Fuente: Gómez-Eguiarte (2013).
El flujo observado de pasajeros durante el año 2010, en la Línea A, se ajustó a modelos probabilísticos teóricos, funciones de densidad, mediante el método de máxima verosimilitud.
La calidad del ajuste obtenido por las densidades de probabilidad propuestas se verificó mediante pruebas de bondad de ajuste: la de Kolmogorov-Smirnov, Anderson-Darling y, ocasionalmente, Ji-cuadrada, validando el ajuste de cada distribución con los datos empíricos. Los resultados obtenidos constituyen un estudio original. El artículo pretende difundir estos alcances, que han sido desarrollados en función de las necesidades y oportunidades encontradas durante la investigación y que no siguen un camino ya trazado anteriormente, proponiendo una metodología apropiada al problema.
Los modelos de funciones de densidad cumplen el principio de independencia estocástica debido a que el flujo de pasajeros en una estación cualquiera (VA) no afecta la demanda de otra. Los modelos obtenidos mediante el ajuste por funciones de distribución no presentan espectros de regresión lineal con datos de variables autocorrelacionadas, son funciones de densidad de probabilidad continuas, con soporte en los reales positivos.
Los resultados alcanzados confirman que es posible ajustar modelos probabilísticos a partir de los datos empíricos que proporcionan las «lecturas» en torniquetes. Tras asignar una distribución de probabilidad a la demanda de pasajeros, los modelos permitirán calcular el comportamiento correspondiente a la Línea A y a cada estación. Los patrones obtenidos develan una forma diferente de modelar la demanda de pasajeros en las estaciones de trenes y otros transportes públicos a partir del flujo descrito por los instrumentos de acceso a las estaciones, teniendo como ventaja el análisis en el lugar donde se origina la demanda, que indica el comportamiento aleatorio de estas oleadas de transeúntes en movimiento.
A reserva de realizar un cálculo económico preciso, se estima que es un procedimiento económicamente viable sobre las encuestas para realizar ajuste por MCO o los estudios poblacionales en la vecindad de las estaciones y sustancialmente más económico que implementar tarjetas inteligentes para describir la ruta que siguen los pasajeros y calcular la demanda de usuarios.
Los resultados aquí mostrados proyectan una ecuación que contiene el valor de los parámetros de localización, dispersión y forma de una función densidad de probabilidad. Las unidades de medición corresponden directamente al número de pasajeros circulantes por las estaciones del Sistema y el tiempo hasta obtener el resultado depende de la disponibilidad con que se obtengan las lecturas en torniquetes, lo cual representa un intervalo menor que el del desarrollo de cuestionarios, calibración de preguntas, aplicación de la encuesta, análisis de resultados, obtención y validación del modelo.
En la Línea A las observaciones se realizaron in situ, excluyendo realizar encuestas y evitando interrelacionar las modalidades de transporte utilizadas en la ZMVM para acceder al tren ligero. Las distribuciones continuas de probabilidad pueden ser vistas como herramientas para tratar con la incertidumbre de eventos aleatorios y son útiles para llevar a cabo cálculos específicos sobre modelos válidos que muestran estos procesos. De no utilizarse el modelo adecuado, se pueden generar errores que consumen recursos y, en ese caso, se pone en riesgo la seguridad de los usuarios de la Línea A. Los modelos aquí obtenidos y validados por pruebas de bondad pueden ayudar a:
- •
Pronosticar el número de viajes esperado por día de la semana.
- •
Planificar el suministro y la utilización de refacciones e insumos que permitan llevar a cabo el mantenimiento y las operaciones de servicio al usuario, conforme a la demanda de pasajeros.
- •
Proveer autoridad para realizar ajustes a las planillas de conducción conforme a la demanda señalada por cada modelo.
- •
Auxiliar en la asignación de tiempos para mantenimiento a material rodante e instalaciones fijas.
Conociendo un modelo de la demanda de usuarios, puede optimizarse la cantidad de recursos para que el Sistema brinde un mejor servicio. Optimizando sus recursos, el Sistema puede avocarse a mejorar otros aspectos de operación detenidos por falta de planeación, financiamiento o escasez de información. Los beneficiarios de este conocimiento son el Sistema y el usuario habitual de Línea A, al permitir el traslado por la ciudad de manera eficiente.
A pesar del rechazo sugerido por alguna de las pruebas de bondad, las distribuciones propuestas se consideran modelos útiles debido a la solidez del algoritmo de ajuste; los modelos expuestos son apropiados para los datos empíricos, sujetos de tomarse en cuenta debido a la escasez de recursos con la que fueron obtenidos. Este trabajo presentó una metodología para llevar a cabo el ajuste de modelos de densidad con datos empíricos del Sistema.
Con datos actualizados, pueden repetirse los procedimientos anteriores y obtener modelos descriptivos y predictivos de la demanda diaria de pasajeros en otras líneas.
Se confirma la validez de particionar el flujo total de pasajeros en clases mutuamente excluyentes al realizar el análisis de esa demanda. Tal afirmación se sostiene al confirmar que los mejores modelos obtenidos corresponden a las clases: laborales, domingos y sábados, respectivamente. El llamado flujo total de la Línea A, que reúne los datos sin discriminarlos por día tipo, resultó con ajustes pobres que caen en la región de rechazo de las pruebas de bondad. Mejores ajustes pueden obtenerse aumentando el tamaño de la muestra en diferentes años: el tamaño muestral presente es insuficiente, especialmente para la categoría sábados.
Los modelos así obtenidos están sujetos a validación a condición de proveer nuevas «lecturas». Estos análisis son perfectibles. Tras verificar la solidez de los modelos encontrados, se puede avanzar en su utilización para realizar simulaciones y cálculos de la demanda de pasajeros en años subsecuentes.
La revisión por pares es responsabilidad de la Universidad Nacional Autónoma de México.