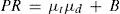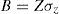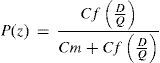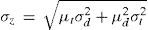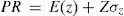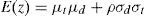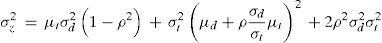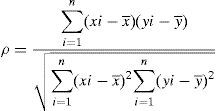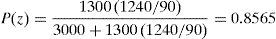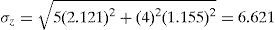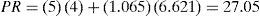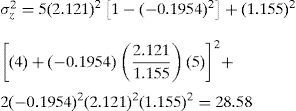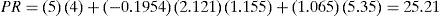Este trabajo presenta un estudio comparativo del cálculo del punto de reorden cuando la demanda diaria de artículos es independiente del tiempo de entrega o cuando ambas variables están correlacionadas.
El estudio se hace para un artículo con demanda y tiempo de entrega normal.
Para el caso ilustrativo no ha habido diferencia significativa del punto de reorden calculado con ambos métodos, lo cual se debe a que la correlación entre ambas variables ha sido baja.
Si el coeficiente de correlación toma valores altos negativos o positivos, entonces las diferencias del punto de reorden calculado con los 2 métodos son significativas. Estas diferencias también dependen del nivel de servicio manejado. Si el coeficiente de correlación es positivo, la metodología tradicional subestima el punto de reorden, y lo sobreestima en caso de que la correlación entre la demanda y el tiempo de entrega sea negativa.
Por esto se recomienda que antes de estimar el punto de reorden, se calcule el coeficiente de correlación entre ambas variables y se apliquen las fórmulas de Wang en caso de que el coeficiente resulte entre −0.5 y −1 o entre 0.5 y 1.
Si el nivel de servicio se incrementa, el punto de reorden también lo hace, requiriéndose un inventario mayor.
This paper presents a comparative study of calculating the reorder point when the daily demand for goods is independent of lead time or when both variables are correlated.
The study is done for an article with normal demand and lead time.
For the illustrative case there has not been significant difference of reorder point calculated with both methods, which is due to the low correlation between the 2 variables.
If correlation coefficient takes negative or positive high values, then the differences in calculated reorder point with the two methods are significant. These differences also depend on the service level managed. If the correlation coefficient is positive, the traditional methodology underestimates the reorder point and it overestimates if the correlation between demand and delivery time is negative.
Therefore it is recommended that before estimating the reorder point, to calculate the correlation coefficient between the 2 variables and apply the Wang equations if the coefficient falls between −0.5 and −1 or between 0.5 and 1.
If the service level increases, the reorder point so does, requiring a larger inventory.
Los modelos de inventarios han sido estudiados de manera intensiva durante el último siglo, debido a que son importantes para un manejo adecuado de los bienes que se tienen en existencia, que muchas veces constituyen una partida muy importante en los estados financieros de las organizaciones, razón por la cual deben ser bien administrados para que cumplan con su función sin incurrir en costos excesivos.
La administración del inventario requiere tomar 3 decisiones básicas (Silver, 2008): 1)¿cada cuándo debe revisarse el sistema del inventario?; 2)¿cuánto debe pedirse al momento de hacer un nuevo pedido?, y 3)¿cuándo es el momento de hacer el nuevo pedido?
La mayoría de los modelos buscan varios objetivos, algunos de los cuales podrían contraponerse entre sí. Entre los objetivos más usuales se cuentan (Silver, 2008):
- •
Minimización de los costos incurridos en el manejo del inventario.
- •
Maximización de los beneficios económicos, incluyendo los ahorros por descuentos.
- •
Maximización de la tasa interna de retorno de la inversión en inventarios.
- •
Determinar una solución factible para la administración del inventario.
- •
Asegurar la flexibilidad en el manejo de un futuro incierto.
De estos, el más común es minimizar los costos, y es el que buscan la mayoría de los modelos de inventarios.
En la administración de inventarios es una práctica común que ante la variación de la demanda y la demora en la entrega de un nuevo pedido de parte del proveedor, las organizaciones definan un stock de seguridad que les permita atender la demanda y no llegar a la penosa situación de tener faltantes de inventario que signifiquen pérdida de ventas y mala imagen ante los consumidores, lo cual en esta época es esencial ante la enorme competencia que se presenta en todos los sectores comerciales y de manufactura (Taha, 2004).
Chikan (2007) afirma que hay un cambio de paradigma respecto al manejo del inventario que debe ponerse en práctica por las organizaciones actuales, de modo que no les represente una desventaja competitiva. El paradigma anterior se basaba en 3 pilares, que eran: el manejo de los inventarios era independiente de otras cuestiones administrativas; su función principal era la de ser un amortiguador en caso de una demanda incierta, y la medida de desempeño se basaba en los costos de mantener el inventario, hacer nuevos pedidos y el de faltantes. El nuevo paradigma propuesto es que ahora los inventarios deben ser parte integral de la cadena de valor y en estrecha relación con otras funciones de la organización, convirtiéndose de esta manera en una herramienta estratégica que logre el beneficio económico y la satisfacción del cliente, y las medidas de su desempeño deberán basarse en su aportación para encontrar mejores soluciones para el consumidor que las que le brindan los competidores (Chikan, 2007).
Para las nuevas métricas del manejo del inventario, Barry (2007) sugiere las siguientes: las tasas inicial y final de órdenes atendidas; las tasas de artículos devueltos y cancelaciones; la rotación del inventario, y el margen de retorno de la inversión.
Uno de los modelos tradicionales para calcular el inventario es el del punto de renovación del pedido, o punto de reorden (PR), que consiste en definir su valor, expresado en unidades de producto, con el cual se hace un nuevo pedido al proveedor una vez que las existencias disminuyen hasta dicho nivel (Izar-Landeta, 2012).
Prácticamente todos los estudios de inventarios que calculan el PR lo hacen asumiendo que la demanda de artículos y el tiempo de entrega de un nuevo pedido de parte del proveedor son independientes.
Este estudio hace un comparativo del cálculo del PR de un producto con demanda y tiempo de entrega con distribución normal de probabilidad, cuando ambas variables no están correlacionadas y cuando lo están. En caso de haber correlación, se aplican las fórmulas desarrolladas por Wang, Zinn y Croxton (2010), en las cuales se incluye el coeficiente de correlación entre el tiempo de entrega y la demanda de artículos.
Luego se analiza cómo afecta a los resultados la variación del coeficiente de correlación, utilizando valores en todo su rango posible, de −1 a +1.Fundamentos teóricos
Uno de los modelos más utilizados para la correcta administración del inventario es el del punto de reorden (PR), que se fundamenta en calcular su valor con base en la demanda de artículos, el tiempo de entrega del proveedor y el stock de seguridad, que es una cantidad adicional que se agrega para protegerse contra eventuales faltantes que pudieran aparecer en caso de que la demanda del tiempo de entrega se incremente.
Sin embargo, todos los modelos conocidos de inventarios asumen que el tiempo de entrega y la demanda son independientes, esto es, que no hay correlación entre ambas variables, lo cual pudiera estar alejado de la realidad, especialmente en algunos casos como el de envíos anticipados de los proveedores en casos de baja demanda procurando mantener sus ventas, en cuyo caso la correlación entre las 2 variables sería positiva; o en caso de que la demanda se incremente, podría pedirse al proveedor que haga entregas de manera más rápida, o en el caso de que la demanda fuera a la baja y el proveedor hiciera entregas más espaciadas, siendo en ambos casos la correlación negativa.
Para artículos que se comportan conforme a la distribución normal de probabilidad, Eppen y Martin (1988) encuentran errores en el cálculo del PR, que pueden corregirse mediante el algoritmo que proponen en este estudio, el cual aplica en caso de que los parámetros de la demanda y tiempo de entrega sean conocidos o desconocidos. Como contraparte, Tyworth y O’Neill (1997) aportan evidencia de que la distribución normal es robusta y confiable para estimar el PR.
Song (1994) encuentra que si el tiempo de entrega aumenta, esto ocasiona un incremento de la demanda del tiempo de entrega y, por consiguiente, un mayor stock de seguridad, aunque no necesariamente un costo óptimo del inventario más elevado. Si el tiempo de entrega tiene más variabilidad (mayor desviación estándar), lleva a una mayor demanda del tiempo de entrega y un mayor costo óptimo. El efecto de la variabilidad se ve afectado por la estructura de costos del inventario, concretamente el de faltantes y de mantenimiento del inventario.
Chopra, Reinhardt y Dada (2004) señalan que 2 medidas para disminuir el inventario sin que se afecte el nivel de servicio son la reducción del tiempo de entrega de los proveedores, y la disminución de la variabilidad de este tiempo de entrega. Si la demanda del tiempo de entrega es normal, estas acciones reducen el inventario si los niveles de servicio son mayores al 50% y es de mayor impacto la variabilidad del tiempo de entrega. Comentan la existencia de un umbral superior al 50% del nivel de servicio, abajo del cual el PR se incrementa ante una disminución de la variabilidad del tiempo de entrega.
Ray (1981) ha desarrollado un método para calcular el PR cuando las demandas están correlacionadas y el tiempo de entrega es aleatorio. Su procedimiento consiste en determinar los 4 momentos de la demanda del tiempo de entrega, los que luego utiliza para calcular los percentiles de la distribución, para finalmente estimar el PR para un nivel de servicio requerido.
Fotopoulos y Wang (1988) han propuesto una metodología para determinar el stock de seguridad cuando las demandas están autocorrelacionadas y los tiempos de entrega siguen una distribución arbitraria. Luego analizan los efectos de violar los supuestos en los que se basan, tales como independencia y normalidad de la demanda y la normalidad del tiempo de entrega, encontrando que el efecto más grande se da cuando se ignora la autocorrelación de la demanda.
Charnes, Marmorstein y Zinn (1995) han estudiado un sistema de revisión periódica con tiempos de entrega determinísticos y una demanda estocástica de covarianza estacional. Desarrollaron un método para obtener el stock de seguridad y obtener una probabilidad exacta de faltantes cuando se conoce la función de autocovarianza de la demanda gaussiana. El modelo no requiere hacer ajustes de los datos a los parámetros de series de tiempos. En este estudio han obtenido las tasas de faltantes para diferentes valores de demandas autocorrelacionadas, incluyendo el caso de ignorar la autocorrelación.
Inderfurth (1995) ha estudiado un sistema de inventarios multietapa para determinar el stock de seguridad, encontrando que ignorar la correlación de la demanda de los artículos lleva a desviaciones significativas del stock óptimo.
Como puede verse, ningún estudio ha calculado PR tomando en cuenta la correlación de la demanda con el tiempo de entrega, que es el objetivo de este trabajo.Metodología
Para calcular PR bajo una demanda y tiempo de entrega normal, sin que haya correlación entre estas variables, se aplica la ecuación (1):
donde: PR=punto de reorden, unidades; μt=tiempo de entrega promedio, días; μd=demanda promedio, unidades/día; B=stock de seguridad, unidades.
El stock de seguridad se obtiene con la siguiente ecuación:
donde: Z=número de desviaciones estandarizadas de la curva normal que corresponde a un área igual al nivel de servicio P(z); σz=desviación estándar de la demanda del tiempo de entrega, unidades.
El nivel de servicio P(z) se calcula con la siguiente ecuación:
donde: Cf=costo de cada faltante, $/faltante, Cm=costo anual de mantenimiento, $/unidad; D=demanda de artículos, unidades/año, Q=cantidad de pedido, unidades/pedido.
La desviación estándar de la demanda del tiempo de entrega para una distribución normal se calcula con la ecuación (4):
donde: σd=desviación estándar de la demanda, unidades/día, σt=desviación estándar del tiempo de entrega, días.Si se tienen datos de la demanda diaria y el tiempo de entrega, es posible calcular el PR para un artículo en inventario.
Si la demanda y el tiempo de entrega están correlacionados, Wang et al. (2010) proponen la siguiente ecuación para obtener PR para un artículo con demanda y tiempo de entrega normal:
siendo E(z) el valor esperado de la demanda del tiempo de entrega, que viene dado por la ecuación (6):donde ρ es el coeficiente de correlación de la demanda y el tiempo de entrega.La varianza de la demanda del tiempo de entrega se estima con la ecuación (7):
con la cual se obtiene la desviación estándar para aplicarla en la ecuación (5). Los otros términos de la ecuación ya han sido definidos previamente.Por su parte el coeficiente de correlación entre 2 variables, x, y, se obtiene con la ecuación (8):
donde xi y yi, son los datos de las variables correlacionadas y X¯ y Y¯ son los valores promedio.Con estas relaciones matemáticas es posible obtener PR mediante la ecuación (5).
A continuación se presenta un caso ilustrativo de un artículo electrónico con demanda y tiempo de entrega normal.
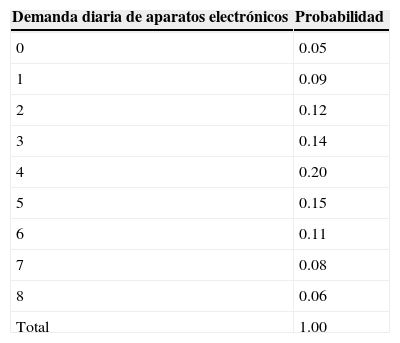
Aplicación a un caso prácticoUna empresa comercial vende aparatos electrónicos, uno de los cuales tiene la distribución de la demanda diaria que se presenta en la tabla 1.
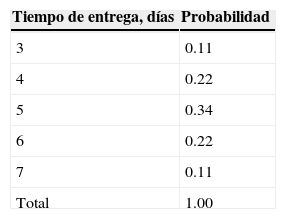
El tiempo de entrega se tiene de registros históricos del proveedor, el cual también es probabilístico, conforme a la distribución de probabilidad que se muestra en la tabla 2.
Además, se tiene la siguiente información:
Costo de faltante: 1,300 $/faltante.
Costo de mantenimiento: 3,000 $/(unidad)(año).
Demanda anual: 1,240 unidades/año.
Cantidad de pedido: 90 unidades/pedido.
Número de pedidos: 13.78 pedidos/año.
Días laborales=310 días/año.
Antes de utilizar las fórmulas de Wang, debe confirmarse que tanto la demanda de artículos como el tiempo de entrega siguen una distribución normal, lo cual se hace mediante la prueba de Kolmogorov-Smirnov (Pardo-Merino y Ruiz-Díaz, 2002), que para la demanda resulta un valor Z de 1.0 y pi de 0.27, mientras que para el tiempo de entrega, Z es 0.707 y un valor pi de 0.699, lo que confirma que ambas variables se ajustan aceptablemente a una distribución normal.
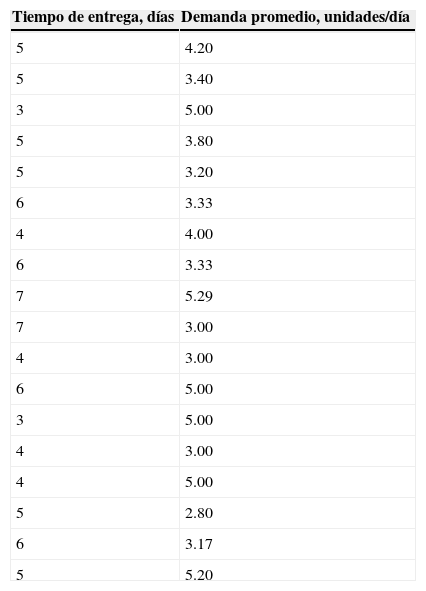
Entonces lo primero es obtener —mediante simulación con base en los datos con que se cuenta para cada tiempo de entrega— la demanda diaria promedio, con la finalidad de obtener el coeficiente de correlación entre ambas variables. Esto genera los datos de la tabla 3, con los cuales al aplicar la ecuación (8) se obtiene el coeficiente de correlación ρ, que resulta en un valor de −0.1954, que es bajo y negativo.
Para los datos de demandas diarias y tiempos de entrega, sus medias y desviaciones estándar son:
μd=4 unidades/día, μt=5 días, σd=2.121 unidades/día, σt=1.155 días
Para obtener el valor P(z) del nivel de servicio, se aplica la ecuación (3):
Que corresponde a un valor Z de 1.065.Por su parte, la desviación estándar de la demanda del tiempo de entrega se calcula con la ecuación (4):
Con lo cual es posible entonces calcular PR mediante la ecuación (1):Que es el PR en caso de que no haya correlación entre la demanda diaria y el tiempo de entrega.Si se considera que hay correlación —dado el valor de ρ—, al aplicar la ecuación (7) se obtiene:
Con lo cual la desviación estándar es 5.35 y PR resulta conforme a la ecuación (5):que es un poco menor al obtenido con las fórmulas tradicionales, debido a que el coeficiente de correlación entre la demanda y el tiempo de entrega es negativo.
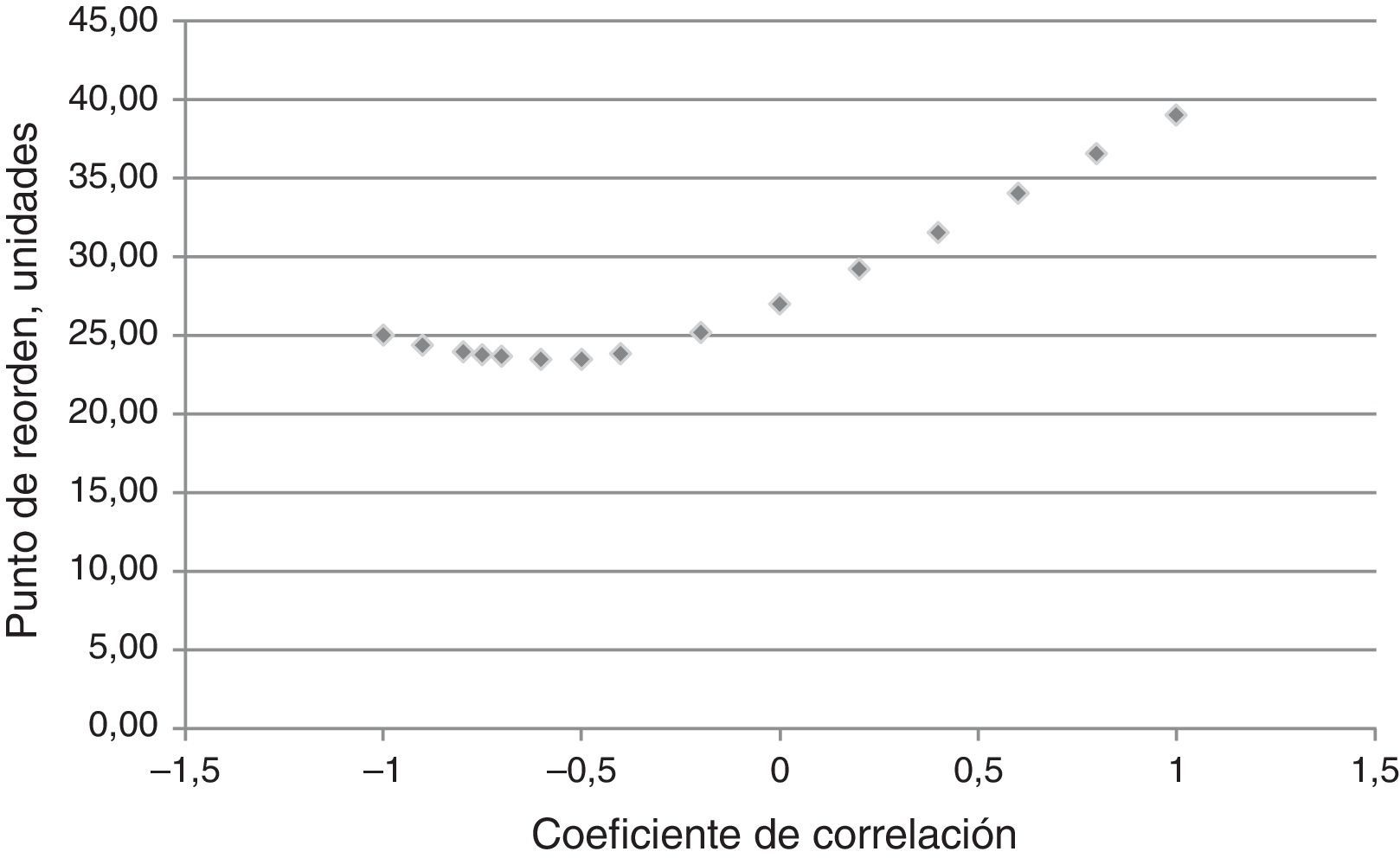
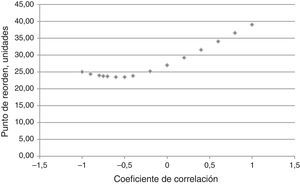
Si se repiten los cálculos con diferentes valores del coeficiente de correlación, se producen los resultados de la figura 1.
En el gráfico de la figura 1 puede observarse que si el coeficiente de correlación aumenta, el PR también lo hace, aunque en el lado izquierdo del gráfico el cambio es un poco diferente, ya que con un coeficiente mínimo (de −1), PR es 25, luego disminuye hasta un valor mínimo de 23.5 para un coeficiente de −0.6 y de ahí se incrementa de manera directa con el valor del coeficiente, hasta alcanzar un máximo de 39 unidades si ρ vale uno.
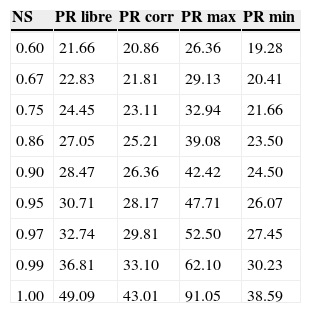
Si se repiten estos cálculos para diferentes valores del nivel de servicio (NS), se obtienen los resultados de la tabla 4, que incluye 4 valores de PR para cada nivel de servicio: el libre (no correlacionado), el correlacionado (con el valor de ρ de −0.1954), el PR máximo y el mínimo.
Puntos de reorden en función del nivel de servicio (NS)
| NS | PR libre | PR corr | PR max | PR min |
|---|---|---|---|---|
| 0.60 | 21.66 | 20.86 | 26.36 | 19.28 |
| 0.67 | 22.83 | 21.81 | 29.13 | 20.41 |
| 0.75 | 24.45 | 23.11 | 32.94 | 21.66 |
| 0.86 | 27.05 | 25.21 | 39.08 | 23.50 |
| 0.90 | 28.47 | 26.36 | 42.42 | 24.50 |
| 0.95 | 30.71 | 28.17 | 47.71 | 26.07 |
| 0.97 | 32.74 | 29.81 | 52.50 | 27.45 |
| 0.99 | 36.81 | 33.10 | 62.10 | 30.23 |
| 1.00 | 49.09 | 43.01 | 91.05 | 38.59 |
Fuente: elaboración propia.
El máximo valor de PR sucedió en todos los casos para un coeficiente ρ de +1, y para el PR mínimo, ρ varió entre −0.5 y −1 dependiendo del nivel de servicio, ya que se dio con −1 para NS=0.599 y −0.5 en un rango de valores de NS mayores al 90%.
En cuanto a las diferencias entre PR libre y correlacionado, son mayores si NS aumenta, ya que en caso de que esta variable se ubique en 100%, la diferencia entre ambos PR es del 14.1%, y únicamente del 3.8% si el nivel de servicio es del 60%. En el caso del PR máximo, que ha sido calculado con un coeficiente de correlación de +1, las diferencias respecto a los demás valores de PR son mayores, ya que para un nivel de servicio del 100%, PR máximo es más del doble del PR obtenido con la ecuación de Wang.
ConclusionesEn primer lugar se ha confirmado que pueden aplicarse las fórmulas sugeridas por Wang et al. (2010) al caso presentado, ya que tanto la demanda como el tiempo de entrega se comportan conforme a la distribución normal de probabilidad.
También se ha visto que, dependiendo del valor del coeficiente de correlación, puede haber diferencias significativas en el valor del PR, lo que implica revisar si efectivamente hay correlación entre la demanda de artículos y el tiempo de su entrega por parte del proveedor, antes de calcular el PR.
En el caso ilustrado la diferencia no ha sido elevada, solo del 7.3%, debido al bajo valor del coeficiente de correlación, lo que haría sugerir que, en casos como este, el PR se obtenga de la manera tradicional.
Los valores máximos de PR han sucedido para un valor del coeficiente de correlación de +1, independientemente del nivel de servicio manejado.
Por su parte, los valores mínimos de PR han sucedido para valores del coeficiente de correlación negativos en un rango de −0.5 a −1, dependiendo del nivel de servicio manejado.
Para niveles de servicio del 90% o más, las diferencias entre PR máximo y PR no correlacionado son significativas, dependiendo del coeficiente de correlación, lo que hace sugerir que si se cuenta con datos de la demanda y el tiempo de entrega, se estime el coeficiente de correlación y con base en su valor se decida cómo calcular el PR para el manejo del inventario.
De acuerdo a lo señalado por Wang et al. (2010), si el coeficiente de correlación es positivo, el cálculo tradicional de PR produce un valor bajo de este, lo que podría ocasionar faltantes del inventario y, en caso de que el coeficiente de correlación sea negativo, el cálculo tradicional de PR resulta alto, teniéndose entonces un inventario excesivo, siendo ambas situaciones perjudiciales para la correcta administración del inventario, ya que en el primer caso habría agotamientos y en el segundo un costo elevado de mantenimiento del inventario.
De los resultados del caso ilustrativo se recomienda que si el coeficiente de correlación se sitúa entre −0.5 y +0.5, el cálculo de PR se haga con la metodología tradicional para la distribución normal; pero si su valor se ubica entre 0.5 y 1, o entre −0.5 y −1, entonces se haga uso de las fórmulas de Wang et al. (2010), con el objetivo de no cometer errores.
También es notorio que con niveles de servicio más elevados, las diferencias entre los valores calculados para el punto de reorden libre o correlacionado son mayores.
Sería de interés hacer un estudio similar para productos con otras distribuciones de probabilidad de su demanda y tiempo de entrega, como pudiera ser el caso de una distribución uniforme, de Poisson o exponencial.
La revisión por pares es responsabilidad de la Universidad Nacional Autónoma de México.