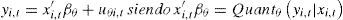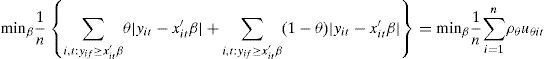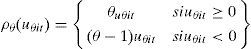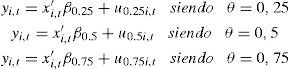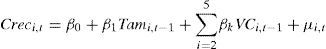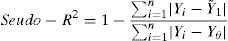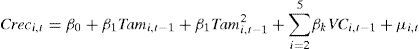Contraste de la ley de Gibrat en la banca comercial brasileña

Resumen

En los últimos años, Brasil ha sido uno de los países con mayores cambios en el sector bancario. El proceso de desregulación iniciado en 2002 ha conllevado el aumento de la presencia de banca extranjera y el incremento de la competencia, entre otros aspectos. En este contexto, el objetivo del presente estudio consiste en contrastar la ley de Gibrat en la banca comercial brasileña durante el periodo 2002-2013 con el objeto de aportar evidencia para la construcción de un modelo de crecimiento para la banca que oriente la política financiera del país. Para ello se emplea la metodología de regresiones cuartílica que consideramos analiza de manera más exhaustiva la relación entre el crecimiento y el tamaño de las entidades que los contrastes empíricos aportados por la evidencia empírica previa. Los resultados obtenidos nos indican que existe una relación no lineal en forma de U invertida entre crecimiento y tamaño en la banca comercial brasileña. Estos resultados nos permiten afirmar que la relativa dispersión de los tamaños de las entidades financieras tenderá a reducirse en el tiempo y con ello la concentración del sector.

Abstract

In recent years Brazil has been one of the countries with major changes in the banking sector. The deregulation process that has taken place since 2002 has brought an increased presence of foreign banks and higher competition, among other aspects. In this context, the objective of this study is to analyze Gibrat's law on Brazilian commercial banks over the period 2002-2013 with the aim of providing evidence for the construction of a banking growth model which guide the country's financial policy. To that end, we employ a methodology based on quartile regressions as a contribution to previous literature. Our overall results reveal the existence of a non-lineal relationship between growth and banks size with an inverted U-shape. These findings allow us to affirm that the relative dispersion of banks size, as well as the sector's concentration, will be reduce in the future years.

Introducción

Durante las últimas décadas el sector financiero ha experimentado cambios significativos debido a la liberalización y desregulación de los mercados, a los cambios tecnológicos y a la crisis financiera internacional que han supuesto un incremento del grado de concentración bancaria y del tamaño de las entidades (Fernholz y Koch, 2016).

Tradicionalmente, los estudios empíricos sobre concentración bancaria se han basado en el contraste de la ley de Gibrat, que implica la ausencia de relación entre tamaño y crecimiento, de modo que todas las entidades tienen las mismas probabilidades de crecer (Alhadeff y Alhadeff, 1964; Rhoades y Yeats, 1974; Yeats, Irons y Rhoades, 1975; Tschoegl, 1983; Wilson y Williams, 2000; Vennet, 2001; Goddard, McKillop y Wilson, 2002; Goddard, Molyneux y Wilson, 2004; Ward y McKillop, 2005; Benito, 2008; Shehzad, de Haan y Sholtens, 2013; Goddard, McKillop y Wilson, 2014; Fernholz y Koch, 2016). Sin embargo, estos estudios presentan 2 importantes limitaciones: se centran en el análisis de los sectores bancarios de países desarrollados y los resultados obtenidos son mixtos. Es por ello conveniente ampliar la evidencia empírica previa con el objeto de obtener resultados concluyentes.

En este sentido, es importante señalar que en los últimos años se ha observado que en la zona euro y el Reino Unido (BOE, 2010) ha descendido el número de activos totales de las entidades, mientras aumentaba en otros países como Brasil (Cull y Martínez Pería, 2013). Prueba de ello es la destacada presencia en el sector bancario brasileño de entidades financieras extranjeras como la española Banco Santander y la británica HSBC que ocupan la quinta y sexta posición en cuota de mercado respectivamente.

En este contexto, el objetivo del presente estudio consiste en analizar el crecimiento de la banca en Brasil durante el periodo 2002-2013 mediante el contraste de la ley de Gibrat e incorporando una serie de novedades metodológicas con respecto a los estudios tradicionales. En primer lugar, analizamos la relación crecimiento-tamaño por cuartiles, ya que consideramos que la obtención de resultados mixtos por parte de la evidencia empírica previa puede depender de la distribución de las tasas de crecimiento de las entidades, llegando a encontrar relaciones diferentes por grupos de entidades. En segundo lugar, realizamos un análisis para detectar si los resultados encontrados por cuartiles difieren significativamente entre ellos. De este modo, el análisis cuartílico nos permite analizar minuciosamente el tipo de relación existente entre el crecimiento y el tamaño de las entidades, encontrando en ocasiones que la relación entre dichas variables es más compleja de lo que se podría suponer en un principio al realizar un análisis sobre la muestra total. Por último, aplicamos un contraste no lineal de la ley de Gibrat con el objeto de presentar resultados concluyentes.

Los principales resultados obtenidos nos muestran que existe una relación significativa entre el crecimiento y el tamaño de las entidades, pero que varía de positiva a negativa entre el primer cuartil y el tercero. La diferencia de los resultados encontrados entre el primer y el tercer cuartil son significativos, lo que confirma la relación no lineal en forma de U invertida entre dichas variables. Estos resultados, por tanto, nos permiten afirmar que la relativa dispersión de los tamaños de las entidades financieras de Brasil tenderá a reducirse en el tiempo. Esto implica una disminución de la concentración sectorial si el número de entidades se mantiene constante.

El resto del trabajo se estructura como se muestra a continuación. En el apartado segundo se presenta una revisión de la literatura previa sobre crecimiento en la banca. En el apartado tercero se presentan las características de la muestra. En el cuarto apartado se desarrolla la metodología empleada. En el quinto apartado se exponen los resultados empíricos obtenidos. Por último, en el sexto apartado se desglosan las conclusiones obtenidas del conjunto del trabajo.

Revisión de la literatura

El estudio empírico del crecimiento bancario se ha ligado tradicionalmente a su relación con el tamaño mediante la ley enunciada por Gibrat (1931), que considera que el crecimiento empresarial es un proceso estocástico que tiende a la concentración de los mercados. Siguiendo la ley de Gibrat, consideramos que la distribución del tamaño se asemeja a una distribución log-normal, ya que cada empresa es objeto de una serie de shocks puramente aleatorios que con el tiempo tiende a producir una distribución asimétrica de este tipo.

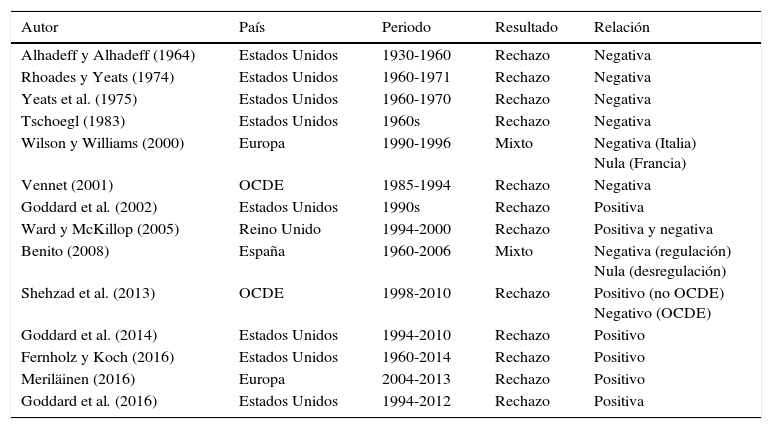
En la tabla 1 se presenta una revisión de trabajos que analizan el crecimiento bancario mediante el contraste de ley de Gibrat. Como podemos ver, estos estudios se centran en el análisis de la banca de Estados Unidos y Europa, presentando resultados no concluyentes. En los primeros estudios se observa una relación negativa entre crecimiento y tamaño bancario, lo que implica que las entidades más pequeñas son las que más crecen (Alhadeff y Alhadeff, 1964; Rhoades y Yeats, 1974; Yeats et al., 1975; Tschoegl, 1983; Wilson y Williams, 2000; Vennet, 2001). Por el contrario, los trabajos más recientes encuentran evidencia de una influencia positiva del tamaño sobre el crecimiento, siendo las entidades de mayor tamaño las que más crecen (Goddard et al., 2002; Shehzad et al., 2013; Goddard et al., 2014; Fernholz y Koch, 2016; Meriläinen, 2016; Goddard, McKillop y Wilson, 2016).

Tabla 1.

Ley de Gibrat en la banca. Relación entre tamaño y crecimiento

Autor	País	Periodo	Resultado	Relación
Alhadeff y Alhadeff (1964)	Estados Unidos	1930-1960	Rechazo	Negativa
Rhoades y Yeats (1974)	Estados Unidos	1960-1971	Rechazo	Negativa
Yeats et al. (1975)	Estados Unidos	1960-1970	Rechazo	Negativa
Tschoegl (1983)	Estados Unidos	1960s	Rechazo	Negativa
Wilson y Williams (2000)	Europa	1990-1996	Mixto	Negativa (Italia) Nula (Francia)
Vennet (2001)	OCDE	1985-1994	Rechazo	Negativa
Goddard et al. (2002)	Estados Unidos	1990s	Rechazo	Positiva
Ward y McKillop (2005)	Reino Unido	1994-2000	Rechazo	Positiva y negativa
Benito (2008)	España	1960-2006	Mixto	Negativa (regulación) Nula (desregulación)
Shehzad et al. (2013)	OCDE	1998-2010	Rechazo	Positivo (no OCDE) Negativo (OCDE)
Goddard et al. (2014)	Estados Unidos	1994-2010	Rechazo	Positivo
Fernholz y Koch (2016)	Estados Unidos	1960-2014	Rechazo	Positivo
Meriläinen (2016)	Europa	2004-2013	Rechazo	Positivo
Goddard et al. (2016)	Estados Unidos	1994-2012	Rechazo	Positiva

Fuente: elaboración propia.

No obstante, también es importante señalar que entre todos estos estudios, tan solo 2 de ellos, Wilson y Williams (2000), y Benito (2008), han encontrado evidencia de aceptación de la ley de Gibrat, justificando este resultado por la influencia del nivel de regulación al que están sometidos los mercados. Concretamente, Wilson y Williams (2000) observan que las entidades financieras francesas tienen la misma probabilidad de crecer, independientemente de su tamaño, y argumentan que dichos resultados son debidos a que el sistema bancario francés se caracteriza por estar muy regulado en los años de estudio. Por otro lado, Benito (2008) contrasta la ley de Gibrat para los bancos españoles en el periodo 1960-2006, desglosando la muestra por periodos de regulación y desregulación. Dichos autores encuentran que en periodos de regulación las entidades pequeñas crecen más deprisa, mientras que en etapas de desregulación no se encuentran diferencias significativas, por lo que todas las entidades crecen en la misma proporción aceptándose la ley de Gibrat.

Por otro lado, también los procesos de integración y reestructuración pueden afectar al contraste de la ley de Gibrat en el sector bancario. Por ello, es preciso tener en cuenta los trabajos de Goddard et al. (2014, 2016). Concretamente, Goddard et al. (2014) analizan el impacto de las salidas y del crecimiento interno generado por los procesos de adquisiciones y fusiones en la distribución del tamaño de las entidades de crédito de Estados Unidos durante el periodo 1994-2010. Por el contrario, Goddard et al. (2016) analizan la influencia de los cambios regulatorios en materia de exigencias de capital ocurridos en el año 2000 en Estados Unidos para un conjunto de 12.046 entidades financieras durante el periodo 1994-2012. Los resultados obtenidos indican que las entidades de mayor tamaño y más jóvenes tienen más probabilidades de sobrevivir y poder crecer, rechazando la ley de Gibrat, encontrando además que las entidades más pequeñas tienen mayor riesgo de desaparecer mediante adquisiciones o quiebras.

En este contexto, consideramos interesante contrastar la ley de Gibrat en el sector bancario de un país emergente como Brasil, ya que en los últimos años se ha producido un cambio en la estructura del mercado bancario brasileño debido a las numerosas reformas estructurales que han permitido la liberalización de los mercados y la entrada de entidades extranjeras. Por otro lado, los resultados obtenidos aportarán evidencia empírica novedosa para el sector bancario debido a la metodología de análisis por cuartiles utilizada.

Base de datos

El sector bancario en Brasil se caracteriza por haber llevado a cabo un proceso de transformación y liberalización que ha permitido que en los últimos 15 años se haya incrementado la presencia de la banca extranjera (Chortareas, Gaza-García y Girardonde, 2011). No obstante, el proceso de internacionalización de las entidades financieras ha favorecido la competencia, lo cual tiene su repercusión en las tasas de crecimiento de las entidades participantes.

Cheng y Liao (2011) destacan que la globalización ha permitido a los bancos extranjeros, especialmente aquellos inmersos en sistemas financieros más desarrollados, expandirse hacia economías emergentes donde en ocasiones han llegado a ser predominantes debido al traslado de gran parte de su negocio como consecuencia de la crisis financiera internacional (Coleman y Feler, 2015). En el caso de Brasil hay que destacar que entre los 10 mayores bancos comerciales por volumen de activos totales se encuentra en tercer lugar el Banco Santander, de origen español, en cuarto lugar el banco HSBS británico y del octavo al décimo lugar el estadounidense Citibank, el suizo Credit Suisse y el también estadounidense JP Morgan Chase. Por lo tanto, una de las razones de la realización de la presente investigación radica en la importancia del sector bancario de Brasil para los principales bancos comerciales a nivel mundial.

El periodo analizado es el comprendido entre los años 2002 y 2013, ya que es a partir del año 2002 cuando Assunção (2013) encuentra evidencia de eliminación de barreras de entrada para la provisión de servicios financieros en Brasil. En este sentido, es preciso indicar que durante estos años de estudio el número de entidades ha ido variando debido a los procesos de entrada de entidades extranjeras, así como de las fusiones y las absorciones que se han llevado a cabo entre entidades nacionales.

Por otro lado, siguiendo el trabajo de Goddard et al. (2004), las principales variables de análisis son recogida en la tabla 2. Concretamente, el crecimiento es medido como la diferencia de logaritmos del tamaño empresarial entre 2 periodos consecutivos, siendo calculado el tamaño empresarial por el logaritmo de la cifra de activos de cada empresa. Entre las variables explicativas del crecimiento se encuentra, en primer lugar, el tamaño. Es más difícil que se produzca mayor concentración cuando se trata de un sector con grandes empresas según Goddard et al. (2004). En segundo lugar, consideramos la rentabilidad de las entidades financieras, medida a partir de la rentabilidad de sus recursos propios.

Tabla 2.

Descripción de las variables del sector bancario brasileño

Variable	Definición	Acrónimo
Crecimiento	Diferencia de logaritmos del tamaño de 2 periodos consecutivos	Crec
Tamaño	Logaritmo natural de la cifra de activos	Tam
Rentabilidad	Rentabilidad de los recursos propios	Rent
Ratio de capital	Relación entre el capital de la entidad y los activos de la misma	Cap
Ratio de morosidad	Relación entre activos impagados y activos totales.	Mor
Ratio de liquidez	Relación de activos líquidos respecto al total de activos	Liq
Off balance sheet	Activos fuera de balance sobre activos totales de la entidad	Obs

Fuente: elaboración propia.

Adicionalmente, hay que tener en cuenta que la banca ha respondido a la concentración y la presión de la competencia ampliando su gama de servicios y productos financieros, incrementando su porcentaje de negocio fuera de balance (off balance sheet [OBS])¹ mejorando la diversificación de su cartera y riesgo. Goddard et al. (2004) encuentran resultados mixtos para diferentes países europeos, señalando que sí existe una relación positiva entre OBS y rentabilidad, encontrando relación negativa para aquellos bancos que han incrementado el nivel de su cartera de OBS, teniendo dificultades para mantener sus tasas de rentabilidad.

Por otro lado, entre los principales indicadores que explican el comportamiento de la banca se encuentran las ratios de capital y de liquidez. Un exceso de capital y liquidez representa una operativa muy conservadora, lo que puede generar que se tengan recursos ociosos, no se aprovechen oportunidades de inversión y, por tanto, vaya en detrimento de la rentabilidad. En este sentido, se incorpora la ratio de morosidad que merma la rentabilidad.

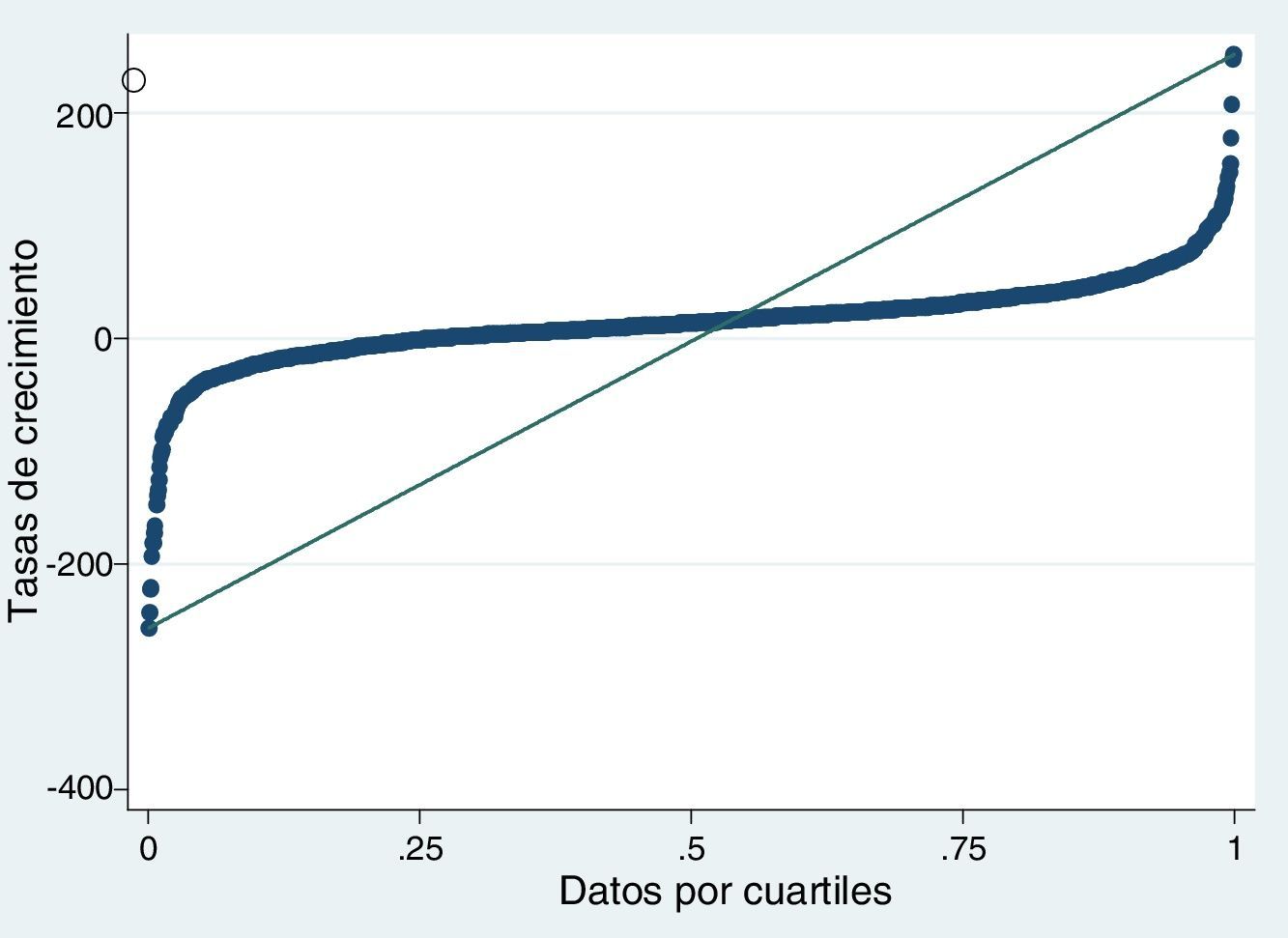
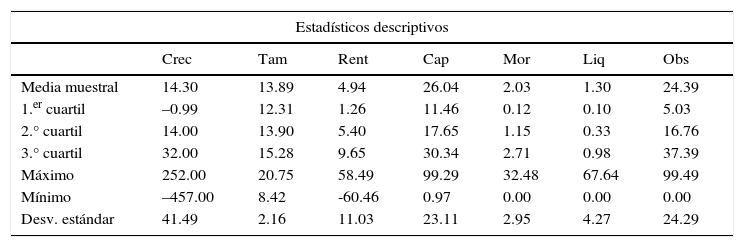
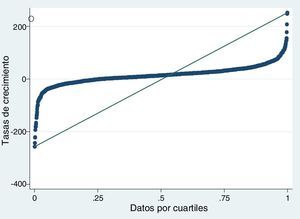
Los estadísticos descriptivos de las variables objeto de estudio se presentan en la tabla 3, tanto para la muestra total como por cuartiles. En relación con los estadísticos descriptivos de la muestra total, es preciso indicar que las entidades en Brasil han crecido de media un 14.30%, situándose el valor del primer cuartil en tasas negativas del 0.99%, la mediana en el 14% y el tercer cuartil en el 32%. Como se puede observar en la figura 1, que representa la distribución de las tasas de crecimiento por cuartiles de las entidades financieras en Brasil, las tasas de crecimiento aumentan por cuartil pero no de manera uniforme, ya que las tasas de crecimiento se distribuyen conforme a una normal, como se muestra en el apartado siguiente.

Tabla 3.

Estadísticos descriptivos y matriz de correlaciones

Estadísticos descriptivos
	Crec	Tam	Rent	Cap	Mor	Liq	Obs
Media muestral	14.30	13.89	4.94	26.04	2.03	1.30	24.39
1.^er cuartil	–0.99	12.31	1.26	11.46	0.12	0.10	5.03
2.° cuartil	14.00	13.90	5.40	17.65	1.15	0.33	16.76
3.° cuartil	32.00	15.28	9.65	30.34	2.71	0.98	37.39
Máximo	252.00	20.75	58.49	99.29	32.48	67.64	99.49
Mínimo	–457.00	8.42	-60.46	0.97	0.00	0.00	0.00
Desv. estándar	41.49	2.16	11.03	23.11	2.95	4.27	24.29

Matriz de correlaciones
	Crec	Tam	Rent	Cap	Mor	Liq	Obs
Crec	1.00
Tam	0.14	1.00
Rent	0.25	0.16	1.00
Cap	–0.17	–0.64	–0.12	1.00
Mor	–0.15	–0.03	–0.19	–0.10	1.00
Liq	–0.00	–0.07	0.04	0.02	–0.06	1.00
Obs	–0.02	–0.01	–0.00	0.25	–0.31	–0.08	1.00

Fuente: elaboración propia.

Figura 1.

Tasas de crecimiento por cuartiles.

Fuente: elaboración propia.

Por otro lado, la banca en Brasil presenta una rentabilidad media del 4.94% y un nivel medio de ratio de capital del 26.04%. La diversificación media de la cartera de productos OBS es de un 24.39%. Además, los niveles de liquidez y la tasa de morosidad media son bajos pero positivos, siendo concretamente del 1.30 y el 2.03%, respectivamente. Por último, la matriz de correlaciones nos muestra cómo el crecimiento está correlacionado positivamente con el tamaño y la rentabilidad, y de manera negativa con el resto de las variables explicadas.

Metodología

Como se ha comentado en la revisión de la literatura, uno de los aspectos más destacados del estudio del crecimiento ha sido la evolución metodológica. Así, los estudios analizados previamente han utilizado diferentes técnicas, como mínimos cuadrados ordinarios (MCO), efectos fijos (FE) y método generalizado de los momentos (GMM), basadas en el desarrollo de la metodología de datos de panel. Esta permite modelizar la heterogeneidad inobservable que existe entre las distintas empresas mediante la descomposición del término de error en 3 componentes, permitiendo además aumentar el número de observaciones, los grados de libertad de los modelos y, por tanto, la consistencia de los resultados.

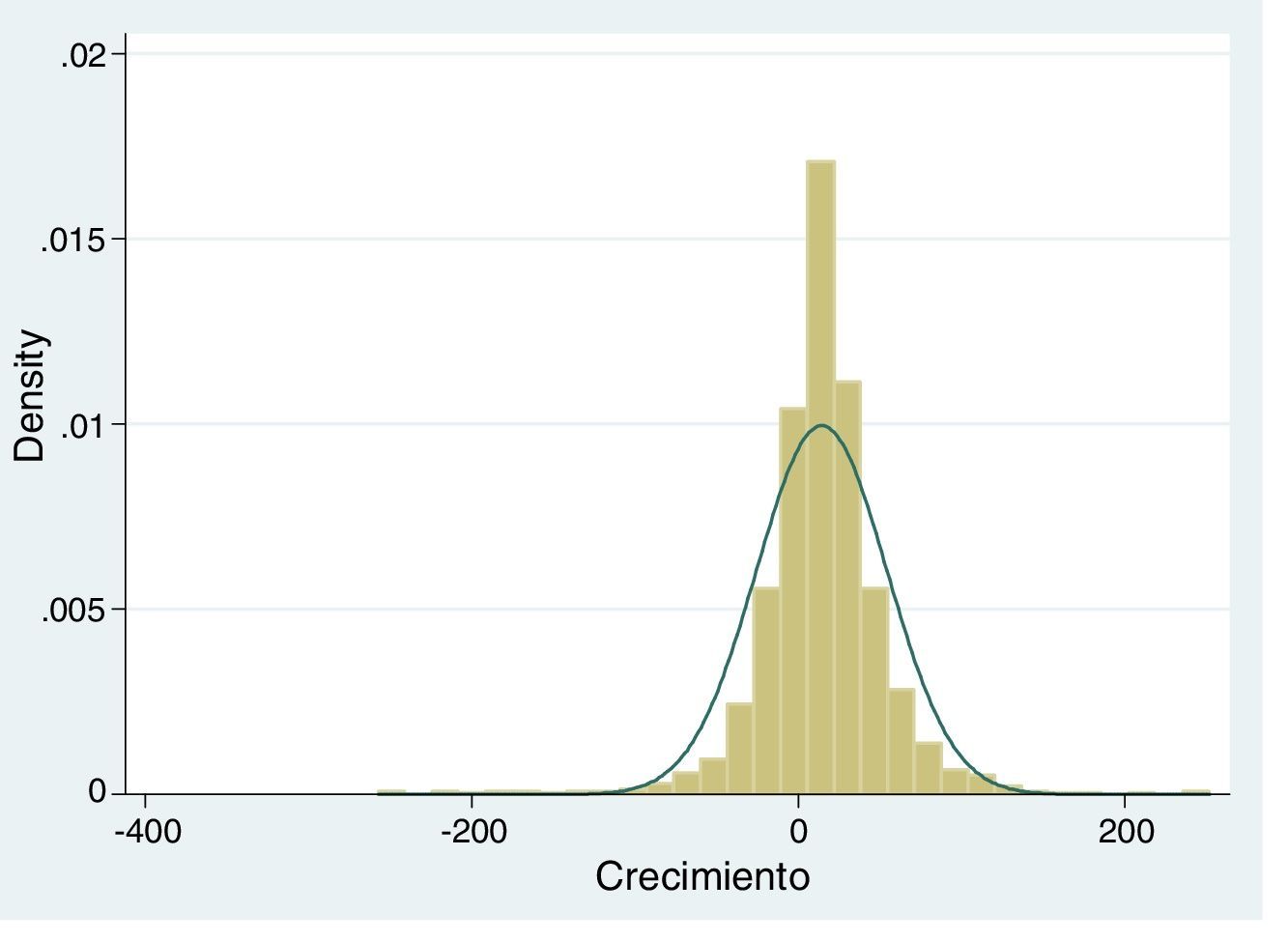
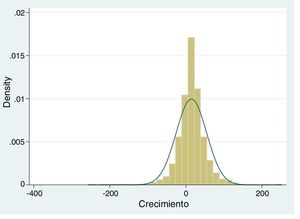
Sin embargo, según Leitão, Nunes y Serrasqueiro (2010), con el uso exclusivo de esos métodos, no es posible contrastar la ley de Gibrat basándose en la distribución del crecimiento de las empresas, ya que para ello lo adecuado es el uso de la metodología de regresión cuartílica, tomando como referencia la distribución del crecimiento del conjunto de empresas de la muestra. De este modo, en la figura 2 se observa la aproximación de la distribución de las tasas de crecimiento de la banca en Brasil a una distribución normal. En dicha figura se observa que existe un mayor número de entidades con tasas positivas de crecimiento, situándose la mayoría en los valores centrales próximos al 14% de crecimiento.

Figura 2.

Distribución del crecimiento de la banca en Brasil (%).

Fuente: elaboración propia.

De este modo, estudios previos han evidenciado cómo la desregulación o un exceso de regulación financiera influía en la variación de los resultados obtenidos del contraste de la ley de Gibrat (Benito, 2008). Este hecho supone la existencia de una relación no lineal entre tamaño y crecimiento empresarial. Por ello consideramos interesante realizar un análisis más exhaustivo del crecimiento en la banca por si existiera un cambio en el signo de la relación entre el tamaño y el crecimiento.

La regresión cuantílica propuesta por Koenker y Basset (1978) busca modelizar la relación existente entre dos variables, una variable dependiente y otra independiente, para distintos cuantiles de la distribución de la variable dependiente, y que puede expresarse del siguiente modo:

donde y_i,t es la variable dependiente, x′i,t el vector de regresores, β es el vector de parámetros a estimar, u es el vector de los residuos y Quand_θ(y_i,t| x_i,t) representa la condición cuantílica θ de y_i,t dado x_i,t. Los valores que puede tomar θ están entre 0 y 1, utilizándose la siguiente expresión para su cálculo:

donde ρ_θ es definida como:

En la presente investigación, como hemos indicado anteriormente, empleamos regresiones cuartílicas que son un caso particular de las regresiones cuantílicas en el que:

Concretamente, se utiliza el modelo lineal multivariante propuesto por Goddard et al. (2002) para analizar el crecimiento y contrastar la ley de Gibrat, que es expresado del siguiente modo:

donde Crec_i,t representa el crecimiento del banco i en el año t, que viene explicado por el tamaño de la entidad en el año anterior representado por Tam_i,t-1, además de por un conjunto de variables de control que representan la rentabilidad, el nivel de solvencia, el porcentaje del negocio fuera del balance, la tasa de liquidez y la tasa de morosidad. Por último, β_k son los parámetros a estimar y μ_i,t el término de error².

Para garantizar la consistencia de los resultados, el estadístico utilizado para la regresión cuantílica es el coeficiente de seudo-R², que depende del cuartil estimado (θ) y viene expresado mediante la siguiente ecuación:

Además, para estimar los parámetros de los diferentes cuantiles, siguiendo a Coad y Rao (2008) y Leitão et al. (2010), usamos el método de la matriz Bootstrap propuesto por Buchinsky (1994, 1998) ya que es considerado como el más adecuado para muestras de pocas observaciones y principalmente por ser válido en presencia de las diferentes formas de heterogeneidad.

Esta metodología es válida para estimar modelos lineales estáticos pero no es la adecuada para estimar modelos lineales dinámicos, ya que en ese caso la metodología adecuada, según Powell (2014), sería llevar a cabo regresiones cuantílicas de datos de panel mediante variables instrumentales (también denominada quantile regresion for panel data [QRPD]).

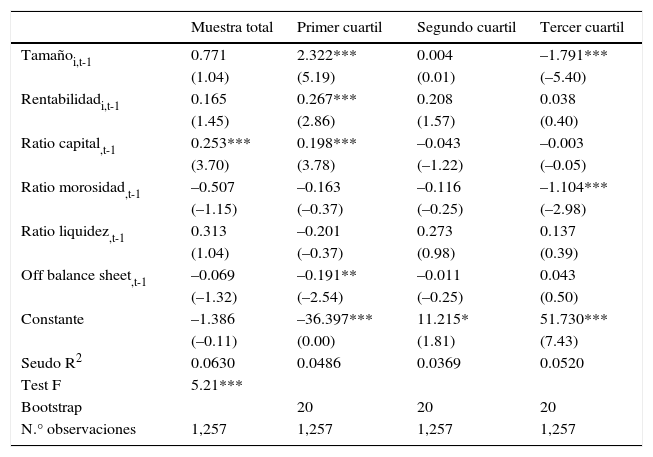
Resultados empíricos

En este apartado se presentan los resultados obtenidos del conjunto de análisis efectuados para el total de entidades financieras comerciales que componen el sistema bancario en Brasil. Concretamente, en la tabla 4 presentamos los resultados obtenidos del contraste de la ley de Gibrat para examinar la relación entre el crecimiento y el tamaño de la banca comercial. En dicha tabla se representan los resultados obtenidos para la muestra total y para cada uno de los cuartiles. Así, se puede observar que para el conjunto de la muestra el tamaño de las entidades no influye significativamente sobre el crecimiento. Este resultado implica la aceptación de la ley de Gibrat, lo que supone que el crecimiento es un proceso aleatorio que no depende del tamaño de las entidades y, por lo tanto, que todas las entidades tienen la misma probabilidad de crecer independientemente de su tamaño.

Tabla 4.

Contraste lineal de la ley de Gibrat. Resultados para la muestra total y por cuartiles

	Muestra total	Primer cuartil	Segundo cuartil	Tercer cuartil
Tamañoi,t-1	0.771	2.322***	0.004	–1.791***
	(1.04)	(5.19)	(0.01)	(–5.40)
Rentabilidadi,t-1	0.165	0.267***	0.208	0.038
	(1.45)	(2.86)	(1.57)	(0.40)
Ratio capital,t-1	0.253***	0.198***	–0.043	–0.003
	(3.70)	(3.78)	(–1.22)	(–0.05)
Ratio morosidad,t-1	–0.507	–0.163	–0.116	–1.104***
	(–1.15)	(–0.37)	(–0.25)	(–2.98)
Ratio liquidez,t-1	0.313	–0.201	0.273	0.137
	(1.04)	(–0.37)	(0.98)	(0.39)
Off balance sheet,t-1	–0.069	–0.191**	–0.011	0.043
	(–1.32)	(–2.54)	(–0.25)	(0.50)
Constante	–1.386	–36.397***	11.215*	51.730***
	(–0.11)	(0.00)	(1.81)	(7.43)
Seudo R^2	0.0630	0.0486	0.0369	0.0520
Test F	5.21***
Bootstrap		20	20	20
N.° observaciones	1,257	1,257	1,257	1,257

Fuente: elaboración propia.

*, **, *** indican significatividad al 1%, 5% y 10% respectivamente.

Sin embargo, los resultados obtenidos para los diferentes cuartiles muestran que la influencia del tamaño sobre el crecimiento varía en función del cuartil que se está analizando. Concretamente, se observa que en el primer cuartil el tamaño influye de manera positiva y significativa sobre el crecimiento, mientras que en el segundo cuartil la influencia no es significativa, pero que en el tercer cuartil la influencia que se encuentra es negativa y significativa.

En cuanto a la influencia del resto de las variables, los resultados obtenidos nos muestran que la rentabilidad ejerce una influencia positiva sobre el crecimiento pero, solo es significativa en el primer cuartil. La ratio de capital también ejerce una influencia positiva sobre el crecimiento, siendo significativa en el primer cuartil y el conjunto de la muestra. Por otro lado, la morosidad ejerce una influencia negativa y significativa en el tercer cuartil y la ratio OBS sobre el primer cuartil. Los resultados obtenidos de los test de buena especificación nos muestran que las variables son significativas conjuntamente.

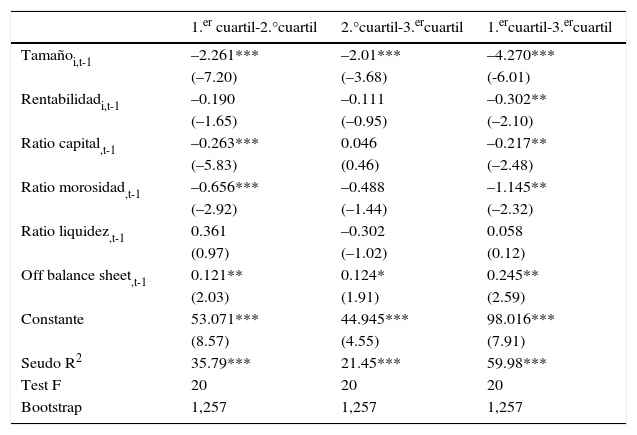
No obstante, en la tabla 5 se presenta el análisis de regresiones intercuartílicas para comprobar que existen diferencias significativas entre los parámetros obtenidos para los diferentes cuartiles. Dicha tabla muestra los resultados de las regresiones intercuartílicas obteniéndose que las diferencias de parámetros obtenidos por cuartiles en la tabla 4 es significativa entre cada uno de los cuartiles para la relación crecimiento-tamaño. Estos resultados son corroborados por la significatividad de los resultados obtenidos en los test de diferencias de los parámetros intercuartílicos.

Tabla 5.

Diferencias entre parámetros intercuartílicos

	1.^er cuartil-2.°cuartil	2.°cuartil-3.^ercuartil	1.^ercuartil-3.^ercuartil
Tamañoi,t-1	–2.261***	–2.01***	–4.270***
	(–7.20)	(–3.68)	(-6.01)
Rentabilidadi,t-1	–0.190	–0.111	–0.302**
	(–1.65)	(–0.95)	(–2.10)
Ratio capital,t-1	–0.263***	0.046	–0.217**
	(–5.83)	(0.46)	(–2.48)
Ratio morosidad,t-1	–0.656***	–0.488	–1.145**
	(–2.92)	(–1.44)	(–2.32)
Ratio liquidez,t-1	0.361	–0.302	0.058
	(0.97)	(–1.02)	(0.12)
Off balance sheet,t-1	0.121**	0.124*	0.245**
	(2.03)	(1.91)	(2.59)
Constante	53.071***	44.945***	98.016***
	(8.57)	(4.55)	(7.91)
Seudo R^2	35.79***	21.45***	59.98***
Test F	20	20	20
Bootstrap	1,257	1,257	1,257

Fuente: elaboración propia.

*, **, *** indican significatividad al 1%, 5% y 10% respectivamente.

En cuanto al resto de las variables, se observa que las principales diferencias intercuartílicas se producen entre el tercer y primer cuartil, siendo las diferencias significativas para las variables de rentabilidad, ratio de capital, morosidad y OBS. No obstante, el primer cuartil muestra diferencias significativas con el segundo cuartil también en la influencia de la ratio de capital y de morosidad.

Los resultados obtenidos en la tabla 4 nos hacen prever que puede existir una relación no lineal entre crecimiento y tamaño, ya que la influencia del tamaño sobre el crecimiento cambia de signo del primer cuartil al tercero. Por esta razón, consideramos interesante contrastar la existencia de no linealidad entre crecimiento y tamaño. Para llevar a cabo este análisis incorporamos al modelo propuesto por Goddard et al. (2002) la variable cuadrática del tamaño expresada por Tam²_i, _t-1, quedando el modelo no lineal del siguiente modo:

Siguiendo la literatura previa se asume que existe causalidad entre el crecimiento y el tamaño. Por tanto, puede surgir un posible problema de endogeneidad que debe ser abordado. Los instrumentos utilizados para solucionar el problema de endogeneidad serán las variables explicativas retardadas, ya que deberán tener la capacidad de aportar la información sobre la variable explicativa.

De este modo, el método elegido para obtener estimaciones consistentes y eficientes es el GMM de diferencias (Arellano y Bond, 1991), que se trata de un método particular de variables instrumentales. Para mostrar la significatividad global del modelo presentamos el test de Wald expresado mediante la F-Snedecor. Para comprobar la validez de los instrumentos se usa el test de Sargan de sobreidentificación de los instrumentos. Por último, se realiza el test estadístico de Arellano y Bond (1991) para comprobar la ausencia de autocorrelación de segundo orden, expresado por m₂.

Los resultados obtenidos en la tabla 6 corroboran que sí existe una relación no lineal entre tamaño y crecimiento, siendo esta cuadrática en forma de U invertida, coincidiendo con las teorías clásicas que defienden que las empresas de menor tamaño tienen un mayor potencial de crecimiento. Por otro lado, los resultados son consistentes y fiables, ya que el modelo es explicado conjuntamente, tal como indica el test de Wald; además, no existe autocorrelación de segundo orden y el modelo no está sobreidentificado, como se puede observar en el test de Arellano y Bond, y el test de Sargan, respectivamente.

Tabla 6.

Contraste no lineal de la ley de Gibrat

	Coeficiente	t-estadístico
Tamañoi,t-1	161.501***	(3.26)
Tamaño^2i,t-1	–6.437*	(1.67)
Rentabilidadi,t-1	–0.292**	(–2.04)
Ratio capital,t-1	2.371***	(4.72)
Ratio morosidad,t-1	–0.227	(–0.27)
Ratio liquidez,t-1	–3.512***	(–3.78)
Off balance sheet,t-1	–0.155	(–0.69)
Test de Wald	21.31***
m2	1.15
Test de Sargan	452.57***
N.°	152

Fuente: elaboración propia. *, **, *** indican significatividad al 1%, 5% y 10% respectivamente.

Conclusiones

La evidencia empírica previa sobre la relación tamaño-crecimiento en el sector bancario no es tan amplia como en el ámbito empresarial, especialmente en economías emergentes como la brasileña. Sin embargo, existen importantes razones económicas que justifican su estudio, como son el importante crecimiento económico que ha experimentado este país en los últimos años, la importancia del sector financiero en su misión de estabilizar y soportar la actividad económica de dicho país y, por último, la fuerte presencia de entidades financieras extranjeras, que se ha visto además incrementada desde el origen de la crisis financiera internacional.

En este contexto, el presente estudio ha tenido por objeto analizar el crecimiento de las entidades financieras de Brasil durante el periodo 2002-2013 mediante el contraste de la ley de Gibrat, considerando el principio del periodo en 2002 debido a ser el año en el que se produjeron los principales cambios regulatorios del sector bancario en Brasil, la liberalización del sector y la entrada de banca comercial extranjera. El presente trabajo ha incorporado 2 análisis novedosos al estudio del crecimiento como es contrastar la ley de Gibrat en la banca comercial en un país emergente y aplicar para dicho análisis la metodología de regresiones cuartílicas con el objeto de analizar minuciosamente la relación tamaño-crecimiento y aportar así evidencia relevante para la construcción de un modelo de crecimiento de la banca que oriente la política financiera del país.

Los resultados del conjunto del trabajo nos indican que existe una relación compleja entre tamaño y crecimiento de tipo no lineal para el conjunto de entidades financieras que operan en Brasil durante los años de estudio. Tras analizar de forma más exhaustiva la influencia del tamaño sobre el crecimiento, encontramos que el tamaño influye de forma cuadrática sobre el crecimiento y experimenta un cambio en el sentido de su influencia sobre el crecimiento en función de los cuartiles analizados. Concretamente, observamos que las entidades de menor tamaño tienen un crecimiento medio esperado positivo mientras que las entidades con un mayor volumen de activos tienen una esperanza de crecimiento de signo negativo. Estos resultados son especialmente relevantes para las autoridades financieras del país ya que nos permite afirmar que en los próximos años disminuirá la concentración del sector, igualándose las cuotas de mercado entre entidades.

En futuras investigaciones sería interesante analizar la interrelación del crecimiento y de la rentabilidad en diferentes economías emergentes, aportando a la literatura un mayor conocimiento del comportamiento del sector bancario en estas economías. Además, debido a la influencia de las ratios de capital, liquidez y diversificación del negocio bancario sobre el crecimiento, sería interesante analizar la influencia del crecimiento sobre los niveles de solvencia y liquidez, de manera que se pueda examinar cómo influye la banca comercial en la función de estabilidad del sector financiero brasileño.

Financiamiento

Este trabajo ha recibido la ayuda financiera de la Junta de Extremadura, concretamente del V Plan Regional de Investigación Desarrollo Tecnológico e Innovación (2014-2017), a través del Grupo de Investigación GIMAF (referencia GR15027).[consultado 13 Oct 2017] Disponible