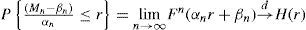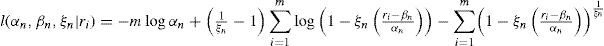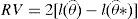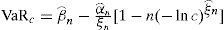El efecto de la volatilidad del peso mexicano en los rendimientos y riesgo de la Bolsa Mexicana de Valores

Resumen

El efecto de las colas pesadas originado por los eventos extremos y los diferentes niveles de asimetría asociados a la alta volatilidad en aglomeraciones en los mercados financieros de economías emergentes requieren de modelos más sofisticados para su modelación. El objetivo de esta investigación es aplicar la teoría de valores extremos (TVE) para cuantificar el riesgo de la cola de los rendimientos diarios de la Bolsa Mexicana de Valores bajo la agregación del riesgo del tipo de cambio durante el periodo de enero de 1971 a diciembre de 2010. Este análisis sugiere el uso de la distribución de valor extremo generalizada y la técnica de bloques máximos para explicar el comportamiento asintótico de los rendimientos extremos. Los resultados empíricos muestran el potencial de la medida VaR basada en la TVE para capturar las propiedades de colas pesadas en los rendimientos de los mercados accionarios altamente volátiles a diferencia de los modelos VaR convencionales. Además, la evidencia empírica demuestra que los inversionistas internacionales con posiciones financieras largas están más propensos a experimentar pérdidas más grandes que los que toman posiciones cortas en el mercado accionario mexicano durante periodos de crisis financieras y depreciaciones de la moneda local.

Abstract

The effect of heavy tails due to rare events and different levels of asymmetry associated with high volatility clustering in the emerging financial markets requires sophisticated models for statistical modelling of such stylized facts. This article applies extreme value theory (EVT) to quantify tail risk on the daily returns of Mexican stock market under aggregation of foreign exchange rate risk from January 1971 to December 2010. This study focuses on the maximum-block method and generalized extreme value distribution (GEVD) to model the asymptotic behavior of extreme returns in US dollars. The empirical results show that EVT-Based VaR measured at high confidence levels performs better than simulation historical and delta-normal VaR models on capturing fat-tails in the returns of highly volatile stock markets. Additionally, international investors holding long positions in Mexican stock market are more prone to experience larger potential losses than investors with short positions during local currency depreciation and financial crisis periods.

Introducción

En la actualidad, los mercados de divisas al contado son los más líquidos y grandes en el nivel global. En su conjunto las operaciones de los mercados de divisas superan a las operaciones bursátiles de los principales mercados de dinero y capital. En los últimos años, el desarrollo de los mercados cambiarios no sólo se ha reflejado de manera positiva en la conducción del comercio nacional e internacional, la política monetaria y la competitividad de los países desarrollados y en vías de desarrollo, sino también en la captación de enormes flujos de capital de inversión directa y de portafolio. En este sentido, el dólar de Estados Unidos, a pesar de los problemas de su economía, es la divisa más importante del mundo porque es la dominante de reservas internacionales y sus transacciones constituyen casi la mitad de las negociaciones globales de divisas; finalmente, es la moneda contractual de una gran mayoría de las transacciones reales y financieras internacionales.

Recientemente, esta divisa ha experimentado un descenso significativo en su valor con respecto a las principales monedas duras y algunas monedas exóticas del mundo durante el periodo 2000-2010; por ejemplo, 30.81%, 19.70%, 23.47%, 40.73%, 20.29% y 7.86% en relación con el dólar canadiense, yen, euro, franco suizo, yuan chino y real brasileño, respectivamente. De ahí que su posición de seigniorage sea continuamente cuestionada; sin embargo, debido a la fragilidad de la economía mexicana y su excesiva dependencia de sus relaciones económicas con Estados Unidos, el dólar ha mantenido su fortaleza frente al peso, a tal grado de alcanzar una apreciación del 31.51% durante el mismo periodo. Desde la segunda mitad de los setenta del siglo pasado, después del colapso del sistema de paridad fija de los tipos de cambio, el comportamiento de la variabilidad del peso mexicano se ha convertido en un tópico de mayor relevancia para la competitividad y desempeño de la actividad económica del país, en particular para el proceso de la inversión de portafolio internacional.

Desde el punto de vista teórico y empírico, la interrelación entre los precios de las acciones y los tipos de cambio ha sido ampliamente documentada aunque con resultados variables para diferentes periodos (Ramasamy y Yeung, 2005). De acuerdo con Michaelides (2003), el fenómeno de la exposición del tipo de cambio extranjero tiene un efecto negativo en el comportamiento de la inversión de portafolio internacional; es decir, reduce su atractivo para los inversionistas adversos al riesgo. Además, evidencia empírica reciente ha demostrado que esta variable macroeconómica juega un papel determinante en la composición, diversificación y rebalanceo del portafolio de inversión como alternativa para reducir el riesgo no sistemático (Hau y Rey, 2004; Gourinchas y Rey, 2005).

Por su parte, la inestabilidad en los mercados cambiarios incrementa significativamente tanto la volatilidad como los rendimientos extremos en los mercados accionarios, creando serios problemas en la estimación exacta de las pérdidas potenciales en las inversiones de portafolio al reducir el desempeño de las medidas convencionales de valor en riesgo (VaR, por sus siglas en inglés) propuestas por el Comité de Basilea.¹ Estas aproximaciones populares utilizadas en la regulación bancaria y la administración del riesgo de mercado en los últimos años se dividen en dos grupos: los métodos paramétricos y los no paramétricos. Los métodos paramétricos conocidos como los modelos delta-normal y GARCH (con innovaciones normales y t-student) suelen subestimar el riesgo de los portafolios de inversión.

Esto se atribuye a su limitado alcance para capturar apropiadamente el efecto de las colas pesadas o anchas originado por los eventos extremos, los cuales se concentran fuera del interior de la distribución de rendimientos (Duffie y Pan, 1997; Vlaar, 2000). Por su parte, el método de simulación histórica o no paramétrico es más eficiente para recoger los eventos extremos originados por desplomes bursátiles, burbujas financieras y devaluaciones en los tipos de cambio que suelen ocurrir no sólo en periodos recesivos, sino también durante auges económicos. No obstante, la naturaleza discreta de los rendimientos en el interior de la distribución empírica y la carencia de información muestral en las colas conllevan a sobrestimar el riesgo de mercado (Zhao et al., 2010; De Jesús y Ortiz, 2011).

En este contexto, una medida de riesgo alternativa más consistente que calcula mejor la severidad de las pérdidas potenciales que exceden el nivel del VaR es la medida de exceso esperado (Expected Shortfall) introducida por Artzner et al., (1997 y 1999), también conocida como valor en riesgo condicional (CVaR). Estas medidas son propuestas en la literatura financiera como medidas de riesgo coherentes, ya que comparten las mismas propiedades cuando se aplican a distribuciones continuas. La medida CVaR, desde el punto de vista financiero, estima el riesgo de la cola de la distribución de manera más eficiente y conservadora al incorporar tanto la frecuencia como el tamaño de los eventos extremos. Además, satisface la propiedad de subaditividad y la condición de convexidad que permite realizar un análisis del riesgo-rendimiento en el contexto de la teoría moderna del portafolio de Markowitz (Rockafellar y Uryasev, 2000). No obstante, la medida CVaR bajo el supuesto de normalidad y para altos niveles de confianza subestima el riesgo al no lograr recoger toda la información de las colas de la distribución de rendimientos. Este problema, en gran medida, afecta el comportamiento de los inversionistas racionales, puesto que no cuentan con suficiente información para tomar decisiones con respecto a la entrada o salida del mercado.

Por lo anterior, el desafío de la cuantificación del riesgo se vuelve una tarea más importante y crucial en las economías emergentes, donde la combinación de un desplome en el mercado de capital y una devaluación abrupta en el tipo de cambio puede propiciar catastróficas pérdidas en las posiciones financieras corta y larga de los inversionistas internacionales, principalmente como resultado de las grandes fluctuaciones en liquidez de los mercados; esto es, variaciones en los precios de los activos y en el volumen de dinero caliente derivado de la exuberancia irracional presente en las inversiones de portafolio y los fondos de cobertura internacionales.

La naturaleza de los movimientos extremos en los mercados accionarios es rara por definición; por ello, su estudio y estimación para altos percentiles, en general, representan una tarea difícil para los académicos y analistas financieros, puesto que se requiere de un conjunto grande de datos y la utilización de técnicas estadísticas más sofisticadas. En años recientes, la teoría de valores extremos (TVE) ha sido utilizada ampliamente por los académicos y los participantes en los mercados financieros con el fin de modelar apropiadamente el comportamiento asintótico de las colas de la distribución de rendimientos en un contexto univariado y, al mismo tiempo, estimar las pérdidas potenciales en términos de moneda local en los países industrializados y emergentes. Sin embargo, la literatura existente sólo ha aplicado la teoría de valores extremos a los rendimientos de los índices bursátiles y los principales tipos de cambio de manera individual, por lo que la evidencia empírica sobre el análisis de los rendimientos financieros extremos incorporando el factor de riesgo del tipo de cambio y aplicando una distribución de colas pesadas es aún muy limitada en la literatura financiera, tanto en economías desarrolladas como emergentes. Contribuyendo a sobreponer esta limitación, el objetivo de esta investigación es aplicar la TVE para estimar el riesgo de la cola en los rendimientos de la Bolsa Mexicana de Valores (BMV) bajo la agregación del efecto de la variabilidad del tipo de cambio peso/dólar estadounidense para el periodo del 2 de enero de 1971 al 31 de diciembre de 2010, que incluye la adopción de varios regímenes cambiarios, inicialmente de una estrategia de tipo de cambio fijo a la final adopción del libre mercado de cambios desde 1996.² La motivación de la investigación es que, como mercado emergente con fundamentos macroeconómicos débiles e importantes cambios estructurales y regulatorios en la actualidad, el Índice de Precios y Cotizaciones de la BMV proporciona una extraordinaria oportunidad para analizar un significante conjunto de datos extremos originados no sólo por las crisis financieras, burbujas especulativas y auges económicos, sino también por las recurrentes devaluaciones y altas depreciaciones del peso mexicano a lo largo de este periodo de estudio. Ante esta situación, la pregunta que surge es la siguiente: ¿cómo se comportan las colas de la distribución de rendimientos de la BMV bajo la agregación del riesgo cambiario?

La presente investigación está estructurada de la siguiente forma. Después de esta introducción, en la sección siguiente se presenta la revisión de la literatura; posteriormente, se hace una descripción de los datos financieros y análisis de sus propiedades estadísticas, así como el comportamiento de la volatilidad condicional, resaltando el comportamiento de las colas pesadas o anchas; más adelante se revisa el marco teórico de la TVE, la aproximación estadística de la distribución de valor extremo generalizada y la presentación de las medidas VaR basadas en la TVE; después se aplica la TVE para estimar el riesgo financiero de los rendimientos de la BMV expresados en dólares; finalmente, en la última parte, se resumen los resultados empíricos y se presentan las conclusiones de este análisis para la administración de riesgos.

Revisión de la literatura

Desde el punto de vista teórico y práctico, el principal problema que han enfrentado académicos y analistas financieros en las diversas aplicaciones financieras, particularmente en aquellas relacionadas con la administración de riesgos, ha sido la selección apropiada de la distribución de probabilidad para la modelación asintótica de los rendimientos financieros. Diversos análisis tradicionales han propuesto la distribución normal para describir el comportamiento de los rendimientos financieros; sin embargo, la presencia de movimientos extremos o atípicos observados en la mayoría de las series financieras ha reducido su potencial para capturar totalmente el exceso de curtosis y los diferentes niveles de asimetría. De hecho, la omisión del fenómeno de las colas pesadas, leptocurtosis y la forma apropiada de la distribución de rendimientos puede generar significativos sesgos en la estimación del VaR y, con ello, insuficientes requerimientos de capital para hacer frente a las pérdidas potenciales derivadas por cambios inesperados en los factores de riesgo de las posiciones de mercado de las instituciones financieras.

Por consiguiente, múltiples modelos han sido sugeridos en la literatura financiera para capturar la asimetría y las colas pesadas de los rendimientos financieros, entre ellos se incluyen las distribuciones α-stable, mixtura de normales, t-student y los procesos de difusión de saltos (Mandelbrot, 1963; Fama, 1965; Hull y White, 1998; Heikkinen y Kanto 2002; Jorion, 1988). Por su parte, el problema de la asimetría presentado en los modelos anteriores ha sido tratado por Azzalini (1985 y 1986), así como Fernandez y Steel (1998), quienes con sólo agregar un parámetro de asimetría obtienen la distribución normal sesga y la distribución t-student sesgada, respectivamente,³ pese a que la mayoría de las distribuciones anteriormente mencionadas recogen apropiadamente los efectos de las colas pesadas o anchas y la asimetría observados en los rendimientos financieros. La carencia de soluciones de forma cerrada y la limitación en el análisis de las colas de manera independiente reducen el potencial de estas distribuciones en la estimación del verdadero riesgo extremo.

En respuesta a las inconsistencias y desventajas que presentan los modelos previos para capturar la magnitud y la probabilidad de los eventos extremos. La TVE proporciona un conjunto de herramientas sólidas para entender y modelar el comportamiento estadístico de los eventos catastróficos raros capturados en las colas de las distribuciones empíricas de las series financieras. Aunque el desarrollo de la TVE se inició en los campos de la hidrología, climatología y seguros, su aceptación como herramienta complementaria en la administración del riesgo cuantitativo en los mercados financieros ha crecido notablemente durante las últimas décadas, principalmente para el caso de economías industrializadas. Un trabajo pionero se atribuye a Longin (2000), quien estima el riesgo de los rendimientos del índice accionario S&P500, y encuentra que la medida VaR basada en la TVE proporciona mejores resultados que los modelos paramétricos. Por su parte, un análisis que modela el riesgo catastrófico en los mercados internacionales de Estados Unidos, Japón y Londres incluye a Cotter (2006). Un trabajo que contribuye a la estimación del parámetro del índice de la cola y cuantificación del riesgo extremo incluye a Danielsson y de Vries (2000). Utilizando datos de frecuencia baja de los índices accionarios DAX y S&P500, McNeil (1999), así como McNeil y Frey (2000) muestran el potencial de la distribución de Pareto generalizada (DPG) en la medición del riesgo relacionado con las colas de la distribución de rendimientos. Asimismo, Gilli y Këllezi (2006) aplican la técnica de valores extremos para medir el VaR y CVaR para los índices accionarios Dow Jones Euro Stoxx 50, FTSE100, Hang Seng, Nikkei225 y S&P500, utilizando la DPG.

Con respecto a la evidencia empírica en los mercados emergentes, destacan los trabajos de Jondeau y Rockinger (2003) y Susmel (2001), quienes emplean la DPG para comparar el comportamiento asintótico de las colas de la distribución entre mercados industrializados y emergentes. Mientras que Gencay y Selcuk (2004) estiman el VaR para diferentes mercados emergentes utilizando como herramienta la TVE y la DPG. Fernandez (2003) presenta evidencia empírica sobre los rendimientos del índice accionario chileno (IPSA). Por su parte, da Silva y Mendes (2003) y Ho et al. (2000) usan la teoría estadística de extremos basada en el procedimiento de bloques máximos para analizar las pérdidas catastróficas en los principales mercados accionarios asiáticos. Assaf (2006) aplica la TVE para analizar los mercados financieros de Egipto, Jordania, Marruecos y Turquía, y encuentra evidencia empírica de que los rendimientos financieros presentan propiedades de colas pesadas significativamente. Analizando la cola inferior de la distribución asintótica de rendimientos en el mercado accionario de Atenas, Tolikas y Brown (2006) muestran que los parámetros de la distribución de valores extremos son muy variables y la cola analizada adopta una tendencia cada vez menos pesada a través del tiempo. Finalmente, un estudio más reciente que analiza los rendimientos extremos y calcula el VaR y CVaR en los mercados accionarios de Brasil y México incluye a De Jesús y Ortiz (2011).

En cuanto a estudios empíricos que han aplicado las técnicas de la TVE para analizar el comportamiento de los rendimientos extremos en los tipos de cambio destaca el trabajo de Danielsson y de Vries (1997), quienes estiman el índice de la cola para rendimientos intradía de tres divisas del mercado Forex.⁴ De manera similar, Loretan y Phillips (1994) aplican la TVE para analizar el comportamiento asintótico de las colas de la distribución de rendimientos para las principales divisas duras de Europa y yen japonés. Por su parte, Hols y de Vries (1991) y Koedijk et al. (1990) proporcionan evidencia empírica para los rendimientos semanales del dólar canadiense y las divisas del Sistema Monetario Europeo con referencia al dólar estadounidense, respectivamente. Cuatro estudios más recientes también aplican la TVE para estimar el VaR de los tipos de cambio. Aggarwal y Qi (2009) analizan el comportamiento asintótico de los valores extremos en los tipos de cambio de nueve países de la región de Asia con respecto al dólar estadounidense y el yen japonés. Asimismo, Gavril (2009) presenta evidencia sobre el desempeño limitado de las metodologías tradicionales VaR y obtiene resultados más confiables aplicando la TVE para el caso del euro con respecto a cuatro divisas: franco suizo, libra esterlina, leu de Rumania y dólar de Estados Unidos. Por su parte, Yang (2010) estima el VaR del yuan de China contra el dólar de Estados Unidos y el euro; emplea para su estudio un modelo GARCH y la teoría de valores extremos. Yang reporta que el ajuste de las colas de la GDP es muy alto y el VaR de gran confiabilidad. Finalmente, Wang, Wu, Chen y Zhou (2010) muestran que el alto grado de ajuste de la distribución de Pareto generalizada para las observaciones de las colas de los rendimientos del yuan chino, permite obtener medidas VaR y CVaR más robustas para la estimación de los riesgos en los tipos de cambio. No obstante, la evidencia empírica sobre valores extremos en los tipos de cambio exóticos de la región de América Latina es casi nula debido a la carencia de datos, en particular para los países de Argentina, Brasil y México.

Descripción y análisis de los datos financieros

Con el fin de estudiar el efecto de la variabilidad del tipo de cambio en los rendimientos y riesgos de la Bolsa Mexicana de Valores esta investigación utiliza los precios de cierre diarios del Índice de Precios y Cotizaciones de la BMV, así como el tipo de cambio para el periodo del 4 de enero de 1971 al 31 de diciembre de 2010. Cabe destacar que el periodo de estudio incluye las principales crisis y devaluaciones del peso mexicano e incluso el choque de la reciente crisis financiera global, cuyo impacto se reflejó en los mercados accionarios y cambiarios de todo el mundo. Ambas series financieras fueron obtenidas de la base de datos de Bloomberg. La serie de los niveles del índice bursátil se transforma a dólares estadounidenses, totalizando 10 047 observaciones después de obtener las series estacionarias; es decir, los rendimientos r_t = 100(ln(P_t)-ln(P_t-1)). La moneda base para los análisis por realizarse es el dólar de Estados Unidos porque en las últimas dos décadas las inversiones internacionales, denominadas en dólares en la Bolsa Mexicana de Valores, han sido mayoritarias, más del 90%, y en relación con la capitalización total los montos de dicha inversión han fluctuado entre 45% y 65%; adicionalmente, la inversión de portafolio extranjera frecuentemente ha sido mayor que la inversión extranjera directa; dada la volatilidad de la Bolsa Mexicana de Valores y los retiros masivos de inversiones en la Bolsa podrían ocasionar gran inestabilidad e incluso crisis de la economía mexicana; finalmente, debe reconocerse que el dólar de Estados Unidos es la divisa de referencia internacional para los inversionistas internacionales.⁵

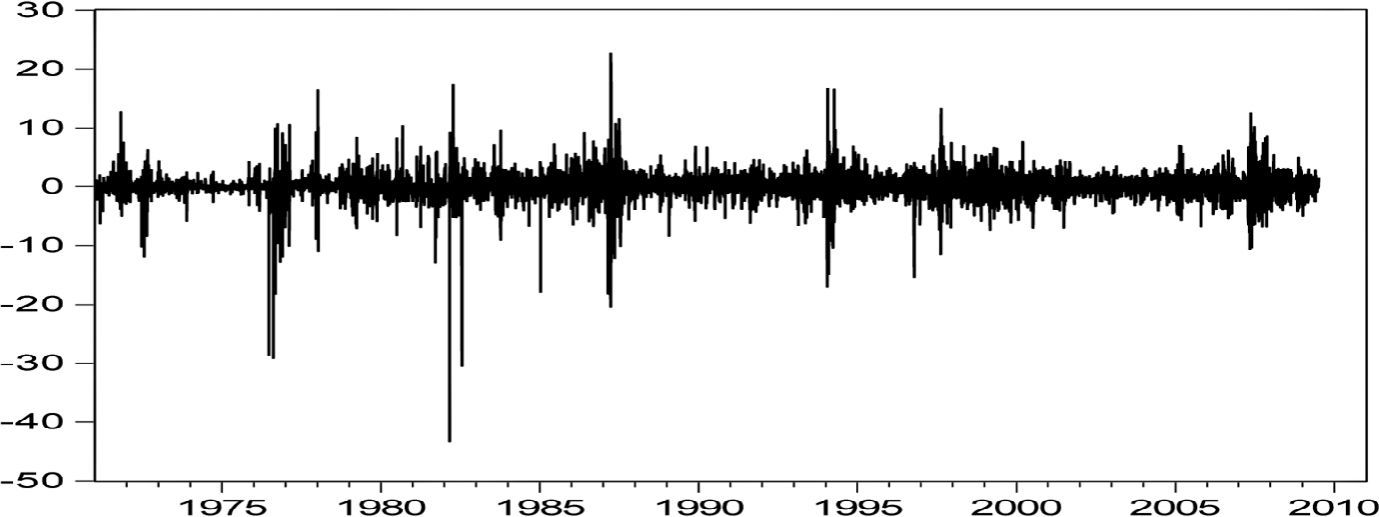
El cuadro 1 resume las propiedades estadísticas de los rendimientos en dólares de la BMV. Durante el periodo de estudio, el índice bursátil ha experimentado un crecimiento espectacular alcanzando un rendimiento promedio positivo de 0.0556% (14.01% anual). La presencia de rendimientos altos y positivos en la BMV se atribuye al hecho de que, como economía emergente, ha logrado una mayor expansión económica que otros países de América Latina y, por ende, ha atraído crecientes inversiones a sus mercados de capital como resultado de sus atractivos rendimientos de la liberalización de los flujos de capital entre países industrializados y emergentes, pero —sobre todo— los esfuerzos de las autoridades por mantener la eficiencia y transparencia en sus respectivos mercados financieros, reduciendo inmediatamente la magnitud de potenciales choques de liquidez negativos. Asimismo, la BMV se ha convertido en un importante mecanismo donde es posible invertir por una gama más amplia de inversionistas sofisticados, en particular, los fondos de pensiones, las aseguradoras y las sociedades de inversión estadounidenses que buscan estrategias de diversificación, formando portafolios grandes de títulos de capital que en gran medida replican a este índice accionario emergente a pesar de que su entorno continúa siendo riesgoso. Por esta razón, los rendimientos expresados en dólares presentan una alta desviación estándar del 2.07% (521.68% anual). Este hecho también es sustentado por la amplia diferencia entre el rendimiento promedio y los rendimientos mínimo y máximo observados, resultado de la alta e inestable volatilidad exhibida a través de tiempo, especialmente en los periodos 1976-1988, 1995-1998 y 2008-2009 cuando se presentaron las principales devaluaciones abruptas en el peso mexicano, como se puede observar en la gráfica 1. De hecho, cabe resaltar que el rendimiento mínimo ocurrió el 6 de agosto de 1982 durante la crisis de la deuda externa, mientras que el rendimiento máximo ocurrió el 18 de noviembre después del desplome del índice accionario S&P500 y durante un periodo de extrema volatilidad. De esta manera, la evidencia confirma que la BMV está asociada a un alto riesgo como consecuencia de la sensibilidad de los rendimientos accionarios a las variaciones del tipo de cambio.

Cuadro 1.

Estadísticas básicas de los rendimientos diarios en dólares de la BMV

Media	Máximo	Mínimo	Desv. Est.	Sesgo	Curtosis	JB
0.0556	22.7033	-43.2673	2.0702	-2.2307	47.0266	819770

Nota: Los resultados de las estadísticas básicas son expresados en porcentajes para el periodo de análisis del 4 de enero de 1971 al 31 de diciembre de 2010. Desv. Est. representa la desviación estándar de los rendimientos; JB es el estadístico Jarque-Bera de la prueba de normalidad.

Gráfica 1.

Rendimientos en dólares de la Bolsa Mexicana de Valores

Asimismo, los rendimientos accionarios se desvían significativamente de la normalidad; es decir, presentan propiedades de colas pesadas o anchas debido al exceso de curtosis (47.02) y sesgo significativamente negativo (-2.23). La evidencia de sesgo negativo demuestra que los rendimientos extremos negativos suelen ocurrir más frecuentemente que los rendimientos extremos negativos; este hallazgo indica que las colas de la distribución de rendimientos presentan diferentes particularidades estadísticas. La pronunciada asimetría cargada a la izquierda observada en los rendimientos de la BMV es principalmente atribuida a las severas y recurrentes devaluaciones experimentadas por el peso mexicano a lo largo de la historia. Este hecho estilizado característico de los mercados accionarios industrializados es opuesto a los resultados obtenidos en las principales economías emergentes de América Latina, donde los rendimientos accionarios en moneda local presentan un ligero comportamiento de asimetría en la distribución de rendimientos (De Jesús y Ortiz, 2011). El hecho estilizado de la asimetría es ampliamente explicado por la alta variabilidad y posibles cambios estructurales que incrementan la volatilidad de los rendimientos financieros.

La gráfica 1 muestra que las series de los rendimientos financieros presentan periodos de tranquilidad donde los precios de los índices accionarios se comportan más o menos estables seguidos de periodos relativamente volátiles, caracterizados por cambios grandes en los precios que generalmente ocurren en racimos; es decir, evidencia de heteroscedasticidad condicional, también comúnmente conocido como el efecto clustering o volatilidad en aglomeraciones demostrado por Engle (1982) y Bollerslev (1986).

De acuerdo con la estimación del cuarto momento, los rendimientos de la serie financiera presentan evidencia de exceso de curtosis extremadamente alta y estadísticamente significativa. Esto confirma que las colas de la distribución de rendimientos de la BMV tienden a ser más pesadas que las colas de la distribución normal, obviamente atribuido a la mayor densidad probabilística. Con base en los estudios empíricos de Fama (1965), Praetz (1972), Blattberg y Gonedes (1974), Kon (1984), Tucker (1992), así como Kim y Kon (1994), el fenómeno de leptocurtosis ha sido significativamente más fuerte en los rendimientos de frecuencia alta o diarios que en los datos de frecuencia baja u horizontes de tiempo más largos. La ausencia de normalidad en los rendimientos financieros también es confirmada por la prueba estadística Jarque-Bera debido su alto valor y probabilidad igual a cero.

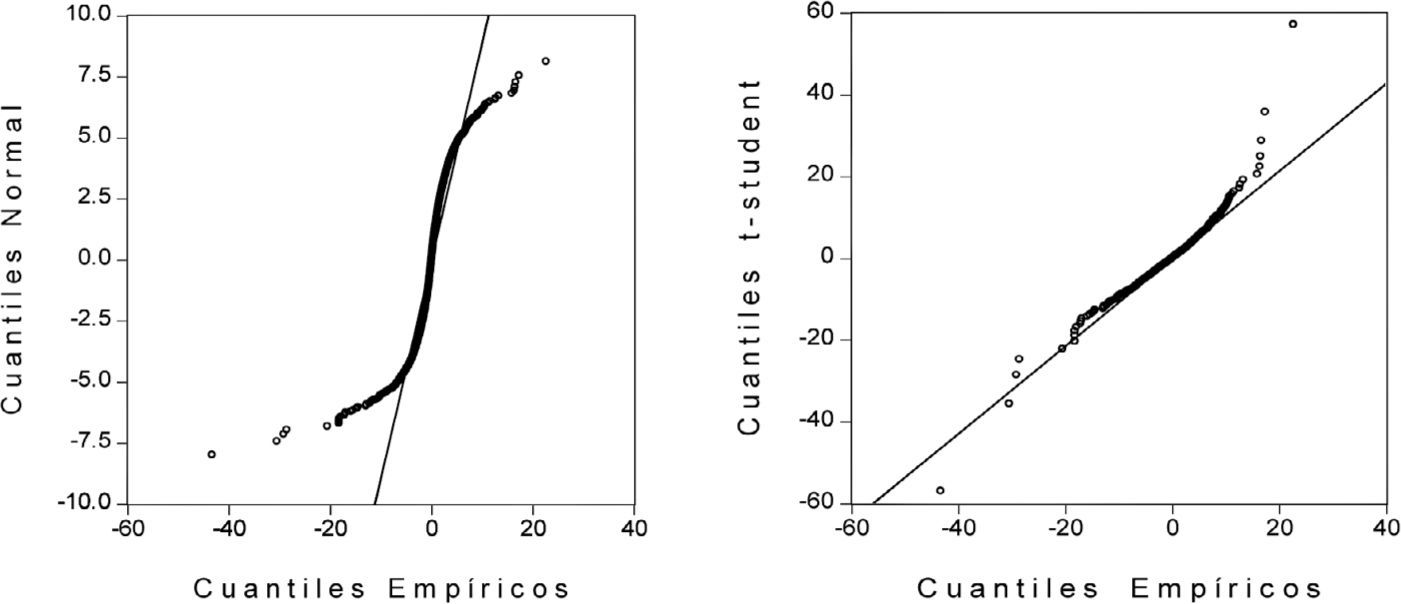
Por otra parte, el gráfico QQ es considerado otra herramienta estadística alternativa que permite explicar la estructura principal en los mercados accionarios y el comportamiento asintótico de los valores extremos capturados en las colas de la distribución de rendimientos de las series financieras. La gráfica 2 muestra los cuantiles de la distribución empírica contra los cuantiles de las distribuciones normal y t-student, respectivamente. En ambas gráficas claramente se puede observar que los rendimientos de la BMV presentan propiedades de colas pesadas o anchas y diferentes niveles de asimetría, puesto que las colas de la distribución empírica son más anchas que las colas de la distribución normal y t-student aunque en menor medida con respecto a esta última. Aunque el fenómeno de las colas pesadas es característico de las series financieras de frecuencia alta, este hecho estilizado es más pronunciado y evidente en los mercados accionarios emergentes que en los industrializados porque si los rendimientos financieros realmente siguen una distribución normal todas las observaciones deberían permanecer sobre la línea recta de 45° cuando se grafican contra los cuantiles de la distribución normal. Sin embargo, las observaciones se desvían de la línea recta en los puntos extremos o colas, presentando mayor variabilidad que las observaciones capturadas en la parte central de la distribución empírica.

Gráfica 2.

Q-Q de los rendimientos diarios contra las distribuciones normal y t-student

De esta manera, el fenómeno de las colas pesadas originado por los eventos extremos o atípicos y los diferentes niveles de asimetría en los rendimientos financieros asociados a la volatilidad en aglomeraciones requieren un trato y estudio especial; esto es, teorías financieras robustas enfocadas específicamente a explorar la naturaleza de la distribución de rendimientos financieros extremos. En este sentido, la técnica de la teoría de valores extremos juega un papel importante en la descripción del comportamiento asintótico de los eventos raros capturados profundamente en las colas de la distribución empírica.

Teoría de valores extremos

Distribución de valor extremo generalizada y estimación de los parámetros

Los eventos atípicos o extremos exhibidos en los mercados financieros son definidos como los rendimientos diarios más pequeños y grandes. Estos movimientos extremos que experimentan los precios de las series financieras están asociados a las correcciones de los mercados financieros durante periodos normales de operación y periodos de extrema volatilidad, derivados de los colapsos financieros tales como las caídas precipitosas en los índices accionarios, crisis financieras, devaluaciones de las monedas, burbujas financieras o escándalos financieros, y que muchas de las veces son producto de los contagios financieros como fue el caso de la crisis subprime. De acuerdo con el análisis empírico de la distribución de frecuencia de pérdidas, Johansen y Sornette (2001) han demostrado que los colapsos financieros presentan características estadísticas muy similares a la de los outliers, por lo que deben ser tratados y estudiados de manera especial con modelos más sofisticados.

Los fundamentos matemáticos de la TVE basados en contribuciones heurísticas y discusiones teóricas fueron originalmente propuestos por Fisher y Tippett (1928) y Gnedenko (1943). Existen dos teorías para modelar el comportamiento de los valores extremos: el procedimiento estadístico de los bloques máximos y la técnica de picos sobre un umbral (Peaks over Threshold).⁶ Este estudio aplica la primera aproximación para analizar los rendimientos de las colas y cuantificar el riesgo catastrófico asumido por los inversionistas internacionales. La técnica de bloques máximos se centra en la colección de observaciones máximas y mínimas extraídas de cada uno de los bloques o submuestras durante un periodo de tiempo fijo. El uso del método de bloques máximos o mínimos reduce la dependencia exhibida en los datos financieros de frecuencia alta ocasionada por la heteroscedasticidad condicional (Diebold et al., 2000). Desafortunadamente, la inexistencia de una regla óptima o método estadístico robusto obliga a seleccionar la longitud del bloque de manera arbitraria.

El teorema de Fisher-Tippett-Gnedenko es la base fundamental de la TVE. Supóngase que R₁, R₂, …,R_n son variables aleatorias independientes e idénticamente distribuidas con función de distribución F_R(r) y definiendo a M_n = Máx {R₁, R₂, …, R_n} como el valor máximo de las variables aleatorias.⁷ Además, si existen dos sucesiones de números normalizadas {β_n} y {α_n}, con α_n > 0 tal que

⁸

Donde es una función de distribución no degenerada, entonces pertenece a una de las siguientes familias:

Gumbel: H(r)=exp{-exp(-r)},-∞

De acuerdo con la reparametrización, sugerida por Jenkinson (1955), esta familia de distribuciones se puede expresar como la distribución de valor extremo generalizada (DVEG); es decir,

Done

Para n suficientemente grande e introduciendo los parámetros de localización β_n y escala α_n > 0 la función de distribución no degenerada se puede expresar de la siguiente manera:

si y sólo si la función de distribución F_R(r) pertenece al máximo dominio de atracción de H_ξn(r) y donde ξ_n = 1/τ representa el índice de la cola de la distribución de valor extremo generalizada.

En este contexto, el signo del índice de la cola es clave para describir el comportamiento de la cola de la distribución asintótica e identificar el tipo de distribución que se utiliza para ajustar los datos financieros reales. De esta manera, si el pará-metro del índice de la cola de la distribución es estrictamente negativo implica que la función de distribución F_R(r) se encuentra en el máximo dominio de atracción de la distribución de Fréchet generalmente válida para modelar las series financieras. Existen varios casos particulares de distribuciones cuyas colas decaen en forma polinomial que incluyen a las distribuciones α-estable, Cauchy, t-student y la mixtura de normales entre las más importantes. Cuando ξ_n > 0 se dice que la función de distribución F_R(r) pertenece al máximo dominio de atracción de la distribución de Weibull, la cual carece de eficiencia para explicar el comportamiento asintótico de los rendimientos de las series financieras. Algunos ejemplos de estos tipos de distribuciones son la uniforme y la beta. Finalmente, si ξ_n = 0, la función de distribución F_R (r) se encuentra en el máximo dominio de atracción de la distribución de Gumbel que incluye a las distribuciones normal, exponencial, gama y lognormal. Esta última distribución se caracteriza por tener una cola pesada o ancha más moderada.

Por su parte, la estimación de los parámetros de la DVEG implica una tarea verdaderamente difícil en el análisis y estimación de los percentiles de los rendimientos financieros extremos, en particular, el parámetro del índice de la cola. En este marco, existen varias técnicas para estimar los parámetros de localización, escala e índice de la cola de la DVEG entre las más potentes se encuentran el método de máxima verosimilitud, el método de momentos y el método de momentos de probabilidad ponderado. Cada uno de estos métodos tiene sus ventajas y desventajas estadísticas, principalmente cuando se depende del tamaño y frecuencia de los eventos raros o atípicos.

En este análisis se emplea el método de máxima verosimilitud en combinación con la técnica de bloques máximos. Este procedimiento proporciona estimadores consistentes y asintóticamente normales, lo cual permite obtener errores estándar e intervalos de confianza. Además, la evidencia empírica ha sustentado que los estimadores de máxima verosimilitud son más eficientes; esto es, satisfacen las condiciones de regularidad al menos para ξ_n > –0.5 e independencia en los datos, incluso las propiedades de los estimadores de máxima verosimilitud aún se cumplen ante la presencia de dependencia en los datos, pero siempre y cuando la interdependencia sea débil (Smith, 1985).

De esta manera, las funciones de verosimilitud de la DVEG para los rendimientos máximos y mínimos están definidas por el logaritmo de la función de densidad conjunta de las observaciones, es decir,

En consecuencia, los parámetros desconocidos de la DVEG son estimados maximizando las funciones de verosimilitud logarítmicas para una muestra específica, la cual se derivará del tamaño del bloque seleccionado.

Prueba de bondad de ajuste

Una importante tarea complementaria, que se debe llevar a cabo una vez que los parámetros desconocidos de la DVEG han sido estimados, es cuantificar la incertidumbre del modelo estimado. En otras palabras, la validación estadística de que tan bueno es el modelo para explicar apropiadamente el comportamiento asintótico de los datos disponibles a través de pruebas de bondad de ajuste. En la literatura, desde un punto de vista estadístico, existen diversas pruebas de bondad de ajuste, entre las más importantes se pueden mencionar la prueba de Kolmogorov, prueba de Sherman y prueba de Anderson-Darling. La mayoría de ellas verifican la bondad de ajuste del modelo estimado comparando las distribuciones teórica y empírica como una medida distancia bajo la hipótesis nula de que los rendimientos financieros siguen una distribución de valor extremo generalizada. Este análisis utiliza la prueba de Anderson-Darling (AD) para validar el modelo estimado, puesto que se centra principalmente en medir las discrepancias en las colas de la distribución asintótica.

El estadístico de la prueba de Anderson-Darling (1954) se define de la siguiente forma:

donde F_n(r) es la función de distribución empírica de la variable aleatoria, F^R(r) es la función de distribución acumulada estimada, en este caso la DVEG, n representa el tamaño de la muestra utilizada para estimar los parámetros desconocidos de la distribución asintótica y r₁ ≤ r₂ ≤ … ≤ r_n es su muestra ordenada.

De hecho, literatura existente ha demostrado que la prueba de Anderson-Darling, en muestras pequeñas, suele ser la más poderosa entre un amplio conjunto de pruebas de bondad de ajuste. Esto se debe a que utiliza una función ponderada que proporciona mayor peso a las observaciones de la región de las colas que a las observaciones concentradas en el interior de la distribución (Stephens, 1976; D’Agostino y Stephens, 1986).

La prueba de razón de verosimilitudes es otro método estadístico alternativo importante que permite sustentar la estabilidad de la distribución de valor extremo generalizada. Este análisis proporciona información adicional acerca de los estimadores del índice de la cola para cada periodo de tiempo o tamaño del bloque y el tipo de distribución asintótica utilizada para ajustar los rendimientos extremos. En otras palabras, la prueba estadística verifica que la estimación del parámetro del índice de la cola es significativamente diferente de cero. Este hecho implica que es inapropiado asumir que la distribución asintótica de los rendimientos extremos se encuentre en el máximo dominio de atracción de la distribución de Gumbel; es decir, la distribución de rendimientos de las series financieras tiene colas más pesadas o anchas que la distribución normal.

El estadístico de la prueba de razón de verosimilitudes se puede expresar de la siguiente forma:

donde l(θ^) es el valor máximo de la función logarítmica de verosimilitud de la distribución de valor extremo generalizada o modelo no restringido y l(θ^*) es el valor máximo de la función logarítmica de la distribución de Gumbel o modelo restringido. El estadístico sigue una distribución Chi cuadrada con un grado de libertad.⁹

Medidas VaR basadas en la teoría de valores extremos

La administración de riesgos cuantitativa en los mercados financieros define a la medida VaR como la máxima pérdida esperada de una posición de mercado o portafolio de inversión durante un horizonte de tiempo para un nivel de confianza dado. En este sentido, el VaR se puede definir como el c – percentil de la distribución de rendimientos F con signo negativo, es decir,

Las implicaciones económicas y financieras derivadas de la distribución de rendimientos extremos en la Bolsa Mexicana de Valores bajo la agregación del riesgo cambiario son ilustradas estimando el VaR para las posiciones financieras larga y corta. Para un nivel de probabilidad el percentil extremo se obtiene invirtiendo la DVEG, utilizando los parámetros de localización, escala e índice de la cola estimados.

De esta manera, el VaR para los rendimientos positivos correspondiente a la posición corta puede ser expresado como

Finalmente, el VaR para los rendimientos negativos correspondiente a la posición larga se puede expresar como

donde n representa el tamaño de la submuestra o bloque seleccionado para obtener los rendimientos extremos máximos o mínimos.

Resultados empíricos

Estimación y prueba de bondad de ajuste de los parámetros de la DVEG

Los hechos estilizados de las colas pesadas o anchas y los diferentes niveles de asimetría, aunados a la alta volatilidad en aglomeraciones exhibidos en los rendimientos en dólares de la Bolsa Mexicana de Valores, sugieren el uso de la teoría de valores extremos para estudiar, de manera independiente, el comportamiento asintótico de los rendimientos extremos capturados en las colas de la distribución empírica. La importancia de analizar ambas colas izquierda y derecha por separado tiene que ver con las severas pérdidas a que están expuestos los inversionistas internacionales cuando toman posiciones financieras largas y cortas en la BMV, respectivamente. El tamaño de la serie de los rendimientos de la BMV permite el uso de la aproximación de los bloques máximos, reduciendo así el fenómeno de la dependencia en los datos financieros de frecuencia alta. Los rendimientos extremos diarios son seleccionados para diferentes periodos; por ejemplo, mensualmente (n=21), trimestralmente (n=63) y semestralmente (n=126).

El cuadro 2 muestra los parámetros estimados de localización, escala e índice de la cola a través del método de máxima verosimilitud para ambos rendimientos extremos y los valores de la probabilidad de las pruebas estadísticas de Anderson-Darling y razón de verosimilitudes. De acuerdo con los resultados, el parámetro de localización se incrementa con el tamaño del bloque o submuestra seleccionada; por ejemplo, para el caso de los rendimientos extremos positivos cambia en tér-minos absolutos de 2.244 a 4.176, mientras que de 2.024 a 4.460 para los rendimientos extremos negativos. Este incremento significativo, similar en el promedio de los rendimientos extremos, obedece a diversos factores tales como los cambios estructurales, los altos índices de inflación, las crisis financieras, los auges económicos, pero especialmente a las recurrentes devaluaciones que ha experimentado la economía mexicana en los últimos cuarenta años, los cuales afectan directamente la dinámica de los rendimientos en dólares de la Bolsa Mexicana de Valores. Otra característica notable en relación con los parámetros de localización estimados es que sus valores son ligeramente más altos para los rendimientos extremos positivos, en particular, para los bloques mensuales y trimestrales. Una posible explicación de este hecho se puede atribuir a la inapropiada implementación de mecanismo de ajuste para mantener fijo al peso mexicano por parte de las autoridades gubernamentales y, así, evitar severas depreciaciones de la moneda en el corto plazo, particularmente durante los setenta y ochenta.

Cuadro 2.

Estimadores de máxima verosimilitud de la distribución de rendimientos extremos

Periodo	Rendimientos máximos			Rendimientos mínimos
	Mensual	Trimestral	Semestral	Mensual	Trimestral	Semestral
βn	2.244 (0.072)	3.369(0.090)	4.176 (0.127)	-2.024 (0.071)	-3.215 (0.107)	-4.460 (0.160)
αn	1.391 (0.058)	1.827(0.088)	2.132 (0.107)	1.356 (0.061)	1.894 (0.096)	2.570 (0.140)
ξn	-0.218 (0.036)	- 0.231 (0.063)	- 0.262 (0.091)	-0.348 (0.039)	- 0.395 (0.084)	- 0.454 (0.114)
p-AD	0.518524	0.655813	0.858987	0.182880	0.649617	0.669597
p-RV	0.0000000	0.0000020	0.0002816	0.0000000	0.0000000	0.0000006

Nota: Los parámetros desconocidos de la DVEG son estimados por el método de máxima verosimilitud. Los valores en paréntesis representan los errores estándar de los estimadores de máxima verosimilitud. En los dos últimos renglones se muestran las probabilidades de las pruebas de bondad de ajuste de Anderson-Darling y razón de verosimilitudes. Los valores p-AD muestran que los parámetros estimados de la DVEG son significativos para un nivel del 5%. Los valores p-RV demuestran que la hipótesis nula de que el índice de la cola es significativamente diferente de cero. Los valores en negritas significan que los índices de la cola son significativos a un nivel del 1% para cualquier tamaño de bloque.

Por su parte, la estimación del parámetro de escala también presenta la misma tendencia creciente a medida que se incrementa la longitud del bloque seleccionado. Considerando la cola derecha de la distribución de rendimientos, el parámetro de escala estimado se incrementa de 1.391 a 2.132, seguido por un incremento de 1.356 a 2.570 para la cola izquierda de la distribución de rendimientos. Estos hallazgos indican que los inversionistas internacionales de portafolio están asociados a un alto riesgo cuando toman posiciones financieras, ya sean cortas o largas, en los mercados accionarios emergentes. Un hecho estilizado que caracteriza a las economías con estructuras financieras y económicas frágiles.

Asimismo, claramente se puede observar que la distribución de rendimientos extremos se encuentra en el máximo dominio de atracción de la distribución de Fréchet. Este hecho se atribuye a que el valor estimado del índice de la cola para ambos rendimientos extremos es menor a cero; es decir, negativo, profundizando más en el comportamiento de las colas de la distribución de rendimientos extremos de la BMV. Los valores del índice de la cola para los rendimientos extremos positivos presentan una ligera variación de –0.218 a –0.262 a medida que el tamaño del bloque cambia de un mes a un semestre. Considerando la cola izquierda de la distribución de rendimientos extremos, todos los valores estimados del índice de la cola reportados tienden a ser cada vez más negativos al oscilar entre –0.348 y –0.454, pero con errores estándar más grandes a medida que se incrementa el tamaño del bloque o submuestra.

El signo negativo de los índices de la cola sustenta que la distribución empírica se encuentra en el máximo dominio de atracción de la distribución de valor extremo generalizada; no obstante, cabe resaltar que la cola de los rendimientos negativos suele ser mucho más pesada o ancha que la cola de los rendimientos extremos positivos; por ejemplo, para un bloque máximo semestral la cola izquierda de la distribución es notablemente más estable y pesada que la cola derecha (–0.454 contra –0.262). Esto se debe a que la economía mexicana ha experimentado una oleada de trastornos profundos que van desde crisis financieras, presiones inflacionarias, depreciaciones persistentes en el peso mexicano, hasta cambios de regímenes dramáticos desde la segunda mitad de los años setenta hasta la primera mitad de 2009, cuando la moneda nacional fue afectada por la crisis subprime originada en el periodo 2007-2008. Estos hallazgos son interesantes y algo sorprendentes comparados con la evidencia empírica de De Jesús y Ortiz (2011), quienes han documentado que el fenómeno de las colas pesadas tiene un comportamiento inverso en la misma BMV, pero para los rendimientos extremos en moneda local, y en donde la cola derecha tiende a ser ligeramente más pesada que la cola izquierda. Además, el comportamiento descendente del parámetro del índice de la cola estimado contradice los hallazgos de Tolikas y Brown (2006), en donde se confirma que la cola izquierda de la distribución de rendimientos extremos tiende a ser menos pesada o ancha a medida que se incrementa el tamaño del bloque. En consecuencia, la relevancia de los resultados empíricos obtenidos probablemente conducirán a estimaciones del VaR más conservadoras y, por consiguiente, suficientes requerimientos de capital a medida que el valor del índice de la cola sea más negativo o menor a cero.

La estabilidad de la distribución de rendimientos extremos de la BMV es sustentada por la prueba de bondad de ajuste de Anderson-Darling para los diferentes tamaños de bloques que se incrementan de un mes a un semestre. Los altos valores de las probabilidades del estadístico de AD que van de 0.1828 a 0.8589 muestran claramente que los parámetros estimados de localización, escala e índice de la cola son estadísticamente significativos a un nivel del 5%, particularmente para los rendimientos extremos negativos y el periodo de tiempo semestral. Este hecho indica que el comportamiento asintótico de los rendimientos extremos de la BMV es mejor explicado por la distribución de valor extremo generalizada. Además, el valor del índice de la cola para los rendimientos extremos negativos y positivos es mayor que –0.50 para cualquier longitud de tiempo seleccionado, indicando así la regularidad de las funciones logarítmicas de verosimilitud que evita, en esencia, la violación del supuesto de las propiedades asintóticas de los estimadores de máxima verosimilitud demostradas por Smith (1985). Por su parte, los valores nulos de las probabilidades de la prueba de razón de verosimilitudes indican que los parámetros estimados del índice de la cola son significativamente diferente de cero a un nivel del 1% para cualquier intervalo de tiempo seleccionado; es decir, se rechaza la hipótesis nula de que la distribución asintótica de los rendimientos extremos se encuentre en el máximo dominio de atracción de la distribución de Gumbel. En consecuencia, los resultados de los parámetros estimados no sólo presentan características muy similares, sino también alta estabilidad para los tres periodos estudiados en ambos rendimientos extremos máximos y mínimos.

Estimación de las medidas VaR basado en la teoría de valores extremos

Para ilustrar el potencial del uso de la distribución de rendimientos extremos de la Bolsa Mexicana de Valores en la estimación del VaR bajo la agregación del riesgo cambiario, este análisis realiza una comparación entre las medidas de valor extremo y las convencionales que incluyen al método delta-normal y el método de simulación histórica con el fin de evaluar el impacto de las diferentes distribuciones en la valuación de los riesgos de las inversiones de portafolio denominados en moneda extranjera; es decir, dólares estadounidenses. En el proceso de estimación de los parámetros de la distribución de valor extremo generalizada se utilizaron diferentes periodos que van desde un mes hasta un semestre. Para obtener una buena estimación del riesgo se utilizan los rendimientos extremos seleccionados sobre un periodo de un semestre, con el fin de omitir observaciones que se encuentran en el centro de la distribución de rendimientos que conllevan a violar las propiedades asintóticas del modelo de estimación. En este sentido, la selección arbitraria de un periodo amplio permite reducir el sesgo en los estimadores, pero incrementa sus errores estándar como resultado del número limitado de observaciones.

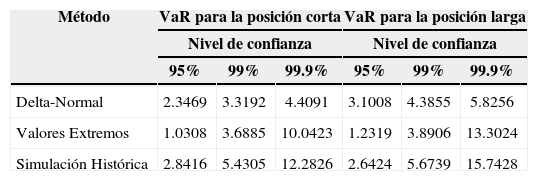
El cuadro 3 muestra los resultados empíricos de la estimación del riesgo extremo para las posiciones financieras corta y larga de las tres metodologías propuestas en el análisis para niveles de confianza del 95%, 99% y 99.9%. Para ambas posiciones financieras se puede observar que el método delta-normal subestima el VaR a diferencia de las medidas de riesgo basadas en las distribuciones empírica y de valores extremos para altos niveles de confianza, excepto para el 95%. Por ejemplo, la máxima pérdida equivale a $2.35 aplicando el método delta-normal contra $1.03 obtenido por el método de valores extremos para la posición corta; en tanto que para la posición larga equivale a $3.10 utilizando la distribución normal contra $1.23 de la distribución de valor extremo generalizada. En consecuencia, los resultados empíricos anteriores confirman la importancia de utilizar el percentil de la distribución de valor extremo generalizada como medida de riesgo en el análisis del VaR para altos niveles de probabilidad. De hecho, la TVE permite obtener mejor información del tamaño y frecuencia de los niveles del perfil del riesgo extremo a que están expuestos los inversionistas internacionales cuando el impacto de la volatilidad en el tipo de cambio afecta los rendimientos de la Bolsa Mexicana de Valores, la cual es omitida por los modelos incondicional y condicional con innovaciones normales.

Cuadro 3.

Estimación de las medidas VaR para las posiciones financieras corta y larga

Método	VaR para la posición corta			VaR para la posición larga
	Nivel de confianza			Nivel de confianza
	95%	99%	99.9%	95%	99%	99.9%
Delta-Normal	2.3469	3.3192	4.4091	3.1008	4.3855	5.8256
Valores Extremos	1.0308	3.6885	10.0423	1.2319	3.8906	13.3024
Simulación Histórica	2.8416	5.4305	12.2826	2.6424	5.6739	15.7428

Nota: Los resultados estimados del VaR para las posiciones financieras corta y larga están expresados en dólares estadounidenses para los niveles de confianza del 95%, 99% y 99.9%.

Sin embargo, analizando los resultados del VaR entre el método de simulación histórica¹⁰ y el modelo de valores extremos se puede observar que el modelo basado en la distribución empírica proporciona estimaciones más conservadoras del riesgo para cualquier nivel de confianza y posición financiera, es decir, sobreestima el riesgo; por ejemplo, para un nivel de confianza del 99.9%, la máxima pérdida en dólares estadounidense obtenida por el método no paramétrico es igual a $15.74 contra $13.30 del método paramétrico basado en la TVE para la posición larga, mientras que en el caso de la posición corta las pérdidas equivalen a $12.28 contra $10.04, respectivamente. La principal razón de este hecho se atribuye a que la distribución empírica suele ser muy densa en el interior como consecuencia de la naturaleza discreta de los rendimientos. Este fenómeno implica que las estimaciones del VaR, que dependen primordialmente de las colas, sean también deter-minados en forma discreta y muchas de las veces de varianza alta. De hecho, esta deficiencia evidente tiene un efecto negativo en la contribución de la modelación correcta del comportamiento estadístico de los rendimientos extremos debido a la importancia de la distribución empírica para la estimación del VaR y otras formas de análisis de riesgo. Por otra parte, la sensibilidad al tamaño de la muestra es otra de la serias debilidades de este modelo no paramétrico, ya que su alcance es muy limitado para estimar pérdidas que ocurren con menor frecuencia dentro del periodo muestral. Asimismo, el método de simulación histórica es insuficiente para proporcionar estimaciones de calidad fuera de la muestra a diferencia del modelo de valor extremo que garantiza estimaciones más precisas del verdadero nivel de riesgo para altos percentiles, incluso dentro de la muestra la estimación precisa del VaR es casi imposible con una muestra pequeña debido a la carencia de información y grandes observaciones adyacentes, profundamente localizados en las colas de la distribución de rendimientos. Finalmente, la evidencia empírica demuestra que los inversionistas internacionales con posiciones largas están más propensos a experimentar pérdidas grandes que los que toman posiciones cortas en el mercado accionario mexicano durante periodos de crisis financieras y depreciaciones de la moneda local.

Conclusiones

El análisis de las características dinámicas y complejas de los mercados accionarios en las economías emergentes es casi imposible a través de los tradicionales modelos paramétricos. Los hechos estilizados de eventos extremos y propiedades de las colas anchas observados en los rendimientos financieros deben ser estudiados con distribuciones relativamente más sofisticadas. Por ello, la modelación correcta de las colas de la distribución de rendimientos de las series financieras es una tarea crucial en el análisis del riesgo, valuación de activos financieros y productos derivados.

Este trabajo de investigación muestra el potencial de la teoría de valores extremos para cuantificar con mayor precisión el riesgo de la cola en los rendimientos diarios de la Bolsa Mexicana de Valores bajo la agregación del efecto de la variabilidad del tipo de cambio para altos niveles de confianza. En cierto grado, los resultados para la BMV son muy similares a los obtenidos por Longin (2000), pero opuestos con los hallazgos de De Jesús y Ortiz (2011). La medida VaR, basada en la distribución de valor extremo generalizada, proporciona información cuantitativa más robusta para analizar el perfil del riesgo extremo en el mercado accionario de México, a diferencia del modelo delta-normal para niveles de confianza mayores al 95%.

Por su parte, el método de simulación es más conservador para estimar el riesgo financiero para cualquier nivel de probabilidad. Sin embargo, el desempeño de los métodos no paramétricos para la estimación de percentiles más altos se reduce notablemente, en particular, para el nivel de probabilidad del 99.9%, propiciado principalmente por la naturaleza discreta de los rendimientos capturados en el interior de la distribución y la falta de información en las colas de la misma. De esta manera, las autoridades regulatorias podrían sugerir a las instituciones financieras el uso de la teoría de valores extremos como herramienta complementaria en la administración de riesgos, ya que les permitirá no sólo medir más exactamente el verdadero riesgo capturado en las colas de la distribución de rendimientos, sino también determinar suficientes requerimientos de capital durante periodos de crisis financieras y devaluaciones. Asimismo, los resultados del VaR sirven como indiciadores cuantitativos a los inversionistas internacionales de portafolio para la eficiente asignación de capital en mercados financieros altamente volátiles. Final-mente, la estimación eficiente del riesgo de mercado permitirá a los inversionistas internacionales, que toman posiciones en la Bolsa Mexicana de Valores, crear estrategias de cobertura apropiadas contra la exposición del tipo de cambio utilizando información generada por la TVE.