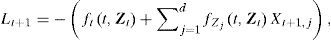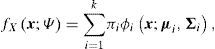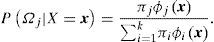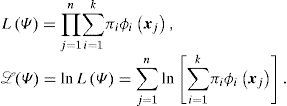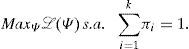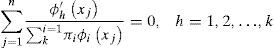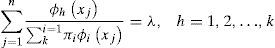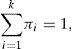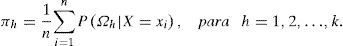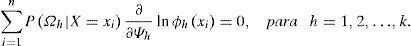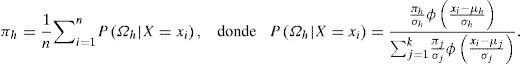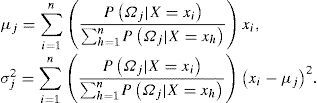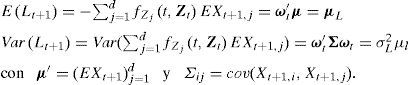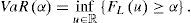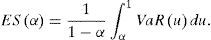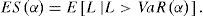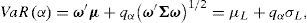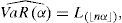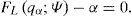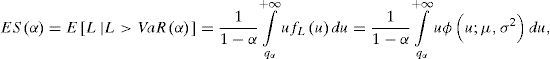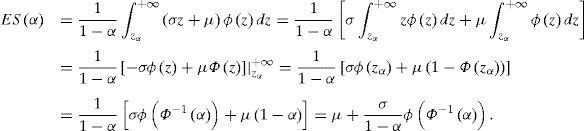Los principales modelos financieros para la estimación del riesgo de mercado suponen que los rendimientos de los activos siguen una distribución Normal o se basan en la distribución empírica. Con frecuencia, el supuesto de normalidad se da por hecho; sin embargo, resulta poco realista debido a las características de exceso de curtosis y de asimetría observadas en el comportamiento real de los retornos. En este trabajo presentamos evidencia de que las mixturas gaussianas finitas constituyen un medio eficiente para modelar la distribución de los rendimientos de los activos financieros. Estudiamos el modelo y derivamos expresiones para las métricas usuales de riesgo de mercado. Ilustramos su aplicación calculando métricas de riesgo para una cartera de activos del mercado mexicano, con el modelo propuesto y comparándolas con modelos ampliamente usados en el mercado.
The most commonly used financial models for the estimation of market risk either assume that asset returns follow a Normal distribution or are based on the empirical distribution. More often than not, the normality assumption is taken for granted. However, it is not realistic due to skewness and excess kurtosis observed in the actual behavior of asset returns. In this work we show evidence that finite Gaussian mixtures are an efficient model for the distribution of asset returns. We study the model and obtain expressions to estimate the usual market risk metrics. We illustrate its application by estimating risk figures for a portfolio of Mexican assets using the proposed model and comparing them against values produced with the most widely used models.
El supuesto de normalidad es frecuente en los modelos financieros. Un ejemplo usual surge en el contexto de administración de riesgos. El valor de una cartera de inversión al tiempo t (Vt) es función del tiempo y de un conjunto de factores de riesgo (Zt ∈ ℝd): Vt=f(t,Zt). Definimos los cambios en los factores de riesgo como Xt=Zt–Zt-1 y la pérdida (positiva) del portafolio como Lt=-(Vt–Vt-1). La aproximación lineal de Lt+1 es:
donde los subíndices de f representan derivadas parciales y solo los cambios Xt+1,j son aleatorios. Si los suponemos Normales, entonces Lt+1 es Normal (ver Propiedad 1, más adelante). Esto da origen al método Delta-Normal para el cálculo de Valor en Riesgo (VaR) descrito por Jorion (2006).Sin embargo, la evidencia empírica muestra que muchos activos financieros tienen rendimientos que no siguen la distribución Normal. En particular, la frecuencia observada de rendimientos extremos es mayor que la probabilidad de dichos rendimientos bajo la Normal. Esta característica se denomina «leptocurtosis», colas anchas o elongación en exceso. También es posible observar alternadamente períodos de alta y baja volatilidad, distribuciones asimétricas o dependencia en las colas en las distribuciones conjuntas. Más grave aún es el hecho de que el supuesto de normalidad con frecuencia no se verifica. Las pruebas de bondad de ajuste del Apéndice B muestran que la Normal no es un modelo adecuado para factores de riesgo representativos del mercado mexicano.
Por otro lado, de acuerdo con el Comité de Basilea (BIS, 2011), «uno de los principales factores desestabilizadores durante la crisis —económica y financiera que estalló en 2007— fue la incapacidad de captar correctamente los mayores riesgos dentro y fuera del balance».
A pesar de lo anterior, el VaR es la medida de riesgo que los reguladores de muchos países promueven para monitorear y controlar el riesgo de mercado (ver, por ejemplo, CNBV, 2005) y que el Comité de Basilea (BIS, 2011) emplea para fijar requerimientos mínimos de capital. Como parte de la respuesta a las deficiencias detectadas, el propio Comité ha propuesto recientemente sustituir el VaR por el déficit esperado (ES, por sus siglas en inglés) como métrica de riesgo de mercado (BIS, 2013).
En este contexto, Behr y Poetter (2009) modelan rendimientos diarios de 10 índices accionarios europeos usando las distribuciones hiperbólica, logF y mixturas gaussianas, concluyendo que el ajuste de estas últimas es ligeramente superior en todos los países. Tan y Chu (2012) modelan los retornos de una cartera de inversión usando una mixtura gaussiana y estiman el VaR. Kamaruzzaman, Isa e Ismail (2012) ajustan una mixtura gaussiana de 2 componentes a los retornos logarítmicos mensuales de 3 índices accionarios en Malasia, y en un trabajo distinto (Kamaruzzaman e Isa, 2013) estiman VaR y ES (usando una expresión que es un caso particular de la ecuación (7), más adelante) para los retornos semanales y mensuales de un índice, encontrando mediante backtesting que las mixturas gaussianas son un modelo apropiado. Zhang y Cheng (2005) usan mixturas gaussianas con distinto número de componentes para estimar el VaR de algunos índices de mercado chinos, acotándolo con el VaR de las componentes y vinculándolo con el comportamiento de los movimientos de precio y la psicología de los inversionistas.
Alexander y Lazar (2002) usan un modelo GARCH(1,1) de mixturas gaussianas para tipos de cambio. Encuentran que un modelo de 2 componentes se desempeña mejor que otros con 3 o más componentes y que un modelo GARCH t-Student. Haas, Mittnik y Paolella (2004) introducen una clase general de modelos GARC(p,q) con mixturas gaussianas para índices accionarios. Sus modelos incluyen procesos individuales de varianza muy flexibles pero al costo de perder parsimonia, ya que sus mejores modelos requieren entre 17 y 22 parámetros para modelar los retornos de solo un índice. Hardy (2001) ajusta un modelo log-Normal de cambio de régimen a los retornos mensuales de 2 índices accionarios y estima tanto VaR como ES usando directamente la función de pagos de una opción de venta europea sobre un índice.
En este trabajo postulamos las mixturas gaussiana finitas como un modelo alternativo a los más ampliamente utilizados: Simulación Histórica (SH) y Delta-Normal, que preserva la parsimonia de los anteriores pero captura explícitamente los períodos de alta volatilidad. Así, comparamos 3 modelos para la estimación de métricas de riesgo, uno de ellos no paramétrico, basado en la distribución empírica de los retornos de los factores de riesgo, y 2 más paramétricos, uno basado en la Normal y otro en una mixtura gaussiana finita.
Este trabajo se organiza en 6 secciones y 3 apéndices. En la sección 2 estudiamos las mixturas gaussianas finitas y algunas propiedades relevantes, y luego, en la sección 3, revisamos el algoritmo EM para la estimación de parámetros. Más adelante, en la sección 4 construimos la variable aleatoria de pérdidas para una cartera cuyo valor fluctúa según los retornos de los factores de riesgo e introducimos 2 métricas de riesgo de mercado y sus estimadores. En la sección 5 proponemos una cartera ficticia pero plausible y calculamos sus métricas de riesgo bajo cada uno de los modelos considerados. En la sección 6 exponemos algunas conclusiones. El Apéndice A contiene el desarrollo de las expresiones para el ES de la Normal y la mixtura Gaussiana, y en el Apéndice B se realizan las pruebas de bondad de ajuste para la Normal y la mixtura gaussiana. Finalmente, el Apéndice C muestra el código desarrollado para los cálculos.
Mixturas gaussianas finitasDecimos que un vector aleatorio X: Ω → ℝd se distribuye de acuerdo a una mixtura (finita) gaussiana (MG) cuando su función de densidad se puede escribir como:
donde ∑i=1kπi=1, πi∈0,1yϕi(⋅,μi,Σi), i=1,…,k son densidades Normales d-variadas con parámetros μi∈ℝd y Σi∈ℝdxd son matrices positivas definidas.En este esquema, se interpreta que existe una partición del espacio muestral Ω=∪i=1i=1Ωi,Ωh∩Ωl=∅,h≠l, tal que cada una de las densidades ϕi rige sobre el subconjunto Ωi. Adicionalmente, πi=PΩi y la probabilidad posterior de cada subconjunto es:
Debido a la linealidad de la integral, la definición anterior se puede escribir en términos de la función de distribución acumulada en lugar de la densidad. Es importante destacar que la familia de mixturas gaussianas finitas es un modelo muy flexible, por lo cual listamos algunas de sus propiedades (ver McLachlan y Peel, 2000):
- 1.
Incluye a la distribución Normal (con k=1).
- 2.
Una mixtura gaussiana finita univariada de k componentes admite 3k-1 parámetros, por lo que es útil para modelar discrepancias continuas de la Normal como asimetría, leptocurtosis, modelos de contaminación, multimodalidad, etc., con frecuencia con k=2 únicamente.
- 3.
No es difícil de simular, por lo que se puede usar en procesos de MonteCarlo o en bootstrap.
- 4.
Se ajusta a hechos estilizados en finanzas, a diferencia de otras distribuciones como la t-Student o la familia de distribuciones hiperbólicas; notoriamente, regímenes de volatilidad de mercado.
- 5.
Es cerrada bajo convolución.
Esta última propiedad es muy importante y se usará más adelante para obtener medidas de riesgo agregadas. Dado que la hereda de la Normal, la enunciamos para ambas distribuciones:
Propiedad 1 (caso Normal). Si X∼Nd(μ, Σ) y lx=−(c+ω′x), entonces l(X)∼N(μl,σl2), donde μl=−(c+ω′μ) y σl2=ω′Σω.
Propiedad 2 (caso mixtura gaussiana). Si X∼MGd(π,{μi}i=1k,{Σi}i=1k) y lx=−ω′x, entonces l(X)∼MG(π,{μlj}j=1k,{σlj2}j=1k), donde μlj=−ω′μj y σlj2=ω′Σjω,j=1,…,k.
En la medida que cada una de las densidades está especificada salvo por el valor de un conjunto de parámetros Ψ=πi,μi,σi2i=1k, la estimación de dichos parámetros puede realizarse mediante máxima verosimilitud. Dada una muestra aleatoria, la función de verosimilitud y su logaritmo se pueden escribir como:
Para simplificar la notación, trabajaremos en una dimensión (d=1). Los estimadores de los parámetros se obtienen resolviendo el problema de optimización:
Utilizando multiplicadores de Lagrange el problema se transforma en encontrar la solución del sistema de 2k+1 ecuaciones:
Este sistema no tiene solución cerrada, pero se puede resolver de forma iterativa aplicando el algoritmo de Esperanza y Maximización (EM) de Dempster, Laird y Rubin (1977).
En el paso de Esperanza se estima la probabilidad posterior, dada la muestra, de cada uno de los subconjuntos de la partición del espacio muestral, mediante:
En el paso de Maximización se obtienen los estimadores de los parámetros de cada una de las k densidades individuales, dadas las probabilidades estimadas arriba.
Para una mixtura gaussiana finita univariada arbitraria, la aplicación del algoritmo EM resulta en:
- 1.
Paso de Esperanza:
- 2.
Paso de Maximización:
El uso del algoritmo EM para mixturas gaussianas finitas puede resumirse de la siguiente manera: dado un conjunto de valores iniciales πj0, μj0 y σj20j=1,…,k, en cada iteración se estiman secuencialmente las probabilidades posteriores de cada elemento de la partición PΩj|X=xi, las probabilidades de membresía πj, las medias μj y las varianzas σj2. Las iteraciones se repiten hasta que se alcance algún criterio de convergencia. Para una discusión detallada sobre la elección de valores iniciales, criterios de convergencia y algunas estrategias para incrementar la rapidez de convergencia, consultar McLachlan y Krishnan (1997).
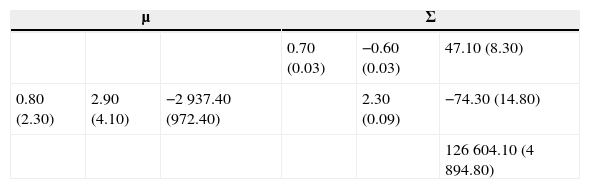
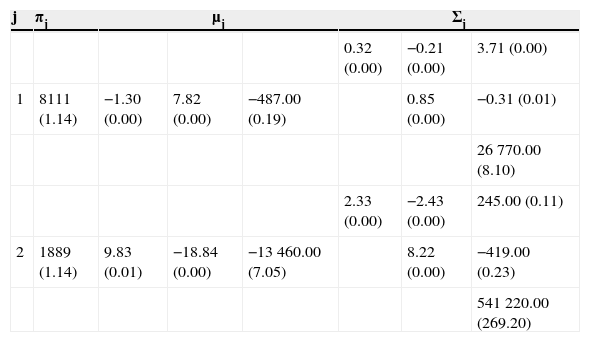
Para estimar los parámetros de las distribuciones supuestas (Normal y mixtura gaussiana) se ha tomado una muestra1 de 1,339 retornos diarios (64 meses a partir de enero de 2008) de la tasa soberana mexicana en pesos de 6 meses (Cetes), el tipo de cambio USDMXN y el Naftrac02. Los estimadores para el supuesto de normalidad son los estimadores insesgados usuales. En el caso de la mixtura gaussiana se programó en VBA de Microsoft Excel una rutina para implementar el algoritmo EM multivariado y se ajustó una mixtura Normal tridimensional de 2 componentes. En las tablas 1 y 2 se muestran los estimadores tanto de la Normal como de la mixtura, respectivamente, con errores estándar entre paréntesis.
Estimadores (×10−4) de la mixtura gaussiana con errores estándar
| j | πj | μj | Σj | ||||
|---|---|---|---|---|---|---|---|
| 0.32 (0.00) | −0.21 (0.00) | 3.71 (0.00) | |||||
| 1 | 8111 (1.14) | −1.30 (0.00) | 7.82 (0.00) | −487.00 (0.19) | 0.85 (0.00) | −0.31 (0.01) | |
| 26770.00 (8.10) | |||||||
| 2.33 (0.00) | −2.43 (0.00) | 245.00 (0.11) | |||||
| 2 | 1889 (1.14) | 9.83 (0.01) | −18.84 (0.00) | −13460.00 (7.05) | 8.22 (0.00) | −419.00 (0.23) | |
| 541220.00 (269.20) | |||||||
Fuente: elaboración propia
Obsérvese que los estimadores de la mixtura gaussiana satisfacen la interpretación usual para el caso de 2 componentes: una de las componentes muestra el comportamiento observado de los retornos durante la mayor parte del tiempo, mientras que la otra componente expone los retornos en situaciones de estrés, por lo que tiene una media bien diferenciada de la primera componente y una dispersión significativamente mayor. Así, por ejemplo, para el factor de riesgo USDMXN se tiene que durante el período de muestra el peso se depreció a un ritmo promedio 0.080% diario, lo cual se descompone en una apreciación promedio diaria de 0.013% durante el 81% del tiempo, con una volatilidad anual de 8.97% y una depreciación promedio diaria de 0.098% durante el restante 19% del tiempo, con una volatilidad anual de 24.12%, 2.7 veces la volatilidad en tiempos usuales.
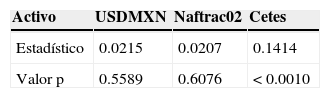
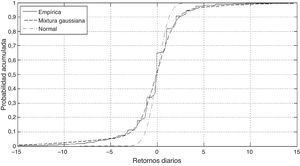
La tabla B.2 del Apéndice B muestra que la mixtura gaussiana de 2 componentes es un modelo adecuado para los retornos tanto del tipo de cambio USDMXN como del Naftrac02, no así para la tasa Cetes, siempre de acuerdo a la prueba de Kolmogorov-Smirnov. La figura B.3 del mismo Apéndice muestra que, a pesar de no pasar la prueba de hipótesis, la bondad de ajuste con la mixtura gaussiana es mejor que con la distribución Normal. Queda abierta la pregunta del número de componentes a incluir en la mixtura gaussiana para pasar la prueba.
Distribución de pérdidas y métricas de riesgoEn esta sección construimos la variable aleatoria de pérdidas mediante un operador lineal que la aproxima para cambios pequeños en los factores de riesgo y definimos las medidas de riesgo a ser calculadas sobre dicha distribución, así como sus estimadores para cada uno de los modelos analizados.
Dada una cartera de activos sujetos a riesgo de mercado, considérese la variable aleatoria de pérdidas diarias de la cartera. En concordancia con la literatura de distribuciones de pérdida se supondrá que las pérdidas son positivas y las utilidades negativas. Su aproximación lineal (delta, en la nomenclatura de cobertura con derivados), en términos de las derivadas parciales respecto del tiempo y los factores de riesgo, está dada por la ecuación (1). Si la función f tiene derivadas de segundo orden no despreciables, la aproximación (1) puede incluirlas, con lo que se tendría un modelo Delta-Gamma.
Los momentos de la variable aleatoria de pérdida son, a partir de la ecuación (1) y suponiendo que ft=0 (lo cual es cierto para incrementos pequeños de tiempo):
En adelante supondremos que los retornos Xt provienen de un proceso estacionario, es decir, son variables aleatorias (Va) independientes e idénticamente distribuidas (iid) y podemos eliminar el subíndice t. A continuación se definen las métricas de riesgo VaR y ES.
Sea L la va de pérdida y FL: ℝ → [0,1] su función de distribución. El VaR para un nivel de confianza α∈0,1 se define como:
Supóngase además que EL<+∞. El ES para un nivel de confianza α∈0,1 se define como:
Obsérvese que el VaR no es más que el percentil α de la distribución de pérdida y que el ES es el promedio de los percentiles sobre todos los niveles de confianza superiores o iguales a α, siempre que la distribución de pérdida sea continua. En tal caso, la siguiente propiedad (ver McNeil, Frey y Embrechts, 2005) provee una herramienta útil de cálculo:
Pasamos ahora a la estimación de las métricas de riesgo. Si la distribución de L es de localización y escala, el cálculo del VaR solo depende de los momentos descritos en la ecuación (2):
donde qα es el percentil α de una distribución FL con parámetros de localización y escala cero y uno, respectivamente.La Propiedad 1 garantiza que bajo el modelo paramétrico Delta-Normal L se distribuye como una Normal univariada, y en este caso la ecuación (4) provee el estimador de VaR. Aun cuando la evidencia estadística indica que la distribución de L no es Normal (ver Apéndice B), conservamos este modelo como parámetro de comparación. Para el modelo SH la distribución de L es la empírica y basta con tomar el estadístico de orden adecuado para obtener:
donde L(j) es el j-ésimo estadístico de orden, n es el tamaño de la muestra y u es el mayor entero que es menor o igual a u. Finalmente, para el modelo Delta-mixtura gaussiana (que denotaremos Delta-MG), la Propiedad 2 garantiza que la distribución de L es una mixtura gaussiana univariada finita, y en tal caso es necesario resolver numéricamente para qα la ecuación:Por lo que respecta al ES, en el Apéndice A se derivan las expresiones para los modelos paramétricos considerados, mientras que para el modelo SH el estimador se construye usando la distribución empírica a partir de la ecuación (3). Las expresiones para los 3 modelos se listan a continuación:
donde zj,α=qα−μj/σj y qα satisface la ecuación (6).Estimación de Valor en Riesgo y déficit esperadoEn esta sección se propone una cartera de activos con exposición a los 3 tipos usuales de factores de riesgo (tasas de interés, precios de acciones y tipos de cambio). Luego se emplea el modelo Delta-MG para el cálculo tanto de VaR como de ES a partir de las sensibilidades de la cartera a los factores de riesgo. Este resultado se compara con los mismos cálculos usando los métodos de SH y Delta-Normal.
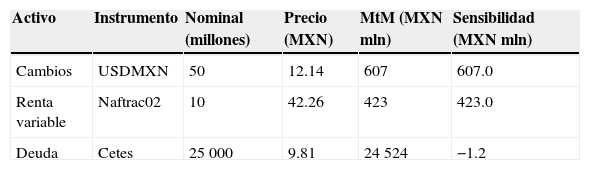
La cartera considerada contiene 3 instrumentos: una posición de 50 millones de dólares (USD), 25,000 millones nominales (MXN) de un bono soberano cupón cero (Cetes) con vencimiento en 6 meses y 10 millones de títulos de Naftrac02, un fondo listado en el mercado bursátil (ETF) que replica el desempeño del Índice de Precios y Cotizaciones (IPC) de la Bolsa Mexicana de Valores. Por simplicidad, este instrumento será tratado como una acción individual y no como un fondo. Así la cartera consta de 3 instrumentos. La tabla 3 muestra para cada uno el valor a mercado al 30 de abril de 2013 y las sensibilidades a los factores de riesgo considerados.
Cartera valorizada a mercado y sensibilidades
| Activo | Instrumento | Nominal (millones) | Precio (MXN) | MtM (MXN mln) | Sensibilidad (MXN mln) |
|---|---|---|---|---|---|
| Cambios | USDMXN | 50 | 12.14 | 607 | 607.0 |
| Renta variable | Naftrac02 | 10 | 42.26 | 423 | 423.0 |
| Deuda | Cetes | 25000 | 9.81 | 24524 | −1.2 |
Fuente: elaboración propia con datos de Bloomberg.
Un aspecto a destacar es que tanto bajo el supuesto de normalidad como usando el modelo de mixtura gaussiana, la media de la distribución de pérdidas de la cartera (Propiedades 1 y 2) es la misma (MXN −533 mil diarios), mientras las desviaciones estándar de dicha distribución son muy similares: MXN 7.325 millones bajo normalidad y MXN 7.308 millones. Es decir, el modelo de mixturas gaussianas no modifica ni el centro de masa ni la dispersión de la distribución de interés, sino que tan solo los segmenta en componentes.
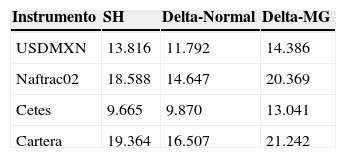
Pasamos ahora a la estimación de medidas de riesgo usando los 3 métodos: SH, Delta-Normal y Delta-MG. En los 3 casos consideramos el vector de ponderaciones como la última columna (sensibilidad) de la tabla 3. El VaR se ha estimado como el percentil 99 de la distribución de pérdidas de la cartera. El cálculo es directo tanto para la distribución empírica como para la Normal (ecuaciones 4 y 5), pero no así para la mixtura gaussiana, por lo que se ha desarrollado un código en Matlab para estimar el percentil deseado de una mixtura gaussiana univariada con un número arbitrario de componentes usando la ecuación 6. La tabla 4 resume el VaR para cada instrumento y la cartera en su conjunto.
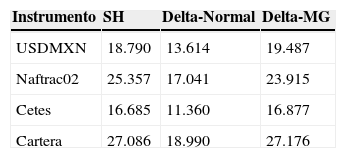
En la tabla 5 se aprecia el ES para cada instrumento y la cartera para cada uno de los 3 modelos estimados según la ecuación 7.
ConclusionesLas pruebas de bondad de ajuste del Apéndice B muestran que la Normal no es un modelo adecuado para ninguno de los factores de riesgo considerados. Las mixturas gaussianas, en cambio, muestran adecuadamente los retornos tanto del tipo de cambio como del ETF, no así los de la tasa de interés, con un ajuste evidentemente mejor que la Normal. Una posible causa de esta falta de ajuste es la combinación de 2 factores: muchos días con cambios muy pequeños en las tasas y que el período elegido incluye toda la crisis crediticia internacional, en el que hubo constantes cambios en la tasa de política monetaria. Ambas situaciones introducen saltos discretos en la tasa de los bonos de corto plazo.
La comparación de las tablas 4 y 5 nos permite afirmar que entre los 3 modelos de riesgo considerados, Delta-Normal es el más agresivo, en el sentido que reporta la menor pérdida potencial tanto para VaR como para ES. Consideramos, sin embargo, que su mayor debilidad radica en que al poseer muy poca masa en la cola de la distribución, de tal suerte que el cambio (propuesto por Basilea III) de migrar de VaR a ES como métrica estándar de riesgo de mercado significa un incremento pequeño de 15% en la cartera estudiada. Si bien esto puede ser benéfico en términos de ahorro de capital, por otro lado puede exponer a las instituciones a pérdidas significativas al ocurrir rachas de alta volatilidad.
Por su parte, el modelo de SH sufre un ajuste significativo del 40% entre VaR y ES. Esto confirma su fuerte dependencia de la muestra utilizada dada la ventana histórica elegida para el ejercicio actual, en la que se observaron retornos muy grandes en comparación con la media de la distribución empírica.
Por último, el modelo de mixturas gaussianas finitas, al incorporar de forma explícita una componente para los períodos de alta volatilidad, entrega los datos de VaR más conservadores: 10% más grandes que SH y 29% mayores que Delta-Normal. Esta es una distribución leptocúrtica que sin embargo es muy versátil y se adapta a la volatilidad observada para cada factor de riesgo. Así, en la cartera estudiada, el ES para el Naftrac02 es solo 17% mayor que el VaR, para el Cete es 29% mayor y para el tipo de cambio es 35%. En contraste con el modelo Normal, las medidas crecen uniformemente un 15%, como se indicó antes.
Si bien las medidas de riesgo obtenidas bajo un modelo u otro pueden parecer más o menos conservadoras, tratándose de requerimientos de capital para una institución financiera, no se desea ser demasiado conservador, por la implicación que tiene mantener capital improductivo. En este sentido, y considerando que no ha sido posible obtener un modelo satisfactorio para los retornos de las tasas de interés, el criterio óptimo de decisión entre modelos debería fundamentarse en una prueba de validación comparando las frecuencias esperadas y observadas de pérdidas en exceso a las pronosticadas. Esto constituye el trabajo inmediato futuro para discriminar objetivamente entre modelos.
En este apéndice se derivan expresiones para el ES de los modelos paramétricos considerados. Primero se hace para la distribución Normal, llenando los detalles de la demostración que se puede encontrar en McNeil et al. (2005). La razón de ello es que el procedimiento resulta de utilidad para obtener el resultado correspondiente para la distribución de mixtura gaussiana finita.
ES para Normal.
Sea L∼N(μ, σ2) y qα=VaRα el percentil α de FL, esto es, FLqα=α. Sea fL⋅=ϕ⋅;μ,σ2 la densidad de L y ϕ⋅=ϕ⋅;0,1 la densidad de la Normal estándar con percentil α igual a zα. Usando la ecuación (3) y la distribución de L, se tiene:
luego se hace el cambio de variable u=σz+μzα=qα−μ/σ,du=σdz:ES para mixtura gaussiana.
Sea ahora L∼MG(π, μ, σ). Antes vimos que qα=VaRα se obtiene resolviendo la ecuación (6). De la definición de ESα, la ecuación (3) y la distribución de L, se tiene
La integral dentro de la suma es la misma que en (8), con la diferencia que el límite de integración depende de la componente específica. Hacemos el cambio de variable u=σjz+μj y definimos zj,α=qα−μj/σj para obtener el resultado análogo a (9):
Obsérvese que zj,α depende de α a través de qα y de la componente a través de los parámetros μj y σj pero no es el percentil α de la distribución de la j-ésima componente, es decir, no es el caso que Φzj,α=α. Dicho de otra forma, μj+σjϕzj,α/Φ−zj,α no es el ESα de la j-ésima componente.
En este apéndice realizamos diversas pruebas de bondad de ajuste para los retornos de los factores de riesgo para cada uno de los modelos paramétricos considerados.
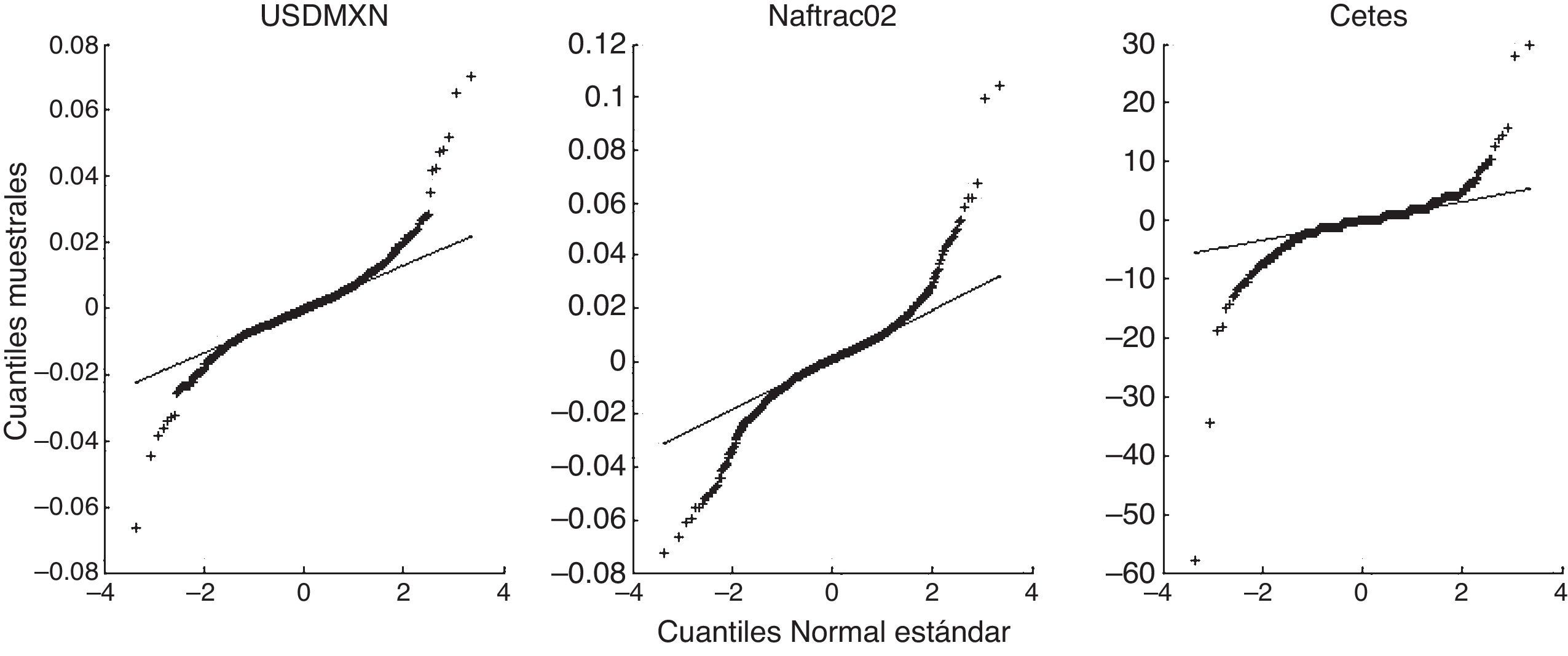
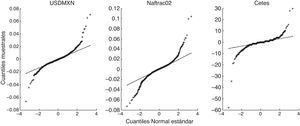
La figura B.1 muestra los gráficos cuantil-cuantil (QQ) para los rendimientos de los factores de riesgo en consideración y la distribución Normal. Como se puede apreciar, el ajuste de la distribución Normal parece pobre, particularmente en las colas de las distribuciones.
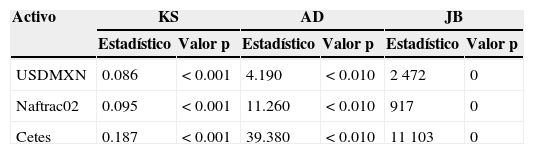
Al aplicar la prueba de Kolmogorov-Smirnov, el valor de p es menor a 0.05, lo cual permite rechazar la hipótesis de normalidad de los datos en los 3 casos. Lo mismo ocurre con las pruebas Jarque-Bera y Anderson-Darling, como se observa en la tabla B.1.
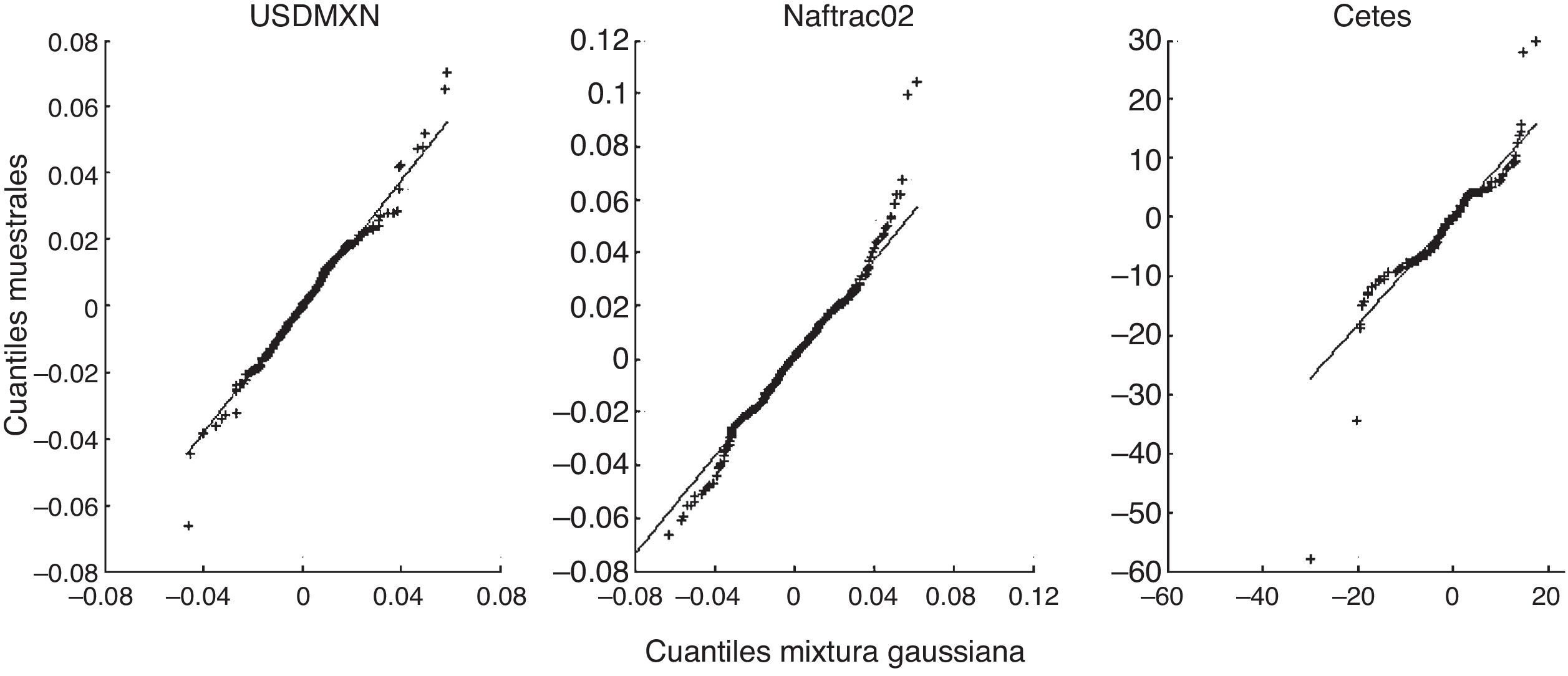
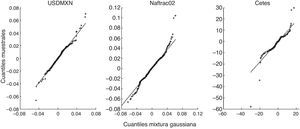
En la figura B.2 se puede apreciar que el ajuste con mixturas gaussianas de 2 componentes es mucho mejor que con la distribución Normal, si bien persiste una falta de ajuste en las colas.
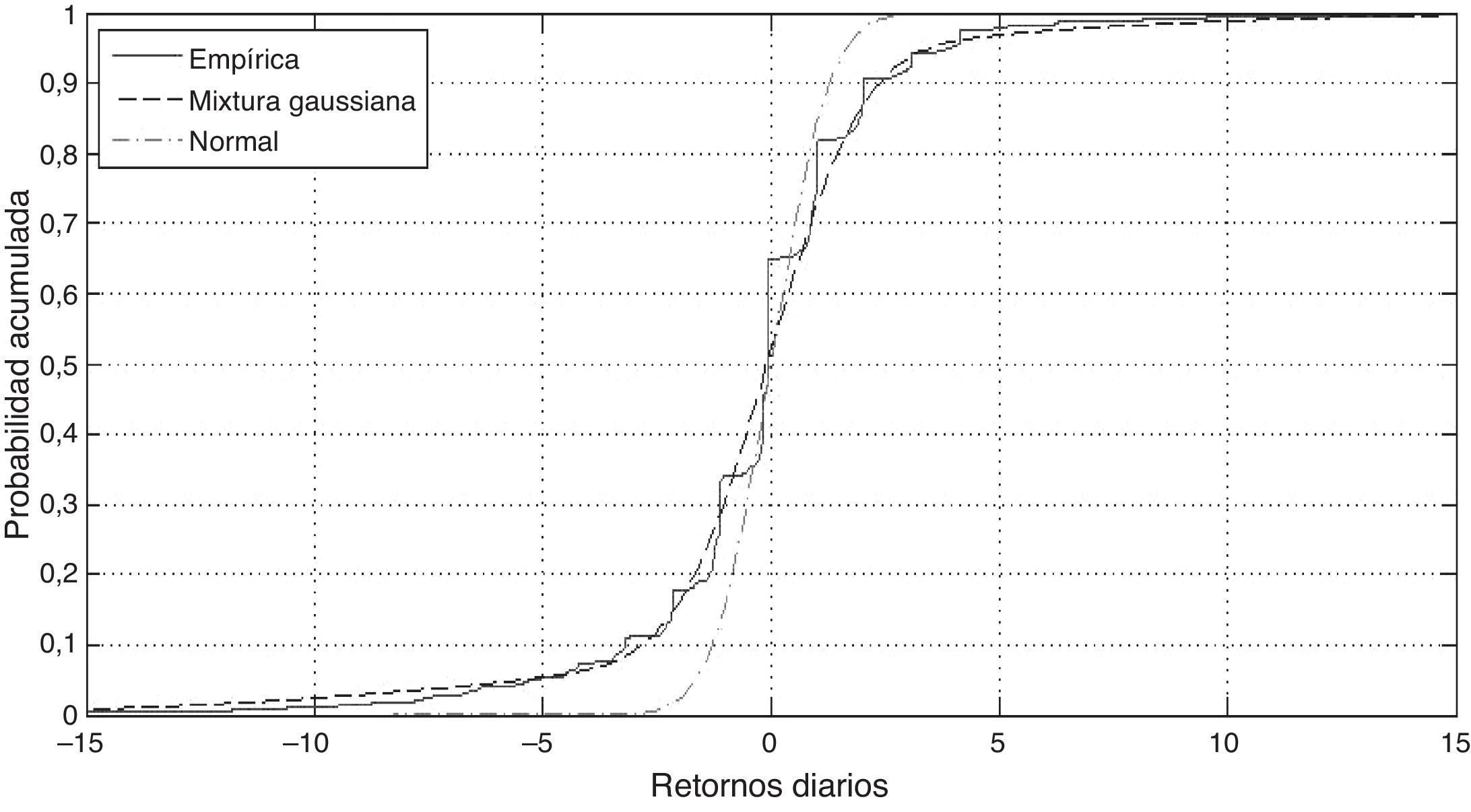
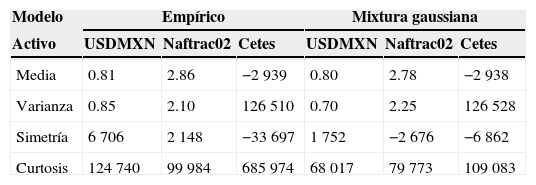
Al realizar la prueba de bondad de ajuste de Kolmogorov-Smirnov (tabla B.2) se puede concluir que el modelo de mixturas gaussianas finitas es razonable para describir los retornos del tipo de cambio y el ETF. En el caso de la tasa de Cetes a 6 meses, existe evidencia para rechazar la hipótesis de que la mixtura gaussiana muestra sus retornos. A pesar de ello, la figura B.3 expone que el ajuste con mixturas gaussianas es sensiblemente mejor que con la Normal. La figura B.3 y la tabla B.3 muestran que la curtosis en exceso contribuye a la falta de ajuste. La curtosis estimada es 3.6 veces la de la Normal, pero la observada es 6.29 veces mayor a la estimada.
Momentos empíricos y estimados (×104)
| Modelo | Empírico | Mixtura gaussiana | ||||
|---|---|---|---|---|---|---|
| Activo | USDMXN | Naftrac02 | Cetes | USDMXN | Naftrac02 | Cetes |
| Media | 0.81 | 2.86 | −2 939 | 0.80 | 2.78 | −2938 |
| Varianza | 0.85 | 2.10 | 126510 | 0.70 | 2.25 | 126528 |
| Simetría | 6706 | 2148 | −33697 | 1752 | −2676 | −6862 |
| Curtosis | 124740 | 99984 | 685974 | 68017 | 79773 | 109083 |
Fuente: Elaboración propia.
En este apéndice se muestra el código VBA desarrollado para ajustar una mixtura gaussiana finita multivariada sin restricciones en el número de componentes ni en los parámetros, así como el código Matlab escrito para encontrar un percentil arbitrario para una mixtura gaussiana univariada arbitraria.
Algoritmo EM para mixturas gaussianas finitas multivariadas.
| Sub EMd()n = WorksheetFunction.Count(Range(«A:A»))d = WorksheetFunction.CountA(Range(«1:1»))tol = 0.00000001maxiter = 200g = 2’ Lee los datosSheets(«Datos»).ActivateFor j = 1 To n For l = 1 To d datos(j, l) = Cells(j + 1, l).Value Next lNext jren = 2’ Lee valores iniciales de los estimadoresitera = 0For k = 1 To g pr(itera, k) = Sheets(«Iteracion»).Cells(2, 1 + k).Value For i = 1 To d mu(itera, k, i) = Sheets(«Iteracion»).Cells(2, 1 + g + (k - 1) * d + i).Value For j = 1 To d vr(itera, k, i, j) = Sheets(«Iteracion»).Cells(2, 1 + (d + 1) * g + (k - 1) * d * d + (i - 1) * d + j).Value If i > j Then vr(itera, k, i, j) = vr(itera, k, j, i) Next j Next iNext k’ Calcula log-verosimilitud de la iteración iniciallogver(itera) = 0For j = 1 To n For l = 1 To d y(l) = datos(j, l) Next l sumando = mix(y, pr, mu, vr, g, itera, d) logver(itera) = logver(itera) + Log(sumando)Next jlogverA(itera) = logver(itera)bandera = TrueWhile bandera itera = itera + 1 For k = 1 To g T1(itera, k) = 0 For i = 1 To d T2(itera, k, i) = 0 For l = 1 To d T3(itera, k, i, l) = 0 Next l Next i For j = 1 To n For l = 1 To d y(l) = datos(j, l) Next l tauij = tau(y, pr, mu, vr, k, itera - 1, g, d) T1(itera, k) = T1(itera, k) + tauij For l = 1 To d T2(itera, k, l) = T2(itera, k, l) + tauij * y(l) Next l yxyt = WorksheetFunction.MMult(WorksheetFunction.Transpose(y), y) For i = 1 To d For l = 1 To d T3(itera, k, i, l) = T3(itera, k, i, l) + tauij * yxyt(i, l) Next l Next i Next j pr(itera, k) = T1(itera, k) / n For l = 1 To d mu(itera, k, l) = T2(itera, k, l) / T1(itera, k) Next l For l = 1 To d y(l) = T2(itera, k, l) Next l yxyt = WorksheetFunction.MMult(WorksheetFunction.Transpose(y), y) For i = 1 To d For l = 1 To d vr(itera, k, i, l) = (T3(itera, k, i, l) - yxyt(i, l) / T1(itera, k)) / T1(itera, k) Next l Next i Next k logver(itera) = 0 For j = 1 To n For l = 1 To d y(l) = datos(j, l) Next l sumando = mix(y, pr, mu, vr, g, itera, d) logver(itera) = logver(itera) + Log(sumando) Next j If itera > 2 Then ak = (logver(itera) - logver(itera - 1)) / (logver(itera - 1) - logver(itera - 2)) logverA(itera) = logver(itera - 1) + (logver(itera) - logver(itera - 1)) / (1 - ak) Else logverA(itera) = logver(itera) End If If Abs(logverA(itera) - logverA(itera - 1)) < tol Or itera = maxiter Then bandera = FalseWendEnd SubFunction tau(y(), pr(), mu(), var(), comp, itera, g, d) As DoubleFor i = 1 To d vmu(i) = mu(itera, comp, i) For j = 1 To d cov(i, j) = var(itera, comp, i, j) Next jNext itau = pr(itera, comp) * fi(y, vmu, cov, d) / mix(y, pr, mu, var, g, itera, d)End FunctionFunction mix(y(), pr(), mu(), var(), g, itera, d) As Doublemix = 0For h = 1 To g For i = 1 To d vmu(i) = mu(itera, h, i) For j = 1 To d cov(i, j) = var(itera, h, i, j) Next j Next i mix = mix + pr(itera, h) * fi(y, vmu, cov, d)Next hEnd FunctionFunction fi(y(), mu(), var(), d) As DoubleFor l = 1 To d z(l, 1) = y(l) - mu(l) zt(1, l) = y(l) - mu(l)Next l varinv = Application.WorksheetFunction.MInverse(var) z = Application.WorksheetFunction.MMult(varinv, z) exponente = Application.WorksheetFunction.MMult(zt, z) fi = (2*3.14159)^(-d/2)*(WorksheetFunction.MDeterm(var))^-0.5*exp(-0.5*exponente(1))End Function |
Código Matlab para VaR de mixturas gaussianas finitas univariadas.
| function [VaR,ES] = GaussianMixtureRisk(GMdist,alpha)if nargin < 2 alpha = [0.99 0.975];else if size(alpha)==1 alpha = [alpha alpha]; endendVaR = nan(GMdist.NDimensions,1);ES = nan(GMdist.NDimensions,1);for j = 1:GMdist.NDimensions mu = GMdist.mu(:, j); sigma = GMdist.Sigma(j, j,:); GMdistobj = gmdistribution(mu, sigma, GMdist.PComponents); VaR(j)=fzero(@(x)cdf(GMdistobj,x)-alpha(1),0); q_alpha = fzero(@(x)cdf(GMdistobj,x)-alpha(2),0); sigmav = nan(GMdist.NComponents,1); for i = 1:GMdist.NComponents sigmav(i) = sqrt(sigma(1,1,i)); end zeta = (q_alpha-mu)./ sigmav; piv = GMdistobj.PComponents’; ES(j)=sum(piv.*normcdf(-zeta).*(mu+sigmav.*normpdf(zeta)./ normcdf(-zeta)))/(1-alpha(2));end |
La revisión por pares es responsabilidad de la Universidad Nacional Autónoma de México.